下载文档原格式
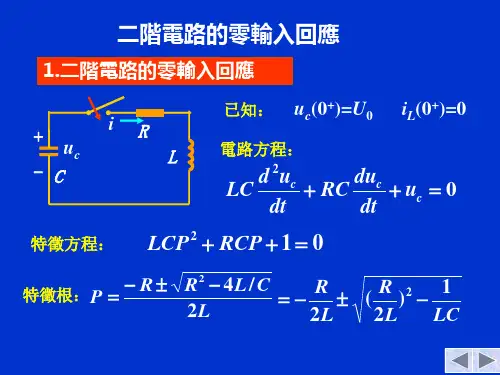
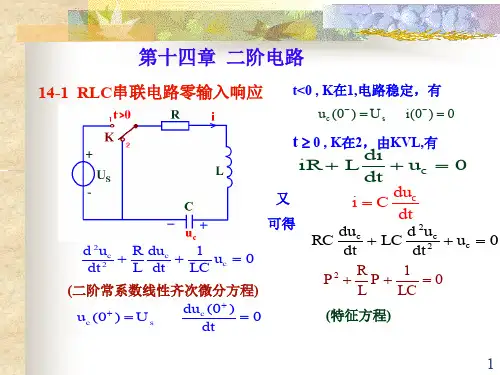
第十四章 状态方程§14-1 电路的状态、状态变量及状态方程一、状态和状态变量经典法分析一阶、二阶电路时，求响应除了要知道电路结构及参数和外加激励之外，还必须知道电路中电容电压，C u 和电感电流C i 的初始值。
有了这些初始值才能确定积分常数，才能确定唯一解．．．，即电路在换路后任意时刻的情况。
C u 及L i 的初始值称为电路的初始状态．．。
只要知道了一个已知电路在换路时的初始状态和换路后作用于电路的外加激励。
就可以确定在换路后任何时刻的电路的响应。
一般意义上的定义： 一个电路在0t t=时的状态．．，是指能完全描述在这一时刻电路性能的最小变量组（的值）。
这个变量组中的每一个变量，称为状态变量。
完全描述电路性能──如果给定0t t=时这组变量的值和0t t ≥时的外加激励，就能完全确定电路在0t t ≥的任何时刻的任一响应。
在电路分析中，这些所谓变量，就是各元件（支路）电流、电压（电荷、磁链）。
最小是指这些变量组中每一个变量都是独立的，不可能用其它变量的线性组合来表示。
相应的，电路中0t t =时刻的其它任何一个电压、电流都可以用状态变量和激励的线性组合来表达。
若一个电路中有几个状态变量)( , ),( ),(21t x t x t x n ，这几个状态变量就构成了一个数学上的矢量)(t X 。
（变量组）)(t X 称为电路的状态矢量。
⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=)( )()()(21t x t x t x t X n 一个电路可以选出多种不同的状态矢量，但其中最容易选取的是由电容电压)(t u C 、电感电流)(t i L 构成的状态矢量。
结合以上定义和讨论可以看出， )(t u C 及)(t i L 确实满足状态变量的基本定义。
所以，一般在电路中将各独立电容的)(t u C ，各独立电感的)(t i L 作为一组状态变量，有时也可以将)(t q 、)(t ψ作为一组状态变量（多用于非线性电路）。
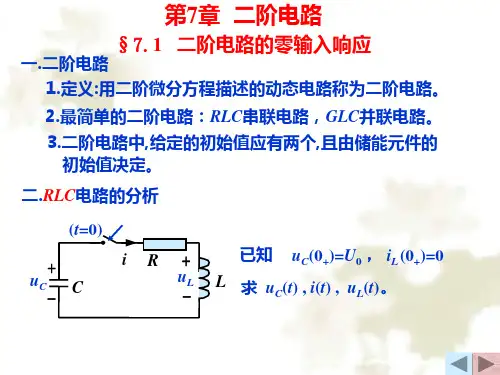
第十四章 状态方程§14-1 电路的状态、状态变量及状态方程一、状态和状态变量经典法分析一阶、二阶电路时，求响应除了要知道电路结构及参数和外加激励之外，还必须知道电路中电容电压，C u 和电感电流C i 的初始值。
有了这些初始值才能确定积分常数，才能确定唯一解．．．，即电路在换路后任意时刻的情况。
C u 及L i 的初始值称为电路的初始状态．．。
只要知道了一个已知电路在换路时的初始状态和换路后作用于电路的外加激励。
就可以确定在换路后任何时刻的电路的响应。
一般意义上的定义： 一个电路在0t t=时的状态．．，是指能完全描述在这一时刻电路性能的最小变量组（的值）。
这个变量组中的每一个变量，称为状态变量。
完全描述电路性能──如果给定0t t=时这组变量的值和0t t ≥时的外加激励，就能完全确定电路在0t t ≥的任何时刻的任一响应。
在电路分析中，这些所谓变量，就是各元件（支路）电流、电压（电荷、磁链）。
最小是指这些变量组中每一个变量都是独立的，不可能用其它变量的线性组合来表示。
相应的，电路中0t t =时刻的其它任何一个电压、电流都可以用状态变量和激励的线性组合来表达。
若一个电路中有几个状态变量)( , ),( ),(21t x t x t x n ，这几个状态变量就构成了一个数学上的矢量)(t X 。
（变量组）)(t X 称为电路的状态矢量。
⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=)( )()()(21t x t x t x t X n 一个电路可以选出多种不同的状态矢量，但其中最容易选取的是由电容电压)(t u C 、电感电流)(t i L 构成的状态矢量。
结合以上定义和讨论可以看出， )(t u C 及)(t i L 确实满足状态变量的基本定义。
所以，一般在电路中将各独立电容的)(t u C ，各独立电感的)(t i L 作为一组状态变量，有时也可以将)(t q 、)(t ψ作为一组状态变量（多用于非线性电路）。
