河北省重点中学2019-2020学年高一下学期期末数学试题

2019—2020学年高一年级下学期期末冲刺满分训练卷第十章 立体几何初步 期末单元测试卷（范围：新教材人教B 版 必修四 考试时间：90分钟 满分：150分）一、选择题（本题共12道小题，每小题5分，共60分）1.以下命题（其中a 、b 表示直线，α表示平面）中，正确的命题是( )A. 若//a b ，b α⊂，则//a αB. 若//a α，//b α，则//a bC. 若//a b ，b α⊥，则a α⊥D. 若//a α，b α⊂，则//a b答案及解析：1.C【分析】根据线线、线面有关定理对选项逐一分析，由此确定正确选项.【详解】对于A 选项，直线a 可能含于平面α，所以A 选项错误.对于B 选项，,a b 可能异面，所以B 选项错误.对于C 选项，由于//a b ，b α⊥，所以a α⊥，所以C 选项正确.对于D 选项，,a b 可能异面，所以D 选项错误.故选：C【点睛】本小题主要考查空间线线、线面位置关系的判断，属于基础题.2.下列命题正确的是（ ）A. 有两个面平行，其余各面都是四边形的几何体叫棱柱。

B. 有两个面平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行的几何体叫棱柱。

C. 绕直角三角形的一边旋转所形成的几何体叫圆锥。

D. 用一个面去截棱锥，底面与截面之间的部分组成的几何体叫棱台。

答案及解析：2.B【分析】根据课本中的相关概念依次判断选项即可.【详解】对于A 选项，几何体可以是棱台，满足有两个面平行，其余各面都是四边形，故选项不正确；对于B ，根据课本中棱柱的概念得到是正确的；对于C ，当绕直角三角形的斜边旋转时构成的几何体不是圆锥，故不正确；对于D ，用平行于底面的平面截圆锥得到的剩余的几何体是棱台，故不正确.故答案为：B.【点睛】这个题目考查了几何体的基本概念，属于基础题.3.在正方体ABCD - A 1B 1C 1D 1中，动点E 在棱BB 1上，动点F 在线段A 1C 1上，O 为底面ABCD 的中心，若1,BE x A F y ==，则四面体O-AEF 的体积( )A. 与x ，y 都有关B. 与x ，y 都无关C. 与x 有关，与y 无关D. 与y 有关，与x 无关答案及解析：3.B【分析】 根据等体积法以及锥体体积公式判断选择.【详解】因为V O －AEF ＝V E －OAF ，所以，考察△AOF 的面积和点E 到平面AOF 的距离的值，因为BB 1∥平面ACC 1A 1，所以，点E 到平面AOE 的距离为定值，又AO ∥A 1C 1，所以，OA 为定值，点F 到直线AO 的距离也为定值，即△AOF 的面积是定值，所以，四面体O-AEF 的体积与x ，y 都无关，选B 。

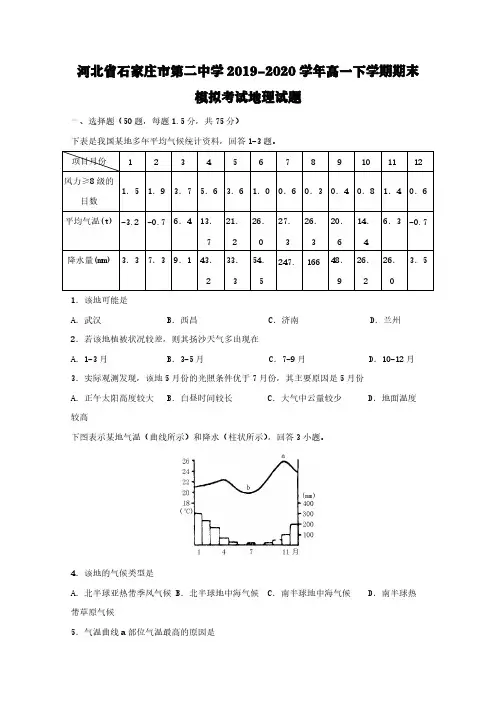
河北省石家庄市第二中学2019-2020学年高一下学期期末模拟考试地理试题一、选择题（50题，每题1.5分，共75分）下表是我国某地多年平均气候统计资料，回答1-3题。

项目月份123456789101112风力≥8级的日数1．51．93．75．63．61．00．60．30．40．81．40．6平均气温(t)-3.2-0.76．413．721．226．27．326．320．614．46．3-0.7降水量(mm)3．37．39．143．233．354．5247.16648．926．226．3．51．该地可能是A．武汉B．西昌C．济南D．兰州2．若该地植被状况较差，则其扬沙天气多出现在A．1-3月B．3-5月C．7-9月D．10-12月3．实际观测发现，该地5月份的光照条件优于7月份，其主要原因是5月份A．正午太阳高度较大B．白昼时间较长 C．大气中云量较少 D．地面温度较高下图表示某地气温（曲线所示）和降水（柱状所示），回答3小题。

4．该地的气候类型是 A．北半球亚热带季风气候 B．北半球地中海气候 C．南半球地中海气候 D．南半球热带草原气候5．气温曲线a部位气温最高的原因是 A．正午太阳高度大，天气晴朗少雨B．太阳直射点位于赤道C．气压带和风带北移D．受高原地形影响6．气温线b部位气温低的原因是A．太阳高度角小B．寒流影响C．云雨较多D．海陆位置影响读下图，甲、乙、丙、丁四个地区的气温雷达图和降水柱状图，回答2题。

7．从气候条件考虑，不适宜乙地区的农业地域类型是A．混合农业B．水稻种植业C．乳畜业D．园艺业8．四个地区中，地带性植被为亚热带常绿硬叶林的是A．甲B．乙C．丙D．丁读世界某地气候资料，回答3题。

9．该种气候类型可能分布在A．巴西利亚B．孟买C．新加坡D．首尔10．该地河流A．冬季有断流B．季节变化大C．有凌汛现象D．年际变化小11．该城市规划建设化学工业区的最理想区域位置是A．西北郊B．东北郊C．西南郊D．城区内下面是2019年“五一”节前几天，我国南、北方两地朋友微信对话截图，根据对话信息回答以下问题。

2019-2020学年荆州市高一下学期期末数学试卷一、单选题（本大题共12小题，共60.0分） 1.已知集合A ={x|−2≤x <5}，B ={x|2<x ≤7}，则A ∩B =( )A. {x|−2<x <5}B. {x|2<x <5}C. {x|2≤x ≤7}D. {x|−2≤x ≤7}2.已知a =0.20.5，b =ln0.2，c =lg11，则( )A. a >b >cB. c >a >bC. a >c >bD. c >b >a3.从含有两件正品a 1，a 2和一件次品b 的3件产品中，按先后顺序任意取出两件产品，每次取出后不放回，则取出的两件产品中恰有一件次品的概率是( )A. 34B. 23C. 12D. 144.函数y =e x (x 2+2x +1)的图象可能是( )A.B.C.D.5. 某校高中三个年级，其中高三有学生1000人，现用分层抽样法抽取一个容量为185的样本，已知在高一抽取了75人，高二抽取了60人，则高中部共有学生( )人．A. 3700B. 2700C. 1500D. 12006.设p ：√2x −1≤1，q ：(x −a)[x −(a −1)]≤0，若p 是q 的充分不必要条件，则实数a 的取值范围是( )A. [1,32]B. (1,32)C. (−∞,1)∪[32，+∞)D. (−∞,1)∪(32,+∞)7.下列说法正确的是( )A. “f(0)=0”是“函数f(x)是奇函数”的充要条件B. 若p ：∃x 0∈R ，x 02−x 0−1>0，则￢p ：∀x ∈R ，x 2−x −1<0C. 若p ∧q 为假命题，则p ，q 均为假命题D. “若α=，则sinα=”的否命题是“若α≠，则sinα≠”8.在锐角中，三个内角满足：，则角与角的大小关系是A.B.C.D.9.已知平面向量a =(1,−2)，b =(2,1)，c =(−4,−2)，则下列说法中错误的是A. c//bB. a ⊥bC. 对同一平面内的任意向量d ，都存在一对实数k 1,k 2，使得d =k 1b +k 2cD. 向量c 与向量a −b 的夹角为45∘10. 已知变量x ，y 之间的一组数据如表：x 1 2 3 4 5 y3.47.59.113.8m若y 关于x 的线性回归方程为 y⏜=3x +1，则m 的值为( ) A. 16 B. 16.2 C. 16.4 D. 16.611. 设实数x ，y 满足约束条件{4x −y −10≤0x +3≥3y x ≥0,y ≥0，若目标函数Z =ax +by ，(其中a >0，b >0)的最大值为3，则2a +3b 的最小值为( )A. 24B. 83C. 8D. 5312. 定义在R 上的奇函数f(x)满足f(1)=0，且对任意的正数a 、b(a ≠b)，有f(a)−f(b)a−b<0，则不等式f(x−2)x−2<0的解集是( )A. (−1,1)∪(2,+∞)B. (−∞,−1)∪(3,+∞)C. (−∞,1)∪(3,+∞)D. (−∞,−1)∪(2,+∞)二、单空题（本大题共3小题，共15.0分）13. 从原点O 向圆x 2+y 2−4y +3=0作两条切线，切点为A ，B ，则OA⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗⃗ 的值为______． 14. 函数y =b +asinx(a <0)的最大值为−1，最小值为−5，则y =tan(3a +b)x 的最小正周期为15. 侧棱长为1，底面边长为√2的正三棱锥的外接球的体积为______ ．三、多空题（本大题共1小题，共5.0分）16. 设函数f(x)=x3+(a−1)x2+ax+b，且f(x)为奇函数，则a+b=(1)，曲线y=f(x)在点(1,f(1))处的切线方程为(2)．四、解答题（本大题共6小题，共70.0分）17. 已知，(1)求的定义域；(2)证明为奇函数；(3)求使>0成立的x的取值范围。

2019年-2020 学年高一数学期末模拟考试试题一．选择题（共10小题）1．已知集合A＝{x|0＜log4x＜1}，B＝{x|e x﹣2≤1}，则A∪B＝（）A．（﹣∞，4）B．（1，4）C．（1，2）D．（1，2]2．某同学用二分法求方程3x+3x﹣8＝0在x∈（1，2）内近似解的过程中，设f（x）＝3x+3x ﹣8，且计算f（1）＜0，f（2）＞0，f（1.5）＞0，则该同学在第二次应计算的函数值为（）A．f（0.5）B．f（1.125）C．f（1.25）D．f（1.75）3．函数的图象大致是（）A．B．C．D．4．函数的零点所在的区间是（）A．B．C．D．5．已知a，b是非零实数，则“a＞b”是“ln|a|＞ln|b|”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件6．函数的值域为（）A．B．C．（0，] D．（0，2]7．若a＞b＞c＞1且ac＜b2，则（）A．log a b＞log b c＞log c a B．log c b＞log b a＞log a cC．log b c＞log a b＞log c a D．log b a＞log c b＞log a c8．已知函数f（x）＝lg（ax2﹣2x+a）的值域为R，则实数a的取值范围为（）A．[﹣1，1] B．[0，1]C．（﹣∞，﹣1）∪（1，+∞）D．（1，+∞）9．若x1是方程xe x＝4的解，x2是方程xlnx＝4的解，则x1•x2等于（）A．4 B．2 C．e D．110．我国古代数学著作《九章算术》有如下问题：“今有蒲生一日，长三尺莞生一日，长一尺蒲生日自半，莞生日自倍．问几何日而长倍？”意思是：“今有蒲草第1天长高3尺，芜草第1天长高1尺以后，蒲草每天长高前一天的一半，芜草每天长高前一天的2倍．问第几天莞草是蒲草的二倍？”你认为莞草是蒲草的二倍长所需要的天数是（）（结果采取“只入不舍”的原则取整数，相关数据：lg3≈0.4771，lg2≈0.3010）A．2 B．3 C．4 D．5二．填空题（共5小题）11．已知x＞0，y＞0，且+＝1，则3x+4y的最小值是2512．函数（a＞0且a≠1）的图象恒过定点P，则点P的坐标为（4，），若点P在幂函数g（x）的图象上，则g（9）＝．13．函数的递减区间是（3，+∞）．14．已知函数f（x）＝有3个零点，则实数a的取值范围是（，1）．15．对于函数f（x），若在定义域内存在实数x0满足f（﹣x0）＝﹣f（x0），则称函数f（x）为“倒戈函数”．设f（x）＝3x+2m﹣1（m∈R，且m≠0是定义在[﹣1，1]上的“倒戈函数”，则实数m的取值范围是．三．解答题（共4小题）16．已知函数的定义域为集合A，集合B＝{x|1＜x＜8}，C＝{x|a ＜x＜2a+1}，（1）求集合（∁R A）∪B；（2）若A∪C＝A，求a的取值范围17．（1）已知5a＝3，5b＝4，用a，b表示log2536．（2）求值．18．已知函数f（x）＝log a（1﹣x），g（x）＝log a（x+3），其中0＜a＜1．（1）解关于x的不等式：f（x）＜g（x）；（2）若函数F（x）＝f（x）+g（x）的最小值为﹣4，求实数a的值．19．某工厂今年初用128万元购进一台新的设备，并立即投入使用，计划第一年维修、保养费用8万元，从第二年开始，每年的维修、保养修费用比上一年增加4万元，该设备使用后，每年的总收入为54万元，设使用x年后设备的盈利总额y万元．（1）写出y与x之间的函数关系式；（2）从第几年开始，该设备开始盈利？（3）使用若干年后，对设备的处理有两种方案：①年平均盈利额达到最大值时，以42万元价格卖掉该设备；②盈利额达到最大值时，以10万元价格卖掉该设备．问哪种方案处理较为合理？请说明理由．2019年-2020 学年高一期末模拟考试试题一．选择题（共10小题）1．已知集合A＝{x|0＜log4x＜1}，B＝{x|e x﹣2≤1}，则A∪B＝（）A．（﹣∞，4）B．（1，4）C．（1，2）D．（1，2]【答案】A【解答】解：A＝{x|1＜x＜4}，B＝{x|x≤2}，∴A∪B＝（﹣∞，4）．故选：A．2．某同学用二分法求方程3x+3x﹣8＝0在x∈（1，2）内近似解的过程中，设f（x）＝3x+3x ﹣8，且计算f（1）＜0，f（2）＞0，f（1.5）＞0，则该同学在第二次应计算的函数值为（）A．f（0.5）B．f（1.125）C．f（1.25）D．f（1.75）【答案】C【解答】解：∵f（1）＜0，f（2）＞0，f（1.5）＞0，∴在区间（1，1.5）内函数f（x）＝3x+3x﹣8存在一个零点该同学在第二次应计算的函数值＝1.25，故选：C．3．函数的图象大致是（）A．B．C．D．【答案】D【解答】解：由，可知当x→﹣∞时，f（x）→﹣∞，排除A，C；当x→+∞时，由指数爆炸可知e x＞x3，则→0，排除B．故选：D．4．函数的零点所在的区间是（）A．B．C．D．【答案】C【解答】解：由于连续函数满足f（）＝﹣2＜0，f（）＝＞0，且函数在区间（，）上单调递增，故函数函数的零点所在的区间为（，）．故选：C．5．已知a，b是非零实数，则“a＞b”是“ln|a|＞ln|b|”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】D【解答】解：由于ln|a|＞ln|b|⇔|a|＞|b|＞0，由a＞b推不出ln|a|＞ln|b|，比如a＝1，b＝﹣2，有a＞b，但ln|a|＜ln|b|；反之，由ln|a|＞ln|b|推不出a＞b，比如a＝﹣2，b＝1，有ln|a|＞ln|b|，但a＜b；∴“a＞b”是“ln（a﹣b）＞0”的既不充分也不必要条件．故选：D．6．函数的值域为（）A．B．C．（0，] D．（0，2]【答案】A【解答】解：令t（x）＝2x﹣x2＝﹣（x﹣1）2+1≤1∵单调递减∴即y≥故选：A．7．若a＞b＞c＞1且ac＜b2，则（）A．log a b＞log b c＞log c a B．log c b＞log b a＞log a cC．log b c＞log a b＞log c a D．log b a＞log c b＞log a c【答案】B【解答】解：因为a＞b＞c＞1，令a＝16，b＝8，c＝2，则log c a＞1＞log a b所以A，C错，则故D错，B对．故选：B．8．已知函数f（x）＝lg（ax2﹣2x+a）的值域为R，则实数a的取值范围为（）A．[﹣1，1] B．[0，1]C．（﹣∞，﹣1）∪（1，+∞）D．（1，+∞）【答案】B【解答】解：函数f（x）＝lg（ax2﹣2x+a）的值域为R，设g（x）＝ax2﹣2x+a，则g（x）能取边所有的正数，即（0，+∞）是g（x）值域的子集，当a＝0时，g（x）＝﹣2x的值域为R，满足条件．当a≠0时，要使（0，+∞）是g（x）值域的子集，则满足得，此时0＜a≤1，综上所述，0≤a≤1，故选：B．9．若x1是方程xe x＝4的解，x2是方程xlnx＝4的解，则x1•x2等于（）A．4 B．2 C．e D．1【答案】A【解答】解：由于x1和x2是函数y＝e x和函数y＝lnx与函数y＝的图象的公共点A和B的横坐标，而A（），B（）两点关于y＝x对称，可得，因此x1x2＝4，故选：A．10．我国古代数学著作《九章算术》有如下问题：“今有蒲生一日，长三尺莞生一日，长一尺蒲生日自半，莞生日自倍．问几何日而长倍？”意思是：“今有蒲草第1天长高3尺，芜草第1天长高1尺以后，蒲草每天长高前一天的一半，芜草每天长高前一天的2倍．问第几天莞草是蒲草的二倍？”你认为莞草是蒲草的二倍长所需要的天数是（）（结果采取“只入不舍”的原则取整数，相关数据：lg3≈0.4771，lg2≈0.3010）A．2 B．3 C．4 D．5【答案】C【解答】设蒲草每天长的高度为数列{a n}，莞草每天长的高度为数列{b n}，由题意得：{a n}为等比数列，求首项为3，公比为，所以通项公式a n＝3•（）n﹣1，前n项和S n＝6[1﹣（）n]，{b n}为等比数列，首项为1，公比为2，所以通项公式b n＝2n﹣1，前n项和T n＝2n﹣1；由题意得设n天莞草是蒲草的二倍，即2n﹣1＝2•6[1﹣（）n]⇒（2n）2﹣13•2n+12＝0⇒2n＝12或1（舍）两边取以10为底的对数，n＝＝＝2+由相关数据可得，n＝4，故选：C．二．填空题（共5小题）11．已知x＞0，y＞0，且+＝1，则3x+4y的最小值是25【答案】25【解答】解：因为x＞0，y＞0，+＝1，所以3x+4y＝（3x+4y）（+）＝13++≥13+2＝25（当且仅当x＝2y 时取等号），所以（3x+4y）min＝25．故答案为：25．12．函数（a＞0且a≠1）的图象恒过定点P，则点P的坐标为（4，），若点P在幂函数g（x）的图象上，则g（9）＝．【答案】（4，）；．【解答】解：对于函数（a＞0且a≠1），令2x﹣7＝1，求得x＝4，y＝，可得它的图象恒过定点P（4，）．点P在幂函数g（x）＝xα的图象上，则4α＝，即22α＝2﹣1，∴α＝﹣，g（x）＝＝，故g（9）＝＝，故答案为：（4，）；．13．函数的递减区间是（3，+∞）．【答案】（3，+∞）【解答】解：由2x2﹣5x﹣3＞0得x＞3或x＜﹣，设t＝2x2﹣5x﹣3，则当x＞3时，函数t为增函数，当x＜﹣时，函数t为减函数，∵y＝log0.1t为减函数，∴要求y＝log0.1（2x2﹣5x﹣3）的递减区间，即求函数t＝2x2﹣5x﹣3的递增区间，即（3，+∞），即函数f（x）的单调递减区间为为（3，+∞）．故答案为：（3，+∞）．14．已知函数f（x）＝有3个零点，则实数a的取值范围是（，1）．【答案】（，1）．【解答】解：∵函数f（x）＝有3个零点，∴a＞0 且y＝ax2+2x+1在（﹣2，0）上有2个零点，∴，解得＜a＜1，故答案为：（，1）．15．对于函数f（x），若在定义域内存在实数x0满足f（﹣x0）＝﹣f（x0），则称函数f（x）为“倒戈函数”．设f（x）＝3x+2m﹣1（m∈R，且m≠0是定义在[﹣1，1]上的“倒戈函数”，则实数m的取值范围是．【解答】解：∵f（x）＝3x+2m﹣1是定义在[﹣1，1]上的“倒戈函数，∴存在x0∈[﹣1，1]满足f（﹣x0）＝﹣f（x0），∴3+2m﹣1＝﹣3﹣2m+1，∴4m＝﹣3﹣3+2，构造函数y＝﹣3﹣3+2，x0∈[﹣1，1]，令t＝3，t∈[，3]，y＝﹣﹣t+2，y∈[﹣，0]，∴﹣＜0，∴﹣，故答案为：[﹣，0）．三．解答题（共4小题）16．已知函数的定义域为集合A，集合B＝{x|1＜x＜8}，C＝{x|a ＜x＜2a+1}，（1）求集合（∁R A）∪B；（2）若A∪C＝A，求a的取值范围【解答】解：（1）∵函数的定义域为集合A，∴A＝{x|}＝{x|﹣1＜x＜2}，∴∁R A＝{x|x≤﹣1或x≥2}，∵集合B＝{x|1＜x＜8}，∴集合（∁R A）∪B＝{x|x≤﹣1或x＞1}．（2）∵A＝{x|}＝{x|﹣1＜x＜2}，C＝{x|a＜x＜2a+1}，A∪C＝A，∴C⊆A，当C＝∅时，a≥2a+1，解得a≤﹣1，当C≠∅时，，解得﹣1＜x．综上，a的取值范围是（﹣∞，]．17．（1）已知5a＝3，5b＝4，用a，b表示log2536．（2）求值．【解答】解：（1）5a＝3，5b＝4，得a＝log53，b＝log54，log2536＝，（2）原式＝﹣1+2＝﹣1﹣2+2＝2.5﹣1＝1.5．18．已知函数f（x）＝log a（1﹣x），g（x）＝log a（x+3），其中0＜a＜1．（1）解关于x的不等式：f（x）＜g（x）；（2）若函数F（x）＝f（x）+g（x）的最小值为﹣4，求实数a的值．【解答】解：（1）不等式即为log a（1﹣x）＜log a（x+3），∵0＜a＜1，∴1﹣x＞x+3＞0，得解为﹣3＜x＜﹣1，（2），由﹣x2﹣2x+3＞0解得其定义域为（﹣3，1），∵h（x）＝﹣x2﹣2x+3z在（﹣3，﹣1）上单调递增，在（﹣1，1）上单调递减，∴h（x）max＝h（﹣1）＝4．∵0＜a＜1，且F（x）的最小值为﹣4，∴log a4＝﹣4．得a﹣4＝4，所以a＝＝．19．某工厂今年初用128万元购进一台新的设备，并立即投入使用，计划第一年维修、保养费用8万元，从第二年开始，每年的维修、保养修费用比上一年增加4万元，该设备使用后，每年的总收入为54万元，设使用x年后设备的盈利总额y万元．（1）写出y与x之间的函数关系式；（2）从第几年开始，该设备开始盈利？（3）使用若干年后，对设备的处理有两种方案：①年平均盈利额达到最大值时，以42万元价格卖掉该设备；②盈利额达到最大值时，以10万元价格卖掉该设备．问哪种方案处理较为合理？请说明理由．（1）由题意可知x年的维修，使用x年后的总保养、维修费用为8x+【解答】解：＝2x2+6x．所以盈利总额y关于x的函数为：y＝54x﹣（2x2+6x）﹣128＝﹣2x2+48x﹣128（x∈N×）．（2）由y＞0，得﹣2x2+48x﹣128＞0，即x2﹣24x+64＜0，解得，由x∈N*，得4≤x≤20．答：第4年该设备开始盈利．（3）方案①年平均盈利，当且仅当，即x＝8时取等号，．所以方案①总利润为16×8+42＝170（万元），方案②y＝﹣2（x﹣12）2+160，x＝12时y取得最大值160，所以方案②总利润为160+10＝170（万元），答：选择方案①处理较为合理．。

玉溪一中2017—2018学年下学期高一年级期末考文科数学试卷注意事项：1.答题前，先将自己的姓名、考号填写在答题卡上。

2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合，则集合中元素的个数为2.已知向量，若，则等于3.已知，则下列不等式中恒成立的是4.公比为的等比数列的各项都是正数，且，则5. 三个数的大小关系为6. 要得到函数的图象，只要将函数的图象向左平移个单位长度 向右平移个单位长度向左平移个单位长度 向右平移个单位长度7．某几何体的三视图如图（1）所示，则该几何体的体积为8．已知，则的值是9．设是两条不同的直线，是两个不同的平面，且，下列命题中正确的是若，则 若，则若，则若，则10.已知，并且是终边上一点，那么的值等于11．如图（2）所示：已知圆锥的母线长为，圆锥的底面半径为，一只蚂蚁从圆锥的底面点出发，沿圆锥侧面爬行一周回到点，则蚂蚁爬行的最短路程长为12.函数则函数的零点个数是第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．13.已知则的最小值为__________．14.已知满足约束条件，则的最小值是__________．15.在中，，，，则_________．16.已知偶函数在上单调递增，且，则满足的的取值范围是__________．三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤。

17．(10分) 已知函数．（1）求的最小正周期；（2）求在区间上的最大值和最小值．18.（12分）已知分别为内角的对边，,（1）若，求；（2）设，且，求的面积.19. (12分)已知等差数列的前项和为，且，．（1）求及；（2）若数列的前项和为，试求并证明不等式成立.20. (12分)如图，在三棱锥中，．（1）求证：平面平面；（2）若，求点到平面的距离.21. (12分)已知直线过点和圆:相交于两点,（1）若圆的圆心，且圆与圆外切，求圆的方程；（2）若弦的长为，求直线的方程.22.（12分）已知函数，且函数的图象过点，（1）求的值；（2）若，求实数的取值范围；（3）若函数有两个零点，求实数的取值范围.玉溪一中2017—2018学年下学期高一年级期末考文科数学试卷答案一、选择题 BBDAA CDADD CC 二、填空题：13.8 14.-5 15.2 16.[][]5,31,1 -三、解答题：共70分。

精练03基本不等式1．【内蒙古赤峰市2019-2020学年高一期末】已知0x >，0y >满足22280x y xy y x +--=，则2y x +的最小值为（ ）A ．B ．4C ．D 【答案】C 【详解】由22280x y xy y x +--=知：(2)8xy x y y x +=+，而0x >，0y >∴182y x x y +=+，则21816(2)(2)()101018y x y x y x x y x y +=++=++≥=∴2y x +≥故选：C2．【湖北省荆州市2019-2020学年高一期末】若正数x ，y 满足21x y +=，则12x y+的最小值为（ ）A ．4B ．3+C ．8D ．9【答案】C 【详解】解：因为正数x ，y 满足21x y +=，所以()12422248x y x y x y y x ⎛⎫++=+++≥+=⎪⎝⎭，当且仅当4x y y x =，即11,42x y ==时取等号， 所以12x y+的最小值为8，故选：C3．【宁夏回族自治区银川一中2019-2020学年高一期末】下列函数的最小值为2的是（ ） A ．1y x x=+B ．1sin (0)sin 2y x x x π=+<<C ．y =D ．1tan (0)tan 2y x x x π=+<< 【答案】D 【详解】 对于A. 1y x x=+,当0x <时，0y <，所以最小值为不是2，A 错误； 对于B. 1sin 0sin 0sin 2y x x x x π⎛⎫=+<<> ⎪⎝⎭，，所以1sin 2sin x x +≥时， 即sin 1x =，此时无解，所以原式取不到最小值2 ，B 错误.对于C.2y =≥2=，此方程无解，则y 的最小值取不到2，C 错误；对于D,1tan (0)tan?2y x x x π=+<<，因为tan 0x >，所以1tan 2tan x x +≥=， 当且仅当tan 1x =，即4x π=时，y 有最小值2，满足，D 正确；故选：D.4．【江西省南昌市2019-2020学年高一期末】已知a ，0b >，且满足21a ab +=，则3a b +的最小值为（ ）A B C ．D ．【答案】C 【详解】 ∵21a ab +=， ∴1b a a=-．即11332a b a a a a a +=+-=+≥=当且仅当2a =时取等号．∴3a b +的最小值为故选：C5．【河北省石家庄市2019-2020学年高一期末】如果x ＞0，y ＞0，且111x y+=，则xy 有（ ）A ．最小值4B ．最大值4C ．最大值14D ．最小值14【答案】A 【详解】x ＞0，y ＞0，且111x y+=，又11x y +≥1，114xy ≤， 即4xy ≥，当2x y ==时取等号, 则xy 有最小值4， 故选：A6．【贵州省毕节市威宁县2019-2020学年高一期末】已知正实数a ，b 满足1a b +=，则2241a ba b--+的最小值为（ ） A ．11 B ．9C ．8D ．7【答案】C 【详解】解：因为正实数a ，b ，且1a b +=，所以2241a b a b--+41a b a b =-+- 41()b a a b =+-+41()()1b a a b =+⋅+- 44b a a b=++4≥ 8=当且仅当4b a a b =即223a b ==时，取等号. 所以2241a b a b--+的最小值为8. 故选：C.7．【广东省佛山市禅城区2019-2020学年高一期末】若0a >，0b >，2a b +=，则下列不等式对一切满足条件的a ，b 恒成立的是（ ）A ．1ab ≤BC ．22a b +≥D ．223a b +≥【答案】A 【详解】对于A ，0a >，0b >，a b ∴+≥12a b+≤=，即1ab ≤，当且仅当1a b ==时取等号，故A 正确；对于B ，224a b =++=+≤2≤，当且仅当1a b ==时取等号，故B 错误； 对于C ， 不妨设32a =，12b =时，23172244a b =+=<+，故B 错误； 对于D ，()2222422+=+-≥-=a b a b ab ，当且仅当1a b ==时取等号，故D 错误. 故选：A8．【广东省佛山市南海区2019-2020学年高一期末】若函数()()40,0af x x x a x=+>>当且仅当2x =时取得最小值，则实数a 的值为（ ） A ．12 B ．24C ．16D ．36【答案】C 【详解】()4af x xx=+≥，等号成立当且仅当24x a =，∴2x ==，解得：16a =，故选：C.9．【黑龙江省哈尔滨市第三十二中学2019-2020学年高一期末】已知0,0x y >>，231x y +=，则48x y +的最小值为（ ）A ．8B ．6C ．D ．【答案】C 【详解】∵00x y >>，，231x y +=，∴232482x y x y ≥+=+= 当且仅当2322x y =即11,46x y ==时，等号成立，所以48x y +的最小值为 故选：C10．【安徽省合肥市第十一中学2019-2020学年高一期末】若正数x ，y 满足x+3y=5xy ，则3x+4y 的最小值是( ) A ．245B ．285C ．5D ．6【答案】C 【详解】 由已知可得31155x y +=，则3194123131234()(34)555555555y x x y x y x y x y +=++=+++≥+=，所以34x y +的最小值5，应选答案C ．11．【山西省晋中市祁县第二中学2019-2020学年高一期末】若两个正实数,x y 满足112x y+=，且不等式2x y m m +<-有解，则实数m 的取值范围是（ ）A ．()1,2-B ．()4,1-C ．()(),12,-∞-+∞ D ．()(),14,-∞-+∞【答案】C 【解析】正实数x ,y 满足112x y+=， 则()111112222224y x x y x y x y x y ⎛⎫+=++=+++= ⎪⎝⎭， 当且仅当1,y x x y ==+取得最小值2. 由2x y m m +<-有解,可得22m m ->， 解得m >2或m <−1. 本题选择C 选项.12．【安徽省宿州市十三所省重点中学2019-2020学年高一期末】已知2m >，0n >，3m n +=，则112m n+-的最小值为（ ） A ．3 B ．4C ．5D ．6【答案】B 【详解】因为2m >，0n >，3m n +=，所以21m n -+=， 则()1111222224222n m m n m n m n m n-⎛⎫+=+-+=++≥+= ⎪---⎝⎭， 当且仅当22n m m n -=-且3m n +=，即51,22m n ==时取等号， 故选：B.13．【安徽省宣城市2019-2020学年高一期末】已知m ，0n >，4121m n+=+，则m n +的最小值为（ ）A ．72B ．7C ．8D ．4【答案】A 【详解】 ∵m ，0n >，4121m n+=+，∴()()4111411911554122122n m m n m n m n m n +⎛⎫⎛⎫++=+++⨯=++≥+= ⎪ ⎪++⎝⎭⎝⎭， 当且仅当411n m m n +=+且4121m n+=+，即2m =，32n =时取等号， 故m n +的最小值72.故选：A.14．【湖北省武汉市部分重点中学（武汉六中等）2019-2020学年高一期末】已知1x >，0y >，且1211x y+=-，则2x y +的最小值为（ ）A ．9B ．10C ．11D ．7+【答案】B 【详解】1x >，10x ->，又0y>，且1211x y+=-， 2(1)21x y x y ∴+=-++[]12(1)211x y x y ⎛⎫=-+++ ⎪-⎝⎭22(1)61y x x y -=++- 262x +-10=， 当且仅当22(1)1y x x y-=-，解得4x =，3y =时等号成立， 故2x y +的最小值为10． 故选：B ．15．【湖南省长沙市长沙县实验中学2019-2020学年高一期末】设正实数x ，y ，z 满足22340x xy y z -+-=，则当xyz取得最大值时，212x y z +-的最大值为（ ）A ．0B ．3C ．94D ．1【答案】D 【详解】由正实数x ，y ，z 满足22340x xy y z -+-=，2234z x xy y ∴=-+．∴22111434432?3xy xy x y z x xy y x y y xy x===-++--， 当且仅当20x y =>时取等号，此时22z y =．∴222122121(1)1122x y z y y y y+-=+-=--+，当且仅当1y =时取等号， 即212x y z+-的最大值是1． 故选：D16．【广东省惠州市2019-2020学年高一期末】函数2241y x x =++的最小值为__. 【答案】3 【详解】函数2241y x x =++， 即()224111y x x =++-+ ()2242114131xx ≥+⋅=-=+， 当且仅当212+=x ，即1x =±时，取等号， 则函数的最小值为3， 故答案为：3.17．【吉林省长春市实验中学2019-2020学年高一期末】已知32310x x k --+⋅->对任意实数x 恒成立，则实数k 的取值范围是________. 【答案】(),221-∞由于不等式32310x x k --+⋅->对任意实数x 恒成立，则3231x x k -<+⋅-，由基本不等式可得323111x x -+⋅-≥=，当且仅当323x x -=⋅时，即当31log 22x =时，等号成立，所以，1k <，因此，实数k 的取值范围是(),1-∞.故答案为：(),1-∞.18．【湖南省长沙市雨花区2019-2020学年高一期末】设1x >，则函数151y x x =++-的最小值为_____ 【答案】8 【详解】1x >，∴函数1115(1)62(1)68111y x x x x x x =++=-++-+=---，当且仅当2x =时取等号． 因此函数151y x x =++-的最小值为8． 故选：A ．19．【湖北省仙桃市、天门市、潜江市2019-2020学年高一期末】已知0a >，0b >，且24ab a b =++，则ab 的最小值为______. 【答案】4 【详解】0a >，0b >，，可得24ab ≥，当且仅当a b =时取等号． )120∴≥，∴21≤-（舍去），4ab ∴≥．故ab 的最小值为4. 故答案为：4．20．【四川省凉山州2019-2020学年高一期末】已知0a >，0b >，1a b +=，则1aa b+的最小值为______． 【答案】3依题意1113a a b a b a a b a b a b ++=+=++≥+=. 当且仅当12a b ==时等号成立. 故答案为：321．【河北省唐山市第一中学2019-2020学年高一期末】若441x y +=，则x y +的取值范围是____________．【答案】(],1-∞- 【详解】由基本不等式可得1144222x y x y x y +++=+≥=⨯=，10x y ∴++≤，解得1x y +≤-.所以，x y +的取值范围是(],1-∞-. 故答案为：(],1-∞-.22．【安徽省淮南市第一中学2019-2020学年高一期末】已知x ，0y >，且194x y+=，则x y +的最小值________． 【答案】4 【详解】 因为x ，0y >，且194x y+=， 所以x y +()11919110104444⎛⎛⎫⎛⎫=++=++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝y x x y x y x y 当且仅当9y xx y=，,即1,3x y ==时，取等号， 所以x y +的最小值为4， 故答案为：423．【山西省2019-2020学年高一期末】已知0a >，0b >，1a b +=，则161a b+的最小值为__________.【答案】25【详解】()1611611617b a a b a b a b a b ⎛⎫+=++=++ ⎪⎝⎭17172425≥+=+⨯= 当且仅当2216a b =，即45a =，15b = 时取等号. 故答案为：2524．【重庆市巴蜀中学2019-2020学年高一半期考试】设2020a b +=，0b >，则当a =____________时，12020a a b+取得最小值. 【答案】20202019-【详解】由已知有： 22212020202020202020a a a a b a b a b a b a a b++=+=++212020≥-+221140392202020202020=-+⨯=， 当且仅当0a <，22020a b a b =时，等号成立. 即222202020192020a a b ⇒=-=. 故答案为：20202019-. 25．【四川省乐山市2019-2020学年高一期末】已知a ，b ，c 均为正数，且abc ＝4a +9b ，则a +b +c 的最小值为_____．【答案】10【详解】49abc a b =+4994a b c ab a b+∴==+9410a b c a b a b ++=+++≥=（当且仅当3,2a b ==时，取等号） 故答案为：10 26．【湖北省仙桃市、天门市、潜江市2019-2020学年高一期末】一家货物公司计划租地建造仓库储存货物，经过市场调查了解到下列信息：每月土地占地费1y （单位：万元）与仓库到车站的距离x （单位：km ）成反比，每月库存货物费2y （单位：万元）与x 成正比；若在距离车站2km 处建仓库，则1y 和2y 分别为10万元和1.6万元.这家公司应该把仓库建在距离车站多少千米处，才能使两项费用之和最小？并求出这个最小值.【答案】5km 处，最小值为8万元..【详解】解：设仓库建在距离车站km x 处时，两项费用之和为y 万元. 根据题意可设1y xλ=，2y x μ=. 由题可知，当2x =时，110y =，2 1.6y =，则20λ=，45μ=. 所以()20405y x x x =+>.根据均值不等式可得8y ≥=， 当且仅当2045x x =，即5x =时，上式取等号. 故这家公司应该把仓库建在距离车站5km 处，才能使两项费用之和最小，且最小值为8万元.27．【安徽省池州市2019-2020学年高一期末】已知函数2(4)()x f x x+=(0)x >． （1）解不等式：f （x ）＞503； （2）求函数f （x ）的最小值．【答案】（1）8|03x x ⎧<<⎨⎩或}6x >；（2）16 【详解】（1）220(4)50()(4)5033x x f x x x x >⎧+⎪=>⇔⎨+>⎪⎩， 208|03264803x x x x x >⎧⎧⇔⇔<<⎨⎨-+>⎩⎩或}6x >. （2）22(4)81616()8816x x x f x x x x x +++===++≥=， 当且仅当16x x =，即4x =时函数2(4)()x f x x+=取得最小值16. 28．【浙江省宁波市慈溪市2019-2020学年高一期末】已知0a >，0b >且3a b +=．（Ⅰ）求11()a b +的最大值及此时a ，b 的值； （Ⅱ）求2231a b a b +++的最小值及此时a ，b 的值． 【答案】（Ⅰ）32a b ==时，11a b ⎛⎫+ ⎪⎝⎭取得最大值为2-；（Ⅱ）6a =-3b =-+32+； 【详解】解：（Ⅰ）1133224233333333333a b a b b a b a a b a b a b a b a b +++=+=+=+++=， 当且仅当33b a a b =且3a b +=，即32a b ==时取等号， 3211423log a b ⎛⎫∴+=- ⎪⎝⎭即最大值为2-， （Ⅱ）3a b +=， ∴223313131(1)121111a b a b a b a b a b a b a b ++=++-+=+-++=++++++ 3113(1)3(1)2()()332314444(1)4(1)a bb a b a a b a b b ++=+++=+++=+++ 当且仅当3(1)44(1)b a a b +=+且3a b +=，即6a =-3b =-+ 29．【黑龙江省哈尔滨市第三中学2019-2020学年高一期末】已知0a >，0b >.（1）求证：()2232a b b a b +≥+； （2）若2a b ab +=，求ab 的最小值.【答案】（1）证明见解析；（2）1.【详解】证明：（1）∵()()222223220a b b a b a ab b a b +-+=-+=-≥， ∴()2232a b b a b +≥+. （2）∵0a >，0b >， ∴22ab a b ab =+≥，即22ab ab ≥， ∴1≥ab ，∴1≥ab .当且仅当1a b ==时取等号，此时ab 取最小值1.和分析法来一起证明，属于中档题.30．【安徽省合肥市第十一中学2019-2020学年高一期末】某村计划建造一个室内面积为800平方米的矩形蔬菜温室，温室内沿左右两侧与后墙内侧各保留1米宽的通道，沿前侧内墙保留3米宽的空地．（1）设矩形温室的一边长为x 米，请用S 表示蔬菜的种植面积，并求出x 的取值范围；（2）当矩形温室的长、宽各为多少时，蔬菜的种植面积最大？最大种植面积为多少．【答案】（1）()80042S x x ⎛⎫=-⋅- ⎪⎝⎭， 4400x <<；（2）长、宽分别为40米，20米时，蔬菜的种植面积最大，最大种植面积为2648m ．【详解】解：（1）矩形的蔬菜温室一边长为x 米，则另一边长为800x 米， 因此种植蔬菜的区域面积可表示()80042S x x ⎛⎫=-⋅- ⎪⎝⎭，由4080020x x->⎧⎪⎨->⎪⎩得： 4400x <<； （2）()8001600 428082808S x x x x =-⋅-=-+≤⎛⎫⎛⎫ ⎪ ⎪⎝-⎝⎭⎭2808160648m =-=， 当且仅当1600x x=，即()404,400x =∈时等号成立． 因此，当矩形温室的两边长、宽分别为40米，20米时，蔬菜的种植面积最大，最大种植面积为2648m ．。

河北省唐山市开滦一中2019-2020学年高一数学下学期期末考试试题（含解析）第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，有且只有一项符合题目要求．1. 在中，，且，则下列结论中正确的是（ ）ABC A B C >>2C π≠A. B. C. D.tan tan A C<tan tan A C>sin sin <A Csin sin A C>【答案】D 【解析】【分析】利用特殊值排除错误选项，利用正弦定理证明正确选项【详解】若，由于,则，所543,,12123124A B C πππππ=====02C A π<<<tan tan A C >以A 选项错误.若，则，74,,1212312A B C ππππ====tan 0tan A C <<，所以BC 选项错误.75sin sinsin sin sin 121212A C πππ==>=在三角形中，大角对大边，由于，所以，由正弦定理得ABC A C >a c >①，是三角形外接圆的半径.2sin 2sin R A R B >R ABC 由①得.所以D 选项正确.sin sin A C >故选：D【点睛】本小题主要考查三角函数的单调性，考查正弦定理，属于基础题.2. 不等式的解集为（ ）112x <A. B. C. D.(,2)-∞(2,)+∞(0,2)(,0)(2,)-∞+∞ 【答案】D 【解析】【分析】移项通分后转为一元二次不等式即可求其解集.【详解】等价于即，112x <202x x -<()20x x ->故不等式的解为或，故解集为，选D.0x <2x >()(),02,-∞+∞ 【点睛】本题考查分式不等式的解，属于基础题.3. 若，则等于（ ）(1,2)OA = (1,1)OB =- ABA.B.C.D.()0,3-()0,1()1,2-()2,3-【答案】A 【解析】【分析】利用向量减法的坐标运算求得.AB【详解】依题意.()()()1,11,20,3AB OB OA =-=--=-故选：A【点睛】本小题主要考查向量减法的坐标运算，属于基础题.4. 已知是等差数列，且，则的值是（ ）{}n a 1415a a +=23a a +A. 20 B. 15C. 10D. 5【答案】B 【解析】【分析】利用等差数列的性质直接求解.【详解】是等差数列，且，{}n a 1423+=+.231415a a a a ∴+==+故选：B.【点睛】本题考查等差数列的性质，属于基础题.5. 下列事件：①任取三条线段，这三条线段恰好组成直角三角形；②从一个三角形的三个顶点各任画一条射线，这三条射线交于一点；③实数a ，b 都不为0，但；220a b +=④明年12月28日的最高气温高于今年12月28日的最高气温．其中为随机事件的是（ ）A. ①②③ B. ①③④C. ①②④D. ②③④【答案】C 【解析】【分析】根据随机事件概念逐一判断，即可选择.【详解】任取三条线段，这三条线段不一定能组成直角三角形，所以①为随机事件；从一个三角形的三个顶点各任画一条射线，这三条射线不一定交于一点，所以②为随机事件；因为当实数a ，b 都不为0时，所以③为不可能事件；220a b +≠明年12月28日的最高气温可能高于今年12月28日的最高气温，所以④为随机事件；故选C ．【点睛】本题考查随机事件概念，考查基本分析判断能力，属基础题.6. 不等式（其中）的解集为（ ）22120x ax a --<0a >AB.C.D.()3,4a a -()4,3a a -()3,4-()2,6a a 【答案】A 【解析】【分析】先因式分解，再根据解的大小写出不等式解集.【详解】22120(3)(4)034,(0)x ax a x a x a a x a a --<∴+-<∴-<<> 故选：A【点睛】本题考查解一元二次不等式，考查基本分析求解能力，属基础题.7. 对于，下列不等式中不正确的是（ ）0,0a b >>A. B.22222a b a b ++⎛⎫ ⎪⎝⎭ (22)2a b ab +…C.22a b ab +⎛⎫⎪⎝⎭…11a b <+【答案】D 【解析】【分析】举例可确定不正确的选项，其它选项可利用作差法证明成立.【详解】当时，满足，即D 不正确；9a b ==0,0a b >>921129a b =>=+，即A 正确；22a b +⎛⎫ ⎪⎝⎭ 222()024a b a b +---=≤∴22222a b a b ++⎛⎫ ⎪⎝⎭…，即B 正确；22222()0222a b a b a b ab ab +--+-=≤∴≤，即C 正确；2222)042(a b a b a b ab ab --=≤∴++⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭…Q 故选：D【点睛】本题考查作差法判断不等式，考查基本分析判断能力，属基础题.8. 羊村村长慢羊羊决定从喜羊羊、美羊羊、懒羊羊、暖羊羊、沸羊羊中选派两只羊去割草，则喜羊羊和美羊羊至少有一只被选中的概率为（ ）A. B. C. D. 710673545【答案】A 【解析】【分析】利用列举法求得所有的可能，结合古典概型概率计算，计算出所求的概率.【详解】依题意从喜羊羊、美羊羊、懒羊羊、暖羊羊、沸羊羊中选派两只羊的可能事件有：（喜羊羊、美羊羊），（喜羊羊、懒羊羊），（喜羊羊、暖羊羊），（喜羊羊、沸羊羊），（美羊羊、懒羊羊），（美羊羊、暖羊羊），（美羊羊、沸羊羊），（懒羊羊、暖羊羊），（懒羊羊、沸羊羊），（暖羊羊、沸羊羊），共种.10其中喜羊羊和美羊羊至少有一只被选中的为：（喜羊羊、美羊羊），（喜羊羊、懒羊羊），（喜羊羊、暖羊羊），（喜羊羊、沸羊羊），（美羊羊、懒羊羊），（美羊羊、暖羊羊），（美羊羊、沸羊羊），共种.7所以喜羊羊和美羊羊至少有一只被选中的概率为.710故选：A【点睛】本小题主要考查古典概型的计算，属于基础题.9. 已知向量，若，则锐角为（ ）31,cos ,cos ,26a b αα⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭ //a b αA. B. C. D. 30°60︒45︒75︒【答案】B 【解析】【分析】根据向量平行坐标表示列方程，解得结果.【详解】因为，所以//a b22311cos cos 264αα=⨯∴=因为为锐角，所以α1cos 602αα=∴=故选：B【点睛】本题考查向量平行坐标表示，考查基本分析求解能力，属基础题.10. 已知的内角的对边分别为．若，则ABC ,,A B C ∠∠∠,,a b c 1sin 4a A =等于（ ）sin sin sin b c aB C A +-+-A. B. 4C. D. 31413【答案】A 【解析】【分析】根据正弦定理可得，代入即可得结果.sin 4,sin 4,sin 4A a B b C c ===【详解】由正弦定理,，即，1 sin 4a A =sin sin b c B C ==sin 4,sin 4,sin 4A a B b C c ===则 ，sin sin sin b c aB C A +-+-14444b c a b c a +-==+-故选：A.【点睛】本题主要考查了正弦定理的应用，实现边角互化是解题的关键，属于基础题.11. 从分别写有1，2，3，4，5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为（ ）A. B. C. D. 1101531025【答案】D 【解析】【分析】先求出基本事件总数，再用列举法求出抽得的第一张卡片上的数大于第二张卡片上的25n =数包含的基本事件个数，由此能求出抽得的第一张卡片上的数大于第二张卡片上的数的概率.【详解】从分别写有1，2，3，4，5的5张卡片中随机抽取1张，放回后再随机抽取1张，基本事件总数，5525n =⨯=抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有：（2，1），（3，1），（3，2），（4，1），（4，2），（4，3），（5，1），（5，2），（5，3），（5，4），共有个基10m =本事件，∴抽得的第一张卡片上的数大于第二张卡片上的数的概率，102255p ==故选：D.【点睛】本题主要考查概率的求法，解题时要认真审题，注意列举法的合理运用，属于基础题.12. 已知数列：，，，…，又，则数{}n a 112,233+123444++12345555+++1114nn n b a a +=⋅列的前n 项的和为（ ）{}n b n S A. B.C.D.1411n ⎛⎫- ⎪+⎝⎭11421n ⎛⎫- ⎪+⎝⎭111n -+1121n -+【答案】C 【解析】【分析】可观察出，然后用裂项相消法即可求出的前项(1)1232112n n n n n a n n +++++===++ {}n b n 和.【详解】因为数列为:，，，，…{}n a 121233+123444++12345555+++所以，(1)1232112n n n n n a n n +++++===++ 所以，1111114(1)1n n n b a a n n n n +=⋅==-++所以的前项和为{}n b n 11111111112233411n n n -+-+-++-=-++故选：C.【点睛】本题考查用裂项相消法求数列的前项和，属于中档题.n 第Ⅱ卷（共90分）二、填空题（每题44分，满分20分，将答案填在答题纸上）13. 某班有男生36人，女生18人，用分层抽样的方法从该班全体学生中抽取一个容量为6的样本，则抽取的女生人数为________．【答案】2【解析】【分析】分层抽样的抽取比例为，抽取的女生人数为抽取比例女生人数．样本容量总体个数⨯【详解】由题意知：分层抽样的抽取比例为，6136189=+抽取的女生人数为．∴11829⨯=故答案为：2．【点睛】本题考查了分层抽样方法，熟练掌握分层抽样的定义是关键，属于基础题．14. 在数列中，，则通项公式________．{}n a 223n S n n =-n a =【答案】45n -【解析】【分析】首先利用得出时的通项公式，把代入此通项公式检验也满足，从而1n n n a S S -=-2n ≥1n =得到数列的通项公式.【详解】当时，，1n =11231a S ==-=-当时，，2n ≥()()12223213145n n n n n a S S n n n -=---+-=--=时，上式也成立，∴，1n =45n a n =-故答案为：.45n -【点睛】本题主要考查了等差数列的通项公式，熟练掌握数列的递推式是解本1n n n a S S -=-题的关键，属于基础题．15. 为组织好“市九运会”，组委会征集了800名志愿者，现对他们的年龄调查统计后，得到如图所示的频率分布直方图，但是年龄在内的数据不慎丢失，依据此图可得：[)25,30（1）年龄分组对应小长方形的高度为________．[)25,30（2）这800名志愿者中年龄在内的人数为________．[)25,40【答案】 (1). (2). 人0.04680【解析】【分析】（1）根据所有矩形的面积和为1，建立方程，即求得年龄分组对应小长方形的高度；[)25,30（2）先利用频率分布直方图求得内的频率，进而求得年龄在内的人数.[)25,40[)25,40【详解】（1）设年龄年龄分组对应小长方形的高度为，[)25,30x 则，解得，(0.010.070.060.02)51x ++++⨯=0.04x =即年龄分组对应小长方形的高度为.[)25,300.04（2）这800名志愿者中年龄在内的频率为，[)25,40(0.040.070.06)50.85++⨯=所以这800名志愿者中年龄在内的人数为人.[)25,408000.85680⨯=故答案为：，人.0.04680【点睛】本题主要考查了频率分布直方图的性质，以及频率分布直方图中频率、频数的计算，着重考查了识图能力，以及运算与求解能力.16. 在中，角所对的边分别为，的平分线交ABC ,,A B C ,,a b c 120,ABC ABC ∠=︒∠于点D ，且，则的最小值为________．AC 1BD =9a c +【答案】16【解析】【分析】先根据三角形面积关系列等量关系，再根据基本不等式求最值.,a c 【详解】因为,ABC ABD BDC S S S =+ 所以11111sin1201sin 601sin 601222ac a c a c =⨯⨯+⨯⨯∴+=因此1199(9)(101016c a a c a c a c a c +=++=++≥+=当且仅当即时取等号911,1c a a c a c =+=44,3a c ==即的最小值为9a c +16故答案为：16【点睛】本题考查三角形面积公式、利用基本不等式求最值，考查综合分析求解能力，属中档题.三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17. 已知等差数列和正项等比数列满足．{}n a {}n b 1124351,10,a b a a b a ==+==（1）求的通项公式；{}n a （2）求数列的前n 项和．{}n b 【答案】（1）；（2）21n a n =-1(31)2n-【解析】【分析】（1）根据条件列公差与公比方程组，解得结果，代入等差数列通项公式即可；（2）根据等比数列求和公式直接求解.【详解】（1）设等差数列公差为，正项等比数列公比为，{}n a d {}n b q 因为，1124351,10,a b a a b a ==+==所以211310,142,03d d q d d q q +++==+∴=>∴= 因此；111(1)221,133n n n n a n n b --=+-⨯=-=⨯=（2）数列的前n 项和{}n b 131(31)132nn n S -==--【点睛】本题考查等差数列以及等比数列通项公式、等比数列求和公式，考查基本分析求解能力，属基础题.18. 某校从参加高一年级期末考试的学生中抽出60名学生，将其物理成绩（均为整数）分成六段后画出如下频率分布直方图．观察图形的信息，回答[)[)[]40,50,50,60,,90,100⋯下列问题：（1）估计这次考试的众数m 与中位数n （结果保留一位小数）；（2）估计这次考试的优秀率（80分及以上为及格）和平均分．【答案】（1），；（2）优秀率，平均分71分.75m =73.3n =30%【解析】【分析】（1）根据众数是最高小矩形中点的横坐标，中位数要平分直方图的面积可得的值；,m n （2）在频率分直方图中，小矩形的面积等于这一组的频率，估计这次考试的优秀率为右边两个小矩形面积之和，平均数为各小矩形面积与底边中点横坐标乘积的和.【详解】（1）众数是最高小矩形中点的横坐标，所以众数为（分）75m =前三个小矩形面积为，0.01100.015100.015100.4⨯+⨯+⨯=∵中位数要平分直方图的面积，∴.0.50.47073.30.03n -=+=（2）依题意，80及以上的分数所在的第五、六组，频率和为，()0.0250.005100.3+⨯=所以，抽样学生成绩的合格率是，30%利用组中值估算抽样学生的平均分：，450.1550.15650.15750.3850.25950.0571⨯+⨯+⨯+⨯+⨯+⨯=估计这次考试的平均分是71分.【点睛】本题考查频率分步直方图，解题的关键是正确运用直方图，在直方图中理解小正方形的面积是这组数据的频率，众数是最高小矩形中点的横坐标，平均数为各小矩形面积与底边中点横坐标乘积的和，属于基础题.19. 在中，，．ABC 120A =︒37c a =（1）求的值；sin C （2）若，求b 的长．7a =【答案】（12）5【解析】【分析】（1）根据正弦定理可求得的值；sin C （2）根据余弦定理列方程解得b 的值.【详解】（1）因为，所以由正弦定理得；37c a =33sin sin sin12077C A === （2）因为，，所以37c a=7a =3c =由余弦定理得2222222cos 7323cos120a b c bc A b b =+-∴=+-⋅2340005b b b b ∴+-=>∴= 【点睛】本题考查正弦定理与余弦定理，考查基本分析求解能力，属基础题.20. 如图，某房地产开发公司计划在一栋楼区内建造一个矩形公园，公园由矩形的休ABCD 闲区（阴影部分）和环公园人行道组成，已知休闲区的面积为1000平方1111D C B A 1111D CB A 米，人行道的宽分别为4米和10米，设休闲区的长为x 米．（1）求矩形所占面积S （单位：平方米）关于x 的函数解析式；ABCD （2）要使公园所占面积最小，问休闲区的长和宽应分别为多少米？1111D C B A【答案】（1）；（2）休闲区的长和宽应分别为1000(20)(8),(0)S x x x =++>1111D C B A 米，米.5020【解析】【分析】（1）先表示休闲区的宽，再表示矩形长与宽，最后根据矩形面积公式得函数解析式，ABCD 注意求函数定义域；（2）根据基本不等式求S 最小值，再根据等号取法确定休闲区的长和宽.1111D C B A 【详解】（1）因为休闲区的长为x 米，休闲区的面积为1000平方米，所以休闲区1111D C B A 的宽为米；从而矩形长与宽分别为米米，1000x ABCD 20x +1000,8x +因此矩形所占面积，ABCD 1000(20)(8),(0)S x x x =++>（2）100020000(20)(8)1160811601960S x x x x =++=++≥+=当且仅当时取等号，此时200008,50x x x ==100020x =因此要使公园所占面积最小，休闲区的长和宽应分别为米，米.1111D C B A 5020【点睛】本题考查函数应用、求函数解析式、利用基本不等式求最值，考查基本分析求解能力，属基础题.21.已知的角、、所对的边分别是、、，设向量，ABC ∆A B C a b c (,)m a b = (sin ,n B =，.sin )A (2,2)p b a =--（1）若，求证：为等腰三角形；//m n ABC ∆（2）若，边长，角，求的面积.m p ⊥ 2c =π3C =ABC ∆【答案】（1）见解析（2【详解】⑴因为，所以，即,其中是的外接圆sin sin a A b B =··22a b a b RR =R ABC ∆半径， 所以，所以为等腰三角形.a b =ABC ∆⑵因为，所以.m p ⊥ ()()220a b b a -+-=由余弦定理可知，，即()22243a b ab a b ab=+-=+-()2340ab ab --=解方程得：（舍去）4ab =1ab =-所以11sin 4sin 223S ab C π==⨯⨯=22. 某市2020年发放汽车牌照14万张，其中燃油型汽车牌照12万张，电动型汽车牌照2万张．为了节能减排和控制汽车总量，从2020年开始，每年电动型汽车牌照按50%增长，而燃油型汽车牌照每一年比上一年减少0.5万张，同时规定一旦某年发放的牌照超过15万张，以后每一年发放的电动型的牌照的数量维持在这一年的水平不变．（1）记2020年为第一年，每年发放的燃油型汽车牌照数构成数列，每年发放的电动型{}n a 汽车牌照数构成数列，完成下列表格，并写出这两个数列的通项公式．{}n b 112a =211.5a =____3a =…12b =______2b =_____3b =…（2）从2020年算起，累计各年发放的牌照数，哪一年开始超过100万张？【答案】（1），（为正整数）；32311,3, 4.5a b b ===0.512.5,1250,26n n n a n -+≤≤⎧=⎨≥⎩n （为正整数）；（2）年132,1,2,324.5,4n n n b n -⎧⎛⎫⨯=⎪ ⎪=⎨⎝⎭⎪≥⎩n 2026【分析】（1）利用列表法，结合等差、等比数列的通项公式，求得数列和的通项公式.{}n a {}n b （2）根据（1）中表格数据得出结论.【详解】（1）依题意列表如下：年份序号na nb 本年度发放累计发放2020112214142021211.53232⨯=14.528.52022311232 4.52⎛⎫⨯= ⎪⎝⎭155442023410.5 4.515592024510 4.514.573.5202569.5 4.51487.52026794.513.5101根据表格数据可知，，，112,0.5a d ==-311a =令，()110n a a n d =+-=即，解得.()()1210.50.512.50n n +-⨯-=-+=25n =所以（为正整数）.0.512.5,1250,26n n n a n -+≤≤⎧=⎨≥⎩n 由表格数据可知，，，132,2b q ==233, 4.5b b ==所以（为正整数）.132,1,2,324.5,4n n n b n -⎧⎛⎫⨯=⎪ ⎪=⎨⎝⎭⎪≥⎩n （2）由（1）表格可知年超过万.2026100【点睛】本小题主要考查等差、等比数列在实际生活中的应用，属于中档题.。

2019-2020 学年度第一学期期末联考高一数学试题第 I 卷（选择题）一、选择题（本大题共 10 小题，每题 5 分，共 50 分．每题只有一个正确答案）1．若 A={0,1,2 } , B = { x 1? x 2} , 则A?B（）{ } { 0,1,2 }{}{1,2 }A ． 1B ．C ． 0,1D ．2． sin15 o cos15o 值为（）A ．1B ．1C．3 D． 324243． 函数 f ( x)1lg(1 x) 的定义域是 ()1 xA ．( － ，－ 1)B ．(1，＋ )C ．(－1，1)∪(1，＋ )D ．(－ ，＋ )4．已知点 P( x,3) 是角终边上一点，且 cos4），则 x 的值为（B ． 55D ． 4A ． 5C ． 45．已知 a0.7 0.8 ,blog 2 0.8, c1.10.8 ，则 a,b, c 的大小关系是（）A ． a b cB ． b a cC ． a c bD ． b c a6．设函数 y ＝ x 3 与 y( 1 )x 2 的图像的交点为 ( x 0，y 0) ，则 x 0 所在的区间是 ()2A ．(0，1)B．(1 ，2) C ．(2 ， 3) D ．(3 ，4)7．在自然界中，存在着大批的周期函数，比方声波，若两个声波随时间的变化规律分别为：y 1 3sin 100 t , y 2 3cos 100 t ，则这两个声波合成后即yy 1 y 2 的振幅为（）A ． 3B ． 6C ． 3 2 D． 6 28．以下函数中，不拥有奇偶性的函数是 ( )A ． yexexB ． y lg1 x1 xC ． ycos2xD ． y sin x cos x9．若 yAsin( x)( A0,0,| |) 的最小值为2，其图像相邻最高点与最低点横坐标之差为2 ，且图像过点（20， 1），则其分析式是（）A ． y 2sin( x )6B． y 2sin( x )3C ． y2sin( x) 2 6xD ． y 2sin( )2 310．如右图，点 P 在半径为 1的半圆上运动， AB 是直径， P当 P 沿半圆弧从 A 到 B 运动时，点 P 经过的行程 x 与 APBxB O A的面积 y 的函数y f ( x) 的图像是以下图中的（）yy11 12OC π2πx OD第 II卷（非选择题）π2πx二、填空题（本大题共 5 小题，每题 5 分，共25 分．将答案填在题后横线上）11．(log29)(log 3 4)．12．把函数y＝ 3sin2 x的图象向左平移个单位获得图像的函数分析是．13．已知tan 2 ，则 cos26．14．若函数f x 知足 f ( x 1) f ( x) ，且当x1,1 时， f x x ，则 f 2 f 3f4．15．函数f ( x)| cos x | cos x 具备的性质有．（将全部切合题意的序号都填上）（ 1）f (x)是偶函数；（ 2）f (x)是周期函数，且最小正周期为；（ 3）f (x)在[, ] 上是增添的；2（ 4）f (x)的最大值为2．三、解答题（本大题共 6 小题，共75 分．解答应写出文字说明、证明过程或演算步骤）16．已知会合M ={x 1 < x < 2}，会合Nx 3x 4 ．2（ 1）求AèB；P ={}（ 2）设会合x a < x < a + 2，若 P 腿(A B) ，务实数 a 的取值范围．117．（本小题满分12 分）已知tan2, tan，此中0,0．3（ 1）求tan() 的值；（ 2）求角的值．18．（本小题满分12 分）已知函数 f (x) sin( x)sin( x) ．32（ 1）求f (x)的最小正周期；3，求 g(x) 在区间[0,] 上的值域．（ 2）若g (x) f ( x)4219．（此题满分12 分）辽宁号航母纪念章从2012 年10 月5 日起开始上市．经过市场检查，获得该纪念章每 1 枚的市场价y(单位 : 元) 与上市时间x(单位 : 天 ) 的数据以下:上市时间x 天41036市场价y 元905190(1) 依据上表数据联合散点图，从以下函数中选用一个适合的函数描绘辽宁号航母纪念章的市场价y与上市时间x 的变化关系并说明原因: ①y ax b ；②y ax 2bx c ；③y a log b x ．(2)利用你选用的函数，求辽宁号航母纪念章市场价最低时的上市天数及最低的价钱．20． ( 本小题满分13 分)已知函数 f (x)cx1, 0 x c，知足 f (c)9 x．2 c 21, c ≤ x128(1)求常数 c 的值；(2)解对于 x 的不等式 f (x)21．821． ( 本小题满分14 分 ) 已知函数mf( )|x|1( x0)．x x（ 1）当m 2时，判断f (x)在(,0) 的单一性，并用定义证明．（ 2）若对随意x R ，不等式 f (2x)0 恒建立，求 m 的取值范围；（ 3）议论f (x)零点的个数．2019-2020 学年度第一学期期末 考高一数学参照答案参照答案： 一、1．A2．B 3 ．C4．D5．B 6 ．B 7 ．C 8 ．D 9 ．C10．A 二、填空11． 4 12． 13 ．3 14． 115．（ 1）（ 3）（4）56三、解答{ x 1 < x < 4}16．解：（ 1） A? B⋯⋯⋯⋯⋯⋯⋯⋯ 6 分 （ 2）由（1） A ? B {x 1 < x < 4 }， ⋯⋯⋯⋯⋯⋯⋯⋯ 9 分ì?a 3 1?1＃a2⋯⋯⋯⋯⋯⋯⋯⋯ 12 分í?2 ? 4?a +1tantan217．解：（ 1） tan()37⋯⋯⋯⋯⋯⋯⋯⋯ 5 分1 tan tan1 ( 2) 131tantan2（ 2） tan(31⋯⋯⋯⋯⋯⋯⋯⋯ 10 分)tan tan111( 2)1 3因 tan2 0,tan0 ，3因此， 022因此2，2故4⋯⋯⋯⋯⋯⋯⋯⋯ 12 分18．解：f (x)( 1 sin x3cos x)cos x⋯⋯⋯⋯⋯⋯⋯⋯ 2 分221 sin x cos x3cos 2 x221sin 2x3(1 cos 2x) ⋯⋯⋯⋯⋯⋯⋯⋯ 4 分441sin(2 x3) 3 ⋯⋯⋯⋯⋯⋯⋯⋯ 6 分24（ 1）因此T 2．⋯⋯⋯⋯⋯⋯⋯⋯ 8 分21（2）g (x)) ，sin(2 x23因 0 ≤ x ≤2 ，因此3 ≤ 2x3 ≤ ，3因此3≤ sin(2 x)≤1，233≤ 1sin(2 x) ≤ 1，423 2因此 g(x) 在区 [0,] 上的 域 [3 ,1] ．⋯⋯⋯⋯⋯⋯⋯⋯ 12 分24 219．解 :(1) ∵跟着 x 的增添， y 的 先减后增，而所 的三个函数中y ax b 和 ya logb x 然都是 函数，不 足 意，∴ yax 2 bx c ．⋯⋯⋯⋯⋯⋯⋯⋯ 4 分(2) 把点 (4 ， 90) ， (10 ， 51) ， (36 ， 90) 代入 yax 2 bx c 中，16a 4b c90得 100a 10bc 51⋯⋯⋯⋯⋯⋯⋯⋯6 分1296a 36b c 90解得 a 110， c 126⋯⋯⋯⋯⋯⋯⋯⋯ 8 分， b1 4 1∴ yx 2 10x 126 (x 20)2 26 ，⋯⋯⋯⋯⋯⋯⋯⋯ 10 分44∴当 x 20 ， y 有最小 y min 26 ．⋯⋯⋯⋯⋯⋯ 11 分答： 宁号航母 念章市 价最低 的上市天数 20 天，最低的价钱 26 元．⋯⋯⋯⋯12 分20．解： (1)∵ f ( c)9 ，即 c c1 9 ，2 8 28解得 c1⋯⋯⋯⋯⋯⋯⋯⋯ 5 分．21 x 1, 0 x 1(2) 由 (1) 得 f ( x)21, 1≤ x2 ，2 4x12由 f ( x)2，适当 0x12 x1 ⋯⋯⋯⋯⋯⋯⋯⋯9 分1，解得4 ；822当1≤ x 1 ，解得 1≤ x5 ． ⋯⋯⋯⋯⋯⋯⋯⋯ 12 分228∴不等式 f ( x)2 1的解集 { x | 2 x 5} ．⋯⋯⋯⋯⋯⋯⋯⋯ 13 分8 4821．分析：（ 1）当 m2 ，且 x0 ， f ( x)x 2 1 是 减的．⋯⋯⋯⋯⋯⋯⋯1 分x明： x 1x 2 0 ，f (x 1)f (x 2 )x 12 1 ( x 22 1)x 1x 2(x 2 x 1 ) (2 2x 1)x 2( x 2 x 1 )2( x 2 x 1)x 1x 2( x 22 ⋯⋯⋯⋯⋯⋯3 分x 1 )(1 ) x 1 x 2又 x 1 x 2 0 ，因此 x 2 x 1 0 ， x 1x 2 0 ，因此 ( x 2 x 1 )(1 2 0)x 1x 2 因此故当f ( x 1 ) f ( x 2 ) 0 ，即 f (x 1) f (x 2 ) ，m 2 ， f ( x) x2在 ( ,0) 上 减的． ⋯⋯⋯⋯⋯⋯⋯⋯ 4 分1 x（ 2）由 f (2 x ) 0 得 | 2x | m x1 0 ，形 (2 x )22x22x(2 x ) 2m 0 ，即 m而 2x(2 x )2(2 x 1)21 ，12 41当 2x即 x1 (2 x (2 x )2 )max ，2 14因此 m⋯⋯⋯⋯⋯⋯⋯⋯ 9 分．4（ 3）由 f (x)0 可得 x | x | xm 0( x 0) ， m x | x | x(x 0)令 g( x)x x | x |x 2 x, xx 2x, x 0作 y g (x) 的 像及直y m ，由 像可得：当 m1 1f ( x) 有 1 个零点．或 m，4 4当 m10 或 m1或 m， f (x) 有 2 个零点；41 14当 0mm0 ， f ( x) 有 3 个零点．⋯⋯⋯⋯⋯⋯⋯⋯ 14 分或44。

一、单选题湖北省荆州市北门中学2019-2020学年高一下学期期末数学试题1. 已知实数集，集合，集合，则（ ）A ．B ．C ．D ．2. 方程的解的个数是（ ）.A ．0个B ．1个C ．2个D ．3个3. 已知a =21.3，b =40.7，c =log 38，则a ，b ，c 的大小关系为（ ）A ．B ．C ．D ．4. 已知奇函数的定义域为，若为偶函数，且，则（ ）A ．B ．C ．D ．5. 若，则下列不等式：①；②；③；④中，正确的不等式是（）A．①④B．②③C．①②D．③④6. 已知函数f（x）=ln（–x2–2x+3），则f（x）的增区间为A．（–∞，–1）B．（–3，–1）C．[–1，+∞）D．[–1，1）7. 体积为的正方体的顶点都在同一球面上，则该球面的表面积为A．B．C．D．8. 函数的图象如图所示，为了得到的图象，则只要将的图象（）A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度9. 如图，已知，若点满足，则（）A．B．C．D．二、填空题三、解答题10.已知向量，满足，，，则与的夹角为（ ）A ．B ．C ．D ．11. 若，，则等于（ ）A ．B ．C ．D ．12. 若实数满足，则的最大值为（）A ．B ．C ．D ．13. 的内角的对边分别为，若，则 ________．14. 已知正四棱锥的底面边长是，侧棱长是，则该正四棱锥的体积为________.15.不等式的解集是________.16. 若关于的方程有实数解，则实数的取值范围是________17. 已知．（1）求的值；（2）求的值．18. 已知关于的不等式.（1）若不等式的解集是或，求的值；（2）若不等式的解集是，求的取值范围；（3）若不等式的解集为，求的取值范围．19. 已知函数，.（1）求的值域；（2）若不等式在上恒成立，求实数的取值范围.20. 已知a，b，c分别是内角A，B，C的对边，且满足．（1）求角A的大小；（2）若，，求的面积．21. 十九大指出中国的电动汽车革命早已展开，通过以新能源汽车替代汽/柴油车，中国正在大力实施一项将重塑全球汽车行业的计划．2018年某企业计划引进新能源汽车生产设备，通过市场分析，全年需投入固定成本2500万元，每生产x（百辆），需另投入成本万元，且．由市场调研知，每辆车售价5万元，且全年内生产的车辆当年能全部销售完．（1）求出2018年的利润L（x）（万元）关于年产量x（百辆）的函数关系式；（利润=销售额-成本）（2）2018年产量为多少百辆时，企业所获利润最大?并求出最大利润．22. 已知函数是定义域为的奇函数.（1）求实数的值；（2）若，不等式在上恒成立，求实数的取值范围；（3）若且在上的最小值为，求的值.。

2019-2020学年辽宁省沈阳二中高一下学期期末考试数学试题说明：1．测试时间：120分钟，总分：150分2．客观题涂在答题卡上，主观题答在答题纸上．第Ⅰ卷（选择题 共60分）一、选择题：（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1．复数2(2)(2)()1a a z a a i a R a ++++∈=-为纯虚数，则a 的值为（ ）A ．1a ≠B ．0a =C ．0a =或2a =-D ．2a =-2．如果α的终边过点(2sin,2cos )66ππ-，则sin α的值等于（ ）A ．12 B ．12-C ．2-D ．3-3．若向量()1,1a =，()2,5b =，()3,c x =，满足条件()824a b c -⋅=，则x 等于（ ）A ．6B ．2C ．4D ．34．关于直线m ﹑n 与平面α﹑β，有下列四个命题，其中真命题的序号是（ ）①//m α，//n β且//αβ，则//m n ； ②m a ⊥，n β⊥且αβ⊥，则m n ⊥； ③m a ⊥，//n β且//αβ，则m n ⊥； ④//m α，n β⊥且αβ⊥，则//m n ． A ．①②B ．③④C ．①④D ．②③5．在ABC 中，2()||BC BA AC AC +⋅=，则ABC 的形状一定是（ ）A ．等边三角形B ．等腰三角形C ．等腰直角三角形D ．直角三角形6．设函数6cos y x =与5tan y x =的图像在y 轴右侧的第一个交点为A ，过点A 作y 轴的平行线交函数sin 2y x =的图像于点B ，则线段AB 的长度为（ ）A ．5B ．352C ．1459D ．257．已知ABC 的三个内角为A ，B ，C ，向量sin (3,sin )A m B =，co s ()s co ,3B n A =．若1cos m n ⋅=+()A B +，则C =（ ）A ．6π B ．3π C ．23π D ．56π 8．《九章算术》问题十：今有方亭，下方五丈，上方四丈．高五丈．问积几何（今译：已知正四棱台体建筑物（方亭）如图，下底边长5a =丈，上底边长4b =丈．高5h =丈．问它的体积是多少立方丈？（ ）A ．75B ．3053C ．3203D ．40039．已知复数1z i =-（i 为虚数单位）是关于x 的方程20x px q ++=（p ，q 为实数）的一个根，则p q +的值为（ ） A ．4B ．2C ．0D ．2-10．已知ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ．ABC 的外接圆的面积为3π，且2cos A22cos cos 13sin sin B C A C -+=+，则ABC 的最大边长为（ ）A ．2B ．3C 3D ．2311．在四面体P-ABC 中，三角形ABC 为等边三角形，边长为3，3PA =，4PB =，5PC =，则四面体P-ABC 外接球表面积为（ ） A ．12πB ．25πC ．809πD ．32411π12．如图，已知OPQ 是半径为1，圆心角为75︒的扇形．点A ，B ，C 分别是半径OP ，OQ 及扇形弧上的三个动点（不同于O ，P ，Q 三点），则ABC 周长的最小值是（ ）A ．61+ B ．62+ C ．261+ D ．262+ 第Ⅱ卷（非选择题 共90分）二、填空题：（本大题共4小题，每小题5分，共20分）13．若z C ∈，且221z i --=，则22z i +-的最小值为_________． 14．如图．在ABC 中，AD AB ⊥，3BC BD =，||1AD =，则AC AD ⋅=_________．15．已知ABC 中，D 是BC 上的点，AD 平分BAC ∠，且2ABDADCSS=，1AD =，12DC =，则AC =_________．16．已知：平面l αβ⋂=，A l ∈，B l ∈，4AB =，C β∈，CA l ⊥，3AC =，D α∈，DB l ⊥， 3.DB =直线AC 与BD 的夹角是60︒，则线段CD 的长为_________．三、解答题：（本大题共6小题，满分70分，写出必要文字说明和演算步骤） 17．（本小题满分10分）已知函数()3sin()(0,||)2f x x πωϕωϕ=+>≤的图像关于直线3x π=对称，且图像上相邻两个最高点的距离为π．（1）求ω和ϕ的值； （2）若32()()263f αππα=<<，求sin()3a π+的值． 18．（本小题满分12分）如图．甲船以每小时302乙船按固定方向匀速直线航行．当甲船位于1A处时，乙船位于甲船的北偏西105︒方向的1B 处，此时两船相距20海里．当甲船航行20min 到达2A 处时，乙船航行到甲船的北偏西120︒方向的2B 处，此时两船相距102海里，问乙船每小时航行多少海里？19．（本小题满分12分）已知a ，b ，c 是同一平面内的三个向量，其中,1)(2a =． （1）若25c =，且//c a ，求c 的坐标；（2）若5||2b =，且()(2)a b a b +⊥-，求a 与b 的夹角θ． 20．（本小题满分12分）如图，四棱锥P-ABCD 中，AP ⊥平面PCD ，//AD BC ，12AB BC AD ==，E ，F 分别为线段AD ，PC 的中点．（1）求证：//AP 平面BEF ； （2）求证：BE ⊥平面P AC ． 21．（本小题满分12分）在ABC 中，内角A ，B ，C 的对边分别是a ，b ，c ，已知3cos sin b A C a =+． （I ）求A 的值：（Ⅱ）若3a =，点D 在边BC 上．且2BD DC =，求AD 的最大值． 22．（本小题满分12分）如图所示的圆锥，顶点为O ，底面半径是5cm ，用一与底面平行的平面截得一圆台，圆台的上底半径为2.5cm ，这个平面与母线OA 交于点B ，线段AB 的长为10cm ．（提示：本题的数据有长度单位） （1）求圆台的体积和圆台的侧面积；（2）把一根绳从线段AB 的中点M 开始到点A ，沿着侧面卷绕．使它成为最短时候，求这根绳的长度； （3）在（2）的条件下，这根绳上的点和圆台上底面上的点的距离中，最短的距离是多少？2019—2020学年度下学期期末考试高一试题数学参考答案及评分标准一、选择题： BCBDD CCBCCDB二、填空题： 13．3 14315．3216．543三、解答题：17．解析：（1）因为()f x 的图像上相邻两个最高点的距离为π，所以()f x 的最小正周期T π=， 从而22Tπω==． 又()f x 的图像关于直线3x π=对称，所以2,32k k Z ππϕπ+=+∈⨯．因为22ππϕ-≤<，所以0k =．所以2236πππϕ=-=-． （2）由（1）得3()3sin(2)226f ααπ=⋅-=， 所以1sin()64πα-=由263ππα<<，得062ππα<-<， 所以22115cos 1sin 16644ππαα⎛⎫⎛⎫⎛⎫-=--=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 15sin sin cos 36264ππππααα⎛⎫⎛⎫⎛⎫+=-+=-=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭． 18．【解析】解法一：如图，连接12A B ，由已知，22102A B =，122030210260A A == ∴1222A A AB =，12218012060A A B ∠=︒-︒=︒ 又12218012060A A B ∠=︒-︒=︒．∴122A A B 是等边三角形，1212102A B A A == 由已知，1120A B =．1211056045B A B ∠=︒-︒=︒在121A B B 中，由余弦定理，得：33212121111122cos45B B A B A B A B A B =+-⋅⋅︒，22220(102)2201022002=+-⨯⨯⨯=． ∴12102B B = 因此乙船的速度的大小为1026030220⨯=（海里/h ）． 答：乙船每小时航行302海里． 解法二：如图，连结2A B ．由已知1220A B =．122030210260A A ==112105B A A ∠=︒， ()cos105cos 4560cos45cos60sin45sin60︒︒︒︒︒︒︒=+=-2(13)-=()sin105sin 4560sin45cos60cos45sin60︒︒︒︒︒︒︒=+=+2(13)+=在211A A B 中，由余弦定理，得22221111211122cos105A B A B A A A B A A ︒=+-⋅⋅222(13)(102)202102204=+-⨯⨯100(43)=+．∴2110(1A B =. 由正弦定理，得1112111221sin sin A B A A B B A A A B ∠=⋅∠42+==． ∴12145A A B ∠=︒，即122604515B A B ︒︒︒∠=-=．cos15sin1054︒︒+==．在122B A B 中，由已知，22A B = 由余弦定理，得22212212221222cos15B B A B A B A B A B ︒=+-⋅⋅22210(1210(12004+=++-⨯+⨯=．∴12B B =6020⨯=海里/h ．答：乙船每小时航行19．解：（1）由于a ，b ，c 是同一平面内的三个向量，其中()2,1a =，若||25c =，且//c a ，可设()2,c a λλλ=⋅=．则由||2c ==，可得2λ=±，∴()4,2c =，或()4,2c =--．（2）∵5||b =，且2a b +与a b -垂直， ∴()()22220a b a b a a b b +-=+⋅-⋅=，化简可得52b a ⋅=-，即cos 5θ⨯=-， ∴cos 1θ=-，故a 与b 的夹角θπ=．20．证明：（1）设AC BE O ⋂=，连结OF ，EC ，由已知可得：//AE BC ，AE AB BC ==， 四边形ABCE 是菱形，O 为AC 中点， 因为F 为PC 中点，所以//OF AP ，//AP 平面BEF ，OF ⊂平面BEF所以AP ∥平面BEF ．（2）由题意知，//ED BC ，ED BC =，所以四边形BCDE 为平行四边形． 因此//BE CD ． 又AP ⊥平面PCD ．所以AP CD ⊥，因此AP BE ⊥． 因为四边形ABCE 为菱形． 所以BE AC ⊥．又AP AC A ⋂=，AP ，AC ⊂平面P AC ， 所以BE ⊥平面P AC ．21．（1）由已知及正弦定理得sin cos 3s s n n i i A C C A B =+． 又()sin sin sin cos cos sin B A C A C A C =+=+，且sin 0C ≠， ∴tan 3A =0A π<<，即3A π=．（2）解法一：设ABC 外接圆的圆心为O ，半径为R ，则由正弦定理得3322sin sin 3a A R π===⨯如图所示，取BC 的中点M ，在Rt BOM 中，322BC BM ==， 222233(3)()22OM OB BM =-=-=；在Rt DOM 中，12OM BD BM =-=， 222231()()122OD OM DM =+=-=． 31AD OD OD O R A +=+=≤，当且仅当圆心O 在AD 上时取等号， 所以AD 31+．解法二：在ABC 中，由正弦定理得：sin sin 3cos A B B A =，因为sin 0B ≠，所以tan 3A =又因为0A π<<，所以3A π=；由正弦定理得：in 23b B =，in 23c C =，在ABD 中，222224cos 24BA BD AD c AD B BA BD c +-+-==⨯在ABC 中，2222292c 6os BA B BC BC AC c b BA c +-+-==⨯所以222244946c D c b c c+-+-=，整理得22221233AD b c =+-， 所以22221(23)(23)233sin sin AD B C =+- 228sin 4sin 2B C =+-44cos22cos2B C =--144cos22cos(2)3B B π=-+- 43sin 23cos2B =+-423sin(2)3B π=+-， 当sin(2)13B π-=，即512B π=时，2AD 取得最大值423+． 所以AD 的最大值为31+．22．（1）作出圆锥的轴截面和侧面展开图，如下图由底面半径是5cm ，上底半径为2.5cm ，可得：10OB =所以，圆锥的高为：515387515c 8m V =，侧面积为：275cm S π=． （2）由圆锥的底面周长可得侧面展开图的弧长为10π，所以，侧面展开图的圆心角为2π，MA ，所以最短时候，绳长为25cm 在直角三角形MOA中可得25cm（3）由侧面展开图可知，距离最短时，就是O到直线AM的距离减OB长．解得：2cm．。

2019-2020学年高一第一学期期末数学试卷一、选择题1．设集合，N＝{x|3x≥1}，则M∩N＝（）A．B．[0，2] C．D．2．设a＝log30.6，b＝30.6，c＝0.63，则a，b，c的大小关系是（）A．a＞b＞c B．a＞c＞b C．b＞c＞a D．c＞b＞a3．函数f（x）＝lg（x2﹣1）的单调递减区间为（）A．（﹣∞，﹣1）B．（﹣∞，0）C．（0，+∞）D．（1，+∞）4．已知向量，，若，则实数m的值为（）A．19 B．3 C．﹣1 D．﹣175．设tan160°＝k，则sin160°＝（）A．B．C．D．6．已知，ln（1+cosα）＝s，，则ln sinα＝（）A．s﹣t B．s+t C．D．7．设函数f（x）＝a sin（πx+α）+b cos（πx+β），其中a，b，α，β都是非零常数，且满足，则f（2020）＝（）A．B．C．D．8．将函数的图象上所有点的横坐标缩短到原来的倍，纵坐标不变，得到y＝g（x）图象，则函数y＝g（x）（）A．关于点对称B．关于点对称C．关于直线对称D．关于直线对称9．设函数f（x）＝，则满足f（x）﹣f（﹣x）＞0的x的取值范围为（）A．B．C．D．10．设函数f（x）的定义域为R，满足f（x）＝2f（x+2），且当x∈[﹣2，0）时，f（x）＝﹣2x（x+2）．若对任意x∈[m，+∞），都有，则m的取值范围是（）A．B．C．D．（二）多项选择题：共2小题，每小题5分，共10分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得3分，有选错的得0分.11．已知定义在区间[﹣π，π]的函数f（x）＝cos x﹣x2，则下列条件中能使f（x1）＜f （x2）恒成立的有（）A．﹣π≤x1＜x2≤0 B．0≤x1＜x2≤πC．|x1|＞|x2| D．x12＜x2212．已知，若sin2θ＝m，cos2θ＝n且m≠n，则下列选项中与恒相等的有（）A．B．C．D．二、填空题：本题4小题，每小题5分，共20分.13．若函数为奇函数，则实数a的值为；14．已知向量，夹角为30°，且，，则＝；15．若在区间[﹣a，a]上是增函数，则正实数a的最大值为；16．已知△ABC中，AB＝AC＝3，D为边BC上一点，，，则的值为．三、解答题17．已知全集U＝R，集合A＝{x|x2﹣4x﹣5≤0}，B＝{x|2≤x≤4}．（1）求A∩（∁U B）；（2）若集合C＝{x|a≤x≤4a，a＞0}，满足C∪A＝A，C∩B＝B，求实数a的取值范围．18．已知函数，x∈R．（1）求函数y＝f（x）的单调递增区间；（2）求时，函数y＝f（x）的值域．19．已知向量，，．（1）求cos（α﹣β）的值；（2）若0＜α＜，﹣＜β＜0，且，求sinα．20．已知函数．（1）求函数y＝f（x）的定义域；（2）若方程f（x）＝1+log a x有两个不等实根，求实数a的取值范围．21．经检测，餐后4小时内，正常人身体内某微量元素在血液中的浓度y1与时间t满足关系式：y1＝4﹣t（0≤t≤4），服用药物N后，药物中所含该微量元素在血液中的浓度y2与时间t满足关系式：y2＝．现假定某患者餐后立刻服用药物N，且血液中微量元素总浓度y等于y1与y2的和．（1）求4小时内血液中微量元素总浓度y的最高值；（2）若餐后4小时内血液中微量元素总浓度y不低于4的累积时长不低于两小时，则认定该药物治疗有效，否则调整治疗方案．请你判断是否需要调整治疗方案．22．已知函数f（x）是定义在R上的奇函数，当x＜0时，．（1）求x＞0时，f（x）的解析式；（2）设x∈[1，2]时，函数g（x）＝2f（x）+m•2x﹣2m，是否存在实数m使得g（x）的最小值为5，若存在，求m的值；若不存在，说明理由．参考答案一、选择题1．设集合，N＝{x|3x≥1}，则M∩N＝（）A．B．[0，2] C．D．【分析】根据交集的定义即可求出．解：集合＝[，+∞}，N＝{x|3x≥1}＝[0，+∞），则M∩N＝[，+∞），故选：D．2．设a＝log30.6，b＝30.6，c＝0.63，则a，b，c的大小关系是（）A．a＞b＞c B．a＞c＞b C．b＞c＞a D．c＞b＞a【分析】利用指数函数对数函数的单调性即可得出．解：a＝log30.6＜0，b＝30.6＞1，c＝0.63∈（0，1），则a，b，c的大小关系是b＞c＞a．故选：C．3．函数f（x）＝lg（x2﹣1）的单调递减区间为（）A．（﹣∞，﹣1）B．（﹣∞，0）C．（0，+∞）D．（1，+∞）【分析】由对数函数的真数大于0求出函数的定义域，在求出内层函数二次函数的减区间得答案．解：由x2﹣1＞0，得x＜﹣1或x＞1，∴函数f（x）＝lg（x2﹣1）的定义域为（﹣∞，﹣1）∪（1，+∞），令t＝x2﹣1，该函数在（﹣∞，﹣1）上单调递减，而外层函数y＝lgt为定义域内的增函数，∴函数f（x）＝lg（x2﹣1）的单调递减区间为（﹣∞，﹣1）．故选：A．4．已知向量，，若，则实数m的值为（）A．19 B．3 C．﹣1 D．﹣17【分析】根据题意，由向量平行的坐标计算公式可得3（m﹣1）＝6，解可得m的值，即可得答案．解：根据题意，向量，，若，则3（m﹣1）＝6，解可得：m＝3，故选：B．5．设tan160°＝k，则sin160°＝（）A．B．C．D．【分析】利用同角三角函数基本关系式即可求解．解：设tan160°＝k＜0，sin160°＞0，可得cos2160°＝＝，可得sin160°＝＝||＝．故选：B．6．已知，ln（1+cosα）＝s，，则ln sinα＝（）A．s﹣t B．s+t C．D．【分析】推导出ln sinα＝ln sin2α＝ln（1﹣cos2α）＝ln[（1+cosα）（1﹣cos α）]，由此能求出结果．解：∵，ln（1+cosα）＝s，，∴ln sinα＝ln sin2α＝ln（1﹣cos2α）＝ln[（1+cosα）（1﹣cosα）]＝（s ﹣t）．故选：C．7．设函数f（x）＝a sin（πx+α）+b cos（πx+β），其中a，b，α，β都是非零常数，且满足，则f（2020）＝（）A．B．C．D．【分析】根据三角函数的诱导公式进行化简即可．解：∵f（2019）＝﹣，∴f（2019）＝a sin（2019π+α）+b cos（2019π+β）＝a sin（π+α）+b cos（π+β）＝﹣a sinα﹣b cosβ＝﹣，即a sinα+b cosβ＝，则f（2020）＝a sin（2020π+α）+b cos（2020π+β）＝a sinα+b cosβ＝，故选：C．8．将函数的图象上所有点的横坐标缩短到原来的倍，纵坐标不变，得到y＝g（x）图象，则函数y＝g（x）（）A．关于点对称B．关于点对称C．关于直线对称D．关于直线对称【分析】根据函数y＝A sin（ωx+φ）的图象变换可求函数g（x）的解析式，进而利用三角函数图象之间的关系进行判断即可．解：将函数y＝sin（x+）图象上所有点的横坐标缩短到原来的倍（纵坐标不变），得到y＝g（x）＝sin（2x+），对于A，由于g（﹣）＝sin（﹣+）＝sin（﹣）＝﹣1，即函数关于（﹣，0）不对称，故错误；对于B，由于g（﹣）＝sin（﹣﹣）＝sin（﹣）＝﹣1，即函数关于（﹣，0）不对称，故错误；对于C，由于g（）＝sin（2×+）＝sin（）＝1，即关于直线对称，故正确；对于D，由于g（）＝sin（2×+）＝sin＝≠1，即不关于直线x＝对称，故错误；故选：C．9．设函数f（x）＝，则满足f（x）﹣f（﹣x）＞0的x的取值范围为（）A．B．C．D．【分析】根据题意，结合函数的解析式按x的范围分3种情况讨论，求出不等式的解集，综合即可得答案．解：根据题意，函数f（x）＝，分3种情况讨论：①，当x＝0时，f（x）﹣f（﹣x）＞0即f（0）﹣f（0）＞0，不成立；②，当x＜0时，﹣x＞0，f（x）﹣f（﹣x）＞0即（x+1）＞4x，解可得：﹣＜x＜0，③，当x＞0时，﹣x＜0，f（x）﹣f（﹣x）＞0即4﹣x＞（﹣x+1），解可得：x＞，综合可得：x的取值范围为（﹣，0）∪（，+∞）；故选：D．10．设函数f（x）的定义域为R，满足f（x）＝2f（x+2），且当x∈[﹣2，0）时，f（x）＝﹣2x（x+2）．若对任意x∈[m，+∞），都有，则m的取值范围是（）A．B．C．D．【分析】由f（x）＝2f（x+2），判断函数值的变化情况，作出函数f（x）的的图象，再确定m所在的区间，求出临界点即可求出结果．解：当x∈[﹣2，0）时，函数f（x）在（﹣2，﹣1）上递增，在（﹣1，0）上递减，所以f（x）max＝f（﹣1）＝2，由f（x﹣2）＝f（x），可得当图象向右平移2个单位时，最大值变为原来的倍，最大值不断变小，由f（x）＝2f（x+2），可得当图象向左平移2个单位时，最大值变为原来的2倍，最大值不断变大，当x∈[0，2）时，f（x）max＝f（1）＝1，当x∈[2，4）时，f（x）max＝f（3）＝，设x∈[0，2），x﹣2∈[﹣2，0），f（x﹣2）＝﹣2x（x﹣2）＝2f（x），即f（x）＝﹣x（x﹣2），由﹣x（x﹣2）＝，解得x＝或x＝，根据题意，当m≥时，f（x）≤恒成立，故选：D．（二）多项选择题：共2小题，每小题5分，共10分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得3分，有选错的得0分.11．已知定义在区间[﹣π，π]的函数f（x）＝cos x﹣x2，则下列条件中能使f（x1）＜f （x2）恒成立的有（）A．﹣π≤x1＜x2≤0 B．0≤x1＜x2≤πC．|x1|＞|x2| D．x12＜x22【分析】由奇偶性的定义和基本函数的单调性，判断f（x）为偶函数，在[0，π]递减，即可得到所求结论．解：定义在区间[﹣π，π]的函数f（x）＝cos x﹣x2，可得f（﹣x）＝cos（﹣x）﹣（﹣x）2＝cos x﹣x2＝f（x），即有f（x）为偶函数，当x∈[0，π]，y＝cos x递减，y＝﹣x2递减，则y＝f（x）为减函数，当x∈[﹣π，0]，y＝f（x）为增函数，可得﹣π≤x1＜x2≤0⇒f（x1）＜f（x2）；0≤x1＜x2≤π⇒f（x1）＞f（x2）；f（x1）＜f（x2）⇔|x2|＜|x1|≤π，故选：AC．12．已知，若sin2θ＝m，cos2θ＝n且m≠n，则下列选项中与恒相等的有（）A．B．C．D．【分析】结合两角差的正切公式及同角基本关系对所求式子进行化简，然后结合选项即可判断．解：由＝＝＝＝＝．由＝＝＝＝＝．故选：AD．二、填空题：本题4小题，每小题5分，共20分.13．若函数为奇函数，则实数a的值为 1 ；【分析】根据f（x）是奇函数即可得出f（﹣x）＝﹣f（x），进而即可得出，从而可得出a的值．解：∵f（x）为奇函数，∴f（﹣x）＝﹣f（x），即＝，∴a＝1．故答案为：1．14．已知向量，夹角为30°，且，，则＝；【分析】直接根据|﹣3|2再代入已知条件即可求解．解：因为向量，夹角为30°，且，则|﹣3|2＝﹣6•+9＝22﹣6×2×||cos30°+9||2＝13⇒||2﹣2||﹣＝0⇒||＝（负值舍）；故答案为：15．若在区间[﹣a，a]上是增函数，则正实数a的最大值为；【分析】求出函数f（x）的单调递增区间，再根据f（x）在区间[﹣，]上是单调增函数求得正实数a的最大值．解：中，令﹣+2kπ≤x﹣≤+2kπ，k∈Z；解得﹣+2kπ≤x≤+2kπ，k∈Z；令k＝0，得﹣≤x≤，所以f（x）在区间[﹣，]上是单调增函数；若f（x）在区间[﹣a，a]上是增函数，令﹣a＝﹣，得a＝，所以正实数a的最大值为．故答案为：．16．已知△ABC中，AB＝AC＝3，D为边BC上一点，，，则的值为．【分析】建立坐标系，设出各点坐标，结合已知条件即可求出结论解：建立如图坐标系；设A（0，b），B（﹣a，0）C（a，0）D（x，0）∴a2+b2＝9；①＝（﹣a，﹣b），＝（x，﹣b），＝（a，﹣b）；∴•＝﹣ax+b2＝6 ②•＝ax+b2＝③；联立②③得b2＝；代入①得a2＝；∴＝b2﹣a2＝＝；故答案为：三、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. 17．已知全集U＝R，集合A＝{x|x2﹣4x﹣5≤0}，B＝{x|2≤x≤4}．（1）求A∩（∁U B）；（2）若集合C＝{x|a≤x≤4a，a＞0}，满足C∪A＝A，C∩B＝B，求实数a的取值范围．【分析】（1）求出A＝{x|﹣1≤x≤5}，∁U B＝{x|x＜2或x＞4}，由此能求出A∩（∁U B）．（2）由C∪A＝A得C⊆A，由C∩B＝B得B⊆C，由此能求出实数a的取值范围．解：（1）由题A＝{x|﹣1≤x≤5}，∁U B＝{x|x＜2或x＞4}，∴A∩（∁U B）＝{x|﹣1≤x＜2或4＜x≤5}．（2）由C∪A＝A得C⊆A，解得，由C∩B＝B得B⊆C，解得1≤a≤2．从而实数a的取值范围为．18．已知函数，x∈R．（1）求函数y＝f（x）的单调递增区间；（2）求时，函数y＝f（x）的值域．【分析】（1）先利用二倍角公式及辅助角公式对已知函数化简，然后结合正弦函数的单调性即可求解；（2）结合正弦函数的最值性质可求、解：＝．（1）令，得，所以函数y＝f（x）的单调递增区间为．（2）得，所以﹣sin（2x+）≤1，则f（x）从而函数y＝f（x）的值域为．19．已知向量，，．（1）求cos（α﹣β）的值；（2）若0＜α＜，﹣＜β＜0，且，求sinα．【分析】（1）根据平面向量的减法法则，表示出﹣，进而表示出，代入已知的，两边平方后利用同角三角函数间的基本关系化简，得到关于cos（α﹣β）的方程，求出方程的解即可得到cos（α+β）的值；（2）根据小于0，得到β的范围，再由α的范围，求出α﹣β的范围，然后由（1）求出的cos（α﹣β）的值及sinβ的值，分别利用同角三角函数间的基本关系求出sin（α﹣β）的值和cosβ的值，把所求式子中的α变为（α+β）﹣β，利用两角差的正弦函数公式化简，将各自的值代入即可求出值．解：（1）∵，，∴．∵，∴，即，∴．（2）∵，∴，∵，∴．∵，∴，∴sinα＝sin[（α﹣β）+β]＝sin（α﹣β）cosβ+cos（α﹣β）sinβ＝20．已知函数．（1）求函数y＝f（x）的定义域；（2）若方程f（x）＝1+log a x有两个不等实根，求实数a的取值范围．【分析】（1）根据对数函数定义域列出＞0，解出即可；（2）方程等价于a＝，其中x∈（1，+∞），令g（x）＝，求出g（x）值域再结合a＞0即可解：（1）根据题意得＞0，解得x＜﹣1或x＞1，则函数的定义域为（﹣∞，﹣1）∪（1，+∞）；（2）方程f（x）＝1+log a x即﹣log a x＝1，整理得＝1，所以a＝，其中x∈（1，+∞），令g（x）＝＝＝，x∈（1，+∞），则g（x）≤，当仅当（x﹣1）2＝2，即x＝+1时取等号，所以a≤＝3﹣2，又因为a＞0，所以a的取值范围是（0，3﹣2）21．经检测，餐后4小时内，正常人身体内某微量元素在血液中的浓度y1与时间t满足关系式：y1＝4﹣t（0≤t≤4），服用药物N后，药物中所含该微量元素在血液中的浓度y2与时间t满足关系式：y2＝．现假定某患者餐后立刻服用药物N，且血液中微量元素总浓度y等于y1与y2的和．（1）求4小时内血液中微量元素总浓度y的最高值；（2）若餐后4小时内血液中微量元素总浓度y不低于4的累积时长不低于两小时，则认定该药物治疗有效，否则调整治疗方案．请你判断是否需要调整治疗方案．【分析】（1）由题意分类写出微量元素在血液内的总浓度y与时间t的关系，再由配方法及基本不等式求最值；（2）分类求解不等式可得t的范围，与2比较大小得结论．解：（1）由题微量元素在血液内的总浓度y与时间t的关系为：当0≤t＜1时，，当时取最大值；当1≤t≤4时，，当时取得最大值．∵，故微元素总浓度最大值为；（2）当0≤t＜1时，，解得0≤t＜1；当1≤t≤4时，，解得1≤t≤2．可知注射药物N后两小时内血液中微量元素总浓度不低于4，则不需要调整治疗方案．22．已知函数f（x）是定义在R上的奇函数，当x＜0时，．（1）求x＞0时，f（x）的解析式；（2）设x∈[1，2]时，函数g（x）＝2f（x）+m•2x﹣2m，是否存在实数m使得g（x）的最小值为5，若存在，求m的值；若不存在，说明理由．【分析】（1）x＞0，则﹣x＜0，，再利用奇函数的性质，即f（x）＝﹣f（﹣x）可得解；（2）通过换元，问题转化为二次函数h（t）在[2，4]上的最小值为5，再通过分类讨论得出结论．解：（1）设x＞0，则﹣x＜0，由当x＜0时，可知，，又f（x）为R上的奇函数，于是，故当x＞0时，；（2）由（1）可知，当x∈[1，2]时，g（x）＝（2x）2+（m+1）2x﹣2m，令t＝2x∈[2，4]，h（t）＝t2+（m+1）t﹣2m，函数g（x）在[1，2]上的最小值为5，即为函数h（t）在[2，4]上的最小值，①当，即m＞﹣5时，函数h（t）在[2，4]上为增函数，于是h（t）min＝h（2）＝6≠5，此时不存在满足条件的实数m；②当，即﹣9≤m≤﹣5时，，解得m＝﹣3或m ＝﹣7，此时m＝﹣7满足题设条件；③当，即m＜﹣9时，函数h（t）在[2，4]上为减函数，于是h（t）min＝h（4）＝2m+20＝5，解得，此时不存在满足条件的实数m；综上，存在m＝﹣7使得函数g（x）的最小值为5．。

2019-2020学年河北省部分重点中学高一（上）期末物理试卷一、选择题：本大题共12小题，每小题4分，共48分．第1～8小题只有一项符合题目要求，第9～12小题有多项符合题目要求．全部选对得4分，少选得2分，有选错的得0分．1．（4分）港珠澳大桥是连接香港、珠海和澳门的巨大桥梁，为香港、澳门和珠江三角洲的经济发展注入了新的动力。

已知港珠澳大桥总长49.968公里，设计速度为100公里/小时。

某辆汽车通过港珠澳大桥的记录显示：12：00进入港珠澳大桥，12：43离开大桥。

下列说法正确的是（）A．题中的“100公里/小时”为瞬时速度B．研究该汽车通过大桥的运动情况时，不可以将汽车看成质点C．该汽车通过港珠澳大桥的位移为49.968kmD．该汽车通过港珠澳大桥的平均速度为69.7km/h2．（4分）下列关于重力和重心的说法正确的是（）A．同一物体在地球上任何地方的重力都相等B．物体静止时，向下的压力就是物体受到的重力C．物体的重心一定在物体上D．用细线将物体悬挂起来，静止时物体的重心一定在悬线所在的直线上3．（4分）斜向上抛出一小球，则小球在空中的受力情况可能正确的是（不计空气阻力）（）A．B．C．D．4．（4分）关于匀变速直线运动，下列说法正确的是（）A．匀减速直线运动中，加速度一定减小B．匀减速直线运动中，加速度的方向有可能和速度方向相同C．匀加速直线运动中，加速度的方向一定和速度方向相同D．匀加速直线运动中，加速度一定增大5．（4分）如图所示，一质量为m的木块靠在竖直粗糙墙壁上，受到水平力F的作用，保持静止，下列说法正确的是（重力加速度为g）（）A．木块受到的摩擦力大于mg，方向竖直向上B．若F增大，木块受到的摩擦力保持不变C．若F增大，木块受到的摩擦力增大D．若F减小，木块一定向下滑动6．（4分）如图所示，物体A、B叠放在斜面上，处于静止状态。

物体B的上表面水平。

下列说法正确的是（）A．物体A受到摩擦力的作用B．物体B受到摩擦力的作用C．斜面对物体B的作用力和物体B受到的重力大小相等D．若物体A、B沿斜面匀速下滑，则物体A受到摩擦力的作用7．（4分）如图所示，小球在竖直向上的拉力作用下从静止开始运动，其v﹣t图象如图所示（竖直向上为正方向，DE段为直线），不计空气阻力，下列说法正确的是（）A．t0～t2时间内，小球先做加速直线运动后做减速直线运动B．t0～t2时间内小球的平均速度一定为C．t3～t4时间内，小球竖直向下做匀减速直线运动D．t3～t4时间内，小球上升的高度为（t4﹣t3）8．（4分）如图所示，AB为半圆的一条直径，O为圆心，P点为圆周上的一点，在P点施加了三个共点力F1、F2、F3，已知F1＝3N，F3＝4N，F2指向O，则这三个力的合力为（）A．0B．1N C．7 N D．7.5N9．（4分）甲、乙两车在平直公路上同向行驶，其v﹣t图象如图所示。

唐山一中2019级高一年级“空中课堂”第一次阶段性测试数学试卷说明：1.考试时间90分钟，满分100分.2.将卷一答案用2B 铅笔涂在答题卡上，卷二用0.5毫米黑色签字笔答在答题卡上. 一、选择题（每题4分，共80分）1. 已知向量a ，b 不共线，且c a b λ=+，()21d a b λ=+-，若c 与d 反向共线，则实数λ的值为（ ） A. 1 B. 12-C. 1或12-D. －1或12-【答案】B 【解析】 【分析】由于c 与d 反向共线，则存在实数k 使()0c kd k =<，即可得到()21a b ka kb λλ+=+-，再根据a ，b 不共线，即可得到方程组，解得即可；【详解】解：由于c 与d 反向共线，则存在实数k 使()0c kd k =<，于是()21a b k a b λλ⎡⎤+=+-⎣⎦．整理得()21a b ka kb λλ+=+-.由于a ，b 不共线，所以有21k k k λλ=⎧⎨-=⎩整理得2210λλ--=，解得1λ=或12λ=-，又k 0<，所以0λ<，故12λ=- 故选：B【点睛】本题考查平面向量的线性运算及平面向量共线基本定理的应用，属于基础题. 2. 在等腰梯形ABCD 中，2AB CD =-.M 为BC 的中点，则AM =（ ） A.1122AB AD + B.3142AB AD + C.3144AB AD + D.1324AB AD + 【答案】B【解析】【详解】取AD 中点N ，连接MN ，∵2AB CD =-，∴//AB CD ，2AB CD =， 又M 是BC 中点，∴//MN AB ，且1()2MN AB CD =+34AB =， ∴1324AM AN NM AD AB =+=+， 故选：B ．【点睛】本题考查平面向量的线性运算，解题可结合平面几何的知识得出直线、线段间关系，从而可得向量的运算表示．3. 平面向量()1,2a =，()4,2b =，c ma b =+（m R ∈），且c 与a 的夹角与c 与b 的夹角互补，则m =（ ） A. 2- B. 1-C. 1D. 2【答案】A 【解析】 【分析】由c 与a 的夹角与c 与b 的夹角的余弦值相加为0求解． 【详解】由已知(4,22)c m m =++，cos ,55c a c a c a cc ⋅<>===，cos ,205c b c b c bcc⋅<>===，∵c 与a 的夹角与c 与b 的夹角互补，5c05c=，解得2m =-．故选：A ．【点睛】本题考查平面向量的夹角，考查平面向量的数量积定义，属于基础题． 4. 在ABC ∆中，,2,1,,AB AC AB AC AB AC E F +=-==为BC 的三等分点，则·AE AF =( )A.89B.109C.259D.269【答案】B 【解析】试题分析：因为AB AC AB AC +=-，所以AB AC ⊥，以点A 为坐标原点，,AB AC 分别为,x y 轴建立直角坐标系，设()()2,00,1AB AC ==，，又E F ，为BC 的三等分点所以，4122,,,3333AE AF ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，所以412210,,33339AE AF ⎛⎫⎛⎫⋅=⋅= ⎪ ⎪⎝⎭⎝⎭，故选B.考点：平面向量的数量积.【一题多解】若AB AC AB AC +=-，则222222AB AC AB AC AB AC AB AC ++⋅=+-⋅，即有0AB AC ⋅=，,E F 为BC 边的三等分点，则()()1133AE AF AC CE AB BF AC CB AB BC ⎛⎫⎛⎫⋅=+⋅+=+⋅+ ⎪ ⎪⎝⎭⎝⎭21123333AC AB AC AB ⎛⎫⎛⎫=+⋅+ ⎪ ⎪⎝⎭⎝⎭22225210(14)099999AC AB AB AC =++⋅=++=,故选B ． 5. 已知等差数列{}n a 的前n 项和为n S ，6350=-≠S S ，则93=S S （ ） A. 18 B. 13C. -13D. -18【答案】D【解析】 【分析】通过等差数列的性质，可得S 3，S 6-S 3，S 9-S 6为等差数列，设635,=-=S a S a ，即可得出结果.【详解】由635S S =-，可设635,=-=S a S a ∵{}n a 为等差数列，∴S 3，S 6-S 3，S 9-S 6为等差数列，即a ，-6a ，96-S S 成等差数列，∴96=13--S S a ，即9=18-S a∴9318=-S S 故选:D.【点睛】本题考查了等差数列的性质，考查了运算求解能力，属于基础题目. 6. 在ABC 中，4B π=，BC 边上的高等于13BC ,则cos A =（ ） A.310B.10 C. 10-D. 31010-【答案】C 【解析】 试题分析：设22,2,5sin cos ,sin ,cos cos 255AD a AB a CD a AC a A ααββ=⇒===⇒====⇒ 10cos()αβ=+=-,故选C.考点：解三角形.7. 在ABC ∆中，角A 、B 、C 所对的边分别为a 、b 、c ，且222b c a bc +=+若2sin sin sin B C A ⋅=，则ABC ∆的形状是（） A. 等腰三角形 B. 直角三角形C. 等边三角形D. 等腰直角三角形 【答案】C 【解析】 【分析】直接利用余弦定理的应用求出A 的值，进一步利用正弦定理得到：b ＝c ，最后判断出三角形的形状．【详解】在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ， 且b 2+c 2＝a 2+bc ．则：2221222b c a bc cosA bc bc +-===，由于：0＜A ＜π， 故：A 3π=．由于：sin B sin C ＝sin 2A ， 利用正弦定理得：bc ＝a 2， 所以：b 2+c 2﹣2bc ＝0， 故：b ＝c ，所以：△ABC 为等边三角形． 故选C ．【点睛】本题考查了正弦定理和余弦定理及三角形面积公式的应用，主要考查学生的运算能力和转化能力，属于基础题型．8. 己知数列{}n a 对于任意p ，*q N ∈有p q p q a a a ++=，若119a =，则36a =（ ） A.136B.19C. 1D. 4【答案】D 【解析】【分析】根据已知关系式求出数列的通项公式后可得结论．【详解】∵对于任意p ，*q N ∈有p q p q a a a ++=，令,1p n q ==，则11n n a a a ++=，∴1119n n a a a +-==， ∴{}n a 是等差数列，公差为19，首项是19，∴11(1)999n n a n =+⨯-=， ∴363649a ==． 故选：D ．【点睛】本题考查等差数列的通项公式，解题关键是在已知条件中对的正整数,p q 赋值，证得数列是等差数列． 9.ABC 中，a ，b ，c 分别为A ∠，B ，C ∠的对边，如果a ，b ，c 成等差数列，30B ∠=︒，ABC 的面积为32，那么b 等于（ ）A.132B. 13C.223+ D. 23【答案】B 【解析】 【分析】由题意可得2b a c =+，平方后整理得22242a c b ac +=-，利用三角形面积可求得ac 的值，代入余弦定理可求得b 的值.【详解】解：∵a ，b ，c 成等差数列， ∴2b a c =+，平方得22242a c b ac +=-，① 又ABC 的面积为32，且30B ∠=︒， 由11sin sin 3022ABCS ac B ac ==⋅︒△1342ac ==，解得6ac =， 代入①式可得222412a c b +=-，由余弦定理得222cos 2a c b B ac +-=，222412312326122b b b ---===⨯， 解得2423b =+ ∴13b =故选：B .【点睛】本题考查等差数列的性质和三角形的面积公式，涉及余弦定理的应用，属于中档题. 10. 己知数列{}n a 满足()1220n n n a a a n N *++-+=∈，且前n 项和为nS，若11927a a =+，则25S =（ ） A.1452B. 145C. 1752D. 175【答案】D 【解析】 【分析】利用等差中项法可判断出数列{}n a 是等差数列，由已知条件计算得出13a 的值，再利用等差数列求和公式以及等差中项的性质可求得25S 的值.【详解】对任意的n *∈N ，1220n n n a a a ++-+=，即122n n n a a a ++=+，所以数列{}n a 为等差数列，91191372a a a a +==+，137a ∴=，由等差数列的求和公式可得()125251325252571752a a S a +===⨯=.故选：D.【点睛】本题考查等差数列求和，同时也考查了等差数列的判断以及等差数列性质的应用，考查计算能力，属于中等题.11. 已知ABC ∆中，满足02,60b B == 的三角形有两解，则边长a 的取值范围是（ ）A32a << B.122a << C. 432a << D. 23a <<【答案】C 【解析】解：由三角形有两解，则满足sin a B b a b <⎧⎨>⎩，即 sin 6022o a a ⎧<⎨>⎩，解得：2＜a ＜ 43，所以边长a 的取值范围（2 43故选C ．12. 已知数列{}n a 中，12213,6,n n n a a a a a ++===-,则2016a =（ ） A. 6 B. 6- C. 3 D. 3-【答案】B 【解析】 【分析】由数列的递推关系21n n n a a a ++=-，可得数列的周期性，再求解即可. 【详解】解:因为21n n n a a a ++=-,①则321n n n a a a +++=-,② ①+②有: 3n n a a +=-,即63n n a a ++=-,则6n n a a +=, 即数列{}n a 的周期为6,又123,6a a ==,得3453,3,6a a a ==-=-，63a =-, 则2016a =633663a a ⨯==-, 故选:D.【点睛】本题考查了数列的递推关系，重点考查了数列周期性的应用，属基础题.13. 数列{a n }通项公式为()2*n a 2n λn n N λR =-+∈∈，，若{a n }是递减数列，则λ的取值范围是（ ）A. (),4∞-B. (],4∞-C. (),6∞-D. (],6∞- 【答案】C 【解析】 【分析】数列{a n }是递减数列，可得a n ＞a n+1，化简解出即可得出． 【详解】∵数列{a n }是递减数列， ∴a n ＞a n+1，∴﹣2n 2+λn ＞﹣2（n+1）2+λ（n+1）， 解得λ＜4n+2， ∵数列{4n+2}单调递增， ∴n ＝1时取得最小值6， ∴λ＜6． 故选C ．【点睛】本题考查了数列的通项公式、单调性，考查了推理能力与计算能力，属于中档题． 14. 已知两个等差数列{}n a 和{}n b 的前n 项和分别为n S 和n T ，且对一切正整数n 都有5327n n S n T n +=+，则99a b 的值为（ ）A.52B.8841C.2817D.4825【答案】B 【解析】 【分析】根据等差数列的性质求解． 【详解】因为{}n a 和{}n b 等差数列，所以12121(21)()(21)2n n n n a a S n a ---+==-，21(21)n n T n b -=-，2121n n nnS b T a --=， 所以917917517388217741a Sb T ⨯+===⨯+．故选：B ．【点睛】本题考查等差数列的前n 项和，考查等差数列的性质，利用等差数列的性质求解是等差数列问题中的重要方法．15. 在等差数列{}n a 中，53a =，1018a =，求12310a a a a ++++=（ ）A. 80B. 81C. 82D. 83【答案】B 【解析】 【分析】利用等差数列的通项公式与求和公式可得：n a ，数列{}n a 的前n 项和n S ，令0n a ，解得4n ，可得：123104102a a a a S S +++⋯+=-+，代入求和公式计算即可． 【详解】设等差数列{}n a 的公差为d ，53a =，1018a =，∴1143918a d a d +=⎧⎨+=⎩，解得19a =-，3d =，93(1)312n a n n ∴=-+-=-，∴数列{}n a 的前n 项和为：2(9312)321222n n n S n n -+-==-，令0n a ，解得4n ，2212310123451041032132122(44)1010812222a a a a a a a a a a S S ∴+++⋯+=----++⋯+=-+=-⨯⨯-⨯+⨯-⨯=故选：B【点睛】本题考查了等差数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．16. 在斜ABC ∆中，设角,,A B C 的对边分别为,,a b c ，已知sin sin sin 4sin cos a A b B c C b B C +-=，CD 是角C 的内角平分线，且CD b =，则cos C （ ） A.18B.34C.23D.16【答案】A 【解析】 【分析】利用正弦定理角化边可构造方程2cos cos bC C a =，由cos 0C ≠可得2a b =；利用ABCACD BCD S S S ∆∆∆=+可构造方程求得3cos 24C =，利用二倍角公式求得结果.【详解】由正弦定理得：22224cos a b c b C +-=则22224cos 2cos cos 22a b c b C bC C ab ab a+-===ABC ∆为斜三角形 cos 0C ∴≠ 2a b ∴=ABC ACD BCD S S S ∆∆∆=+ 1112sin sin 2sin 22222C Cb b C b b b b ∴⋅=⋅+⋅即：2sin 4sin cos 3sin 222C C CC ==()0,C π∈ 0,22C π⎛⎫∴∈ ⎪⎝⎭ sin 02C ∴≠ 3cos 24C ∴= 291cos 2cos 1212168C C ∴=-=⨯-= 本题正确选项：A【点睛】本题考查解三角形的相关知识，涉及到正弦定理化简边角关系式、余弦定理和三角形面积公式的应用、二倍角公式求三角函数值等知识；关键是能够通过面积桥的方式构造方程解出半角的三角函数值.17. 在ABC 中，角,,A B C 的对边分別为,,a b c ，若1b =，()2sin 3cos 3ccos a B C A =，点G 是ABC 的重心，且133AG =，则ABC 的面积为（ ） A.3B.3 C.323 D.33或3【答案】D 【解析】 【分析】利用正弦定理化简已知条件，求得sin A 的值，由此求得π3A =或2π3A =，利用()2214AD AB AC =+和余弦定理列方程，求得面积的两种取值.【详解】由题可知2sin sin 3sin cos 3sin cos A B A C C A -=，2sin sin 3sin A B B =，则3sin A =3A π=或23π.又13AG =，延长AG 交BC 于点D ，所以13AD =因为()12AD AB AC =+，所以()2214AD AB AC =+，即()2221||2cos 4AD b c bc A =++，当3A π=时，3c =，所以ABC ∆的面积为133sin 24bc A =；当23A π=时，4c =，所以ABC ∆的面积为1sin 32bc A =.故选D. 【点睛】本小题主要考查利用正弦定理解三角形，考查向量运算，考查三角形的面积公式，属于中档题.18. 在ABC 中，2AB =，6C π=，则3AC BC 的最大值为（ ）A.7 B. 7 C. 37 D. 7【答案】D 【解析】 【分析】首先根据已知条件得到4sin =BC A ，4sin =AC B ，从而得到()347ϕ=+AC BC A ，再利用三角函数的性质即可得到最大值。