第五章.竖向荷载作用下的框架内力计算
- 格式：doc
- 大小：1.35 MB
- 文档页数：12
下载文档原格式
合集下载
框架在竖向荷载作用下内力计算
Mik MiFk 2Mi'k Mk' i
…3.6.4
或
Mik MiFk Mi'k (Mi'k Mk' i ) …3.6.5
➢ 根据算得的各杆端弯矩值，作最后的弯矩图并求得 相应的剪力图和轴力图。
例题：
0.463
A2
结点B2与结点A2分配系数相同
(2)计算固端弯矩:
mA2B2
1 12
q2l 2
1 12
10
82
53.333kN
gm
mB2 A2
1 12
q2l 2
1 12
10 82
53.333kN gm
(3)循环过程B2
A2
4、还原-叠加、结点不平衡弯矩再分配一次
6、计算框架梁其他截面的弯矩 计算框架梁截面的剪力 计算框架柱的轴力
结点A1：
S A1A2 4(0.9ic2 ) S A1A0 4ic1
S A1B1 4ib
S 4(ic1 0.9ic2 ib ) 4 2.478
A1
A1A2
S A1A2 S
4 0.9 1 0.363 4 2.478
A1
A1A0
S A1A0 S
4 0.801 4 2.478
1 0.0133E 12
ic 2
EIc H2
1 1 0.0666E 4 12
1 0.0166E 12
ib
EIb L
1 1 0.1029E 8Βιβλιοθήκη 121 0.0129E 12
相对线刚度: 设：ic2 1
则 ic1 0.801
ib 0.777
2、把框架以按层拆为两个开口框架
H2=4000
第五章.竖向荷载作用下的框架内力计算
第五章.竖向荷载作⽤下的框架内⼒计算5.1 计算单元的确定取6号轴线⼀榀框架进⾏计算，计算宽度为(6.6+6.6)/2=6.6m 。
如图下图所⽰横向框架荷载传递图5.2 荷载计算5.2.1 恒荷载的计算 1、五层、（1）q 、q 0、q 0′、q 0″分别为⼥⼉墙、边跨横梁(⾛道纵梁)、⾛道横梁、次梁⾃重（扣除板⾃重），为均布荷载形式；β为考虑梁粉刷⾃重时的放⼤系数，取β=1.05。
⼥⼉墙：q=3.47×0.9=3.12 kN/m 边跨横梁（⾛道纵梁）：q 0=1.05×0.3×(0.6-0.1)×25=3.94kN/m ⾛道横梁：q 0′=1.05×0.3×(0.4-0.1)×25=2.36kN/m 次梁：q 0″=1.05×0.2×(0.5-0.1)×25=2.1kN/m（2）q 1、q 1′分别为屋⾯板⾃重传给横梁的梯形和三⾓形荷载等效为均布荷载值 q 1=[1-2×(3.3/6.6×2) 2+(3.3/6.6×2)3]×4.38×3.3/2=6.44kN/mq 1′=85×4.38×3.0/2=4.11kN/m（3）q 2、q 2′分别为屋⾯板⾃重传给纵梁上的梯形和三⾓形荷载等效为均布荷载值梯形：q 2=[1-2×(3.0/6.6×2) 2+(3.0/6.6×2)3]×4.38×3.0/2=5.96kN/m三⾓形：q 2′=85×4.38×3.3/2=4.52kN/mP 1为由板传给次梁及次梁⾃重传给纵梁的集中⼒ P 1= q 1×6.6+ q 0″×6.6/2=49.43kNP 2为由板传给外纵梁及外纵梁、⼥⼉墙⾃重传给柱⼦的集中⼒ P 2=（ q 2′+ q 0+q ）×3.3×2=76.42 kNP 3为由板传给内纵梁及内纵梁⾃重传给柱⼦的集中⼒。
框架施工图—内力分析及侧移计算(建筑构造)
（2） 侧移刚度d的确定 侧移刚度d表示柱上下两端有单位侧移时在柱中产生的 剪力。根据假定（1），梁柱线刚度之比无穷大，则各 柱端转角为零，由结构力学的两端无转角但有单位水平 位移时杆件的杆端剪力方程，柱的侧移刚度d可写成：
V 12 i
d= =
c
D
h2
EI
i=
c
h
内力分析及侧移计算
（3）同层各柱剪力的确定
（5
柱端弯矩确定以后，根据节点平衡条件可确定梁的弯矩。
对于边柱节点（图(a)），有Mb=Mc1+Mc2 对于中柱节点（图1(b))
Mb1=ib1/(ib1+ib2)(Mc1+Mc2 Mb2=ib2/(ib1+ib2)(Mc1+Mc2)
内力分析及侧移计算
如图所示，从框架中任取一柱AB，根据转角位移方
内力分析及侧移计算
分层法
认为某层框架梁上的荷载只给本层梁及与本层梁相连的框架产 生剪力和弯矩
进行弯矩分配后叠加，叠加后的不平衡弯矩再分配但不传递
内力分析及侧移计算
2 框架在水平荷载作用下内力的近似计算——反弯点法和D值法
A 反弯点法 反弯点法基本假定: （1） 在进行各柱间的剪力分配时，假定梁与柱的线
（2） 在确定各柱的反弯点位置时，假定除底层柱以
多层多跨框架所受水平荷载主要是风荷载及水平 地震作用。一般可简化为作用在框架节点上的集中 荷载，其弯矩图如图(a)所示。它的特点是，各杆的 弯矩图都是直线形，每杆都有一个零弯矩点，称为 反弯点。框架在水平荷载作用下的变形情况如图(b) 所示
内力分析及侧移计算
程，柱两端剪力为：
V
=
12ic h2
6ic h
第五章 框架结构
4. 构件截面惯性矩
计算框架梁截面惯矩时应考虑楼板的影响， 计算框架梁截面惯矩时应考虑楼板的影响，楼板在 梁端附近对其截面弯曲刚度影响较小， 梁端附近对其截面弯曲刚度影响较小，跨中对梁的截面 弯曲刚度影响较小。为方便设计， 弯曲刚度影响较小。为方便设计，假定沿梁轴线截面刚 度不变。 度不变。 1) 现浇楼盖：中框架取 现浇楼盖： ; 边框架取 0 2) 装配整体式楼盖：中框架取 装配整体式楼盖： 架取
5.2 多层框架结构竖向荷载作用下 的内力与侧移计算方法
竖向荷载作用可采用弯矩分配法，迭代法， 竖向荷载作用可采用弯矩分配法，迭代法， 分层法计算。 分层法计算。
水平荷载作用下可采用迭代法，无剪 水平荷载作用下可采用迭代法， 力分配法，反弯点法， 值法 值法(修正反弯点 力分配法，反弯点法，D值法 修正反弯点 法）计算
3.纵横向框架承重方案 纵横向框架承重方案
两个方向的框架梁均布置为主梁。当楼面荷载较 有较大开孔，柱网为方形或接近正方形， 大，有较大开孔，柱网为方形或接近正方形，均可考 两个方向刚度均大， 虑纵横向框架承重方案，两个方向刚度均大，抗震性 框架柱为双向偏压构件（空间框架） 能好，框架柱为双向偏压构件（空间框架）。
1.横向框架承重方案 横向框架承重方案 横向布置框架主梁 纵向布置联系梁 优点：横向刚度大， 优点：横向刚度大， 抗震性好.纵向有利 抗震性好 纵向有利 于采光.通风 于采光 通风 2.纵向框架承重方案 纵向框架承重方案 纵向布置框架主梁，横向为联系梁. 纵向布置框架主梁，横向为联系梁 优点：纵向刚度大，有利于布置较大空间的房屋， 优点：纵向刚度大，有利于布置较大空间的房屋， 方便布置管线， 方便布置管线，可调整房屋的不均匀沉降 缺点：横向刚度差， 缺点：横向刚度差，进深受预制板长度的影响
框架结构的内力和位移计算(精)
假定： （1）平面结构假定； （2）忽略柱的轴向变形； （3）D值法考虑了结点转角， 假定同层结点转角相等
2019/3/19
27
D 值法
计算方法 1、D值——修正抗侧刚度的计算 水平荷载作用下，框架不仅有侧移， 且各结点有转角，设杆端有相对位 移 ，转角 、 ，转角 1 2 位移方程为：
2019/3/19
22
反弯点法
2、剪力的计算 根据假定1：
V1 j d1 j j
Vij d ij j
Vij , d ij
——第j层第I根柱的剪力及其抗侧刚度
第j层总剪力
V pj
Vpj V1 j V2 j Vmj
2019/3/19 23
反弯点法
V1 j
第j层各柱剪力为
M ( z) N B
M(z)——上部水平荷载对坐标Z力矩总和 B——两边柱轴线间的距离
N
2019/3/19 44
柱轴向变形产生的侧移
N j
任意水平荷载下柱轴向变形产生的第j层处侧移 把框架连续化，根据单位荷载法：
2 ( NN / EA)dz
N j 0
Hj
N ( H j z) / B
框架结构的内力和位移计算荷载和设计要求51计算简图计算简图计算简图计算简图计算简图52竖向荷载作用下的近似计算方法分层法分层法分层法分层法力学知识回顾分层法计算过程构件弯矩图53水平荷载作用下内力近似计算方法反弯点法反弯点法弯点法反弯点法反弯点法反弯点法反弯点法反弯点法54水平荷载作用下内力近似计算方法d55水平荷载作用下侧移的近似计算梁柱刚度比k中柱
2019/3/19
9
计算简图
二、结构构件的截面抗弯刚度 考虑楼板的影响，框架梁的截面抗弯刚度应适当提高 现浇钢筋混凝土楼盖： 中框架：I＝2I0 边框架：I＝1.5I0 装配整体式钢筋混凝土楼盖： 截面形式选取： 框架梁跨中截面： 中框架：I＝1.5 I0 T型截面 边框架：I＝1.2 I0 框架梁支座截面： 装配式钢筋混凝土楼盖： 矩形截面 中框架：I＝I0 边框架：I＝I0 注：I0为矩形截面框架梁的截面惯性矩
第五章 高层建筑结构近似计算详解
构 设
• 忽略梁、柱轴向变形及剪切变形；
计 • 等截面杆件，以杆件轴线作为框架计
土 木
算轴线； • 竖向荷载作用下，结构无侧移。
系
结
构
一
5.2 框架结构的近似计算方法
高 5.2.1竖向荷载作用下内力近似计算
层
—分层力矩分配法
建 筑
计算假定：
结 构
• 框架的侧移和侧移力矩忽略不计;
设 • 每层梁荷载对其它层梁和柱的影响忽
构 设
底层柱： y=2/3
计 ⑹ 计算柱端弯矩；
土 木
柱上端弯矩 Mitj Vijh1 y
系 结
柱上端弯矩 Mibj Vijhy
构
一
5.2.2水平荷载作用下的近似计算
高 层
⑺ 由柱端弯矩、结点平衡，计算
建 筑
梁端弯矩；
结 构 设 计
M
l bi
M
t ij
Mb i1, j
ibl ibl ibr
计
则
土
木 系
为刚度修正系数，小于1，与梁柱刚度相
结 对大小有关（见表）；
构
D为结点有转角时柱的抗侧刚度，小于d。
一
高 层 建 筑 结 构 设 计 土 木 系 结 构 一
5.2.2水平荷载作用下的近似计算
框架结构同一层各柱侧移相等，
高 层
层剪力按柱的抗侧刚度分配：
建
筑
结
构
设
计
土
—框架结构i层总剪力 ；
木
—i层第j根柱分配到的剪力；
系 结
—i层第j根柱的抗侧刚度；
构 一
—i层全部柱的抗侧刚度之和。
5.2.2水平荷载作用下的近似计算
4_竖向荷载作用下框架内力计算
4_竖向荷载作用下框架内力计算在结构设计过程中，框架结构是一种常见的结构形式。
在实际工程中，框架结构会受到各种荷载的作用。
竖向荷载是一种重要的荷载形式，常见的竖向荷载包括自重、活荷载和附加荷载等。
在框架结构内力计算中，需要首先确定结构的几何特征，包括框架的截面形状、材料参数和受力情况等。
然后根据几何特征和力学原理，分析结构的受力平衡和变形情况，最终得到内力的计算结果。
下面将以一个简单的框架结构为例，介绍竖向荷载作用下框架内力计算的基本步骤。
1.框架结构的受力分析首先，需要绘制框架的受力图。
在竖向荷载作用下，框架的受力主要包括竖向荷载的作用力、支座反力和框架内部的轴力、剪力和弯矩等。
通过受力分析，可以将框架结构简化为若干个矩形梁和柱，以便进行进一步的计算。
2.框架结构的力学模型化将框架结构进行力学模型化，即将结构划分为若干个杆件和节点，并确定节点的受力情况。
杆件的长度、截面形状和材料参数等需要根据实际情况进行设定，以便计算杆件的受力。
3.杆件的受力计算根据竖向荷载作用下杆件的受力平衡和变形情况，可以得到杆件的轴力、剪力和弯矩等。
对于轴力，可以利用静力平衡原理进行计算。
对于剪力和弯矩，可以根据杆件的受力分布和形状进行计算，常用的方法包括截面法和弯矩传递法等。
4.框架结构的内力计算根据杆件的受力计算结果，可以得到框架结构内各个节点的内力情况。
根据节点的受力平衡条件，可以计算出节点上的轴力、剪力和弯矩等。
此外，还需要考虑支座反力的作用，以及与其他荷载（如横向荷载）的叠加效应。
5.内力的承载能力和设计校核根据内力计算结果，可以对框架结构的承载能力进行评估和校核。
根据设计规范和材料参数，结合强度和稳定性要求，进行构件的截面尺寸校核。
如果结构的承载能力满足要求，则结构设计合理；否则，需要进行后续的调整和优化。
总的来说，竖向荷载作用下框架内力计算是结构设计中的重要环节。
通过合理的受力分析和计算，能够得到准确的内力计算结果，从而为结构设计和施工提供科学的依据。
框架结构竖向荷载作用下的内力计算
框架结构竖向荷载作用下的内力计算框架结构是由梁柱等构件组成的，在受到竖向荷载作用下，会引起构件内力的产生。
了解框架结构竖向荷载作用下的内力计算对于结构的设计和分析非常重要。
下面将详细介绍框架结构竖向荷载作用下的内力计算方法。
首先，通过建立结构模型来描述框架结构。
结构模型中包括构件、节点和连接关系。
构件可以是梁或柱，节点是构件之间的连接点，连接关系表示构件之间的刚性约束。
在竖向荷载作用下，框架结构的内力主要有两种情况：梁内力和柱内力。
1.梁内力计算：在竖向荷载作用下，梁会产生弯矩和剪力。
根据梁的基本理论，可以得出计算弯矩和剪力的公式。
-弯矩计算：弯矩是由竖向荷载作用在梁上引起的。
根据弯矩的定义，弯矩M等于施加在梁上的力乘以力臂。
当梁需要承受重力荷载时，弯矩的计算公式为M=w*l^2/8，其中w为荷载大小，l为梁的跨度。
-剪力计算：剪力是由竖向荷载作用在梁上引起的。
根据剪力的定义，剪力V等于施加在梁上的力。
当梁需要承受重力荷载时，剪力的计算公式为V=w*l/2，其中w为荷载大小，l为梁的跨度。
2.柱内力计算：在竖向荷载作用下，柱会产生压力和拉力。
根据柱的基本理论，可以得出计算压力和拉力的公式。
-压力计算：压力是由竖向荷载作用在柱上引起的。
根据力学平衡原理，压力P等于施加在柱上的荷载之和。
当柱需要承受多个重力荷载时，压力的计算公式为P=∑w，其中w为荷载大小。
-拉力计算：拉力是由竖向荷载作用在柱上引起的。
和压力类似，拉力T等于施加在柱上的荷载之和。
在实际计算过程中，需要考虑梁和柱的截面形状和材料性质，以及节点和连接部位的刚性约束等因素。
同时，还需要考虑结构的整体平衡条件和节点处的力的平衡条件。
在计算过程中，可以使用静力平衡原理和弹性力学理论来进行分析。
通过平衡方程和应变-位移关系等基本原理，可以建立结构方程组，并通过求解方程组得到内力的值。
总结起来，框架结构竖向荷载作用下的内力计算是一个复杂的过程，需要考虑多个因素和使用多种方法。
框架钢结构内力计算
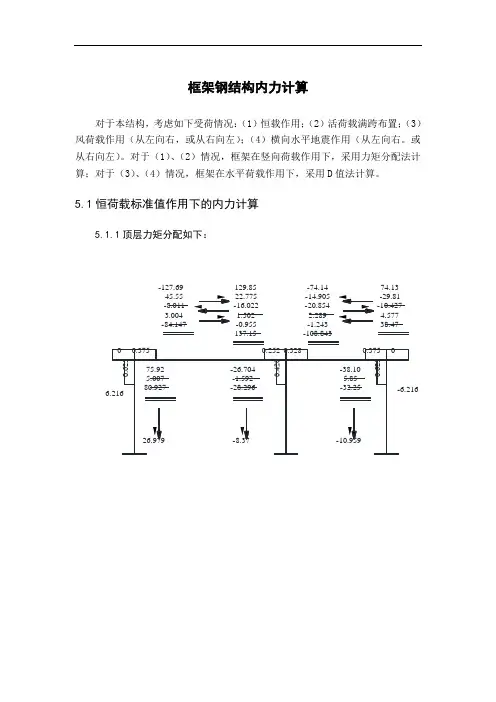
框架钢结构内力计算对于本结构，考虑如下受荷情况：（1）恒载作用；（2）活荷载满跨布置；（3）风荷载作用（从左向右，或从右向左）；（4）横向水平地震作用（从左向右。
或从右向左）。
对于（1）、（2）情况，框架在竖向荷载作用下，采用力矩分配法计算；对于（3）、（4）情况，框架在水平荷载作用下，采用D值法计算。
5.1恒荷载标准值作用下的内力计算5.1.1顶层力矩分配如下：-127.6945.55-8.0113.004-84.147129.8522.775-16.0221.502-0.955137.1574.13-29.81-10.4274.57738.47-74.14-14.905-20.8542.289-1.243-108.843顶层-10.544-8.757三层5.1.3二层力矩分配如下：-11.212-9.203二层0.174.50.185.48.4760.1420.21500.326.265.39-193.8428.684-7.4521.297-171.311214.6814.342-14.9050.649-0.240214.526114.81-18.451-9.7092.08788.737-114.81-9.226-19.4181.044-0.313-142.72382.4253.72686.15142.455-27.815-0.449-28.264-26.5183.00-23.518底层-42.825-0.691-43.516-21.758-40.854.62-36.23-18.11453.7412.42955.85818.724-9.422-7.83928.99-28.99叠加可得到最终的梁端、柱端弯矩。
其次求各层梁的最大弯矩，由于各层梁的最大弯矩求法相同，故此处列举顶层梁AC做实例。
由力矩分配法已求得：第一个集中力处剪力同理在顶梁AC段，第二个集中荷载处，剪力变号，故此处弯矩最大。
同理可求得其它梁的最大弯矩及梁端剪力，列表如下：梁剪力表层号 4 3 2 1 AC跨69.98 117.48 114.67 115.3566.95 101.83 100.62 101.3019.35 38.39 37.18 37.86 16.45 23.45 23.77 24.45 -32.15 -39.99 -39.67 -38.99 -34.19 -55.64 -53.72 -53.04 -81.79 -119.08 -117.16 -116.48 -84.55 -133.30 -129.93 -129.25CD跨62.91 96.97 93.99 92.50 59.88 81.32 79.94 78.45 12.28 17.88 16.50 15.01 9.38 2.94 3.10 1.61 -38.22 -60.50 -60.34 -61.83 -41.26 -76.15 -74.39 -75.88（注：表中单位为kN）梁跨最大弯矩，柱轴力计算如下表：层号4 上146.14 220.49 117.42101.05 48.96 下154.23 228.57 125.503 上401.64 536.69 331.59137.85 65.51 下408.84 543.90 338.212 上647.40 843.20 537.07134.70 64.06 下654.60 850.40 544.271 上893.84 1147.53 744.036132.41 62.77 下907.62 1161.31 757.82柱的剪力可根据平衡方程求出。
竖向荷载作用下框架结构的内力计算
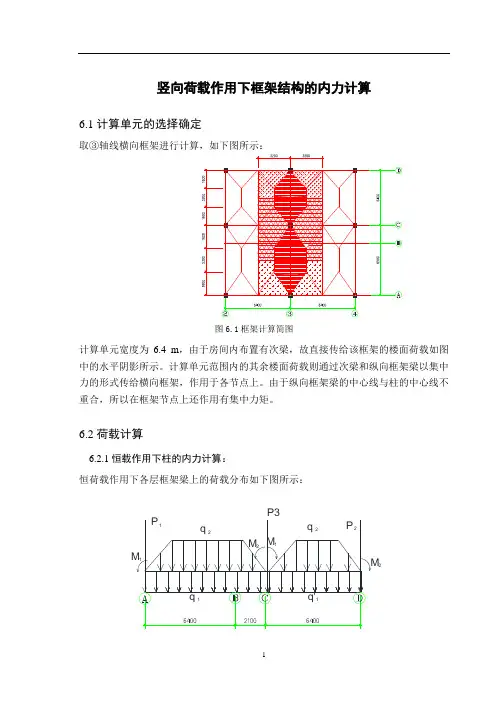
竖向荷载作用下框架结构的内力计算6.1计算单元的选择确定取③轴线横向框架进行计算，如下图所示：图6.1框架计算简图计算单元宽度为6.4 m，由于房间内布置有次梁，故直接传给该框架的楼面荷载如图中的水平阴影所示。
计算单元范围内的其余楼面荷载则通过次梁和纵向框架梁以集中力的形式传给横向框架，作用于各节点上。
由于纵向框架梁的中心线与柱的中心线不重合，所以在框架节点上还作用有集中力矩。
6.2荷载计算6.2.1恒载作用下柱的内力计算：恒荷载作用下各层框架梁上的荷载分布如下图所示：2图6.2恒荷载作用下各层框架梁上的荷载分布图（1）、对于顶层屋面，q1、q1＇代表横梁自重，为均布荷载形式。
q1=0.3×0.75×25=5.625kN/mq1＇=0.3×0.75×25=5.625kN/mq2为屋面板传给横梁的梯形荷载。
q2=5.29×3.2=16.928kN/mP1、P2分别由边纵梁、中纵梁直接传给柱的恒载，它包括主梁自重、次梁自重、楼板重等重力荷载，计算如下：P1=6.4*0.3*0.75*25+8.5/2*0.25*0.6*25+5.29*3.2*1.6+(5.3+8.5)*1.6*5.29/4=108.223KN P2=6.4*0.3*0.75*25+6.4/2*0.25*0.6*25+5.29*3.2*1.6 +(3.2+6.4)*1.6*5.29/4=95.398KN P3=6.4*0.3*0.75*25+(8.5+6.4)*0.5*0.25*0.6*25+5.29*3.2*1.6*2++(3.2+6.4)*1.6*5.29/4= 190.64KN集中力矩M1=P1e1=108.223×（0.6 -0.3）/2=16.23kN·mM2=P2e2=147.23×（0.6 -0.3）/2=14.31kN·m（2）、对于3层，包括梁自重和其上横墙自重，为均布荷载，其它荷载的计算方法同第顶层。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5.1 计算单元的确定取6号轴线一榀框架进行计算，计算宽度为(6.6+6.6)/2=6.6m 。
如图下图所示横向框架荷载传递图5.2 荷载计算5.2.1 恒荷载的计算 1、五层、（1）q 、q 0、q 0′、q 0″分别为女儿墙、边跨横梁(走道纵梁)、走道横梁、次梁自重（扣除板自重），为均布荷载形式；β为考虑梁粉刷自重时的放大系数，取β=1.05。
女儿墙：q=3.47×0.9=3.12 kN/m 边跨横梁（走道纵梁）：q 0=1.05×0.3×(0.6-0.1)×25=3.94kN/m 走道横梁：q 0′=1.05×0.3×(0.4-0.1)×25=2.36kN/m 次梁：q 0″=1.05×0.2×(0.5-0.1)×25=2.1kN/m（2）q 1、q 1′分别为屋面板自重传给横梁的梯形和三角形荷载等效为均布荷载值 q 1=[1-2×(3.3/6.6×2) ²+(3.3/6.6×2) ³]×4.38×3.3/2=6.44kN/mq 1′=85×4.38×3.0/2=4.11kN/m（3）q 2、q 2′分别为屋面板自重传给纵梁上的梯形和三角形荷载等效为均布荷载值 梯形：q 2=[1-2×(3.0/6.6×2) ²+(3.0/6.6×2) ³]×4.38×3.0/2=5.96kN/m三角形：q 2′=85×4.38×3.3/2=4.52kN/mP 1为由板传给次梁及次梁自重传给纵梁的集中力 P 1= q 1×6.6+ q 0″×6.6/2=49.43kNP 2为由板传给外纵梁及外纵梁、女儿墙自重传给柱子的集中力 P 2=（ q 2′+ q 0+q ）×3.3×2=76.42 kNP 3为由板传给内纵梁及内纵梁自重传给柱子的集中力。
P 3=（q 2′+ q 2+ q 0）×3.3×2=95.17kNP 4为由板传给边框架横梁及边框架横梁自重传给柱子的集中力 P 4= q 1×6.6+ q 0×6.6/2=55.51 kNP 5为由板传给走道横梁及走道横梁自重传给柱子的集中力 P 5= q 1′×6.6+ q 0′×3.0/2=30.67 kN P A = P 1 +P 2 =125.85 kN P C = P 1 +P 3 =144.6 kN P D = P 1 +P 3 =144.6 kN P E = P 1 +P 2 =125.85 kN(4)由于梁偏心作用而在梁端产生的弯矩 M A =( P A )e=125.85×(0.6-0.3)/2=18.88kN ⋅m M C =( P C )e=144.6×(0.6-0.3)/2=21.69kN ⋅m M D =( P D )e=144.6×(0.6-0.3)/2=21.69kN ⋅m M E =( P E )e=125.85×(0.6-0.3)/2=18.88kN ⋅m 2、一~四层：（1）q 、q 0、q 0′、q 0″分别为外纵梁、边跨横梁(走道纵梁)、走道横梁、次梁自重（扣除板自重，包括填充墙重），为均布荷载形式；β为考虑梁粉刷自重时的放大系数，取β=1.05。
外纵梁：q=1.05×0.3×(0.6-0.1)×25+2.77×3.3=13.08 kN/m 边跨横梁（走道纵梁）：q 0=1.05×0.3×(0.6-0.1)×25+1.6×3.3=9.22kN/m 走道横梁：q 0′=1.05×0.3×(0.4-0.1)×25+1.6×3.3=7.64kN/m 次梁：q 0″=1.05×0.2×(0.5-0.1)×25+1.6×3.3=7.38kN/m（2）q 1、q 1′分别为楼面板自重传给横梁的梯形和三角形荷载等效为均布荷载值 q 1=[1-2×(3.3/6.6×2) ²+(3.3/6.6×2) ³]×3.39×3.3/2=4.98kN/mq 1′=85×3.39×3.0/2=3.18kN/m（3）q 2、q 2′分别为楼面板自重传给纵梁上的梯形和三角形荷载等效为均布荷载值 梯形：q 2=[1-2×(3.0/6.6×2) ²+(3.0/6.6×2) ³]×3.39×3.0/2=4.62kN/m三角形：q 2′=85×3.39×3.3/2=3.50kN/mP 1为由板传给次梁及次梁自重传给纵梁的集中力 P 1= q 1×6.6+ q 0″×6.6/2=57.22kNP 2为由板传给外纵梁及外纵梁自重传给柱子的集中力 P 2=（q 2′+ q ）×3.3×2=109.43 kNP 3为由板传给内纵梁及内纵梁自重传给柱子的集中力。
P 3=（q 2′+ q 2+ q 0）×3.3×2=114.44kNP 4为由板传给边框架横梁及边框架横梁自重传给柱子的集中力 P 4= q 1×6.6+ q 0×6.6/2=46.70 kNP 5为由板传给走道横梁及走道横梁自重传给柱子的集中力 P 5= q 1′×6.6+ q 0′×3.0/2=32.45 kN P A = P 1 +P 2 =166.65 kN P C = P 1 +P 3 =171.66 kN P D = P 1 +P 3 =171.66 kN P E = P 1 +P 2 =166.65 kN(4)由于梁偏心作用而在梁端产生的弯矩 M A =( P A )e=166.65×(0.6-0.3)/2=25.00kN ⋅mM C =( P C )e=171.66×(0.6-0.3)/2=25.75kN ⋅m M D =( P D )e=171.66×(0.6-0.3)/2=25.75kN ⋅m M E =( P E )e=166.65×(0.6-0.3)/2=25.00kN ⋅m 5.2.2 活荷载计算《建筑结构荷载规范》5.1.2规定：当楼面梁从属面积超过25m 2时，应取折减系数0.9。
本设计中楼面梁的从属面积：6.6×3.3=21.78m 2<25m 2，故活荷载不需要折减。
1、 五层q 1、q 1′分别为房间传给边横梁的梯形荷载和走道板传给走道横梁上的三角形荷载等效为均布荷载值q 1=[1-2×(3.3/6.6×2) ²+(3.3/6.6×2) ³]×0.5×3.3/2=0.74kN/mq 1′=85×0.5×3.0/2=0.47kN/mq 2、q 2′分别为房间传给纵梁上的梯形和三角形荷载等效为均布荷载值 梯形：q 2=[1-2×(3.0/6.6×2) ²+(3.0/6.6×2) ³]×0.5×3.0/2=0.68kN/m三角形：q 2′=85×0.5×3.3/2=0.52kN/mP 为房间通过纵梁传给柱的集中力 P A = P E = q 2×6.6=4.49 kN P C = P D =（ q 2+ q 2′）×6.6 =7.92 kNM 为由于梁偏心作用而在梁端产生的弯矩 M A = M E = ( P A )e=4.49×(0.6-0.3)/2=0.67kN ⋅m M C = M D = ( P C )e=7.92×(0.6-0.3)/2=1.19kN ⋅m2、 一~四层q 1、q 1′分别为房间传给边横梁和走道横梁上的荷载等效为均布荷载值 q 1=[1-2×(3.3/6.6×2) ²+(3.3/6.6×2) ³]×2.0×3.3/2=2.96kN/mq 1′=85×2.0×3.0/2=1.88kN/mq 2、q 2′分别为房间传给纵梁上的梯形和三角形荷载等效为均布荷载值 梯形：q 2=[1-2×(3.0/6.6×2) ²+(3.0/6.6×2) ³]×2.0×3.0/2=2.72kN/m三角形：q 2′=85×2.0×3.3/2=2.08kN/mP 为房间通过纵梁传给柱的集中力 P A = P E = q 2×6.6=17.95 kN P C = P D =（ q 2+ q 2′）×6.6 =31.68 kNM 为梁偏心作用而在梁端产生的弯矩 M A = M E = ( P A )e=17.95×(0.6-0.3)/2=2.69kN ⋅m M C = M D = ( P C )e=31.68×(0.6-0.3)/2=4.75kN ⋅m各层梁上作用的恒荷载各层梁上作用的活荷载5.3 内力计算梁端、柱端弯矩均采用弯矩二次分配法计算。
5.3.1 弯矩计算弯矩计算简图恒荷载弯矩计算1、 五层由均布荷载产生的弯矩： M AC =-M CA =-1/12×10.38×6.62=-37.68kN·mM CD =-M DC =-1/12×6.47×3.02=-4.85kN·m M DE =-M ED =-1/12×10.38×6.62=-37.68kN·m 2、一~四层由均布荷载产生的弯矩： M AC =-M CA =-1/12×14.20×6.62=-51.55kN·m M CD =-M DC =-1/12×10.82×3.02=-8.12kN·mM DE =-M ED =-1/12×14.20×6.62=-51.55kN·m 活荷载弯矩计算1、 五层由分布荷载产生的弯矩： M AC =-M CA =-1/12×0.74×6.62=-2.69kN·mM CD =-M DC =-1/12×0.47×3.02=-0.56kN·mM DE =-M ED =-1/12×0.74×6.62=-2.69kN·m 2、一~四层由分布荷载产生的弯矩： M AC =-M CA =-1/12×2.96×6.62=-6.82kN·mM CD =-M DC =-1/12×1.88×3.02=-1.41kN·mM DE =-M ED =-1/12×2.96×6.62=-6.82kN·m 5.3.2 横向框架内力计算 1、转动刚度122ql梁柱线刚度取前面计算结果，分配系数按与节点连接方式形式可得各个杆件的转动刚度比值计算。