第八章 点的合成运动
- 格式:ppt
- 大小:865.00 KB
- 文档页数:28

第八章 点的合成运动8-1 如图所示,光点M 沿y 轴作谐振动,其运动方程为:0=x , )cos(β+=kt a y 如将点M 投影到感光记录纸上,此纸以等速e v 向左运动。
求点M 在记录纸上的轨迹。
解:把动坐标系'''y x O 固连在纸上,M 点的相对运动的运动方程为 t v x e '=,)cos('β+=kt a y 消去t 即可得到M 点在记录纸上的轨迹方程)'cos('eβ+=x v ka y8-3 水流在水轮机工作轮入口处的绝对速度m/s 15a =v ,并与直径成︒=60β角,如图所示,工作轮的半径m 2=R ,转速r/min 30=n 。
为避免水流与工作轮叶片相冲击,叶片应恰当地安装,以使水流对工作轮的相对速度与叶片相切。
求在工作轮外缘处水流对工作轮的相对速度的大小方向。
解:取水轮机工作轮入口处的一滴水为动点M ,动坐标系建立在工作轮上,速度分析图(a ),设θ为r v 与'x 轴的夹角。
M 点的牵连速度为m/s 283.630π2e =⨯==n R v ω 方向与'y 轴平行,由图(a )︒=-︒=+︒sin30)sin(90)sin(60ra e v v v θθ 前一等式得)60sin(cos a e θθ+︒=v v即 ︒︒-=60cos 60sin tan a a e v v v θ把m/s 283.6e =v 及m/s 15a =v 代入解得'4841︒=θ后一等式得m/s 1.10cos 30sin a r =︒=v v θ8-5 杆OA 长l ,由推杆推动而在图面内绕点O 转动,如图所示。
假定推杆的速度为v ,其弯头高为a 。
试求杆端A 的速度的大小(表示为推杆至点O 的速度x 的函数)。
解:取推杆上与AO 杆接触的B 点为动点,动系固连在AO 上,B 点速度分析如图。
设OA 角速度为ωv v =a ,ϕωsin a e v OB v =⋅=,ϕωsin v OB =⋅ 以 22sin a x aOBa +==ϕ代入上式得,22ax va+=ω 最终得 22a ax lavl v +==ω,方向如图8-7 在图a 和b 所示的两种机构中,已知mm 20021==a O O ,rad/s 31=ω。
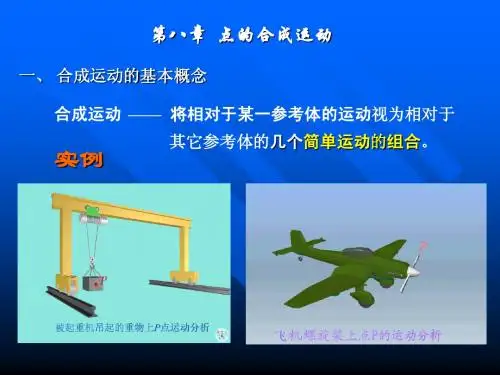



潍坊学院机电系讲稿专用纸如车轮上的点P的运动,如果以地面作为参考系,点的轨迹是旋轮线,而如果以小车作为参考系,点的轨迹则是一个圆。
相对于地面是直线运动,相对于旋转的工件,是,因此,车刀在工件的表面上切出螺旋线。
在实际问题中,往往不仅要知道物体相对地球的运动,而且有时要知道被观察物体相对于地面运动着的参考系的运动情况。
例如在运动着的飞机、车船上观察飞机、车船潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸动系上与动点相重合的点相对于定系的速度、加速度称为牵连速度、牵连加速度。
6. 动点和动系的选择基本原则:(1)动点对动系要有相对运动。
(2)动点的相对运动轨迹要明确、容易确定。
具体选择方法:(1)选择持续接触点为动点。
(2)对没有持续接触点的问题,一般不选择接触点为动点。
根据选择原则具体问题具体分析。
实例见PPT。
潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸内的绝对位移绕固定轴O limlim11M M MM '+='M M MMM M '+='11潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸在定系和动系中的矢径分别用r 和r ′表示。
k z j y i x r r ''+''+''+='r潍坊学院机电系讲稿专用纸和为未知量,暂设潍坊学院机电系讲稿专用纸当牵连运动是定轴转动时,动点的绝对加速度并不等于牵连加速度与相对加速之矢量和。
牵连运动是定轴转动时点的加速度合成定理和角加速度α 绕定系Oxyz 的轴z 转动;动系)分析动系的单位矢量k j i''',,对时间的一阶导数以角速度e ω绕定轴z 转动,则角速度矢e ω沿潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸0=r v ③ r e v//ω r e v⊥, 此时 e k a =ω2是由于牵连运动和相对运动的相互影响而产生的潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸。






第八章 点的合成运动我们都知道,物体的运动与选定的参考体有关,参考体不同,物体的运动状态就不同。
如沿直线轨道行驶的火车,对于车上的观察者来说,轮缘上点M 的轨迹就是一个圆,而对于地上的观察者来说,M 点的轨迹是旋轮线。
显然,点M 相对于两个参考体的速度和加速度也不同。
本章的任务是研究点的相对于不同参考体的运动之间的关系。
通过上例可以得出,M 点相对于地面的运动可以看成是M 点相对于车厢的圆周运动与车厢相对于地面平动的合成,这样的运动称为合成运动。
因此,我们总可以把复杂运动分解为几个简单运动。
先研究这些简单运动,然后再加以合成。
通常我们把固定在地球上的坐标系成为定参考系,以oxyz 坐标系表示。
固定在其它相对于地球运动的参考体上的坐标系称为动参考系,以坐标系表示。
上例中,动参考系固定在车厢上。
,,,,z y x o 用点的合成运动理论分析点的运动时,必须选定两个参考系,区分三种运动。
§8-1 相对运动 牵连运动 绝对运动三种运动的定义:(1) 动点相对于定参考系的运动,称为绝对运动。
(2) 动点相对于动参考系的运动,称为相对运动。
(3) 动参考系相对于定参考系的运动,称为牵连运动。
在分析这三种运动时,必须明确:(1)站在什么地方看物体的运动(2)看哪个物体的运动应指出动点的绝对运动和相对运动都是指点的运动,它可能作直线运动也可能作曲线运动,而牵连运动则是指参考体(参考系)的运动。
实际上是刚体运动,它可能作平动,定轴转动或其它复杂运动。
动点在相对运动中的轨迹,速度和加速度称为相对轨迹,相对速度和相对加速度。
动点在绝对运动中的轨迹,速度和加速度称为绝对轨迹,绝对速度和绝对加速度。
由于动参考系的运动是刚体运动,在一般情况下,刚体上各点的速度和加速度是不同的,但是动参考系上对动点运动有直接影响的是参考系上与动点相重合的那点,这点称作牵连点。
因此定义:在动参考系上与动点相重合的那点的速度和加速度称为动点的牵连速度和牵连加速度。
第八章 点的合成运动8-1 M 点沿 y 轴作谐运动,运动方程为: x 0,y acos kt 。
如将 M 点放映到银幕上,此银幕以 匀速 v 向左运动。
试分析 M 点的牵连、相对和绝对运动,并求 M 点映在银幕上的轨迹。
答案:相对运动方程 x vt ;相对运动轨迹 y acoskt8-2 M 点沿圆盘直径 AB 以 v 匀速运动,当开始时, M 点在圆盘中心,且直径 AB 与 Ox 轴重合。
如圆盘 以匀角速度 w 绕 O 轴转动,求 M 点的绝对轨迹。
答案:轨迹方程: r vy acos x v8-3 半径为r 的齿轮Ⅱ由曲柄OA 带动沿同样半径的固定齿轮Ⅰ而滚动,曲柄以角速度w0绕O 轴转动。
设在曲柄OA 上固连一动系,试求动齿轮上B、C、D 三点的牵连速度。
答案:v eC r, veB5r, veD3r8-4 河的两岸相互平行,设各处河水流速均匀且不随时间改变。
一船由点 A 朝与岸垂直的方向等速驶出,经10min 到达对岸,这时船到达点 B 下游120m 的点C。
为使船从点 A 能垂直到达对岸的点 B ,船应逆流并保持与直线AB成某一角度的方向航行。
再此情况下,船经12.5min 到达对岸。
求河宽L、船对水的相对流速v r和水的流速v的大小。
答案:L 200m ;v r 0.333m/s ;v 0.2m/s8-5 水流在水轮机工作轮入口处的绝对速度v a 15m/s ,并与铅垂直径成60 角。
工作轮的半径R 2m ,转速n 30r/min 。
为避免水流对工作轮叶片想冲击,叶片应恰当的安装,以使水流对工作轮的相对速度与叶片相切。
求在工作轮外缘处水流对工作轮的相对速度的大小和方向。
8-6 矿砂从传送带A落到另一传送带B,其绝对速度v1 4m/s,方向与铅直线成30 角。
设传送带 B 与水平面成15 角,其速度v2 2m/s。
求此时矿砂对于设传送带 B 的相对速度。
并问设传送带 B 的速度为多大时,矿砂的相对速度才能与它垂直?答案:v r 3.982m/s ;当传送带B的速度v2 1.035m/s时,v r才与带垂直。