大学物理电磁学公式总结
- 格式:doc
- 大小:21.86 KB
- 文档页数:4

大学物理公式总结引言:大学物理是自然科学中的一门基础学科,掌握物理公式是学好物理的关键。
物理公式是在长期实验和理论研究的基础上总结、归纳出来的。
在这篇文章中,我将为大家总结一些常见的大学物理公式,并简要介绍这些公式的应用。
1. 动力学公式:1.1 牛顿第二定律:F = ma(F代表力,m代表物体质量,a代表物体加速度)牛顿第二定律是经典力学的基石,描述了物体受到的力和其加速度之间的关系。
它可以用于解释物体在受力作用下的运动状态。
1.2 动能公式:K = (1/2)mv^2(K代表动能,m代表物体质量,v代表物体速度)动能公式是描述物体动能与质量以及速度之间关系的公式。
它告诉我们,当物体速度增加时,其动能也会增加。
1.3 势能公式:U = mgh(U代表势能,m代表物体质量,g代表重力加速度,h代表物体高度)势能公式是描述物体势能与质量、重力加速度以及高度之间关系的公式。
它可以用于解释物体在重力场中的储能情况。
2. 热力学公式:2.1 热力学第一定律:Q = ΔU + W(Q代表系统吸收的热量,ΔU代表系统内能的变化,W代表系统对外界做的功)热力学第一定律描述了系统内能的变化与热量和功之间的关系。
根据这个公式,我们可以推导出热功定理和热机效率等重要概念。
2.2 热容公式:Q = mcΔT(Q代表系统吸收的热量,m代表物体质量,c代表物质的比热容,ΔT代表温度变化)热容公式描述了物体吸收的热量与其质量、比热容和温度变化之间的关系。
它可以用于计算物体在受热或冷却过程中需要吸收或释放的热量。
3. 电磁学公式:3.1 库仑定律:F = k * (|q1 * q2| / r^2)(F代表电场力,k代表库仑常数,q1和q2代表电荷量,r代表距离)库仑定律描述了两个电荷之间的相互作用力与它们的电荷量以及距离之间的关系。
这个定律是电磁学的基础之一,用于解释电荷之间的相互作用。
3.2 电路定律:3.2.1 欧姆定律:V = IR(V代表电压,I代表电流,R代表电阻)欧姆定律是描述电路中电压、电流和电阻之间关系的基本定律。
静电场小结均匀带电长直圆柱面均匀带电球体四、静电场高斯定理 点电荷电势点电荷系电势连续带电体电势 九、几种典型电场的电势、库仑定律、电场强度 三、场强迭加原理 点电荷场强 六、静电场的环流定理连续带电体场强 '丄一:「八、电势迭加原理均匀带电球面五、几种典型电荷分布的电场强度1r>R1均匀带电球面均匀带电长直圆柱面均匀带电球体 均匀带电球面均 匀 带 电 长 直 圆 柱体无限大均匀带电平面 六、 静电场的环流定理七、 电势八、 电势迭加原理点电荷电势点电荷系电势连续带电体电势 九、 几种典型电场的电势一、 库仑定律 二、 电场强度三、 场强迭加原理点电荷场强点电荷系强连续带电体场强 四、 静电场高斯定理五、 几种典型电荷分布的电场强度均匀带电球面均匀带电长直圆柱面均匀带电球体 均匀带电球面均 匀 带 电 长 直 圆 柱体无限大均匀带电平面 六、 静电场的环流定理七、 电势八、 电势迭加原理点电荷电势点电荷系电势连续带电体电势 九、 几种典型电场的电势一、 库仑定律 二、 电场强度三、 场强迭加原理点电荷场强点电荷系强连续带电体场强 四、 静电场高斯定理五、 几种典型电荷分布的电场强度均匀带电球面均匀带电长直圆柱面均匀带电球体 均匀带电球面均 匀 带 电 长 直 圆 柱体无限大均匀带电平面 六、 静电场的环流定理七、 电势八、 电势迭加原理点电荷电势点电荷系电势连续带电体电势 九、 几种典型电场的电势一、 库仑定律 二、 电场强度三、 场强迭加原理点电荷场强点电荷系强连续带电体场强 四、 静电场高斯定理五、 几种典型电荷分布的电场强度均匀带电球面均匀带电长直圆柱面均匀带电球体 均匀带电球面均 匀 带 电 长 直 圆 柱体无限大均匀带电平面 六、 静电场的环流定理七、 电势八、 电势迭加原理点电荷电势点电荷系电势连续带电体电势九、 几种典型电场的电势一、 库仑定律 二、 电场强度三、 场强迭加原理点电荷场强点电荷系强连续带电体场强 四、 静电场高斯定理五、 几种典型电荷分布的电场强度均匀带电球面。

引言概述:物理公式是大学物理课程中不可或缺的一部分,它们是描述自然现象的数学表达式。
本文将介绍一些大学常用的物理公式,包括力学、热力学、电磁学和光学公式等。
这些公式不仅在学习物理理论和解题中起到重要的作用,而且在工程、科学研究和实际应用中也具有广泛的应用价值。
正文内容:一、力学公式1.1运动学公式1.1.1位移公式s=ut+(1/2)at^21.1.2速度公式v=u+at1.1.3加速度公式a=(vu)/t1.2动力学公式1.2.1牛顿第二定律F=ma1.2.2动能公式Ek=(1/2)mv^21.2.3动量公式p=mv1.3静力学公式1.3.1弹性力公式F=kx1.3.2引力公式F=G(m1m2)/r^21.3.3摩擦力公式Ff=μFn二、热力学公式2.1热传导公式2.1.1热传导方程q=kΔT/L2.1.2热导率公式k=(QL)/(AΔT)2.2热膨胀公式2.2.1线膨胀公式ΔL=αL0ΔT2.2.2体膨胀公式ΔV=βV0ΔT2.3热力学循环公式2.3.1热转化效率公式η=(W_net/Q_h)100%2.3.2卡诺循环效率公式η_C=(T_hT_c)/T_h三、电磁学公式3.1电场公式3.1.1电场强度公式E=F/q3.1.2电势差公式V=W/q3.2磁场公式3.2.1磁场强度公式B=F/(qv)3.2.2磁场感应公式ε=BLv3.3法拉第电磁感应公式3.3.1法拉第电磁感应定律ε=dΦ/dt3.3.2洛伦兹力公式F=q(E+vxB)四、光学公式4.1光速公式4.1.1光速定义c=λf4.1.2光速在介质中的速度v=c/n4.2折射公式4.2.1斯涅尔定律n1sin(θ1)=n2sin(θ2)4.2.2光线传播路径差公式Δx=d(n1)(cot(θ2)cot(θ1))4.3球面镜公式4.3.1球面镜公式1/f=(n1)(1/R11/R2)五、总结本文介绍了大学常用的物理公式,涵盖了力学、热力学、电磁学和光学等方面。

大学物理电磁学公式总结第一章(静止电荷的电场)1.电荷的基本性质:两种电荷,量子性,电荷守恒,相对论不变性。
2. 库仑定律:两个静止的点电荷之间的作用力F =kq 1q 2r 2e r =q 1q 24πε0r 2e r3. 电力叠加原理:F=ΣF i4. 电场强度:E=Fq 0, q 0为静止电荷5. 场强叠加原理:E=ΣE i用叠加法求电荷系的静电场:E =∑q i4πε0r i2e ri i (离散型) E=∫dq4πε0r 2e r q(连续型)6. 电通量:Φe=∫E •dS s7. 高斯定律:∮E •dS s=1ε0Σq int 8. 典型静电场:1) 均匀带电球面:E=0 (球面内)E=q4πε0r 2e r (球面外)2) 均匀带电球体:E=q4πε0R3r =ρ3ε0r (球体内)E=q4πε0r 2e r (球体外)3) 均匀带电无限长直线: E=λ2πε0r ,方向垂直于带电直线4) 均匀带电无限大平面:E=σ2ε0,方向垂直于带电平面9. 电偶极子在电场中受到的力矩:M=p×E第九章 静电场知识点:1、 用积分方法计算连续带电体电场强度,场强叠加是矢量叠加;首先进行矢量分解,再把同方向的相加;2、 运用高斯定理,计算电荷均匀分布、对称带电体周围空间的场强和电势;关键是分析场强分布特点,选好封闭曲面;(1)电荷在表面均匀分布的带电圆筒;(选择一个封闭圆柱曲面) (2)电荷在表面均匀分布的带电球壳;(选择一个封闭球面) (3)电荷均匀分布的无穷大平面;(选择一个封闭圆柱曲面)3、 根据电势定义用积分方法计算连续带电体的激发的电势,要获得积分路径上场强的分布;电势叠加是标量叠加; 4、 电场强度环路定理一些问题辨识:1、理解高斯定理的内容:(1)只有封闭曲面内的电荷,才对该封闭曲面的电通量有贡献;(2)曲面以外的任何电荷,对该封闭曲面的电通量没有贡献;(3)这里强调的是封闭曲面,如果只是一个有限曲面,是封闭曲面的一部分,里外的电荷对该部分是有电通量贡献的:(4)里、外的电荷都对曲面上的各点产生场强;2、场强等于零的空间点,电势可以不为零;电势为零的空间点,场强可以不为零;1、 有关静电场的论述,正确的是( )(1) 只有封闭曲面内的电荷才对该封闭曲面的电通量有贡献;√(2) 无论封闭曲面内的电荷的位置如何改变,只要不离开该封闭曲面,而且电荷代数和不变,该封闭曲面的电通量就不变;√(3) 封闭曲面内部的任何电荷的位置的改变,尽管不离开该封闭曲面,而且电荷代数和不变,该封闭曲面的电通量也要发生改变;×(4) 封闭曲面外的电荷激发的场强对该封闭曲面上的任何面元的电通量的贡献为零;×(5) 如果封闭曲面的电通量为零,则该封闭曲面上任何面元上的电场强度一定为零;×(6) 如果封闭曲面的电通量不为零,则该封闭曲面上任何面元的电通量的一定不为零;×(7) 电场强度为零的空间点,电势一定为零;×(8) 在均匀带电的球壳内部,电场强度为零,但电势不为零;√计算场强的三种方法,按照问题的实际情况选择最方便的方法: (1) 根据连续带电体的积分公式; (2) 采用高斯定理;(3) 先获得电势分布公式,然后计算偏导数;z z y x U E y z y x U E x z y x U E z y x ∂∂-=∂∂-=∂∂-=),,(;),,(;),,(计算电势分布首先计算场强分布,再计算电势分布;➢ 第三章(电势)1. 静电场是保守场:∮E •dr L=0 2. 电势差:φ1 –φ2=∫E •dr (p2)(p1)电势:φp =∫E •dr (p0)(p) (P0是电势零点) 电势叠加原理:φ=Σφi 3. 点电荷的电势:φ=q 4πε0r电荷连续分布的带电体的电势:φ=∫dq4πε0r4. 电场强度E 与电势φ的关系的微分形式:E=-grad φ=-▽φ=-(∂φ∂x i+∂φ∂y j+∂φ∂z k)电场线处处与等势面垂直,并指向电势降低的方向;电场线密处等势面间距小。

大学物理电磁学公式大学物理电磁学是物理学中的一个重要分支,研究电场和磁场以及它们之间的相互作用。
在学习和研究电磁学的过程中,我们经常会接触到一系列重要的公式。
以下是一些常见的大学物理电磁学公式的详细介绍。
1. 库仑定律(Coulomb's Law):库仑定律描述了两个点电荷之间相互作用力的大小和方向。
它的数学表达式为:F = k * |q1 * q2| / r²其中,F为两个电荷所受的力,k为库仑常数,q1和q2分别为两个电荷的大小,r为两个电荷之间的距离。
2. 电场强度(Electric Field Intensity):电场强度描述了电荷在某一点周围的电场的强弱。
对于一个点电荷,其电场强度的数学表达式为:E = k * |q| / r²其中,E为电场强度,k为库仑常数,q为电荷的大小,r为点电荷到被测点之间的距离。
3. 电势能(Electric Potential Energy):电势能描述了电荷由于存在于电场中而具有的能量。
对于一个点电荷,其电势能的数学表达式为:U = k * |q1 * q2| / r其中,U为电势能,k为库仑常数,q1和q2分别为两个电荷的大小,r为两个电荷之间的距离。
4. 电势差(Electric Potential Difference):电势差描述了电场中两个点之间的电势能的差异。
对于两个点电荷之间的电势差,其数学表达式为:ΔV = V2 - V1 = -∫(E · dl)其中,ΔV为电势差,V1和V2分别为两个点的电势,E为电场强度,dl为路径元素。
5. 电场线(Electric Field Lines):电场线用于可视化电场的分布情况。
电场线从正电荷流向负电荷,并且密集的电场线表示电场强度较大,稀疏的电场线表示电场强度较小。
6. 电场的高斯定律(Gauss's Law for Electric Fields):电场的高斯定律描述了电场通过一个闭合曲面的总通量与该闭合曲面内的电荷量之间的关系。

大学物理电磁学公式总结汇总——WORD文档,下载后可编辑修改——大学物理电磁学公式总结1定律和定理1. 矢量叠加原理:任意一矢量可看成其独立的分量的和。
即:=∑ (把式中换成、、、、、就分别成了位置、速度、加速度、力、电场强度和磁感应强度的叠加原理)。
2. 牛顿定律: =m (或 = );牛顿第三定律:′= ;万有引力定律:3. 动量定理:→动量守恒:条件4. 角动量定理:→角动量守恒:条件5. 动能原理: (比较势能定义式: )6. 功能原理:A外+A非保内=ΔE→机械能守恒:ΔE=0条件A外+A 非保内=07. 理想气体状态方程:或P=nkT(n=N/V,k=R/N0)8. 能量均分原理:在平衡态下,物质分子的每个自由度都具有相同的平均动能,其大小都为kT/2。
克劳修斯表述:不可能把热量从低温物体传到高温物体而不产生其它影响。
开尔文表述:不可能从单一热源吸取热量,使之完全变为有用的功而不产生其它影响。
实质:在孤立系统内部发生的过程,总是由热力学概率小的宏观状态向热力学概率大的状态进行。
亦即在孤立系统内部所发生的过程总是沿着无序性增大的方向进行。
9. 热力学第一定律:ΔE=Q+A10.热力学第二定律:孤立系统:ΔS>0(熵增加原理)11. 库仑定律:(k=1/4πε0)12. 高斯定理: (静电场是有源场)→无穷大平板:E=σ/2ε013. 环路定理: (静电场无旋,因此是保守场)θ2Ir P o Rθ1I14. 毕奥—沙伐尔定律:直长载流导线:无限长载流导线:载流圆圈:,圆弧:电磁学1. 定义:= /q0 单位:N/C =V/mB=Fmax/qv;方向,小磁针指向(S→N);单位:特斯拉(T)=104高斯(G) ① 和:=q( + × )洛仑兹公式②电势:电势差:电动势: ( )③电通量:磁通量:磁通链:ΦB=NφB单位:韦伯(Wb)Θ ⊕-q +qS④电偶极矩: =q 磁矩: =I =IS⑤电容:C=q/U 单位:法拉(F)乘自感:L=Ψ/I 单位:亨利(H)乘互感:M=Ψ21/I1=Ψ12/I2 单位:亨利(H)⑥电流:I = ; 乘位移电流:ID =ε0 单位:安培(A)⑦乘能流密度:2. 实验定律① 库仑定律:②毕奥—沙伐尔定律:③安培定律:d =I ×④电磁感应定律:ε感= –动生电动势:感生电动势: ( i为感生电场)乘⑤欧姆定律:U=IR( =ρ )其中ρ为电导率3. 乘定理(麦克斯韦方程组)电场的高斯定理: ( 静是有源场)( 感是无源场)磁场的高斯定理: ( 稳是无源场)( 感是无源场)电场的环路定理: (静电场无旋)(感生电场有旋;变化的磁场产生感生电场)安培环路定理: (稳恒磁场有旋)(变化的电场产生感生磁场)4. 常用公式①无限长载流导线:螺线管:B=nμ0I② 带电粒子在匀强磁场中:半径周期磁矩在匀强磁场中:受力F=0;受力矩③电容器储能:Wc= CU2 乘电场能量密度:ωe= ε0E2 电磁场能量密度:ω= ε0E2+ B2乘电感储能:WL= LI2 乘磁场能量密度:ωB= B2 电磁场能流密度:S=ωV④ 乘电磁波:C= =3.0×108m/s 在介质中V=C/n,频率f=ν=波动学大学物理电磁学公式总结2概念(2113定义和相关公式)1. 位置矢量:,其5261在直角坐标系中: ; 角位置:4102θ16532. 速度:平均速度:速率: ( )角速度:角速度与速度的关系:V=rω3. 加速度:或平均加速度:角加速度:在自然坐标系中其中(=rβ),(=r2 ω)4. 力: =m (或 = ) 力矩: (大小:M=rFcosθ方向:右手螺旋法则)5. 动量:,角动量: (大小:L=rmvcosθ方向:右手螺旋法则)6. 冲量:(= Δt);功: (气体对外做功:A=∫PdV)mg(重力) → mgh-kx(弹性力) → kx2/2F= (万有引力) → =Ep(静电力) →7. 动能:mV2/28. 势能:A保= –ΔEp不同相互作用力势能形式不同且零点选择不同其形式不同,在默认势能零点的情况下:机械能:E=EK+EP9. 热量:其中:摩尔热容量C与过程有关,等容热容量Cv与等压热容量Cp之间的关系为:Cp= Cv+R10. 压强:11. 分子平均平动能: ;理想气体内能:12. 麦克斯韦速率分布函数: (意义:在V附近单位速度间隔内的分子数所占比率)13. 平均速率:方均根速率: ;最可几速率:14. 熵:S=KlnΩ(Ω为热力学几率,即:一种宏观态包含的微观态数)15. 电场强度: = /q0 (对点电荷: )16. 电势: (对点电荷 );电势能:Wa=qUa(A= –ΔW)17. 电容:C=Q/U ;电容器储能:W=CU2/2;电场能量密度ωe=ε0E2/218. 磁感应强度:大小,B=Fmax/qv(T);方向,小磁针指向(S→N)。
大学物理(电磁学)参考公式第一章:一段带电直棒中垂线上一点的场强: 21220)4(4L x x LE +=πελ均匀带电细圆环轴线上任一点场强: 23220)(4x R qxE +=πε 电偶极子在匀强电场中所受的力矩:E P M ϖϖρ⨯= 高斯定理:∑⎰=⋅=Φint1qS d E e εϖρ第三章:静电场的环路定理:0d =⋅⎰Lr E ϖϖ; 电势的定义: ⎰⋅=0d P Pr E ϖϖϕ 均匀带电圆环轴线上一点的电势: 2/1220)(4x R q+=πεϕ 静电场的能量: ⎰⎰==VVeV E V w W d 2d 2ε移动电荷时电场力做功: 212112)(W W q A -=-=ϕϕ第五章:各向同性电介质中的电极化强度与电场强度的关系:()E P r ρρ10-=εε 电介质表面的面束缚电荷密度:n e P P ρρ⋅=='θσcos电介质中封闭面内的体束缚电荷:intq P ds '=-⋅⎰v v Ñ 电位移矢量:0D E P ε=+v v v电位移矢量D ρ的高斯定理:∑⎰=⋅int 0q s d D s ρρ 平行板电容器的电容:dSC r εε0=圆柱形电容器的电容:()120ln 2R R L C r επε=球形电容器的电容:122104R R R R C r -=επε电容器并联:∑=i C C 电容器串联:∑=iC C 11 电容器的能量:QU CU C Q W 21212122=== 静电场的总能量:dV E dV W e ⎰⎰==22εω 第七章: 一个运动电荷在另外的运动电荷周围所受的力 B v q E q F ϖϖϖϖ⨯+=霍尔电压 nqbIBU H =载流导线L 在磁场中受的力 ⎰⨯=L B l Id F ϖϖϖ载流线圈在均匀磁场中受的力矩 B e SI B m M n ϖϖϖωϖ⨯=⨯=线圈磁矩在磁场中的势能 B m W m ϖϖ⋅-=第八章:电流元产生的磁场(毕-萨定律)024r Idl e dB rμπ⨯=v vv磁通连续定理 ⎰=⋅S S d B 0ϖϖ 直线电流的磁场 ()210cos cos 4θθπμ-rIB =圆电流轴线上的磁场 ()2322202x R IR B +=μ载流直螺线管轴线上的磁场 ()120cos cos 2θθμ-=nIB运动电荷产生的磁场 204r e v q B rϖϖϖ⨯=πμ 安培环路定理⎰∑=⋅LI r d B int 0μϖϖ推广的安培环路定理 ⎰⎰⎰⋅⎪⎪⎭⎫ ⎝⎛∂∂+=⎪⎭⎫ ⎝⎛⋅+=⋅S c L s c S d t E J S d E dt d I r d B ϖϖϖϖϖϖϖ0000εμεμ 第九章:磁化强度 r 01M rB μμμ-r r= 磁化电流密度n j M e '=⨯r v r磁场强度 00BrB H M μμμ-v vr v == H 的环路定理0int LH dr I ⋅=∑⎰v vÑ第十章: 法拉第电磁感应定律: 动生电动势:感生电场:互感系数:211212M i i ψψ==互感电动势: 两个载流线圈的总磁能:自感系数:L Iψ=自感电动势:L d dI L dt dt εψ=-=- 自感磁能: 磁场能量密度: (非铁磁质) 磁场总磁能: (非铁磁质)d dtεΦ=-()bb ab ne aaE dl v B dlε=⋅=⨯⋅⎰⎰r r r r rd d d d LSd E l B s dt t εΦ=⋅=-==-⋅⎰⎰r r r rÑ感感1221212d dIM dt dtεψ=-=-2112121d dI M dt dtεψ=-=-212m WLI =221122121122m W L I L I M I I =++2122m B BH ωμ==12m m VVW dV BHdVω==⎰⎰。
大学物理磁学总结大学物理磁学总结篇一:大学物理电磁学公式总结免费下载普通物理学教程——大学物理电磁学公式总结(各种归纳差不多都一样)?第一章(静止电荷的电场)1.电荷的基本性质:两种电荷,量子性,电荷守恒,相对论不变性。
2. 库仑定律:两个静止的点电荷之间的作用力 F3. 电力叠加原理:F=ΣFi kq1q2r2 =?? 4πε0r2?? q1q2 4. 电场强度:0为静止电荷q ??5.场强叠加原理: E=ΣEi 用叠加法求电荷系的静电场:E= i E= ??6. 电通量:Φe= ?? ?? qi4πε0ridq ??? (离散型) (连续型) ?? 4πε0r2??7. 高斯定律:?=int s ε018. 典型静电场:1) 均匀带电球面:E=0 (球面内) 2) 均匀带电球体:qqq 4πε0r2 ????(球面外)ρ??ε0 4πε0R?? =3 ??(球体内) 4πε0r2λ(球体外)方向垂直于带电直线 3) 均匀带电无限长直线: 2πε0r? 4) 均匀带电无限大平面:ε0 ,方向垂直于带电平面9. 电偶极子在电场中受到的力矩:M=p×E ? 第三章(电势)1.静电场是保守场:?=0 L2. 电势差:φ1 –φ2=(p1) 电势:φp= ??? (P0是电势零点) (p)电势叠加原理:φ=Σφi3. 点电荷的电势:q4πε0r (p0) (p2) dq 电荷连续分布的带电体的电势:φ= 4πεr4. 电场强度E与电势φ的关系的微分形式: E=-gradφ=-▽φ=-(i) ?x ?y ?z ?φ?φ?φ电场线处处与等势面垂直,并指向电势降低的方向;电场线密处等势面间距小。
5. 电荷在外电场中的电势能:=qφ移动电荷时电场力做的功:A12=q(φ1 –φ2)=1-2 电偶极子在外电场中的电势能:=-p?E ? 第四章(静电场中的导体)1. 导体的静电平衡条件: Eint=0,表面外紧邻处Es⊥表面或导体是个等势体。
大学物理电磁学知识点磁感应强度(magneticfluxdensity),描述磁场强弱和方向的物理量,是矢量,常用符号B表示,国际通用单位为特斯拉(符号为T)。
磁感应强度也被称为磁通量密度或磁通密度。
在物理学中磁场的强弱使用磁感应强度来表示,磁感应强度越大表示磁感应越强;磁感应强度越小,表示磁感应越弱。
磁感应强度的定义公式磁感应强度公式B=F/(IL)磁感应强度是由什么决定的磁感应强度的大小并不是由F、I、L来决定的,而是由磁极产生体本身的属性。
如果是一块磁铁,那么B的大小之和这块磁铁的大小和磁性强弱有关。
如果是电磁铁,那么B与I、匝数及有无铁芯有关。
物理网很多文章都建议同学们采用类比的方法来理解各个物理量。
我们用电阻R来做个对比。
R的计算公式是R=U/I;可一个导体的电阻R大小并不是由U或者I来决定的。
而是由其导体自身属性决定的,包括电阻率、长度、横截面积。
同样,磁感应强度B也不是由F、I、L来决定的,而是由磁极产生体本身的属性。
如果同学们有时间,可以把静电场中电容的两个公式来对比着复习、巩固下。
B为矢量,方向与磁场方向相同,并不是在该处电流的受力方向,运算时遵循矢量运算法则(左手定则)。
描述磁感应强度的磁感线在磁场中画一些曲线,用(虚线或实线表示)使曲线上任何一点的切线方向都跟这一点的磁场方向相同(且磁感线互不交叉),这些曲线叫磁感线。
磁感线是闭合曲线。
规定小磁针的北极所指的方向为磁感线的方向。
磁铁周围的磁感线都是从N极出来进入S极,在磁体内部磁感线从S极到N极。
磁感线都有哪些性质呢⒈磁感线是徦想的,用来对磁场进行直观描述的曲线,它并不是客观存在的。
⒉磁感线是闭合曲线;磁铁的磁感线,外部从N指向S,内部从S指向N;⒊磁感线的疏密表示磁感应强度的强弱,磁感线上特定点的切线方向表示该点的磁场方向。
⒋任何两条磁感线都不会相交,也不能相切。
磁感线(不是磁场线)的性质与电场线的性质对比来记忆。
磁感应强度B的所有计算式磁感应强度B=F/IL磁感应强度B=F/qv磁感应强度B=ξ/Lv磁感应强度B=Φ/S磁感应强度B=E/v其中,F:洛伦兹力或者安培力q:电荷量v:速度ξ:感应电动势E:电场强度Φ:磁通量S:正对面积磁通量磁通量是闭合线圈中磁感应强度B的累积。
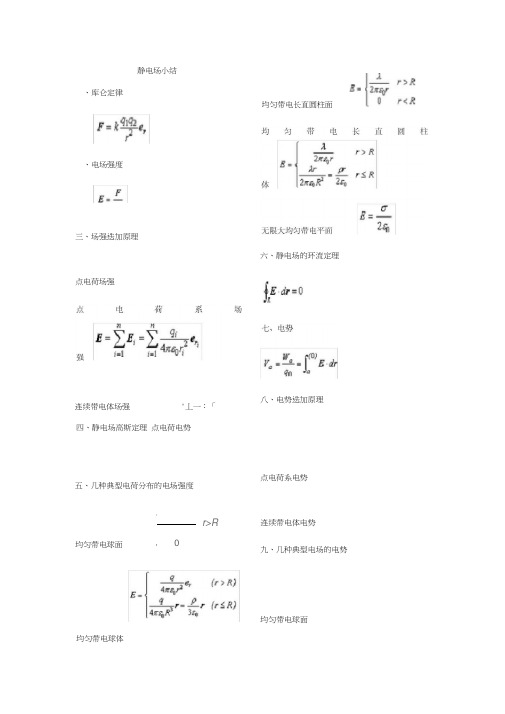
大学物理电磁学公式总结
➢ 第一章(静止电荷的电场)
1. 电荷的基本性质:两种电荷,量子性,电荷守恒,相对论不变性。
2. 库仑定律:两个静止的点电荷之间的作用力
F =
kq 1q 2r 2
e r =
q 1q 2
4πε0r 2
e r
3. 电力叠加原理:F=ΣF i
4. 电场强度:E=F
q
, q 0为静止电荷
5. 场强叠加原理:E=ΣE i
用叠加法求电荷系的静电场:
E =∑q i
4πε0r i 2e ri i (离散型) E=∫dq
4πε0r 2
e r q
(连续型)
6. 电通量:Φe=∫E •dS s
7. 高斯定律:∮E •dS s
=1
ε0
Σq int 8. 典型静电场:
1) 均匀带电球面:E=0 (球面内)
E=
q 4πε0r 2
e r (球面外)
2) 均匀带电球体:E=
q 4πε0R
3
r =ρ3ε0
r (球体内)
E=
q
4πε0r 2
e r (球体外) 3) 均匀带电无限长直线:
E=
λ
2πε0r ,方向垂直于带电直线
4) 均匀带电无限大平面:
E=
σ
2ε0
,方向垂直于带电平面
9. 电偶极子在电场中受到的力矩:
M=p×E
➢ 第三章(电势)
1. 静电场是保守场:
∮E •dr L
=0 2. 电势差:φ1 –φ2=∫E •dr (p2)
(p1)
电势:φp =∫E •dr (p0)
(p) (P0是电势零点) 电势叠加原理:φ=Σφi 3. 点电荷的电势:φ=
q 4πε0r
电荷连续分布的带电体的电势:
φ=∫dq
4πε0
r
4. 电场强度E 与电势φ的关系的微分形式:
E=-gradφ=-▽φ=-(∂φ∂x
i +∂φ∂y
j +∂φ
∂z
k )
电场线处处与等势面垂直,并指向电势降低的方向;电场线密处等势面间距小。
5. 电荷在外电场中的电势能:W=q φ
移动电荷时电场力做的功:
A 12=q(φ1 –φ2)=W 1-W 2
电偶极子在外电场中的电势能:W=-p •E
➢ 第四章(静电场中的导体)
1. 导体的静电平衡条件:E int =0,表面外紧邻处Es ⊥表面 或导体是个等势
体。
2. 静电平衡的导体上电荷的分布:
Q int =0,σ=ε0E
3. 计算有导体存在时的静电场分布问题的基本依据:
高斯定律,电势概念,电荷守恒,导体经典平衡条件。
4. 静电屏蔽:金属空壳的外表面上及壳外的电荷在壳内的合场强总为零,
因而对壳内无影响。
➢ 第五章(静电场中的电介质)
1. 电介质分子的电距:极性分子有固有电距,非极性分子在外电场中产生
感生电距。
2. 电介质的极化:在外电场中固有电距的取向或感生电距的产生使电介质
的表面(或内部)出现束缚电荷。
电极化强度:对各向同性的电介质,在电场不太强的情况下
P=ε0(εr -1)E =ε0X E
面束缚电荷密度:σ’=P•e n 3. 电位移:D =ε0E +P
对各向同性电介质:D =ε0εr E =εE D 的高斯定律:∮D •dS S =q 0int 4. 电容器的电容:C=Q
U
5. 平行板电容器:C=
ε0εr S d
并联电容器组:C=ΣC i 串联电容器组:1
C
=Σ1
C i
6. 电容器的能量:
W=
12Q 2C
=12
CU 2=1
2
QU
7. 电介质中电场的能量密度:ωe =ε0εr E 2
2
=DE
2
➢ 第六章(恒定电流)
1. 电流密度:J =nq v
电流:I=∫J •dS s
电流的连续性方程:∮J •dS s =-dq int dt
2. 恒定电流:∮J •dS s
=0 恒定电场:稳定电荷分布产生的电场
∮E •dr s
=0 3. 欧姆定律:U=IR J=σE (微分形式)
电阻:R=ρl
S
4. 电动势:非静电力反抗静电力移动电荷做功,把其它种形式的能量转换
为电势能,产生电势升高。
Ε=A ne
q =∮E ne•dr L。