训练28

第一周、有效倾听第一天：审视自己的倾听习惯（一）练习：在与他人交流的时候，集中注意力倾听，不对比，不关刻意关注负面信息，不思考接下来该这么应答，并且把倾听之后的感悟写出来，不少于50个字。

第二天：审视自己的倾听习惯（二）练习：在与他人交流之时，集中注意力，不刻意逃避对方的话题，不刻意的讨好迎合对方，不要强行表达自己的观点，学会少说多听，并且把倾听之后的感悟写出来，不少于50个字。

第三天：纠正自己的倾听习惯（一）练习：在与他人交流的时候，集中注意力，适当的时候要有眼神交流，学会用自己的话解释一下对方的观点，让对方觉得我们是理解对方的，适当的时候可以对别人说，我理解你说的，并且把倾听之后的感悟写出来，不少于50个字。

第四天：纠正自己的倾听习惯（二）练习：在与他人交流的时候，集中注意力，倾听对方的话之后，学会表达自己的感受，感受没有好坏之分，就是感觉而已，我们也不需要完全认同对方的观点，学会从他观点中找到自己真正认同的观点，表达认同，并且把倾听之后的感悟写出来，不少于50个字。

第五天：练习有效倾听练习：在于对方交流时，集中注意力，保持适当的眼神交流，学会解释对方表达的内容，适当的做出感受反馈，并且表示理解对方的观点，同时学会找到自己认同的点，表示认同，整个过程尽可能保持全情的专注，并且把倾听之后的感悟写出来，不少于50个字。

第六天：练习有效倾听练习：在于对方交流时，集中注意力，保持适当的眼神交流，学会解释对方表达的内容，适当的做出感受反馈，并且表示理解对方的观点，同时学会找到自己认同的点，表示认同，整个过程尽可能保持全情的专注，并且把倾听之后的感悟写出来，不少于50个字。

第七天：总结练习：总结一下本周所学以及实践的感悟，不少于200字！第二周、肢体交流第一天：审视自己的肢体习惯（一）1、面部动作1）表情太多2）面无表情2、头部动作1）摇头晃脑2）低头作业：与别人正常的交流，同时留意自己与人交流时的习惯，是否存在表情太多，或者面无表情的情况，另外，是否有摇头晃脑，或者习惯性低头不与他人对视的情况，如果有，不要否定自己，也不要攻击自己，试着先接纳这样的自己，然后在打卡处写出自己的感悟。

精心整理28个语言训练技巧1、教孩子用话语表示要大小便 方法： a.选择特定的语言(如撒尿，“西--西--”，尿哗哗等)，作为让孩子大小便时的习惯用语。

b.孩子用动作表示要大小便，如往下拉裤子、抱小腹部时，让孩子跟c.( 谁?” c.a.当孩子指着某物说出它的名称时，你要说：“××在这儿”或“××在那儿”。

b.和孩子做游戏时，把孩子喜欢的小玩具藏起来，问他：“××在哪儿呢?”等待孩子回答。

如果孩子不回答，你把小玩具拿出来，对他说：“××在这儿(那儿)哪!”并让孩子重复说这些话。

当孩子重复说或主动说时，就表扬他。

4、说否定句“不”、“没有”方法： a.让孩子看几种物品，并告诉他物品的名称。

然后把这些物品藏起来，让他反复跟着说：“××没有啦”，如果孩子不说，你就让他跟着你重复说。

b.你指着各种物品或身体的某全部位说：“不是××”。

如，你指着眼睛说：“不是鼻子”，指着杯子说：“不是筷子”。

然后再指其他物品或身体的某c.菜、c.a.让孩子好好看着你把一些物品放进盒子、杯子或盘子里，然后问他：“××在哪儿?”让孩子回答。

b.当家人离开家或房间时，告诉孩子他们的去处，然后问他：“××(爸爸)到哪儿去了?”让孩子回答。

c.在房间里孩子看得到的地方放些物品，问孩子：“××在哪儿?”先让孩子回答物品放的地方，然后再让他把这些物品拿来。

7、说出听到的声音是什么方法：a.当听到某种声音时，立即问孩子：“这是什么声音?”然后带他去找声音的来源，说出发出声音的物品的名称或动物名。

c.c.b.你做些动作游戏，如刷牙、洗手、扫地等，让孩子猜一猜你在做什么。

c.把球、匙子、饭碗和香皂各一个放在桌子上，然后问孩子：“吃饭时使用什么?”、“拍的时候使用什么?”、“喝水的时候使用什么?”如果孩子回答正确，你再问他这些物品是做什么用的。

专题28高中数学等差等比数列证明专题训练【方法总结】1．等差数列的四个判定方法(1)定义法：a n ＋1－a n ＝d (常数)(n ∈N *)⇔{a n }是等差数列．(2)等差中项法：2a n ＋1＝a n ＋a n ＋2(n ∈N *)⇔{a n }是等差数列．(3)通项公式法：a n ＝pn ＋q (p ，q 为常数，n ∈N *)⇔{a n }是等差数列．(4)前n 项和公式法：S n ＝An 2＋Bn (A ，B 为常数，n ∈N *)⇔{a n }是等差数列．提醒：(1)定义法和等差中项法主要适合在解答题中使用，通项公式法和前n 项和公式法主要适合在选择题或填空题中使用．(2)若要判定一个数列不是等差数列，则只需判定存在连续三项不成等差数列即可．2．等比数列的四个判定方法(1)定义法：a n ＋1a n＝q (q 是不为0的常数，n ∈N *)⇔{a n }是等比数列． (2)等比中项法：a 2n ＋1＝a n ·a n ＋2(a n ·a n ＋1·a n ＋2≠0，n ∈N *)⇔{a n }是等比数列．(3)通项公式法：a n ＝cq n (c ，q 均是不为0的常数，n ∈N *)⇔{a n }是等比数列．(4)前n 项和公式法：S n ＝k ·q n －k (k 为常数且k ≠0，q ≠0，1)，则{a n }是等比数列．提醒：(1)定义法和等比中项法主要适合在解答题中使用，通项公式法和前n 项和公式法主要适合在选择题或填空题中使用．(2)若要判定一个数列不是等比数列，则只需判定存在连续三项不成等比数列即可．【高考真题】1．(2022·全国甲理文) 记S n 为数列{a n }的前n 项和．已知2S n n＋n ＝2a n ＋1． (1)证明：{a n }是等差数列；(2)若a 4，a 7，a 9成等比数列，求S n 的最小值．【题型突破】1．已知等差数列{a n }的前n 项和为S n ，且a 3＝7，a 5＋a 7＝26．(1)求a n 及S n ；(2)令b n ＝S n n(n ∈N *)，求证：数列{b n }为等差数列． 2．已知数列{a n }中，a 1＝35，a n ＝2－1a n －1(n ≥2，n ∈N *)，数列{b n }满足b n ＝1a n －1(n ∈N *)． (1)求证：数列{b n }是等差数列；(2)求数列{a n }中的最大项和最小项，并说明理由．3．在数列{a n }中，a 1＝4，na n ＋1－(n ＋1)a n ＝2n 2＋2n ．(1)求证：数列⎩⎨⎧⎭⎬⎫a n n 是等差数列；(2)求数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和S n ． 4．数列{a n }满足a 1＝1，na n ＋1＝(n ＋1)a n ＋n (n ＋1)，n ∈N *．(1)求证：数列⎩⎨⎧⎭⎬⎫a n n 是等差数列； (2)设b n ＝3n ·a n ，求数列{b n }的前n 项和S n ．5．若数列{a n }的前n 项和为S n ，且满足a n ＋2S n S n －1＝0(n ≥2)，a 1＝12． (1)求证：⎩⎨⎧⎭⎬⎫1S n 成等差数列； (2)求数列{a n }的通项公式．6．已知数列{a n }的前n 项和为S n ，且2S n ＝3a n －3n ＋1＋3(n ∈N *)．(1)设b n ＝a n 3n ，求证：数列{b n }为等差数列，并求出数列{a n }的通项公式； (2)设c n ＝a n n －a n 3n ，T n ＝c 1＋c 2＋c 3＋…＋c n ，求T n ． 7．(2021·全国乙)设S n 为数列{a n }的前n 项和，b n 为数列{S n }的前n 项积，已知2S n ＋1b n＝2． (1)证明：数列{b n }是等差数列；(2)求{a n }的通项公式．8．(2014·全国Ⅰ)已知数列{a n }的前n 项和为S n ，a 1＝1，a n ≠0，a n a n ＋1＝λS n －1，其中λ为常数．(1)证明：a n ＋2－a n ＝λ；(2)是否存在λ，使得{a n }为等差数列？并说明理由．9．设数列{a n }的前n 项和为S n ，且满足a n －12S n －1＝0(n ∈N *)． (1)求数列{a n }的通项公式；(2)是否存在实数λ，使得数列{S n ＋(n ＋2n )λ}为等差数列？若存在，求出λ的值；若不存在，请说明理由．10．若数列{b n }对于任意的n ∈N *，都有b n ＋2－b n ＝d (常数)，则称数列{b n }是公差为d 的准等差数列．如数列c n ，若c n ＝⎩⎪⎨⎪⎧4n －1，n 为奇数，4n ＋9，n 为偶数，则数列{c n }是公差为8的准等差数列．设数列{a n }满足a 1＝a ，对于n ∈N *，都有a n ＋a n ＋1＝2n ．(1)求证：{a n }是准等差数列；(2)求{a n }的通项公式及前20项和S 20．11．已知数列{a n }的首项a 1>0，a n ＋1＝3a n 2a n ＋1(n ∈N *)，且a 1＝23． (1)求证：⎩⎨⎧⎭⎬⎫1a n －1是等比数列，并求出{a n }的通项公式； (2)求数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和T n ．12．已知数列{a n }的前n 项和为S n ，n ∈N *，a 1＝1，a 2＝32，a 3＝54，且当n ≥2时，4S n ＋2＋5S n ＝8S n ＋1＋S n － 1．(1)求a 4的值；(2)证明：⎩⎨⎧⎭⎬⎫a n ＋1－12a n 为等比数列． 13．已知数列{a n }的前n 项和S n 满足S n ＝2a n ＋(－1)n (n ∈N *)．(1)求数列{a n }的前三项a 1，a 2，a 3；(2)求证：数列⎩⎨⎧⎭⎬⎫a n ＋23(－1)n 为等比数列，并求出{a n }的通项公式． 14．已知在正项数列{a n }中，a 1＝2，点A n (a n ，a n ＋1)在双曲线y 2－x 2＝1上，数列{b n }中，点(b n ，T n )在直线y ＝－12x ＋1上，其中T n 是数列{b n }的前n 项和． (1)求数列{a n }的通项公式；(2)求证：数列{b n }是等比数列．15．已知数列{a n }满足：a 1＝1，a n ＋1＝⎩⎪⎨⎪⎧a n ＋1，n 为奇数，2a n ，n 为偶数(n ∈N *)，设b n ＝a 2n －1． (1)求b 2，b 3，并证明b n ＋1＝2b n ＋2；(2)①证明：数列{b n ＋2}为等比数列；②若a 2k ，a 2k ＋1,9＋a 2k ＋2成等比数列，求正整数k 的值．16．(2019·全国Ⅱ)已知数列{a n }和{b n }满足a 1＝1，b 1＝0，4a n ＋1＝3a n －b n ＋4，4b n ＋1＝3b n －a n －4．(1)证明：{a n ＋b n }是等比数列，{a n －b n }是等差数列；(2)求{a n }和{b n }的通项公式．17．(2018·全国Ⅰ)已知数列{a n }满足a 1＝1，na n ＋1＝2(n ＋1)a n ，设b n ＝a n n． (1)求b 1，b 2，b 3；(2)判断数列{b n }是否为等比数列，并说明理由；(3)求{a n }的通项公式．18．已知数列{a n }的前n 项和为S n ，a 1＝1，a n >0，S 2n ＝a 2n ＋1－λS n ＋1，其中λ为常数．(1)证明：S n ＋1＝2S n ＋λ；(2)是否存在实数λ，使得数列{a n }为等比数列，若存在，求出λ；若不存在，说明理由．19．设等差数列{a n }的前n 项和为S n ，a ＝(a 1，1)，b ＝(1，a 10)，若a·b ＝24，且S 11＝143，数列{b n }的前n项和为T n ，且满足12n a -＝λT n －(a 1－1)(n ∈N *)．(1)求数列{a n }的通项公式及数列⎩⎨⎧⎭⎬⎫1a n a n ＋1的前n 项和M n ； (2)是否存在非零实数λ，使得数列{b n }为等比数列？并说明理由．20．已知数列{a n }满足a 1＝1，a n ＋1＝2a n ＋λ(λ为常数)．(1)试探究数列{a n＋λ}是不是等比数列，并求a n；(2)当λ＝1时，求数列{n(a n＋λ)}的前n项和T n．。

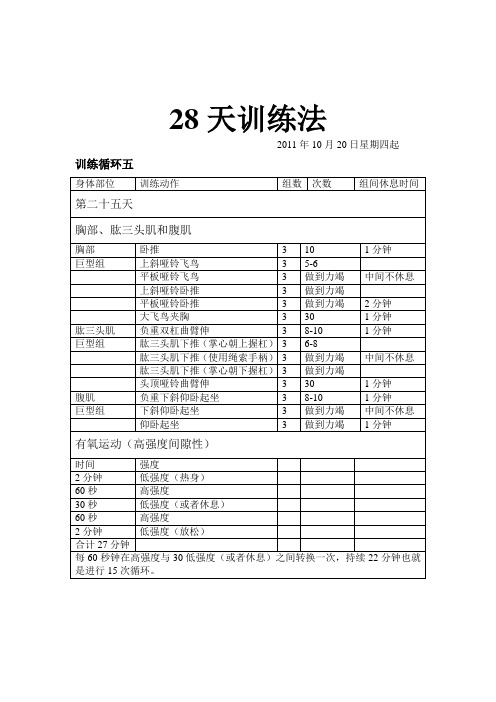
28天训练法2011年10月20日星期四起训练循环五身体部位训练动作组数次数组间休息时间第二十五天胸部、肱三头肌和腹肌胸部卧推 3 10 1分钟巨型组上斜哑铃飞鸟 3 5-6平板哑铃飞鸟 3 做到力竭中间不休息上斜哑铃卧推 3 做到力竭平板哑铃卧推 3 做到力竭2分钟大飞鸟夹胸 3 30 1分钟肱三头肌负重双杠曲臂伸 3 8-10 1分钟巨型组肱三头肌下推（掌心朝上握杠）3 6-8肱三头肌下推（使用绳索手柄）3 做到力竭中间不休息肱三头肌下推（掌心朝下握杠）3 做到力竭头顶哑铃曲臂伸 3 30 1分钟腹肌负重下斜仰卧起坐 3 8-10 1分钟巨型组下斜仰卧起坐 3 做到力竭中间不休息仰卧起坐 3 做到力竭1分钟有氧运动（高强度间隙性）时间强度2分钟低强度（热身）60秒高强度30秒低强度（或者休息）60秒高强度2分钟低强度（放松）合计27分钟每60秒钟在高强度与30低强度（或者休息）之间转换一次，持续22分钟也就是进行15次循环。

身体部位训练动作组数次数组间休息时间第二十六天背部、肱二头肌和前臂背部硬拉 3 8-10 1分钟巨型组高位下拉机颈后下拉 3 6-8高位下拉机颈前下拉 3 做到力竭中间不休息掌心朝后握杆下拉 3 做到力竭2分钟坐姿拉索划船 3 30 1分钟肱二头肌曲柄杠铃弯举 3 8-10 1分钟巨型组上斜哑铃弯举 3 6-8坐姿弯举 3 做到力竭中间不休息站姿哑铃交替弯举 3 做到力竭1分钟前臂正握杠铃腕弯举 3 6-8 中间不休息超级组反握杠铃腕弯举 3 做到力竭1分钟有氧运动（高强度间隙性）26、27、28天时间强度2分钟低强度（热身）60秒高强度30秒低强度（或者休息）60秒高强度2分钟低强度（放松）合计29分钟每60秒钟在高强度与30秒低强度（或者休息）之间转换一次，持续2415分钟，也就是16次循环。

28天把体脂减少5%计划。

身体部位训练动作组数次数组间休息时间第二十七天肩膀、斜方肌和腹肌肩膀杠铃推举 3 8-10 1分钟斯密斯机宽握杠铃划船 3 8-10 2分钟巨型组俯身哑铃侧平举 3 5-6站姿哑铃侧平举 3 做到力竭中间不休息哑铃前平举 3 做到力竭休息2分钟斜方肌颈后杠铃耸肩 3 8-10 中间不休息超级组杠铃耸肩 3 做到力竭坐姿弯举 3 做到力竭2分钟腹肌悬挂举腿 4 做到力竭中间不休息超级组拉索负重卷腹 4 8-10 1分钟有氧运动（高强度间隙性）时间强度2分钟低强度（热身）60秒高强度30秒低强度（放松）60秒高强度2分钟放松合计29分钟每60秒钟在高强度与30秒低强度（或者休息）之间转换一次，持续2415分钟，也就是16次循环。

AComplete the following passage with the words or phrases in the box. Each word can only be used once（将下列单词或词组填入空格。

每空格限填一词，每词只能填一次）：A．seriousB．machineC．prizeD．observingE．impossibleF．interested inG．inventorH．marathonI．usefulWelcome to the Amazing Kids Website! Here you can read about clever children all over the world.Gina, who is thirteen years old, got first 1 in the" Young Cook of the Year" competition and is now writing her own recipe（食谱）book for kids. "I want it to be fun to read and easy enough for children to use," she says. Gina learned by 2 her father, who's also good at cooking, in the kitchen. She wants to encourage other children to cook because" everyone needs to eat, so it's a skill that will always be 3 !"Fourteen-year-old Bren used to love running until he had a 4 car accident three years ago. He lost part of one leg and didn't even expect to walk again. Now he's an athlete who has recently completed a 5 . "After my accident I wanted to give up," he says. "But now I'm happy to be alive and able to continue running. "Helga has always been good at science, but she thought it was too difficult to become an 6 . Then she heard about an accident that had happened when a car hit a train in her town. "That gave me an idea," says the clever sixteen-year-old girl. It took her over a year to invent a special 7 that tells car drivers when a train is coming. One company is already 8 selling it, so it may be in the shops soon!BChoose the best answer（根据短文内容，选择最恰当的答案）：One day, Tony walked home from the park where he had baseball practice. His sister Lara was home from college, and he was excited to show off his baseball uniform.As he approached his house, Tony saw Lara's car parked in the driveway and hurried. He decided to go around to the back door to surprise his sister.When he got to the door, he noticed a yellow sticky note on the door. On the sticky note was a word he didn't know. Tony shrugged（耸肩）and opened the door.Inside the kitchen, Tony observed that everything had a tiny sticky（黏性的）note on it—the sink, table, chairs, refrigerator, oven, and microwave. Even the flowers had a sticky note on them! Each note had a different word on it. He raised his eyebrows and went into the family room to find his sister.Again, he found tiny sticky notes everywhere. The couch, recliner, TV, stereo, and bookshelves were all labeled with strange words. And where was Lara?He went up the sticky-note-labeled staircase to his room. Just as Tony had suspected（怀疑）, his room was plastered（粘贴）with notes. His bed, lamp, closet, and desk all wore sticky notes. Even his baseball bat had a note on it! What was going on?"Hey, kiddo," he heard his sister say. Tony turned around as Lara was putting a sticky note on his light switch."What are you doing?" Tony asked. Lara explained to Tony that the words were Spanish for the things they were stuck on. The notes were helping Lara learn Spanish!1．Tony wanted to show his sister ________.A．his new uniformB．his baseball gloveC．his baseball batD．an autographed baseball2．Why didn't Tony use the front door?A．It was locked.B．It had a note on it.C．Lara was using it.D．He wanted to surprise Lara.3．What did Tony observe when he got home?A．His sister was not at home.B．He noticed an envelope on the door.C．Everything has a tiny stick note on it.D．His parents were waiting for him at home.4．What did NOT have a sticky note on it when Tony first got home?A．Flowers in the kitchen.B．His bedroom light switch.C．The stereo.D．The couch.5．What was Lara doing?A．She was playing.B．She was learning Spanish.C．She was giving a lesson.D．She was practicing baseball.6．What can we learn from the story?A．Tony is a good student.B．The parents are teachers of Spanish.C．Tony and his sister are learning Spanish.D．Tony's sister is a good college student.CChoose the words or expressions and complete the passage（选择最恰当的单词或词语完成短文）：When I was fifteen I went to a summer camp. There were lots of great 1 but there was one thing I was really scared（害怕的）about: climbing the wall.The wall is a kind of rock that people use to learn how to climb. It is very tall. We were all supposed to climb the wall, but I knew I couldn't get to the top because I am 2 heights. I was ashamed and I didn't want anyone to knowthat I was scared. I thought they would all laugh at me. I practiced my excuse: "I'm not scared, you know. I suffer from vertigo（眩晕）. "The day came. It was time to climb the wall. The sun was shining but everyone was very quiet that morning. I took photographs at the bottom of the wall and tried to 3 . Everyone in the group went up. Then the moment came. It was my turn. I was so scared that all I could think about was my excuse. Someone said," shall I take your camera?" and I answered," I'm not scared, you know. I suffer from vertigo." The 4 was that I was more than scared. I was terrified. The camp leader said," Don't worry, you don't have to do anything you don't want to do." I was surprised. Everyone was understanding. No one 5 .The next day, the leader asked me if I wanted to try the wall on my own, 6 the others watching. Although I was still very nervous I agreed and climbed slowly to the top with his help. I was still shaking when I came down, but I was really happy and relieved（释然的）too. For me, climbing the wall was a real achievement.1．A．activitiesB．operationsC．accidentsD．exams2．A．poor atB．good atC．afraid ofD．fond of3．A．goB．hideC．appearD．run4．A．truthB．situationC．storyD．reason5．A．jumpedB．cheeredC．smiledD．laughed6．A．withB．withoutC．amongD．behindDRead the passage and fill in the blanks with suitable words（在短文的空格内填入适当的词，使其内容通顺。

天天练文言断句专练(二)基础过关．用斜线()给下面文言文中的画线部分断句。

(限处)今以百金与抟黍以示儿子儿子必取抟黍矣以和氏之璧与百金以示鄙人鄙人必取百金矣以和氏之璧道德之至言以示贤者贤者必取至言矣。

其知弥精，其所取弥精；其知弥粗，其所取弥粗。

(选自《吕氏春秋》)答案：今以百金与抟黍以示儿子儿子必取抟黍矣以和氏之璧与百金以示鄙人鄙人必取百金矣以和氏之璧道德之至言以示贤者贤者必取至言矣原文：今以百金与抟黍以示儿子，儿子必取抟黍矣；以和氏之璧与百金以示鄙人，鄙人必取百金矣；以和氏之璧、道德之至言以示贤者，贤者必取至言矣。

【参考译文】假如现在把百金与黄鸟摆在一个小孩面前，小孩肯定选取黄鸟；把和氏璧和百金摆在一个粗鄙无知的人面前，粗鄙无知的人肯定选取百金；把和氏璧、有关道德的至理名言摆在贤者面前，贤者肯定选取至理名言。

他们的知识越精深，所选取的东西越精妙；他们的知识越粗浅，所选取的东西越粗陋。

．用斜线()给下面文言文中的画线部分断句。

(限处)文公问箕郑曰：“救饿奈何？”对曰：“信。

”公曰：“安信？”曰：“信名，信事，远者归信义。

信名则群臣守职善恶不逾百事不怠信事则不失天时百姓不逾信义则近亲劝勉而”(之矣。

)选自《韩非子》答案：信名则群臣守职善恶不逾百事不怠信事则不失天时百姓不逾信义则近亲劝勉而远者归之矣原文：信名，则群臣守职，善恶不逾，百事不怠；信事，则不失天时，百姓不逾；信义，则近亲劝勉，而远者归之矣。

【参考译文】晋文公问箕郑说：“怎样救济饥荒？”箕郑回答说：“守信用。

”晋文公说：“怎样守信用呢？”箕郑说：“在名位、政事、道义上都要守信用。

在名位上守信用，那么群臣就会尽职尽责，好的坏的不会混杂，各种政事不会懈怠；在政事上守信用，那么就不会错过天时，百姓就不会逾越自己的本职；在道义上守信用，那么亲近的人就敢于规劝勉励，远方的人也会前来归顺。

”．用斜线()给下面文言文中的画线部分断句。

(限处)唐震字景实，会稽人。

基础过关训练28 赤壁赋［基础演练］1．下列加点字读音有误的一项是()A．窈．窕（yǎo)冯．(píng）虚御风棹．(zhào）B．嫠．（lí）妇愀．(qiū）然酾．(shī）酒C．横槊．(shuò）渚．(zhǔ) 蜉蝣．．(fú yóu)D．无尽藏．（zàng) 藉．(jiè) 壬．(rén)戌2．下列各句中字形无误的一组是（)A．壬戊之秋，七月既望B．飘飘乎如遗世独立，羽化而登仙C．月明星稀，乌雀南飞D．寄蜉蝣于天地,渺沧海之一栗3．下列各句中没有通假字的一组是（)A．扁鹊望桓侯而还走B．山川相缪C．寄蜉蝣于天地D．冯虚御风4．下列各句中加点词的古今意义相同的一项是()A．所以．．游目骋怀,足以极视听之娱B．渺沧海．．之一粟C．白露．．横江D．凌万顷之茫然．．5．下列各句中加点字解释错误的一项是(）A．①举酒属．客（劝人饮酒）②徘徊于斗牛．．之间(斗宿星和牛宿星）B．①倚歌而和．之（同声相应，唱和)②余音袅袅．．(形容声音婉转悠长。

）C．①方其破荆州，下．江陵(往下游走)②击空明．．兮溯流光(澄明的水波)D．①山川相缪．,郁乎苍苍（同“缭”,盘绕）②酾酒．．临江，横槊赋诗（斟酒)6．与“苏子与客泛舟游于赤壁之下”中的“于”字意义用法相同的一项是（)A．况吾与子渔樵于．江渚之上B．托遗响于．悲风C．此非孟德之困于．周郎者乎D．月出于．东山之上7．下列各句的句式特点和其他三句不同的是（）A．而今安在哉?B．何为其然也?C．沛公安在?D．此非孟德之困于周郎者乎8．黄州赤壁因为苏轼的吟诵而声名大振。

春节晚会上，有一副对联写到了江南两省富有人文特色的自然景观。

把对联补齐,并说明分别是哪两个省拟出来的。

上联:八百里凭岳阳壮阔省份下联：赤壁揽黄鹤风流省份9．下列文学文化常识解释错误的一项是（）A．既望：过了望日后的第一天,通常指农历每月十六日.望：农历每月十五日.B．美人：指所思慕的人，古人作品中常用美人来作为圣主贤臣或美好理想的象征。

专题28 利用乘法公式和因式分解简便计算【例题讲解】用简便方法进行计算．（1）21.4×2.3+2.14×27+214×0.5．（2）22100007525-． （3）（2112-）×2211(1)(1)34-⨯-⨯…×（21110-）． （4）1952+195×10+52． 1191010⨯⨯⨯195×5+521．用简便方法计算2008﹣4016×2007+2007的结果是_____．2．利用因式分解计算：22111021198⨯-⨯的结果是______．3．利用因式分解简便运算：2252.847.2-＝_____．4．利用因式分解计算2221000252248=-__________． 5．计算：2222020200119=200119--⨯__． 6．利用因式分解计算：3.4614.70.5414.729.4⨯+⨯-=______.7．利用因式分解计算：2022+202×196+982=______．8．利用乘法公式简便计算．(1)4.3212＋8.642×0.679＋0.6792；(2)2020×2022－20212．9．利用因式分解计算(1)2900894906-⨯(2)2.6815.731.415.7 1.32⨯-+⨯10．利用因式分解计算：（1）21 3.1462 3.1417 3.14⨯+⨯+⨯；（2）22758258-．11．利用因式分解进行简便运算：（1）2920.217220.2120.21⨯+⨯- （2）2210119810199+⨯+12．利用因式分解进行简便计算：（1）3×852﹣3×152；（2）20212﹣4042×2019+20192．13．利用因式分解计算：225652443524⨯-⨯．14．计算：（要求：应用因式分解巧算，写明计算过程）（1）7749.124.12525⨯-⨯； （2）1.1 2.5 2.29 2.50.61 2.5⨯+⨯+⨯； （3）20.9990.9990.001+⨯；（4）已知2004+=a b ，1003=ab ，求22222-+a b a b ab 的值．15．简便计算：（1）227.29 2.71-；（2）2.887.680.48⨯+⨯-⨯；（3）2200820081664-⨯+．16．用简便方法计算：（1）8502﹣1700×848+8482（2）2221111()1()1()232021⎡⎤⎡⎤⎡⎤-⨯-⨯⋯⨯-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦17．简便计算（1）221.2229 1.3334⨯-⨯ （2）2220220219698⨯++18．利用因式分解计算：（1）222222221009998974321-+-+⋯+-+-（2）()()()()2483212451515151++++⋅⋯⋅+（3）()()4222222n n n ++-19．用简便方法计算：（1）22429171-（2）2220220219698⨯++20．利用因式分解计算：22015201520152016+-⨯21．利用因式分解计算：（1）342+34×32+162（2）38.92-2×38.9×48.9+48.9222．计算：①2032﹣203×206+1032②20192﹣2018×2020．23．用简便方法计算．（1）227.29 2.71-（2）44134 23.7 1.35555 -⨯+⨯-⨯24．利用因式分解计算：3232 2018320182015 201820182019-⨯-+-25．利用因式分解简便计算：11 1009922⨯26．利用因式分解计算：（1）9788597879788⨯+⨯+⨯；（2）23.86 3.86 3.85-⨯. 27．利用乘法公式计算：（1）2201920182020-⨯. （2）299.8.专题28 利用乘法公式和因式分解简便计算【例题讲解】用简便方法进行计算．（1）21.4×2.3+2.14×27+214×0.5．（2）22100007525-． （3）（2112-）×2211(1)(1)34-⨯-⨯…×（21110-）． 221191010⨯⨯⨯195×5+52，1．用简便方法计算2008【答案】1．【分析】共三项，其中4016是2×2008，用完全平方公式分解因式即可解答.【解答】20082﹣4016×2007+20072，＝20082﹣2×2008×2007+20072，＝（2008﹣2007）2，＝1．【点评】此题考查公式法在有理数计算中的应用，正确分析出所应用的公式是解题的关键. 2．利用因式分解计算：22111021198⨯-⨯的结果是______．【答案】8800【分析】先提出11，再根据平方差公式计算即可．【解答】原式=2211(10298)⨯-=11(10298)(10298)⨯+⨯-=112004⨯⨯=8800．故答案为：8800．【点评】本题主要考查了应用因式分解计算，掌握平方公式是解题的关键．即22()()a b a b a b -=+-．3．利用因式分解简便运算：2252.847.2-＝_____．【答案】560【分析】利用平方差法进行因式分解，再进行计算；【解答】原式＝()()52.847.252.847.2+⨯-＝100 5.6⨯＝560．故答案为：560．【点评】本题考查利用公式法因式分解进行简便运算．熟练掌握公式法因式分解是解题的关键．4．利用因式分解计算2221000=__________．5．计算：2020200119=--__．6．利用因式分解计算：______.【答案】29.4【分析】根据提取公因式法，提取公因数14.7，进行简便计算，即可. 【解答】原式=(3.46+0.542)14.7-⨯=214.7⨯=29.4故答案为：29.4.【点评】本题主要考查提取公因式法分解因式，提取公因数14.7，进行简便计算，是解题的关键.7．利用因式分解计算：2022+202×196+982=______．【答案】90000．【分析】将式子改写为完全平方公式的形式进行计算.【解答】原式2220222029898=+⨯⨯+2(20298)=+2300=90000=．故答案为90000．【点评】本题考查利用完全平方公式计算，熟练掌握公式的形式是关键.8．利用乘法公式简便计算．(1)4.3212＋8.642×0.679＋0.6792；(2)2020×2022－20212．【答案】(1)25(2)-1【分析】（1）根据完全平方公式计算即可；（2）根据平方差公式计算即可【解答】（1）4.3212＋8.642×0.679＋0.6792224.3212 4.3210.6790.679=+⨯⨯+()24.3210.679=+ 25=25=（2）2020×2022－20212()()220211202112021=-+-222=202112021--1=-【点评】本题考查了利用乘法公式简便计算，掌握乘法公式是解题的关键．9．利用因式分解计算(1)2900894906-⨯ (2)2.6815.731.415.7 1.32⨯-+⨯【答案】(1)36(2)31.4【分析】（1）先将894906⨯变形为()()a b a b +-的形式，再利用平方差公式求解；（2）先提取公因式15.7，再进行计算即可．【解答】（1）解：2900894906-⨯222222290090(9006)(9006)(9006)9609000630--⨯+=--=-+==（2）解：2.6815.731.415.7 1.32⨯-+⨯15.7(2.682 1.32)15.7231.4=⨯-+=⨯= 【点评】本题考查通过因式分解进行简化计算，解题关键是提取公因式或根据数字特点将所求式子进行变形后利用公式求解．10．利用因式分解计算：（1）21 3.1462 3.1417 3.14⨯+⨯+⨯；（2）22758258-．【答案】（1）314；（2）508000【分析】（1）利用提取公因式法计算；（2）应用平方差公式计算．【解答】解：（1）原式 3.14(216217)314=⨯++=；（2）原式(758258)(758258)1016500508000=+-=⨯=．【点评】本题考查因式分解的应用，属于基础题型．11．利用因式分解进行简便运算：（1）2920.217220.2120.21⨯+⨯- （2）2210119810199+⨯+【答案】（1）2021；（2）40000【分析】（1）观察式子，利用提公因式法进行求解；（2）根据式子的特点，利用完全平方公式进行求解．【解答】（1）解：原式()20.2129721=⨯+-20.21100=⨯2021=．（2）解：原式2210129910199=+⨯⨯+()210199=+ 2200=40000=【点评】本题考查因式分解的应用，解题的关键是根据每个式子中的特点选择适当的因式分解的方法（如提公因式法、公式法等），从而简化计算．12．利用因式分解进行简便计算：（1）3×852﹣3×152； （2）20212﹣4042×2019+20192．【答案】（1）21000；（2）4【分析】（1）提取公因式，利用平方差公式进行因式分解计算即可；（2）对原式进行变形，利用完全平方公式直接分解因式计算即可．【解答】解：（1）3×852﹣3×152=3×（852-152）=3×（85+15）×（85-15）=3×100×70=21000；（2）20212﹣4042×2019+20192=20212-2×2021×2019+20192=（2021-2019）2=22=4．【点评】本题考查了因式分解的应用，熟练掌握平方差公式和完全平方公式是解题的关键． 13．利用因式分解计算：225652443524⨯-⨯．【答案】3120000【分析】先提取24，再利用平方差公式即可求解．【解答】225652443524⨯-⨯=()2224565435⨯-=()()24565435565435⨯+⨯-=241000130⨯⨯=3120000．【点评】此题主要考查因式分解的运用，解题的关键是熟知平方差公式的运用．14．计算：（要求：应用因式分解巧算，写明计算过程）（1）7749.124.12525⨯-⨯； （2）1.1 2.5 2.29 2.50.61 2.5⨯+⨯+⨯；（3）20.9990.9990.001+⨯； 2222）a (a -原式()1003200420062006=⨯-=-．【点评】本题考查了因式分解的应用，掌握因式分解的方法是解题的关键．15．简便计算：（1）227.29 2.71-；（2）2.887.680.48⨯+⨯-⨯； （3）2200820081664-⨯+．【答案】（1）45.8；（2）80；（3）4000000【分析】（1）利用平方差公式即可求解；（2）提取8，故可求解；（3）利用完全平方公式即可求解．【解答】（1）227.29 2.71-=()()7.29 2.717.29 2.71+⨯-=10×4.58=45.8；（2）2.887.680.48⨯+⨯-⨯=()8 2.87.60.4⨯+-=8×10=80（3）2200820081664-⨯+=2220082200888-⨯⨯+=()220088-=20002=4000000．【点评】此题主要考查因式分解的应用，解题的关键是熟知提公因式法、公式法分解因式．16．用简便方法计算：（1）8502﹣1700×848+8482（2）2221111()1()1()⎡⎤⎡⎤⎡⎤-⨯-⨯⋯⨯-⎢⎥⎢⎥⎢⎥ 112021⎛⨯⨯+ ⎝20222021⨯⨯⨯20202021⨯⨯⨯【点评】本题考查了因式分解的应用，熟练掌握完全平方公式、平方差公式是解本题的关键．（1）221.2229 1.3334⨯-⨯ （2）2220220219698⨯++【答案】（1）6.332；（2）90000【分析】（1）先利用同底数幂的乘法变形，再利用平方差公式计算；（2）利用完全平方公式变形计算．【解答】解：（1）221.2229 1.3334⨯-⨯=22221.2223 1.3332⨯-⨯=()()221.2223 1.3332⨯-⨯=223.666 2.666-=()()3.666 2.666 3.666 2.666+-=6.332；（2）2220220219698+⨯++=2220222029898+⨯⨯+=()220298+=90000【点评】本题考查了同底数幂的乘法，平方差公式，完全平方公式，计算时注意乘法公式的应用．18．利用因式分解计算：（1）222222221009998974321-+-+⋯+-+-（2）()()()()2483212451515151++++⋅⋯⋅+（3）()()4222222n n n ++-（1）22429171-（2）2220220219698⨯++【答案】（1）154800；（2）90000.【分析】（1）利用平方差公式进行计算即可得到答案；（2）把原式化为：2220222029898+⨯⨯+，再利用完全平方公式进行计算即可得到答案．【解答】解：（1）22429171-()()429171429171=+-600258154800=⨯=（2）2220220219698⨯++2220222029898=+⨯⨯+()220298=+ 230090000.==【点评】本题考查的是利用平方差公式与完全平方公式进行简便计算，掌握两个公式的特点是解题的关键．20．利用因式分解计算：22015201520152016+-⨯【答案】0【分析】先提取公因数2015进行分解，然后再进行计算即可．【解答】22015201520152016+-⨯=()2015120152016⨯+-=20150⨯0=．【点评】本题考查了利用因式分解进行计算，熟练掌握提公因式法是解此题的关键．21．利用因式分解计算：（1）342+34×32+162 （2）38.92-2×38.9×48.9+48.92【答案】（1）2500；（2）100．【分析】（1）转化为完全平方公式形式，计算即可；（2）根据完全平方公式计算即可．【解答】解：（1）342+34×32+162=342+2×34×16+162=(34+16)2=502=2500；（2）38.92-2×38.9×48.9+48.92=(38.9-48.9)2=(-10)2=100．【点评】本题考查了根据完全平方公式因式分解，熟练掌握完全平方式的特点是解题关键．22．计算：①2032﹣203×206+1032 ②20192﹣2018×2020．【答案】①10000；②1．【分析】①根据完全平方公式计算即可；②根据平方差公式计算即可．【解答】解：①原式＝2032﹣2×203×103+1032＝（203﹣103）2＝1002＝10000； ②原式＝20192﹣（2019﹣1）×（2019+1）＝20192﹣（20192﹣1）＝20192﹣20192+1＝1．【点评】本题主要考查了平方差公式以及完全平方公式，熟记公式是解答本题的关键．平方差公式：()()22a b a b a b +-=-．完全平方公式：()2222a b a ab b ±=±+．23．用简便方法计算．（1）227.29 2.71-（2）4413423.7 1.3-⨯+⨯-⨯24．利用因式分解计算：322018320182015-⨯-25．利用因式分解简便计算：10099⨯（1）9788597879788⨯+⨯+⨯；（2）23.86 3.86 3.85-⨯.【答案】（1）97800；（2）0.0386【分析】（1）提取公因式978后进行计算；（2）提取公因式3.86后进行计算.【解答】(1)原式()9788578=⨯++97800=.(2)原式()3.86 3.86 3.85=⨯-0.0386=.【点评】本题考查利用因式分解对有理数进行简便运算，利用提取公因式因式分解是解答此题的关键.27．利用乘法公式计算：（1）2201920182020-⨯. （2）299.8.【答案】（1）1（2）9960.04【分析】(1)观察算式，把2018和2020分别用2019-1和2019+1表示，利用平方差公式对这一部分进行运算，然后再去括号相加减即可；(2)将99.8表示成100-0.2，然后利用完全平方公式展开运算即可.【解答】（1）原式22019(20191)(20191)=--⨯+()2222019201911=--=（2）原式2(1000.2)=-2210021000.20.2=-⨯⨯+9960.04=【点评】本题考查了乘法公式，熟练掌握平方差公式和完全平方公式并运用是解题的关键.。