初三数学阶段测试圆和二次函数

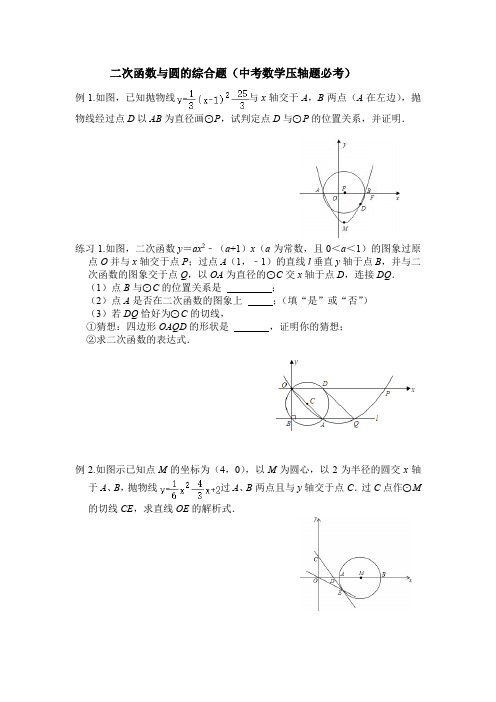
二次函数与圆的综合题（中考数学压轴题必考）例1.如图，已知抛物线与x轴交于A，B两点（A在左边），抛物线经过点D以AB为直径画⊙P，试判定点D与⊙P的位置关系，并证明．练习1.如图，二次函数y＝ax2﹣（a+1）x（a为常数，且0＜a＜1）的图象过原点O并与x轴交于点P；过点A（1，﹣1）的直线l垂直y轴于点B，并与二次函数的图象交于点Q，以OA为直径的⊙C交x轴于点D，连接DQ．（1）点B与⊙C的位置关系是；（2）点A是否在二次函数的图象上；（填“是”或“否”）（3）若DQ恰好为⊙C的切线，①猜想：四边形OAQD的形状是，证明你的猜想；②求二次函数的表达式．例2.如图示已知点M的坐标为（4，0），以M为圆心，以2为半径的圆交x轴于A、B，抛物线过A、B两点且与y轴交于点C．过C点作⊙M 的切线CE，求直线OE的解析式．练习2.平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴，设平行于x轴的直线交抛物线y＝﹣x2﹣x+2于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径；若不存在，请说明理由．练习3.如图，抛物线y＝﹣x2﹣x+2与x轴交于A（﹣4，0），B（2，0），与y 轴交于点C（0，2）．以AB为直径作⊙M，直线经过点E（﹣1，﹣5），并且与⊙M相切，求该直线的解析式．练习4.如图，抛物线y＝﹣x2+x+2．经过A、B、C三点，A点坐标为（4，0），B点坐标为（﹣1，0），以AB的中点P为圆心，AB为直径作⊙P的正半轴交于点C，M为抛物线的顶点，试说明直线MC与⊙P的位置关系，并证明你的结论．练习5.如图，抛物线与x轴交于A、B两点，与y轴交于C点．以AB为直径作⊙M．（1）求出M的坐标并证明点C在⊙M上；（2）若P为抛物线上一动点，求出当CP与⊙M相切时P的坐标；练习6.在平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴于点C，过点C作圆的切线交x轴于点D．（1）求点C的坐标和过A，B，C三点的抛物线的析式；（2）求点D的坐标：（3）设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径，若不存在，请说明理由．练习7.如图，在平面直角坐标系中，已知OA＝n，OC＝m，⊙M与y轴相切于点C，与x轴交于A，B两点，∠ACD＝90°，抛物线y＝ax2+bx+c经过A，B，C三点．（1）求证：∠OCA＝∠OBC；（2）若A（x1，0），B（x2，0），且x1，x2满足x1+x2＝5，x1•x2＝4，求点C 的坐标和抛物线的解析式；（3）若△ACD≌△ABD，在四边形ABDC内有一点P，且点P到四边形四个顶点的距离之和P A+PB+PC+PD最小，求此时距离之和的最小值及P点的坐标（用含n的式子表示）．练习8.已知二次函数y＝mx2+（m﹣3）x﹣3（m＞0）（1）求证：它的图象与x轴必有两个交点；（2）这条抛物线与x轴交于两点A、B（A在B左），与y轴交于点C，顶点为D，sin∠ABD＝，⊙M过A、B、C三点，求⊙M的面积；（3）在（2）的条件下，抛物线上是否存在点P，使P A是⊙M的切线？若存在，求出P点的坐标，若不存在，说明理由．例3.如图，抛物线y＝ax2+bx+c（a，b，c是常数，a≠0）的对称轴为y轴，且经过（0，0）和（，）两点，点P在该抛物线上运动，以点P为圆心的⊙P总经过定点A（0，2）．（1）求a，b，c的值；（2）求证：在点P运动的过程中，⊙P始终与x轴相交；（3）设⊙P与x轴相交于M（x1，0），N（x2，0）（x1＜x2）两点，当△AMN 为等腰三角形时，求圆心P的纵坐标．练习9.已知：如图，抛物线y＝ax2+bx+1的图象关于y轴对称，且抛物线过点（2，2），点P为抛物线上的动点，以点P为圆心的⊙P与x轴相切，当点P运动对，⊙P始终经过y轴上的一个定点E．（1）求抛物线的解析式；（2）当⊙P的半径为时，⊙P与y轴交于M、N两点，求MN的长；（3）求定点E到直线y＝kx﹣8k的距离的最大值．练习10.已知：直线y＝﹣x﹣4分别交x、y轴于A、C两点，抛物线y＝ax2+bx （a＞0）经过A、O两点，且顶点B的纵坐标为﹣2（1）判断点B是否在直线AC上，并求该抛物线的函数关系式；（2）以点B关于x轴的对称点D为圆心，以OD为半径作⊙D，试判断直线AC与⊙D的位置关系，并说明理由；（3）若E为⊙D的优弧AO上一动点（不与A、O重合），连接AE、OE，问在抛物线上是否存在点P，使∠POA：∠AEO＝2：3？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．练习11.已知A是x轴正半轴上一个动点，以线段OA为直径作⊙B，圆心为点B，直径OA＝m，线段EF是⊙B的一条弦，EF∥x轴，点C为劣弧EF的中点，过点E作DE垂直于EF，交抛物线C1：y＝ax2+bx（a＞0）于点G，抛物线经过点O和点A．（1）求证：DG＝m；（2）拖动点A，如果抛物线C1与⊙B除点O和点A外有且只有一个交点，求b的值；（3）拖动点A，抛物线C1交⊙B于点O、E、F、A，①求证：DE＝m﹣；②直接写出FC2的值（用a，m的代数式表示）练习13.如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A．B两点，开口向下的抛物线经过点A，B，且其顶点P在⊙C上．（1）求∠ACB的大小；（2）写出A，B两点的坐标；（3）由圆与抛物线的对称性可知抛物线的顶点P的坐标为（1，3），求出抛物线的解析式；（4）在该抛物线上是否存在一点D点，使线段OP与CD互相平分？若存在，求出点D的坐标；若不存在，请说明理由．例4.如图1，抛物线y＝ax2+3ax（a为常数，a＜0）与x轴交于O，A两点，点B 为抛物线的顶点，点D是线段OA上的一个动点，连接BD并延长与过O，A，B三点的⊙P相交于点C，过点C作⊙P的切线交x轴于点E．（1）①求点A的坐标；②求证：CE＝DE；（2）如图2，连接AB，AC，BE，BO，当，∠CAE＝∠OBE时，①求证：AB2＝AC•BE；②求的值．练习14.如图1，已知圆O的圆心为原点，半径为2，与坐标轴交于A，C，D，E 四点，B为OD中点．（1）求过A，B，C三点的抛物线解析式；（2）如图2，连接BC，AC．点P在第一象限且为圆O上一动点，连接BP，交AC于点M，交OC于点N，当MC2＝MN•MB时，求M点的坐标；（3）如图3，若抛物线与圆O的另外两个交点分别为H，F，请判断四边形CFEH的形状，并说明理由．练习15.如图，二次函数与x轴的一个交点A的坐标为（﹣3，0），以点A为圆心作圆A，与该二次函数的图象相交于点B，C，点B，C的横坐标分别为﹣2，﹣5，连接AB，AC，并且满足AB⊥AC．过点B作BM⊥x轴于点M，过点C作CN⊥x轴于点N．（1）求该二次函数的关系式；（2）经过点B作直线BD，在A点右侧与x轴交于点D，与二次函数的图象交于点E，使得∠ADB＝∠ABM，连接AE，求证：AE＝AD；（3）若直线y＝kx+1与圆A相切，请求出k的值．例5.已知抛物线y＝ax2+bx+5（a≠0）经过A（5，0），B（6，1）两点，且与y 轴交于点C．（1）求抛物线y＝ax2+bx+5（a≠0）的函数关系式；（2）如图1，连接AC，E为线段AC上一点且横坐标为1，⊙P是△OAE外接圆，求圆心P点的坐标；（3）如图2，连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F；①点E在运动过程中四边形OEAF的面积是否为定值？如果是，请求出这个定值；如果不是，请说明理由；②求出当△AEF的面积取得最大值时，点E的坐标．练习16.如图1，已知抛物线y＝﹣x2+bx+c经过点A（1，0），B（﹣5，0）两点，且与y轴交于点C．（1）求b，c的值．（2）在第二象限的抛物线上，是否存在一点P，使得△PBC的面积最大？求出点P的坐标及△PBC的面积最大值．若不存在，请说明理由．（3）如图2，点E为线段BC上一个动点（不与B，C重合），经过B、E、O 三点的圆与过点B且垂直于BC的直线交于点F，当△OEF面积取得最小值时，求点E坐标．练习17.如图1，抛物线y＝+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C，顶点为D．（1）求抛物线的解析式；（2）如图2，以AB为直径在x轴上方画半圆交y轴于点E，圆心为G，P为半圆上一动点，连接DP，点Q为PD的中点．①判断点C、D与⊙G的位置关系，并说明原因；②当点P沿半圆从点B运动到点A时，求线段AQ的最小值．练习18.如图1，二次函数y＝ax2﹣3ax+b（a、b为参数，其中a＜0）的图象与x 轴交于A、B两点，与y轴交于点C，顶点为D．（1）若b＝﹣10a，求tan∠CBA的值（结果用含a的式子表示）；（2）若△ABC是等腰三角形，直线AD与y轴交于点P，且AP：DP＝2：3．求抛物线的解析式；（3）如图2，已知b＝﹣4a，E、F分别是CA和CB上的动点，且EF＝AB，若以EF为直径的圆经过点C，并交x轴于M、N两点，求MN的最大值．课后练习1.抛物线y＝ax2+bx﹣4交x轴于A（﹣2，0），B（4，0）两点，交y轴于点C，点P是介于B、C之间的抛物线上的动点（包括B、C两点），点E是△ABP 的外接圆圆心．（1）求抛物线的解析式；（2）如图1，当P为抛物线的顶点时，求圆心E的坐标；（3）如图2，作PH⊥x轴于点H，延长PH交⊙E于点Q，当P从C点出发，沿该抛物线运动到B点，求点Q在这个运动过程中的路径长．2.如图，在正方形OABC中，AB＝4，点E是线段OA（不含端点）边上一动点，作△ABE的外接圆交AC于点D．抛物线y＝ax2﹣x+c过点O，E．（1）求证：∠BDE＝90°；（2）如图1，若抛物线恰好经过点B，求此时点D的坐标；（3）如图2，AC与BE交于点F．①请问点E在运动的过程中，CF•AD是定值吗？如果是，请求出这个值，如果不是，请说明理由；②若，求点E坐标及a的值．。

圆为背景的二次函数综合训练卷1．如图，已知点A的坐标是（﹣1，0），点B的坐标是（9，0），以AB为直径作⊙O′，交y轴的负半轴于点C，连接AC，BC，过A，B，C三点作抛物线．（1）求抛物线的解析式；（2）点E是AC延长线上一点，∠BCE的平分线CD交⊙O′于点D，连接BD，求直线BD的解析式；（3）在（2）的条件下，抛物线上是否存在点P，使得∠PDB=∠CBD？如果存在，请求出点P的坐标；如果不存在，请说明理由．第三问改成，在（2）的条件下，点P是直线BC下方的抛物线上一动点，当点P运动到什么位置时，△PCD的面积是△BCD面积的三分之一，求此时点P的坐标．2．在平面直角坐标系xOy中，当图形W上的点P的横坐标和纵坐标相等时，则称点P为图形W的“梦之点”.（1）已知⊙O的半径为1.①在点E（1,1），,M(－2，－2)中，⊙O的“梦之点”为；②若点P位于⊙O内部，且为双曲线（k≠0）的“梦之点”，求k的取值范围.（2）已知点C的坐标为（1，t），⊙C的半径为，若在⊙C上存在“梦之点”P，直接写出t的取值范围.（3）若二次函数的图象上存在两个“梦之点”，求二次函数图象的顶点坐标.3．如图，在平面直角坐标系中，圆D与轴相切于点C(0,4)，与轴相交于A、B两点，且AB=6（1）D点的坐标是，圆的半径为；（2）求经过C、A、B三点的抛物线所对应的函数关系式；（3）设抛物线的顶点为F,试证明直线AF与圆D相切；（4）在轴下方的抛物线上，是否存在一点N，使面积最大，最大面积是多少？并求出点坐标.4．（2018年山东省济宁市中考数学模拟）如图，抛物线y=ax2+bx﹣3与x轴交于A，B两点，与y轴交于C点，且经过点（2，﹣3a），对称轴是直线x=1，顶点是M．（1）求抛物线对应的函数表达式；（2）经过C，M两点作直线与x轴交于点N，在抛物线上是否存在这样的点P，使以点P，A，C，N为顶点的四边形为平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由；（3）设直线y=﹣x+3与y轴的交点是D，在线段BD上任取一点E（不与B，D重合），经过A，B，E三点的圆交直线BC于点F，试判断△AEF的形状，并说明理由；（4）当E是直线y=﹣x+3上任意一点时，（3）中的结论是否成立（请直接写出结论）．5．已知，如图，点M在x轴上，以点M为圆心，2.5长为半径的圆交y轴于A、B两点，交x轴于C（x1，0）、D（x2，0）两点，（x1＜x2），x1、x2是方程x（2x+1）=（x+2）2的两根．（1）求点C、D及点M的坐标；（2）若直线y=kx+b切⊙M于点A，交x轴于P，求PA的长；（3）⊙M上是否存在这样的点Q，使点Q、A、C三点构成的三角形与△AOC相似？若存在，请求出点的坐标，并求出过A、C、Q三点的抛物线的解析式；若不存在，请说明理由．6．如图，抛物线y=ax2+bx+c（a≠0）与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．（1）求抛物线的解析式；（2）若点D为该抛物线上的一个动点，且在直线AC上方，当以A、C、D为顶点的三角形面积最大时，求点D的坐标及此时三角形的面积；（3）以AB为直径作⊙M，直线经过点E（﹣1，﹣5），并且与⊙M相切，求该直线的解析式．7．如图①已知抛物线y=ax2﹣3ax﹣4a（a＜0）的图象与x轴交于A、B两点（A在B的左侧），与y的正半轴交于点C，连结BC，二次函数的对称轴与x轴的交点为E．（1）抛物线的对称轴与x轴的交点E坐标为_____，点A的坐标为_____；（2）若以E为圆心的圆与y轴和直线BC都相切，试求出抛物线的解析式；（3）在（2）的条件下，如图②Q（m，0）是x的正半轴上一点，过点Q作y轴的平行线，与直线BC交于点M，与抛物线交于点N，连结CN，将△CMN沿CN翻折，M的对应点为M′．在图②中探究：是否存在点Q，使得M′恰好落在y轴上？若存在，请求出Q的坐标；若不存在，请说明理由．8．如图，O是平面直角坐标系的原点．在四边形OABC中，AB∥OC，BC⊥x轴于C，A（1，1），B（3，1），动点P 从O点出发，沿x轴正方向以2个单位/秒的速度运动．设P点运动的时间为t秒（0＜t＜2）．（1）求经过O、A、B三点的抛物线的解析式；（2）过P作PD⊥OA于D，以点P为圆心，PD为半径作⊙P，⊙P在点P的右侧与x轴交于点Q．①则P点的坐标为_____，Q点的坐标为_____；（用含t的代数式表示）②试求t为何值时，⊙P与四边形OABC的两边同时相切；③设△OPD与四边形OABC重叠的面积为S，请直接写出S与t的函数解析式．9．已知x轴上有点A（1，0），点B在y轴上，点C（m，0）为x轴上一动点且m＜﹣1，连接AB，BC，tan∠ABO=，以线段BC为直径作⊙M交直线AB于点D，过点B作直线l∥AC，过A，B，C三点的抛物线为y=ax2+bx+c，直线l与抛物线和⊙M的另一个交点分别是E，F．（1）求B点坐标；（2）用含m的式子表示抛物线的对称轴；（3）线段EF的长是否为定值？如果是，求出EF的长；如果不是，说明理由．（4）是否存在点C（m，0），使得BD=AB？若存在，求出此时m的值；若不存在，说明理由．10．在平面直角坐标系中，抛物线y=x2+（k﹣1）x﹣k与直线y=kx+1交于A、B两点，点A在点B的左侧．（1）如图1，当k=1时，直接写出A，B两点的坐标；（2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；（3）如图2，抛物线y=x2+（k﹣1）x﹣k（k＞0）与x轴交于点C、D两点（点C在点D的左侧），是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切？若存在，请求出k的值；若不存在，请说明理由．[来源:]11．如图，抛物线与x轴交于A、B两点，与y轴交于点C.直线经过抛物线与坐标轴的两个交点B和C。

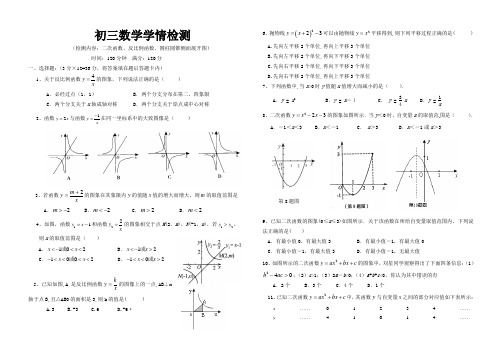
初三数学学情检测（检测内容：二次函数、反比例函数、圆柱圆锥侧面展开图） 时间：120分钟 满分：120分 一、选择题：（3分×12=36分，将答案填在题后答题卡内） 1、关于反比例函数4y x=的图象，下列说法正确的是（ ） A ．必经过点（1，1）B ．两个分支分布在第二、四象限C ．两个分支关于x 轴成轴对称D ．两个分支关于原点成中心对称2、函数2y x =与函数1y x-=在同一坐标系中的大致图像是（ ）3、若函数xm y 2+=的图象在其象限内y 的值随x 值的增大而增大，则m 的取值范围是 A ．2->mB ．2-<mC ．2>mD ．2<m4、如图，函数11y x =-和函数22y x=的图象相交于点M (2，m )，N (-1，n )，若12y y >，则x 的取值范围是（ ）A ．102x x <-<<或B ．12x x <->或C ．1002x x -<<<<或D ．102x x -<<>或5、已知如图,A 是反比例函数xky =的图像上的一点,AB ⊥x 轴于点B,且△ABO 的面积是3,则k 的值是( )A.3B.-3C.6D.-6·6、抛物线()223y x =+-可以由抛物线2y x =平移得到,则下列平移过程正确的是( )A.先向左平移2个单位,再向上平移3个单位B.先向左平移2个单位,再向下平移3个单位C.先向右平移2个单位,再向下平移3个单位D.先向右平移2个单位,再向上平移3个单位7、下列函数中,当x >0时y 值随x 值增大而减小的是（ ）．A ．y = x 2B ．y = x －１C ． y = 34xD ．y = 1x8、二次函数223y x x =--的图象如图所示．当y ＜0时，自变量x 的取值范围是（ ）． A ．－1＜x ＜3B ．x ＜－1C ． x ＞3D ．x ＜－1或x ＞3第8题图9、已知二次函数的图象(0≤x ≤3)如图所示．关于该函数在所给自变量取值范围内，下列说法正确的是( )A ．有最小值0，有最大值3B ．有最小值－1，有最大值0C ．有最小值－1，有最大值3D ．有最小值－1，无最大值10、如图所示的二次函数2y ax bx c =++的图象中，刘星同学观察得出了下面四条信息：（1）240b ac ->；（2）c >1；（3）2a －b <0；（4）a +b +c <0。

2023年九年级数学中考专题：二次函数与圆综合压轴题1．如图1，在平面直角坐标系中，O为坐标原点，已知抛物线与x轴交于，两点，与y轴交于点C．(1)求抛物线解析式；(2)如图2，M是抛物线顶点，的外接圆与x轴的另一交点为D，与y轴的另一交点为E．①求；②若点N是第一象限内抛物线上的一个动点，在射线上是否存在点P，使得与相似？如果存在，请求出点P的坐标；(3)点Q是拋物线对称轴上一动点，若为锐角，且，请直接写出点Q 纵坐标的取值范围．2．【概念学习】在平面直角坐标系中，对于已知的点和图形，给出如下定义：如果图形上存在一点，使得当时，，则称点为图形的一个“垂近点”．(1)【初步理解】若图形为线段，，，在点、、、中，是线段的“垂近点”的为________；(2)【知识应用】若图形为以坐标原点为圆心，2为半径的圆，直线与轴交于点、与轴交于点，如果线段上的点都是的“垂近点”，求的取值范围；(3)若图形为抛物线，以点为中心，半径为的四边形，轴，轴，如果正四边形上存在“垂近点”，直接写出的取值范围．3．在平面直角坐标系xOy中，已知抛物线y＝x2﹣2x﹣3与x轴交于A、B两点，与y 轴交于C点，D为抛物线顶点．(1)连接AD，交y轴于点E，P是抛物线上的一个动点．①如图一，点P是第一象限的抛物线上的一点，连接PD交x轴于F，连接，若，求点P的坐标．②如图二，点P在第四象限的抛物线上，连接AP、BE交于点G，若，则w 有最大值还是最小值？w的最值是多少？(2)如图三，点P是第四象限抛物线上的一点，过A、B、P三点作圆N，过点作轴，垂足为I，交圆N于点M，点在运动过程中，线段是否变化？若有变化，求出MI的取值范围；若不变，求出其定值．(3)点Q是抛物线对称轴上一动点，连接OQ、AQ，设AOQ外接圆圆心为H，当的值最大时，请直接写出点H的坐标．4．如图1，在平面直角坐标系中，已知抛物线y＝ax2＋bx－4(a≠0)经过点A(－2，0)和点B(4，0)．（1）求这条抛物线所对应的函数表达式；（2）点P为抛物线上第一象限内一点，若S△ABC＝2S△PBC，求点P的坐标；（3）如图2，点D是第二象限内抛物线上一点，过点D作DF⊥x轴，垂足为F，△ABD 的外接圆与DF相交于点E．试问：线段EF的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由．5．如图，抛物线经过点，，直线AC的解析式为，且与y轴相交于点C，若点E是直线AB上的一个动点，过点E作轴交AC于点F．（1）求抛物线的解析式；（2）点H是y轴上一动点，连结EH，HF，当点E运动到什么位置时，四边形EAFH 是矩形?求出此时点E，H的坐标；（3）在（2）的前提下，以点E为圆心，EH长为半径作圆，点M为上以动点，求的最小值．6．已知二次函数的图象经过点A（2，0），B（，0），C（0，4），点为二次函数第二象限内抛物线上一动点，轴于点，交直线于点，以为直径的圆⊙M与交于点．（1）求这个二次函数的关系式；（2）当三角形周长最大时．求此时点点坐标及三角形的周长；（3）在（2）的条件下，点N为⊙M上一动点，连接BN，点Q为BN的中点，连接HQ，求HQ的取值范围．7．如图，在平面直角坐标系中，抛物线，y与轴交于A、B两点，与轴交于点C．（1）求点A、B、C的坐标；（2）如图1，连接BC，点D是抛物线上一点，若∠DCB=∠ABC，求点D的坐标；（3）如图2，若点P在以点O为圆心，OA长为半径作的圆上，连接BP、CP，请你直接写出CP+BP的最小值．8．如图，在平面直角坐标系中，半径为1的圆的圆心在坐标原点，且与两坐标轴分别交于、、、四点，点坐标为．抛物线与轴交于点，与直线交于点、，且、分别与圆相切于点和点．（1）求抛物线的解析式．（2）过点作圆的切线交的延长线于点，判断点是否在抛物线上，说明理由．（3）抛物线对称轴交轴于点，连接并延长交于点，求点的坐标．9．如图，在平面直角坐标系中，抛物线交y轴于点，交x轴于两点．(1)求此抛物线的解析式；(2)已知点P是抛物线上的一个动点，且位于A、C两点之间，问：当点P运动到什么位置时，的面积最大？并求出此时P点的坐标和的最大面积；(3)过点B作线段的垂线交抛物线于点D，如果以点C为圆心的圆与直线相切，请判断抛物线的对称轴l与有怎样的位置关系，并给出证明．10．如图，直线与x轴交于点B，与y轴交于点C，抛物线经过B、C两点，且与x轴交于另一点A．（1）求抛物线的解析式．（2）点P是线段BC下方的抛物线上的动点（不与点B、C重合），过P作PD∥y轴交BC 于点D，以PD为直径的圆交BC于另一点E，求DE的最大值及此时点P的坐标；（3）当（2）中的DE取最大值时，将△PDE绕点D旋转，当点P落在坐标轴上时，求点E的坐标．11．直角坐标系xOy中，有反比例函数上的一动点P，以点P为圆心的圆始终与y轴相切，设切点为A（1）如图1，⊙P运动到与x轴相切时，求OP2的值．（2）设圆P运动时与x轴相交，交点为B、C，如图2，当四边形ABCP是菱形时，①求出A、B、C三点的坐标．②设一抛物线过A、B、C三点，在该抛物线上是否存在点Q，使△QBP的面积是菱形ABCP 面积的？若存在，求出所有满足条件的Q点的坐标；若不存在，说明理由．12．已知：如图，在平面直角坐标系xOy中，以点P（2，）为圆心的圆与y轴相切于点A，与x轴相交于B、C两点（点B在点C的左边）．（1）求经过A、B、C三点的抛物线的解析式；（2）在（1）中的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的．如果存在，请直接写出所有满足条件的M点的坐标；如果若不存在，请说明理由；（3）如果一个动点D自点P出发，先到达y轴上的某点，再到达x轴上某点，最后运动到（1）中抛物线的顶点Q处，求使点D运动的总路径最短的路径的长．13．已知，如图，二次函数y＝﹣x2+bx+c的图象经过点A(﹣1，0)，B(3，0)，点E为二次函数第一象限内抛物线上一动点，EH⊥x轴于点H，交直线BC于点F，以EF为直径的圆⊙M与BC交于点R.(1)求这个二次函数关系式.(2)当△EFR周长最大时.①求此时点E点坐标及△EFR周长.②点P为⊙M上一动点，连接BP，点Q为BP的中点，连接HQ，求HQ的最大值.14．如图所示，对称轴为直线的抛物线与轴交于、两点，与轴交于点，点在抛物线对称轴上并且位于轴的下方，以点为圆心作过、两点的圆，恰好使得弧的长为周长的．(1)求该抛物线的解析式；(2)求的半径和圆心的坐标，并判断抛物线的顶点与的位置关系；(3)在抛物线上是否存在一点，使得？若存在，求出所有符合条件的点的坐标；若不存在，请说明理由．15．已知抛物线y＝ax2+bx+5（a≠0）经过A（5，0），B（6，1）两点，且与y轴交于点C．(1)求抛物线y＝ax2+bx+5（a≠0）的函数关系式；(2)如图1，连接AC，E为线段AC上一点且横坐标为1，⊙P是△OAE外接圆，求圆心P 点的坐标；(3)如图2，连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F；①点E在运动过程中四边形OEAF的面积是否为定值？如果是，请求出这个定值；如果不是，请说明理由；②求出当△AEF的面积取得最大值时，点E的坐标．16．如图1，已知圆O的圆心为原点，半径为2，与坐标轴交于A，C，D，E四点，B 为OD中点．(1)求过A，B，C三点的抛物线解析式；(2)如图2，连接BC，AC．点P在第一象限且为圆O上一动点，连接BP，交AC于点M，交OC于点N，当MC2＝MN•MB时，求M点的坐标；(3)如图3，若抛物线与圆O的另外两个交点分别为H，F，请判断四边形CFEH的形状，并说明理由．17．已知一次函数：与轴交于点，与轴交于点．抛物线（、为常数）过定点，连接，点为线段上一动点．（1）求出点的坐标；（2）过作于点，于点，设点横坐标为，长度为，试求关于的函数解析式；（3）①当，时，该抛物线上存在唯一的点使，求此时抛物线的解析式；②过点作交线段于点，连接并延长交的外接圆于点，当点在上移动时，求的最大值．18．已知抛物线经过，，三个点．（1）求抛物线的解析式；（2）如图1，作的外接圆，为上方半圆上一点，当时，求的长；（3）如图2，直线与抛物线交于，两点，与轴交于点，作轴的平行线，分别与线段、抛物线交于，两点（点与点，不重合），点为射线上一点，当与相似时，求的最大面积．参考答案：1．(1)(2)①；②存在，或或或(3)或2．(1)，；(2)；(3)或时，正方形上存在抛物线的“垂近点”．3．(1)①，②w有最小值，w的最值是(2)不变，(3)或4．（1）；（2）；（3）为定值．5．（1）；（2），；（3）6．（1）；（2）F（，4），△EFD的周长为；（3）．7．（1），，；（2），；（3）8．（1）；（2）点在抛物线上；（3）9．（1）；（2），；（3）相交，10．（1）y=x2﹣x﹣2；（2）m=2时，DE有最大值，此时P；（3），或E或11．（1）16；（2）①A（0，），B（2，0），C（6，0）；②存在，满足条件的Q点有（0，），（14，），（8，）和（6，0）．12．（1）．（2）存在，点M的坐标为（0，），（3，0），（4，），（7，）．（3）．13．(1)y＝﹣x2+2x+3；(2)①E(，)，周长为+；②HQ的最大值大为：+.14．(1)(2)2，，点在上(3)存在，，，15．(1)抛物线解析式为y＝x2﹣x+5(2)圆心P点的坐标为（，）(3)①四边形OEAF的面积是定值，这个定值为；②当△OEF的面积取得最小值时，E点坐标为（，）16．(1)y＝﹣x2+x+2；(2)M（，）；(3)四边形CFEH是矩形．17．（1）；（2）（）；（3）①；②18．（1）；（2）；（3）．。

图① 图②xy O 1 BAOM二次函数、圆复习测试卷姓名： 得分：一、选择题(每题3分，共计30分)1、向上发射一枚炮弹，经x 秒后的高度为y 公尺，且时间与高度关系为y =ax 2bx 。

若此炮弹在第7秒与第14秒时的高度相等，则再下列哪一个时间的高度是最高的（ ） A.第8秒 B. 第10秒 C.第12秒 D.第15秒2、如图①是一个横断面为抛物线形状的拱桥，当水面在l 时，拱顶 （拱桥洞的最高点）离水面2m ，水面宽4m ．如图②建立平面直角 ；坐标系，则抛物线的关系式是（ ） A ．22y x =- B ．22y x = C ．212y x=-D ．212y x =3、在同一坐标系中一次函数y ax b =+和二次函数2y ax bx =+的图象可能为（ ） ？4、已知二次函数2y ax bx c =++(a ≠0)的图象开口向上，并经过点(-1，2)，(1，0) . 下列结论正确的是( )A. 当x >0时，函数值y 随x 的增大而增大B. 当x >0时，函数值y 随x 的增大而减小C. 存在一个负数x 0，使得当x <x 0时，函数值y 随x 的增大而减小；当x > x 0时，函数值y 随x 的增大而增大D. 存在一个正数x0，使得当x<x0时，函数值y 随x 的增大而减小；当x>x0时，函数值y 随x 的增大而增大)5、已知二次函数2(0)y ax bx c a =++≠的图象如图所示，则下列结论：0ac >①；②方程20ax bx c ++=的两根之和大于0；③ 0a b c -+<， ④y 随x 的增大而增大；其中正确的个数（ ）A ．4个B ．3个C ．2个D ．1个6、如果两个圆心角相等，那么（ ）A ．这两个圆心角所对的弦相等;B ．这两个圆心角所对的弧相等C ．这两个圆心角所对的弦的弦心距相等;D ．以上说法都不对:（第7题 ） （第8题） （第9题） （第10题） 7、如图，⊙O 的直径为10，圆心O 到弦AB 的距离OM 的长为3，则弦AB 的长是（ ）A ．4B ．6C ．7D ．8O x y O ` O x y O x yA ！C DO BAC 21EDOBACED BACPO/8、如图，A、B、C三点在⊙O上，∠AOC=100°，则∠ABC等于（）．A．140°B．110°C．120°D．130°9、如图，AD是⊙O的直径，AC是弦，OB⊥AD，若OB=5，且∠CAD=30°，则BC等于（）．A．3 B．3C．5-123D．510、如图，AB与⊙O切于点C，OA=OB，若⊙O的直径为8cm，AB=10cm，那么OA的长是（）A41B．40.14.60C D二、填空题（每题3分，共计30分）11、若二次函数cbxxy++=2的图象经过点（2，0）和点（0，1），则函数关系式为．?12、已知二次函数232)1(2-++-=aaxxay的图象的最低点在x轴上，则a= ．13、将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值是cm214、P为⊙O内一点，OP=3cm，⊙O半径为5cm，则经过P点的最短弦长为________；•最长弦长为_______．•—（第15题）（第16题）（第17题）（第18题）（第19题）15、如图，A、B是⊙O的直径，C、D、E都是圆上的点，则∠1+∠2=_______．16、如图，AB和DE是⊙O的直径，弦AC∥DE，若弦BE=3，则弦CE=________．17、如图，已知△ABC为⊙O内接等边三角形，BC=•1，∠A=•60°，则⊙O•半径为_______．18、如图，AB为⊙O直径，BD切⊙O于B点，弦AC的延长线与BD交于D点，若AB=10，AC=8，则DC长为________．.19、如图，P为⊙O外一点，PA、PB为⊙O的切线，A、B为切点，弦AB与PO交于C，⊙O半径为1，PO=2，则∠AOB=________．20、已知二次函数2y ax bx c=++的图象与x轴交于点(20)-，、1(0)x，，且112x<<，与y轴的正半轴的交点在(02)，的下方.列结论：①420a b c-+=；②0a b<<；③20a c+>；④210a b-+>其中正确结论的个数是个．三、解答题（7+6+7+8+7+7+8+10）21、如图，以平行四边形ABCD的顶点A为圆心，AB为半径作圆，分别交BC、AD于E、F，若∠D=50°，求弧BE的度数和弧EF的度数．&22、用6m 长的铝合金型材做一个形状如图所示的矩形窗框。

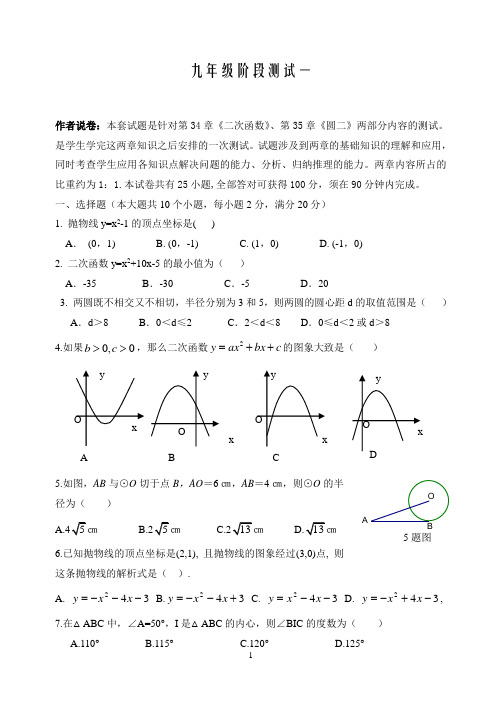
1九年级阶段测试一作者说卷：本套试题是针对第34章《二次函数》、第35章《圆二》两部分内容的测试。

是学生学完这两章知识之后安排的一次测试。

试题涉及到两章的基础知识的理解和应用，同时考查学生应用各知识点解决问题的能力、分析、归纳推理的能力。

两章内容所占的比重约为1：1.本试卷共有25小题,全部答对可获得100分，须在90分钟内完成。

一、选择题（本大题共10个小题，每小题2分，满分20分） 1. 抛物线y=x 2-1的顶点坐标是( )A ． (0，1) B. (0，-1) C. (1，0) D. (-1，0) 2. 二次函数y=x 2+10x-5的最小值为（ ）A ．-35B ．-30C ．-5D ．203. 两圆既不相交又不相切，半径分别为3和5，则两圆的圆心距d 的取值范围是（ ） A ．d ＞8 B ．0＜d ≤2 C ．2＜d ＜8 D ．0≤d ＜2或d ＞84.如果0,0b c >>，那么二次函数2y ax bx c =++的图象大致是（ ）5.如图，AB 与⊙O 切于点B ，AO ＝6㎝，AB ＝4㎝，则⊙O 的半径为（ ）6.已知抛物线的顶点坐标是(2,1), 且抛物线的图象经过(3,0)点, 则这条抛物线的解析式是（ ）.A. 342---=x x y B.342+--=x x y C. 342--=x x y D. 342-+-=x x y , 7.在△ABC 中，∠A=50°，I 是△ABC 的内心，则∠BIC 的度数为（ ） A.110° B.115° C.120° D.125°BAO5题图28.已知点A （1,1y ）、B （2,2y -）、C （3,2y -）在函数()21122-+=x y 上，则1y 、2y 、3y 的大小关系是( )A.1y ＞2y ＞3yB.1y ＞3y ＞2yC.3y ＞1y ＞2yD.2y ＞1y ＞3y 9.Rt △ABC 中，∠C=90°，∠AC=3cm ，BC ＝4cm ，给出下列三个结论： ①以点C 为圆心1.3 cm 长为半径的圆与AB 相离；②以点C 为圆心，2.4cm 长为半径的圆与AB 相切；③以点C 为圆心，2.5cm 长为半径的圆与AB 相交．上述结论中正确的个数是（ ） A ．0个 B ．l 个 C ．2个 D ．3个10.根据下列表格中二次函数2y ax bx c =++的自变量x 与函数值y 的对应值， 判断方程20ax bx c ++=（0a a b c ≠，，，为常数）的一个解x 的范围是（ ）Ａ．6 6.17x <<Ｂ．6.17 6.18x << Ｃ．6.18 6.19x <<Ｄ．6.19 6.20x <<二、填空题（共5个小题，每小题3分，共15分）11.已知二次函数的图象开口向下，且经过原点。

九年级数学圆、二次函数试题考试时间：60分钟一、选择题（共10小题，满分35分）1.（3分）将二次函数34-2+=x x y 通过配方可化为k h x a y +=2)-(的形式，结果为（）A.1-)2-(2x y =B.3)2-(2+=x yC.3)2(2++=x yD.1-)2(2+=x y 2.（3分）关于二次函数12-2+=x y ，下列说法中正确的是（）A.它的开口方向是向上B.当1-<x ，y 随x 的增大而增大C.它的原点坐标是（-2,1）D.当0=x 时，y 有最大值是21-3.（3分）二次函数c bx ax y ++=2与一次函数c ax y +=，它们在同一直角坐标系中的图象大致是（）4.（3分）若点)1-(1y M ，，)1(2y N ，，)27(3y P ，都在抛物线)0(1422m m mx mx y 上，则下列结论正确的是（）A.321y y yB.231y y yC.213y y yD.312y y y5.（3分）抛物线2x y 向上平移2个单位长度，再向左平移3个单位长度，得到的抛物线表达式（）A.2)3(2x yB.2-)3(2x yC.3)2(2x yD.3-)2(2x y 6.（4分）关于圆的性质有以下四个判断：①垂直于弦的直线平分弦，②平分弦的直径垂直于弦，③在同圆或等圆中，相等的弦所对的圆周角相等，④在同圆或等圆中，相等的圆周角所对的弦相等，则四个判断中正确的是（）A.①③ B.②③ C.①④ D.②④7.（4分）如图，在○·O 中，直径CD 弦AB ，若30C ，则BOD 的度数是（）A.30 B.40 C.50D.608.（4分）如图，○·O 的半径为6，点C B A 、、在○·O 上，且45BCA ，则点O 到弦AB 的距离为（）A.3B.6C.23D.269.（4分）从如图所示的二次函数c bx ax y 2的图像中，观察得出下面五条信息：①0c ；②0abc ；③0c b a ；④032b a ；⑤08b c .你认为其中正确的信息的个数为（）A.2个 B.3个 C.4个 D.5个10.（4分）如图，在平面直角坐标系中，C （0，4），A （3，0），○·A 半径为2，P 为○·A 上任意一点，E 的PC 的中点，则OE 的最小是（）A.1 B.23C.2D.2二、填空题（共10小题，满分35分）11.（3分）如图所示的抛物线是二次函数2245a x ax y 的图象，那么a 的值是。

九年级上数学阶段性测试（2010.11）(时间90分钟，满分120分)一、选择题（每小题4分，共48分）1．抛物线 y ＝x 2 不具有的性质是（ ）A 、开口向上B 、与 y 轴不相交C 、对称轴是 y 轴D 、最低点是原点2.把抛物线22y x =-向上平移1个单位，得到的抛物线是（ ） A ．22(1)y x =-+B ．22(1)y x =--C ．221y x =-+D ．221y x =--3. 下面的图形中，对称轴最少的是（ ）。

A 、 长方形B 、 正方形C 、 圆D 、等腰三角形4. (08湖南长沙)二次函数c bx ax y ++=2的图象如图所示，则下列关系式不正确的是（ ） A 、a ＜0 B 、abc ＞0 C 、c b a ++＞0 D 、ac b 42-＞0 5. 如图，A 、B 、C 是⊙O 上的三点，∠BAC=30°则∠BOC 的大小是（ ）A ．60○B ．45○C ．30○D ．15○第4题图 第5题图 6. 抛物线247y x x =--的顶点坐标是（ ） A ．(211)-， B ．(27)-， C ．(211)，D ．(23)-，7.二次函数y=x 2-6x+5的图象与x 轴交于A 、B 两点，与y 轴交于点C ，则△ABC 的面积为（ ） A. 15 B. 10 C.20 D.308. 圆的半径为13cm ，两弦AB CD ∥，24cm AB =，10cm CD =，则两弦AB CD ，的距离是( )cm A.7 B.8 C.7或17 D.1或15 9. 在反比例函数k y x=中，当x ＞0时，y 随x 的增大而增大，则二次函数22y kx kx =+图像大致是（ ）A B C D..10. 下列图形中阴影部分的面积相等的是（ ）Ａ．③④Ｂ．②③ Ｃ．①④Ｄ．①②11.如图，已知EF 是⊙O 的直径，把A ∠为60的直角三角板ABC 的一条直角边BC 放在直线EF 上，斜边AB 与⊙O 交于点P ，点B 与点O 重合；将三角形ABC 沿OE 方向 平移，使得点B 与点E 重合为止．设POF x =∠，则x 的取值 范围是（ ） Ａ．60120x ≤≤ Ｂ．3060x ≤≤ Ｃ．3090x ≤≤Ｄ．30120x ≤≤12 (08河北)如图，正方形ABCD 的边长为10，四个全等的小正方形的对称中心分别在正方形ABCD 的顶点上，且它们的各边与正方形ABCD 各边平行或垂直．若小正方形的边长为x ，且010x <≤，阴影部分的面积为y ，则能反映y 与x 之间函数关系的大致图象是（ ）二、填空题（每小题34分，共15分） 13.已知二次函数的解析式是c x x y ++=22，其抛物线与x 轴有且只有一个交点， 则c= ．14. 如图所示，在⊙O 中，AB 是⊙O 的直径，∠ACB 的角 平分线CD 交⊙O 于D ，则∠ABD ＝__________度．x A ．xB ．xC ．x D ．1A题1115. 如图所示的抛物线是二次函数2231y ax x a =-+-的图象，那么a 的值是 ．16.已知二次函数c bx ax y ++=2(a 、b 、c 是常数)，图象如图所示，则当x 满足的条件是 时，y17. 如图所示，△ABC A (－1，3)、B (－2，－2)、C (4△ABC三、解答题（共57分）18.（本题7分）于（-3，0）和（1，0），且过点（1）求二次函数的表达式， （2）在图中画出它的图象；19. （本题7分）如图，在⊙O 中，AB 为⊙O 的弦，C 、D 是直线AB 上两点，且AC ＝BD求证：△OCD 为等腰三角形。

九年级数学上二次函数与圆阶段测试一、选择题(30分）1.下列关系式中，属于二次函数的是(x 为自变量)( )A .B.C .D .2. 抛物线y=2(x-3)2的顶点在( )A . 第一象限B . 第二象限C . x 轴上D . y 轴上4.抛物线的对称轴是( )A . x=-2B .x=2C . x=-4D .x=45.已知二次函数y=ax 2+bx+c 的图象如图所示，则下列结论中，正确的是()A . ab>0，c>0 B.ab>0，c<0C . ab<0，c>0D . ab<0，c<0 6.如图，AB 是⊙O 的直径， BC=BD ，∠A=25º，则∠BOD 的度数为( )A . 25ºB .50ºC .100ºD .150º7.两圆半径分别为5cm 和10cm ，圆心距为12cm ，则这两圆的位置关系为()A . 外离B .外切C .相交D .内切 8.一条弦把圆分成2:3两部分，那么这条弦所对的圆周角的度数为( )A . 108ºB .72ºC .216º或144ºD .108º、72º9. 已知抛物线和直线在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线1-=x ，()111,y x P ，()222,y x P 是抛物线上的点，()333,y x P 是直线 上的点，且211x x <<-，13-<x ，则1y 、2y 、3y 的大小关系是()A .y 1<y 2<y 3B . y 2<y 3<y 1C .y 3<y 1<y 2D . y 2<y 1<y 310.把抛物线的图象向左平移2个单位，再向上平移3个单位，所得的抛物线的函数关系式是()A .B .C .D .A BD CO二、填空题（24分）11. 若将二次函数y=x2-2x+3配方为y=(x-h)2+k的形式，则y=________________.12.在半径为9cm的圆中，60º的圆心角所对的弦长为________________.13.若抛物线y=x2-2x-3与x轴分别交于A、B两点，则AB的长为________________.14. 抛物线y=x2+bx+c，经过A(-1，0)，B(3，0)两点，则这条抛物线的解析式为_____________.15.已知二次函数y=ax2+bx+c的图象交x轴于A、B两点，交y轴于C点，且△ABC是直角三角形，请写出一个符合要求的二次函数解析式________________.16.在距离地面2m高的某处把一物体以初速度v0(m/s)竖直向上抛物出，在不计空气阻力的情况下，其上升高度s(m)与抛出时间t(s)满足：(其中g是常数，通常取10m/s2).若v0=10m/s，则该物体在运动过程中最高点距地面_________m.17.试写出一个开口方向向上，对称轴为直线x=2，且与y轴的交点坐标为(0，3)的抛物线的解析式为______________.18.已知抛物线y=x2+x+b2经过点，则y1的值是_________.三、解答下列各题（64分）19.（10分）若二次函数的图象的对称轴方程是，并且图象过A(0，-4)和B(4，0)(1)求此二次函数图象上点A关于对称轴对称的点A′的坐标；(2)求此二次函数的解析式；20.（14分）在直角坐标平面内，点O为坐标原点，二次函数y=x2+(k-5)x-(k+4) 的图象交x轴于点A(x1，0)、B(x2，0)，且(x1+1)(x2+1)=-8.(1)求二次函数解析式；(2)将上述二次函数图象沿x轴向右平移2个单位，设平移后的图象与y轴的交点为C，顶点为P，求△POC的面积.21.（14分）已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，点C(0，5)，另抛物线经过点(1，8)，M为它的顶点.(1)求抛物线的解析式；(2)求△MCB的面积S△MCB.22.（14分）某商店销售一种商品，每件的进价为2.50元，根据市场调查，销售量与销售单价满足如下关系：在一段时间内，单价是13.50元时，销售量为500件，而单价每降低1元，就可以多售出200件.请你分析，销售单价多少时，可以获利最大.23.（12分）如图，线段AB经过圆心O，交⊙O于点A、C，∠A=∠B=30º，边BD交⊙O于点D，试说明BD是⊙O的切线。

2024--2025学年人教版九年级上册数学期中测试题（二次函数~圆）1.下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．2.如图，将绕点顺时针旋转得到，点的对应点恰好落在边上，则的度数为（）A．B．C．D．3.已知抛物线，下列结论错误的是（）A．抛物线开口向上B．抛物线的对称轴为直线C．抛物线的顶点坐标为D．当时，y随x的增大而减小4.已知(﹣3，)，(﹣2，)，(1，)是抛物线上的点，则（）A．B．C．D．5.如果点在第三象限，点关于原点的对称点在（）．A．第一象限B．第二象限C．第三象限D．第四象限6.如图，是的切线，为切点，经过圆心，若，则的长度是（）A．B．C．D．7.如图，在中，弦相交于点P，若，，则的大小是（）A．B．C．D．8.如图，正六边形内接于，半径为6，则这个正六边形的边心距为（）A．4B．C．D．9.如图，正六边形和正方形有公共边，连接交于点，则的度数为（）A．B．C．D．10.二次函数y＝ax2+bx+c的部分图象如图，则下列说法正确的有（）①abc＞0；②2a-b=0；③a-b+c≥am2+bm+c；④当x＜1时，y＞0；⑤9a-3b+c=0A．2个B．3个C．4个D．5个11.已知二次函数的图象与轴有交点，则的取值范围是_______．12.一个球从地面竖直向上弹起时的速度为米/秒，经过（秒）时球距离地面的高度（米）适用公式，那么球弹起后又回到地面所花的时间（秒）______．13.如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形．若母线长l为9cm，圆锥的底面圆的半径r为3cm，则扇形的圆心角为__°．14.如图，是的直径，点C、D、E在上，若，则的度数为_________________．15.如图，在平面直角坐标系xOy中，点A，B的坐标分别是，，是的外接圆，则点M的坐标为___________．16.如图所示，抛物线形拱桥的顶点距水面2时，测得拱桥内水面宽为12．当水面升高1后，拱桥内水面的宽度为___________．17.如图，AB是⊙O的直径，BC切⊙O于点B，AC交⊙O于点D．若⊙O的半径为3，∠C＝40°，则的长为__．（结果保留π）18.在，，，，为的内切圆，与三边的切点为、、，则的半径为______．19.圆形拱门屏风是中国古代家庭中常见的装饰隔断，既美观又实用，彰显出中国元素的韵味，如图，是一款拱门的示意图，其中拱门最下端分米，为的中点，为拱门最高点，圆心在线段上，分米，求拱门所在圆的半径．20.如图，点是等边三角形内一点，且，，，若将绕点逆时针旋转后得到，求的长和的角度．21.如图，点E与F分别在正方形的边与上，，以点A为旋转中心，将按顺时针方向旋转得到．已知，，求的长．22.如图，在平面直角坐标系中，已知点，，.（1）画出绕点逆时针旋转后的图形，并写出点的坐标；（2）将（1）中所得先向左平移4个单位，再向上平移2个单位得到，画出，并写出点的坐标；（3）若可以看作绕某点旋转得来，直接写出旋转中心的坐标.23.某校准备用32米长的围栏修建一边靠墙的矩形菜地，已知墙体的最大可用长度为16米，在与墙平行的一边，要留一扇2米宽的门，设的长为x米，矩形菜地的面积为y平方米．(1)请用含有x的代数式表示y，并写出自变量x的取值范围；(2)如果该矩形菜地的面积为平方米，则的长．24.2023年中国杭州获得第十九届亚运会主办权，作为唯一申办城市，杭州成为继北京和广州之后，中国第三个举办亚运会的城市，亚运之城喜迎五湖之客，很多商家都紧紧把握这一商机．某商家销售一批具有中国文化意义的吉祥玩具，已知每个玩具的成本为元，销售单价不低于成本价，且不高于成本价的倍，在销售过程中发现，玩具每天的销售量y（个）与销售单价x（元）满足如图所示的一次函数关系．(1)求y与x的函数关系式；(2)当玩具的销售单价为多少元时，该商家获得的利润最大？最大利润是多少元？25.如图，BE是⊙O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C．(1)若∠ADE＝25°，求∠C的度数；(2)若AC＝，CE＝4，求阴影部分的面积．26.如图，以的边为直径作交边于点，恰有．(1)求证：与相切；(2)在上取点，使得．①求证：；②若，，求阴影部分的面积．27.如图，已知抛物线与轴交于、两点，与轴交于点，连接．(1)求抛物线的解析式；(2)若点为线段上的一动点（不与、重合），轴，且交抛物线于点，交轴于点，当的面积最大时，求点的坐标．。