牛头刨床的连杆机构运动分析
- 格式:doc
- 大小:301.51 KB
- 文档页数:14


一·机构简介·1.1牛头刨床的组成牛头刨床主要由床身、滑枕、刀架、工作台、横梁、进给机构和变速机构等组成。
(1)床身床身内部有变速机构和曲柄摇杆机构。
床身的顶面有水平导轨,滑枕沿水平导轨作往复直线运动。
在床身前面有垂宜导轨,横梁带动工作台沿垂直导轨升降。
2)滑枕滑枕的前端有环状T形槽,用来安装刀架和调节刀架的偏转角度:滑枕的内部装有调整滑枕行程位置的机构,它是由一对锥齿轮和丝杠组成。
滑枕的下部有两条燕尾型导轨,它与床身上部的水平导轨配合。
在曲柄摇杆机构的带动下,滑枕在床身水平导轨上作往复直线运动。
(3)横梁与工作台校梁安装在床身前部垂直导轨上。
横梁的底部装有升降丝杠,使校梁能沿着床身前部的垂直导轨作上下移动。
工作台和滑板连接在一起,安装在横梁水平导轨上,转动安装在校梁凹框内的横向进给丝杠,工作台就沿着横梁的水平导轨作横向移动。
工作台的前部底下装有支架,以防止工作台在刨削过程中产生向下倾斜和振动现象。
工作台的上平面和两侧面均制有T形槽、v 形槽和圆孔,用来固定不同形状的工件或夹具。
(4)刀架刀架用于装夹刨刀,并使刨刀沿着垂直方向和倾斜方向移动。
刀架由手柄、丝杠、刻度转盘、夹刀座、拍板、拍板座、滑板等组成。
刻度转盘6用T形职栓5紧固在滑枕前端的“环”状T形槽内。
可按加工的需要作160’的回转。
刻度转盘6与滑板13通过导轨相配合,只要摇动丝杠3上端的手柄1,就可使滑板13沿着刻度转盘6上的导轨移动,通过刻度环2来控制背吃刀量的大小。
拍板10与拍板座11的凹槽相配合,用铰链销7连接。
在拍板10的孔内装有夹刀座8刨刀就装在它的槽孔内,拍板10可以绕铰链销7向前上方拾起,这样可避免滑枕回程时刨刀与工件已加工。
(5)进给机构进给机构主要用来控制工作台横向进给运动的大小。
(6)变速机构操纵变速机构的手柄,可以把各种不同的转速传递到曲柄摆杆机构而改变格杆在相同时间间隔内的摆动次数。
(7)曲柄摇杆机构主要作用是把电动机的旋转运动转换为滑枕的往复直线运动。

牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是对于结构型式及尺寸参数已定的具体机构,按主动件的位置、速度和加速度来确定从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量,运动参数又是机械动力学分析的依据,所以机构的运动分析是机械设计过程中必不可少的重要环节。
以计算机为手段的解析方法,由于解算速度快,精确度高,程序有一定的通用性,已成为机构运动分析的主要方法。
连杆机构作为在机械制造特别是在加工机械制造中主要用作传动的机构型式,同其他型式机构特别是凸轮机构相比具有很多优点。
连杆机构采用低副连接,结构简单,易于加工、安装并能保证精度要求。
连杆机构可以将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件,实现间歇运动,满足给定的运动要求,完成机器的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动,实现工件的切削。
工作台的横向运动即是进给运动,实现对切削精度的控制。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成,其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时,通过六杆机构驱动刨刀作往复移动。
刨刀右行时,当刨刀处于工作行程时;要求刨刀的速度较低且平稳,以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时,刨刀不工作,称为空行程,此时要求刨刀的速度较高以提高生产率。
由此可见,牛头刨床的纵向运动特性对机床的性能有决定性的影响。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成,其中实现刨头切削运动的六杆机构是一个关键机构。
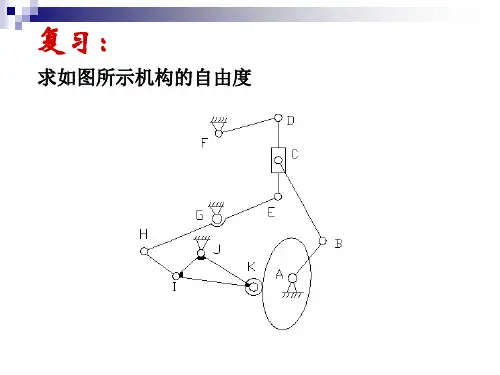
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件,刨刀装在C点上。
假设已知各构件的尺寸如表1所示,原动件1以等角速度ω1=1rad/s沿着逆时针方向回转,要求分析各从动件的角位移、角速度和角加速度以及刨刀C点的位移、速度和加速度的变化情况。


目录一、课程设计任务书21.工作原理及工艺动作过程22.原始数据及设计要求4二、设计说明书51.画机构的运动简图52.对位置4点进展速度分析和加速度分析63.对位置9点进展速度分析和加速度分析9速度分析图:104.对位置9点进展动态静力分析12心得体会16谢辞17参考文献18一、课程设计任务书1.工作原理及工艺动作过程牛头刨床是一种用于平面切削加工的机床。
刨床工作时,如图(1-1〕所示,由导杆机构2-3-4-5-6带动刨头6和刨刀7作往复运动。
刨头右行时,刨刀进展切削,称工作行程,此时要求速度较低并且均匀;刨头左行时,刨刀不切削,称空回行程,此时要求速度较高,以提高生产率。
为此刨床采用有急回作用的导杆机构。
刨头在工作行程中,受到很大的切削阻力,而空回行程中那么没有切削阻力。
切削阻力如图(b〕所示。
Y图〔1-1〕(b)2.原始数据及设计要求曲柄每分钟转数n2,各构件尺寸及重心位置,且刨头导路x-x位于导杆端点B所作圆弧高的平分线上。
要求作机构的运动简图,并作机构两个位置的速度、加速度多边形以及刨头的运动线图。
以上内容与后面动态静力分析一起画在1号图纸上。
二、设计说明书1.画机构的运动简图1、以O4为原点定出坐标系,根据尺寸分别定出O2点,B点,C点。
确定机构运动时的左右极限位置。
曲柄位置图的作法为:取1和8’为工作行程起点和终点所对应的曲柄位置,1’和7’为切削起点和终点所对应的曲柄位置,其余2、3…12等,是由位置1起,顺ω2方向将曲柄圆作12等分的位置〔如下列图〕。
图1-2取第I 方案的第4位置和第9位置〔如下列图1-3〕。
图 1-32. 对位置4点进展速度分析和加速度分析〔a 〕 速度分析 取速度比例尺l μ=mm s m001.0对A 点:4A V = 3A V + 34A A V方向:4BO ⊥A O 2⊥ //B O 4大小: ? √ ?4A V =l μ⨯4pa =sm mm mmsm673239.0239.673001.0=⨯ 4ω=AO A l V 44=sr mmsm38431.1486334.0673239.0= 34A A V =l μ43a a l =sm mm mmsm156326.0326.156001.0=⨯ V 5B = V 4B =4ω⨯B O l 4=s m 747530.0对于C 点:C V = B V + CB V 方向: //'XX B O 4⊥BC ⊥大小: ? √ ?C V =l μ⨯pc l =mm sm001.0sm mm 749708.0708.749=⨯ CB V =l μ⨯bc l =mmsm001.0sm mm 0490895.00895.49=⨯ 5ω=bcl CBl u V =s r 363626.0 速度分析图:图 1-4(b)加速度分析 选取加速度比例尺为a μ=mm s m2001.0对于A 点:4A a = n A a 4 + t A a 4 = 3A a + k A A a 34 + 34rA A a 方向:A →4OB O 4⊥ A →2O B O 4⊥//B O 4 大小: √ ? √√ ? 由于3A a =22ωA O l 2=234263.4smKA A a 34=24ω34A A V =2432808.0s mnA a 4=24ωA O l 4=2931975.0s m ,根据加速度图1-5可得:t A a 4=a μ''a n l =2549416.0sm, r A A a 34=a μ''a k l =2298112.3sm 。

牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是对于结构型式及尺寸参数已定的具体机构,按主动件的位置、速度和加速度来确定从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量,运动参数又是机械动力学分析的依据,所以机构的运动分析是机械设计过程中必不可少的重要环节。
以计算机为手段的解析方法,由于解算速度快,精确度高,程序有一定的通用性,已成为机构运动分析的主要方法。
连杆机构作为在机械制造特别是在加工机械制造中主要用作传动的机构型式,同其他型式机构特别是凸轮机构相比具有很多优点。
连杆机构采用低副连接,结构简单,易于加工、安装并能保证精度要求。
连杆机构可以将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件,实现间歇运动,满足给定的运动要求,完成机器的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动,实现工件的切削。
工作台的横向运动即是进给运动,实现对切削精度的控制。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成,其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时,通过六杆机构驱动刨刀作往复移动。
刨刀右行时,当刨刀处于工作行程时;要求刨刀的速度较低且平稳,以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时,刨刀不工作,称为空行程,此时要求刨刀的速度较高以提高生产率。
由此可见,牛头刨床的纵向运动特性对机床的性能有决定性的影响。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成,其中实现刨头切削运动的六杆机构是一个关键机构。
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件,刨刀装在C点上。
假设已知各构件的尺寸如表1所示,原动件1以等角速度ω1=1rad/s沿着逆时针方向回转,要求分析各从动件的角位移、角速度和角加速度以及刨刀C点的位移、速度和加速度的变化情况。

机械原理课程设计编程说明书设计题目: 牛头刨床的设计及运动分析(1)指导老师: 席本强, 郝志勇设计者: 迟宇学号: **********班级: 液压09-1班2011年6月30号辽宁工程技术大学机械原理课程设计任务书五、要求:1)作机构的运动简图(A4或A3图纸)。
2)用C语言编写主程序调用子程序, 对机构进行运动分析, 并打印出程序及计算结果。
3)画出导轨4的角位移, 角速度, 角加速度的曲线。
4)编写设计计算说明书。
指导教师:开始日期: 2010年6月26日完成日期: 2010年6月30日目录1.设计要求及参数 (1)2.数学模型 (2)3.程序框图 (4)4.程序清单及运行结果 (5)5.设计总结 (14)6.参考文献 (14)一、设计要求及参数已知: 曲柄每分钟转数n2, 各构件尺寸及重心位置, 且刨头导路X-X位于导杆端点B所作圆弧的平分线上, 数据见下表要求:(1)作机构的运动简图(2)用C语言编写主程序调用子程序, 对机构进行运动分析, 动态显示, 并打印程序及运算结果。
(3)画出导轨4的角位移Ψ, 角速度Ψ’, 角加速度Ψ”。
(4)编写设计计算说明书二、数学模型如图四个向量组成封闭四边形, 于是有0321=+-Z Z Z按复数式可以写成a (cos α+isin α)-b(cos β+isin β)+d(cos θ3+isin θ3)=0(1)由于θ3=90º, 上式可化简为a (cos α+isin α)-b(cos β+isin β)+id=0(2)根据(2)式中实部、虚部分别相等得acos α-bcos β=0(3)asin α-bsin β+d=0(4)(3)(4)联立解得 β=arctan acosaasinad + (5)b=2adsina d2a 2++ (6)将(2)对时间求一阶导数得ω2=β’=baω1cos(α-β)(7)υc =b ’=-a ω1sin(α-β)(8)将(2)对时间求二阶导数得ε3=β”=b1[a ε1cos(α-β)- a ω21sin(α-β)-2υc ω2] (9)a c =b ”=-a ε1sin(α-β)-a ω21cos(α-β)+b ω22(10)ac 即滑块沿杆方向的加速度, 通常曲柄可近似看作均角速转动, 则ε1=0。

设计题目:牛头刨床附图1:导杆机构的运动分析与动态静力分析附图2:齿轮机构的设计目录一.设计题目…………………………….……………………. .4二. 牛头刨床机构简介……………………………….………. .4三.机构简介与设计数据……………………………………. .. .5四. 设计内容…………….………………………….…………. .6五. 体会心得 (14)一、设计题目:牛头刨床1.)为了提高工作效率,在空回程时刨刀快速退回,即要有急回运动,行程速比系数在1.4左右。
2.)为了提高刨刀的使用寿命和工件的表面加工质量,在工作行程时,刨刀要速度平稳,切削阶段刨刀应近似匀速运动。
3.)曲柄转速在64r/min,刨刀的行程H在300mm左右为好,切削阻力约为9000N,其变化规律如图所示。
二、牛头刨床机构简介牛头刨床是一种用于平面切削加工的机床,如图4-1。
电动机经皮带和齿轮传动,带动曲柄2和固结在其上的凸轮8。
刨床工作时,由导杆机构2-3-4-5-6带动刨头6和刨刀7作往复运动。
刨头右行时,刨刀进行切削,称工作行程,此时要求速度较低并且均匀,以减少电动机容量和提高切削质量,刨头左行时,刨刀不切削,称空回行程,此时要求速度较高,以提高生产率。
为此刨床采用有急回作用的导杆机构。
刨刀每切削完一次,利用空回行程的时间,凸轮8通过四杆机构1-9-10-11与棘轮带动螺旋机构(图中未画),使工作台连同工件作一次进给运动,以便刨刀继续切削。
刨头在工作行程中,受到很大的切削阻力(在切削的前后各有一段约5H的空刀距离,见图4-1,b),而空回行程中则没有切削阻力。
因此刨头在整个运动循环中,受力变化是很大的,这就影响了主轴的匀速运转,故需安装飞轮来减小主轴的速度波动,以提高切削质量和减小电动机容量。
三、机构简介与设计数据3.1机构简介牛头刨床是一种用于平面切削加工的机床。
电动机经皮带和齿轮传动,带动曲柄2和固结在其上的凸轮8。

牛头刨床的综合与分析(课程设计说明书) 牛头刨床的综合与分析(课程设计说明书) 目录一、设计题目与原始数据一、设计题目与原始数据- - 1 1 - - 二、牛头刨床示意图二、牛头刨床示意图- - 2 2 - - 三、导杆机构设计三、导杆机构设计- - 2 2 - - 四、机构的运动分析四、机构的运动分析- - 4 4 - - 五、机构动态静力分析五、机构动态静力分析- - 9 9 - - 六、飞轮设计六、飞轮设计- - 1313 - - 七、设计凸轮轮廓曲线七、设计凸轮轮廓曲线- - 1515 - - 八、齿轮设计及绘制啮合图八、齿轮设计及绘制啮合图- - 1515 - - 九、解析法九、解析法- - 1616 - - 1.导杆机构设计.- 16 - 2.机构运动分析.- 17 - 3.凸轮轮廓曲线设计.- 19 - 4. 齿轮机构设计.- 22 - 十、本设计的思想体会十、本设计的思想体会- - 2222 - - 参考文献参考文献- - 2222 - - 附附录录- - 2323 - - 辽宁工业大学课程设计说明书(论文)- 1 - 一、设计题目与原始数据1.题目:牛头刨床的综合与分析2.原始数据:刨头的行程H=550mm 行程速比系数K=1.6 机架长LO2O3=400mm 质心与导杆的比值LO3S4/LO3B=0.5 连杆与导杆的比值LBF/LO3B=0.3 刨头重心至 F 点距离XS6=160mm 导杆的质量m4=15 刨头的质量m6=58 导杆的转动惯量JS4=0.7 切割阻力FC=1300N 切割阻力至O2的距离YP=175mm 构件 2 的转速n2=80 许用速度不均匀系数[δ]=1/40 齿轮Z1、Z2的模数m12=15 小齿轮齿数Z1=18 大齿轮齿数Z2=46 凸轮机构的最大摆角φmax=16º 凸轮的摆杆长LO4C=140mm 凸轮的推程运动角δ0=60º 凸轮的远休止角δ01=10º 凸轮的回程运动角δ0 =60º 凸轮机构的机架长Lo2o4=150mm 凸轮的基圆半径ro=55mm 凸轮的滚子半径rr=15mm 辽宁工业大学课程设计说明书(论文)- 2 - 二、牛头刨床示意图如图1 所示图 1 三、导杆机构设计1、已知:行程速比系数K=1.6 刨头的行程H=550mm 机架长度LO2O3=400mm 连杆与导杆的比LBF/LO3B=0.3 2、各杆尺寸设计如下A、求导杆的摆角:辽宁工业大学课程设计说明书(论文)- 3 - ψmax =180°×(K-1)/(K+1)=180°×(1.6-1)/(1.6+1)=42°B、求导杆长:LO3B1=H/[2sin(ψmax/2)]=550/[2sin(42°/2)]=776mm C、求曲柄长:LO2A =LO2O3×sin(ψmax/2)=400×sin21°=142mm D、求连杆长:LBF=LO3B×LBF/LO3B=776×0.3=233mm E、求导路中心到O3的距离:LO3M =LO3B-LDE/2=LO3B{1-[1-cos(ψmax/2)]/2}=750mm F、取比例尺:μL=0.005m/mm 在1#图纸中央画机构位置图,机构位置图见1#图纸。

目录一、概述1.1、课程设计的目的——————————————— 21.2、工作原理—————————————————— 21.3、设计要求—————————————————— 31.4、设计数据—————————————————— 41.5、创新设计内容及工作量———————————— 4二、牛头刨床主传动机构的结构设计与分析2.1、方案分析—————————————————— 52.2、主传动机构尺寸的综合与确定————————— 52.2、杆组拆分—————————————————— 62.4、绘制刀头位移曲线图————————————— 7三、牛头刨床主传动机构的运动分析及程序3.1、解析法进行运动分析————————————— 83.2、程序编写过程(计算机C语言程序)—————— 103.3、计算数据结果——————————————— 123.4、位移、速度和加速度运动曲线图与分析————— 13四、小结心得体会——————————————————— 18五、参考文献参考文献——————————————————— 19一、概述1.1、课程设计的目的目的:机械课程创新设计是培养学生机械系统方案设计能力的技术基础课程,他是机制专业课程学习过程中的一个重要实践环节。
其目的是以机制专业课程的学习为基础,进一步巩固和加深所学的基本理论、基本概念和基本知识,培养学生分析和解决与本专业课程有关的具体机械所涉及的实际问题的能力,使学生熟悉机械系统设计的步骤及方法,其中包括选型、运动方案的确定、运动学和动力学的分析和整体设计等,并进一步提高计算、分析、计算机辅助设计、绘图以及查阅和使用文献的综合能力。
1.2、工作原理牛头刨床是一种靠刀具的往复直线运动及工作台的间歇运动来完成工件的平面切削加工的机床。
图1为其参考示意图。
电动机经过减速传动装置(皮带和齿轮传动)带动执行机构(导杆机构和凸轮机构)完成刨刀的往复运动和间歇移动。
《机械原理》课程设计计算说明书设计题目:牛头刨床学院:机械工程学院专业班级:机自1421班学生姓名:郭文超学号: 03320142108指导教师:赵楠2016年07月04日——2016年07月07日目录工作原理 (3)一.设计任务 (4)二.设计数据 (4)三.设计要求 (5)1、运动方案设计 (5)2、确定执行机构的运动尺寸 (5)3、进行导杆机构的运动分析四.设计方案选定五.1.32.381111 (12)13工作原理.牛头刨床是一种用于平面切削加工的机床,如图a)所示。
电动机经过皮带和齿轮传动,带动曲柄2和固结在其上的凸轮8。
刨床工作时,由导杆机构2-3-4-5-6带动刨头6和刨刀7作往复运动。
刨头左行时,刨刀不切削,称为空回行程,此时要求速度较高,以提高生产率。
为此刨床采用有急回运动的导杆10-11各有一段0.05H(a)(b)图d表2求出刨头3的速度、加速度,将过程详细地写在说明书中。
四.设计方案选定如图所示,牛头刨床的主传动机构采用导杆机构、连杆滑块机构组成的5杆机构。
采用导杆机构,滑块与导杆之间的传动角r始终为90o,且适当确定构件尺寸,可以保证机构工作行程速度较低并且均匀,而空回行程速度较高,满足急回特性要求。
适当确定刨头的导路位置,可以使压力角 尽量小。
五.机构的运动分析1.3点速度分析当曲柄位于3点时如上图已知:ω04=2πn/60=7.536rad/sV A4 = V A3A4 + V A3方向:⊥杆4 ∥杆4 ⊥杆2大小:??√已知:V A3=ω04×L2 =7.536×110=828.96mm/s 作图得:V A4=670.05MM/Sω04=V A4/L AO4=670.05/513.91=1.306rad/s V B=ω04×L4=1.306 ×810=1057.86mm/sVc= V B + V CB方向:∥X-X √⊥杆BC大小:?√?由作图法得::V C2和3在A点处的转其大小等于ω22lO2A,方向由A指向O2。
机械原理课程设计说明书系部名称: 机电系专业班级: 04机制三班姓名:学号: **********目录概述 (3)设计项目...............................1.设计题目 (4)2.机构简介 (4)3.设计数据 (4)设计内容...............................1.导杆机构的设计 (5)2.凸轮机构的设计 (12)3.齿轮机构的设计 (17)设计体会 (20)参考文献 (21)附图·····························概述一、机构机械原理课程设计的目的:机械原理课程设计是高等工业学校机械类专业学生第一次较全面的机械运动学和动力学分析与设计的训练,是本课程的一个重要实践环节。
其基本目的在于:(1)进一步加深学生所学的理论知识,培养学生独立解决有关本课程实际问题的能力。
(2)使学生对于机械运动学和动力学的分析设计有一较完整的概念。
(3)使学生得到拟定运动方案的训练,并具有初步设计选型与组合以及确定传动方案的能力。
(4)通过课程设计,进一步提高学生运算、绘图、表达、运用计算机和查阅技术资料的能力。
二、机械原理课程设计的任务:机械原理课程设计的任务是对机械的主体机构(连杆机构、凸轮机构、齿轮机构以及其他机构)进行设计和运动分析、动态静力分析,并根据给定机器的工作要求,在此基础上设计凸轮、齿轮;或对各机构进行运动分析。
要求学生根据设计任务,绘制必要的图纸,编写说明书。
三、械原理课程设计的方法:机械原理课程设计的方法大致可分为图解法和解析法两种。
图解法几何概念较清晰、直观;解析法精度较高。
牛头刨床机构的运动特点
牛头刨床机构的运动特点是指它在工作时产生的机构运动特征。
牛头刨床机构是一种将直线运动转化为往复运动的机械结构,其主要特点包括:
1. 往复运动:牛头刨床机构通过曲轴和连杆组成,使得工作台面能够以往复运动的方式进行刨削操作。
这种往复运动是机构的基本特点,能够有效地实现工作过程中的刨削加工。
2. 快速往复:牛头刨床机构的刨床行程通常较长,且具有快速往复的特点。
它能够在短时间内完成一次完整的刨削过程,提高生产效率。
3. 平稳可靠:牛头刨床机构的运动稳定性较好,能够在工作过程中保持平稳的运动状态,避免产生过大的振动和冲击力,保证加工质量和切削工具的寿命。
4. 节能高效:牛头刨床机构在运动时能够利用较少的能量来完成工作,实现能耗的节约。
同时,其运动速度较快,能够提高生产效率,减少加工时间。
5. 方向可逆:牛头刨床机构的运动方向是可逆的,可以根据需要进行前后或上下刮削,具有较好的灵活性和适应性。
总的来说,牛头刨床机构的运动特点是往复、快速、平稳可靠、节能高效和方向可逆。
这些特点使得牛头刨床机构成为一种常用的刨削设备,广泛应用于金属加工和木工加工等领域。
目录一、概述 (1)1、设计目的 (1)2、设计任务 (1)3、设计方法 (1)二、牛头刨床机构简介 (2)1、牛头刨床的组成机构 (2)2、牛头刨床的工作原理 (3)三、导杆机构方案设计1、拟定运动方案2、方案机构的选择四、传动导杆机构的运动分析1、位置分析2、速度分析3、加速度分析五、齿轮机构设计1、齿轮的设计要求2、齿轮计算六、课程设计自我评价与心得七、参考文献一、概述1、设计目的机械原理课程设计是培养学生掌握机械系统运动方案设计能力的技术基础课程,它是机械原理课程学习过程中的一个重要实践环节。
机械原理课程设计目的在于巩固和加深所学的理论知识,培养学生独立解决有关本课程实际问题的能力,使学生对于常用机构(连杆机构、凸轮机构和齿轮机构)设计和运动分析有比较完整的认识,。
以及熟悉机械系统设计的步骤及方法,其中包括选型、运动方案的确定、运动学和动力学的分析和整体设计等,进一步提高设计计算和解决工程技术问题的能力2、设计任务本课程设计要求在规定的时间里按题目任务要求完成设计工作,并上交设计说明书一份。
设计说明书内容包括:1.题目介绍。
2.机构方案。
绘制原理图,说明原动件,从动件等的工作原理。
3.设计说明。
自由度计算,主要尺寸计算、选取等。
4.特点。
说明设计的特色,主要优缺点等。
3、设计方法机械原理课程设计的主要方法有图解法、解析法、实验法。
①图解法是利用已知的条件和某些几何关系,通过几何作图求得的结果。
此法概念清晰、形象直观,但是作图繁琐,精度不高。
②解析法是通过建立数学模型,编制框图和程序,借助计算机求出结果。
该方法精度高、速度快、能解决较复杂的问题。
③实验法是通过建立模型、计算机动态演示与仿真、CAD等,使设计的产品得以实现。
二、牛头刨床机构简介1、牛头刨床的组成机构如图1所示:图1图中:1—工作台;2—刀架;3—滑枕;4—床身;5—减速传动装置;6—带动执行机构;7—手柄;8—滑板。
2、牛头刨床工作原理牛头刨床是一种用于平面切削加工的机床。
牛头刨床的典型机构及其调整图1 B6065牛头刨床的主传动系统1、2—滑动齿轮组 3、4—齿轮 5—偏心滑块 6—摆杆 7—下支点 8—滑枕9—丝杠 10—丝杠螺母 11—手柄 12—轴 13、14—锥齿轮B6065牛头刨床的传动系统如图1所示,其典型机构及其调整概述如下。
(1)变速机构如图1的变速机构由1、2两组滑动齿轮组成,轴Ⅲ有3×2=6种转速,使滑枕变速。
(2)摆杆机构摆杆机构中齿轮3带动齿轮4转动,滑块5在摆杆6的槽内滑动并带动摆杆6绕下支点7转动,于是带动滑枕8作往复直线运动。
(3)行程位置调整机构松开手柄11,转动轴12,通过13、14锥齿轮转动丝杠9,由于固定在摆杆6上的丝杠螺母10 不动,丝杠9带动滑枕8改变起始位置。
(4)滑枕行程长度调整机构滑枕行程长度调整机构见图2。
调整时,转动轴1,通过锥齿轮5、6,带动小丝杠2转动使偏心滑块7移动,曲柄销3带动偏心滑块7改变偏心位置,从而改变滑枕的行程长度。
图2 滑枕行程长度的调整1—轴(带方榫) 2—小丝杠 3—曲柄销 4—曲柄齿轮 5、6—锥齿轮 7—偏心滑块图3 滑枕往复运动速度的变化(5)滑枕往复直线运动速度的变化滑枕往复运动速度在各点上都不一样,见图3。
其工作行程转角为α,空行程为β,α>β,因此回程时间较工作行程短,即慢进快回。
(6)横向进给机构及进给量的调整横向进给机构及进给量的调整如图4所示。
齿轮2与图1中的齿轮4是一体的,齿轮2带动齿轮1转动,连杆3摆动棘爪4,拨动棘轮5使丝杆6转一个角度,实现横向进给。
反向时,由于棘爪后面是斜的,爪内弹簧被压缩,棘爪从棘轮顶滑过,因此工作台横向自动进给是间歇的。
图4 B6065牛头刨床运动及调整1、2—齿轮 3—连杆 4—棘爪 5—棘轮 6—丝杆 7—棘轮护盖工作台横向进给量的大小取决于滑枕每往复一次时棘爪所能拨动的棘轮齿数。
因此调整横向进给量,实际是调整棘轮护盖7的位置。
牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是对于结构型式及尺寸参数已定的具体机构,按主动件的位置、速度和加速度来确定从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量,运动参数又是机械动力学分析的依据,所以机构的运动分析是机械设计过程中必不可少的重要环节。
以计算机为手段的解析方法,由于解算速度快,精确度高,程序有一定的通用性,已成为机构运动分析的主要方法。
连杆机构作为在机械制造特别是在加工机械制造中主要用作传动的机构型式,同其他型式机构特别是凸轮机构相比具有很多优点。
连杆机构采用低副连接,结构简单,易于加工、安装并能保证精度要求。
连杆机构可以将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件,实现间歇运动,满足给定的运动要求,完成机器的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动,实现工件的切削。
工作台的横向运动即是进给运动,实现对切削精度的控制。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成,其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时,通过六杆机构驱动刨刀作往复移动。
刨刀右行时,当刨刀处于工作行程时;要求刨刀的速度较低且平稳,以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时,刨刀不工作,称为空行程,此时要求刨刀的速度较高以提高生产率。
由此可见,牛头刨床的纵向运动特性对机床的性能有决定性的影响。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成,其中实现刨头切削运动的六杆机构是一个关键机构。
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件,刨刀装在C点上。
假设已知各构件的尺寸如表1所示,原动件1以等角速度ω1=1rad/s沿着逆时针方向回转,要求分析各从动件的角位移、角速度和角加速度以及刨刀C点的位移、速度和加速度的变化情况。
图1 牛头刨床的六连杆机构简图表1 六连杆机构的尺寸参数(单位:mm )l 1 l 3 l 4 h h 1 h 2 1809601609004601102 六连杆机构的运动分析方程杆件1为主动件,六杆机构的运动随杆件1的位置变化而发生周期性变化。
在一个变化周期中,可以把杆件1的角位置分成36等分(θ1取362 πn ,其中n 取整数0~35,对应时间s 362πn t =),分别研究θ1在不同取值下杆件机构的位置参数和运动参数的变化。
3s 的长度与刨刀的运动行程成正比,因此可以用5S 表征刨刀的行程,用5S 关于时间的一阶导数5s来表征刨刀的运动速度,用5S 关于时间的二阶导数5s 来表征刨刀的加速度。
1)位置方程由图可知2θ=3θ,故未知量有3θ、4θ(x 轴与4l所成的的角度)、3S (直线BD 的长度)、5S (直线GC 的长度)。
利用两个封闭图形ABDEA 和EDCGE ,建立两个封闭矢量方程,由此可得:⎭⎬⎫+=++=+' s l l s l l l l56431643 (1) 把(1)式分别向x 轴、y 轴投影得:⎪⎪⎭⎪⎪⎬⎫=+=++=++=+ h l l s l l l h s l l h s l 33445334411133441123344sin sin cos cos sin sin sin cos cos cos θθθθθθθθθθ(2) 在(2)式中包含3s 、5s 、3θ、4θ四个未知数,消去其中三个可得到只含4θ一个未知数的方程:[][]{}[][]0sin sin sin 2sin cos cos sin sin 244111234424224244112244111=-+--+-++-+ θθθθθθθθl l h l hl h l l l h l l h (3)当1θ取不同值时,用牛顿迭代法解(3)式,可以求出每个4θ的值,再根据方程组(2)可以求出其他杆件的位置参数3s 、5s 、3θ的值:⎪⎪⎭⎪⎪⎬⎫-+=+=-= 3441113334453443sin sin sin cos cos )sin arcsin(θθθθθθθl l h s l l s l l h (4)2)速度方程对(2)式对时间求一次导数并把结果写成矩阵的形式得:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----00cos sin 0cos cos 01sin sin 00cos cos sin 0sin sin cos 1111143443344334433344333θθωωωθθθθθθθθθθl l v v l l l l l s l s C e B (5)其中C v 为刨刀的水平速度,v eB 为滑块2相对于杆3的速度。
由于每个1θ对应的3s 、3θ、4θ已求出,方程组式(5)的系数矩阵均为常数,采用按列选主元的高斯消去法可求解(式Ⅳ)可解得角速度ω3、ω4、eB v 、C v 。
3)加速度方程把式Ⅳ对时间求导得矩阵式:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡----------=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----00sin cos 0sin sin 00cos cos 00sin sin cos cos 0cos cos sin sin 0cos cos 01sin sin 00cos cos sin 0sin sin cos 11111114344433344433344433333344433333343443344334433344333θωθωωωωθωθωθωθωθωθωθθωθωθωθθωααl l v v l l l l l s v l s v a a θl θl θl θl θl θs θθl θs θC eBe B eBC e B(6)同样采用按列选主元的高斯消去法可求解(6)可得角加速度3α、4α、eB a 、C a 。
3 程序流程图4 Matlab程序编写%主程序开始l1=180;l3=960;l4=160;h=900;h1=460;h2=110;theta1=linspace(0,35*pi/18,36);%定义常量和已知参数,l1代表杆1的长度,l3代表杆3的长度,l4代表杆4的长度,h表示EG 的长度,h1表示AE的竖直距离,h2表示AE的水平距离,theta1表示角θ1的不同值。
theta3=zeros(1,36);theta4=zeros(1,36);s3=zeros(1,36);s5=zeros(1,36);t est=zeros(1,36);vBe=zeros(1,36);vc=zeros(1,36);omega1=ones(1,36);omeg a3=zeros(1,36);omega4=zeros(1,36);aBe=zeros(1,36);ac=zeros(1,36);alph a1=zeros(1,36);alpha3=zeros(1,36);alpha4=zeros(1,36);A=zeros(4,4);dA=zeros(4,1);%定义最终的结果数据,当θ1取不同值时,theta3表示θ3的值,theta4表示θ4的值,s3表示BD的长度,s5表示GC的长度,vBe表示B点在杆3上运动的速度,vc表示杆5的运动速度,即牛头刨刀的速度,omega3表示杆3的转动角速度,omega4表示杆4的转动角速度,aBe表示B点在杆3上运动的角加速度,ac表示杆5的加速度,即牛头刨刀的加速度,alpha3表示杆3的角加速度,alpha4表示杆4的角加速度,矩阵A,dA表示线性方程组的系数矩阵。
i=0; %i为循环变量,在循环结构中使用。
syms THETA1THETA4 %定义符号变量,为以下计算做准备。
fun1=((h1+l1*sin(THETA1)-l4*sin(THETA4))^2+(h2+l1*cos(THETA1)-l4*cos(THETA4))^2)*(l4^2*sin(THETA4)^2+h^2-2*h*l4*sin(THETA4))-l3^2*(h1+ l1*sin(THETA1)-l4*sin(THETA4))^2;%定义迭代法中要求解的关于THETA4的方程。
x0=0; %定义在牛顿迭代法中的变量THEA4的初值。
for i=1:36 %用循环结构求当theta1取不同值时,theta3值。
fun2=subs(fun1,THETA1,theta1(i));%把不同的THETA1的值代入要求解的方程。
[theta4(i),EA,it]=NEWTON(fun2,'THETA4',x0,0.0001,1000);%用牛顿迭代法求得THEATA4,并赋值到theta4的数组中。
x0=theta4(i); %把这次计算的解作为下一次计算的初值。
endfor i=1:36%用循环结构求当theta1的值取不同值时,theta3、s3、s5的取值。
因为theta3的值可能的取值范围为[0,π],对theta3求解时应分以下两种情况讨论。
if sign(h2+l1*cos(theta1(i))-l4*cos(theta4(i)))>0 %theta3<π/2 theta3(i)=asin((h-l4*sin(theta4(i)))/l3);else theta3(i)=pi-asin((h-l4*sin(theta4(i)))/l3); %theta3>π/2 endtest(i)=h1+l1*sin(theta1(i))-l4*sin(theta4(i));s5(i)=l4*cos(theta4(i))+l3*cos(theta3(i));s3(i)=(h1+l1*sin(theta1(i))-l4*sin(theta4(i)))/sin(theta3(i)); endfor i=1:36%用循环结构求当theta1的值取不同值时vBe、omega3、omega4、vc的值。
A(1,1)=cos(theta3(i));A(1,2)=-s3(i)*sin(theta3(i));A(1,3)=-l4*sin(theta4(i));A(2,1)=sin(theta3(i));A(2,2)=s3(i)*cos(theta3(i));A(2,3)=l4*cos(theta4(i));A(3,2)=-l3*sin(theta3(i));A(3,3)=-l4*sin(theta4(i));A(4,2)=l3*cos(theta3(i));A(4,3)=l4*cos(theta4(i));dA(1,1)=-omega1(1,1)*l1*sin(theta1(i));dA(2,1)=omega1(1,2)*l1*cos(theta1(i));x=gauss(A,dA);%用按列选主元的高斯消去法求解。