全等三角形拓展题

全等三角形的提高拓展训练知识点睛全等三角形的性质：对应角相等，对应边相等，对应边上的中线相等，对应边上的高相等，对应角的角平分线相等，面积相等． 寻找对应边和对应角，常用到以下方法：(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边． (2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角． (3)有公共边的，公共边常是对应边． (4)有公共角的，公共角常是对应角． (5)有对顶角的，对顶角常是对应角．(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角)，一对最短边(或最小角)是对应边(或对应角)．要想正确地表示两个三角形全等，找出对应的元素是关键． 全等三角形的判定方法：(1) 边角边定理(SAS )：两边和它们的夹角对应相等的两个三角形全等． (2) 角边角定理(ASA )：两角和它们的夹边对应相等的两个三角形全等． (3) 边边边定理(SSS )：三边对应相等的两个三角形全等．(4) 角角边定理(AAS )：两个角和其中一个角的对边对应相等的两个三角形全等． (5) 斜边、直角边定理(HL )：斜边和一条直角边对应相等的两个直角三角形全等． 全等三角形的应用：运用三角形全等可以证明线段相等、角相等、两直线垂直等问题，在证明的过程中，注意有时会添加辅助线．拓展关键点：能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系．而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础．例题精讲板块一、截长补短【例1】 (06年北京中考题)已知ABC ∆中，60A ∠=，BD 、CE 分别平分ABC ∠和.ACB ∠，BD 、CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．DOECB AND【例2】 如图，点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外)，作60DMN ∠=︒，射线MN 与DBA ∠外角的平分线交于点N ，DM 与MN 有怎样的数量关系?【变式拓展训练】如图，点M 为正方形ABCD 的边AB 上任意一点，MN DM ⊥且与ABC ∠外角的平分线交于点N ，MD 与MN 有怎样的数量关系？【例3】 已知：如图，ABCD 是正方形，∠F AD =∠F AE . 求证：BE +DF =AE .【例4】 以ABC ∆的AB 、AC 为边向三角形外作等边ABD ∆、ACE ∆，连结CD 、BE 相交于点O ．求证：OA 平分DOE ∠．NC D EB M A F E DCBA O ED CBA【例5】 (北京市、天津市数学竞赛试题)如图所示，ABC ∆是边长为1的正三角形，BDC∆是顶角为120︒的等腰三角形，以D 为顶点作一个60︒的MDN ∠，点M 、N 分别在AB 、AC 上，求AMN ∆的周长．【例6】 五边形ABCDE 中，AB =AE ，BC +DE =CD ，∠ABC +∠AED =180°， 求证：AD 平分∠CDE板块二、全等与角度【例7】如图，在ABC ∆中，60BAC ∠=︒，AD 是BAC ∠的平分线，且AC AB BD =+，求ABC ∠的度数.【例8】在等腰ABC ∆中，AB AC =，顶角20A ∠=︒，在边AB 上取点D ，使AD BC =， 求BDC ∠.DCB A NM D CB AC EDBADCBA NMC【例9】(“勤奋杯”数学邀请赛试题) 如图所示，在ABC ∆中，AC BC =，20C ∠=︒，又M 在AC 上，N 在BC 上，且满足50BAN ∠=︒，60ABM ∠=︒，求NMB ∠.【例10】 在四边形ABCD 中，已知AB AC =，60ABD ︒∠=，76ADB ︒∠=，28BDC ︒∠=，求DBC ∠的度数.【例11】 (日本算术奥林匹克试题) 如图所示，在四边形ABCD 中，12DAC ︒∠=，36CAB ︒∠=，48ABD ︒∠=，24DBC ︒∠=，求ACD ∠的度数.【例12】 (河南省数学竞赛试题) 在正ABC ∆内取一点D ，使DA DB =，在ABC ∆外取一点E ，使DBE DBC ∠=∠，且BE BA =，求BED ∠.【例13】 (北京市数学竞赛试题) 如图所示，在ABC ∆中，44BAC BCA ︒∠=∠=，M 为ABC∆内一点，使得30MCA ︒∠=，16MAC ︒∠=，求BMC ∠的度数.全等三角形证明经典20题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBDADBCM CA B即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2 又∵CD=DE∴⊿ADC ≌⊿GDE （AAS ） ∴EG=AC ∵EF//AB ∴∠DFE=∠1 ∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC3. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD又∵AE=AB ，AD=AD∴⊿AED ≌⊿ABD （SAS ） ∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C4. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE 证明：在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ，CDB ABA CDF2 1 E所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC所以△ADC ≌△AFC （SAS ） 所以AD ＝AF所以AE ＝AF ＋FE ＝AD ＋BE5. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

第一种情况：当∠B 是直角时，如图 1，△ABC 和△DEF 中，AC＝DF，BC＝EF，∠B
＝∠E＝90°，根据“HL”定理，可以知道 Rt△ABC≌Rt△DEF．
第二种情况：当∠B 是锐角时，如图 2，BC＝EF，∠B＝∠E＜90°，在射线 EM 上有点
28．如图，△ABC 和△EBD 中，∠ABC＝∠DBE＝90°，AB＝CB，BE＝BD，连接 AE，CD，
AE 与 CD 交于点 M，AE 与 BC 交于点 N．
（1）求证：AE＝CD；
（2）求证：AE⊥CD；
（3）连接 BM，有以下两个结论：①BM 平分∠CBE；②MB 平分∠AMD．其中正确的
学习了三角形全等的判定方法（即“SAS”“ASA”“AAS”“SSS”）和直角三角形全等的判
定方法（即“HL”）后，小聪继续对“两个三角形满足两边和其中一边的对角对应相等”
的情形进行研究
小聪将命题用符号语言表示为：在△ABC 和△DEF 中，AC＝DF，BC＝EF，∠B＝∠E．
小聪的探究方法是对∠B 分为“直角、钝角、锐角”三种情况进行探究．
．（填写序号）
13．已知：如图，BD 为△ABC 的角平分线，且 BD＝BC，E 为 BD 延长线上的一点，BE＝
BA，过 E 作 EF⊥AB，F 为垂足，下列结论：①△ABD≌△EBC；②∠BCE+∠BCD＝180°；
③AD＝EF＝EC；④AE＝EC，其中正确的是
（填序号）
14．如图，两个边长均为 2 的正方形重叠在一起，O 是正方形 ABCD 的中心，则阴影部分
P、Q（点 Q 是不同于点 F 的点），若以 O、P、Q 为顶点的三角形与△OFP 全等，则符
合条件的点 P 的坐标为

全等三角形的提高拓展训练知识点睛全等三角形的性质：对应角相等，对应边相等，对应边上的中线相等，对应边上的高相等，对应角的角平分线相等，面积相等． 寻找对应边和对应角，常用到以下方法：(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边． (2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角． (3)有公共边的，公共边常是对应边． (4)有公共角的，公共角常是对应角． (5)有对顶角的，对顶角常是对应角．(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角)，一对最短边(或最小角)是对应边(或对应角)．要想正确地表示两个三角形全等，找出对应的元素是关键． 全等三角形的判定方法：(1) 边角边定理(SAS )：两边和它们的夹角对应相等的两个三角形全等． (2) 角边角定理(ASA )：两角和它们的夹边对应相等的两个三角形全等． (3) 边边边定理(SSS )：三边对应相等的两个三角形全等．(4) 角角边定理(AAS )：两个角和其中一个角的对边对应相等的两个三角形全等． (5) 斜边、直角边定理(HL )：斜边和一条直角边对应相等的两个直角三角形全等． 全等三角形的应用：运用三角形全等可以证明线段相等、角相等、两直线垂直等问题，在证明的过程中，注意有时会添加辅助线．拓展关键点：能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系．而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础．例题精讲板块一、截长补短【例1】 (06年北京中考题)已知ABC ∆中，60A ∠=，BD 、CE 分别平分ABC ∠和.ACB ∠，BD 、CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．DOECB AD【例2】 如图，点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外)，作60DMN ∠=︒，射线MN 与DBA ∠外角的平分线交于点N ，DM 与MN 有怎样的数量关系?【变式拓展训练】如图，点M 为正方形ABCD 的边AB 上任意一点，MN DM ⊥且与ABC ∠外角的平分线交于点N ，MD 与MN 有怎样的数量关系？【例3】 已知：如图，ABCD 是正方形，∠F AD =∠F AE . 求证：BE +DF =AE .【例4】 以ABC ∆的AB 、AC 为边向三角形外作等边ABD ∆、ACE ∆，连结CD 、BE 相交于点O ．求证：OA 平分DOE ∠．NC D EB M A F E DCB A O ED CA【例5】 (北京市、天津市数学竞赛试题)如图所示，ABC ∆是边长为1的正三角形，BDC∆是顶角为120︒的等腰三角形，以D 为顶点作一个60︒的MDN ∠，点M 、N 分别在AB 、AC 上，求AMN ∆的周长．【例6】 五边形ABCDE 中，AB =AE ，BC +DE =CD ，∠ABC +∠AED =180°， 求证：AD 平分∠CDE板块二、全等与角度【例7】如图，在ABC ∆中，60BAC ∠=︒，AD 是BAC ∠的平分线，且AC AB BD =+，求ABC ∠的度数.D CB ANM D CB AC EDBA【例8】在等腰ABC ∆中，AB AC =，顶角20A ∠=︒，在边AB 上取点D ，使AD BC =，求BDC ∠.【例9】(“勤奋杯”数学邀请赛试题) 如图所示，在ABC ∆中，AC BC =，20C ∠=︒，又M 在AC 上，N 在BC 上，且满足50BAN ∠=︒，60ABM ∠=︒，求NMB ∠.【例10】 在四边形ABCD 中，已知AB AC =，60ABD ︒∠=，76ADB ︒∠=，28BDC ︒∠=，求DBC ∠的度数.【例11】 (日本算术奥林匹克试题) 如图所示，在四边形ABCD 中，12DAC ︒∠=，36CAB ︒∠=，48ABD ︒∠=，24DBC ︒∠=，求ACD ∠的度数.CDBADCBAANMCBA【例12】 (河南省数学竞赛试题) 在正ABC ∆内取一点D ，使DA DB =，在ABC ∆外取一点E ，使DBE DBC ∠=∠，且BE BA =，求BED ∠.【例13】 (北京市数学竞赛试题) 如图所示，在ABC ∆中，44BAC BCA ︒∠=∠=，M 为ABC∆内一点，使得30MCA ︒∠=，16MAC ︒∠=，求BMC ∠的度数.M CA B全等三角形证明经典50题（含答案）1.已知：AB=4，AC=2，D是BC中点，AD是整数，求AD延长AD到E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52.已知：D是AB中点，∠ACB=90°，求证：12 CD ABADB C3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

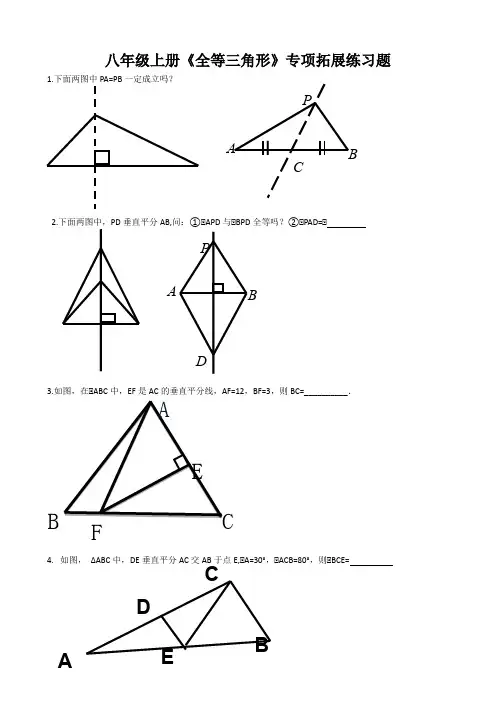
八年级上册《全等三角形》专项拓展练习题 1.下面两图中PA=PB 一定成立吗？2.下面两图中，PD 垂直平分AB,问：①△APD 与△BPD 全等吗？②△PAD=△3.如图，在△ABC 中，EF 是AC 的垂直平分线，AF=12，BF=3，则BC=__________．4. 如图， ΔABC 中，DE 垂直平分AC 交AB 于点E,△A=30°，△ACB=80°，则△BCE=P A BC PA B DE B C FA E BA C D5.已知：QA=QB 求证：点Q在线段AB的垂直平分线上QA B6.如图，△DBC=△DCB, AB=AC,连结AD，E为AD上任一点，试判断BE与CE的数量关系，并说明理由。

AEB CD7. 如图，△ABC中，边AB、BC的垂直平分线l，m交于点O。

求证：O在AC的垂直平分线上8.已知：如图，AB=AC, △BAC=120°，AB 边的垂直平分线交BC 于点F ，连接AF 。

问：△AFC 是什么形状？9. 如图所示，在ΔABC 中，边BC 的垂直平分线MN 分别交AB 于点M,交BC 于点N, ΔBMC 的周长为23,且BM=7,求BC 的长。

10.如图，△ABC 中，△CAB=120º，AB ，AC 的垂直平分线分别交BC 于点E 、F ，则△EAF等于 度。

A CF B E AB C M N11.如图，AD 是△ABC 的角平分线，DE 、DF 分别是△ABD 和△ACD 的高。

求证：AD 垂直平分EF 。

12. 在△ABC 中，AB=AC ，AB 的中垂线与AC 所在的直线相交所得的锐角为50°，则∠B=______.A FB CD E。

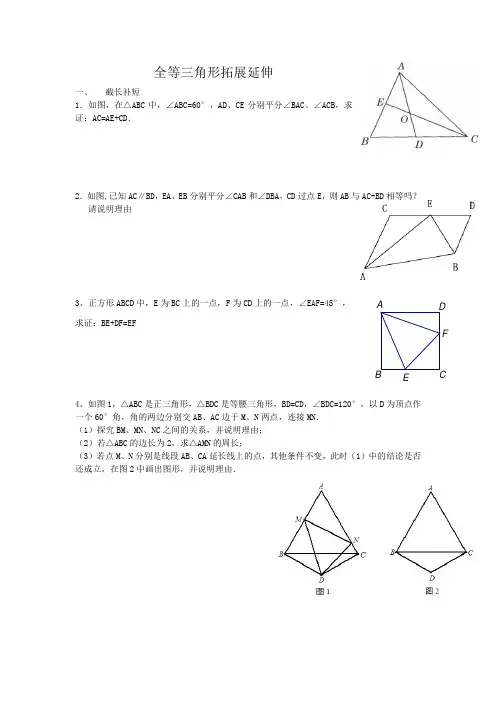
FE D CB A全等三角形拓展延伸一、 截长补短1．如图，在△ABC 中，∠ABC=60°，AD 、CE 分别平分∠BAC 、∠ACB ，求证：AC=AE+CD ．2．如图,已知AC ∥BD ，EA 、EB 分别平分∠CAB 和∠DBA ，CD 过点E ，则AB 与AC+BD 相等吗？请说明理由3、正方形ABCD 中，E 为BC 上的一点，F 为CD 上的一点，∠EAF=45°， 求证：BE+DF=EF4、如图1，△ABC 是正三角形，△BDC 是等腰三角形，BD=CD ，∠BDC=120°，以D 为顶点作一个60°角，角的两边分别交AB 、AC 边于M 、N 两点，连接MN ． （1）探究BM 、MN 、NC 之间的关系，并说明理由； （2）若△ABC 的边长为2，求△AMN 的周长；（3）若点M 、N 分别是线段AB 、CA 延长线上的点，其他条件不变，此时（1）中的结论是否还成立，在图2中画出图形，并说明理由．5、用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD．把一个含60°角的三角尺与这个菱形叠合，如果使三角尺60°角的顶点与点A重合，两边分别与AB、AC重合，将三角尺绕A点按逆时针方向旋转．（1）当三角尺的两边分别与菱形的两边BC、CD相交于点E、F时，通过观察或测量BE、CF 的长度，你能得出什么结论？证明你的结论．（2）当三角尺的两边分别与菱形的两边BC、CD的延长线相交于点E、F时，你在（1）中得到的结论还成立吗？简要说明理由．（3）在（1）的图形中证明四边形AECF的面积等于菱形ABCD的面积的一半．．6、已知正方形ABCD，一等腰直角三角板的一个锐角顶点与A重合，将此三角板绕A点旋转时，两边分别交直线BC、CD于M、N．（1）当M、N分别在边BC、CD上时（如图1），求证：BM+DN=MN；（2）当M、N分别在边BC、CD所在的直线上时（如图2，图3），线段BM、DN、MN之间又有怎样的数量关系，请直接写出结论；（3）在图3中，作直线BD交直线AM、AN于P、Q两点，若MN=10，CM=8，求AP的长．7．（1）如图1，在正方形ABCD 中，M 是BC 边（不含端点B 、C ）上任意一点，P 是BC 延长线上一点，N 是∠DCP 的平分线上一点．若∠AMN =90°，求证：AM =MN ． （2）若将（1）中的“正方形ABCD ”改为“正三角形ABC ”（如图2），N 是∠ACP 的 平分线上一点，则当∠AMN =60°时，结论AM =MN 是否还成立？请说明理由．（3）若将（1）中的“正方形ABCD ”改为“正n 边形ABCD ……X ”，请你作出猜想： 当∠AMN = °时，结论AM =MN 仍然成立．（直接写出答案，不需要证明）8、如图，一个含45°的三角板HBE 的两条直角边与正方形ABCD 的两邻边重合，过E 点作EF ⊥AE 交∠DCE 的角平分线于F 点，试探究线段AE 与EF 的数量关系，并说明理由．9、.如图①、②、③中，点E 、D 分别是正△ABC 、正四边形ABCM 、正五边形ABCMN 中以C点为顶点的相邻两边上的点，且BE = CD ，DB 交AE 于P 点． ⑴求图①中，∠APD 的度数；⑵图②中，∠APD 的度数为___________，图③中，∠APD 的度数为___________； ⑶根据前面探索，你能否将本题推广到一般的正n 边形情况．若能，写出推广问题和结论；若不能，请说明理由．MNPCBA图2M NPDCEBA 图1D CB AEDFCBA10．如图1，△ABC 的边BC 直线l 上，AC ⊥BC ，且AC=BC ；△EFP 的边FP 也在直线l 上，边EF 与边AC 重合，且EF=FP ．(1)在图1中，请你通过观察、测量，猜想并写出AB 与AP 所满足的数量关系和位置关系；(2)将△EFP 沿直线l 向左平移到图2的位置时，EP 交AC 于点Q ，连接AP ，BQ ．猜想并写出BQ 与AP 所满足的数量关系和位置关系，请证明你的猜想；(3)将△EFP 沿直线l 向左平移到图3的位置时，EP 的延长线交AC 的延长线于点Q ，连接AP ，BQ ．你认为(2)中所猜想的BQ 与AP 的数量关系和位置关系还成立吗?若成立，给出证明；若不成立，请说明理由．11、 已知：如图，△ABC 、△DCE 都是等边三角形，B 、C 、E 在一条直线上，连接AE 、BD 交于点F ，（1）求证：AE=BD ； （2）求证：CF 平分∠BFE 。

全等三角形的提高拓展训练知识点睛全等三角形的性质：对应角相等，对应边相等，对应边上的中线相等，对应边上的高相等，对应角的角平分线相等，面积相等．寻找对应边和对应角，常用到以下方法：(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边． (2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角． (3)有公共边的，公共边常是对应边． (4)有公共角的，公共角常是对应角． (5)有对顶角的，对顶角常是对应角．(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角)，一对最短边(或最小角)是对应边(或对应角)．要想正确地表示两个三角形全等，找出对应的元素是关键． 全等三角形的判定方法：(1) 边角边定理(SAS )：两边和它们的夹角对应相等的两个三角形全等． (2) 角边角定理(ASA )：两角和它们的夹边对应相等的两个三角形全等． (3) 边边边定理(SSS )：三边对应相等的两个三角形全等．(4) 角角边定理(AAS )：两个角和其中一个角的对边对应相等的两个三角形全等． (5) 斜边、直角边定理(HL )：斜边和一条直角边对应相等的两个直角三角形全等．全等三角形的应用：运用三角形全等可以证明线段相等、角相等、两直线垂直等问题，在证明的过程中，注意有时会添加辅助线．拓展关键点：能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系．而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础．例题精讲板块一、截长补短【例1】 已知ABC ∆中，60A ∠=，BD 、CE 分别平分ABC ∠和.ACB ∠，BD 、CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．D OECBA【例2】 如图，点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外)，作60DMN ∠=︒，射线MN 与DBA ∠外角的平分线交于点N ，DM 与MN 有怎样的数量关系?【变式拓展训练】如图，点M 为正方形ABCD 的边AB 上任意一点，MN DM ⊥且与ABC ∠外角的平分线交于点N ，MD 与MN 有怎样的数量关系？【例3】 已知：如图，ABCD 是正方形，∠F AD =∠F AE . 求证：BE +DF =AE .【例4】 以ABC ∆的AB 、AC 为边向三角形外作等边ABD ∆、ACE ∆，连结CD 、BE 相交于点O ．求证：OA 平分DOE ∠．NEB M A DF AB C D EO O E D C B A _ F _ E_ D_ C _ B _ A _ N _ C _ D _ E _ B _ M _ A【例5】 如图所示，ABC ∆是边长为1的正三角形，BDC ∆是顶角为120︒的等腰三角形，以D 为顶点作一个60︒的MDN ∠，点M 、N 分别在AB 、AC 上，求AMN ∆的周长．【例6】 五边形ABCDE 中，AB =AE ，BC +DE =CD ，∠ABC +∠AED =180°，求证：AD 平分∠CDE板块二、全等与角度【例7】如图，在ABC ∆中，60BAC ∠=︒，AD 是BAC ∠的平分线，且AC AB BD =+，求ABC∠的度数.【例8】在等腰ABC ∆中，AB AC =，顶角20A ∠=︒，在边AB 上取点D ，使AD BC =，求BDC ∠.D CB A N MDCB AC ED BA DC BA【例9】 如图所示，在ABC ∆中，AC BC =，20C ∠=︒，又M 在AC 上，N 在BC 上，且满足50BAN ∠=︒，60ABM ∠=︒，求NMB ∠.【例10】 在四边形ABCD 中，已知AB AC =，60ABD ︒∠=，76ADB ︒∠=，28BDC ︒∠=，求DBC∠的度数.【例11】 如图所示，在四边形ABCD 中，12DAC ︒∠=，36CAB ︒∠=，48ABD ︒∠=，24DBC ︒∠=，求ACD ∠的度数.【例12】 在正ABC ∆内取一点D ，使DA DB =，在ABC ∆外取一点E ，使DBE DBC ∠=∠，且BE BA =，求BED ∠.CDB ADCBAD E C B A NMCBA【例13】 如图所示，在ABC ∆中，44BAC BCA ︒∠=∠=，M 为ABC ∆内一点，使得30MCA ︒∠=，16MAC ︒∠=，求BMC ∠的度数.M C A B全等三角形证明经典50题（含答案）1.已知：AB=4，AC=2，D是BC中点，AD是整数，求AD延长AD到E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52.已知：D是AB中点，∠ACB=90°，求证：12 CD AB3.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2 证明：连接BF和EF。

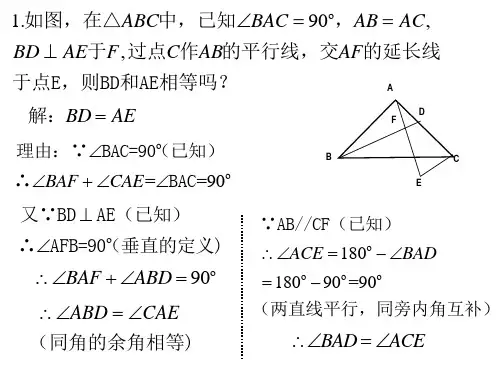
三角形全等实际应用专项训练（25题）一、解答题1．如图，有两个长度相等（BC=EF）的滑梯靠在一面墙上，已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，求证：∠ABC+∠DFE=90°．2．杨阳同学沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙O，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息汇集如下：如图，AB∠OH∠CD，相邻的平行线间的距离相等，AC，BD相交于O，OD∠CD．垂足为D，已知AB=18米，请根据上述信息求标语CD的长度．3．一次演习中，红军与蓝军在河边激战，蓝军在河北岸Ｑ处，如图，因不知河宽，红军很难瞄准蓝军，聪明的红军指挥官站在南岸Ｏ处调整好自己的帽子，使视线恰好擦过帽舌边沿看到蓝军兵营Ｑ处，然后后退到B点，这时他的视点恰好能落在O处，于是他下令测量他脚站的B处与O点之间的距离，并下令按这个距离炮轰蓝军兵营，红军能命中吗？说明理由．4．如图，两根旗杆AC与BD相距12m，某人从B点沿AB走向A，一定时间后他到达点M，此时他仰望旗杆的顶点C和D，两次视线夹角为90°，且CM=DM．已知旗杆AC的高为3m，该人的运动速度为0.5m/s，求这个人走了多长时间？5．如图，A、B两点分别位于一个假山两边，请你利用全等三角形的知识设计一种测量A、B间距离的方案，并说明其中的道理．（1）测量方案：（2）理由：6．如图，为了测量一池塘的宽AB，在岸边找到一点C，连接AC，在AC的延长线上找一点D，使得DC=AC，连接BC，在BC的延长线上找一点E，使得EC=BC，测出DE=60m，试问池塘的宽AB 为多少？请说明理由．7．如图，一根电线杆MN直立在水平地面上的点N处，分别用钢丝绳AB，AC将它加固，两根钢丝绳分别固定在地面上的点B,C处，点B,N,C在同一条直线上，小明测得BN=CN，两根钢丝绳相等吗？请说明理由.8．如图所示,A、B 两点分别位于一个池塘的两端，小明想用绳子测量A、B 间的距离，但绳子不够长,请你利用三角形全等的相关知识帮他设计一种方案测量出A、B间的距离,写出具体的方案,并解释其中的道理,9．图为人民公园的荷花池，现要测量此荷花池两旁A、B两棵树间的距离（不能直接测量），请你根据所学三角形全等的知识，设计一种测量方案求出AB的长（要求画出草图，写出测量方案和理由）．10．如图，在一个风筝ABCD中，AB=AD，BC=DC，分别在AB、AD的中点E、F处挂两根彩线EC、FC．求证：EC=FC．11．已知如图，要测量水池的宽AB，可过点A作直线AC∠AB，再由点C观测，在BA延长线上找一点B′，使∠ACB′=∠ACB，这时只要量出AB′的长，就知道AB的长，对吗？为什么？12．如图，AD是一段斜坡，AB是水平线，现为了测斜坡上一点D的铅直高度（即垂线段DB的长度），小亮在D处立上一竹竿CD，并保证CD=AB，CD∠AD，然后在竿顶C处垂下一根细绳．（细绳末端挂一重锤，以使细绳与水平线垂直）．细绳与斜坡AD交于点E，此时他测得DE=2米，求DB的长度．13．有一座小山，现要在小山A、B的两端开一条隧道，施工队要知道A、B两端的距离，于是先在平地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD=CA，连接BC并延长到E，使CE=CB，连接DE，那么量出DE的长，就是A、B的距离，你能说说其中的道理吗？14．一块三角形玻璃损坏后，只剩下如图所示的残片，你对图中作哪些数据测量后就可到建材部门割取符合规格的三角形玻璃并说明理由．15．如图，一条输电线路需跨越一个池塘，池塘两侧A，B处各立有一根电线杆，但利用现有皮尺无法直接测量出A，B的距离，请你根据所学三角形全等的知识，设计一个方案，测出A，B 的距离（要求画出图形，写出测量方案和理由）16．如图所示，C、D分别位于路段A、B两点的正北处与正南处，现有两车分别从E、F两处出发，以相同的速度直线行驶，相同时间后分别到达C、D两地，休整一段时间后又以原来的速度直线行驶，最终同时到达A、B两点，那么CE与DF平行吗？为什么？17．如图，操场上有两根旗杆间相距12m，小强同学从B点沿BA走向A，一定时间后他到达M 点，此时他测得CM和DM的夹角为90°，且CM=DM，已知旗杆AC的高为3m，小强同学行走的速度为0.5m/s，则：（1）请你求出另一旗杆BD的高度；（2）小强从M点到达A点还需要多长时间？18．某中学八年级同学到野外开展数学综合实践活动，在营地看到一池塘，同学们想知道池塘两端的距离.某同学设计了如下测量方案：先取一个可直接到达池塘的两端的点A，B的点E，连接AE，BE，分别延长AE至点D，BE至点C，使得ED=AE，EC=BE.再测出CD的长度即可知道AB之间的距离.他的方案可行吗？请说明理由.19．如图，两车从路段MN的两端同时出发，以相同的速度行驶，相同时间后分别到达A，B两地，两车行进的路线平行．那么A,B两地到路段MN的距离相等吗？为什么？20．课间，小明拿着老师的等腰三角板玩，不小心掉到两墙之间，如图，求证：∠ADC∠∠CEB．二、综合题（提升）21．解答题（1）问题发现如图1，∠ABC和∠ADE均为等边三角形，点D在边BC上，连接CE．请填空：①∠ACE的度数为；②线段AC、CD、CE之间的数量关系为．（2）拓展探究如图2，∠ABC和∠ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D在边BC上，连接CE．请判断∠ACE的度数及线段AC、CD、CE之间的数量关系，并说明理由．22．解答题（1）如图1，以∠ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG，连接EG，试判断∠ABC与∠AEG面积之间的关系，并说明理由．（2）园林小路，曲径通幽，如图2所示，小路由白色的正方形理石和黑色的三角形理石铺成．已知中间的所有正方形的面积之和是a平方米，内圈的所有三角形的面积之和是b平方米，这条小路一共占地多少平方米．23．如图，∠ABC中，∠ACB=90°，AC=BC=1，将∠ABC绕点C逆时针旋转得到∠A1B1C，旋转角为ɑ（0°＜ɑ＜90°），连接BB1．设CB1交AB于点D，A1B1分别交AB，AC于点E，F．（1）求证：∠BCD∠∠A1CF；（2）若旋转角ɑ为30°，①请你判断∠BB1D的形状；②求CD的长．24．琪琪家门前有一条小河，村里准备在河面上架上一座桥，但河宽AB无法直接测量，（1）爱动脑的小明想到了如下方法：在与AB垂直的岸边BF上取两点C，D，使CD=，再引出BF的垂线DG，在DG上取一点E，并使A、C、E在一条直线上，这时测出线段的长度就是AB的长。

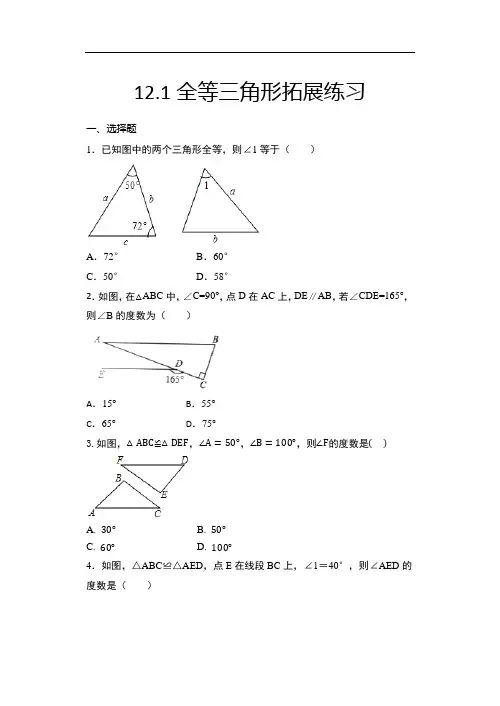
12.1全等三角形拓展练习一、选择题1．已知图中的两个三角形全等，则∠1等于（）A．72°B．60°C．50°D．58°2．如图，在△ABC中，∠C=90°，点D在AC上，DE∥AB，若∠CDE=165°，则∠B的度数为（）A．15°B．55°C．65°D．75°3.如图，△ABC≌△DEF，∠A=50°，∠B=100°，则∠F的度数是()A. 30°B. 50°C. 60°D. 100°4．如图，△ABC≌△AED，点E在线段BC上，∠1＝40°，则∠AED的度数是（）A．70°B．68°C．65°D．60°5．如图，△ABC≌△CDA，并且AB＝CD，那么下列结论错误的是( )A．∠1＝∠2 B．CA＝ACC．∠D＝∠B D．AC＝BC6.已知△DEF≌△ABC，AB=AC，且△ABC的周长是23cm，BC=4cm，则△DEF中必有一边的长为()A. 9cm或4cmB. 9.5cm或9cmC. 4cm或9.5cmD. 9cm7．如图，已知△ABE≌△ACD，下列选项中不能被证明的等式是（）A．AD＝AE B．DB＝AEC．DF＝EF D．DB＝EC8．如图，把△ABC沿DE折叠，当点A落在四边形BCDE内部时，则∠A 与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是( )．A．∠A=∠1+∠2B．2∠A=∠1+∠2C．13∠A=∠1+∠2D．∠A=2∠1+2∠29.如图，△ABC≌△A′B′C′，其中∠A=36°，∠C′=24°，则∠B=()A. 150°B. 120°C. 90°D. 60°10．如图，△AEB≌△DFC，AE⊥BC，DF⊥BC，垂足分别为E、F，∠B ＝25°，则∠D等于（）A．80°B．65°C．48°D．28°11．如图，△ABC≌△EFD，且AB＝EF，EC＝4，CD＝3，则AC＝（）A．3B．4C．7D．8二、填空题12．如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC ＝120°．以D为顶点作一个60°角，使其两边分别交AB于点M，交AC 于点N，连接MN，则△AMN的周长为_____．13.如图，∠C=∠CAM=90°，AC=8，BC=4，P，Q两点分别在线段AC 和射线AM上运动，且PQ=AB.若△ABC与△PQA全等，则AP的长度为_________．14．如图，若△ABC≌△A1B1C1，且∠A＝110°，∠B＝40°，则∠C1＝______°．15如果△ABC≌△ADC，AB=AD，∠B=70°，BC=3cm，那么∠D=______ ，DC=______ cm．16．已知△ABC≌△A′B′C′，A与A′，B与B′是对应点，△A′B′C′周长为9cm，AB＝3cm，BC＝4cm，则A′C′＝cm．17．如图，已知△ABC≌△ADE，若AB＝7，AC＝3，则BE的值为．三、解答题18．如图，点A，B，C在同一直线上，点E在BD上，且△ABD≌△EBC，BC=．2cmAB=，3cm（1）求DE的长；（2）判断AC与BD的位置关系，并说明理由．（3）判断直线AD与直线CE的位置关系，并说明理由．19.如图，已知△ACE≌△DBF.CE=BF，AE=DF，AD=8，BC=2．(1)求AC的长度；(2)试说明CE//BF．20．如图，已知△ABC≌△DBE，点D在AC上，BC与DE交于点P，若AD=DC=2.4，BC=4.1．（1）若∠ABE=162°，∠DBC=30°，求∠CBE的度数；（2）求△DCP与△BPE的周长和．21．如图，CD⊥AB于点D，BE⊥AC于点E，△ABE≌△ACD，∠C=42°，AB=9，AD=6，G为AB延长线上一点．（1）求∠EBG的度数．（2）求CE的长．答案1．D2．D3. A4．A5．D6. C7．B8．B9. B10．B11．C12． 613. 8或414．3015 .70°；316．2．17．4△≌△，18．解：（1）ABD EBC∴==，2cm==，BE ABBD BC3cmDE BD BE∴=-=．1cm⊥．理由：（2）AC BD△≌△，ABD EBC∴．∠=∠ABD EBC又A，B，C在同一直线上，∠︒．∴=EBC90∴⊥．AC BD（3）直线AD与直线CE垂直．理由：如图，延长CE交AD于F．ABD EBC △≌△， D C ∴∠=∠．在Rt ABD △中，90A D ∠+∠=︒，90A C +∠=∴∠︒，90AFC ∴∠=︒，即直线AD 与直线CE 垂直．19. 解：(1)∵△ACE≌△DBF ， ∴AC =BD ，则AB =DC ， ∵BC =2， ∴2AB +2=8， 解得：AB =3， 故AC =3+2=5；(2)∵△ACE≌△DBF ， ∴∠ECA =∠FBD ， ∴CE//BF ．20． 解：（1）∵∠ABE=162°，∠DBC=30°， ∴∠ABD+∠CBE=132°， ∵△ABC ≌△DBE ， ∴∠ABC=∠DBE ，∴∠ABD=∠CBE=132°÷2=66°， 即∠CBE 的度数为66°； （2）∵△ABC ≌△DBE ， ∴DE=AD+DC=4.8，BE=BC=4.1，△DCP 和△BPE 的周长和=DC+DP+CP+BP+PE+BE=DC+DE+BC+BE=15.4． 故答案是：（1）66°；（2）15.421．（1）∵△ABE≌△ACD，∴∠EBA=∠C=42°，∴∠EBG=180°-42°=138°；（2）∵△ABE≌△ACD，∴AC=AB=9，AE=AD=6，∴CE=AC-AE=9-6=3．。

全等三角形综合应用知识点：1、全等三角形的判定方法：2、角平分线的性质与判定：例题讲解2016武汉江汉区压轴题．（本题12分）△ABC是等腰三角形，AB＝AC，AD是△ABC的中线，以AC为边作等边△ACE，BE分别与直线AD、AC交于点F、G，连接CF(1) ①如图1，若△ABC、△ACE位于AC异侧，求∠EFC的度数②试判断线段EF、DF、AF之间的数量关系，并说明理由(2) 若△ABC、△ACE位于AC同侧，试完成备用图，并直接写出线段EF、DF、AF之间的数量关系解：(1) ①∵AB＝AE，∴设∠ABE＝∠AEB＝α∵AB＝AC，AD是△ABC的中线∴设∠BAD＝∠CAD＝β又2α＋2β＋60°＝180°，α＋β＝60°∴∠AFE＝∠DFC＝α＋β＝60°∴∠EFC＝180°－60°－60°＝60°②过点C作CH⊥BE于H∵∠AEB＋∠AEC＝60°，∠ABE＋∠BAD＝60°∴∠BAD＝∠HEC可证：△ABD≌△EHC（AAS）∴HE＝AD易证：△CFH≌△CFD（AAS）∴FH＝DF∴EF－FH＝AF－DF即EF－AF＝2DF(3) 作图、证明的过程一样AF－EF＝2DF2016武珞路中学．（本题10分）已知等边三角形ABC，M为AB上的一点，以CM为边作等边△CMN，连接BN(1) 求证：AM＝BN(2) 作MH⊥BC于H，连接AH．若AH∥MN，AM＝1，求CH的长证明：(1) △ACM ≌△BCN （SAS ）(2) 由(1)知：△ACM ≌△BCN∴∠CBN ＝∠MAC ＝60°∴∠MBN ＝60°＋60°＝120过点M 作MD ∥BC 交AC 于D∴△AMD 为等边三角形∴AM ＝AD ＝BN ，∠ADM ＝60°∴BM ＝CD ，∠MDC ＝120°在△BMN 和△DCM 中⎪⎩⎪⎨⎧=∠=∠=DMBN CDM MBN DCBM∴△BMN ≌△DCM （SAS ）∴∠BMN ＝∠DCM∵AH ∥MN∴∠BMN ＝∠BAH ＝∠DCM在△BAH 和△ACM 中⎪⎩⎪⎨⎧∠=∠=∠=∠A C M BAH CA AB CAM ABH ∴△BAH ≌△ACM （ASA ）∴BH ＝AM ＝1∴BM ＝HC∵MH ⊥BC ，∠MBH ＝60°∴BM ＝2BH ＝2∴CH ＝22016武珞路中学．（本题10分）如图1，已知等腰△ABC 中，AB ＝AC ，AD 为BC 边上的中线，以AB 为边向外作等边△ABE ，直线CE 与直线AD 交于点F(1) 若AF ＝10，DF ＝3，试求EF 的长(2) 若以AB 为边向内作等边△ABE ，其它条件均不改变，请用尺规作图补全图2（保留作图痕迹），找出EF 、AF 、DF 三者的数量关系，并证明你的结论．解：(1) 设∠BAD ＝∠CAD ＝α，∠AEC ＝∠ACE ＝β在△ACE 中，2α＋60＋2β＝180°，α＋β＝60°连接BF∴∠BFD＝∠CFD＝60°∴BF＝CF＝2DF＝6在EC上截取EG＝CF，连接AG∴△AEG≌△ACF（SAS）∴∠EAG＝∠CAF，AG＝AF∴∠GAF＝60°∴△AFG为等边三角形∴EF＝EG＋GF＝AF＋FC＝10＋6＝16(2) 尺规作图：先作AB的垂直平分线，再利用半径得到等边设∠BAD＝∠CAD＝α，∠ACE＝∠AEC＝β∴∠CAE＝180°－2β∴∠BAE＝2α＋180－2β＝60°，β－α＝60°∴∠BAD＝∠BEF在AF上截取AG＝EF，连接BG可知：△ABG≌△EBF（SAS）∴AG＝EF，BG＝BF∴△BFG为等边三角形∴AF＝AG＋GF＝BF＋EF＝2DF＋EF武汉二中广雅中学2016．（本题12分）在△ABC中，AB＝AC，∠BAC＝α（0＜α＜60°），以线段BC为边在△ABC内作等边△DBC(1) 如图1，∠ABD＝_______（用含α的式子表示）(2) 如图2，∠BCE＝150°，∠ABE＝60°，判断△ABE的形状并加以证明(3) 在(2)的条件下，连接DE，若∠DEC＝45°，求α的值例1、（1）在⊿ABC中，∠B=∠C，与⊿ABC全等的三角形有一个角是130°，那么⊿ABC中与这个角对应的角是（）A、∠A B、∠B C、∠C D、∠B或∠C（2）如图1，亮亮书上的三角形被墨迹污染了一部分，很快他根据所学知识，画出了一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A、SSSB、SASC、AASD、ASA（3）如图2，AD平分∠BAC，BF⊥AD于D，交AC于F，DE∥AC，∠BAD=30°，则∠BDE=______例2、如图3，OM平分AOB，AO=OB，AD与BC相交于M。

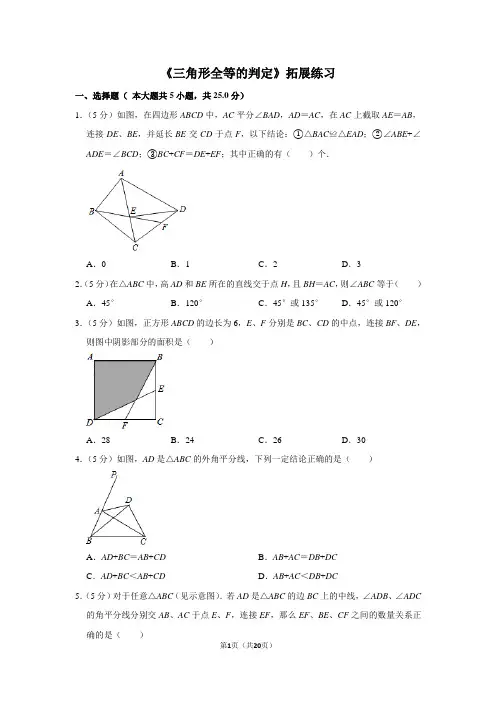
《三角形全等的判定》拓展练习一、选择题（本大题共5小题，共25.0分）1．（5分）如图，在四边形ABCD中，AC平分∠BAD，AD＝AC，在AC上截取AE＝AB，连接DE、BE，并延长BE交CD于点F，以下结论：①△BAC≌△EAD；②∠ABE+∠ADE＝∠BCD；③BC+CF＝DE+EF；其中正确的有（）个．A．0B．1C．2D．32．（5分）在△ABC中，高AD和BE所在的直线交于点H，且BH＝AC，则∠ABC等于（）A．45°B．120°C．45°或135°D．45°或120°3．（5分）如图，正方形ABCD的边长为6，E、F分别是BC、CD的中点，连接BF、DE，则图中阴影部分的面积是（）A．28B．24C．26D．304．（5分）如图，AD是△ABC的外角平分线，下列一定结论正确的是（）A．AD+BC＝AB+CD B．AB+AC＝DB+DCC．AD+BC＜AB+CD D．AB+AC＜DB+DC5．（5分）对于任意△ABC（见示意图）．若AD是△ABC的边BC上的中线，∠ADB、∠ADC 的角平分线分别交AB、AC于点E、F，连接EF，那么EF、BE、CF之间的数量关系正确的是（）A．BE+CF＞EF B．BE+CF≥EF C．BE+CF＜EF D．BE+CF＝EF二、填空题（本大题共5小题，共25.0分）6．（5分）如图，在平面直角坐标系中，点A的坐标为（1，0），点B的坐标为（1，4），C 的坐标为（﹣2，6），如果存在点D，使得△ABD与△ABC全等，那么点D的坐标．（写出所有可能的情况）7．（5分）若满足∠AOB＝30°，OA＝4，AB＝k的△AOB的形状与大小是唯一的，则k的取值范围是．8．（5分）如图，在Rt△ABC中，∠ACB＝90°，EF⊥AB于点D，交BC的延长线于点E．若AB＝EF且BE＝16，CF＝6，则AC＝．9．（5分）如图，已知四边形ABCD中，AB＝10厘米，BC＝8厘米，CD＝12厘米，∠B＝∠C，点E为AB的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为时，能够使△BPE与△CQP全等．10．（5分）如图，在△P AB中，P A＝PB，M、N、K分别是P A、PB、AB上的点，且AM＝BK，BN＝AK．若∠MKN＝50°，则∠P的度数为．三、解答题（本大题共5小题，共50.0分）11．（10分）如图，在△ABC中，D为AB上一点，E为AC中点，连接DE并延长至点F，使得EF＝ED，连CF．（1）求证：CF∥AB（2）若∠ABC＝50°，连接BE，BE平分∠ABC，AC平分∠BCF，求∠A的度数．12．（10分）如图，点A，B，C，D在一条直线上，且AB＝CD，若∠1＝∠2，EC＝FB．求证：∠E＝∠F．13．（10分）阅读下面材料：小明遇到这样一个问题：如图1，在四边形ABCD中，E是BC的中点，AE是∠BAD的平分线，AB∥DC，求证：AD＝AB+DC．小明发现以下两种方法：方法1：如图2，延长AE、DC交于点F；方法2：如图3，在AD上取一点G使AG＝AB，连接EG、CG．（1）根据阅读材料，任选一种方法，证明：AD＝AB+DC；用学过的知识或参考小明的方法，解决下面的问题：（2）如图4，在四边形ABCD中，AE是∠BAD的平分线，E是BC的中点，∠BAD＝60°，∠ABC＝180°﹣∠BCD，求证：CD＝CE．14．（10分）如图，在△ABC中，AD⊥BC，垂足为D，AD＝CD，点E在AD上，DE＝BD，M、N分别是AB、CE的中点．（1）求证：△ADB≌△CDE；（2）求∠MDN的度数．．15．（10分）如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且AD＝CD．（1）求证：△ABD≌△CFD；（2）已知BC＝7，AD＝5，求AF的长．《三角形全等的判定》拓展练习参考答案与试题解析一、选择题（本大题共5小题，共25.0分）1．（5分）如图，在四边形ABCD中，AC平分∠BAD，AD＝AC，在AC上截取AE＝AB，连接DE、BE，并延长BE交CD于点F，以下结论：①△BAC≌△EAD；②∠ABE+∠ADE＝∠BCD；③BC+CF＝DE+EF；其中正确的有（）个．A．0B．1C．2D．3【分析】只要证明△BAC≌△EAD，∠ABE＝∠ACD，FE＝FC即可解决问题．【解答】解：∵AB＝AE，AC＝AD，∠BAC＝∠EAD，∴△BAC≌△EAD（SAS），故①正确，∴∠ACB＝∠ADE，BC＝DE，∵AB＝AE，AC＝AD，∴∠ABE＝∠AEB，∠ACD＝∠ADC，∴∠BAE+2∠ABE＝180°，∠CAD+2∠ACD＝180°，∵∠BAE＝∠CAD，∴∠ABE＝∠ACD，∴∠ABE+∠ADE＝∠ACD+∠ACB＝∠BCD，故②正确，∵∠CEF＝∠AEB，∠ABE＝∠AEB，∠ABE＝∠ACD，∴∠FEC＝∠ECF，∴EF＝CF，∴BC+CF＝DE+EF，故③正确，故选：D．【点评】本题考查全等三角形的判定和性质，等腰三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．2．（5分）在△ABC中，高AD和BE所在的直线交于点H，且BH＝AC，则∠ABC等于（）A．45°B．120°C．45°或135°D．45°或120°【分析】根据题意画出两个图形，证△HBD≌△CAD，推出AD＝DB，推出∠DAB＝∠DBA，根据三角形内角和定理和等腰三角形的性质求出∠ABD，即可求出答案．【解答】解：分为两种情况：①如图1，∵AD、BE是△ABC的高，∴∠ADC＝∠BDH＝90°，∠BEC＝90°，∴∠C+∠CAD＝90°，∠C+∠HBD＝90°，∴∠CAD＝∠HBD，在△HBD和△CAD中，∴△HBD≌△CAD（AAS），∴BD＝AD，∵∠ADB＝90°，∴∠ABC＝∠BAD＝45°，②如图2，∵AD⊥BC，BE⊥AC，∴∠ADC＝∠HDB＝∠AEH＝90°，∴∠H+∠HAE＝∠C+∠HAE＝90°，∴∠H＝∠C，∵在△HBD和△CAD中，，∴△HBD≌△CAD（AAS），∴AD＝BD，∴∠DAB＝∠DBA，∵∠ADB＝90°，∴∠ABD＝45°，∴∠ABC＝180°﹣45°＝135°；故选：C．【点评】本题考查了全等三角形的性质和判定，等腰三角形的性质和判定，垂直定义，三角形的内角和定理等知识点的应用，用了分类讨论思想．3．（5分）如图，正方形ABCD的边长为6，E、F分别是BC、CD的中点，连接BF、DE，则图中阴影部分的面积是（）A．28B．24C．26D．30【分析】连接BD，可看出阴影部分的面积等于正方形的面积+一个三角形的面积，用相似求出三角形的面积，阴影部分的面积可证．【解答】解：连接BD，EF．设DE交BF于G．∵阴影部分的面积＝△ABD的面积+△BDG的面积（G为BF与DE的交点），∴△ABD的面积＝正方形ABCD的面积＝×36＝18，∵△BCD中EF为中位线，∴EF∥BD，EF＝BD，∴△GEF∽△GBD，∴DG＝2GE，∴△BDE的面积＝△BCD的面积．∴△BDG的面积＝△BDE的面积＝△BCD的面积＝×18＝6．∴阴影部分的面积＝18+6＝24．故选：B．【点评】本题考查正方形的性质，正方形的四个边长相等，关键是连接BD，把阴影部分分成两部分计算．4．（5分）如图，AD是△ABC的外角平分线，下列一定结论正确的是（）A．AD+BC＝AB+CD B．AB+AC＝DB+DCC．AD+BC＜AB+CD D．AB+AC＜DB+DC【分析】在AP上截取AF＝AC．首先证明△DAF≌△DAC（SAS），再根据三角形的三边关系即可解决问题；【解答】解：在AP上截取AF＝AC．∵AF＝AC，∠DAF＝∠DAC，AD＝AD，∴△DAF≌△DAC（SAS），∴DF＝DC，∴BD+DF＞BF，∴BD+DC＞AB+AC．故选：D．【点评】本题考查了全等三角形的性质和判定，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．5．（5分）对于任意△ABC（见示意图）．若AD是△ABC的边BC上的中线，∠ADB、∠ADC 的角平分线分别交AB、AC于点E、F，连接EF，那么EF、BE、CF之间的数量关系正确的是（）A．BE+CF＞EF B．BE+CF≥EF C．BE+CF＜EF D．BE+CF＝EF 【分析】延长ED到H，使DE＝DH，连接CH，FH，证△EFD≌△HFD，推出EF＝FH，证△BDE≌△CDH，推出BE＝CH，在△CFH中，由三角形三边关系定理得出CF+CH ＞FH，代入求出即可．【解答】证明：延长ED到H，使DE＝DH，连接CH，FH，∵AD是△ABC的中线，∴BD＝DC，∵DE、DF分别为∠ADB和∠ADC的平分线，∴∠1＝∠4＝∠ADB，∠3＝∠5＝∠ADC，∴∠1+∠3＝∠4+∠5＝∠ADB+∠ADC＝×180°＝90°，∵∠1＝∠2，∴∠3+∠2＝90°，即∠EDF＝∠FDH，在△EFD和△HFD中，，∴△EFD≌△HFD（SAS），∴EF＝FH，在△BDE和△CDH中，，∴△BDE≌△CDH（SAS），∴BE＝CH，在△CFH中，由三角形三边关系定理得：CF+CH＞FH，∵CH＝BE，FH＝EF，∴BE+CF＞EF．故选：A．【点评】本题考查了全等三角形的性质和判定，三角形的三边关系定理的应用，题目比较好，但是有一定的难度．二、填空题（本大题共5小题，共25.0分）6．（5分）如图，在平面直角坐标系中，点A的坐标为（1，0），点B的坐标为（1，4），C 的坐标为（﹣2，6），如果存在点D，使得△ABD与△ABC全等，那么点D的坐标（4，6）；（﹣2，﹣2）；（4，﹣2）．（写出所有可能的情况）【分析】由条件可以知道要使△ABD与△ABC全等，则点C与点D关于直线AB、AB的中点或AB的垂直平分线对称，再根据点C的坐标就可以求出D的坐标．【解答】解：∵点A的坐标为（1，0），点B的坐标为（1，4），C的坐标为（﹣2，6），∴当点D与点C关于AB对称时，△ABD与△ABC全等，此时D（4，6）；当点D与点C关于AB的垂直平分线对称时，△ABD与△ABC全等，此时D（﹣2，﹣2）；当点D与点C关于AB的中点对称时，△ABD与△ABC全等，此时D（4，﹣2）；故答案为：（4，6）；（﹣2，﹣2）；（4，﹣2）．【点评】本题考查了全等三角形的性质，坐标与图形的性质的运用，轴对称的性质的运用，解题时注意分类思想的运用．7．（5分）若满足∠AOB＝30°，OA＝4，AB＝k的△AOB的形状与大小是唯一的，则k的取值范围是k＝2或k≥4．【分析】分两种情况讨论，依据∠AOB＝30°，OA＝4，AB＝k的△AOB的形状与大小是唯一的，即可得到k的取值范围．【解答】解：如图所示，以点A为圆心，2为半径画弧，弧线与射线OB有唯一交点B，即△AOB的形状与大小是唯一的；以A为圆心，大于等于4为半径画弧，弧线与射线OB（不含端点）有唯一交点B'，即△AOB'的形状与大小是唯一的；综上所述，k的取值范围是k＝2或k≥4．故答案为：k＝2或k≥4．【点评】本题主要考查了全等三角形的判定，需要通过三角形的角与边的关系来判断，考虑最特殊的两种情况，即直角三角形以及等腰三角形．8．（5分）如图，在Rt△ABC中，∠ACB＝90°，EF⊥AB于点D，交BC的延长线于点E．若AB＝EF且BE＝16，CF＝6，则AC＝10．【分析】利用AAS证明△ACB≌△ECF，推出BC＝CF＝6，AC＝EC，求出EC即可解决问题；【解答】解：∵∠ACB＝90°，EF⊥AB于点D，∴∠ECF＝∠ACB＝∠ADF＝90°，∴∠A+∠B＝90°，∠E+∠B＝90°，∴∠A＝∠E，在△ACB和△ECF中，，∴△ACB≌△ECF（AAS），∴AC＝EC，BC＝CF＝6，∵BE＝16，∴AC＝EC＝BE﹣BC＝16﹣6＝10，故答案为10．【点评】本题考查全等三角形的判定和性质，解题的关键是正确寻找全等三角形的全等的条件，属于中考常考题型．9．（5分）如图，已知四边形ABCD中，AB＝10厘米，BC＝8厘米，CD＝12厘米，∠B＝∠C，点E为AB的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为3厘米/秒或厘米/秒时，能够使△BPE与△CQP全等．【分析】分两种情况讨论，依据全等三角形的对应边相等，即可得到点Q的运动速度．【解答】解：设点P运动的时间为t秒，则BP＝3t，CP＝8﹣3t，∵∠B＝∠C，∴①当BE＝CP＝5，BP＝CQ时，△BPE与△CQP全等，此时，5＝8﹣3t，解得t＝1，∴BP＝CQ＝3，此时，点Q的运动速度为3÷1＝3厘米/秒；②当BE＝CQ＝5，BP＝CP时，△BPE与△CQP全等，此时，3t＝8﹣3t，解得t＝，∴点Q的运动速度为5÷＝厘米/秒；故答案为：3厘米/秒或厘米/秒．【点评】本题考查了全等三角形的性质和判定的应用，解决问题的关键是掌握全等三角形的对应边相等．10．（5分）如图，在△P AB中，P A＝PB，M、N、K分别是P A、PB、AB上的点，且AM＝BK，BN＝AK．若∠MKN＝50°，则∠P的度数为80°．【分析】由△MAK≌△KBN，推出∠AMK＝∠BKN，由∠BKM＝∠A+∠AMK＝∠MKN+∠BKN，推出∠A＝∠MKN＝50°，推出∠A＝∠B＝50°，由此即可解决问题．【解答】解：∵P A＝PB，∴∠A＝∠B，在△MAK和△KBN中，，∴△MAK≌△KBN（SAS），∴∠AMK＝∠BKN，∵∠BKM＝∠A+∠AMK＝∠MKN+∠BKN，∴∠A＝∠MKN＝50°，∴∠A＝∠B＝50°，∴∠P＝180°﹣2×50°＝80°．故答案为80°．【点评】本题考查全等三角形的判定和性质、等腰三角形的性质，三角形的外角的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．三、解答题（本大题共5小题，共50.0分）11．（10分）如图，在△ABC中，D为AB上一点，E为AC中点，连接DE并延长至点F，使得EF＝ED，连CF．（1）求证：CF∥AB（2）若∠ABC＝50°，连接BE，BE平分∠ABC，AC平分∠BCF，求∠A的度数．【分析】（1）求出∴△AED≌△CEF，根据全等得出∠A＝∠ACF，根据平行线的判定得出即可；（2）求出∠A＝∠ACB，根据三角形内角和定理求出即可．【解答】（1）证明：∵在△AED和△CEF中∴△AED≌△CEF（SAS），∴∠A＝∠ACF，∴CF∥AB；（2）解：∵AC平分∠BCF，∴∠ACB＝∠ACF，∵∠A＝∠ACF，∴∠A＝∠ACB，∵∠A+∠ABC+∠ACB＝180°，∠ABC＝50°，∴2∠A＝130°，∴∠A＝65°．【点评】本题考查了全等三角形的性质和判定、平行线的性质和判定、三角形内角和定理等知识点，能综合运用定理进行推理是解此题的关键．12．（10分）如图，点A，B，C，D在一条直线上，且AB＝CD，若∠1＝∠2，EC＝FB．求证：∠E＝∠F．【分析】求出∠DBF＝∠ACE，AC＝DB，根据SAS推出△ACE≌△DBF，根据全等三角形的性质得出即可．【解答】证明：∵∠1+∠DBF＝180°，∠2+∠ACE＝180°．又∵∠1＝∠2，∴∠DBF＝∠ACE，∵AB＝CD，∴AB+BC＝CD+BC，即AC＝DB，在△ACE和△DBF中，∴△ACE≌△DBF（SAS），∴∠E＝∠F．【点评】本题考查了全等三角形的性质和判定，能求出△ACE≌△DBF是解此题的关键．13．（10分）阅读下面材料：小明遇到这样一个问题：如图1，在四边形ABCD中，E是BC的中点，AE是∠BAD的平分线，AB∥DC，求证：AD＝AB+DC．小明发现以下两种方法：方法1：如图2，延长AE、DC交于点F；方法2：如图3，在AD上取一点G使AG＝AB，连接EG、CG．（1）根据阅读材料，任选一种方法，证明：AD＝AB+DC；用学过的知识或参考小明的方法，解决下面的问题：（2）如图4，在四边形ABCD中，AE是∠BAD的平分线，E是BC的中点，∠BAD＝60°，∠ABC＝180°﹣∠BCD，求证：CD＝CE．【分析】（1）方法1：如图2，延长AE、DC交于点F，证明△ABE≌△FCE（ASA）即可解决问题方法2：如图3，在AD上取一点G使AG＝AB，连接EG、CG．想办法证明DC＝DG即可解决问题；（2）如图4中，作CM∥AB交AE的延长线于M，CM交AD于N，连接EN．只要证明△CNE≌△CND（ASA）即可解决问题；【解答】解：（1）方法1：如图2，延长AE、DC交于点F；∵AB∥DF，∴∠B＝∠ECF，∵BE＝EC，∠BEA＝∠CEF，∴△ABE≌△FCE（ASA），∴AB＝CF，∵EA平分∠BAD，∴∠BAE＝∠DAF＝∠F，∴AD＝DF，∴AD＝CD+AB．方法2：如图3，在AD上取一点G使AG＝AB，连接EG、CG．∵AB＝AG，∠BAE＝∠GAE，AE＝AE，∴△BAE≌△GAE（SAS），∴BE＝EG＝EC，∠AEB＝∠AEG，∴∠EGC＝∠ECG，∵∠BEG＝∠EGC+∠ECG，∴∠BEA＝∠ECG，∴AE∥CG，∴∠EAG＝∠CGD，∵AB∥CD，AE∥CG，∴∠BAE＝∠DCG，∴∠DCG＝∠DGC，∴CD＝DG，∴AD＝AB+CD．（2）证明：如图4中，作CM∥AB交AE的延长线于M，CM交AD于N，连接EN．由（1）可知：AN＝NM，AE＝EM，∴EN平分∠ANM，∵∠BAD＝60°，MN∥AB，∴∠MND＝∠BAD＝60°，∴∠ENM＝∠ENA＝60°，∴∠CND＝∠CNE，∵∠B+∠ECN＝180°，∠ABC＝180°﹣∠BCD，∴∠NCE＝∠NCD，∵CN＝CN，∴△CNE≌△CND（ASA），∴CE＝CD．【点评】本题考查全等三角形的判定和性质，平行线的性质，角平分线的定义，等腰三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．14．（10分）如图，在△ABC中，AD⊥BC，垂足为D，AD＝CD，点E在AD上，DE＝BD，M、N分别是AB、CE的中点．（1）求证：△ADB≌△CDE；（2）求∠MDN的度数．．【分析】（1）由垂直的定义得到∠ADB＝∠ADC＝90°，根据已知条件即可得到结论；（2）根据全等三角形的性质得到∠BAD＝∠DCE，根据直角三角形的性质得到AM＝CN，由△ADM≌△CDN，可得∠ADM＝∠CDN，再根据∠CDN+∠ADN＝90°，可得∠ADM+∠ADN＝90°，即可得出∠MDN＝90°．【解答】解：（1）∵AD⊥BC，∴∠ADB＝∠ADC＝90°，在△ABD与△CDE中，，∴△ABD≌△CDE（SAS）；（2）∵△ABD≌△CDE，∴∠BAD＝∠DCE，AB＝CE，∵M、N分别是AB、CE的中点，∴AM＝AB，CN＝CE，∴AM＝CN，在△ADM和△CDN中，，∴△ADM≌△CDN（SAS），∴∠ADM＝∠CDN，∵∠CDN+∠ADN＝90°，∴∠ADM+∠ADN＝90°，∴∠MDN＝90°．【点评】本题考查了全等三角形的判定和性质，直角三角形斜边上中线的性质，熟练掌握全等三角形的性质定理是解题的关键．15．（10分）如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且AD＝CD．（1）求证：△ABD≌△CFD；（2）已知BC＝7，AD＝5，求AF的长．【分析】（1）由ASA证明△ABD≌△COD即可；（2）理由全等三角形的性质即可解决问题；∵【解答】（1）证明：证明：∵AD⊥BC，CE⊥AB，∴∠ADB＝∠CDF＝∠CEB＝90°，∴∠BAD+∠B＝∠FCD+∠B＝90°，∴∠BAD＝∠FCD，在△ABD和CFD中，，∴△ABD≌△CFD（ASA），（2）∵△ABD≌△CFD，∴BD＝DF，∵BC＝7，AD＝DC＝5，∴BD＝BC﹣CD＝2，∴AF＝AD﹣DF＝5﹣2＝3．【点评】此题考查了全等三角形的判定与性质的应用，证明三角形全等是解决问题的关键，属于中考常考题型．。

GF CF （全等三角形的对应边相等)
G E 2 1 B D 3
A
F
4 C
在△GEF中，有GE GF EF (三角形任意两边和大于第三边）
BE CF EF (等量代换）
10.如图1，已知点C为线段AB上一点，△ACM,△BCN是两个 等边三角形 （1）试说明：AN=BM； (2)若把原题中：“△ACM , △BCN 是 两个等边三角形”换成两个正方形（如图2），AN与BM的
EAF AFE
6.如图，已知AD是△ABC的中线，BE交AC于点E，交AD于点F， 且AE EF , 求证AC BF
A
E F
∵AFE BFD （对顶角相等） EAF G (等量代换）
B D
C
G
△ACG为等腰三角形 AC CG
AC BF (等量代换）
∵AD BC（已知） ∴ADB=ADG 90o （垂直的定义）
在△ADB和△ADG中
C G D B
AB=AG，B AGD
△ADB≌△ADG(SAS)
（全等三角形的对应边、角相等） （公共边） AD AD （已证） ADB=ADG 又∵B 2C （已知） DB DG （辅助线作法） AGD 2C
（全等三角形的对应边相等）
7.如图，已知点D是BC的中点，BOF CAE，CE AD于点E , BF AD交AD的延长线于点F，试说明：AO 2DE
A
在△BOF 和△CAE中 （已知） BOD CAE （已证） BFD CEA BF CE （已证） △BOF≌△CAE ( AAS )
AN BM
（全等三角形的对应边相等)
10.如图1，已知点C为线段AB上一点，△ACM,△BCN是两个 等边三角形 （1）试说明：AN=BM； (2)若把原题中：“△ACM , △BCN 是 两个等边三角形”换成两个正方形（如图2），AN与BM的 关系如何？请说明理由。

全等三角形的提高拓展训练知识点睛全等三角形的性质：对应角相等，对应边相等，对应边上的中线相等，对应边上的高相等，对应角的角平分线相等，面积相等．寻找对应边和对应角，常用到以下方法：(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边． (2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角． (3)有公共边的，公共边常是对应边． (4)有公共角的，公共角常是对应角． (5)有对顶角的，对顶角常是对应角．(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角)，一对最短边(或最小角)是对应边(或对应角)．要想正确地表示两个三角形全等，找出对应的元素是关键． 全等三角形的判定方法：(1) 边角边定理(SAS )：两边和它们的夹角对应相等的两个三角形全等． (2) 角边角定理(ASA )：两角和它们的夹边对应相等的两个三角形全等． (3) 边边边定理(SSS )：三边对应相等的两个三角形全等．(4) 角角边定理(AAS )：两个角和其中一个角的对边对应相等的两个三角形全等． (5) 斜边、直角边定理(HL )：斜边和一条直角边对应相等的两个直角三角形全等．全等三角形的应用：运用三角形全等可以证明线段相等、角相等、两直线垂直等问题，在证明的过程中，注意有时会添加辅助线．拓展关键点：能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系．而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础．例题精讲板块一、截长补短【例1】 已知ABC ∆中，60A ∠=，BD 、CE 分别平分ABC ∠和.ACB ∠，BD 、CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．【例2】 如图，点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外)，作60DMN ∠=︒，射线MN 与DBA ∠外角的平分线交于点N ，DM 与MN 有怎样的数量关系?【变式拓展训练】如图，点M 为正方形ABCD 的边AB 上任意一点，MN DM ⊥且与ABC ∠外角的平分线交于点N ，MD 与MN 有怎样的数量关系？【例3】 已知：如图，ABCD 是正方形，∠FAD =∠FAE . 求证：BE +DF =AE .【例4】 以ABC ∆的AB 、AC 为边向三角形外作等边ABD ∆、ACE ∆，连结CD 、BE 相交于点O ．求证：OA 平分DOE ∠．【例5】 如图所示，ABC ∆是边长为1的正三角形，BDC ∆是顶角为120︒的等腰三角形，以D 为顶点作一个60︒的MDN ∠，点M 、N 分别在AB 、AC 上，求AMN ∆的周长．_F _E_D_C _B _A _N _C _D _E _B _M _A【例6】五边形ABCDE中，AB=AE，BC+DE=CD，∠ABC+∠AED=180°，求证：AD平分∠CDE板块二、全等与角度【例7】如图，在ABC∠的平分线，且AC AB BD=+，求ABC∠∠=︒，AD是BAC∆中，60BAC的度数.【例8】在等腰ABC∠=︒，在边AB上取点D，使AD BC=，A∆中，AB AC=，顶角20求BDC∠.【例9】如图所示，在ABC∠=︒，又M在AC上，N在BC上，且满足C=，20∆中，AC BC∠=︒，求NMB∠.ABMBAN50∠=︒，60【例10】 在四边形ABCD 中，已知AB AC =，60ABD ︒∠=，76ADB ︒∠=，28BDC ︒∠=，求DBC∠的度数.【例11】 如图所示，在四边形ABCD 中，12DAC ︒∠=，36CAB ︒∠=，48ABD ︒∠=，24DBC ︒∠=，求ACD ∠的度数.【例12】 在正ABC ∆内取一点D ，使DA DB =，在ABC ∆外取一点E ，使DBE DBC ∠=∠，且BE BA =，求BED ∠.【例13】 如图所示，在ABC ∆中，44BAC BCA ︒∠=∠=，M 为ABC ∆内一点，使得30MCA ︒∠=，16MAC ︒∠=，求BMC ∠的度数.全等三角形证明经典50题（含答案）1.已知：AB=4，AC=2，D是BC中点，AD是整数，求ADAB CD延长AD到E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52.已知：D是AB中点，∠ACB=90°，求证：12 CD AB3.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF和EF。

全等三角形的提高拓展训练知识点睛全等三角形的性质：对应角相等，对应边相等，对应边上的中线相等，对应边上的高相等，对应角的角平分线相等，面积相等． 寻找对应边和对应角，常用到以下方法：(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边． (2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角． (3)有公共边的，公共边常是对应边． (4)有公共角的，公共角常是对应角． (5)有对顶角的，对顶角常是对应角．(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角)，一对最短边(或最小角)是对应边(或对应角)．要想正确地表示两个三角形全等，找出对应的元素是关键． 全等三角形的判定方法：(1) 边角边定理(SAS )：两边和它们的夹角对应相等的两个三角形全等． (2) 角边角定理(ASA )：两角和它们的夹边对应相等的两个三角形全等． (3) 边边边定理(SSS )：三边对应相等的两个三角形全等．(4) 角角边定理(AAS )：两个角和其中一个角的对边对应相等的两个三角形全等． (5) 斜边、直角边定理(HL )：斜边和一条直角边对应相等的两个直角三角形全等． 全等三角形的应用：运用三角形全等可以证明线段相等、角相等、两直线垂直等问题，在证明的过程中，注意有时会添加辅助线．拓展关键点：能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系．而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础．例题精讲板块一、截长补短【例1】 (06年北京中考题)已知ABC ∆中，60A ∠=，BD 、CE 分别平分ABC ∠和.ACB ∠，BD 、CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．DOECB AND【例2】 如图，点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外)，作60DMN ∠=︒，射线MN 与DBA ∠外角的平分线交于点N ，DM 与MN 有怎样的数量关系?【变式拓展训练】如图，点M 为正方形ABCD 的边AB 上任意一点，MN DM ⊥且与ABC ∠外角的平分线交于点N ，MD 与MN 有怎样的数量关系？【例3】 已知：如图，ABCD 是正方形，∠FAD =∠FAE . 求证：BE +DF =AE .【例4】 以ABC ∆的AB 、AC 为边向三角形外作等边ABD∆、ACE ∆，连结CD 、BE 相交NCDE BMAFEDCBA OEDCBA于点O．求证：OA平分DOE∠．【例5】(北京市、天津市数学竞赛试题)如图所示，ABC∆是边长为1的正三角形，BDC∆是顶角为120︒的等腰三角形，以D为顶点作一个60︒的MDN∠，点M、N分别在AB、AC上，求AMN∆的周长．【例6】五边形ABCDE中，AB=AE，BC+DE=CD，∠ABC+∠AED=180°，求证：AD平分∠CDEA NMD CBACE DBA板块二、全等与角度【例7】如图，在ABC∆中，60BAC∠=︒，AD是BAC∠的平分线，且AC AB BD=+，求ABC∠的度数.【例8】在等腰ABC∆中，AB AC=，顶角20A∠=︒，在边AB上取点D，使AD BC=，求BDC∠.【例9】(“勤奋杯”数学邀请赛试题) 如图所示，在ABC∆中，AC BC=，20C∠=︒，又M在AC上，N在BC上，且满足50BAN∠=︒，60ABM∠=︒，求NMB∠. NMCB A【例10】 在四边形ABCD 中，已知AB AC =，60ABD ︒∠=，76ADB ︒∠=，28BDC ︒∠=，求DBC ∠的度数.【例11】 (日本算术奥林匹克试题) 如图所示，在四边形ABCD 中，12DAC ︒∠=，36CAB ︒∠=，48ABD ︒∠=，24DBC ︒∠=，求ACD ∠的度数.【例12】 (河南省数学竞赛试题) 在正ABC ∆内取一点D ，使DA DB =，在ABC ∆外取一点E ，使DBE DBC ∠=∠，且BE BA =，求BED ∠.【例13】 (北京市数学竞赛试题) 如图所示，在ABC ∆中，44BAC BCA ︒∠=∠=，M 为ABC∆内一点，使得30MCA ︒∠=，16MAC ︒∠=，求BMC ∠的度数.全等三角形证明经典20题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求ADMCAB_延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2 又∵CD=DE∴⊿ADC ≌⊿GDE （AAS ） ∴EG=AC ∵EF//AB ∴∠DFE=∠1 ∵∠1=∠2 ∴∠DFE=∠DGE ∴EF=EG ∴EF=ACADBCBA CDF2 1 E3. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ） ∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C4. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE 证明：在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥ABCDB A所以∠CEB＝∠CEF＝90°因为EB＝EF，CE＝CE，所以△CEB≌△CEF所以∠B＝∠CFE因为∠B＋∠D＝180°，∠CFE＋∠CFA＝180°所以∠D＝∠CFA因为AC平分∠BAD所以∠DAC＝∠FAC又因为AC＝AC所以△ADC≌△AFC（SAS）所以AD＝AF所以AE＝AF＋FE＝AD＋BE5. 如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

专题1.10探索全等三角形的条件（3）-角角边（AAS ）（拓展提高）一、单选题1．如图，在四边形ABCD 中，点E 在边AD 上，BCE ACD ∠=∠，40BAC D ∠=∠=︒，AB DE =，则BCE ∠的度数为（ ）A ．80︒B ．90︒C ．100︒D ．110︒【答案】C 【分析】通过证明△ABC ≌△DEC ，可得AC =DC ，从而40CAD D ∠=∠=︒，然后求出∠ACD 的值，进而可求BCE ∠的度数．【详解】解：∵BCE ACD ∠=∠，∴BCE ACE ACD ACE ∠-∠=∠-∠，∴∠ACB =∠DCE ．在△ABC 和△DEC 中ACB DCE BAC D AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABC ≌△DEC ，∴AC =DC ，∴40CAD D ∠=∠=︒，∴∠ACD =180°-40°-40°=100°，∴∠BCE =∠BCA +∠ACE =∠DCE +∠ACE =∠ACD =100°，故选C ．【点睛】本题主要考查了全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS 、SAS 、ASA 、AAS 和HL ）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．也考查了等腰三角形的性质．2．如图，在四边形ABCD 中，AB //DC ，E 为BC 的中点，连接DE 、AE ，AE ⊥DE ，延长DE 交AB 的延长线于点F ．若AB ＝5，CD ＝3，则AD 的长为（ ）A ．2B ．5C ．8D ．11【答案】C 【分析】由“AAS ”可证△BEF ≌△CED ，可得EF ＝DE ，BF ＝CD ＝3，由线段垂直平分线的性质可得AD ＝AF ＝8．【详解】解：∵E 为BC 的中点，∴BE ＝EC ，∵AB ∥CD ，在△BEF 与△CED 中，F CDE BEF CED BE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BEF ≌△CED （AAS ）∴EF ＝DE ，BF ＝CD ＝3，∴AF ＝AB +BF ＝8，∵AE ⊥DE ，EF ＝DE ，∴AF ＝AD ＝8，故选：C ．【点睛】本题考查全等三角形的判定与性质，以及垂直平分线的判定与性质，准确推导出全等三角形并理解线段垂直平分线的性质是解题关键．3．如图，在ABC 中，AB AC ⊥，AD BC ⊥，BE 平分ABC ∠，交AD 于点E ，//EF AC ，下列结论中一定成立的是（ ）A ．ABE DFE ∠=∠B ．AE ED =C ．AD DC = D ．AB BF =【答案】D 【分析】先利用等角的余角相等得到∠C=∠BAD ，再根据平行线的性质得∠C=∠BFE ，则∠BAD=∠BFE ，于是可根据“AAS”可判断△ABE ≌△FBE ，所以AB=BF ．【详解】解：∵AB ⊥AC ，AD ⊥BC ，∴∠BAD+∠CAD=90°，∠CAD+∠C=90°，∴∠C=∠BAD ，∵EF ∥AC ，∴∠C=∠BFE ，∴∠BAD=∠BFE ，∵BE 平分∠ABC ，∴∠ABE=∠FBE ，在△ABE 和△FBE 中，BAD BFE ABE FBE BE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△FBE ，∴AB=BF ．故选：D ．【点睛】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．也考查了平行线的性质和全等三角形的判定与性质．4．如图，在OAB 和△OCD 中，OA OB =，OC OD =，OA OC >，40AOB COD ∠=∠=︒，连接AC ，BD 交于点M ，连接OM ．下列结论：①AC BD =；②40AMB ∠=︒；③OM 平分BOC ∠；④MO 平分BMC ∠．其中一定正确的为（ ）A．①②③B．①②④C．①③④D．②③④【答案】B【分析】由SAS证明△AOC≌△BOD得出∠OCA=∠ODB，AC=BD即可判断①；由全等三角形的性质得出∠OAC=∠OBD，由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD，得出∠AMB=∠AOB=40°，即可判断②；作OG⊥MC于G，OH⊥MB于H，则∠OGC=∠OHD=90°，由AAS证明△OCG≌△ODH（AAS），得出OG=OH，由角平分线的判定方法得出MO平分∠BMC，即可判断④；由∠AOB=∠COD，得出当∠DOM=∠AOM时，OM平分∠BOC，假设∠DOM=∠AOM，由△AOC≌△BOD得出∠COM=∠BOM，由MO平分∠BMC得出∠CMO=∠BMO，推出△COM≌△BOM，得OB=OC，而OA=OB，所以OA=OC 即可判断③；【详解】∵∠AOB=∠COD=40°，∴∠AOB+∠AOD=∠COD+∠AOD，即∠AOC=∠BOD，在△AOC和△BOD中，OA OBOC ODAOC BOD=⎧⎪=⎨⎪∠=∠⎩，∴△AOC≌△BOD（SAS），∴∠OCA=∠ODB，AC=BD，故①正确；∴∠OAC=∠OBD，由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD，∴∠AMB=∠AOB=40°，故②正确；作OG⊥MC于G，OH⊥MB于H，如图所示：则∠OGC=∠OHD=90°，在△OCG和△ODH中OCA ODBOGC OHD OC OD∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△OCG≌△ODH（AAS），∴OG=OH，∴MO平分∠BMC，故④正确；∵∠AOB=∠COD，∴当∠DOM=∠AOM时，OM平分∠BOC，假设∠DOM=∠AOM，∵△AOC≌△BOD∴∠COM=∠BOM，∵MO平分∠BMC∴∠CMO=∠BMO，在△COM和△BOM中，COM BOMOM OMCMO BMO∠∠⎧⎪=⎨⎪∠=∠⎩，∴△COM≌△BOM（ASA）∴OB=OC，∵OA=OB，∴OA=OC与OA＞OC矛盾，故③错误；故选：B．【点睛】本题考查了全等三角形的判定与性质，三角形的外角性质，角平分线的判定等知识，证明三角形全等是解题的关键；．5．如图，AP平分∠BAF，PD⊥AB于点D，PE⊥AF于点E，则△APD与△APE全等的理由是（）A．SSS B．SAS C．SSA D．AAS【答案】D【分析】求出∠PDA=∠PEA=90°，∠DAP=∠EAP，根据AAS推出两三角形全等即可．【详解】解：∵PD ⊥AB ，PE ⊥AF ，∴∠PDA=∠PEA=90°，∵AP 平分∠BAF ，∴∠DAP=∠EAP ，在△APD 和△APE 中DAP EAP PDA PEA AP AP ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△APD ≌△APE （AAS ），故选：D ．【点睛】本题考查了全等三角形的判定的应用，注意：全等三角形的判定定理有SAS ，ASA ，AAS ，SSS ．6．如图，在Rt △ABC 中，∠B ＝90°，BC ＝2，过A 点作AD ∥BC ；AE ⊥AC ，AC ＝AE ，AD ＝3，连接DE ，则△ADE 的面积为（ ）A ．3B ．6C ．12D ．18【答案】A 【分析】通过过E 作EF ⊥DA ，交DA 延长于F ，将三角形ABC 转移到三角形AFE 构造确定，求出三角形ADE 的高EF ，利用面积公式即可求出．【详解】过E 作EF ⊥DA ，交DA 延长于F ，∵AE ⊥AC ，∴∠EAF+∠FAC=90º，∵AD ∥BC ，∠B ＝90°，∴∠BAF+∠B=180º，∴∠BAF=90º，∴∠BAC+∠FAC=90º，∴∠EAF=∠BAC ，∠F=∠B ，∴△AEF ≌△ACB(AAS)，∴EF=BC=2，∴S △ADE=11AD EF=3222⨯⨯=3， 故选择：A ．【点睛】本题考查三角形的面积问题，利用辅助线构造三角形全等，解决三角形ADE 的高是解题关键．二、填空题7．如图，已知//AD BC ，AB BC ⊥，CD DE ⊥，CD ED =，3AD =，4BC =，则ADE 的面积为________．【答案】32【分析】知道AD 的长，只要求出AD 边上的高，就可以求出△ADE 的面积；过点D 作DG ⊥BC 于G ，过点E 作EF ⊥AD 交AD 的延长线于F ，构造出△EDF ≌△CDG ，求出GC 的长，即为EF 的长，利用三角形的面积公式解答即可．【详解】解：过点D 作DG ⊥BC 于G ，过点E 作EF ⊥AD 交AD 的延长线于F ，如图所示：则四边形ABGD 是矩形，∵∠EDF +∠FDC =90°，∠GDC +∠FDC =90°，∴∠EDF =∠GDC ，在△EDF 和△CDG 中，F DGC EDF GDC DE DC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△EDF ≌△CDG （AAS ），∴EF =CG =BC -BG =BC -AD =4-3=1，∴S △ADE =12 AD •EF =12×3×1=32， 故答案为：32．【点睛】本题考查了全等三角形的判定与性质、矩形的判定与性质、三角形面积计算等知识，通过作辅助线构造△EDF ≌△CDG 是解题的关键．8．如图，在面积为36的四边形ABCD 中，∠ADC =∠ABC =90°，AD =CD ，DP ⊥AB 于点P ，则DP 的长是_____【答案】6【分析】作DE ⊥BC ，交BC 延长线于E ，如图，则四边形BEDP 为矩形，再利用等角的余角相等得到∠ADP =∠CDE ，则可利用“AAS ”证明△ADP ≌△CDE ，得到DP =DE ，S △ADP =S △CDE ，所以四边形BEDP 为正方形，S 四边形ABCD =S 正方形BEDP ，根据正方形的面积公式得到DP 2=36，易得DP =6．如图，作DE ⊥BC ，交BC 延长线于E ，∵DP ⊥AB ，ABC =90°，∴四边形BEDP 为矩形，∴∠PDE =90°，即∠CDE +∠PDC =90°，∵∠ADC =90°，即∠ADP +∠PDC =90°，∴∠ADP =∠CDE ，在△ADP 和△CDE 中APD CED ADP CDE AD DC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADP ≌△CDE ，∴DP =DE ，S △ADP =S △CDE ，∴四边形BEDP 为正方形，S 四边形ABCD =S 正方形BEDP ，∴DP 2=36，∴DP =6．故答案为6．【点睛】本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．也考查了正方形和矩形的性质．本题的关键的作辅助线构造两个全等的三角形．9．如图，在△ABC 中，点D 为AB 延长线上一点，点E 为AC 中点，过C 作CF //AB 交射线DE 于F ，若BD ＝1，CF ＝5，则AB 的长度为_____．【答案】4【分析】根据CF ∥AB 就可以得出∠A =∠ECF ，∠ADE =∠F ，证明△ADE ≌△CFE 就可以求出答案．【详解】∵CF ∥AB ，∴∠ADE =∠F ，∠FCE =∠A ．∵点E 为AC 的中点，∴AE =EC ．∵在△ADE 和△CFE 中，ADE F FCE A AE EC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADE ≌△CFE （AAS ）．∴AD =CF =5，∵BD =1，∴AB =AD -BD =5-1=4．故答案为：4．【点睛】本题考查了全等三角形的判定及性质，平行线的性质，解答时证明三角形全等是关键． 10．如图，△ABC 中，AB ＝AC ，点E 在AB 的延长线上，点D 在边AC 上，且EB ＝CD ＝4，线段DE 交边BC 于点F ，过点F 作FG ⊥DE 交线段CE 于点G ，CE ⊥AC ，△GEF 的面积为5，则EG 的长_____．【答案】5【分析】过D 作//DH AB 交BC 于H ，求出EF DF =，延长GC 到M ，使EG GM =，连接DM ，DG ，根据三角形的面积公式求出即可．【详解】解：过D 作//DH AB 交BC 于H ，则,DHC ABC EBF DHF ∠=∠∠=∠，∵AB AC =，∴A ABC CB =∠∠，∴DHC ACB ∠=∠，∴DH CD =，∵BE CD =，∴DH BE =，在BEF 与HDF 中EBF DHF BFE HFD BE DH ∠=∠⎧⎪∠=∠⎨⎪=⎩∴BEF HDF ≌（AAS ），∴EF DF =，延长GC 到M ，使EG GM =，连接DM ，DG ，∵5,,S EFG EF DF EG MG ===，∴5S DFG S EFG ==，5510S DGM S DGE ==+=，∴101020S DEM =+=，∵4,DC AC CE =⊥， ∴12S DEM EM DC =⨯⨯， ∴12042EM =⨯⨯，解得：=10EM ， ∴11052EG MG ==⨯=， 故答案为：5．【点睛】本题考查了全等三角形的性质和判定，等腰三角形的性质和判定，能综合运用定理进行推理是解此题的关键．11．如图，在△ABC 中，点D ，E 在AC 边上，且AE ＝ED ＝DC ．点F ，M 在AB 边上，且////EF DM BC ，延长FD 交BC 的延长线于点N ，则EF BN的值＝_____．【答案】14【分析】首先证明13EF BC ＝∶∶，再利用全等三角形的性质证明EF ＝CN 即可解决问题． 【详解】解：////EF DM BC AE DE CD ，＝＝， ∴13EF AE BC AC ==， 在EFD △与CND △中，EDF CDN FED NCD ED DC ∠=∠⎧⎪∠=∠⎨⎪=⎩，EFD CND AAS ∴≌（），EF CN ∴＝，13CN BC ∴∶＝∶，1CN BN ∴＝∶∶4，∴14EF BN =， 故答案为14． 【点睛】本题考查平行线分线段成比例定理，全等三角形的判定和性质，关键在于熟练掌握两个知识点的基本性质和定理，该类型题属常考题．12．如图，在等边ABC 中，12AC =，点O 在边AC 上，且4AO =，点P 是边AB 上的一动点．连结OP ，将线段OP 绕点O 逆时针旋转60︒得到线段OD ．要使点D 恰好落在边BC 上，则AP 的长为______．【答案】8【分析】根据AC =12，AO =4，求出OC =8，再根据等边三角形的性质得∠A =∠C =60°，再根据旋转的性质得OD =OP ，∠POD =60°，根据三角形内角和和平角定义得∠AOP +∠APO +∠A =180°，∠AOP +∠COD +∠POD =180°，利用等量代换可得∠APO =∠COD ，然后证出△AOP ≌△CDO ，得出AP =CO =8．【详解】解：∵AC =12，AO =4，∴OC =8，∵△ABC 为等边三角形，∴∠A =∠C =60°，∵线段OP 绕点D 逆时针旋转60°得到线段OD ，要使点D 恰好落在BC 上，如图所示，∴OD =OP ，∠POD =60°，∵∠AOP +∠APO +∠A =180°，∠AOP +∠COD +∠POD =180°，∴∠AOP +∠APO =120°，∠AOP +∠COD =120°，∴∠APO =∠COD ，在△AOP 和△CDO 中，A C APO COD OP OD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AOP ≌△CDO （AAS ），∴AP =CO =8，故答案为8．【点睛】本题考查了旋转的性质、等边三角形的性质、全等三角形的判定与性质，熟练掌握对应点到旋转中心的距离相等、对应点与旋转中心所连线段的夹角等于旋转角，旋转前、后的图形全等是本题的关键． 13．如图，AE AB ⊥，且,AE AB BC CD =⊥，且BC CD =，请按照图中所标注的数据，计算图中实线所围成的图形的面积S 是___________．【答案】50【分析】求出∠F=∠AGB=∠EAB=90°，∠FEA=∠BAG ，根据AAS 证△FEA ≌△GAB ，推出AG=EF=6，AF=BG=2，同理CG=DH=4，BG=CH=2，求出FH=14，根据阴影部分的面积=S 梯形EFHD -S △EFA -S △ABC -S △DHC 和面积公式代入求出即可．【详解】解：∵AE ⊥AB ，EF ⊥AF ，BG ⊥AG ，∴∠F=∠AGB=∠EAB=90°，∴∠FEA+∠EAF=90°，∠EAF+∠BAG=90°，∴∠FEA=∠BAG ，在△FEA 和△GAB 中，∵F BGA FEA BAG AE AB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△FEA ≌△GAB （AAS ），∴AG=EF=6，AF=BG=2，同理CG=DH=4，BG=CH=2，∴FH=2+6+4+2=14，∴梯形EFHD 的面积是12×（EF+DH ）×FH=12×（6+4）×14=70， ∴阴影部分的面积是S 梯形EFHD -S △EFA -S △ABC -S △DHC =70-12×6×2-12×（6+4）×2-12×4×2 =50．故答案为50．【点睛】本题考查了三角形的面积，梯形的面积，全等三角形的性质和判定等知识点，关键是把不规则图形的面积转化成规则图形的面积．14．如图，△ABC中，AB=AC，BH⊥AC，垂足为点H，BD平分∠ABH，点E为BH上一点，连接DE，∠BDE=45°，DH：CH=3：2，BE=10，则CH=____．【答案】4【分析】延长DE交BC于F，根据等腰三角形的性质，三角形内角和定理和角平分线的性质，由AAS证明△BEF≌△DCF，再根据全等三角形的性质即可求解．【详解】解：延长DE交BC于F，∵AB=AC，设∠A=2α，则∠ABC=∠ACB=90°-α，∵BH⊥AC，∴∠HBC=90°-∠ACB=α，∠A+∠ABH=90°，∵BD平分∠ABH，∴∠DBH=12∠ABH=45°-α，∴∠DBF=45°-α+α=45°，∴∠BDF=∠DBF=45°，∠DFB=∠DFC=90°，∴DF=BF，∵∠DFB=∠DHB=90°，∴∠CDF=∠EBF ，在△BEF 和△DCF 中，CDF EBF BFE DFC BF DF ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△BEF ≌△DCF （AAS ），∴BE=CD=CH+DH=10，∵DH ：CH=3：2，∴CH=4．故答案为：4．【点睛】考查了全等三角形的判定与性质，等腰三角形的性质，题目关键是得到∠DBF=45°，利用全等三角形的性质得到BE=CD ．三、解答题15．如图AOB ∠是一个锐角．（1）用尺规作图法作出AOB ∠的平分线OC ；（2）若点P 是OC 上一点，过点P 作PD OA ⊥于点D ，PE OB ⊥于点E ，求证：OD OE =．【答案】（1）见解析；（2）见解析【分析】（1）根据要求作出图形即可．（2）利用全等三角形的性质证明即可．【详解】解：（1）如图，射线OC 即为所求作．（2）由作图可知，∠POD =∠POE ，∵PD ⊥OA ，PE ⊥OB ，∴∠PDO =∠PEO =90°，在△POD 和△POE 中，PDO PEO POD POE OP OP ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△POD ≌△POE （AAS ），∴OD =OE ．【点睛】本题考查作图-基本作图，角平分线的定义，全等三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．16．如图，,,//AD BF EC AB DE ∠∠＝＝．求证：AC DF ＝．【答案】证明见解析【分析】由已知//AB DE ，可得∠B ＝∠E ，由BF ＝EC ，可得BC ＝EF ，易证ABC DEF △≌△，即可得出AC ＝DF ．【详解】证明：∵//AB DE ，,B E ∴∠∠＝,BF CE ＝,BC EF ∴＝在ABC 和DEF 中，,A D B E BC EF ∠=∠⎧⎪∠=∠⎨⎪=⎩，ABC DEF AAS ∴≌（），AC DF ∴＝．【点睛】本题主要考查了全等三角形的判定及性质，解题的关键是证出ABC DEF △≌△． 17．如图，在ABC 中，90ACB ∠=︒，AC BC =，点E 是ACB ∠内部一点，分别过A 、B 两点作,AD CE BE CE ⊥⊥，垂足分别为点D 、E ，求证：AD BE DE =+【答案】见解析【分析】由全等三角形的性质可得BE =DC ，AD =CE ，即可求解．【详解】解：证明：BE CE ⊥，AD CE ⊥，90E ADC ∴∠=∠=︒，90EBC BCE ∴∠+∠=︒．90BCE ACD ∠+∠=︒，EBC DCA ∴∠=∠，在BCE ∆和CAD ∆中，E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()BCE CAD AAS ∴∆≅∆；BCE CAD ∆≅∆，BE DC ∴=，AD CE =，AD CE CD DE BE DE ∴==+=+．【点睛】本题考查了全等三角形的判定和性质，掌握全等三角形的判定是本题的关键．18．如图，四边形ABCD 中，//AD BC ，E 为CD 的中点，连结BE 并延长交AD 的延长线于点F ．（1）求证：BCE FDE ≌；（2）连结AE ，当,2,1AE BF BC AD ⊥==时，求AB 的长．【答案】（1）见解析；（2）3【分析】（1）利用AAS 即可证明；（2）由BCE ≌FDE 可得BE FE =，2BC FD ==，从而证明AEB △≌AEF ，得到AB AF =，可得A B ．【详解】解：（1）∵//AD BC ，∴CBE DFE ∠=∠，∵E 为CD 中点，∴CE DE =，在BCE 和FDE 中，CBE DFE BEC FED CE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴BCE ≌FDE （AAS ）．（2）由（1）中BCE ≌FDE ，∴BE FE =，2BC FD ==，∵AE BF ⊥，∴90AEB AEF ∠=∠=︒，在AEB △和AEF 中，AE AE AEB AEF BE FE =⎧⎪∠=∠⎨⎪=⎩，∴AEB △≌AEF （SAS ），∴AB AF =，而123AF AD DF =+=+=，∴3AB =．【点睛】本题考查了全等三角形的判定和性质，关键是根据AAS 和SAS 证明三角形全等．19．已知：在矩形ABCD 中，点E 在BC 边上，连接DE ，且DE BC =，过点A 作AF DE ⊥于点F ．求证：AB AF =；【答案】见解析【分析】由“AAS ”可证ADF DEC △≌△，可得AF CD AB ==．【详解】证明：∵四边形ABCD 是矩形，AF DE ⊥，∴//,,,90AD BC AD BC AB CD C AFD ==∠=∠=︒，∴ADE DEC ∠=∠，∵DE BC =，∴AD DE =，在ADF 和DEC 中，90AFD C ADE DEC AD DE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴()ADF DEC AAS ≌，∴AF CD =，∴AF AB =.【点睛】本题考查了矩形的性质，全等三角形的判定和性质，灵活运用这些性质解决问题是本题的关键． 20．如图，点C 、F 、E 、B 在同一直线上，点A 、D 分别在BC 两侧，AB ∥CD ，BE ＝CF ，∠A ＝∠D ． （1）求证：AB ＝DC ；（2）若AB ＝CE ，∠B ＝30°，求∠D 的度数．【答案】（1）见解析；（2）75°．【分析】（1）由两直线平行，内错角相等得到∠B ＝∠C ，继而证明△ABF ≌△CDE （AAS ），据此解题； （2）由（1）△ABF ≌△CDE 得，AB ＝CD ，BF ＝CE ，证明△ABF 是等腰三角形，再根据三角形内角和180°解题．【详解】证明：（1）∵//AB CD ，∴∠B ＝∠C ，∵BE ＝CF ，∴BF CE =，在△ABF 和△CDE 中，A DBC BF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABF ≌△CDE （AAS ），∴AB ＝CD ；（2）∵△ABF ≌△CDE ，∴AB ＝CD ，BF ＝CE ，∵AB ＝CE ，∠B ＝30°，∴AB ＝BF ，∴∠A ＝∠AFB ，∴△ABF 是等腰三角形，∴∠A ＝()1801180307522B ︒-∠=︒-︒=︒， ∴∠D ＝∠A ＝75°．【点睛】本题考查平行线的性质、全等三角形的判定与性质、等腰三角形的判定与性质、三角形内角和的应用等知识，是重要考点，难度较易，掌握相关知识是解题关键．。

《第十二章全等三角形》重难点易错点思维拓展一、认真选一选，你一定很棒！1. 如图：AD=AC，AB平分∠DAC，下列结论错误的是（）A：△ADB≌△ACB B：△ADE≌△ACE C：△EDB≌△ECB D：△AED≌△CEB2. 如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A.SSSB.SA SC.AASD.ASA3. 下列各作图题中，可直接用“边边边”条件作出三角形的是（）A．已知腰和底边，求作等腰三角形B．已知两条直角边，求作等腰三角形C．已知高，求作等边三角形D．已知腰长，求作等腰直角三角形4. 如图，已知AB∥CD，AB=CD，AE=FD，则图中的全等三角形有（）A、1对B、2对C、3对D、4对5. 如图，△ABD和△ACE都是等边三角形，则ΔADC≌ΔABE的根据是（）（A）SSS （B）SAS （C）ASA （D）AAS6. 如图4，AC=AD，BC=BD，那么全等三角的对数是（）A.1 B．2 C．3 D．47. 如图所示，表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（）Ａ．1处Ｂ．2处Ｃ．3处Ｄ．4处8. 下列命题中正确的有（）个①三个内角对应相等的两个三角形全等；②三条边对应相等的两个三角形全等；③有两角和一边分别相等的两个三角形全等；④等底等高的两个三角形全等．A．1 B．2 C．3 D．49. 如图，已知：△ABC≌△DEF，AC∥DF，BC∥EF.则不正确的等式是（）（A）AC=DF （B）AD=BE （C）DF=EF （D）BC=EF10. 如图，P是∠BAC的平分线AD上一点，PE⊥AB于E，PF⊥AC于F，下列结论中不正确的是（）A．PE PF== B．AE AFC．△APE≌△APF D．AP PE PF=+11. 如图，△A BC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分为三个三角形，则S△ABO︰S△BCO︰S△CAO等于（）A．1︰1︰1 B．1︰2︰3 C．2︰3︰4 D．3︰4︰5二、仔细填一填，你一定很准！12. 如图：在四边形ABCD中，点E在边CD上，连接AE、BE并延长AE交BC的延长线于点F，给出下列5个关系式：：①AD∥BC，②，DE=EC③∠1=∠2，④∠3=∠4，⑤AD+BC=AB。

FED C BA 全等三角形经典题目原创一. 基本篇基本类型（ 1 ）证明两个三角形全等例1 ：如图,点B 在AE 上,∠CAB=∠DAB,要使ΔABC ≌ΔABD,可补充的一个条件是 .基本类型（ 2 ）证明两个角相等例2已知：如图，AB=AC,AD=AE, ∠1=∠3,那么∠E=∠D 吗？为什么？基本类型（ 3 ）证明两条线段相等例3 :已知：∠ACB=∠ADB=90°，AC=AD ，P 是AB 上任意一点，求证：CP=DP基本类型（4）判定、性质综合应用例4 、如图, A,E,B,D 在同一直线上, AB=DE,AC=DF,AC ∥ DF,在ΔABC 和ΔDEF, (1)求证: ΔABC ≌ΔDEF;(2)你还可以得到的结论是 .(写出一个,不再添加其他线段,不再表注或使用其他字母)E D C B A基本类型（6）实际问题应用例5. 如图，仪器ABCD可以用来平分一个角，其中AB=AD，BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们落在角的两边上，沿AC画一条射线AE，AE就是∠PRQ的平分线。

你能说明其中的道理吗？二. 提高篇拓展专题（1）构造全等类证明线段和差问题（方法截长补短）例2. 如图,已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，则AB与AC+BD相等吗？请说明理由。

拓展专题（2）复杂图形（探索）类问题例1. 原题：如图,A是CD上的一点,△ABC , △ADE 都是正三角形,求证CE=BD变式1（深度挖掘）:在原题条件不变的前提下,可以探求以下结论:(1)求证:AG=AF;(2)连结GF,求证△AGF是正三角形;(3)求证GF//CD拓展专题（3）运动变化类问题例1. 如图1，在△ABC中，AB=AC，∠BAC=90°，分别过点B、C作点过点A的直线AD的垂线，垂足分别为E、F。

探索(1)当直线AD在三角形内部旋转时，求证：AE=BE+EF。

专题10 全等三角形创新题【专题综述】随着课程改革的不断深入，一大批格调清新、设计独特的开放型、探究型、操作型等创新题纷纷在各地中考试卷上闪亮登场。

近年来，有关全等三角形的创新题更令人耳目一新、目不暇接；试题以它的新颖性、思辨性摒弃模式、推陈出新，创造性地描绘了一个绚丽多姿的图形世界。

【方法解读】一、实际应用型例1 如图1，一块三角形模具的阴影部分已破损．只要从残留的模具片中度量出哪些边、角，就可以不带'''？请简要说明理残留的模具片到店铺加工一块与原来的模具ABC的形状和大小完全相同的模具A B C由．【举一反三】如图所示，太阳光线AC与A′C′是平行的，AB表示一棵塔松，A′B′表示一棵小杨树，同一时刻两棵树的影长相等，已知塔松高6米，则小杨树高______.【来源】北师大版七年级数学下册第四章三角形单元检验题二、操作探索型例2 复习“全等三角形”的知识时，老师布置了一道作业题：“如图2，已知在△ABC中，AB=AC，P是△ABC 内部任意一点，将AP绕A顺时针旋转至AQ，使∠QAP=∠BAC，连接BQ、CP，则BQ=CP．”小亮是个爱动脑筋的同学，他通过对图2的分析，证明了△ABQ≌△ACP，从而证得BQ=CP之后，将点P移到三角形ABC之外，原题中的条件不变，发现“BQ=CP”仍然成立，请你就图3给出证明．【举一反三】在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．（1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE= 度；（2）设∠BAC= α，∠DCE= β．①如图2，当点D在线段CB上，∠BAC≠90°时，请你探究α与β之间的数量关系，并证明你的结论；α与β之②如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，并直接．．写出此时间的数量关系（不需证明）．【来源】北京市第四十四中学2017—2018学年度上期期中测试八年级数学试题三、开放探究型例3 如图4，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E、F，BE=CF．（1）图中有几对全等的三角形？请一一列出；A. ②③B. ①②C. ①③D. ①②③【来源】浙江杭州余杭区2016-2017学年八年级上学期期末数学试题4.已知：∠MON=α，点P是∠MON角平分线上一点，点A在射线OM上，作∠APB=180°-α，交直线ON 于点B，PC⊥ON于C.（1）如图1，若∠MON=90°时，求证：PA=PB；（2）如图2，若∠MON=60°时，写出线段OB，OA及BC之间的数量关系，并说明理由；（3）如图3，若∠MON=60°时，点B在射线ON的反向延长线上时，（2）中结论还成立吗？若不成立，直接写出线段OB，OA及BC之间的数量关系（不需要证明）.【来源】北京师大附中2017-2018学年上学期初中八年级期末考试数学试卷5.在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．（1）如图一，若△ABC是等边三角形，且AB=AC=2,点D在线段BC上，①求证：∠BCE+∠BAC=180°；②当四边形ADCE的周长取最小值时，求BD的长．（2）若∠BAC 60°，当点D在射线．．上移动，则∠BCE和∠BAC 之间有怎样的数量关系？并说明理．．BC由.【来源】浙江省吴兴区2017-2018学年八年级上学期期终模拟数学试题6.如图，点B、D、E、C在一条直线上，△ABD≌△ACE，AB和AC，AD和AE是对应边，除△ABD≌△ACE外，图中还有其他全等三角形吗？若有，请写出来，并证明你的结论。