苏教版初三数学《锐角三角函数》7.2 正弦余弦
- 格式：doc
- 大小：244.48 KB
- 文档页数：5
下载文档原格式
合集下载
新苏科版九年级数学下册《7章锐角三角函数7.2正弦、余弦》教案_18
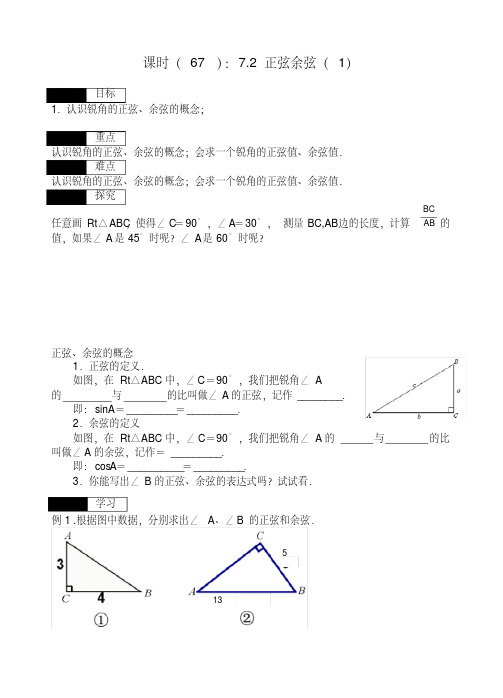
课时（ 67 ）：7.2正弦余弦（1）学习目标1．认识锐角的正弦、余弦的概念；学习重点认识锐角的正弦、余弦的概念；会求一个锐角的正弦值、余弦值．学习难点认识锐角的正弦、余弦的概念；会求一个锐角的正弦值、余弦值．自主探究任意画Rt △ABC ，使得∠C ＝90°，∠A ＝30°，测量BC,AB 边的长度，计算AB BC的值，如果∠A 是45°时呢？∠A 是60°时呢？正弦、余弦的概念1．正弦的定义．如图，在Rt △ABC 中，∠C ＝90°，我们把锐角∠A的与的比叫做∠A 的正弦，记作________．即：sinA ＝_________＝_________．2．余弦的定义如图，在Rt △ABC 中，∠C ＝90°，我们把锐角∠A 的与的比叫做∠A 的余弦，记作＝_________．即：cosA ＝__________＝_________．3．你能写出∠B 的正弦、余弦的表达式吗？试试看．例1 .根据图中数据，分别求出∠A 、∠B 的正弦和余弦．例题学习135例2 如图，在等边△ABC 中，AD ⊥BC,垂足为D.求sin ∠BAD.思考：由例2知道，sin30°= 12，如何求cos30°？你会求60°角的正弦、余弦吗？比较大小：sin40° sin80°;cos40° cos80°拓展延伸例3：.如图，⊙0是△ABC 的外接圆,AD 是⊙O 的直径,若⊙O 的半径为5，AC=6，则cosB 的值是1.如图,直角三角形ABC 中，斜边AB 的长为m ，∠B=40°，则直角边BC 的长是（）A ．msin40°B ．mcos40°C ．mtan40°D ．2、如图，△ABO 的顶点都是小正方形组成的网格中的格点，则cos ∠OAB 等于（）效果检测班级学号姓名等第1．在Rt △ABC 中,∠C ＝90°,BC ＝3,sinA ＝0．6,则AC ＝_ _,AB ＝___, tanB ＝_ __．2．在Rt △ABC 中，锐角A 的对边和邻边同时扩大100倍，sinA 的值（）A ．扩大100倍B ．缩小100倍C ．不变D ．不能确定3．已知∠A,∠B 为锐角(1)若∠A ＝∠B ，则sinA sinB ；(2)若∠A<∠B ，则sinA sinB ；cosA cosB ；tanA tanB4.在Rt △ABC 中,∠C ＝90°, cosA ＝35，BC ＝12,求斜边AB 上的中线CD 长.tan 40m o C A B D B。
苏科版数学九年级下7.2锐角三角函数—正弦、余弦课件(共16张PPT)
B
在△ABC中, ∠C=90°.
A C
我们把锐角A的对边a与斜边c的比叫做 ∠A的正弦,记作sinA. 我们把锐角A的邻边b与斜边c的比叫做 ∠A的余弦,记作cosA.
∠A的对边 a sinA = = 斜边 c
∠A的邻边 b cosA = = 斜边 c
整合提升
1.如图，Rt△ABC中，∠ACB=90°，CD⊥AB 于D若AC= 5 BC=2 ， 求∠A的三角函数值和sin∠ACD的值.
AD 4 tan B . BD 3
个性展示
3. 在Rt△ABC中,∠B=900,AC=200,sinA=0.6.求: △ABC 的周长和面积
5 4 .在△ABC中，∠C=90°，sinA= 13 ，△ABC的周长
为60，求△ABC的面积。
课堂小结
锐角A的正弦、余弦和正切都是∠A的三角函数
例1.根据图中数据,分别求出∠A, ∠B 的正弦,余弦.
A
C
3
C
3
4 ①
B
A
4 ②
B
已知:如图, ∠ACB=90°,CD⊥AB,垂足为D
(1)sinA ( AC ) BC (
( AB
A
)
)
C D B
CD (2)sinB ( )
(3)cosACD
(4)tanA CD (
CD (
( AC
)
, cosBCD
) , tanB (
( BC
)
)
A计算器 ,求值（精确到0.01）:
α sinα 10º 20º 30º 40º 50º 60º 70º 80º
0.17 0.34 0.5 0.87 0.64 0.77 0.77 0.64 0.87 0.5 0.94 0.34 0.98 0.17
在△ABC中, ∠C=90°.
A C
我们把锐角A的对边a与斜边c的比叫做 ∠A的正弦,记作sinA. 我们把锐角A的邻边b与斜边c的比叫做 ∠A的余弦,记作cosA.
∠A的对边 a sinA = = 斜边 c
∠A的邻边 b cosA = = 斜边 c
整合提升
1.如图，Rt△ABC中，∠ACB=90°，CD⊥AB 于D若AC= 5 BC=2 ， 求∠A的三角函数值和sin∠ACD的值.
AD 4 tan B . BD 3
个性展示
3. 在Rt△ABC中,∠B=900,AC=200,sinA=0.6.求: △ABC 的周长和面积
5 4 .在△ABC中，∠C=90°，sinA= 13 ，△ABC的周长
为60，求△ABC的面积。
课堂小结
锐角A的正弦、余弦和正切都是∠A的三角函数
例1.根据图中数据,分别求出∠A, ∠B 的正弦,余弦.
A
C
3
C
3
4 ①
B
A
4 ②
B
已知:如图, ∠ACB=90°,CD⊥AB,垂足为D
(1)sinA ( AC ) BC (
( AB
A
)
)
C D B
CD (2)sinB ( )
(3)cosACD
(4)tanA CD (
CD (
( AC
)
, cosBCD
) , tanB (
( BC
)
)
A计算器 ,求值（精确到0.01）:
α sinα 10º 20º 30º 40º 50º 60º 70º 80º
0.17 0.34 0.5 0.87 0.64 0.77 0.77 0.64 0.87 0.5 0.94 0.34 0.98 0.17
苏科版九年级数学下册第七章《锐角三角函数》教学案
_________________. ________________________. ……AC C CB BB斜边c对边呢？20m13m如图，在Rt△ABC中，∠C＝90°，AC＝12，BC＝5，则sinA＝_____知道一边长及一锐角的三角函数值，其它各边的长和另一锐角的三角函数值。
cosB=1312,AC ＝10，求△ABC 的周长和斜三个角，在直角三角形中，已知有一个角是直角，我们把利用已知的元素求出末知元素的过程，叫做解直角三角形。
像上述的就是由两条直角边这两个元素，利用勾股定BA年湖北仙桃）如图所示，小华同学在距离某建筑物6米的点°，则广告牌的高度B的高度，在平地上C处测得建筑物顶方向前进12 m到达D处，在D处测得°，则建筑物ABA50CB．为了测量停留在空中的气球的高度，小明先站在地面上某点处观测BC°方向，距离灯塔80海里的的南偏东34°方向上如，我们可以利用测角仪测出∠ECB 度数，用皮尺量出CE 的长度，而后按一定的比例尺(例如1:500)出图形，进而求出物体的高度。
， ＝a b ，cota ＝b a（余0＜cosA ＜1，tinA ×cotAa sina cosa tana cota30°45°60°、( )、2.8cm。
CD.参考答案：7.1正切(1) 1. 35 2.4 7.2正弦、余弦（一） 1.21，21,23,23. 2．A 3．D 4． BC=6,cosB=53。
7.2正弦、余弦（二）1．60,13120 2．4 3．6 7．3特殊角的三角函数 1．(1)-1.5 (2) 312．45°，60° 3．23 4．B 5．C 6．156 7.4由三角函数值求锐角1．(1) 60° (2) 30° (3) 60° (4) 23.3° （5）38.3° (6)41.9° 2．14.5° 3．105 m。
苏科版数学九年级下册7.2《正弦、余弦》(第1课时)讲教学设计
苏科版数学九年级下册7.2《正弦、余弦》（第1课时）讲教学设计一. 教材分析苏科版数学九年级下册7.2《正弦、余弦》这一节主要介绍了正弦和余弦的概念以及它们的性质。
学生需要了解正弦和余弦的定义，掌握它们的性质，并能够运用正弦和余弦知识解决实际问题。
本节课的内容是学生学习三角函数的基础，对于学生来说具有重要的意义。
二. 学情分析学生在学习本节课之前，已经学习了角的度量、弧度制等知识，对于角度有一定的了解。
同时，学生还学习了锐角三角函数的概念，对于三角函数有一定的认识。
但是，学生对于正弦和余弦的性质以及运用正弦和余弦解决实际问题还比较陌生，需要教师通过实例进行讲解和引导。
三. 教学目标1.了解正弦和余弦的定义，掌握它们的性质。
2.能够运用正弦和余弦知识解决实际问题。
3.培养学生的数学思维能力，提高学生的数学素养。
四. 教学重难点1.正弦和余弦的定义。
2.正弦和余弦的性质。
3.运用正弦和余弦解决实际问题。
五. 教学方法采用问题驱动法、实例教学法、小组合作法等教学方法。
通过问题引导学生思考，通过实例让学生理解正弦和余弦的性质，通过小组合作让学生互相讨论和交流，提高学生的学习效果。
六. 教学准备1.准备正弦和余弦的实例，用于讲解和引导学生理解正弦和余弦的性质。
2.准备一些实际问题，用于巩固学生对正弦和余弦的运用。
3.准备教学PPT，用于辅助教学。
七. 教学过程1.导入（5分钟）通过提问方式引导学生回顾锐角三角函数的概念，为新课的学习做好铺垫。
2.呈现（10分钟）教师通过PPT呈现正弦和余弦的定义，让学生初步了解正弦和余弦的概念。
然后，通过实例讲解正弦和余弦的性质，让学生理解并掌握正弦和余弦的性质。
3.操练（10分钟）学生分组合作，利用正弦和余弦的性质解决实际问题。
教师巡回指导，为学生提供帮助。
4.巩固（10分钟）教师通过PPT呈现一些实际问题，让学生独立解决。
学生展示解题过程，教师进行点评和指导。
5.拓展（10分钟）教师引导学生思考正弦和余弦在实际生活中的应用，让学生发挥想象，提高学生的创新能力。
九年级下册数学课件(苏科版)正弦余弦 第一课时
2、同角的正弦、余弦关系： sin 2A+cos 2A=1
(1) 已知sinA= 且∠B=90º—∠A,求cosB; (2) 已知sin35º=0.5736,求cos55º; (3) 已知cos47º6’=0.6807,求sin42º54’.
（4）已知sin67º18’=0.9225,求cos______ =0.9225。
B
c a
A
bC
sin A与cos A有什么关系？
同角的正弦、余弦关系： sin 2A+cos 2A=1
计算：(1)
已知sinα=
2 5
（2）若sinα+cos α=1
求sinαcos α
求COSα
若关于x的一元二次方程4x2-2（m+1）x+m=0的 两个根是一个直角三角形的两锐角的正弦，求 m的值。
B
A
C
1、互为余角的正弦、余弦关系： sin A= cos (90°-A) cos A= sin (90°-A)
我们发现：30º，45º， 60º这三个特殊角的正弦 值分别等于它们的余角的 余弦值。
B
对于任意锐角的正弦值，是否也等于它的余 角的余弦值呢？
c
a
sinA= cosB=
sinA= cosB
A
= cos (90º-A)
b
C
∠B=90º-∠A
任意锐角的余弦值等于它的余角的正弦值. sinA=cos(90º-A), cosA=sin(90º-A)
正弦与余弦的关系： 任意锐角的正弦值等于它的余角的余弦值； 任意锐角的余弦值等于它的余角的正弦值.
sinA=cos(90º-A), cosA=sin(90º-A)
考考你：
(1) 已知sinA= 且∠B=90º—∠A,求cosB; (2) 已知sin35º=0.5736,求cos55º; (3) 已知cos47º6’=0.6807,求sin42º54’.
（4）已知sin67º18’=0.9225,求cos______ =0.9225。
B
c a
A
bC
sin A与cos A有什么关系？
同角的正弦、余弦关系： sin 2A+cos 2A=1
计算：(1)
已知sinα=
2 5
（2）若sinα+cos α=1
求sinαcos α
求COSα
若关于x的一元二次方程4x2-2（m+1）x+m=0的 两个根是一个直角三角形的两锐角的正弦，求 m的值。
B
A
C
1、互为余角的正弦、余弦关系： sin A= cos (90°-A) cos A= sin (90°-A)
我们发现：30º，45º， 60º这三个特殊角的正弦 值分别等于它们的余角的 余弦值。
B
对于任意锐角的正弦值，是否也等于它的余 角的余弦值呢？
c
a
sinA= cosB=
sinA= cosB
A
= cos (90º-A)
b
C
∠B=90º-∠A
任意锐角的余弦值等于它的余角的正弦值. sinA=cos(90º-A), cosA=sin(90º-A)
正弦与余弦的关系： 任意锐角的正弦值等于它的余角的余弦值； 任意锐角的余弦值等于它的余角的正弦值.
sinA=cos(90º-A), cosA=sin(90º-A)
考考你：
苏科版数学九年级下册7.2《正弦、余弦》(第1课时)讲说课稿
苏科版数学九年级下册7.2《正弦、余弦》（第1课时）讲说课稿一. 教材分析苏科版数学九年级下册7.2《正弦、余弦》这一课时，是在学生学习了锐角三角函数的基础上进行授课的。
本节课的主要内容是正弦和余弦的概念、性质及其应用。
通过本节课的学习，学生能够掌握正弦和余弦的定义，理解它们的性质，并能运用正弦和余弦解决一些实际问题。
教材通过丰富的例题和练习题，帮助学生巩固所学知识，提高解题能力。
二. 学情分析在进入九年级下册的学习之前，学生已经掌握了锐角三角函数的相关知识，对三角函数有一定的认识。
但是，对于正弦和余弦的概念、性质及其应用，学生可能还比较陌生。
因此，在教学过程中，我需要引导学生逐步理解正弦和余弦的定义，通过举例、讲解、练习等方式，让学生逐步掌握它们的性质和应用。
三. 说教学目标1.知识与技能目标：学生能够理解正弦和余弦的概念，掌握它们的性质，并能运用正弦和余弦解决一些实际问题。
2.过程与方法目标：通过观察、思考、讨论等方法，学生能够自主探究正弦和余弦的性质，培养学生的探究能力和合作意识。
3.情感态度与价值观目标：学生能够体验数学与实际生活的联系，增强对数学的兴趣和自信心。
四. 说教学重难点1.教学重点：正弦和余弦的概念、性质及其应用。
2.教学难点：正弦和余弦的性质的理解和运用。
五. 说教学方法与手段在本节课的教学过程中，我将采用以下教学方法与手段：1.情境教学法：通过生活实例引入正弦和余弦的概念，让学生感受数学与实际生活的联系。
2.引导发现法：在讲解正弦和余弦的性质时，引导学生观察、思考、讨论，发现其中的规律。
3.练习法：通过丰富的练习题，让学生巩固所学知识，提高解题能力。
六. 说教学过程1.导入：以生活实例引入正弦和余弦的概念，激发学生的学习兴趣。
2.新课讲解：讲解正弦和余弦的定义，通过例题和练习题，让学生掌握它们的性质。
3.课堂讨论：引导学生观察、思考、讨论正弦和余弦的性质，培养学生的探究能力和合作意识。
初中数学九年级下册苏科版7.2正弦、余弦优秀教学案例
（四）反思与评价
1.教师引导学生对所学知识进行反思，总结正弦、余弦函数的性质及应用。
2.学生进行自我评价，发现自身不足，明确后续学习目标。
3.教师对学生的学习过程和成果进行评价，关注学生的成长和发展，给予鼓励和指导。
本节课的教学策略旨在充分发挥学生的主体作用，引导学生主动探究、合作学习，提高学生的数学素养。通过情景创设、问题导向、小组合作、反思与评价等教学手段，激发学生的学习兴趣，培养学生的数学思维能力，促进学生的全面发展。
四、教学内容与过程
（一）导入新课
1.利用多媒体展示生活中常见的周期性现象，如钟表走动、海浪起伏等，引导学生关注数学与现实生活的联系。
2.提出引导性问题：“这些周期性现象背后是否存在共同的数学规律？”激发学生思考和探究欲望。
3.回顾已学过的锐角三角函数知识，为学生学习正弦、余弦函数奠定基础。
（二）讲授新知
（一）情景创设
1.利用多媒体展示生活中常见的周期性现象，如钟表走动、海浪起伏等，让学生感受数学与现实生活的紧密联系。
2.设计具有挑战性的数学问题，激发学生探究欲望，引导学生主动参与到学习过程中。
3.创设轻松、愉快的学习氛围，鼓励学生大胆提问、发表见解，增强学生的自信心。
（二）问题导向
1.教师提出引导性问题，引导学生思考正弦、余弦函数的定义及性质。
3.小组合作与实践操作：在学生小组讨论环节，教师组织学生进行小组合作，分享学习心得，培养学生合作学习的习惯。同时，教师还引导学生进行实践性任务，如制作正弦、余弦函数的演示道具，增强学生的动手能力，使学生在实践中巩固所学知识。
4.反思与评价：在总结归纳环节，教师引导学生对所学知识进行反思，总结正弦、余弦函数的性质及应用。同时，学生进行自我评价，发现自身不足，明确后续学习目标。教师对学生的学习过程和成果进行评价，关注学生的成长和发展，给予鼓励和指导，使得学生在评价中不断进步。
1.教师引导学生对所学知识进行反思，总结正弦、余弦函数的性质及应用。
2.学生进行自我评价，发现自身不足，明确后续学习目标。
3.教师对学生的学习过程和成果进行评价，关注学生的成长和发展，给予鼓励和指导。
本节课的教学策略旨在充分发挥学生的主体作用，引导学生主动探究、合作学习，提高学生的数学素养。通过情景创设、问题导向、小组合作、反思与评价等教学手段，激发学生的学习兴趣，培养学生的数学思维能力，促进学生的全面发展。
四、教学内容与过程
（一）导入新课
1.利用多媒体展示生活中常见的周期性现象，如钟表走动、海浪起伏等，引导学生关注数学与现实生活的联系。
2.提出引导性问题：“这些周期性现象背后是否存在共同的数学规律？”激发学生思考和探究欲望。
3.回顾已学过的锐角三角函数知识，为学生学习正弦、余弦函数奠定基础。
（二）讲授新知
（一）情景创设
1.利用多媒体展示生活中常见的周期性现象，如钟表走动、海浪起伏等，让学生感受数学与现实生活的紧密联系。
2.设计具有挑战性的数学问题，激发学生探究欲望，引导学生主动参与到学习过程中。
3.创设轻松、愉快的学习氛围，鼓励学生大胆提问、发表见解，增强学生的自信心。
（二）问题导向
1.教师提出引导性问题，引导学生思考正弦、余弦函数的定义及性质。
3.小组合作与实践操作：在学生小组讨论环节，教师组织学生进行小组合作，分享学习心得，培养学生合作学习的习惯。同时，教师还引导学生进行实践性任务，如制作正弦、余弦函数的演示道具，增强学生的动手能力，使学生在实践中巩固所学知识。
4.反思与评价：在总结归纳环节，教师引导学生对所学知识进行反思，总结正弦、余弦函数的性质及应用。同时，学生进行自我评价，发现自身不足，明确后续学习目标。教师对学生的学习过程和成果进行评价，关注学生的成长和发展，给予鼓励和指导，使得学生在评价中不断进步。
新苏科版九年级数学下册《7章锐角三角函数7.2正弦、余弦》教案_30
A的邻边 b
即：cos A
斜边
c
归纳小结：
锐角 A 的正弦、余弦、正切都是∠ A 的 三角函数 .
注意 :
A
（1） sinA、 cosA 和 tanA 都是比值，没有单位。
（2） sinA、 cosA 和 tanA 的值取决于角的大小，与所在三角形的边长无关。
三、性质探究，深化概念
练一练：
斜边 c 邻边 b
,sinB=
sinA=
,sinB=
思考 ：在直角三角形中，∠ A 的邻边与斜边的比值是否变化？
发现：当直角三角形的一个锐角的大小已确定时 余弦的定义：在直角三角形 ABC 中，
,它的邻边与斜边的比值也确定。
我们把锐角∠ A 的邻边 b 与斜边 c 的比叫做∠ A 的 __________,记作 __________,
求 cosB 的值 .
A
O
B
C
6.如图，在 ABC 中， AD 是 BC 边上的高， tan B (1)求证 : AC BD ; (2)若 sin C 12 ， BC 12 ，求 ABC 的面积 13
cos DAC .
D
第 5题
第 6题
教学过程
一、情景导入，引出概念
1.观察思考
如图 1，在 12 12 的正方形网格（每个小正方形的边长为 1 ）中，将 MAN 如图放置．
(1) 在网格中取一个格点 B ，过 B 作 BC AN ,垂足为 C ．从 ABC 中，你能读出哪些信息？
(2) 在网格中取另一个格点 D ，过 D 作 DE AN ，
2.相等的锐角的正弦值相等，余弦值也相等 .
3.正弦值随着锐角的增大而增大，余弦值随着锐角的增大而减小
苏教版九年级下册数学教学课件：7.2《正弦、余弦(2)》
B
5
2．sinA＝____，cosA＝____；
A
C
3．sinB＝____，cosB＝____；
12
4．tanA＝____，tanB＝____．
3
7.2 正弦、余弦（2）
通过计算，你 有何发现？
1
sinA＝cosB，cosA＝sinB，tanA＝ ．
tanB
A 12
B
5
C
4
7.2 正弦、余弦（2）
6
7.2 正弦、余弦（2）
一把梯子靠在一堵墙上，若梯子与地面的 夹角是68°，而梯子底部离墙脚1.5 m，求梯子 的长度（精确到0.1 m）（参考数据：sin68°≈ 0.9272， cos68°≈ 0.3746，tan68°≈ 2.475） ．
7
7.2 正弦、余弦（2）
畅所欲言
1．对于一个角的正弦、余弦，你有了什么新 的认识？和你的同伴交流一下！
初中数学 九年级(下册)
7.2 正弦、余弦（2）
1
7.2 正弦、余弦（2）
正弦
sinA＝∠A斜的边对边
＝
a c
三
角 函
余弦
cosA＝∠A斜的边邻边
＝
b c
数
正切
tanA＝∠ ∠AA的 的对 邻边 边
＝
a b
2
7.2 正弦、余弦（2）
如图，在Rt△ABC 中，∠C＝90°，AC＝12，BC＝5．
1．AB＝______；
2．你还有什么收获或困惑吗？
8
9
小明在放风筝时，他的手离地面的距离AD＝ 1m．假设风筝线AB是一条直线段，当AB＝95 m时， 测得风筝线与水平线所成角为35°，求此时风筝的高 度（精确到1m）（参考数据：sin35°≈0.5736， cos35°≈0.8192，tan35°≈0.7002）．
苏科版九年级数学下册7.2 正弦、余弦课件
正弦、余弦
tanA= BC
B
AC
AC
tanB= △ABC的周长为36，且AB=AC=10，
求tanB.
答案tanB=3/4
A
B
D
C
如图,小明沿着某斜坡
向上行走了13m,他的相对
位置升高了5m.
5m
A
可求出∠A的对边与斜边之比为5/13
如果他沿着斜坡行走了26m,那么他的相 对位置升高了多少? 10M
∠A的正弦,记作sinA.
sinA = ∠A的对边 = a
斜边
c
我们把锐角A的邻边a与斜边c的比叫做 ∠A的余弦,记作cosA.
cosA = ∠A的邻边 = b
斜边
c
例1.根据图中数据,分别求出∠A, ∠B 的正弦,余弦.
A
3
C4
B
A
①
C
3
4
B
②
1.在△ABC中, ∠C=90°,AB=2,AC=1,则sinB的值 是___1___.
正弦 sinA = ∠A的对边 = a
斜边 c
三
角 函
余弦 cosA = ∠A的邻边 = b
斜边 c
数
正切
tanA = ∠A的对边 = a ∠A的邻边 b
如图，⊙O是△ABC的外接圆，AD是⊙O的直径．若⊙O的半径为， AC=3，则cosB的值为
如图，已知⊙0的半径为1，锐角△ABC内接于⊙0，BD⊥AC于点D,OM⊥AB于点M， 求sin∠CBD的值。
可求出∠A的对边与斜边之比为5/13
以上情况下∠A的邻边与斜边的比值又如何？
B
由刚才分析可知:
A
C
当直角三角形的一个锐角的大小确定时, 它的对边与斜边的比值,邻边与斜边的比值也 就确定.
tanA= BC
B
AC
AC
tanB= △ABC的周长为36，且AB=AC=10，
求tanB.
答案tanB=3/4
A
B
D
C
如图,小明沿着某斜坡
向上行走了13m,他的相对
位置升高了5m.
5m
A
可求出∠A的对边与斜边之比为5/13
如果他沿着斜坡行走了26m,那么他的相 对位置升高了多少? 10M
∠A的正弦,记作sinA.
sinA = ∠A的对边 = a
斜边
c
我们把锐角A的邻边a与斜边c的比叫做 ∠A的余弦,记作cosA.
cosA = ∠A的邻边 = b
斜边
c
例1.根据图中数据,分别求出∠A, ∠B 的正弦,余弦.
A
3
C4
B
A
①
C
3
4
B
②
1.在△ABC中, ∠C=90°,AB=2,AC=1,则sinB的值 是___1___.
正弦 sinA = ∠A的对边 = a
斜边 c
三
角 函
余弦 cosA = ∠A的邻边 = b
斜边 c
数
正切
tanA = ∠A的对边 = a ∠A的邻边 b
如图，⊙O是△ABC的外接圆，AD是⊙O的直径．若⊙O的半径为， AC=3，则cosB的值为
如图，已知⊙0的半径为1，锐角△ABC内接于⊙0，BD⊥AC于点D,OM⊥AB于点M， 求sin∠CBD的值。
可求出∠A的对边与斜边之比为5/13
以上情况下∠A的邻边与斜边的比值又如何？
B
由刚才分析可知:
A
C
当直角三角形的一个锐角的大小确定时, 它的对边与斜边的比值,邻边与斜边的比值也 就确定.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
7.2正弦余弦（1）
1．在Rt△ABC中,∠C＝90°, AC＝7．AB＝25．则sinA＝_____ cosB＝_______tanB＝_______．2．在Rt △ABC中,∠C＝90°,BC＝3,sinA＝0．6,则AC＝______AB＝________
tanB＝__________．
3．在Rt△ABC中,∠C＝90°,AC ＝2,cosA＝0．8,则BC＝______ cos B＝______ tanA＝_____．4．在Rt△ABC中，锐角A的对边和邻边同时扩大100倍，sinA的值（）A．扩大100倍B．缩小100倍C．不变D ．不能确定
5．已知∠A,∠B为锐角
(1)若∠A＝∠B，则sinA sinB ；
(2)若∠A<∠B，则sinA sinB；cosA cosB；tanA tanB
6．如图，在Rt△ABC中，∠C＝90°，BC＝10，cos A＝12
13
，求：AB、sinB
7．如图：在Rt△ABC中，∠C＝90°，BC＝20，sinA＝4
5
, 求△ABC的周长．
8.在Rt△ABC中,∠C＝90°, cosA＝3
5
，BC＝12,求斜边AB上的中线CD长.
A
B
A
B
C
答案
1.24247
,, 252525
2. 4,5,4 3
3. 1.5,3
5
,
3
4
4.C
5.＝,<,>,<
6.AB＝26,sinB＝12 13
7.60
8.15
2
7.2正弦余弦（2）
1．已知Rt △ABC 中，∠C ＝90°，AB ＝m ，40B ∠=，则BC 的长是（ ）
A ．sin 40m
B ．cos 40m
C ．tan 40m
D
．
tan 40
m
2．如图，为了测量河两岸A 、B 两点的距离，在与AB 垂直的方向点C 处测得AC ＝a ，∠ACB ＝α，那么
AB 等于（ ）
A ．a ·sin α
B ．a ·tan α
C ．a ·cos α
D ．αtan a
3．在Rt △ABC 中，∠C ＝900，∠A 、∠B 的对边分别是a 、b ，且满足022
=--b ab a ，则tanA 等于
（ ）
151515
1222
A B C D -+±⋅⋅
⋅⋅
4．以直角坐标系的原点O 为圆心，以1为半径作圆.若点P 是该圆上第一象限内的一点，且OP 与x 轴正方向组成的角为α，则点P 的坐标为
( )
A ．(cos α,1)
B ．(1,sin α)
C ．(si n α,cos α)
D ．(cos α,sin α)
5．如图，在△ABC 中，∠C ＝90°，AC ＝8cm ，AB 的垂直平分线MN 交AC 于D ，连结BD ，若cos ∠BDC ＝
5
3
，则BC 的长是 ( ) A 、4cm
B 、6cm
C 、8cm
D 、10cm
二、填空题（每题5分，共25分）
6．在Rt △ABC 中，∠ACB ＝900，SinB ＝
27
则cosB ．
7．某人想沿着梯子爬上高4米的房顶，梯子的倾斜角（梯子与地面的夹角）不能大于60°，否则就有危
险，那么梯子的长至少为_________米．
8．在Rt △ABC 中， ∠C ＝90︒，AB ＝4，AC ＝1，则cos A 的值是_______． 9．已知α是锐角，s in α＝ a+2，则a 的取值范围是 10．一等腰三角形的两边长分别为4cm 和6cm ，则其底角的余弦值为________．
A
B C
a α
B
N
A
C
D
M
D
O
C
A
B
F
E
B C
A D
B A
C
D 11．平行四边形ABCD 中，AB ＝4cm, BC ＝6cm ，它们的夹角为600，求AC 长．
12．在△ABC 中，∠C ＝90°，D 是BC 的中点，且∠ADC ＝50°，AD ＝2，求tanB 的值.（保留两个有效数字）（参考数据：sin50°≈0.76，cos50°≈0.64，tan50°≈1.19）
13．已知正方形ABCD 中，CE ＝3DE ，AF ⊥BE ，求sin ∠BAF ．
14．如图，四边形ABCD 中，∠B ＝∠D ＝90°，∠A ＝150°，AB ＝5，CD ＝15，求AD 、BC 的长．
15．如图，⊙O 是△
ABC 的外接圆，AD 是⊙O 的直径，若⊙O 的半径为
2
3
，2 AC ，求B sin 的值．
答案 1．B
A B C
D
2．B 3．C 4．D 5．A
6．35 7
7．83 3
8．1 4
9．－2＜a＜－1
10．2
3
或
3
4
11．27cm 12．tanB≈0.59 13．
5
3
14．
53
3
AD=,
253
3
BC=
15．
2 sin
3
B=。