三种基本结构框图的程序语句知识解析
- 格式:ppt
- 大小:173.00 KB
- 文档页数:20

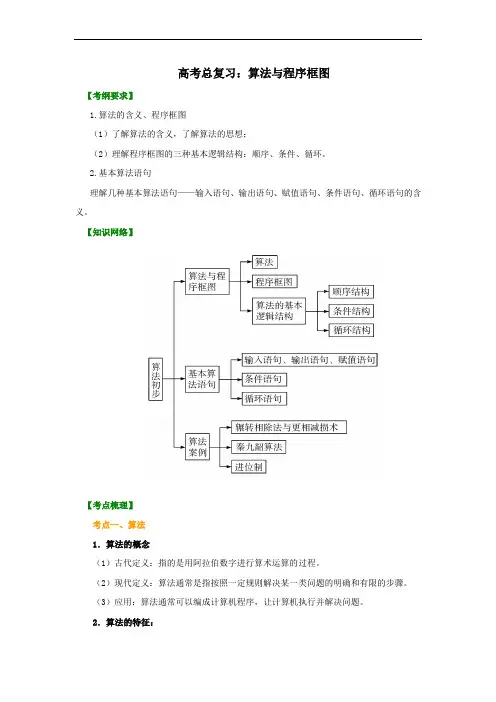
高考总复习:算法与程序框图【考纲要求】1.算法的含义、程序框图(1)了解算法的含义,了解算法的思想;(2)理解程序框图的三种基本逻辑结构:顺序、条件、循环。
2.基本算法语句理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义。
【知识网络】【考点梳理】考点一、算法1.算法的概念(1)古代定义:指的是用阿拉伯数字进行算术运算的过程。
(2)现代定义:算法通常是指按照一定规则解决某一类问题的明确和有限的步骤。
(3)应用:算法通常可以编成计算机程序,让计算机执行并解决问题。
2.算法的特征:①指向性:能解决某一个或某一类问题;②精确性:每一步操作的内容和顺序必须是明确的;算法的每一步都应当做到准确无误,从开始的“第一步”直到“最后一步”之间做到环环相扣,分工明确.“前一步”是“后一步”的前提,“后一步”是“前一步”的继续.③有限性:必须在有限步内结束并返回一个结果;算法要有明确的开始和结束,当到达终止步骤时所要解决的问题必须有明确的结果,也就是说必须在有限步内完成任务,不能无限制的持续进行.④构造性:一个问题可以构造多个算法,算法有优劣之分。
3.算法的表示方法:(1) 用自然语言表示算法: 优点是使用日常用语, 通俗易懂;缺点是文字冗长, 容易出现歧义;(2) 用程序框图表示算法:用图框表示各种操作,优点是直观形象, 易于理解。
要点诠释:泛泛地谈算法是没有意义的,算法一定以问题为载体。
考点二:程序框图1. 程序框图的概念:程序框图又称流程图,是最常用的一种表示法,它是描述计算机一步一步完成任务的图表,直观地描述程序执行的控制流程,最便于初学者掌握。
2.程序框图常用符号:连接点用于连接另一页或另一部分的框图注释框框中内容是对某部分流程图做的解释说明3.画程序框图的规则:(1)使用标准的框图的符号;(2)框图一般按从上到下、从左到右的方向画;(3)除判断框图外,大多数框图符号只有一个进入点和一个退出点。





专题37 程序框图的应用一.学习目标1.了解算法的含义,了解算法的思想;理解程序框图的三种基本逻辑结构:依次结构、条件结构、循环结构.2.理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.3.初步了解几个典型的算法案例.二.学问要点1.算法通常是指可以用计算机来解决某一类问题的程序或步骤,必需是明确和有序的,而且能够在有限步之内完成.2.程序框图又称流程图,是一种用规定的图形、指向线及文字说明来精确、直观地表示算法的图形.通常程序框图由程序框和流程线组成,一个或几个程序框的组合表示算法中的一个步骤,流程线带方向箭头,依据算法进行的依次将程序框连接起来.3.三种基本逻辑结构(1)依次结构是由若干个依次执行的处理步骤组成的,其结构形式为:(2)条件结构是指算法的流程依据给定的条件是否成立而选择执行不同的流向的结构形式,即:(3)循环结构是指从某处起先,依据肯定的条件反复执行处理某一步骤的状况.反复执行的处理步骤称为循环体.循环结构又分为当型循环和直到型循环.结构形式为:4.基本算法语句(1)输入、输出语句和赋值语句:输入语句格式:INPUT“提示内容”;变量;输出语句格式:PRINT“提示内容”;表达式;赋值语句格式:变量=表达式.(2)条件语句:①框图:②条件语句格式:IF—THEN格式IF 条件THEN语句体END IFIF—THEN—ELSE格式IF 条件THEN语句体1ELSE 语句体2END IF5.循环语句循环语句的格式①UNTIL语句②WHILE语句DO循环体LOOP UNTIL条件WHILE条件循环体WEND③依次结构是每个算法结构都含有的,而对于循环结构有重复性,条件结构具有选择性没有重复性,并且循环结构中必定包含一个条件结构,用于确定何时终止循环体.循环结构和条件结构都含有依次结构.④利用循环结构表示算法,第一要先确定是利用当型循环结构,还是直到型循环结构;其次要选择精确的表示累计的变量;第三要留意在哪一步起先循环,满意什么条件不再执行循环体.6.算法案例(1)辗转相除法与更相减损术①辗转相除法:求两个正整数的最大公约数的方法,用较大的数m除以较小的数n得到余数r,反复操作,直到余数为0为止,即m=nt+r(0≤r<n).因此要用“后测试型”循环语句表示,其程序如下:INPUT m,nDOr=m MOD nm=nn=rLOOP UNTIL r=0PRINT mEND(2)秦九韶算法n次多项式f(x)=a n x n+a n-1x n-1+…+a1x+a0=(a n x n-1+a n-1x n-2+…+a1)x+a0…=(…((a n x+a n-1)x+a n-2)x+…+a1)x+a0得到递推公式v0=a n且v k=v k-1x+a n-k,其中k=1,2,…,n其算法可用循环语句来实现.(3)进位制①将十进制数化为二进制数的算法称为除2取余法;将十进制数化为k进制数的算法称为除k取余法.②将k进制数化为十进制数的算法步骤为:第一步:从左到右依次取k进制数a n a n-1…a1a0(k)各位上的数字乘以k的幂,k的幂从n起先取值,每次递减1,递减到0,即a n·k n,a n-1·k n-1,…,a1·k,a0·k0;其次步:把全部积加起来,就得到十进制数.三.高考类型分析例1. (1)执行下面的程序框图,假如输入的t∈[-1,3],则输出的s属于( )A.[-3,4] B.[-5,2]C.[-4,3] D.[-2,5](2)执行下面的程序框图,若输入的ε的值为0.25,则输出的n的值为____.(3)阅读如下程序框图,假如输出i=5,那么在空白矩形框中应填入的语句为( )A.S=2*i-2 B.S=2*i-1C.S=2*i D.S=2*i+4【分析】(1)条件结构、框图功能是求分段函数的值域.(2)依据运行依次计算出1F1的值,当1F1≤ε时输出n的值,结束程序.n为循环次数.(3)依据程序框图表示的算法对i的取值进行验证.【解析】(1)因为t∈[-1,3],当t∈[-1,1)时,s=3t∈[-3,3);当t∈[1,3]时,s =4t-t2=-(t2-4t)=-(t-2)2+4∈[3,4],所以s∈[-3,4].(3)当i=2时,S=2×2+1=5<10;当i=3时,仍旧循环,解除D;当i=4时,S=2×4+1=9<10;当i=5时,不满意S<10,即此时S≥10,输出i.此时A项求得S=2×5-2=8,B项求得S=2×5-1=9,C项求得S=2×5=10,故只有C项满意条件.【评析】(1)循环结构中的条件推断循环结构中的条件是高考常考的学问点,主要是限制循环的变量应当满意的条件是什么.满意条件则进入循环或者退出循环,此时要特殊留意当型循环与直到型循环的区分.(2)条件结构中的条件推断条件结构中条件的推断关键是明确条件结构的功能,然后依据“是”的分支成立的条件进行推断.例2(1)下面程序运行的结果为( )n=10S=100DOS=S-nn=n-1LOOP UNTIL S<=70PRINT nENDA.4 B.5 C.6 D.7【解析】第一次循环后,S=90,n=9,90>70,不满意要求,接着运行;其次次循环后,S=81,n=8,81>70,不满意要求,接着运行;第三次循环后,S=73,n=7,73>70,不满意要求,接着运行;第四次循环后,S=66,n=6,66<70,满意条件,结束循环.【点评】1.在用WHILE语句和UNTIL语句编写程序解决问题时,肯定要留意它们的格式及条件的表述方法.WHILE语句中是当条件满意时执行循环体,而UNTIL语句中是当条件不满意时执行循环体.(2)下面程序运行后输出的结果为( )a=0j=1WHILE j<=5a=(a+j) MOD 5j=j+1ENDaA.0 B.1 C.2 D.4【解析】当j=1时,余数a=1;当j=2时,余数a=3;当j=3时,余数a=1;当j=4时,余数a=0;当j=5时,余数a=0;当j=6时,不满意条件,此时退出循环.【点评】1.在解答本题时,易错选D而导致错误,错误缘由是:对循环过程不理解,误认为j=1时,余数a=0,即j=1时,没有执行第一次循环.其错误过程如下:当j=1时,余数a=0;当j=2时,余数a=2;当j=3时,余数a=0;当j=4时,余数a=4;当j=5时,余数a=4.2.解决算法语句的有关问题时,还有以下几点易造成失误,备考时要高度关注:(1)对基本算法语句的功能及格式要求不熟识.(2)条件语句中的嵌套结构混乱,不能用分段函数例3(1)用辗转相除法或更相减损术求375和85的最大公约数;(2)用秦九韶算法计算f(x)=x5+2x4+3x3+4x2+5x+6在x=2时的值;(3)将七进制数235(7)转化为八进制数.【解析】(1)用辗转相除法:375=85×4+3585=35×2+1535=15×2+515=3×5+0∴375与85的最大公约数为5.用更相减损术:375-85=290290-85=205205-85=120120-85=3585-35=5050-35=1535-15=2020-15=515-5=1010-5=5.∴375与85的最大公约数为5.(3)先化成十进制,再化成八进制.235(7)=2×72+3×7+5=124∴124=174(8),即235(7)=174(8).【点评】驾驭三种特殊算法的求解思想和方法是顺当解决问题的前提和必要条件.例4某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.(1)分别求出按程序框图正确编程运行时输出y的值为i的概率P i(i=1,2,3);(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.甲的频数统计表(部分)运行次数n 输出y的值为1的频数输出y的值为2的频数输出y的值为3的频数30 14 6 10…………2 100 1 027 376 697乙的频数统计表(部分)运行次数n 输出y的值为1的频数输出y的值为2的频数输出y的值为3的频数30 12 11 7…………2 100 1 051 696 353当n=2 100时,依据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并推断两位同学中哪一位所编写程序符合算法要求的可能性较大;(3)按程序框图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.(2)当n =2 100时,甲、乙所编程序各自输出y 的值为i(i =1,2,3)的频率如下:输出y 的值为1的频数 输出y 的值为2的频数 输出y 的值为3的频数 甲1 0272 100 3762 100 6972 100 乙 1 0512 100 6962 100 3532 100 比较频率趋势与概率,可得乙同学所编程序符合算法要求的可能性较大.(3)随机变量ξ可能的取值为0,1,2,3.P (ξ=0)=C 03×⎝ ⎛⎭⎪⎫130×⎝ ⎛⎭⎪⎫233=827, P (ξ=1)=C 13×⎝ ⎛⎭⎪⎫131×⎝ ⎛⎭⎪⎫232=49, P (ξ=2)=C 23×⎝ ⎛⎭⎪⎫132×⎝ ⎛⎭⎪⎫231=29, P (ξ=3)=C 33×⎝ ⎛⎭⎪⎫133×⎝ ⎛⎭⎪⎫230=127, 故ξ的分布列为ξ 01 2 3 P 827 49 29 127所以,E ξ=0×827+1×49+2×29+3×127=1. 即ξ的数学期望为1.例5依据如图所示的程序框图,将输出的x,y的值依次分别记为x1,x2,x3,…,x k…;y1,y2,y3,…,y k….(1)分别求数列{x k}和{y k}的通项公式;(2)令z k=x k y k,求数列{z k}的前k项和T k,其中k∈N*,k≤2 017.(2)T k =x 1y 1+x 2y 2+…+x k y k=1×(3-1)+3×(32-1)+…+(2k -1)(3k -1)=1×3+3×32+…+(2k -1)·3k -[1+3+…+(2k -1)].令S k =1×3+3×32+…+(2k -1)·3k ,①则3S k =1×32+3×33+…+(2k -1)·3k +1,② ①-②得-2S k =3+2·32+2·33+…+2·3k -(2k -1)·3k +1 =2(3+32+…+3k )-3-(2k -1)·3k +1 =2×3×(1-3k )1-3-3-(2k -1)·3k +1 =3k +1-6-(2k -1)·3k +1 =2(1-k )·3k +1-6,∴S k =(k -1)·3k +1+3.又∵1+3+…+(2k -1)=k (1+2k -1)2=k 2, ∴T k =(k -1)·3k +1+3-k 2. 【点评】以程序框图或算法语句为题设条件常与统计问题、数列问题、函数问题综合,求解时关键是将程序框图或算法语句转化翻译.四.方法总结1.了解算法思想,理解算法含义的关键在于体现程序或步骤的明确性和有限性.2.深刻理解算法的三种逻辑结构特征,需通过实际例子体会算法流程的全过程,认清所解决问题的实质.如解决分段函数的求值问题时,一般采纳条件结构设计算法;如累加求和,累乘求积等问题,往往包含循环过程,特别适合计算机处理,这类问题许多程序框图都用循环结构进行设计,同时也要留意三种基本结构的共同特点.3.特殊提示的是,程序框图主要包括三个部分:(1)弄清相应操作框的内容;(2)带箭头的流程线及推断框的条件;(3)框内外必要的文字说明和算法功能.读懂流程图要从这三方面探讨,流程线反映了流程执行的先后依次,主要看箭头方向,框内外文字说明白操作内容以及流向.4.(1)辗转相除法与更相减损术是求两个正整数的最大公约数的两种方法,关键是驾驭这两种算法的操作步骤,计算时应仔细、细心,确保中间结果的精确性,因为下一次计算要用到上一次计算的结果.(2)利用“除k取余法”将十进制数化为k进制数时,要把各步所得余数从下到上排,切莫把依次弄错.(3)利用秦九韶算法计算多项式的值的关键是正确地将多项式改写,然后由内向外逐次计算.由于本次计算用到上一次计算的结果,同样应仔细、细致地计算每一步,确保每一步结果的精确性.。
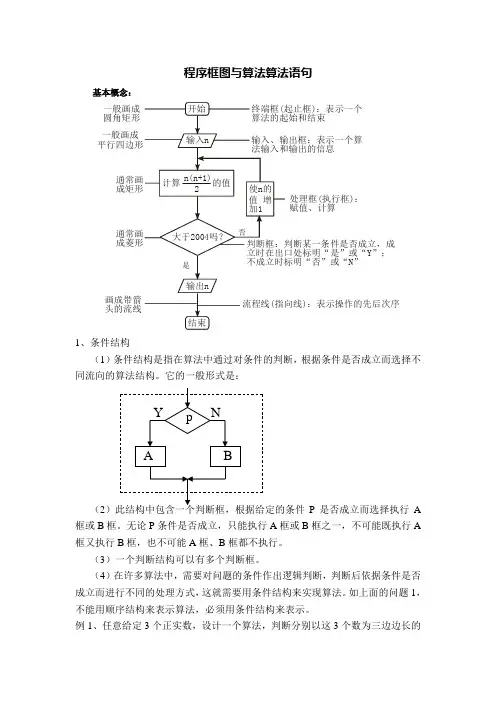
程序框图与算法算法语句基本概念:一般画成圆角矩形 一般画成画成带箭头的流线处理框(执行框):赋值、计算1、条件结构(1)条件结构是指在算法中通过对条件的判断,根据条件是否成立而选择不同流向的算法结构。
它的一般形式是:(2P是否成立而选择执行A 框或B框。
无论P条件是否成立,只能执行A框或B框之一,不可能既执行A 框又执行B框,也不可能A框、B框都不执行。
(3)一个判断结构可以有多个判断框。
(4)在许多算法中,需要对问题的条件作出逻辑判断,判断后依据条件是否成立而进行不同的处理方式,这就需要用条件结构来实现算法。
如上面的问题1,不能用顺序结构来表示算法,必须用条件结构来表示。
例1、任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在。
画出这个算法的程序框图。
评注:凡必须根据条件作出判断,然后再决定进行哪一个步骤的问题,在画程序框图时,必须引入判断框,应用条件结构。
例 1、读如下列框图分析此算法的功能2、循环结构(1)需要重复执行同一操作的结构称为循环结构。
即从某处开始,按照一定条件反复执行某一处理步骤。
反复执行的处理步骤称为循环体。
循环结构有两种形式:当型循环结构和直到型循环结构。
(2)循环结构不是永无终止的“死循环”,一定要在某个条件下终止循环,这就需要条件结构来判断。
因此,循环结构中一定包含条件结构。
(3)循环结构在程序框图中也是利用判断框来表示,判断框内写上条件,两个出口分别对应着条件成立和条件不成立时时执行的不同指令,其中一个指向循环体,然后再从循环体回到判断框的入口处。
(4)在循环结构中都有一个计数变量和累加变量。
计数变量用于记录循环次数,累加变量用于输出结果。
计数变量和累加变量一般是同步执行的,累加一次,计数一次。
例 1 结合前面学过的算法步骤,利用三种基本逻辑结构画出程序框图,表示用“二分法”求方程x 2-2=0(x>0)的近似解的算法. 算法分析:(1)算法步骤中的“第一步”“第二步”和“第三步”可以用顺序结构来表示(如下图):(2)算法步骤中的“第四步”可以用条件结构来表示(如下图).在这个条件结构中,“否”分支用“a=m”表示含零点的区间为[m,b],并把这个区间仍记成[a,b];“是”分支用“b=m ”表示含零点的区间为[a,m],同样把这个区间仍记成[a,b].(3)算法步骤中的“第五步”包含一个条件结构,这个条件结构与“第三步”“第四步”构成一个循环结构,循环体由“第三步”和“第四步”组成,终止循环的条件是“|a-b|<d或f(m)=0”.在“第五步”中,还包含由循环结构与“输出m”组成的顺序结构(如下图).(4)将各步骤的程序框图连接起来,并画出“开始”与“结束”两个终端框,就得到了表示整个算法的程序框图(如下图).点评:在用自然语言表述一个算法后,可以画出程序框图,用顺序结构、条件结构和循环结构来表示这个算法,这样表示的算法清楚、简练,便于阅读和交流.例2 高中某班一共有40名学生,设计算法流程图,统计班级数学成绩良好(分数>80)和优秀(分数>90)的人数.分析:用循环结构实现40个成绩的输入,每循环一次就输入一个成绩s,然后对s的值进行判断.设两个计数器m,n,如果s>90,则m=m+1,如果80<s≤90,则n=n+1.设计数器i,用来控制40个成绩的输入,注意循环条件的确定.解:程序框图如下图:例3、设计一个计算1+2+3+…+1000的值的算法,并画出程序框图。


图形符号名称功能终端框(起止框)表示一个算法的起始和结束输入、输出框表示一个算法输入和输出的信息处理框(执行框)赋值、计算判断框判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”流程线连接程序框连接点连接程序框图的两部分三种逻辑结构可以用如下程序框图表示:顺序结构条件结构循环结构变式训练观察下面的程序框图,指出该算法解决的问题.解:这是一个累加求和问题,共99项相加,该算法是求100991431321211⨯++⨯+⨯+⨯ 的值.例2 已知一个三角形三条边的边长分别为a ,b ,c ,利用海伦—秦九韶公式设计一个计算三角形面积的算法,并画出程序框图表示.(已知三角形三边边长分别为a,b,c ,则三角形的面积为S=))()((c p b p a p p ---),其中p=2c b a ++.这个公式被称为海伦—秦九韶公式)算法步骤如下:第一步,输入三角形三条边的边长a,b,c.第二步,计算p=2c b a ++. 第三步,计算S=))()((c p b p a p p ---.第四步,输出S.程序框图如下:点评:很明显,顺序结构是由若干个依次执行的步骤组成的,它是最简单的逻辑结构,它是任何一个算法都离不开的基本结构.顺序结构可以用程序框图表示为语句n语句n+1件是______________. 答案:i>10.构),如图1所示.执行过程如下:条件成立,则执行A框;不成立,则执行B框.图1 图2应用示例例1 任意给定3个正实数,设计一个算法,判断以这3个正实数为三边边长的三角形是否存在,并画出这个算法的程序框图.算法步骤如下:第一步,输入3个正实数a,b,c.第二步,判断a+b>c,b+c>a,c+a>b是否同时成立.若是,则存在这样的三角形;否则,不存在这样的三角形.程序框图如右图:随堂练习1、设计算法判断一元二次方程ax2+bx+c=0是否有实数根,并画出相应的程序框图. 相应的程序框图如右:2、(1)设计算法,求ax+b=0的解,并画出流程图.程序框图如下:第3课时循环结构当型循环结构直到型循环结构直到型循环结构是程序先进入循环体,然后对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.当型循环结构是在每次执行循环体前,先对条件进行判断,当条件满足时,执行循环体,否则终止循环.应用示例例1设计一个计算1+2+……+100的值的算法,并画出程序框图.第一步,令i=1,S=0.第二步,若i≤100成立,则执行第三步;否则,输出S,结束算法.第三步,S=S+i.第四步,i=i+1,返回第二步.当型循环直到型循环变式训练例1 设计框图实现1+3+5+7+…+131的算法.第一步,赋初值i=1,sum=0.第二步,sum=sum+i,i=i+2.第三步,如果i≤131,则反复执第二步;否则,执行下一步.第四步,输出sum.第五步,结束.程序框图如右图知能训练设计一个算法,求1+2+4+…+249的值,并画出程序框图.(2)算法步骤中的“第四步”可以用条件结构来表示(如下图).在这个条件结构中,“否”分支用“a=m”表示含零点的区间为[m,b],并把这个区间仍记成[a,b];“是”分支用“b=m ”表示含零点的区间为[a,m],同样把这个区间仍记成[a,b].(3)算法步骤中的“第五步”包含一个条件结构,这个条件结构与“第三步”“第四步”构成一个循环结构,循环体由“第三步”和“第四步”组成,终止循环的条件是“|a-b|<d或f(m)=0”.在“第五步”中,还包含由循环结构与“输出m”组成的顺序结构(如下图).(4)将各步骤的程序框图连接起来,并画出“开始”与“结束”两个终端框,就得到了表示整个算法的程序框图(如下图).解:将实际问题转化为数学模型,该问题就是要求1+2+4+……+263的和.程序框图如下:点评:对于开放式探究问题,我们可以建立数学模型(上面的题目可以与等比数列的定义、性质和公式联系起来)和过程模型来分析算法,通过设计算法以及语言的描述选择一些成熟的办法进行处理.例3 乘坐火车时,可以托运货物.从甲地到乙地,规定每张火车客票托运费计算方法是:行李质量不超过50 kg 时按0.25元/kg ;超过50 kg 而不超过100 kg 时,其超过部分按0.35元/kg ;超过100 kg 时,其超过部分按0.45元/kg .编写程序,输入行李质量,计算出托运的费用.分析:本题主要考查条件语句及其应用.先解决数学问题,列出托运的费用关于行李质量的函数关系式.设行李质量为x kg ,应付运费为y 元,则运费公式为:y=⎪⎩⎪⎨⎧>-+⨯+⨯≤<-+⨯≤<,100),100(45.05035.05025.0,10050),50(35.05025.0,500,25.0x x x x x x整理得y=⎪⎩⎪⎨⎧>-≤<-≤<.100,1545.0,10050,535.0,500,25.0x x x x x x要计算托运的费用必须对行李质量分类讨论,因此要用条件语句来实现.解:算法分析:第一步,输入行李质量x.第二步,当x≤50时,计算y=0.25x,否则,执行下一步.第三步,当x≤100,计算y=0.35x-5,否则,计算y=0.45x-15.第四步,输出y.程序框图如下:课堂小节(1)进一步熟悉三种逻辑结构的应用,理解算法与程序框图的关系.(2)根据算法步骤画出程序框图.作业习题1.1B组1、2.设计感想本节是前面内容的概括和总结,在回忆前面内容的基础上,选择经典的例题,进行了详尽的剖析,这样降低了学生学习的难度.另外,本节的练习难度适中,并且多为学生感兴趣的问题,这样为学生学好本节内容作好充分准备,希望大家喜欢这一节课.。

《程序框图与算法的基本逻辑结构》讲义一、引言在当今数字化的时代,计算机程序已经深入到我们生活的方方面面。
从智能手机中的各种应用,到工业生产中的自动化控制,无一不是通过程序来实现的。
而程序的核心就是算法,算法的设计和表达则离不开程序框图。
程序框图是一种直观、清晰地展示算法流程的工具,它能够帮助我们更好地理解和设计算法。
在这篇讲义中,我们将深入探讨程序框图与算法的基本逻辑结构。
二、程序框图的基本概念程序框图,又称为流程图,是用一些规定的图形、流程线及文字说明来准确、直观地表示算法的图形。
它由一些图形符号和连接这些符号的流程线组成。
常见的图形符号包括:1、起止框:表示算法的开始和结束,通常是一个圆角矩形。
2、输入输出框:用于表示数据的输入或输出,一般是一个平行四边形。
3、处理框:用于表示对数据的处理操作,如计算、赋值等,是一个矩形。
4、判断框:用于根据条件决定程序的流向,是一个菱形。
5、流程线:用于连接各个图形符号,表示算法的执行顺序。
通过这些图形符号的组合和连接,我们可以清晰地展示算法的步骤和逻辑。
三、算法的基本逻辑结构算法的基本逻辑结构主要有三种:顺序结构、选择结构和循环结构。
1、顺序结构顺序结构是最简单的算法结构,也是最基本的结构。
在顺序结构中,算法的执行按照从上到下的顺序依次进行,每一个步骤都必须在前一个步骤完成后才能执行。
例如,要计算两个数的和,首先输入两个数 a 和 b,然后进行相加运算 c = a + b,最后输出结果 c。
这个过程就是按照顺序结构进行的。
2、选择结构选择结构也称为条件结构,是根据给定的条件进行判断,然后根据判断的结果决定执行不同的分支。
例如,判断一个数是否为正数,如果是正数则输出“该数为正数”,否则输出“该数为非正数”。
这里就用到了选择结构,通过判断条件来决定输出不同的结果。
3、循环结构循环结构是指在一定条件下,重复执行一段算法。
循环结构分为当型循环和直到型循环。
当型循环是在满足条件时执行循环体,直到条件不满足时退出循环。
算法 初步要求层次重难点算法及其程序框图算法的含义A (1)算法的含义、程序框图① 了解算法的含义,了解算法的思想.② 理解程序框图的三种基本逻辑结构:顺序、条件分支、循环. (2)基本算法语句理解几种基本算法语句――输入语句、输出语句、赋值语句、条件语句、循环语句的含义.程序框图的三种基本逻辑结构B 基本算法语句A一、算法的概念与描述1.算法的概念:由基本运算及规定的运算顺序所构成的完整的解题步骤,或者看成按照一定规则解决某一类问题的明确的和有限的步骤,称为算法(algorithm ). 通常可以编成计算机程序,让计算机执行并解决问题.2.算法的特征:⑴有穷性:算法必须在执行有限步后结束,通常还理解为实际上能够容忍的合理限度; ⑵确定性:算法的每一个步骤必须有确定的含义;⑶可行性:组成算法的每个步骤和操作必须是相当基本的,原则上都是能精确地执行的; ⑷输入:有零个或多个输入: ⑸输出:有一个或多个输出.知识内容高考要求模块框架程序框图与算法3.算法的描述:⑴用自然语言;⑵用数学语言;⑶用算法语言(程序设计语言);⑷用程序框图(流程图).4.算法的三种基本逻辑结构:顺序结构、条件(分支)结构和循环结构.⑴顺序结构:最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的.如下图,只有在执行完A框指定的操作后,才能接着执行B框指定的操作;⑵条件(分支)结构:在一个算法中,用来处理需要根据条件是否成立有不同的流向的结构.常见的条件结构的程序框图有下面两种形式:⑶循环结构:从某处开始,按照一定的条件反复执行某些步骤的情况,就是循环结构,其中反复执行的步骤称为循环体.常见的循环结构的框图对应为:<教师备案>1.在画程序框图时,从开始框沿箭头必须能到达结束框,特别是条件分支结构应沿每条支路都能到达结束框,流程线必须加箭头表示顺序.2.对于循环结构有如下需要注意的情况:⑴循环结构非常适合计算机处理,因为计算机的运算速度非常快,执行成千上万次的重复计算,只不过是一瞬间的事,且能保证每次的结果都正确;⑵循环结构要有中止循环体的条件,不能无休止的运算下去,循环结构中一定包含条件结构,如i n≤就是中止循环的条件;⑶循环结构的关键是,要理解“累加变量”和“用1i 代替i”,S是一个累加变量,i是计数变量,每循环一次,S和i都要发生变化,这两步要重复计算若干次;⑷一种循环结构是先判断i n≤是否成立,若是,执行循环体;若否,则中止循环,像这样,每次执行循环体前对控制循环条件进行判断,条件满足时执行循环体,不满足则停止,称为当型循环.除了当型循环外,常用的循环结构还有直到型循环.5.程序框图的概念:用一些通用的图形符号构成的一张图来表示算法,称为程序框图(简称框图).常用图形符号:<教师备案>1.画程序框图的规则:⑴ 使用标准的框图的符号;⑵ 框图一般按从上到下、从左到右的方向画;⑶ 除判断框外,大多数框图符号只有一个进入点和一个退出点.判断框是具有超过一个退出点的惟一符号;⑷ 一种判断框是“是”与“不是”两分支的判断,而且有且仅有两个结果;另一种是多分支判断,有几种不同的结果;⑸ 在图形符号内描述的语言要非常简练清楚.2.画程序框图要注意的几点:⑴起、止框是任何流程不可少的,表示程序的开始和结束; ⑵输入、输出框可以用在算法中任何需要输入、输出的位置; ⑶算法中间要处理数据或计算,可分别写在不同的处理框内;⑷当算法要求你对两个不同的结果进行判断时,要写在判断框内; ⑸一个算法步骤到另一个算法步骤用流程线连结;⑹如果一个框图需要分开来画,要在断开处画上连结点,并标出连结的号码.如:用海伦公式求任意三角形的面积的程序框图,其中断开处画上连结点,并标出连结的号码.(1)(1)二.基本算法语句Basic语言(A版)1.将算法转变成计算机能够理解和能在计算机上实现的程序,这就需要程序语言,每一种程序语言都包含一些基本的语句,程序语言的基本语句结构:输入语句、输出语句、赋值语句、条件语句、循环语句.2.赋值语句:表明赋给某一个变量一个具体的确定值的语句.一般格式:变量=表达式.其中,“=”叫做赋值号.作用:先计算出赋值号右边表达式的值,然后将它赋给左边的变量,使该变量的值等于表达式的值.3.输入语句:在每次程序运行时,用于输入相应的初始数据的语句,我们主要介绍键盘输入语句.一般格式:INPUT “提示内容”;变量例:INPUT “Maths=”;a,INPUT “Chinese=”;bc=(a+b)/2END表示输入数学与语文的成绩,其中c表示它们的平均数.4.输出语句:以某种形式把求解结果输出的语句.一般格式:PRINT “提示内容”;表达式如上例中输出平均成绩可以用:PRINT “The average=”;(a+b)/25.条件语句:处理条件结构的算法语句.有以下两种基本格式:一般格式1:IF 条件THEN语句体END IF计算机执行语句时,先对IF后的条件进行判断,如果(IF)条件符合,那么(THEN)执行语句体,否则执行END IF之后的语句.一般格式2:IF 条件THEN语句体1ELSE语句体2END IF计算机执行语句时,先对IF后条件进行判断,如果(IF)条件符合,那么(THEN)执行语句体1,否则(ELSE)执行语句体2.6.循环语句:处理算法中的循环结构的语句;有两种基本语句:UNTIL语句和WHILE语句,前者称为直到型循环语句,后者称为当型循环语句.UNTIL语句:DO循环体LOOP UNTIL 条件WHILE语句的一般格式:WHILE 条件循环体WENDScilab程序语言(B版)1.将算法转变成计算机能够理解和能在计算机上实现的程序,这就需要程序语言,每一种程序语言都包含一些基本语句,程序语言的基本语句结构:输入语句、输出语句、赋值语句、条件语句、循环语句.2.赋值语句:表明赋给某一个变量一个具体的确定值的语句.一般格式:变量名=表达式;其中“=”叫做赋值号.作用:先计算出赋值号右边表达式的值,然后将它赋给左边的变量,使该变量的值等于表达式的值.3.输入语句:在每次程序运行时,用于输入相应的初始数据的语句,我们主要介绍键盘输入语句. Scilab 中的输入语句常用的是:“input”; 一般格式:变量名=input (“提示内容”) 例:a=input (“x1”);b=input (“x2”);aver=(a+b )/2表示输入1x ,2x 的值,求它们的算术平均数, 在Scilab 界面内运行结果如下: -->a=input ("x1");b=input ("x2");aver=(a+b )/2 x1-->此时通过键盘输入x1的值,如4,再按“Enter”键,界面出现: x2-->输入x2的值,如6,再按“Enter”键,这时界面出现: aver = 5.4.输出语句:以某种形式把求解结果输出的语句.Scilab 中有:print ,write ,format ,printf ,disp 等输出语句,主要介绍print 语句: 一般格式:print (%io (2),表达式);其中参数%io (2)表示在屏幕上输出. 5.条件语句:处理条件分支结构的算法语句. Scilab 程序语言中常用的条件语句为if 语句. 一般格式:if 表达式语句序列1; else语句序列2; end最简格式:if 表达式语句序列1; end6.循环语句:处理算法中的循环结构的语句; Scilab 有两种循环语句:for 循环和while 循环. for 循环的格式:for 循环变量=初值:步长:终值循环体; endwhile 语句的一般格式:while 表达式(即条件)循环体; end<教师备案>1.计算机能够直接或间接理解的程序语言有很多种,比如C 语言,Basic 语言,以及一些应用数学软件:Matlab ,Mathsmatics ,Scilab 对应的计算机语言.这里的基本语句结构在这些语言中都是存在的,但是对应不同的程序语言,都会有自己的输入指令与方法.这里是以一种语言为例,让大家理解程序语句的含义,为以后深入学习程序设计打下基础. 2.赋值语句:⑴赋值号左边只能是变量名,而不是表达式;如3m =是错误的; ⑵赋值号左右不能对换,是将赋值号右边的表达式的值赋给左边的变量;如x y =表示用y 的值替代变量x 原先的值,与y x =不同;⑶不能利用赋值语句进行代数式(或符号)的演算;如21(1)(1)y x x x =-=+-是不能实现的;并且在一个赋值语句中,只能给一个变量赋值;⑷赋值号与数学中的等号的意义不同,执行赋值语句后,右面表达式的值会赋给左边,如果左边变量原来有一个值,会自动被冲掉,如1N N =+表示将N 的原值加1再赋给N ,即N 的值加1.3.输入语句:在某些算法中,变量的初值要根据情况经常地改变,一般我们把程序与初始数据分开,每次算题时,即使初始数据改变,也不必改变程序部分,只要程序运行时,输入相应的数据即可,这个过程在程序语言中,用“输入语句”来控制.输入语句中还有read输入语句等.输入语句要求输入的一般都是具体的常数,也可输入单个或多个字符,格式为:变量名=input(“提示内容”,“string”),string表示输入字符型变量.4.循环语句:for语句:先把初值赋给循环变量,记下终值和步长,循环变量增值到超过终值时,执行end后面的语句,不超过时,执行for后面的语句;循环变量起计数作用,控制算法中循环次数,有初值与终值,步长是指循环变量每次增加的值,步长为1时,可以省略;while语句:先判断条件是否成立,并在符合条件时,执行循环体;直到某次不符合时,跳到end后面的语句.对应的基本框图是:5.在程序语言中,乘、除、乘方、求平方根、绝对值,分别用下列符号表示:*、/、^、sqrt()、abs ().程序语言中,一般“=”为赋值号,“==”表示等号.≥、≤、≠分别写成:>=、<=、<>.在程序中,如果赋值语句后面用分号隔开,则被赋值的变量不会输出,一般不随便使用逗号或句号,而是直接使用回车或空格.在Scilab语句中,变量名一般用一个字母表示,不可以用几个字母表示.如可以用s表示变量名,但不能用sum表示变量名,但在有些程序语言中,可以用多个字母表示变量名.三.算法案例1.更相减损术——求两个整数的最大公约数的算法如何找到一种算法,对任意两个正整数都能快速地求出它们的最大公约数呢?更相减损术的步骤:以两个数中较大的数减去较小的数,以差数和较小的数构成一对新的数,对这一对数再用大数减小数,以同样的操作一直做下去,直到产生一对相等的数,此数就是这两个数的最大公约数.等值算法:用“更相减损术”设计出来的算法求最大公约数的算法称为“等值算法”,用等值算法可以求任意两个正整数的最大公约数.<教师备案>《九章算法》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数.以具体的例子来说明更相减损术求最大公约数的原理:以求117和182的最大公约数为例:,,,,,,,,(117182)(11765)(6552)(5213)(1339)(1326)(1313)→→→→→→每次操作后得到的两个数与前两个数的最大公约数相同,而且逐渐减少,故总能得到相等的两个数,即为所求的最大公约数.2.辗转相除法又称欧几里得算法,是由欧几里得在公元前300年左右首先提出来的求两个数的最大公约数的算法。