高中数学高一数学期末三校联考试卷

2024—2025学年度上学期高三10月联合教学质量检测高三数学试卷本试卷共5页 满分150分，考试用时120分钟注意事项：1. 答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码贴在答题卡上的指定位置.2. 选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.3. 非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.4. 考试结束后，请将本试卷和答题卡一并上交.一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题所给的四个选项中，只有一项是符合题目要求的）1. 已知集合{}21A x x =-<，{}3B x a x a =<<+，若{}15A B x x ⋃=<<，则a =（）A. 0B. 1C. 2D. 3【答案】C 【解析】【分析】先求出集合A ，再根据并集得出参数的值.【详解】因为()1,3A =,()1,5A B ⋃=，又因为(),3B a a =+，所以35,a +=即a =2.故选：C.2. 如图，在ABC V 中，点D 是BC 边的中点，3AD GD = ，则用向量AB ，AC表示BG 为（ ）A. 2133BG AB AC=-+u u u u r uu r u u u r B. 1233BG AB AC=-+u u u r u uu r u u u r C. 2133BG AB AC=-u u u r u u u r u u u r D. 2133BG AB AC=+u u u r u u u r u u u r【答案】A 【解析】【分析】利用向量的线性运算求解即可.【详解】3AD GD =，故23AG AD = ，则()2212133233B C G BA BA BA AG AD AB A AB AC =+=+=+⨯+=-+.故选：A3. 在等比数列{}n a 中，记其前n 项和为n S ，已知3212a a a =-+，则84S S 的值为（ ）A. 2 B. 17 C. 2或8D. 2或17【答案】D 【解析】【分析】根据等比数列通项公式求得1q =或2q =-，再利用等比数的求和公式求解即可.【详解】解：由等比数列的通项公式可得21112a q a q a =-+，整理得220q q +-=，解得1q =或2q =-．当q =1时，1841824S a S a ==；当2q =-时，()()814844184111117111a q S q q q S q a q q ---====-+--．所以84S S 的值为2或17．故选：D ．4. 每年10月1日国庆节，根据气象统计资料，这一天吹南风的概率为25%，下雨的概率为20%，吹南风或下雨的概率为35%，则既吹南风又下雨的概率为（ ）A. 5% B. 10%C. 15%D. 45%【答案】B 【解析】【分析】根据概率公式直接得出结论.【详解】由题知，既吹南风又下雨的概率为25%20%35%10%+-=.故选:B5. 若直线:3l y kx k =+-与曲线:C y =恰有两个交点，则实数k 的取值范围是（ ）A. 4,+3∞⎛⎫⎪⎝⎭B. 43,32⎛⎤⎥⎝⎦C. 40,3⎛⎫ ⎪⎝⎭D. 43,32⎡⎫⎪⎢⎣⎭【答案】B 【解析】【分析】先得到直线过定点()1,3P ，作出直线l 与曲线C ，由图求出直线l 过点()1,0A -时的斜率和直线l 与曲线C 相切时的斜率即可树形结合得解.【详解】由()313y kx k k x =+-=-+可知直线l 过定点()1,3P ，曲线:C y =两边平方得()2210x y y +=≥，所以曲线C 是以()0,0为圆心，半径为1且位于直线x 轴上方的半圆，当直线l 过点()1,0A -时，直线l 与曲线C 有两个不同的交点，此时3032k k k =-+-⇒=，当直线l 与曲线C 相切时，直线和圆有一个交点，圆心()0,0到直线l的距离1d ，两边平方解得43k =，所以结合图形可知直线l 与曲线C 恰有两个交点，则4332k <≤.故选：B.6. 已知()ππsin 0,32f x x ωϕωϕ⎛⎫⎛⎫=++>< ⎪⎪⎝⎭⎝⎭为偶函数，()()sin g x x ωϕ=+，则下列结论不正确的A. π6ϕ=B. 若()g x 的最小正周期为3π，则23ω=C. 若()g x 在区间()0,π上有且仅有3个最值点，则ω的取值范围为710,33⎛⎫⎪⎝⎭D. 若π4g ⎛⎫= ⎪⎝⎭，则ω的最小值为2【答案】D 【解析】【分析】先根据()f x 是偶函数求ϕ判断A 选项；根据最小正周期公式计算可以判断B 选项；据有且仅有3个最值点求范围判断C 选项；据函数值求参数范围结合给定范围求最值可以判断D 选项.【详解】()ππsin 0,32f x x ωϕωϕ⎛⎫⎛⎫=++>< ⎪⎪⎝⎭⎝⎭为偶函数，则πππππ,Z,,,3226k k ϕϕϕ+=+∈<∴=∣∣A 选项正确；若()g x 的最小正周期为3π，由()sin()g x x ωϕ=+则2π23π,3T ωω==∴=，B 选项正确；πππ(0,π),(,π)666x x ωω∈+∈+ 若()g x 在区间()0,π上有且仅有3个最值点，则5ππ7π710π,26233ωω<+≤<≤,C 选项正确；若π()sin(6g x x ω=+ πππsin +446g ω⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，则πππ+2π463k ω=+或ππ2π+2π463k ω=+，Z k ∈，则 283k ω=+或28,Z k k ω=+∈，又因为0ω>，则ω的最小值为23，D 选项错误.故选:D.7. 已知()612a x x x ⎛⎫-- ⎪⎝⎭的展开式中，常数项为1280-，则a =（ ）A. ―2B. 2C. D. 1【解析】【分析】根据已知条件，结合二项式定理并分类讨论，即可求解.【详解】由题意，62a x x ⎛⎫- ⎪⎝⎭的通项公式为()()6662166C 2C 2rr r r r rr r a T x a x x ---+-⎛⎫=⋅=- ⎪⎝⎭，令620r -=，则3r =，令621r -=-，则72r =不符合题意，所以()612a x x x ⎛⎫-- ⎪⎝⎭的常数项为()3336C 21280a --=-，解得2a =-．故选：A .8. 已知函数22()log f x x mx x =-+，若不等式()0f x >的解集中恰有两个不同的正整数解，则实数m的取值范围是（ ）A. 23log 33,89+⎡⎫⎪⎢⎣⎭B. 23log 33,94+⎛⎫⎪⎝⎭C. 23log 33,94+⎡⎫⎪⎢⎣⎭ D. 23log 33,89+⎛⎫⎪⎝⎭【答案】C 【解析】【分析】不等式()0f x >可化为2log 1xmx x-<，利用导数分析函数()2log x g x x =的单调性，作函数()1h x mx =-，()2log xg x x=的图象，由条件结合图象列不等式求m 的取值范围.【详解】函数22()log f x x mx x =-+的定义域为(0,+∞)，不等式()0f x >化为：2log 1xmx x-<．令()1h x mx =-，()2log x g x x=，()2222221log e log log e log x xx x g x x x --='=，故函数()g x 在()0,e 上单调递增，在()e,∞+上单调递减．当1x >时，()0g x >，当1x =时，()0g x =，当01x <<时，()0g x <，当x →+∞时，()0g x →，当0x >，且0x →时，()g x ∞→-，画出()g x 及()h x 的大致图象如下，因为不等式()0f x >的解集中恰有两个不同的正整数解，故正整数解为1,2．故()()()()2233h g h g ⎧<⎪⎨≥⎪⎩，即22log 2212log 3313m m ⎧-<⎪⎪⎨⎪-≥⎪⎩，解得23log 3943m +≤<.故选：C.二、多项选择题（本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对得6分，部分选对的得部分分，有选错的得0分）9. 已知复数232023i i i i 1iz ++++=+ ，则下列结论正确的是（ ）A. 1i 2z -=-B. 1i 2z -=C. 1i 2z +=-D. z =【答案】ACD 【解析】【分析】利用234i+i +i +i 0=对分子化简，然后利用复数的除法化简，可求共轭复数、复数的模依次判断即可得出结果.【详解】因为i,411,42i ,i,431,4nn k n k k n k n k=+⎧⎪-=+⎪=∈⎨-=+⎪⎪=⎩Z ，所以234i+i +i +i 0=，所以()()()()2342323202323505i+i +i +i i i i 1i i i i i i i i 111i 1i 1i 1i 1i 1i 1i 22z +++--++++++-======-++++++- ，所以A 正确，B 错误，111i i=222z +=---，C 准确，所以z ==D 正确.故选：ACD10. “费马点”是由十七世纪法国数学家费马提出并征解的一个问题. 该问题是：“在一个三角形内求作一点，使其与此三角形的三个顶点的距离之和最小”.意大利数学家托里拆利给出了解答，当 ABC V 的三个内角均小于120°时，使得120AOB BOC COA ︒∠=∠=∠=的点O 即为费马点；当 ABC V 有一个内角大于或等于120°时，最大内角的顶点为费马点.下列说法正确的是（ ）A. 正三角形的的费马点是正三角形的中心B. 若P 为ABC V 的费马点, 且 0PA PB PC ++=u u r u u r u u u r r，则ABC V 一定为正三角形C. 若ABC V 三边长分别为2D. ABC V 的内角A ，B ，C 所对的边分别为a ，b ， c ， π22A ,bc ∠==，若点P 为ABC V 的费马点，则PA PB PB PC PC PA ⋅+⋅+⋅=.【答案】ABC 【解析】【分析】对A ，根据正三角形中心的性质结合费马点定义易判断；对B ，取AB 的中点D ，由0PA PB PC ++=可得点P 是ABC V 的重心，再结合条件可得点P 是ABC V 的中心，得证；对C ，利用三角形旋转，结合费马点定义，构造正三角形转化线段长求解；对D ，由向量数量积定义，结合费马点定义和三角形等面积法列式求解.【详解】对于A ，如图O 是正三角形ABC 的中心，根据正三角形的性质易得o 120AOB AOC BOC ∠=∠=∠=，所以点O 是正三角形ABC 的费马点，故A 正确；对于B ，如图，取AB 的中点D ，则2PA PB PD += ，因为0PA PB PC ++=，所以2PC PD =-u u u r u u u r，所以,,C P D 三点共线，且点P 是ABC V 的重心，又点P 是ABC V 费马点，则o 120APB APC BPC ∠=∠=∠=，则o 60APD BPD ∠=∠=，又AD BD =，易得PA PB =，同理可得PC PB =，所以PA PB PC ==所以点P 是ABC V 的外心，所以点P 是ABC V 的中心，即ABC V 是正三角形.故B 正确；对于C ，如图，在Rt ABC △中，1AB =，BC =，2AC =，o 30ACB ∠=，点O 是Rt ABC △的费马点，将COA 绕点C 顺时针旋转o 60，得到CED △，易证COE ，ACD 是正三角形，则OC OE =，OA DE =，CD AC =，且点,,,B O E D 共线，所以o90BCD ∠=，所以BD ===又OA OB OC DE OE OB DB ++=++==，的.故C 正确；对于D ，由费马点定义可得o 120APB APC BPC ∠=∠=∠=，设PA x =，PB y =，PC z =，,,0x y z >，由ABC PAB PAB PAB S S S S =++V V V V，可得111122222xy xz yz ++=⨯，整理得xy yz xz ++=，所以111222PA PB PB PC PC PA xy yz xz ⎛⎫⎛⎫⎛⎫⋅+⋅+⋅=⋅-+⋅-+⋅- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ()1122xy yz xz =-++=-=，故D 错误.故选：ABC.【点睛】关键点点睛：解答本题首先要理解费马点的含义，解答D 选项的关键在于利用三角形等面积法求出xy yz xz ++=.11. 在四面体ABCD 中，棱AB 的长为4，AB BD ⊥，CD BD ⊥，2BD CD ==，若该四面体的体积为）A. 异面直线AB 与CD 所成角的大小为π3B. AC的长可以为C. 点D 到平面ABCD. 当二面角A BC D --是钝角时，其正切值为【答案】ACD【解析】【分析】根据等体积法可结合三角形的面积公式可得sin CDE ∠=A ，根据余弦定理即可求解B ，根据等体积法即可求解C ，根据二面角的几何法，结合同角关系即可求解D.【详解】在平面ABD 内过D 作DE AB ∥，且ED AB =,由于AB BD ⊥，故四边形ABDE 为矩形，CD BD ⊥，DE BD ⊥，BD DE C = ，CD ⊂平面CDE ，DE ⊂平面CDE ，故BD ⊥平面CDE ，故11233C ABD C EDA B CDE CDE CDE V V V S BD S ---===⋅=⨯=，11sin 24sin 4sin 22CDE S CD DE CDE CDE CDE=⋅⋅∠=⨯⨯∠=∠故1124sin 233C ABD CDE V S CDE -=⨯=⨯∠⨯=，因此sin CDE ∠=由于()0,CDE π∠∈，所以3CDE π∠=或23π，由于CDE ∠为异面直线AB 与CD 所成角或其补角，故异面直线AB 与CD 所成角的大小为3π，A 正确，当23CDE π∠=时，CE ===,由于BD ⊥平面CDE ，AE BD ，∴AE ⊥平面CDE ，CE ⊂平面CDE ，故AE CE ⊥，此时AC ==当3CDE π∠=时，CE ===,由于BD ⊥平面CDE ，AE BD ，∴AE ⊥平面CDE ，CE ⊂平面CDE ，故AE CE ⊥，此时4AC ==,故B 错误，由于BC ==,4AB =,当AC =cos BAC ∠==sin BAC ∠=，11sin 422ABC S AB AC BAC =⋅⋅∠=⨯⨯= ,当4AC =时，161683cos 2444BAC +-∠==⨯⨯，故sin BAC ∠=，1sin 2ABC S AB AC BAC =⋅∠= ,故点D 到平面ABC的距离为d ===,C 正确，当4AC =时，4AB AC ==,2CD BD ==,取BC 中点为O ，连接OA ,OD ,则AOD ∠即为二面角A BC D --的平面角，12OD BC ===,AO ==所以22cos 0AOD ∠===<,故AOD ∠为钝角，符合题意，此时sin tan cos AODAOD AOD∠∠==∠，当4AC =，由于2DBCS =，点A 到平面BDC距离为d ===,设A 在平面BDC 的投影为H ,则AH =,故HD==HC ==,因此点O 为以D ,C为圆心，以半径为,显然交点位于BC ,同D 的一侧，故此时二面角A BC D --为锐角，不符合要求，故D 正确，故选：ACD三、填空题（本大题共3小题，每小题5分，共15分）12. 已知,a b +∈R ，41a b +=，则aba b+的最大值是________．【答案】19【解析】的【分析】先求出11a b+的最小值，再将aba b +化为111a b+，即可求得答案.【详解】因为,a b +∈R ，41a b +=，故()111144559b a a b a b a b a b ⎛⎫+=++=++≥+= ⎪⎝⎭，当且仅当4b a a b=，结合41a b +=，即11,63==a b 时等号成立，所以11119ab a b a b =≤++，即ab a b +的最大值是19，故答案为：1913. 刻画空间的弯曲性是几何研究的重要内容，在数学上用曲率刻画空间弯曲性．规定：多面体的顶点的曲率等于2π与多面体在该点的面角之和的差（多面体的面的内角叫做多面体的面角，角度用弧度制），多面体面上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和．例如：正四面体（四个面都是等边三角形围成的几何体）在每个顶点有3个面角，每个面角是π3，所以正四面体在每个顶点的曲率为π2π3π3-⨯=，故其总曲率为4π．我们把平面四边形ABCD 外的点P 连接顶点A 、B 、C 、D 构成的几何体称为四棱锥，根据曲率的定义，四棱锥的总曲率为______．【答案】4π【解析】【分析】根据曲率的定义求解即可.【详解】由定义可得多面体的总曲率2π=⨯顶点数各面内角和，因为四棱锥有5个顶点，5个面，分别为4个三角形和1个四边形，所以任意四棱锥的总曲率为()2π5π42π14π⨯-⨯+⨯=.故答案为：4π.14. 过双曲线22221(0,0)y x a b a b-=>>的上焦点1F ，作其中一条渐近线的垂线，垂足为H ，直线1F H 与双曲线的上､下两支分别交于,M N ，若3NH HM =，则双曲线的离心率e =__________.【解析】【分析】设双曲线右焦点为2F ，HM t =，3NH t =，由题意结合双曲线定义可依次求出1F H 、1OF 、1F M 、1F N 、2F N 和2F M ，接着分别在1Rt F OH 、12F MF △和12F NF △中结合余弦定理求出1cos OF M ∠，进而建立等量关系式求出t ，从而求得2b a =，进而由离心率公式即可得解.【详解】设双曲线右焦点为2F ，由题()10,F c ，双曲线的一条渐近线方程为ay x b=-即0ax by +=，过该渐近线作垂线，则由题1F H b =，1OF c =，设HM t =，则由题3NH t =，1F M b t =-，13F N b t =+，所以232F N b t a =+-，22F M b t a =-+，所以在1Rt F OH 中，111cos F H bOF M OF c∠==①，在12F MF △中，()()()()()22222211221112||||22cos 222F M F F F M b t c b t a OF M b t c F M F F +--+--+∠==-⋅②，在12F NF △中，()()()()()22222211221112||||3232cos 2322F N F F F N b t c b t a OF M b t c F N F F +-++-+-∠==+⋅③，由①②得()()()()()2222222b t c b t a bb tc c-+--+=-，化简解得ab t a b =+，由①③得()()()()()2223232232b t c b t a b b t c c++-+-=+，化简解得()3ab t b a =-，所以()23ab abb a a b b a =⇒=+-，故双曲线的离心率c e a====.【点睛】思路点睛：依据题意设双曲线右焦点为2F ，HM t =，则结合双曲线定义可得1Rt F OH 、12F MF △和12F NF △的边长均是已知的，接着结合余弦定理均可求出三个三角形的公共角1OF M ∠的余弦值1cos OF M ∠，从而可建立等量关系式依次求出t 和2b a =，进而由离心率公式得解.四、解答题（本大题共5小题，共77分.解答应写出必要的文字说明、证明过程或演算步骤）15. 设n S 为数列{}n a 的前n 项和，满足()*1N n n S a n =-∈.（1）求数列{}n a 的通项公式；（2）记22212n n T S S S =+++ ，求n T .【答案】（1）1()2n n a = （2）1235111((3232n nn n T --=+-⋅【解析】【分析】（1）应用1n n n S S a --=，再结合等比数列定义及通项公式计算即可；（2）先化简得出21111()()24n n n S --+=，再应用分组求和及等比数列前n 项和公式计算.小问1详解】因为数列{a n }的前n 项和，满足1n n S a =-，当2n ≥时，可得111n n S a --=-，两式相减得1n n n a a a -=-，即12n n a a -=，所以112n n a a -=，令1n =，可得1111S a a =-=，解得112a =，所以数列{a n }构成首项为12，公比为12的等比数列，所以{a n }的通项公式为1111()(222n nn a -=⋅=.【小问2详解】由（1）知1(2nn a =，可得11(2nn S =-，所以222111111()]12()()1((22224[1n n n n n n S -=-⋅=+=-+-，【则222121111()[1()]244(111)111124n n n n T S S S -⋅-=+++=+++-+-- 1235111()()3232n n n --=+-⋅.16. 如图，正四棱台ABCD EFGH -中，24,EG AC MN ==上为上下底面中心的连线，且MN 与侧面.（1）求点A 到平面MHG 的距离；（2）求二面角E HM G --的余弦值.【答案】（1（2）23-【解析】【分析】（1）由题意建立空间直角坐标系，求得平面法向量，利用点面距向量公式，可得答案；（2）求得两个平面的法向量，利用面面角的向量公式，可得答案.【小问1详解】由题意，易知,,MN MA MB 两两垂直，分别以,,MA MB MN 为,,x y z 轴建立直角坐标系，如下图：则()()()()1,0,0,0,0,0,0,2,1,2,0,1A M H G --，取()()0,2,1,2,0,1MH MG =-=-，设平面MHG 的法向量(),,n x y z = ，则2020n MH y z n MG x z ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩，令2z =，则1,1x y ==，所以平面MHG 的一个法向量()1,1,2n =，取()1,0,0MA = ，点A 到平面MHG的距离MA n d n ⋅===.【小问2详解】由（1）可知()()()()2,0,1,0,2,1,0,0,0,2,0,1E H M G --，取()()()()2,2,0,2,0,1,2,2,0,2,0,1HE ME HG MG ===-=-，设平面EHM 的法向量()1111,,m x y z = ，则11111122020m HE x y m ME x z ⎧⋅=+=⎪⎨⋅=+=⎪⎩ ，令11x =-，则221,2y z ==，所以平面EHM 的一个法向量()11,1,2m =-，设平面HMG 的法向量()2222,,m x y z = ，则22222222020m HG x y m MG x z ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩ ，令21x =，则111,2y z ==，所以平面EHG 的一个法向量()21,1,2m =，设二面角E HM G --的大小为θ，则12121142cos 1143m m m m θ⋅-++=-=-=-++⋅ .17. 某汽车公司最新研发了一款新能源汽车，并在出厂前对100辆汽车进行了单次最大续航里程（理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程）的测试.现对测试数据进行整理，得到如下的频率分布直方图：（1）估计这100辆汽车的单次最大续航里程的平均值x （同一组中的数据用该组区间的中点值代表）；（2）由频率分布直方图计算得样本标准差s 的近似值为49.75.根据大量的汽车测试数据，可以认为这款汽车的单次最大续航里程X 近似地服从正态分布()2,N μσ，其中μ近似为样本平均数x ，σ近似为样本标准差S.（ⅰ）利用该正态分布，求()250.25399.5P X <<；（ⅱ）假设某企业从该汽车公司购买了20辆该款新能源汽车，记Z 表示这20辆新能源汽车中单次最大续航里程位于区间（250.25，399.5）的车辆数，求E （Z ）；参考数据：若随机变量ξ服从正态分布()2,N μσ，则()0.6827P μσξμσ-<<+=，()()220.9545,330.99731P P μσξμσμσξμσ-<<+=-<<+=.（3）某汽车销售公司为推广此款新能源汽车，现面向意向客户推出“玩游戏，送大奖”活动，客户可根据抛掷硬币的结果，操控微型遥控车在x 轴上从原点O 出发向右运动，已知硬币出现正、反面的概率都12，客户每掷一次硬币，遥控车向右移动一次，若掷出正面，则遥控车向移动一个单位，若掷出反面，则遥控车向右移动两个单位，直到遥控车移到点（59，0）（胜利大本营）或点（60，0）（失败大本营）时，游戏结束，若遥控车最终停在“胜利大本营”，则可获得购车优惠券.设遥控车移到点(),0n 的概率为()160n P n ≤≤，试证明数列{}1n n P P --是等比数列()259n ≤≤，求出数列{}()160n P n ≤≤的通项公式，并比较59P 和60P 的大小.【答案】（1）300 （2）（ⅰ）0.8186；（ⅱ）16.372（3）证明见解析，158211,159362111,60362n n n P n -⎧⎛⎫-⋅-≤≤⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪+⋅= ⎪⎪⎝⎭⎩，5960P P >【解析】【分析】（1）根据平均数的求法求得正确答案.（2）（ⅰ）根据正态分布的对称性求得正确答案.（ⅱ）根据二项分布的知识求得正确答案.（3）根据已知条件构造等比数列，然后利用累加法求得n P ，利用差比较法比较59P 和60P 的大小.【小问1详解】2050.12550.23050.453550.24050.05300x ≈⨯+⨯+⨯+⨯+⨯=.【小问2详解】（ⅰ）0.95450.6827(250.25399.5)0.68270.81862P X -<<=+=.（ⅱ））∵Z 服从二项分布()20,0.8186B ，∴()200.818616.372E Z =⨯=.【小问3详解】当359n ≤≤时，()12112111,222n n n n n n n P P P P P P P -----=+-=--，1221111131,,222244P P P P ==⨯+=-=.∴{}1(259)n n P P n --≤≤是以14为首项，12-为公比的等比数列，2111(259)42n n n P P n --⎛⎫-=⋅-≤≤ ⎪⎝⎭.22132111111,,,(259)44242n n n P P P P P P n --⎛⎫⎛⎫-=-=⋅-⋯-=⋅-≤≤ ⎪⎪⎝⎭⎝⎭.累加得：115816058111422111111,(259),1362236212n n n n P P P n P P --⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎛⎫⎛⎫⎝⎭-==-⋅-≤≤==+⋅ ⎪ ⎪⎝⎭⎝⎭+.∴158211,159362111,60362n n n P n -⎧⎛⎫-⋅-≤≤⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪+⋅= ⎪⎪⎝⎭⎩∵58585960111111033232P P ⎛⎫⎛⎫⎛⎫-=-⨯=-> ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，∴5960P P >.注：比较59P 和60P 的另一个过程：58596059592112111,13623622P P P P ⎛⎫=-⋅>-==-<< ⎪⎝⎭.18. 已知函数()1e xx f x +=.（1）求函数()f x 的极值；（2）若不等式()e ln 1xf x a x +≥恒成立，求实数a 的取值范围；（3）已知直线l 是曲线()y f x =在点()(),t f t 处的切线，求证：当1t >时，直线l 与曲线()y f x =相交于点()(),s f s ，其中s t <.【答案】（1）极大值为1，没有极小值 （2）[]e,0- （3）证明见解析【解析】【分析】（1）求导，利用导数判断()f x 的单调性和极值；（2）根据题意可得ln 0x a x +≥恒成立，构建()ln ,0g x x a x x =+>，分类讨论a 的符号，利用导数求最值，结合恒成立问题分析求解；（3）根据导数的几何意义可得当1t >时，方程2110e e ex t tx tx t t ++++-=有小于t 的解，构建()211e e ex t tx tx t t h x +++=+-，其中x t <，1t >，利用导数研究函数零点分析证明.小问1详解】由题意可知：()f x 的定义域为R ，且()ex xf x '-=，令()0f x '=时，0x =，则x ，f ′(x )，()f x 的关系为x(),0∞-0(0,+∞)f ′(x )+0-()f x 单调递增极大值单调递减所以，当0x =时，()f x 取到极大值为1，没有极小值.【小问2详解】若()e ln 1xf x a x +≥，即ln 0x a x +≥恒成立，设()ln ,0g x x a x x =+>，则()1a x a g x x x'+=+=，①当0a =时，则()0g x x =>恒成立，符合题意；②当0a >时，则()0g x '≥，可知()g x 在(0,+∞)上单调递增，因为11e e 10a a g --⎛⎫=-< ⎪⎝⎭，所以ln 0x a x +≥不恒成立；③当0a <时，x ，()g x '，()g x 的关系为x()0,a -a-(),a ∞-+()g x '-+【()g x 单调递减极小值单调递增可知()g x 的最小值为()()min ln g x a a a =-+-，则()ln 0a a a -+-≥，因为0a <，则()1ln 0a --≥，解得e 0a ≤-<；综上所述：实数a 的取值范围是[]e,0-.【小问3详解】因为()1e x x f x +=，()e x x f x '-=，则()1e t tf t +=，e t t k -=即切点坐标为1,e t t t +⎛⎫⎪⎝⎭，切线l 斜率为e tt k -=，可得l 的方程为()1e e t t t t y x t +--=-，即21e et tt t t y x -++=+，联立方程21e e 1e t txt t t y x x y ⎧-++=+⎪⎪⎨+⎪=⎪⎩，可得2110e e e x t tx tx t t ++++-=，由题可知：当1t >时，方程2110e e ex t tx tx t t ++++-=有小于t 的解，设()211e e ex t tx tx t t h x +++=+-，其中x t <，1t >且()0h t =，则()e e x t x t h x '-=+，设()()F x h x ='，则()1e xx F x '-=，因为1t >，x ，()F x '，F (x )的关系为x(),1∞-1()1,t ()F x '-+F (x )单调递减1e et t -+，单调递增可知F (x )的最小值()()()min 10F x F F t =<=，且()1e 0e ttF -=+>，可知()01,1x ∃∈-，使()00F x =，当()0,x x ∞∈-时，()0F x >，即h ′(x )>0；当()0,x x t ∈时，()0F x <，即h ′(x )<0；可知h (x )在()0,x ∞-内单调递增；在()0,x t 内单调递减，可知h (x )的最大值()()()0max 0h x h x h t '=>=，且()()2110e t t h -+-=<，可知h (x )存在小于t 的零点，所以当1t >时，直线l 与曲线y =f (x )相交于点()(),s f s ，其中s t <，得证.【点睛】方法点睛：两招破解不等式的恒成立问题（1）分离参数法第一步：将原不等式分离参数，转化为不含参数的函数的最值问题；第二步：利用导数求该函数的最值；第三步：根据要求得所求范围．（2）函数思想法第一步：将不等式转化为含待求参数的函数的最值问题；第二步：利用导数求该函数的极值；第三步：构建不等式求解．19. 蝴蝶定理因其美妙的构图，像是一只翩翩起舞的蝴蝶，一代代数学名家蜂拥而证，正所谓花若芬芳蜂蝶自来．如图，已知圆M 的方程为222()x y b r +-=，直线x my =与圆M 交于()11,C x y ，()22,D x y ，直线x ny =与圆M 交于()33,E x y ，()44,F x y ．原点O 在圆M 内．设CF 交x 轴于点P ，ED 交x 轴于点Q ．（1）当0b =，r =，12m =-，2n =时，分别求线段OP 和OQ 的长度；（2）①求证：34121234y y y y y y y y ++=．②猜想|OP |和|OQ |的大小关系，并证明．【答案】（1）53OP OQ == （2）①证明见解析；②猜测OP OQ =，证明见解析.【解析】【分析】（1）联立直线与圆的方程，可求,,,C D E F 各点的坐标，利用直线的两点式方程，可得直线CF 和ED 的方程，并求它们与x 轴的交点坐标，可得问题答案.（2）①联立直线与圆的方程，求出两根之和与两根之积，找到相等代换量，从而证明成立.②分别求出点P 和点Q 的横坐标表达式，结合①中的结论，从而证明成立.【小问1详解】当0b =，r =，12m =-，2n =时，圆M ：225x y +=，直线CD ：12x y =-，由22512x y x y ⎧+=⎪⎨=-⎪⎩⇒12x y =⎧⎨=-⎩或12x y =-⎧⎨=⎩，故()1,2C -，()1,2D -；直线EF ：2x y =，由2252x y x y⎧+=⎨=⎩⇒21x y =⎧⎨=⎩或21x y =-⎧⎨=-⎩，故()2,1E ，()2,1F --.所以直线CF :122112y x ++=+-+，令0y =得53x =-，即5,03P ⎛⎫- ⎪⎝⎭；直线ED :122112y x --=---，令0y =得53x =，即5,03Q ⎛⎫ ⎪⎝⎭.所以：53OP OQ ==.【小问2详解】①由题意：22b r <.由()222x y b r x my ⎧+-=⎪⎨=⎪⎩⇒()()222my y b r +-=⇒()2222120m y by b r +-+-=，则1y ，2y 是该方程的两个解，由韦达定理得：12222122211b y y m b r y y m ⎧+=⎪⎪+⎨-⎪⋅=⎪+⎩，所以1222122y y b y y b r +=⋅-.同理可得：3422342y y b y y b r +=⋅-，所以34121234y y y y y y y y ++=⋅⋅.②猜测OP OQ =，证明如下：设点(),0P p ，(),0Q q .因为,,C P F 三点共线，所以：414100y y x p x p --=--⇒411414x y x y p y y -=-，又因为点C 在直线x my =上，所以11x my =；点F 在直线x ny =上，所以44x ny =.所以()1441141414y y n m ny y my y p y y y y --==--；同理因为,,E Q D 三点共线，可得：()2323y y n m q y y -=-.由①可知：34121234y y y y y y y y ++=⋅⋅⇒12341111y y y y +=+⇒14321111y y y y -=-⇒23411423y y y y y y y y --=⋅⋅⇒231414230y y y y y y y y ⋅⋅+=--， 所以()()14231423y y n m y y n m p q y y y y --+=+--()23141423y y y y n m y y y y ⎛⎫=-+ ⎪--⎝⎭0=.即p q =-，所以OP OQ =成立.【点睛】关键点点睛：本题的关键是联立直线与圆的方程，结合一元二次方程根与系数的关系，进行化简处理，设计多个字母的运算，整个运算过程一定要小心、仔细.。

新人教A版辽宁三校高一下学期数学期末考试卷少向左平移()个单位.A. B. C. D.12.阅读程序框图，当输入x的值为-25时，输出x的值为()A.-1B.1C.3D.9卷Ⅱ二、填空题(本大题共4个小题，每空5分，共20分，把正确答案填在题中横线上)13.已知14. 若为锐角，且sin6=13，则sin的值为________.15.在△ABC中，已知BAC=60，ABC=45，BC= ，则AC=16.定义在R上的偶函数f(x)是最小正周期为的周期函数，且当时，，则的值是三、解答题(本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤)17.(本小题满分10分)已知(1)化简 ;(2)若是第三象限角，且cos( )= ，求的值.本文导航 1、首页2、高一下学期数学期末考试卷-23、高一下学期数学期末考试卷-318. (本小题满分12分)如图，某中学甲、乙两班共有25名学生报名参加了一项测试.这25位学生的考分编成的茎叶图，其中有一个数据因电脑操作员不小心删掉了(这里暂用x来表示)，但他清楚地记得两班学生成绩的中位数相同.(1)求这两个班学生成绩的中位数及x的值;(2)如果将这些成绩分为优秀(得分在175分以上，包括175分)和过关，若学校再从这两个班获得优秀成绩的考生中选出3名代表学校参加比赛，求这3人中甲班至多有一人入选的概率.19. (本小题满分12分) 已知函数f(x)=2sinx4cosx4+3cosx2.(1)求函数f(x)的最小正周期及最值;(2)令g(x)=f x+3，判断函数g(x)的奇偶性，并说明理由.20.(本小题满分12分) 在△ABC中，中线长AM=2.(1)若OA=-2OM，求证：OA+OB+OC(2)若P为中线AM上的一个动点，求PA(PB+PC)的最小值.21. (本小题满分12分)在△ABC中，a，b，c分别为内角A，B，C的对边，且2asinA=(2b+c)sinB+(2c+b)sinC.(1)求A的大小;(2)求sinB+sinC的最大值.22. (本小题满分12分)设函数f(x)=sin(2x+0)，y=f(x)图象的一条对称轴是直线x=8.(1)求(2) 求函数y=f(x)的单调增区间;(3)画出函数y=f(x)在区间[0，]上的图象.2019年新人教A版辽宁三校高一下学期数学期末考试卷，愿考生学业有成。

杭高2023学年第一学期期末考试高一数学参考答案（答案在最后）命题：1.本试卷分试题卷和答题卡两部分.本卷满分150分，考试时间120分钟.2.答题前务必将自己的学校、班级、姓名用黑色字迹的签字笔或钢笔填写在答题卡规定的地方.3.答题时，请按照答题卡上“注意事项”的要求，在答题卡相应的位置上规范答题，在本试题卷上答题一律无效.4.考试结束后，只需上交答题卡.第Ⅰ卷一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若角α终边上一点()43P ,-，则sin α=（）A.3 B.45-C.35D.34-【答案】C 【解析】【分析】根据三角函数的定义可求sin α的值.【详解】因为()43P ,-，故5OP =，故3sin 5α=，故选：C.2.已知2log 0.5a =，0.52b =，sin 2c =，则,,a b c 的大小关系为（）A.a b c <<B.b<c<aC.c<a<bD.a c b<<【答案】D 【解析】【分析】分别利用函数2log y x =、2x y =和sin y x =的单调性，对“2log 0.5a =，0.52b =，sin 2c =”三个因式进行估值即可.【详解】因为函数2log y x =是增函数，且0.51<，则22log 0.5log 10a =<=，因为函数2x y =是增函数，且0.50>，则0.50221b =>=，因为正弦函数sin y x =在区间π3π[,22上是减函数，且π2π2<<，所以π0sin πsin 2sin 12c =<=<<，所以a c b <<，故选：D.3.函数2lg 43()()f x x x =+-的单调递减区间是（）A.3,2⎛⎤-∞ ⎥⎝⎦B.3,2⎡⎫+∞⎪⎢⎣⎭C.31,2⎛⎤- ⎥⎝⎦D.3,42⎡⎫⎪⎢⎣⎭【答案】D 【解析】【分析】计算出函数定义域后结合复合函数的单调性计算即可得.【详解】由()()243lg f x x x =+-可得，2430x x+->，解得()1,4x ∈-，故()f x 的定义域为()1,4-，由ln y x =为增函数，令243t x x =+-，对称轴为32x =，故其单调递减区间为3,42⎡⎫⎪⎢⎣⎭，所以()()243lg f x x x =+-的单调递减区间为3,42⎡⎫⎪⎢⎣⎭.故选：D.4.“01a <<且01b <<”是“log 0a b >”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据两者之间的推出关系可得条件关系.【详解】若01a <<且01b <<，则log log 10a a b >=，故log 0a b >成立，故“01a <<且01b <<”是“log 0a b >”的充分条件.若log 0a b >，则log log 1a a b >，故11a b >⎧⎨>⎩或0101a b <<⎧⎨<<⎩，故“01a <<且01b <<”不是“log 0a b >”的必要条件，故“01a <<且01b <<”是“log 0a b >”的充分不必要条件.故选：A.5.设函数()f x 51,11,1x x x a x -<⎧=⎨+≥⎩.若4()95f f ⎡⎤=⎢⎥⎣⎦，则a 等于（）A.12B.2C.13D.3【答案】B 【解析】【分析】按照从内到外的原则，先计算4()5f 的值，再代入4()95f f ⎡⎤=⎢⎥⎣⎦，即可求出a 的值.【详解】由于函数()f x 51,11,1x x x a x -<⎧=⎨+≥⎩，且415<，则44(51355f =⨯-=，且31>，所以34()(3)195f f f a ⎡⎤==+=⎢⎥⎣⎦，即38a =，得2a =.故选：B.6.已知函数()24f x x ax =-+在()1,2上有且只有一个零点，则实数a 的取值范围是（）A.[)8,10 B.()8,10 C.[)4,5 D.()4,5【答案】D 【解析】【分析】根据题意将零点问题转化为函数图象公共点问题进而求解答案即可.【详解】因为函数()24f x x ax =-+在()1,2上有且只有一个零点，所以24x ax +=，即4x a x+=在()1,2上有且只有一个实根，所以4y x x=+与y a =的函数图象在()1,2x ∈时有一个公共点，由于4y x x =+在()1,2单调递减，所以442121a +<<+，即45a <<.故选：D7.已知()()π2sin 03⎛⎫=+> ⎪⎝⎭f x x ωω在2π0,3⎛⎫⎪⎝⎭上单调递增，则ω的取值范围是（）A.(]0,4 B.10,4⎛⎤ ⎝⎦C.10,4⎛⎫ ⎪⎝⎭D.(]0,1【答案】B 【解析】【分析】先求出π3x ω+取值范围，再由()f x 在2π0,3⎛⎫⎪⎝⎭上单调递增得2πππ332ω+≤，最后结合题意求出ω的取值范围即可.【详解】因为2π0,3x ⎛⎫∈ ⎪⎝⎭，0ω>，所以ππ2ππ,3333x ω⎛⎫+∈+ ⎪⎝⎭，要使得()f x 在2π0,3⎛⎫ ⎪⎝⎭上单调递增，则2πππ332ω+≤，解得14ω≤，又由题意可知0ω>，所以104ω<≤，故选：B8.中国早在八千多年前就有了玉器，古人视玉为宝，玉佩不再是简单的装饰，而有着表达身份、感情、风度以及语言交流的作用.不同形状.不同图案的玉佩又代表不同的寓意.如图1所示的扇形玉佩，其形状具体说来应该是扇形的一部分（如图2），经测量知4AB CD ==，4BC =，8AD =，则该玉佩的面积为（）A.16π3- B.32π3-C.16π3D.32π3【答案】B【解析】【分析】取AD 的中点为M ，连接BM 、CM ，延长AB ，CD 交于点O ，利用平面几何知识得到扇形的圆心角，进而利用扇形面积公式和三角形的面积公式计算求得该玉佩的面积.【详解】如图，取AD 的中点为M ，连接BM ，CM ，延长AB ，CD 交于点O ，由题意，△AOB 为等腰三角形，又∵AB CD =，∴AD //BC ，又∵M 为AD 的中点，8,4AD BC ==，∴AM 与BC 平行且相等，∴四边形ABCM 为平行四边形，∴4MC AB ==，同理4CM AB ==，∴△ABM ，△CDM 都是等边三角形，∴△BOC 是等边三角形，∴该玉佩的面积138844234S π=⨯⨯⨯-⨯⨯=32π3-.故选：B.二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9.已知函数()f x 的图象是连续不断的，且有如下对应值表：x1234567()f x 4-2-1421-3-在下列区间中，函数()f x 必有零点的区间为（）A.(1,2)B.(2,3)C.(5,6)D.(5,7)【答案】BCD 【解析】【分析】根据零点存在定理可判断零点所在区间.【详解】由所给的函数值表知，()()()()()()()()120,230,560,570,f f f f f f f f ><<<由零点存在定理可知：()f x 在区间()()()2,3,5,6,5,7内各至少有一个零点，故选：BCD.10.设函数()πsin 2,6f x x x ⎛⎫=+= ⎪⎝⎭R ，若ππ,22α⎛⎫∈- ⎪⎝⎭，函数()f x α+是偶函数，则α的值可以是（）A.π6-B.π3-C.π6D.π3【答案】BC 【解析】【分析】由题意可得()πsin 226f x x αα⎛⎫+=++⎪⎝⎭，结合偶函数的性质与ππ,22α⎛⎫∈- ⎪⎝⎭计算即可得.【详解】()πsin 226f x x αα⎛⎫+=++ ⎪⎝⎭，又其为偶函数，则图像关于y 轴对称，则ππ2π,62k k α+=+∈Z ，得ππ,62k k α=+∈Z ，又ππ,22α⎛⎫∈- ⎪⎝⎭，则π6α=或π3α=-.故选：BC.11.已知函数())ln1f x x x =++.则下列说法正确的是（）A.()1lg3lg 23f f ⎛⎫+= ⎪⎝⎭B.函数()f x 的图象关于点()0,1对称C.对定义域内的任意两个不相等的实数12,x x ，()()12120f x f x x x -<-恒成立.D.若实数,a b 满足()()2f a f b +>，则0a b +>【答案】ABD 【解析】【分析】选项A 、B ，先利用函数解析式得出结论：()()2f x f x -+=，由于1lglg33=-，只需验证()()lg3lg32f f +-=是否成立即可；选项B ，需验证点()(,)x f x 和点()(,)x f x --关于点()0,1对称即可；选项C ，利用复合函数单调性的“同增异减”的原则判断即可；选项D ，将不等式()()2f a f b +>转化为()()()2f a f b f b >-=-的形式，借助函数()f x 单调性判断即可.【详解】对于A 、B 选项，对任意的x ∈R ，0x x x >+≥，所以函数())ln1f x x x =++的定义域为R ，又因为()())()1])1f x f x x x x x -+=+-++++22ln(1)22x x =+-+=，由于()()()1lg3lg lg3lg323f f f f ⎛⎫+=+-= ⎪⎝⎭，故A 正确；由于函数()f x 满足()()2f x f x -+=，所以任意点()(,)x f x 和点()(,)x f x --关于点()0,1对称，故函数()f x 的图象关于点()0,1对称，故B 正确；对于C 选项，对于函数())ln h x x =+0x x x >+≥，得该函数的定义域为R ，()()))()22lnlnln 10h x h x x x x x -+=-+=+-=，即()()h x h x -=-，所以函数()h x 为奇函数，当0x ≥时，内层函数u x =为增函数，外层函数ln y u =为增函数，所以函数()h x 在[)0,∞+上为增函数，故函数()h x 在(],0-∞上也为增函数，因为函数()h x 在R 上连续，故函数()h x 在R 上为增函数，又因为函数1y x =+在R 上为增函数，故函数()f x 在R 上为增函数，故C 不正确；对于D 选项，由()()2f x f x -+=，得2()()f x f x -=-，因为实数a ，b 满足()()2f a f b +>，所以()()()2f a f b f b >-=-，同时函数()f x 在R 上为增函数，可得a b >-，即0a b +>，故D 正确.故选：ABD.12.函数()lg f x x =，有0a b <<且()()22a b f a f b f +⎛⎫==⎪⎝⎭，则下列选项成立的是（）A.1ab =B.14a <C.3<<4b D.517328a b +<<【答案】ACD 【解析】【分析】利用对数性质判断选项A ；再利用零点存在定理判断得3<<4b ，从而判断选项B 、C 、D.【详解】因为()lg ,f x x =有0a b <<且()()2,2a b f a f b f +⎛⎫== ⎪⎝⎭所以lg lg =a b ，即lg lg a b -=，得lg lg 0a b +=所以1ab =，且()()0,1,1,.a b ∞∈∈+所以A 正确22112lg 2lg lg 24b b b b b +++==（因为12b b+>），故22142,b b b=++即4324210,b b b -++=()()321310b b b b ----=，令()3231,g b b b b =---当13b <<时，()3222313310g b b b b b b b =---<---<当4b >时，()32222314311(1)10g b b b b b b b b b b b =--->---=--=-->，而()()30,40,g g 故()0g b =在()3,4之间必有解，所以存在b ，使得3 4.b <<所以C 正确111,43a b ⎛⎫=∈ ⎪⎝⎭，所以B 不正确11517,2238a b b b +⎛⎫⎛⎫=+∈ ⎪ ⎪⎝⎭⎝⎭，所以D 正确故选：ACD【点睛】方法点睛：已知函数有零点（方程有根）求参数值（取值范围）常用的方法：（1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决；（3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解.第Ⅱ卷三、填空题：本题共4小题，每小题5分，20分.13.计算：23(log 9)(log 4)⋅=____________.【答案】4【解析】【分析】根据题意，由换底公式代入计算，即可得到结果.【详解】()()23log 9log 4=lg 9lg 2×lg 4lg 32lg 3lg 2=×2lg 2lg 3＝4.故答案为：414.写出一个同时满足以下三个条件①定义域不是R ，值域是R ；②奇函数；③周期函数的函数解析式___________.【答案】()()πtan ,πZ 2f x x x k k =≠+∈（答案不唯一）.【解析】【分析】联想正切函数可得结果.【详解】满足题意的函数为()tan f x x =，(Z)2x k k ππ≠+∈（答案不唯一）.故答案为：()tan f x x =，(Z)2x k k ππ≠+∈（答案不唯一）.15.已知()f x 为定义在R 上的奇函数，且又是最小正周期为T 的周期函数，则πsin 32T f ⎡⎤⎛⎫+ ⎪⎢⎥⎝⎭⎣⎦的值为____________．【答案】2【解析】【分析】根据函数的周期和奇偶性得到02T f ⎛⎫=⎪⎝⎭，进而得到ππsin sin 3232T f ⎡⎤⎛⎫+== ⎪⎢⎥⎝⎭⎣⎦.【详解】因为()f x 的最小正周期为T ，故222T T T f f T f ⎛⎫⎛⎫⎛⎫=-=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，又()f x 为奇函数，故22T T f f ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭，故22T T f f ⎛⎫⎛⎫=-⎪ ⎪⎝⎭⎝⎭，即202T f ⎛⎫= ⎪⎝⎭，解得02T f ⎛⎫= ⎪⎝⎭，故ππsin sin 3232T f ⎡⎤⎛⎫+== ⎪⎢⎥⎝⎭⎣⎦.故答案为：3216.对于任意实数,a b ，定义{},min ,,a a ba b b a b ≤⎧=⎨>⎩.设函数()3f x x =-+，()2log g x x =，则函数{}()min (),()h x f x g x =的最大值是_______.【答案】1【解析】【分析】画出()f x 和()g x 的图象，得到()h x 的图象，根据图象得到最大值.【详解】在同一坐标系中，作出函数()(),f x g x 的图象，依题意，()h x 的图象为如图所示的实线部分，令23log 2x x x -+=⇒=,则点()2,1A 为图象的最高点，因此()h x 的最大值为1，故答案为：1四、解答题：本题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤.17.已知cos sin 3cos sin θθθθ-=-+.（1）求tan θ的值；（2）求222sin 113cos +-θθ的值.【答案】（1）2-（2）132【解析】【分析】（1）根据题意整理可得sin 2cos θθ=-，进而可得结果；（2）根据齐次式问题分析求解，注意“1”的转化.【小问1详解】因为cos sin 3cos sin θθθθ-=-+，整理得sin 2cos θθ=-，所以sin tan 2cos θθθ==-；【小问2详解】因为tan 2θ=-，所以2222222222222sin 12sin sin cos 3sin cos 13cos sin cos 3cos sin 2cos θθθθθθθθθθθθ++++==-+--()()22223tan 1tan 321213222θθ⨯-+==--+=-.18.已知集合{}1217A xx =≤-≤∣，函数()f x =的定义域为集合B ．（1）求A B ⋂；（2）若{}M xx m =≤∣，求R M B ⋃=时m 的取值范围．【答案】（1）{34}A B xx ⋂=<≤∣（2）[)3,+∞【解析】【分析】（1）解一次与二次不等式，结合具体函数定义域的求法化简集合,A B ，再利用交集的运算即可得解；（2）利用集合的并集结果即可得解.【小问1详解】集合{}{}121714A xx x x =≤-≤=≤≤∣∣，由2230x x -->，得1x <-或3x >，则集合{1B xx =<-∣或3}x >，所以{34}A B xx ⋂=<≤∣.【小问2详解】因为R M B ⋃=，{}M xx m =≤∣，则3m ≥，故m 的取值范围是[)3,+∞．19.已知()sin()f x x π=-223，（1）求()f x 的最小正周期和对称轴方程；（2）求()f x 在闭区间,44ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值．【答案】（1）最小正周期为π；对称轴方程为5,122k x k Z ππ=+∈；（2）()max 1f x =，()min 2f x =-；【解析】【分析】（1）由正弦函数的性质计算可得；（2）由x 的取值范围，求出23x π-的取值范围，再由正弦函数的性质计算可得；【详解】解：（1）因为()2sin 23f x x π⎛⎫=- ⎪⎝⎭，所以最小正周期22T ππ==，令2,32x k k Z πππ-=+∈，解得5,122k x k Z ππ=+∈，故函数的对称轴为5,122k x k Z ππ=+∈（2）因为,44x ππ⎡⎤∈-⎢⎥⎣⎦，所以52,366x πππ⎡⎤-∈-⎢⎥⎣⎦，所以当236x ππ-=，即4x π=时函数取得最大值()max 14f x f π⎛⎫== ⎪⎝⎭，当232x ππ-=-，即12x π=-时函数取得最小值()min 212f x f π⎛⎫=-=- ⎪⎝⎭20.已知函数()f x 为定义在R 上的偶函数，当0x ≥时，()1432xx f x +=-⨯.（1）求()f x 的解析式；（2）求方程()8f x =-的解集.【答案】（1）()11432,0432,0x x xx x f x x +--+⎧-⨯≥=⎨-⨯<⎩（2）{}2,1,1,2--【解析】【分析】（1）根据偶函数的性质直接求解即可；（2）根据题意先求0x ≥时符合题意的解，再结合偶函数对称性求出方程解集即可.【小问1详解】因为函数()f x 为定义在R 上的偶函数，当0x ≥时，()1432xx f x +=-⨯，所以任取0x <，则0x ->，此时()()1432xx f x f x --+=-=-⨯，所以()11432,0432,0x x xx x f x x +--+⎧-⨯≥=⎨-⨯<⎩【小问2详解】当0x ≥时，令()14328xx f x +=-⨯=-，即()226280xx -⨯+=，令2x t =，则2680t t -+=，解得2t =或4t =，当22x t ==时，1x =，当24x t ==时，2x =，根据偶函数对称性可知，当0x <时，符合题意的解为=1x -，2x =-，综上，原方程的解集为{}2,1,1,2--21.已知函数()222cos 1f x x x =+-.（1）求()f x 的单调递增区间；（2）若π102313f α⎛⎫-=⎪⎝⎭，π,π2α⎛⎫∈ ⎪⎝⎭，求πsin 4α⎛⎫+ ⎪⎝⎭的值.【答案】（1）πππ,π,Z36k k k ⎡⎤-++∈⎢⎥⎣⎦（2）26【解析】【分析】（1）由降幂公式和辅助角公式化简函数解析式，整体代入法求单调递增区间；（2）由π102313f α⎛⎫-= ⎪⎝⎭，代入函数解析式解出cos α和sin α，由两角和的正弦公式求解πsin 4α⎛⎫+ ⎪⎝⎭的值.【小问1详解】()222cos 12cos 2f x x x x x =+-=+1π2sin 2cos 22sin 2226x x x ⎛⎫⎛⎫=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭，令Z 262πππ2π22π,k x k k -+≤+≤+∈，解得2ππ2π22πZ ,33k x k k -+≤≤+∈，即ππππ,Z 36k x k k -+≤≤+∈，所以()f x 的单调递增区间为πππ,π,Z 36k k k ⎡⎤-++∈⎢⎥⎣⎦.【小问2详解】由π102313f α⎛⎫-=⎪⎝⎭得5sin 213πα⎛⎫-= ⎪⎝⎭，所以5cos 13α=-，又因为π,π2α⎛⎫∈⎪⎝⎭，所以12sin 13α==，所以πππsin sin cos cos sin 44426ααα⎛⎫+=+= ⎪⎝⎭.22.已知函数()22log f x x =-，()()21,11,1x x g x f x x ⎧-≤⎪=⎨->⎪⎩.（1）求()g x 的最大值；（2）若对任意[]14,16x ∈，2R x ∈，不等式()()()12212kf x f xg x ⋅>恒成立，求实数k 的取值范围.【答案】（1）1（2）1,2⎛⎫+∞ ⎪⎝⎭【解析】【分析】（1）根据分段函数性质讨论函数单调性与最值，结合指数函数和对数函数相关知识求解最值即可；（2）根据题意转化为对任意[]14,16x ∈，()()21121kf x f x ⋅>恒成立，代入函数表达式进行化简，令21log ,24m x m =≤≤，将不等式化为()()2211k m m --->，结合二次函数相关知识分类讨论即可.【小问1详解】当1x ≤时，()21xg x =-，此时022x <≤，1211x -<-≤，则()0211xg x ≤=-≤；当1x >时，()()211log g x f x x =-=-单调递减，此时()()11g x g <=，综上所述，当1x =时，取得()g x 的最大值1；【小问2详解】因为对任意[]14,16x ∈，2R x ∈，不等式()()()21122kf x f xg x ⋅>恒成立，且()21g x ≤，所以对任意[]14,16x ∈，()()21121kf x f x ⋅>恒成立，由题意得，()()()()()()22112121212122log 22log 22log 1log kkf x f x x x k x x ⋅=--=---，令21log ,24m x m =≤≤，则不等式可化为()()2211k m m --->，即()2223230m k m k +--+>对任意[]2,4m ∈恒成立，令()()[]222323,2,4h m m k m k m =+--+∈，则函数图象开口向上，对称轴()233222k km --=-=⨯，当322k -≤，即1k ≥-时，()()()min 2843230h m h k k ==+--+>，解得12k >，符合题意；当3242k -<<时，即51k -<<-时，()2min 323022k k k h m h --+-⎛⎫==> ⎪⎝⎭，即2230k k -+<，不等式无解，该情况舍去；当342k-≥时，即5k ≤-时，()()()min 43283236110h m h k k k ==+--+=+>，解得116k >-，不符合题意，该情况舍去.综上所述，实数k 的取值范围为1,2∞⎛⎫+⎪⎝⎭.【点睛】结论点睛：本题考查不等式的恒成立与有解问题，可按如下规则转化：一般地，已知函数()[],,y f x x a b =∈，()[],,y g x x c d=∈（1）若[]1,x a b ∀∈，[]2,x c d ∀∈，总有()()12f x g x <成立，故()()2max min f x g x <；（2）若[]1,x a b ∀∈，[]2,x c d ∃∈，有()()12f x g x <成立，故()()2max max f x g x <；（3）若[]1,x a b ∃∈，[]2,x c d ∃∈，有()()12f x g x <成立，故()()2min min f x g x <；（4）若[]1,x a b ∀∈，[]2,x c d ∃∈，有()()12f x g x =，则()f x 的值域是()g x 值域的子集．。

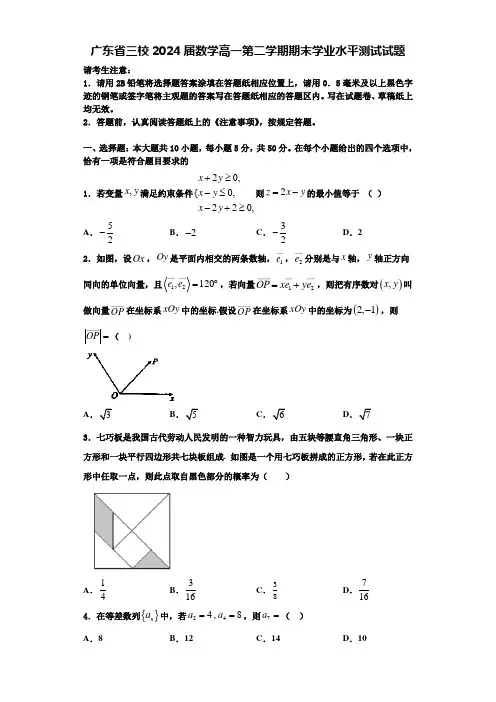
广东省三校2024届数学高一第二学期期末学业水平测试试题请考生注意：1．请用2B 铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。

写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题：本大题共10小题，每小题5分，共50分。

在每个小题给出的四个选项中，恰有一项是符合题目要求的1．若变量,x y 满足约束条件20,{0,220,x y x y x y +≥-≤-+≥则2z x y =-的最小值等于 （ ）A ．52-B ．2-C ．32-D ．22．如图，设Ox ，Oy 是平面内相交的两条数轴，1e ，2e 分别是与x 轴，y 轴正方向同向的单位向量，且12,120e e =︒，若向量12OP xe ye =+，则把有序数对(),x y 叫做向量OP 在坐标系xOy 中的坐标.假设OP 在坐标系xOy 中的坐标为()2,1-，则OP =（ )A ．3B ．5C ．6D ．73．七巧板是我国古代劳动人民发明的一种智力玩具，由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成. 如图是一个用七巧板拼成的正方形，若在此正方形中任取一点，则此点取自黑色部分的概率为（ ）A ．14B ．316C ．38D ．7164．在等差数列{}n a 中，若244,8a a ==，则7a =（ ） A ．8B ．12C ．14D ．105．设R a ∈，若不等式221148x x ax x x x++-+≥-恒成立，则实数a 的取值范围是( ) A ．[2,12]-B ．[2,10]-C ．[4,4]-D ．[4,12]-6．若a 、b 、c >0且a (a ＋b ＋c )＋bc ＝4－23，则2a ＋b ＋c 的最小值为( ) A ． 3－1 B ． 3＋1 C ．23＋2D ．23－27． 下列赋值语句正确的是 ( ) A ．S ＝S ＋i 2 B ．A ＝－A C ．x ＝2x ＋1D ．P ＝8．函数cos tan y x x =⋅（302x π≤<且2x π≠）的图像是下列图像中的（ ） A ． B ．C ．D ．9．下列函数中，既是偶函数又在(,0)-∞上是单调递减的是 A ．cos y x =-B ．lg y x =C ．21y x =-D ．x y e -=10．记max{,,}a b c 为实数,,a b c 中的最大数.若实数,,x y z 满足222363x y z x y z ++=⎧⎨++=⎩则max{||,||,||}x y z 的最大值为（ ）A ．32B ．1C ．73D ．23二、填空题：本大题共6小题，每小题5分，共30分。

“三校生”职业高中高一年级期末考试数学试题一、是非选择题：本大题共10小题，每小题3分，共30分。

对每小题的命题作出判断，对的选A,错的选B 。

1.{}c b a a ,,⊆ ……………………………………………( ) 2.如果c a c b b a >>>则,,…………………………………( ) 3.a a =2………………………………………………( )4.若b a >，则b a 11< ……………………………………( )5.9log 3log )93(log 333+=+………………………………( )6.函数53+=x y 是在实数集上的增函数………………( )7.函数532+-=x x y ）（3>x 有最小值，无最大值……( )8.24log 3log 32= ………………………………………( )9.函数)1lg(2+=x y 的图像关于坐标原点对称…………( )10.xy 31-=函数的定义域为()∞+，1…………………( ) 二、单项选择题：本大题共8小题，每小题5分，共40分。

11.已知12)(+=x x f ,那么=)1(f …………………( ) A ．1 B ．2 C ．3 D.412.的是且000>>>xy y x ……………………………( ) A ．充分条件 B ．必要条件C ．充要条件D ．既不是充分条件也不是必要条件13.不等式0)2(1>++-x x ）（的解集为………………( ) A.(1,2) B.(-2,1) C.()()+∞∞-,21, D.R14.若n m )21()21(>，则n m ,的大小关系为……………( )n D.m n C.m n B .m n A.m ≤≥<>15.已知函数n x x f =)(的图像过点（3,9）则=)1(f ( ) A.1 B.-1 C.2 D.316.集合{}02≤x x 的子集个数是…………………( ) A.0 B.1 C.2 D.3 17.下列大小比较不正确的是………………( ) A.5log 5.0log 22> B.4.002>π C.1.0lg 1lg > D.322.02.0<18.函数()+∞=,0)(在x f y 上是减函数，若),23()(-<x f x f 则x 的取值范围是……………………( )1A.32<<x B.0>x C.1<x D.10<<x三、填空题：本大题共6小题，每小题5分，共30分。

2021-2022学年广东省广州市三校联考高一下学期期末数学试题一、单选题1．若集合{}{}21,0,1,2A x Z x B =∈-<<=，则A B ⋃=（ ） A ．(2,1)- B ．{1,0}- C ．(2,1]{2}-⋃ D ．{1,0,1,2}-【答案】D【分析】根据已知条件求出集合A ，再利用并集的定义即可求解. 【详解】由题意可知{}}{211,0A x Z x =∈-<<=-，又{}0,1,2B =， 所以}{{}1,00,1,2{1,0,1,2}A B =-=-．故选：D ．2．设i 为虚数单位，若复数()()1i 1i a -+是实数，则实数a 的值为（ ） A ．－1 B ．0 C ．1 D ．2【答案】C【分析】由复数乘法法则化复数为代数形式，再由复数的分类求解． 【详解】2(1i)(1i)1i i i 1(1)i a a a a a -+=+--=++-，它是实数， 则10a -=，1a =． 故选：C ．3．已知π1tan 33α⎛⎫-= ⎪⎝⎭，则πtan 23α⎛⎫+ ⎪⎝⎭的值为（ ）A ．43B ．34C ．34-D ．43-【答案】C【分析】首先将π1tan 33α⎛⎫-= ⎪⎝⎭转化为πtan 36α⎛⎫+= ⎪⎝⎭，再将未知角π23α+向已知角π6α+转化，根据倍角公式求出πtan 23α⎛⎫+ ⎪⎝⎭的值. 【详解】因为π1tan 33α⎛⎫-= ⎪⎝⎭，所以πcos -απππ13tan tan =3ππ623sin -αtan 33ααα⎛⎫⎪⎡⎤⎛⎫⎛⎫⎝⎭+=--== ⎪ ⎪⎢⎥⎛⎫⎛⎫⎝⎭⎝⎭⎣⎦- ⎪ ⎪⎝⎭⎝⎭，所以22π2tan ππ2336tan 2tan 2π361341tan 6αααα⎛⎫+ ⎪⎡⎤⨯⎛⎫⎛⎫⎝⎭+=+===- ⎪ ⎪⎢⎥-⎛⎫⎝⎭⎝⎭⎣⎦-+ ⎪⎝⎭. 故选：C.4．在ABC 中，若45,60,32A B BC ===，则AC =（ ） A ．33 B ．43 C ．3 D ．23【答案】A【分析】已知三角形中两角和其中一角的对边，可以用正弦定理求另一角的对边. 【详解】在ABC 中，由正弦定理得， sin sin BC AC A B =，即32sin45sin60AC=， 解得：AC 33=. 故选：A.5．设m ，n 是两条不同的直线，α，β是两个不同的平面，则下列说法错误的是（ ） A ．若m n ⊥，m α⊥，n β⊥，则αβ⊥ B ．若//m n ，m α⊥，//n β，则αβ⊥ C ．若m n ⊥，//m α，//n β，则//αβ D ．若//m n ，m α⊥，n β⊥，则//αβ【答案】C【分析】利用线面垂直的判定性质、面面垂直的判定推理判断A ，B ；举例说明判断C ；利用线面垂直的判定性质判断D 作答.【详解】对于A ，因m n ⊥，m α⊥，当n ⊂α时，而n β⊥，则αβ⊥，当n α⊄时，在直线m 上取点P ，过P 作直线//n n '，则m n '⊥，过直线,m n '的平面l γα⋂=，如图，由m α⊥得m l ⊥，于是得////l n n '，而n β⊥，则l β⊥，而l α⊂，所以αβ⊥，A 正确；对于B ，若//m n ，m α⊥，则n α⊥，又//n β，则存在过直线n 的平面δ，使得c δβ⋂=， 则有直线//c n ，即有c α⊥，所以αβ⊥，B 正确；对于C ，如图，在长方体1111ABCD A B C D -中，平面ABCD 为平面α，直线11A B 为直线m ，平面11ADD A 为平面β，直线11B C 为直线n ，满足m n ⊥，//m α，//n β，而AD αβ⋂=，C 不正确；对于D ，若//m n ，m α⊥，则n α⊥，又n β⊥，于是得//αβ，D 正确. 故选：C6．锐角ABC 中，内角A ､B ､C 的对边分别为a ，b ，c ，S 为ABC 的面积，且2a =，23AB AC S ⋅=，则b 的取值范围为（ ）A ．()3,4 B ．()2,4 C ．()0,4 D ．()2,+∞【答案】A【分析】根据23AB AC S ⋅=即可得出cos 3sin bc A bc A =，从而求出3tan A =即可得出6A π=，根据ABC 为锐角即可得出32B ππ<<，然后根据正弦定理可得出4sin b B =，从而可求出b 的范围.【详解】因为23AB AC S ⋅=，所以1cos 2323sin 2bc A S bc A ==，3tan A =，又(0,)A π∈，所以6A π=，若ABC 为锐角三角形，则02B π<<，62A B B ππ+=+>，所以32B ππ<<3sin 1B <<，sin sin b a B A =，sin 4sin (23,4)sin a B b B A ==∈， 故选：A.7．已知实数(),1,a b ∈+∞，且22log log 3log log 2b a a b +=+，则（ ） A ．a b b << B b a b << C ．b a a << D a b a <<【答案】B【分析】对22log log 2log log 2a b a b -<-，利用换底公式等价变形，得222211log log log log a b a b -<-，结合1y x x =-的单调性判断b a <，同理利用换底公式得232311log log log log a b a b-<-，即23log log a b >，再根据对数运算性质得22log log a b >，结合2log y x =单调性， a b >，继而得解.【详解】由22log log 3log log 2b a a b +=+，变形可知22log log 2log log 2a b a b -<-， 利用换底公式等价变形，得222211log log log log a b a b-<-， 由函数()1f x x x=-在()0,∞+上单调递增知，22log log a b <，即a b <，排除C ，D ； 其次，因为23log log b b >，得23log log 3log log 2b a a b +>+，即23log log 2log log 3a b a b ->-，同样利用()1f x x x=-的单调性知，23log log a b >， 又因为323log log log b b b =>，得22log log a b >，即a b >，所以b a b <<.故选：B.8．如图（1）所示，已知球的体积为36π，底座由边长为12的正三角形铜片ABC 沿各边中点的连线垂直向上折叠成直二面角所得，如图（2）所示．则在图（1）所示的几何体中，下列结论中正确的是（ ）A ．CD 与BE 是异面直线B ．异面直线AB 与CD 所成角的大小为45°C ．由A 、B 、C 三点确定的平面截球所得的截面面积为3πD ．球面上的点到底座底面DEF 的最大距离为336++ 【答案】C【分析】取,DF EF 中点N ，M ，利用给定条件证明//,//BC DE AB DF ，推理判断A ，B ；求出ABC 外接圆半径，结合球面截面圆性质计算判断C ，D 作答. 【详解】取,DF EF 中点N ，M ，连接,,,,,AB BC AC BM MN CN ，如图，因BEF 为正三角形，则BM EF ⊥，而平面BEF ⊥平面DFE ，平面BEF 平面DFE EF =，BM ⊂平面BEF ，于是得BM ⊥平面DFE ，同理CN ⊥平面DFE ，即//BM CN ，BM CN == 因此，四边形BCNM 是平行四边形，有////BC NM DE ，则直线CD 与BE 在同一平面内，A 不正确；由选项A ，同理可得//AB DF ，则异面直线AB 与CD 所成角等于直线DF 与CD 所成角60，B 不正确；由选项A 知，132BC MN DE ===，同理可得3AB AC ==，正ABC 外接圆半径r = 由A 、B 、C 三点确定的平面截球所得的截面圆是ABC 的外接圆，此截面面积为3π，C 正确；体积为36π的球半径R ，由34π36π3R =得3R =，由选项C 知，球心到平面ABC 的距离d ==由选项A ，同理可得点A 到平面DFE 的距离为即平面ABC 与平面DFE 的距离为所以球面上的点到底座底面DEF 的最大距离为3R d BM ++=+D 不正确. 故选：C 二、多选题9．某高中有学生500人，其中男生300人，女生200人，希望获得全体学生的身高信息，按照分层抽样的原则抽取了容量为50的样本，经计算得到男生身高样本均值为170cm ，方差为172cm ；女生身高样本均值为160cm ，方差为302cm .下列说法中正确的是（ ）A ．男生样本容量为30B ．每个女生被抽入到样本的概率均为25C ．所有样本的均值为166cmD ．所有样本的方差为46.22cm 【答案】ACD【分析】分层抽样等比例性质求男女生样本容量，再由古典概型的概率求每个女生被抽入到样本的概率判断A 、B ；利用均值、方差公式，结合男、女的样本的均值和方差求样本总体均值方差判断C 、D.【详解】A ：由3005030500⨯=人，正确； B ：由2005020500⨯=人，故每个女生被抽入到样本的概率为20120010=，错误； C ：所有样本的均值为170301602016650⨯+⨯=cm ，正确；D ：男生方差30211(170)1730i i x =-=∑，女生方差20211(160)3020i i y =-=∑，所有样本的方差302022111[(166)(166)]50i i i i x y ==-+-∑∑302022111[(1704)(1606)]50i i i i x y ===--+-+∑∑ 303020202211111[(170)8(170)480(160)12(160)720]50i i i i i i i i x x y y =====---++-+-+∑∑∑∑ 1[510480600720]50=+++46.2=2cm ，正确. 故选：ACD10．2020年前8个月各月社会消费品的零售总额增速如图所示，则下列说法正确的有（ ）A ．受疫情影响，1~2月份社会消费品的零售总额明显下降B ．社会消费品的零售总额前期增长较快，后期增长放缓C ．与6月份相比，7月份社会消费品的零售总额名义增速回升幅度有所扩大D ．与4月份相比，5月份社会消费品的零售总额实际增速回升幅度有所扩大 【答案】AB【分析】根据图象和图中的数据逐个分析判断即可【详解】对于选项A ：由图可知，1~2月份社会消费品的零售总额名义增速和实际增速都小于0，所以1~2月份社会消费品的零售总额明显下降，故选项A 正确；对于选项B ：由图可知，社会消费品的零售总额前期增长较快，后期增长较缓，所以选项B 正确；对于选项C ：由图可知，6月份社会消费品的零售总额名义增速回升幅度为()()1.8 2.81--=，7月份社会消费品的零售总额名义增速回升幅度为()()1.1 1.80.7---=，所以选项C 错误；对于选项D ：由图可知，4月份社会消费品的零售总额实际增速间升幅度为()()9.118.19---=，5月份社会消费品的零售总额实际增速回升幅度为()()3.79.1 5.4---=，所以选项D 错误.故选：AB.11．如图，在菱形ABCD 中，2AB =，60ABC ∠=︒，M 为BC 的中点，将△ABM 沿直线AM 翻折成1AB M ，连接1B C 和1B D ，N 为1B D 的中点，则（ ）A ．平面1B MC ⊥平面AMCD B ．线段CN 的长为定值C ．当三棱锥1B AMD -的体积最大时，三棱锥1B AMD -的外接球的表面积为12π D ．二面角1B AD M --的最大值为30° 【答案】ABD【分析】对于A ，由已知可得△ABC 为等边三角形，则AM CM ⊥，由翻折性质知，AM ⊥平面1B MC ，再由面面垂直的判定可得结论，对于B ，取AD 中点E ，由三角形中位线定理可得1EN AB ∥，1112EN AB ==，由等角定理得130NEC B AM ∠=∠=︒，然后在△NEC 中由余弦定理可求出CN 长，对于C ，由题意可知将三棱锥1B AMD -的顶点放置在长宽高分别为231的长方体的顶点处，从而可求出其外接球的半径，进而可求出球的表面积，对于D ，过作1B F MC ⊥，垂足为F ，过F 作FG AD ⊥，垂足为D ，可和1B GF ∠即为二面角1B AD M --的平面角，当1B M MC ⊥时，1B F 取得最大值1，从而可求出其角度【详解】对于A ，如图所示，在菱形ABCD 中，2AB =，60ABC ∠=︒，所以△ABC 为等边三角形，又M 是BC 的中点，所以AM CM ⊥，由翻折性质知，又因为1B M ，CM ⊂平面1B MC ，1B M CM M ⋂=，所以AM ⊥平面1B MC ，因为AM ⊂平面AMCD ，所以平面1B MC ⊥平面AMCD ，故A 正确；对于B ，如图所示，取AD 中点E ，则1EN AB ∥，1112EN AB ==，在菱形ABCD 中， CE AM ∥，3CE AM ==，因为NEC ∠和1B AM ∠的两边方向相同，则由等角定理得130NEC B AM ∠=∠=︒，在△NEC 中，由余弦定理可得22232cos 1321312CN EN CE EN CE NEC =+-⋅∠=+-⨯⨯⨯=，所以1CN =，即CN 长为定值，故B 正确；对于C ，由题意可知当平面1AB M ⊥平面AMD 时，三棱锥1B AMD -的体积最大，由A 项已证知此时1B M ⊥平面AMD ，易知90DAM ∠=︒，所以AM AD ⊥，故可将三棱锥1B AMD -的顶点放置在长宽高分别为231的长方体的顶点处，此时三棱锥的外接球即为长方体的外接球，则长方体的外接球半径()222123122r =++为248r ππ=，故C 错误；对于D ，如图所示，由选项A 可知，平面1B MC ⊥平面AMCD ，在平面1B MC 中，过1B 作1B F MC ⊥，垂足为F ，在平面AMCD 中，过F 作FG AD ⊥，垂足为G ，因为平面1B MC ⊥平面AMCD ，1B F MC ⊥，平面1B MC平面AMCD MC =，1B F ⊂平面1B MC ，所以1B F ⊥平面AMCD ，1B GF ∠即为二面角1B AD M --的平面角．11tan B FB GF FG∠=，在菱形ABCD 中，已知FG 3AM ⊥平面1B MC ，11B M =知，点1B 的在以M 为圆心的圆弧上，所以当1B M MC ⊥时，1B F 取得最大值1，此时1113tan 33B F B GF FG ∠===，因为1B GF ∠为锐角，所以130B GF ∠=︒，故D 正确，故选：ABD ．12．如图，正方体1111ABCD A B C D -棱长为1，P 是1A D 上的一个动点，下列结论中正确的是（ ）A ．BP 3B ．PA PC +22+C ．当P 在直线1AD 上运动时，三棱锥1B ACP -的体积不变 D ．以点B 21AB C 6【答案】BCD【分析】当1BP A D ⊥时，BP 最小，结合正三角形性质，求得B 到直线1A D 的距离判断A ，将平面11DCB A 翻折到平面1ADA 上，求得P A +PC 的最小值判断B ，由题可得1//A D 平面1AB C ，进而可得三棱锥1B ACP -的体积不变，判断C ，根据球的截面的性质可得以点B 21AB C 的交线即为1AB C 的内切圆，即可判断D. 【详解】对于A ，当1BP A D ⊥时，BP 最小，由于112A B BD A D ==B ∴到直线1A D 的距离36222d =⋅=，故A 错误； 对于B ，将平面11DCB A 翻折到平面1ADA 上，如图，连接AC ，与1A D 的交点即为点P ，此时PA PC +取最小值AC ，在三角形ADC 中，135ADC ∠=,222cos13522AC AD CD AD CD =+-⋅=+，故B 正确；对于C ，由正方体的性质可得11//A D B C ，1A D ⊄平面1AB C ， 1//A D ∴平面1AB C ，P ∴到平面1AB C 的距离为定值，又1AB CS为定值，则1P AB C V -为定值，即三棱锥1B ACP -的体积不变，故C 正确；对于D ，由于1BD ⊥平面1AB C ，设1BD 与平面1AB C 交于Q 点， 1133BQ BD ∴==，设以B 2为半径的球与面1AB C 交线上任一点为G ，22BG ∴=，22236236QG ⎛⎫⎛⎫∴=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭， G ∴在以Q 为圆心，66为半径的圆上，由于1AB C 231623=， 故此圆恰好为1AB C 的内切圆，完全落在面1AB C 内， ∴交线长为662π=，故D 正确．故选：BCD. 三、填空题13．欧拉公式i e cos isin x x x =+（i 为虚数单位）是由瑞士著名数学家欧拉提出的，它将i 42ie π______．【答案】1i -i 1-+【分析】利用复数三角形式以及复数的除法化简所求复数，利用共轭复数的定义可得结果.【详解】由已知可得i422e cosisin44πππ=+=， ()()()()i42i 1i 2i2i 2i i 1i 1i1i 1i 1i 22e i -====-=+++-+， i 42ie1i -.故答案为：1i -.14．如图所示是利用斜二测画法画出的水平放置的ABC 的直观图，已知A C y '''∥轴，B C x '''∥轴且22A C B C ''''==，则ABC 的周长为___________.【答案】422+或224+【分析】由斜二测画法还原原图即可求解【详解】先由斜二测画法得AC BC ⊥，2AC BC ==，即可求解.由题意得，AC BC ⊥，且2AC BC ==，则4422AB =+=，则ABC 的周长为2222422++=+. 故答案为：422+.15．如图，在ABC 中，3BC BA BC =⋅=，点P 为边BC 上的一动点，则PA PC ⋅的最小值为___________.【答案】1-【分析】设BP BC λ=，[]0,1λ∈，用BC 、BA 表示PA 、PC ，再计算PA PC ⋅的最小值．【详解】由题意，设BP BC λ=，[]0,1λ∈，所以PA PB BA BP BA BC BA λ=+=-+=-+，()1PC BC λ=-. 又3BC =，3BA BC ⋅=，所以()()()()2111PA PC BC BA BC BC BA BC λλλλλ⋅=-+⋅-=--+-⋅()()229319123λλλλλ=-+-=-+22913λ⎛⎫=-- ⎪⎝⎭，当23λ=时，PA PC ⋅取得最小值1-. 故答案为：1-. 四、双空题16．如图，四棱台1111ABCD A B C D -上下底面都为正方形且侧棱长都相等，且1112A B AB =．设E 、F 、G 分别是棱11AB BC C D 、、的中点，过E 、F 、G 的平面与1AA 交于点H ，则1AHAA 值为___________；若四棱台1111ABCD A B C D -的高2，体积为14，则该四棱台外接球的表面积为_________．【答案】2340π 【分析】第一空；作辅助线，作出过E 、F 、G 的平面与1AA 的交点，利用平行线性质即可求得答案；第二空，求得棱台的上下底面的棱长，以及侧棱长，判断外接球的球心的位置，列出等式，求得外接球半径，即可求得其表面积.【详解】如图连接FE ,并延长交DA 延长线于M ,设11A D 的中点为P ,连接GP ,AC, 则11//,PG AC ,而由题意可知11//A C AC ,又//EF AC ,故//PG EF , 故P ∈平面EFG ,而M ∈平面EFG ,故连接PM ，交1AA 于H , H 点即为过E 、F 、G 的平面与1AA 的交点，设Q 为AD 中点，连接FQ,则//,FQ AB FQ AB = ,因为E 为AB 中点， 故1122AE AB FQ == ，故12AM AQ AD == , 因为11//,//A P AD A P AM ∴ ,则1111112122A DA H A D AH AM AD ===,所以123AH AA =；设四棱台上底面棱长为a ,则下底面棱长为2a ,由四棱台1111ABCD A B C D -的高2，体积为14，可得22221(44)2143a a a a ⋅⨯= ，解得3a =，对于四棱台，21116116,26,()422AC AC CC ==+=,则21617(26)422AC =-+故得22211171124022AC CC AC +-=+-< ， 即190AC C ∠>,由棱台的性质可知外接球球心位于对角面11AAC C 所在平面上， 故由此可知外接球球心在棱台的外部，即底面ABCD 的外部，设球心到面ABCD 的距离为1h ，则到面1111D C B A 的距离为12h +，是外接球半径为R ， 则222221166,((2)R h R h =+=++ ，解得210R =, 故外接球的表面积为24π40πR =, 故答案为：2;40π3【点睛】本题综合考查了棱台以及球的相关知识，涉及到棱台体积以及球的表面积的计算，解答时要发挥空间向想象力，明确空间的点线面的位置关系，注意空间和平面的转化. 五、解答题17．在复平面xOy 内，向量AB 对应的复数1z ，向量BC 对应的复数2z ，123i 2i z +=-，23i2iz +=-. (1)求向量AC 对应的复数；(2)若点()11,P x y ，()22,Q x y ，则三角形POQ 的面积为122112x y x y -.计算三角形ABC 的面积.【答案】(1)23i +； (2)12.【分析】（1）利用共轭复数的意义及复数除法运算分别求出1z ，2z ，再借助复数与向量的关系求解作答.（2）由（1）求出AC ，BC 的坐标，再利用给定公式计算作答. 【详解】(1)依题意，1224i z =-，即112i z =-，则112i z ，()()()()23i 2i 55i 1i2i 2i 5z +++===+-+，因为AC AB BC =+，所以向量AC 对应的复数为：()()1212i 1i 23i z z +=+++=+. (2)依题意，()11,OP x y =，()22,OQ x y =，则POQ △的面积为122112x y x y -， 由（1）知，AC 对应的复数为23i +，即有(2,3)AC =，AB 对应的复数为12i +，即有(1,2)AB =，所以ABC 的面积为11132222⨯⨯-⨯=.18．“2021年全国城市节约用水宣传周”已于5月9日至15日举行、成都市围绕“贯彻新发展理念，建设节水型城市”这一主题，开展了形式多样，内容丰富的活动，进一步增强全民保护水资源，防治水污染，节约用水的意识.为了解活动开展成效，某街道办事处工作人员赴一小区调查住户的节约用水情况，随机抽取了300．名业主进行节约用水调查评分，将得到的分数分成6组：[)70,75，[)75,80，[)80,85，[)85,90，[)90,95，[]95,100，得到如图所示的频率分布直方图．(1)求a 的值，并估计这300名业主评分的众数和中位数；(2)若先用分层抽样的方法从评分在[)90,95和[]95,100的业主中抽取5人，然后再从抽出的这5位业主中任意选取2人作进一步访谈： ①写出这个试验的样本空间；②求这2人中至少有1人的评分在[]95,100概率． 【答案】(1)0.200a =；众数为87.5；中位数为85；(2){}12,A A ，{}13,A A ，{}11,A B ，{}12,A B ，{}23,A A ，{}21,A B ，{}22,A B ，{}31,A B ，{}32,A B ，{}12,B B ；710P =【分析】（1）由频率分布直方图的的性质，所有小矩形的面积之和为1，可解得a 的值，由中位数的定义，找到频率之和为0.5的点，众数估计值为最高小矩形的中点； （2）首先根据两个分组的人数之比，采用分层抽样的方法，得到每个分组抽取的人数，根据古典概型的概率计算公式求解即可【详解】(1)第三组的频率为1(0.0200.0250.0300.0350.050)50.200-++++⨯=， 0.2000.0405a ∴== 又第一组的频率为0.02550.125⨯=，第二组的频率为0.03550.175⨯=，第三组的频率为0.200.∴前三组的频率之和为0.1250.1750.2000.500++=， ∴这300名业主评分的中位数为85.众数为859087.52+=． (2)由频率分布直方图，知评分在[90,95)的人数与评分在[]95,100的人数的比值为3:2. ∴采用分层抽样法抽取5人，评分在[90,95)的有3人，评分在[]95,100有2人.不妨设评分在[90,95)的3人分别为123,,A A A ；评分在[]95,100的2人分别为12,B B ， 这个试验的样本空间为：{}12,A A ，{}13,A A ，{}11,A B ，{}12,A B ，{}23,A A ，{}21,A B ，{}22,A B ，{}31,A B ，{}32,A B ，{}12,B B ；②从5人中任选2人的所有可能情况有共10种.其中选取的2人中至少有1人的评分在[]95,100的情况有：{}11,A B ，{}12,A B ，{}21,A B ，{}22,A B ，{}31,A B ，{}32,A B ，{}12,B B 共7种.故这2人中至少有1人的评分在[]95,100的概率为710P =. 19．如图，在四棱锥P ABCD -中，平面PAD ⊥平面,ABCD BC ∥平面1,2PAD BC AD =，90ABC ∠=︒，E 是PD 的中点．(1)求证：BC AD ∥；(2)求证：平面PAB ⊥平面PAD ；(3)若M 是线段CE 上任意一点，试判断线段AD 上是否存在点N ，使得MN ∥平面PAB ？请说明理由． 【答案】(1)见解析 (2)见解析(3)当N 为AD 中点时，MN ∥平面PAB . 【分析】（1）由线面平行的性质定理即可证明.（2）由面面垂直的性质定理证得BA ⊥平面PAD ，又因为BA ⊂平面PAB ，所以平面PAB ⊥平面PAD .（3）取AD 的中点N ，连接,CN EN ，由线面平行的判定定理证明EN ∥平面PAB ，CN 平面PAB ，所以平面CNE 平面PAB ，再由面面平行的性质定理可证得MN ∥平面PAB .【详解】(1)BC ∥平面,PAD BC ⊂平面,ABCD 平面PAD 平面ABCD AD =, 所以BC AD ∥.(2)因为平面PAD ⊥平面,ABCD 平面PAD 平面ABCD AD =，BA AD ⊥，所以BA ⊥平面PAD ，又因为BA ⊂平面PAB ，所以平面PAB ⊥平面PAD . (3)取AD 的中点N ，连接,CN EN ，,E N 分别为,PD AD 的中点，所以EN PA ∥，EN ⊄平面PAB ，PA ⊂平面PAB ，所以EN ∥平面PAB ，又因为12BC AD =，BC AD ∥，所以四边形ABCN 为平行四边形， 所以CN AB ∥，CN ⊄平面PAB ，AB 平面PAB ，所以CN 平面PAB ，CN NE ⋂，所以平面CNE 平面PAB ，又因为MN ⊂平面CNE ，所以MN ∥平面PAB .线段AD 上存在点N ，使得MN ∥平面PAB .20．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且()22sin sin sin 6sin sin sin B C A B C A +=+.(1)求tan A ；(2)若5a =10b =ABC 的面积. 【答案】(1)1tan 3A = (2)答案见解析【分析】（1）利用正弦定理和余弦定理得到2cos 6sin bc A bc A =，即可求出1tan 3A =；（2）先由1tan 3A =求出10sin A =310cos A =利用余弦定理解得1c =或5c =.代入ABC 的面积求面积即可.【详解】(1)因为()22sin sin sin 6sin sin sin B C A B C A +=+，所以2226sin b c a bc A +=+， 所以2cos 6sin bc A bc A =， 所以1tan 3A =.(2)因为510a b =<=，1tan 3A =， 所以10sin 10A =，310cos 10A =. 由余弦定理2222cos a b c bc A =+-， 可得231051021010c c =+-⨯，即2650c c -+=， 解得1c =或5c =.当1c =时，ABC 的面积为11101sin 10122102bc A =⨯⨯⨯=；当5c =时，ABC 的面积为11105sin 10522102bc A =⨯⨯⨯=.21．如图，在三棱台111ABC A B C -中，11A B 与1A C 、11B C 都垂直，已知3AB =，15A A AC ==．(1)求证：平面1A BC ⊥平面ABC ；(2)直线1A B 与底面ABC 所成的角的大小θ为多少时，二面角1A AC B --的余弦值为21 (3)在（2）的条件下，求点C 到平面11A ABB 的距离． 【答案】(1)证明见解析； (2)π3θ=； (3)3【分析】（1）证明平面1A BC ⊥平面ABC 面面垂直，即证AB ⊥平面1A BC 线面垂直，即证AB BC ⊥，1AB A C ⊥线线垂直；（2）根据面面垂直的性质定理作出1A BD θ∠=，根据二面角的定义作出1A ED ∠为二面角1A AC B --的平面角，根据解三角形以及Rt Rt ABC DEC ，得()121cos 5DE θ-=，进而表示出115tan 3A D A ED DE ∠==，再利用三角恒等变换公式求出θ； （3）点C 到平面11A ABB 的距离即为点C 到平面1A AB 的距离．注意到1Rt Rt ABC ABA ≅，并结合11A ABC C A AB V V --=可知，点C 到平面1A AB 的距离即点1A 到平面ABC 的距离，再利用第（2）问求1A D 的长即可.【详解】(1)∵11A B 与1A C 、11B C 都垂直，又由棱台的性质11//AB A B ， ∴AB BC ⊥，1AB A C ⊥，又1BC AC C =， ∴AB ⊥平面1A BC ，又AB 平面ABC ．故平面1A BC ⊥平面ABC ．(2)由（1）知，平面1A BC ⊥平面ABC ．如图所示，过1A 作1A D BC ⊥于D ，则1A D ⊥平面ABC ， ∴1A BD ∠是1A B 与平面ABC 所成的角，即1A BD θ∠=． 作DE AC ⊥于E ，则1A ED ∠为二面角1A AC B --的平面角． 在Rt ABC △中，易得4BC =．在1Rt A DB 中，14A B =，14sin A D θ=，4cos BD θ=，44cos CD θ=-． 由Rt Rt ABC DEC ，得()121cos 5DE θ-=． ∵121cos 14A ED ∠=，∴115tan 3A D A ED DE ∠==，即()5sin 531cos 3θθ=-， 于是，sin 3cos 3θθ+=，π2sin 33θ⎛⎫+= ⎪⎝⎭，注意到π02θ<≤，故π3θ=．(3)点C 到平面11A ABB 的距离即为点C 到平面1A AB 的距离．15AC AA ==，1π2ABC ABA ∠=∠=，3AB =， 1Rt Rt ABC ABA ∴≅，又由11A ABC C A AB V V --=可知，点C 到平面1A AB 的距离即点1A 到平面ABC 的距离，由（2）知，1A D ⊥平面ABC，且14sin 4A D θ=== 于是，C 到平面1A AB的距离为22．若函数()f x 满足()32f x f x π⎛⎫=+ ⎪⎝⎭且()R 44f x f x x ππ⎛⎫⎛⎫+=-∈ ⎪ ⎪⎝⎭⎝⎭，则称函数()f x 为“M 函数”.(1)试判断()4sin 3x f x =是否为“M 函数”，并说明理由； (2)函数()f x 为“M 函数”，且当,4x ππ⎡⎤∈⎢⎥⎣⎦时，()sin f x x =，求()y f x =的解析式，并写出在30,2π⎡⎤⎢⎥⎣⎦上的单调递增区间； (3)在（2）的条件下，当()3,N 22k x k πππ⎡⎤∈-+∈⎢⎥⎣⎦时，关于x 的方程()f x a =（a 为常数）有解，记该方程所有解的和为()S k ，求()3S .【答案】(1)不是，理由见解析(2)答案见解析(3)()7,020,01330,2401a a a S a a ππππ=⎧⎪⎪<<=⎪⎪=⎨=⎪⎪⎪<<⎪⎩【分析】（1）根据“M 函数”的定义判断可得出结论； （2）分析可知函数()f x 是周期为32π的周期函数，且()2f x f x π⎛⎫=- ⎪⎝⎭，分()33,Z 242k k x k ππππ⎡⎤∈++∈⎢⎥⎣⎦、()33,Z 2224k k x k ππππ⎡⎤∈-+∈⎢⎥⎣⎦两种情况分析，结合题意可出函数()f x 的解析式，进而可得出函数()f x 30,2π⎡⎤⎢⎥⎣⎦上的单调递增区间； （3）作出函数()f x 在,2ππ⎡⎤-⎢⎥⎣⎦上的图象，数形结合可得实数a 在不同取值下，方程()f x a =的根之和，再结合函数()f x 的周期性可求得()3S 的值.【详解】(1)解：函数()4sin 3x f x =不是为“M 函数”，理由如下：因为44sin sin 43433x f x x πππ⎡⎤⎛⎫⎛⎫⎛⎫+=+=+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦， 44sin sin 43433x f x x πππ⎡⎤⎛⎫⎛⎫⎛⎫-=-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，所以，()R 44f x f x x ππ⎛⎫⎛⎫+≠-∈ ⎪ ⎪⎝⎭⎝⎭， 因此，函数()4sin 3x f x =不是为“M 函数”. (2)解：函数()f x 满足()32f x f x π⎛⎫=+ ⎪⎝⎭，所以，函数()f x 为周期函数，且周期为32T π=， 因为()R 44f x f x x ππ⎛⎫⎛⎫+=-∈ ⎪ ⎪⎝⎭⎝⎭，则()()R 2f x f x x π⎛⎫=-∈ ⎪⎝⎭. ①当()33,Z 242k k x k ππππ⎡⎤∈++∈⎢⎥⎣⎦时，()3,Z 24k x k πππ⎡⎤-∈∈⎢⎥⎣⎦， 则()()33sin Z 22k k f x f x x k ππ⎛⎫⎛⎫=-=-∈ ⎪ ⎪⎝⎭⎝⎭； ②当()33,Z 2224k k x k ππππ⎡⎤∈-+∈⎢⎥⎣⎦，则()3,Z 224k x k πππ⎡⎤-∈-∈⎢⎥⎣⎦， 则()3,Z 224k x k ππππ⎛⎫⎡⎤--∈∈ ⎪⎢⎥⎝⎭⎣⎦， 所以，()()333sin cos Z 22222k k k f x f x x x k πππππ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=--=--=-∈ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦. 综上所述，()()()333cos ,Z 22224333sin ,Z 2242k k k x x k f x k k k x x k ππππππππππ⎧⎛⎫--≤≤+∈ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+<≤+∈ ⎪⎪⎝⎭⎩， 所以，函数()f x 在30,2π⎡⎤⎢⎥⎣⎦上的单调递增区间为,42ππ⎛⎤ ⎥⎝⎦、3,2ππ⎡⎤⎢⎥⎣⎦. (3)解：由（2）可得函数()f x 在,2ππ⎡⎤-⎢⎥⎣⎦上的图象如下图所示，下面考虑方程()f x a =在区间,2ππ⎡⎤-⎢⎥⎣⎦的根之和. ①当202a ≤<或1a =时，方程()f x a =有两个实数解，其和为2π； ②当2a =()f x a =有三个实数解，其和为34π； ③21a <<时，方程()f x a =有四个实数解，其和为π. 当()3,N 22k x k πππ⎡⎤∈-+∈⎢⎥⎣⎦时，关于x 的方程()f x a =（a 为常数）有解，记该方程所有解的和为()S k ，所以，当0a =时，()()334123722S πππ=-⨯+⨯++=；当0a <<1a =时，()()33241232042S πππ⎡⎤=⨯⨯+⨯++=⎢⎥⎣⎦；当a =()()33341233042S πππ⎡⎤=⨯⨯+⨯++=⎢⎥⎣⎦；1a <<时，()()33441234042S πππ⎡⎤=⨯⨯+⨯++=⎢⎥⎣⎦. 因此，()7,020,01330,401a a a S a a ππππ=⎧⎪⎪<<=⎪⎪=⎨=⎪⎪⎪<<⎪⎩.。

2023—2024学年浙江省杭高三校高一上学期期末数学试卷一、单选题1. 若角终边上一点，则（）A．B．C．D．2. 已知，，，则的大小关系为（）A．B．C．D．3. 函数的单调递减区间是（）A．B．C．D．4. “且”是“”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件5. 设函数.若，则等于（）A．B．C．D．6. 已知函数在上有且只有一个零点，则实数的取值范围是（）A．B．C．D．7. 已知在上单调递增，则的取值范围是（）A．B．C．D．8. 中国早在八千多年前就有了玉器，古人视玉为宝，玉佩不再是简单的装饰，而有着表达身份、感情、风度以及语言交流的作用.不同形状.不同图案的玉佩又代表不同的寓意.如图1所示的扇形玉佩，其形状具体说来应该是扇形的一部分（如图2），经测量知，，，则该玉佩的面积为（）A．B．C．D．二、多选题9. 已知函数的图象是连续不断的，且有如下对应值表：在下列区间中，函数必有零点的区间为（）A．B．C．D．10. 设函数，若，函数是偶函数，则的值可以是（）A．B．C．D．11. 已知函数.则下列说法正确的是（）A．B．函数的图象关于点对称C．对定义域内的任意两个不相等的实数，恒成立.D．若实数满足，则12. 函数，有且，则下列选项成立的是（）A．B．C．D．三、填空题13. 计算： ____________ .14. 写出一个同时满足以下三个条件①定义域不是R，值域是R；②奇函数；③周期函数的函数解析式 ___________ .15. 已知为定义在R上的奇函数，且又是最小正周期为的周期函数，则的值为 ____________ ．16. 对于任意实数，定义. 设函数，，则函数的最大值是_______ .四、解答题17. 已知.(1)求的值；(2)求的值.18. 已知集合，函数的定义域为集合．(1)求；(2)若，求时的取值范围．19. 已知，（1）求的最小正周期和对称轴方程；（2）求在闭区间上的最大值和最小值．20. 已知函数为定义在上的偶函数，当时，.(1)求的解析式；(2)求方程的解集.21. 已知函数.(1)求的单调递增区间；(2)若，，求的值.22. 已知函数，.(1)求的最大值；(2)若对任意，，不等式恒成立，求实数的取值范围.。