二重积分的计算

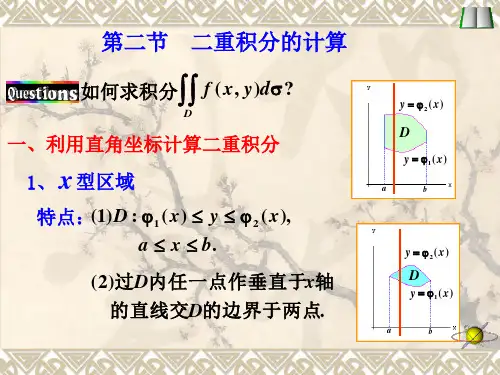
二重积分的计算方法本文在介绍二重积分的计算方法前，先来介绍与二重积分有关的性质，最后总结出二重积分的计算步骤.（一）二重积分的性质性质1 设，为常数，则⎰⎰[f (x, y) +g(x, y)]d=⎰⎰f (x, y)d+⎰⎰g(x, y)d.D D D性质2 如果闭区域D 被有限条曲线分为有限个部分闭区域，则在D 上的二重积分等于在各部分闭区域上的二重积分的和⎰⎰f (x, y)d=⎰⎰f (x, y)d+⎰⎰f (x, y)d.D D1 D2性质3 如果在D 上，f (x, y) =1 ，是D 的面积，则⎰⎰1d=⎰⎰d=.D D性质4 如果在D 上，f (x, y) ≤g(x, y) ，则特别地，有⎰⎰f (x, y)d≤⎰⎰g(x, y)d.D D⎰⎰f (x, y)d≤⎰⎰ f (x, y) d.D D性质5 设M ，m 分别是f (x, y) 在闭区域D 上的最大值和最小值，是D 的面积，则m≤⎰⎰f (x, y)d≤M.D性质6 （二重积分的中值定理）设函数f (x, y) 在平面闭区域D 上连续，是D 的面积，则存在(,) ∈D ，使得⎰⎰f (x, y)d=Df (,).（二）二重积分的计算方法1.利用对称性和奇偶性进行判断（1）利用积分区域的对称性和被积函数的奇偶性①若积分区域D 关于y 轴对称，且被积函数f (x, y) 关于x 具有奇偶性，则1⎧⎪2⎰⎰ f (x , y )dxdy , f (x , y )关x 于为偶函数 ⎰⎰ f (x , y )dxdy = ⎨ D 1 ， D ⎪⎩0, f (x , y )关于x 为奇函数其中 D 1 为 D 在 y 轴右侧的部分.②若积分区域 D 关于 x 轴对称，且被积函数 f (x , y ) 关于 y 具有奇偶性，则⎧⎪2⎰⎰ f (x , y )dxdy , f (x , y )关y 于为偶函数⎰⎰ f (x , y )dxdy = ⎨ D 1， D ⎪⎩0, f (x , y )关于y 为奇函数其中 D 1 为 D 在 x 轴上方的部分.（2） 利用变量的对称性①若积分区域 D 关于 y = x 对称，则⎰⎰ f (x , y )dxdy = ⎰⎰ f ( y , x )dxdy .DD②若积分区域 D 关于 y = -x 对称，则⎰⎰ f (x , y )dxdy = ⎰⎰ f (- y ,-x )dxdy .DD2. 利用直角坐标计算二重积分（1） 适合先 y 后 x 的积分区域（ X 型区域）若积分区域 D 由不等式1 (x ) ≤ y ≤ 2 (x ) ， a ≤ x ≤ b 确定，则b 2 ( x )⎰⎰ f (x , y )dxdy = ⎰adx ⎰( x )f (x , y )dy .D1（2） 适合先 x 后 y 的积分区域（ X 型区域）若积分区域 D 由不等式 1 ( y ) ≤ x ≤2( y ) ， c ≤ y ≤ d 确定，则d2 ( y) ⎰⎰ f (x , y )dxdy = ⎰cdy ⎰ ( y ) f (x , y )dx .D1在化二重积分为二次积分时，为了计算简便，需要选择恰当的二次积分的次序，这时, 1既要考虑积分区域 D 的形状，又要考虑被积函数 f (x , y ) 的特性。

探秘二重积分的计算方法
二重积分是高等数学中的一个重要概念，用于求解平面上某个区域内的面积，也被称为二重积分面积公式。

下面，我们将探讨二重积分的简单计算方法。

首先，二重积分的计算需要先确定被积函数和积分区域。

假设被积函数为f(x,y)，积分区域为D，其在直角坐标系下的边界可以用以下公式表示：
∬f(x,y)dxdy = ∫∫f(x,y)dA
接下来，我们需要根据积分区域D的形状来确定积分的范围。

当积分区域为直角坐标系下有界区域时，我们可以采用以下方法求解：
1. 积分区域为矩形时，通常采用先对x积分后对y积分的方法，即：
∫∫f(x,y)dA = ∫ab∫cd f(x,y)dxdy
其中，积分范围为a≤x≤b，c≤y≤d。

2. 积分区域为三角形时，可采用先对y积分后对x积分的方法，即：
∫∫f(x,y)dA=∫cd∫h1(x)h2(x) f(x,y)dydx
其中，积分范围为c≤y≤d，h1(x)≤y≤h2(x)。

3. 积分区域为梯形时，可采用换元法将积分区域转化为矩形的形式，即：
∫∫f(x,y)dA=∫ab∫g1(y)g2(y) f(x,y)dxdy
其中，积分范围为g1(y)≤x≤g2(y)，a≤y≤b。

以上是二重积分计算的基本方法，希望能对您有所帮助。

二重积分定义法计算二重积分定义法计算是一种使用二重积分的基本定义来计算积分的方法。

下面是一个使用定义法计算二重积分的例子: 假设我们要计算以下二重积分:∫∫[a,b] x^2 dy我们可以使用二重积分的定义来计算这个积分。

根据定义，二重积分等于被积函数在积分区间内的立体面积乘以积分常数。

因此，我们可以将积分常数设为 c，并将积分区间重新写成 [a,b]。

这样，我们就可以将积分式子化简为:∫∫[a,b] x^2 dy = (b-a) x^3 / 3 |[a,b]现在我们可以使用二重积分的定义来计算这个积分。

根据定义，我们可以将积分区间 [a,b] 分成两个部分:[a,c] 和 [c,b]。

其中，c 是积分常数。

我们可以分别计算这两个部分的面积，然后将两个部分的面积相加起来。

对于第一部分 [a,c],我们可以将积分式子写成:∫[a,c] x^2 dy = x^3 |[a,c] - 3x^2 |[a,c]根据积分的基本公式，我们可以将第一部分的面积计算为:A1 = x^3 |[a,c] - 3x^2 |[a,c] = (c-a) x^3 - 3(c-a) x^2 对于第二部分 [c,b],我们可以将积分式子写成:∫[c,b] x^2 dy = x^3 |[c,b] - 3x^2 |[c,b]根据积分的基本公式，我们可以将第二部分的面积计算为:A2 = x^3 |[c,b] - 3x^2 |[c,b] = (b-c) x^3 - 3(b-c) x^2因此，整个二重积分的值等于:∫∫[a,b] x^2 dy = A1 + A2 = (c-a) x^3 - 3(c-a) x^2 + (b-c) x^3 - 3(b-c) x^2= (b-a) x^3 - 6(b-a) x^2 + 3(b-a) x^3 - 3(b-a) x^2= (b-a) x^3 - 9(b-a) x^2因此，我们使用二重积分定义法计算得出的结果为:∫∫[a,b] x^2 dy = (b-a) x^3 - 9(b-a) x^2这个结果与我们使用其他方法计算得出的结果应该是一致的。

二重积分的计算与应用在数学的领域中，二重积分是一种重要的数学工具，广泛应用于各个科学领域。

本文将探讨二重积分的计算方法以及其在实际问题中的应用。

一、二重积分的定义与计算方法二重积分是对二元函数在某个有界区域上的积分运算。

设有函数f(x, y) 定义在平面上的有界闭区域 D 上，记作：∬D f(x, y)dxdy其中，D 表示平面上一个有界区域，f(x, y) 表示在此区域内的函数，dxdy 表示对 x, y 的积分。

二重积分可以通过以下两种常用方法进行计算：1. 直角坐标系下的二重积分计算在直角坐标系下，二重积分可以表示为：∬D f(x, y)dxdy其中，D 表示 x 轴与 y 轴所围成的区域，f(x, y) 表示在此区域内的函数。

使用直角坐标系下的计算方法可以将二重积分转化为两个一重积分的运算，具体过程如下：将 D 区域划分为若干个小矩形或小平行四边形；在每个小矩形或小平行四边形上取一点(xi, yj)；设Δxi 和Δyj 分别为小矩形或小平行四边形的宽度和高度；计算 f(xi, yj) 与Δxi Δyj 的乘积的和，即为所求的二重积分。

2. 极坐标系下的二重积分计算在极坐标系下，二重积分可以表示为：∬D f(x, y)dxdy其中，D 表示极坐标系下的一个有界区域，f(x, y) 表示在此区域内的函数。

使用极坐标系下的计算方法可以将二重积分转化为一重积分的运算，具体过程如下：将 D 区域在极坐标系下表示为R ≤ r ≤ S, α ≤ θ ≤ β；将x = rcosθ，y = rsinθ 进行替换，使得函数 f(x, y) 转化为 F(r, θ)；计算F(r, θ) 与 r 的积分后再对θ 进行积分，即为所求的二重积分。

二、二重积分的应用1. 几何应用二重积分可用于计算平面图形的面积。

通过在直角坐标系或极坐标系下进行适当的变换，将图形转化为简单的几何图形（如矩形、圆、扇形等），然后进行二重积分的计算，便可得到所求图形的面积。

二重积分计算方法引言二重积分是高等数学中的重要内容，常用于计算平面区域上的面积、质量、重心等问题。

计算二重积分时，需要掌握一些常见的计算方法，本文将介绍三种常见的计算方法：直角坐标系下的累次积分法、极坐标系下的累次积分法以及变量代换法。

直角坐标系下的累次积分法直角坐标系下的累次积分法是最常用的计算二重积分的方法之一。

对于平面上的一个区域D，可以将其分解为若干个小矩形区域，然后通过对每个小矩形区域进行积分求和，从而得到整个区域的二重积分值。

具体步骤如下： 1. 将区域D划分为若干个小矩形区域，每个小矩形区域的面积可以通过计算两个相邻顶点之间的距离得到。

2. 对每个小矩形区域进行积分，积分的上限和下限分别是该小矩形区域在x轴和y轴上的边界。

3. 将每个小矩形区域的积分结果求和，得到整个区域D的二重积分值。

极坐标系下的累次积分法在一些特殊的情况下，采用极坐标系进行计算可以简化计算过程。

极坐标系下，平面上的点由极径和极角两个参数决定，适用于具有旋转对称性的问题。

具体步骤如下： 1. 将直角坐标系下的二重积分转换为极坐标系下的二重积分。

极坐标系下，二重积分的积分变量可以表示为r和θ。

2. 将区域D在极坐标系下表示出来，确定积分的上限和下限。

3. 对每个小区域进行积分，积分的上限和下限分别是在极坐标系下的边界。

4. 将每个小区域的积分结果求和，得到整个区域D的二重积分值。

变量代换法变量代换法是一种常用的计算二重积分的方法，通过引入新的变量进行积分变换，从而简化计算过程。

具体步骤如下： 1. 引入新的变量，将二重积分中的自变量进行变换。

2. 将原来的二重积分转换为新的变量下的二重积分。

3. 对新的二重积分进行计算，可以使用上述的直角坐标系下的累次积分法或者极坐标系下的累次积分法。

4. 将计算得到的结果转换回原来的变量，得到整个区域D的二重积分值。

总结本文介绍了三种常见的二重积分计算方法：直角坐标系下的累次积分法、极坐标系下的累次积分法以及变量代换法。

二重积分公式1. 二重积分的定义二重积分是对二维平面上的某个区域进行积分的概念。

它是将一个函数在该区域内进行“求和”的过程。

设函数 f(x, y) 在平面区域 D 上有界，划分 D 为 m 行 n 列的小矩形，其中每个小矩形的面积为∆S。

取 D 中的一组任意点（ξi,j，ηi,j），构造函数值与面积的乘积f(ξi,j, ηi,j)⋅ ∆S，然后对所有小矩形内的乘积进行求和，即可得到二重积分的近似值。

当 m 和 n 均趋于无穷大，且∆S 趋于零时，如果此极限存在，则称此极限值为函数 f(x, y) 在区域 D 上的二重积分，记为∬Df(x, y)dS。

2. 二重积分的计算方法2.1 通过极坐标变换计算二重积分对于某些特殊的平面区域，在直角坐标系下求解二重积分可能会比较困难。

这时可以利用极坐标变换来简化计算。

设平面区域 D 在极坐标下的表示是 R（r，θ），且区域 D 内的任意一点（x, y）与极坐标下的点（r，θ）存在一一对应关系。

则二重积分∬Df(x, y)dS 可以改写为∬Rf(r cosθ, r sinθ)r dr dθ。

在极坐标下，面积微元dS = r dr dθ。

因此，对于函数 f(r cosθ, r sinθ)，可以进行类似于直角坐标系下的计算方法，将其转化为对 r 和θ 的积分来求得二重积分的值。

2.2 通过直角坐标系计算二重积分除了利用极坐标变换来计算二重积分外，直角坐标系下的计算方法也是常用的。

对于平面区域 D，利用直角坐标系划分为 m 行 n 列的小矩形，每个小矩形的面积为∆S。

取每个小矩形的中点（ξi,j，ηi,j），构造函数值与面积的乘积f(ξi,j, ηi,j)⋅ ∆S，然后对所有小矩形内的乘积进行求和，即可得到二重积分的近似值。

将 m 和 n 均趋于无穷大，且∆S 趋于零时可以得到二重积分的精确值。

2.3 利用重积分的性质简化计算在实际计算二重积分时，有时可以根据重积分的性质进行简化。