基尔霍夫定律的相量表达式

由相量形式KVL有 : V V 1 V 2 600 8090 (V)
（2）相量图解法
60 j80 10053.1 (V) 故 : |V | 100(V)
相量法的三个基本公式


UR RIR


U L jL IL

1
UC

j
C
IC
以上公式是在电压、电流关联参考方向的条件
错误的写法
1 u
C i
1
C

U I
(2) 容抗的绝对值和频率成反比。
0, XC , 直流开路( 隔直作用) ;
XC
, XC 0, 高频短路（旁路作用）;

(3) 由于容抗的存在使电流领先电压。
4、受控源 如果受控源（线性）的控制电压或电流是正弦量， 则受控源的电压或电流将是同一频率的正弦量。
i 超前u 90° I
0
所示，反映电压电流瞬时 值关系的波形图如图(b)所示。由此图可以看出电容电流超 前于电容电压90°，当电容电压由负值增加经过零点时，其 电流达到正最大值。
容抗
I= CU
U 1
I C
容抗的物理意义：
X
C
定义

1
C
(1) 表示限制电流的能力；
相量关系
+
U R R I
U R
-
有效值关系：UR = RI 相位关系：u , i 同相
I
R
U
相量图
相量模型
2. 电感
时域
频域
i(t)
i(t) 2I cost
+ u (t)
u(t) L di(t)

电压相量，如图(c)所示，从相量图上容易看出各正弦电压
的相位关系。
值得注意的是回路中全部电压有效值之代数和并不一
定等于零，本题中 US=10U1+U2+U3=6+8+12=26
即一般说来
n
Uk 0
k 1Biblioteka 关于复数的几个公式1. 假设复数 c rθ a jb
则有 c a2 b2 θ arctan b a
uk (t) Re[U kme jt ] Re[ 2U k e jt ]
代入KVL方程中得到
n uk (t) n Re[Ukmejt ] 0
k 1
k 1
n
n
uk (t) Re[
2Uke jt ] 0
k 1
k 1
由于上式适用于任何时刻t，其相量关系也必须成立，
j ej180 cos180 jsin180 1 1 j2 ej180 1180
模型，图中各电流参考方向均与时域模型相同，仅将
时域模型中各电流符号 iS、i、i1、i2 用相应的相量符
号 IS、I、I1、I2 表示，并计算出电流相量 。
I1 1060 A
I2 5 90 A
列出图(b)相量模型中结点1的KCL方程，其相量形式
为
I I1 I2 0
§8－3 基尔霍夫定律的相量形式
一、基尔霍夫电流定律的相量形式
基尔霍夫电流定律(KCL)叙述为：对于任何集中参数 电路中的任一结点，在任何时刻，流出该结点的全部支路 电流的代数和等于零。其数学表达式为
n
ik (t) 0
k 1
假设电路中全部电流都是相同频率ω的正弦电流，则 可以将它们用振幅相量或有效值相量表示为以下形式

4.6.1用相量法分析串联电路 对于RLC串联电路来说，其阻抗为
Z = Z R + Z L + Z C = R + jωL + 1 jωC
1 = R + j ωL − ωC
1 = R 2 + ωL − ωC
2
ωL −
arctg R
1 ωC
(4-53)
0 • •
=U L =UC
•
•
为参考向量，相量图如
故电流表的读数为 即(1) (2)
2 A = I R + (I C − I L ) 2 A
A = 5 2 + (25 − 20) 2 = 7.07 A
图4-26 例4-9相量图
A = 5 + ( 25 − 10) = 40.31A
2 2
从【例4-9】题的解法二，可以体会到应用向量图分析电路的要点，那就是： （1）首先要选好一个参考相量，这个参考相量的选择，必须能方便地将电路 中其它电压、电流相量，根据电路的具体结构及参数特点逐一画出，把所给的 条件转化成相量图中的几何关系。 （2）最后根据相量图中的相量关系，使问题得到解决。一般对串联电路，选 电流作参考方向较方便，如【例4-8】题。对并联电路，则选电压作参考相量较 方便，如【例4-9】题。有些问题通过相量图分析将很直观和简便。
2 2 U S = U R + U L = 30 2 + 60 2 = 67.08V
图4-24例4-8解法二图
由题解图4-24b）可得
2 U S = U R + (U C − U L ) 2 = 15 2 + (100 − 80) 2 = 258V

电路相量图的原理及应用1. 什么是电路相量图电路相量图是一种用于表示电路中电压、电流及其相位信息的图形工具。

相量图使用矢量的长度和角度来表示电压和电流的振幅和方向。

通过使用相量图，我们可以更直观地理解和分析电路中的信号传输和变换。

2. 电路相量图的原理在电路相量图中，电压和电流被表示为复数的形式，其中实部表示振幅，虚部表示相位。

根据欧姆定律和基尔霍夫定律，我们可以推导出电阻、电容和电感的相量图表示。

•电阻的相量表示为：Z R=R•电容的相量表示为：$Z_C = \\frac{1}{j\\omega C} = \\frac{-j}{\\omega C}$•电感的相量表示为：$Z_L = j\\omega L$3. 电路相量图的应用3.1 直流电路分析通过使用电路相量图，我们可以更加简洁和方便地分析直流电路。

相量图可以帮助我们计算电流和电压的大小和方向，从而更好地理解和解决直流电路中的问题。

例如，当我们需要计算电阻串联电路中总电阻时，可以将每个电阻的相量图相加得到总阻抗。

3.2 交流电路分析在交流电路中，相量图发挥着重要的作用。

交流电压和电流的相量图可以用于计算电路中电压的幅值、相位和频率响应。

通过将电路的各个元件转换为相量图形式，我们可以方便地计算电路中电压和电流的大小和相位差，进而计算功率、阻抗和电流的分布。

3.3 三相电路分析在三相电路分析中，电路相量图也是必不可少的工具。

通过将三相电压和电流表示为相量的形式，我们可以更好地理解和分析三相电路中的功率传输、电压平衡和相序问题。

3.4 系统稳定性分析电路相量图可以用于分析系统的稳定性。

通过计算电路的传输函数，并绘制相量图，我们能够评估系统的稳定性和抗干扰能力。

相量图可以帮助我们观察电路中的衰减、相位移和共振频率。

4. 总结电路相量图是一种重要的工程工具，它帮助我们直观地理解和分析电路中的信号传输和变换。

通过使用电路相量图，我们可以更好地计算电压和电流的大小、相位差和频率响应。

电工基础
正弦量的表示法：
解析式： i(t ) I m sin(t ) A
i
Im
最大值相量： I m I m
有效值相量： I I
最大值： I m
I
Im
I
有效值： I
平均值：
I
I
电工基础
例：写出下列正弦量的相量形式：
i1 (t ) 5 2 sin(t 53.1) A
2
虚数
用 j 代替
虚部 实部
i
B a jb
j
复数 A a jb 代数式
0
D
b
A
C a jb
D a jb
复数的模
r

0
1
r a 2 b2

复数矢量与实轴正方向的夹角
a
C
0
取值在正180度到负180度之间
a r cos
0
电工基础
三、正弦量的相量表示法： re j r cos jr sin
Im
t
正弦交流电
I me j (t ) I m cos(t ) jI m sin(t )
用 I me
I me
j (t )
代
jt
替
I m sin(t ) I mt
加减用代 数式运算
A B a1 jb1 a2 jb2 (a1 a2 ) j (b1 b2 ) A B a1 jb1 (a2 jb2 ) (a1 a2 ) j (b1 b2 )
A B
A
A B
A
B B
1
1

电流与电压同相
电工基础
三、电感元件的相量形式： 电感元件的相量形式：
i
L
Z L = ωL∠90 = jωL = j 2πfL
ɺ I
ZL
相量图
+
u
−
ɺ U
ϕi
ɺ I
+
ɺ U
−
i (t ) = I m sin(ωt + ϕi ) A u (t ) = U m sin(ωt + ϕ u )V
u(t ) = L ⋅
Q=
ωt
t
2 UC
XC
电 源
i 电
源
(var) : 电容元件 电
u
电工基础
例：求电流及电容元件的电压和无功功率，并画相量图。 求电流及电容元件的电压和无功功率，并画相量图。 ɺ ZC C = 10µF i C I
+
u
解： X C =
− u (t ) = 100 2 sin(1000t + 30 )V
ɺ UC
电工基础
u (t ) = U m sin(ωt + ϕ u )V
ϕ
ɺ I +1
电流与电压同相
ɺ I = I∠ϕi (A) ɺ U = U∠ϕ u (V )
ɺ U Z= ɺ = Z ∠ϕ z I
u(t ) = R ⋅ i(t )
= R ⋅ I m sin(ωt + ϕ i )
大小关系： 大小关系： m = R ⋅ I m U
ϕ z = ϕu − ϕi
电工基础
电感元件的功率： 电感元件的功率：
1）瞬时功率: 瞬时功率:
p ( t ) = u ( t )i ( t )

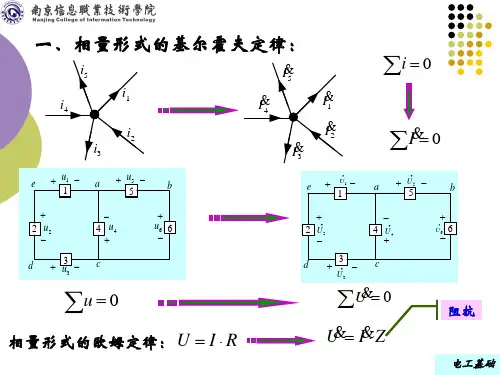
第一章习题1－1 指出图1－1所示电路中A 、B 、C 三点的电位。

图1－1 题 1－1 的电路解：图（a ）中，电流 mA I 51226.=+=, 各点电位 V C = 0 V B = 2× = 3V V A = (2+2)× = 6V图（b ）中，电流mA I 1246=+=， 各点电位 V B = 0 V A = 4×1 = 4V V C =－ 2×1 = －2V|图（c ）中，因S 断开，电流I = 0， 各点电位 V A = 6VV B = 6V V C = 0图（d ）中，电流mA I 24212=+=， 各点电位 V A = 2×(4+2) =12V V B = 2×2 = 4V V C = 0图（e ）的电路按一般电路画法如图，电流mA I 12466=++=， 各点电位 V A = E 1 = 6VV B = (－1×4)+6 = 2V ?V C = －6V1－2 图1－2所示电路元件P 产生功率为10W ，则电流I 应为多少 解：由图1－2可知电压U 和电流I 参考方向不一致，P = －10W ＝UI 因为U ＝10V, 所以电流I ＝－1A ）图 1－2 题 1－2 的电路1－3 额定值为1W 、10Ω的电阻器，使用时通过电流的限额是多少 解：-根据功率P = I 2 R A R P I 3160101.===1－4 在图1－3所示三个电路中，已知电珠EL 的额定值都是6V 、50mA ，试问哪个电珠能正常发光图 1－3 题 1－4 的电路解：图（a ）电路，恒压源输出的12V 电压加在电珠EL 两端，其值超过电珠额定值，不能正常发光。

图（b ）电路电珠的电阻Ω=Ω==120120506K R .，其值与120Ω电阻相同，因此电珠EL 的电压为6V ，可以正常工作。

图（c ）电路，电珠与120Ω电阻并联后，电阻为60Ω，再与120Ω电阻串联，电珠两端的电压为V 4126012060＝＋⨯小于额定值，电珠不能正常发光。

U
i
L
u
U IX L di jX L 则 uL X L L dt jL u 2 IL sin(t 90 )
jX C
i 2 I sin t
UI
I
u领先 i 90°
U I jX L
0
I2XL
设
i
C
u
iC
du dt
1 j C 1 j C
？
？
单一参数正弦交流电路的分析计算小结
电路 电路图 基本 参数 （正方向） 关系
i 复数 阻抗 设 电压、电流关系 瞬时值 有效值 相量图 相量式 功率 有功功率 无功功率
u 2U sin t
I
U IR
U
R
u
u iR
R
则
U IR
UI
0
i 2 I sin t
设
u、 i 同相
图 KVL的相量形式
回路的电压方程： 其KVL相量表达式为：
u1 u 2 u 3 u 4 0
U1 U 2 U 3 U 4 0
小 结
电路参数
R L
基本关系 复阻抗
u iR
R
I
U
U
电路参数
基本关系
复阻抗
电路参数
jX L j L
di uL dt
项目十九 电路基本定律的相量形式
电压、电流瞬时值的关系符合欧姆定律、基尔霍 夫定律 。
i
R
u
L
uR uL
u uR uL di iR L dt
电流、电压相量符合相量形式的欧姆定律、 基尔霍夫定律。
I

R
W直 =I 2RT
T i 2 ( t ) Rd t R W交 0
例 周期电压如图所示。求其有效值U。 u(t)/V 2 1 0
1 2 3 4 5 6
t/s
解 根据有效值的定义，有
1 U T

T 0
u 2 ( t )dt
2 3 1 1 2 2 2 0 1 dt 1 2 dt 2 0 dt 1.29 V 3
有效值也称均方根值(root-mean-square，简记为 rms。)
正弦电压有效值与最大值的关系： 1 U Um 或 U m 2U 2
工程上说的正弦电压、电流一般指有效值，如设备铭牌 额定值、电网的电压等级等。但绝缘水平、耐压值指的是 最大值。 测量中，电磁式交流电压、电流表读数均为有效值。 * 注意区分电压、电流的瞬时值、有效值、最大值的符号。
频率f : 每秒钟完成循环的次数，单位：Hz(赫兹) 。
关系 : f 1 T
2f
2 T
小常识
* 电网频率： 中国 50 Hz
美国 、日本 60 Hz * 有线通讯频率：300 - 5000 Hz
* 无线通讯频率： 30 kHz - 3×104 MHz
i(t)=Imcos( t + φ)
例 + u + u1
U1 U2 U3
u1 (t ) 3 2 cos 314t V
-
u2 (t ) 4 2 cos (314t 90o ) V 求u。 + u2 u(t ) u (t ) u (t ) 5 2 cos (314t 53.1o ) V 1 2 U2 490 V U1 30o V
u, i u i O

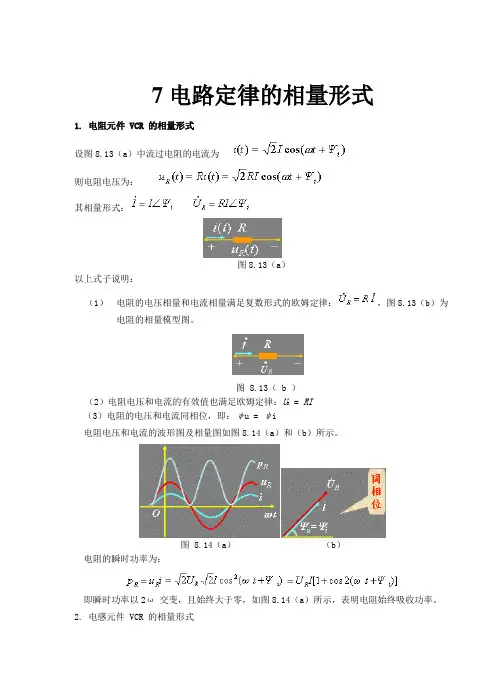
7电路定律的相量形式1. 电阻元件 VCR 的相量形式设图8.13（a）中流过电阻的电流为则电阻电压为：其相量形式：图8.13（a）以上式子说明：（1）电阻的电压相量和电流相量满足复数形式的欧姆定律：，图8.13（b）为电阻的相量模型图。

图 8.13（ b ）（2）电阻电压和电流的有效值也满足欧姆定律：U R = RI（3）电阻的电压和电流同相位，即：ψu = ψi电阻电压和电流的波形图及相量图如图8.14（a）和（b）所示。

图 8.14（a）（b）电阻的瞬时功率为：即瞬时功率以2ω交变，且始终大于零，如图8.14（a）所示，表明电阻始终吸收功率。

2. 电感元件 VCR 的相量形式设图 8.15（a）中流过电感的电流为则对应的相量形式分别为：图 8.15 （ a ）（ b ）以上式子说明：（1）电感的电压相量和电流相量满足关系：，其中X L=ωL=2πfL ，称为感抗，单位为Ω(欧姆)，图8.16（b）为电感的相量模型图。

（2）电感电压和电流的有效值满足关系：，表示电感的电压有效值等于电流有效值与感抗的乘积。

（3）电感电压超前电流相位，即：电感电压和电流的波形图及相量图如图8.16（a）和（b）所示。

注意:（1）感抗表示限制电流的能力；（2）感抗和频率成正比如图8.16（c）所示，当；电感电压和电流的波形图及相量图如图8.16（a）和（b）所示。

图 8.16 （a）（b）（c）电感的瞬时功率为：即电感的瞬时功率以 2ω交变，有正有负，如图8.16（a）所示。

电感在一个周期内吸收的平均功率为零。

3. 电容元件 VCR 的相量形式图 8.17 （ a ）（ b ）设图8.17（a）中电容的电压为：则对应的相量形式分别为：以上式子说明：（1）电容的电压相量和电流相量满足关系：其中X C =1/ωC ，称为容抗，单位为Ω(欧姆)，图8.17（b）为电容的相量模型图。

（2）电容电压和电流的有效值满足关系：，表示电容的电压有效值等于电流有效值与容抗的乘积。

相量形式的推导
01
通过三角函数和复数的关系，将交流电路中的电压和电流用相 量表示。
02
利用相量图，通过几何方法分析电路，得出各支路电流和元件
上电压的关系。
通过相量的运算（加、减、乘、除等），推导出电路的阻抗、
03
导纳等参数，进而求解交流电路的各种问题。
相量形式的应用场景
交流电路分析
控制系统分析
利用相量形式分析交流电路，可以方便地 得出各支路电流和元件上电压的关系，计 算电路的功率、阻抗、导纳等参数。
3
相量形式的图解分析
通过相量图，可以直观地表示出电压和电流的相 位关系以及元件之间的相互作用，方便理解和分 析电路。
相量形式的优势与局限性
优势 • 简化了交流电路的计算过程。
• 通过相量图可以直观地理解电路的工作原理。
相量形式的优势与局限性
相量形式的优势与局限性
01
局限性
02
• 对于瞬态分析或非线性分析，相量形式可能不够 精确或复杂。
为了更好地适应这一发展趋势，需要进一步深入研究基尔霍夫定律的相量形式在复杂交流电路中的应用， 包括对非线性元件的处理、多频段电路的分析以及高性能计算在交流电路分析中的应用等。
此外，随着智能电网和物联网技术的发展，交流电路的应用领域也在不断扩展，需要进一步探索基尔霍 夫定律的相量形式在智能电网和物联网中的应用。
基尔霍夫定律的相量形式
contents
目录
• 引言 • 基尔霍夫定律的相量形式 • 相量形式与正弦稳态电路 • 相量形式在交流电路分析中的作用 • 基尔霍夫定律的相量形式与实际应用 • 结论
01 引言
基尔霍夫定律的重要性
在电路分析中，基尔霍夫定律 是基本的定律之一，它为电路 分析提供了基础。

60 53.13 (V )
U L j LI 240 36.87 (V )
U C
I
1
j C
160 143 .13 (V )
电路的相量图
一、相量图
相关的电压和电流相量在复平面上组成。 在相量图上，除了按比例反映各相量的模外， 最重要的是确定各相量的相位关系。
二、相量图的画法
选择某一相量作为参考相量， 而其他有关相量就根据它来加以确定。 参考相量的初相可取为零， 也可取其他值，视不同情况而定。
• 1、掌握正弦量的三要素和有效值 • 2、掌握电感、电容元件电流电压关系的
相量形式及基尔霍夫定律的相量形式 • 3、掌握阻抗、导纳、有功功率、无功功
率、视在功率和功率因数的概念 • 4、熟练掌握正弦电路分析的相量方法
• 5、了解频率特性的概念
预备知识——复数
一、复数的形式
1、代数形式
F = a + jb
1、串联电路
取电流为参考相量，从而确定各元件的电压相量； 表达KVL的各电压相量可按向量求和的方法作出。 2、并联电路 取电压为参考相量，从而确定各元件的电流相量； 表达KCL的各电流相量可按向量求和的方法作出。 3、串并联电路 从局部开始
以上一节中例题为例
I 4 53.13 ( A) U R 60 53.13 (V ) U L 240 36.87 (V ) UC 160 143 .13 (V )
2、角频率ω
i
反映正弦量变化的快慢
Im
单位 rad/s ωT=2π ω=2πf
2π O
π 2π ωt
i
f=1/T
频率f 的单位为赫兹（Hz）
周期T的单位为秒（s）
工频，即电力标准频率：f =50Hz,

时域列写微分方程
相量形式代数方程
相量模型：电压、电流用相量；元件用复数阻抗或导纳。
例1
A C 解
已知 U AB 50V, U AC 78V, 问：U BC ?
30
I
j40 jXL
B
U AB (30 I )2 (40 I )2 50 I
I 1A, U R 30 1 30V, U L 40 1 40V
I
+ U _ 15 j20 -j10
I1
I2
I3
例5：图示电路I1=I2=5A，U＝50V，总电压与总电流同 相位，求I、R、XC、XL。 解法1 0 设 I jXL
U C UC 0
0

+
则
I 1 50 A


I 2 j5 A
U
_
R I
jXC + UC
0 (直流) X L 0, 短路 , , X L , 开路
O

U jX L I jLI ,
jB U j 1 U 1 U I L L j L
相量表达式
波形图及相量图 uL pL i
O
UL
电压超前 电流90°
2 t
A 4 cos 100t 120 A
0
sin t sin t cos t cos t
4 cos 100t 300 A i2 4sin 100t 60 A
cos t sin t 2 sin t sin t 2
相量模型中结点①的KCL方 程相量形式为
I I 1 I 2 10600 5 900 5 j8.66 j5 5 j3.66

基尔霍夫定律网孔电流方程基尔霍夫定律(Kirchhoff laws)是电路中电压和电流所遵循的基本规律，是分析和计算较为复杂电路的基础，1845年由德国物理学家G.R.基尔霍夫（Gustav Robert Kirchhoff，1824～1887）提出。

基尔霍夫（电路）定律包括基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL）。

基尔霍夫（电路）定律既可以用于直流电路的分析，也可以用于交流电路的分析，还可以用于含有电子元件的非线性电路的分析。

1、先了解支路、节点、回路和网孔的概念。

(1)支路：由一个或几个元件首尾相接构成的无分支电路。

如：E1R1、R2、R3三条支路。

(2)节点：三条或三条以上支路的汇合点。

如B、E两个节点。

(3)回路：电路中任何闭合回路。

如ABEFA和BCDEB两条回路。

(4)网孔：内部不包含支路的回路。

如ABEFA和BCDEB两个网孔。

电路中的网孔数等于独立回路数。

2、基尔霍夫定律：分为电压定律和电流定律：(1)基尔霍夫电压定律对于电路中任何一个闭合回路，回路中各电阻上的电压降的代数和等于各电动势的代数和。

I1R1+I2R2-I3R3=E1+E2+E3(2)基尔霍夫电流定律对于任何节点而言，流入节点的电流总和必定等于流出节点的电流总和。

如上图：I2、I4、I5为流出节点的电流，I1、I3为流入节点的电流。

根据基尔霍夫定律，有I1+I3=I2+I4+I5.基尔霍夫定律的数学表达式1、基尔霍夫电流定律的表达式是：∑I=02、它的含义是：任一时刻，流入某结点的各电流矢量和为0.也可扩展到任一时刻，流入某封闭区间的各电流矢量和为0.基尔霍夫电流定律的本质是物质不灭在电学中的体现。

3、在交流电中使用基尔霍夫电流定律需注意，各交流电流的瞬时值符合∑i=0、相量值也符合∑I =0(这里的I 具有相量角度)，但有效值不符合∑I=0.所以KCL在交流电路一定要用瞬时值或相量来进行计算。

基尔霍夫第一定律表达式为∑i(t)=0.即对于任何节点，在任一时刻流出(或流入)该节点的电流代数和恒等于零。

1.电压电流电流的参考方向可以任意指定，分析时：若参考方向与实际方向一致，则i>0，反之i<0。

电压的参考方向也可以任意指定，分析时：若参考方向与实际方向一致，则u>0反之u<0。

2．功率平衡一个实际的电路中，电源发出的功率总是等于负载消耗的功率。

3．全电路欧姆定律：U=E-RI4．负载大小的意义：电路的电流越大，负载越大。

电路的电阻越大，负载越小。

5．电路的断路与短路电路的断路处：I＝0，U≠0 电路的短路处：U＝0，I≠0 。

基尔霍夫定律：1．几个概念：支路：是电路的一个分支。

结点：三条（或三条以上）支路的联接点称为结点。

回路：由支路构成的闭合路径称为回路。

网孔：电路中无其他支路穿过的回路称为网孔。

2．基尔霍夫电流定律：（1）定义：任一时刻，流入一个结点的电流的代数和为零。

或者说：流入的电流等于流出的电流。

（2）表达式：i进总和=0 或：i进=i出（3）可以推广到一个闭合面。

3．基尔霍夫电压定律（1）定义：经过任何一个闭合的路径，电压的升等于电压的降。

或者说：在一个闭合的回路中，电压的代数和为零。

或者说：在一个闭合的回路中，电阻上的电压降之和等于电源的电动势之和。

电位的概念（1）定义：某点的电位等于该点到电路参考点的电压。

（2）规定参考点的电位为零。

称为接地。

（3）电压用符号U表示,电位用符号V表示（4）两点间的电压等于两点的电位的差。

（5）注意电源的简化画法。

四．理想电压源与理想电流源1．理想电压源（1）不论负载电阻的大小，不论输出电流的大小，理想电压源的输出电压不变。

理想电压源的输出功率可达无穷大。

（2）理想电压源不允许短路。

2．理想电流源（1）不论负载电阻的大小，不论输出电压的大小，理想电流源的输出电流不变。

理想电流源的输出功率可达无穷大。

（2）理想电流源不允许开路。

3．理想电压源与理想电流源的串并联（1）理想电压源与理想电流源串联时，电路中的电流等于电流源的电流，电流源起作用。

正弦稳态电路的特点：激励和稳态响应统一频率。
相量法是分析求解正弦电流电路稳态响应的一种有效工具。
1、相量：

I

IΨ为正弦量
i(t)
对应的相量。

i(t)2Isiω n tΨ () II Ψ
相量的模表示正弦量的有效值 正弦量的相量表示: 相量的幅角表示正弦量的初相位
加一个小圆点是用来和普通的复数相区别(强调它与正 弦量的联系)，同时也改用“相量”，而不用“向量”， 是因为它表示的不是一般意义的向量，而是表示一个正弦
N
线性
w1
w2
N
线性
w非
线性
不适用 ③ 相量法可以用来求强制分量是正弦量的任意常系数 线
性微分方程的特解，即可用来分析正弦稳态电路。
8. 4 电路定律的相量形式
VCR、KCL和KVL
一、电阻、电感和电容的VCR
1. 电阻 i(t)
+
uR(t) R -

I
+

UR
R
-
相量模型
时域形式：
已i知 (t)2Isiω n t Ψ (i)
(3) 初相位(initial phase angle)y ：反映了正弦量的计时起点。
(wt+y )表示正弦量随时间变化的
进程,称之为相位角。它的大小决定该
i(t)=Imsin(w t+y)
i
T
时刻正弦量的值。 Im
y/w O
2 twt
同一个正弦量，计时起点不同，初相位不同。 i
一般规定：| | 。
恰好等于初相位之差
j >0， u 领先(超前)I j 角，或i 落后(滞后) u j 角(u 比 i 先

第一章：电路模型和电路定理 一．电流、电压、功率概念1.电流的参考方向可以任意指定，分析时：假设参考方向与实际方向一致，则i>0，反之i<0。

电压的参考方向也可以任意指定，分析时：假设参考方向与实际方向一致，则u>0反之u<0。

2． 功率平衡一个实际的电路中，电源发出的功率总是等于负载消耗的功率。

3．欧姆定律：，，运用欧姆定理的时候要先判断电压与电流方向是否关联，如果不关联需要加负号 4． 电路的断路与短路电路的断路处：I ＝0，U≠0 电路的短路处：U ＝0，I≠0 三． 基尔霍夫定律 1． 几个概念：支路：是电路的一个分支。

结点：三条〔或三条以上〕支路的联接点称为结点。

回路：由支路构成的闭合路径称为回路。

网孔：电路中无其他支路穿过的回路称为网孔。

2． 基尔霍夫电流定律：〔1〕 定义：任一时刻，流入一个结点的电流的代数和为零。

或者说：流入的电流等于流出的电流。

〔2〕 表达式：i 进总和=0 或： i 进=i 出 〔3〕 可以推广到一个闭合面。

3． 基尔霍夫电压定律〔1〕 定义：经过任何一个闭合的路径，电压的升等于电压的降。

或者说：在一个闭合的回路中，电压的代数和为零。

或者说：在一个闭合的回路中，电阻上的电压降之和等于电源的电动势之和。

〔2〕基尔霍夫电压定律可以推广到一个非闭合回路 第二章电阻电路的等效变换概念：两个两端电路，端口具有相同的电压、电流关系,则称它们是等效的电路。

对外等效，对内不等效2. 串联电路的总电阻等于各分电阻之和，各电阻顺序连接，流过同一电流，串联电阻具有分压作用，Ri u =i u R =Gu R u i ==u R R R u 2111+=u R R R u 2122+=3.电阻并联等效电导等于并联的各电导之和，并联电阻具有分流作用4. 电阻的Y 形连接和形连接的等效变换，。

假设三个电阻相等(对称)，则有5． 理想电压源〔1〕 不管负载电阻的大小，不管输出电流的大小，理想电压源的输出电压不变。