《单位圆与周期性》

《单位圆与周期性》教学设计教材首先通过对终边相同角的正、余弦函数值的分析得出公式，使学生初步了解函数的周期性，进而给出周期函数的定义。

特别探究正弦函数、余弦函数的周期、最小正周期，以便于后续的学习和应用。

【知识与能力目标】1、掌握终边相同角的正弦、余弦函数值间的关系2、理解周期函数的定义；熟知正、余弦函数的周期、最小正周期。

【过程与方法目标】通过对周期函数的定义和三角函数周期的推导，提高学生分析、探究、解决问题的能力。

【情感态度价值观目标】1、使学生认识到事物之间是有联系的，终边相同角的三角函数值相等；2、学习转化的思想，培养学生严谨治学、一丝不苟的科学精神。

【教学重点】掌握终边相同角的正弦、余弦函数值间的关系【教学难点】理解周期函数的定义；熟知正、余弦函数的周期、最小正周期。

电子课件调整、相应的教具带好、熟悉学生名单、电子白板要调试好。

一、复习导入部分复习回顾正、余弦函数的定义、定义域、值域、在各个象限的符号。

二、探究新知： 阅读教材P 16～P 17练习以上部分，完成下列问题。

1、终边相同的角的正弦、余弦函数值的关系。

(1)终边相同的角的正弦函数值相等，即sin(x ＋2k π)＝sin x (k ∈Z )。

(2)终边相同的角的余弦函数值相等，即cos(x ＋2k π)＝cos x (k ∈Z )。

2、一般地，对于函数f (x )，如果存在非零实数T ，对定义域内的任意一个x 值，都有f (x ＋T )＝f (x )，则称f (x )为周期函数，T 称为这个函数的周期。

3、特别地，正弦函数、余弦函数是周期函数，称2k π(k ∈Z ，k ≠0)是正弦函数、余弦函数的周期，其中2π是正弦函数、余弦函数正周期中最小的一个，称为最小正周期。

三、例题解析求下列各角的三角函数值。

(1)sin ⎝ ⎛⎭⎪⎫－236π；(2)cos 1 500°； (3)sin 174π；(4)cos 253π。

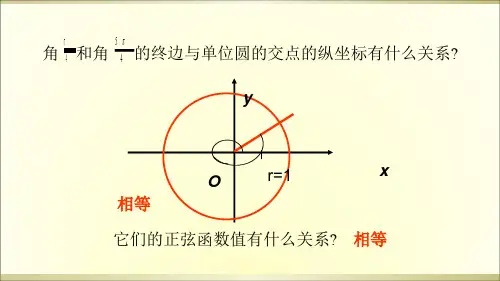
《单位圆与周期性》教学设计本课时编写：双辽一中张敏◆教材分析本节是根据在单位圆中，任意角的正弦、余弦函数定义得到函数的特征，通过分析两个等式直接下了定义。

由于定义来的突然，学生对于应用的理解很低，因此本教案设计了两个例题和一个变式训练，算是抛砖引玉。

◆教学目标【知识与能力目标】了解并掌握周期性的定义；【过程与方法目标】积极讨论，踊跃展示，大胆质疑，探究周期性的规律．【情感态度价值观目标】在学习中感悟数学概念的合理性、严谨性、科学性．感悟数学的本质，培养追求真理的精神．通过本节的学习，使同学们对正弦函数与余弦函数有了一个全新的认识，通过对定义的应用，提高学生分析、解决问题的能力．◆教学重难点【教学重点】周期性的定义.【教学难点】周期性的应用.◆课前准备多媒体课件教学过程一、新知探究提出问题：（1）观察下图，根据前面学的知识，在单位圆中，由任意角的正弦、余弦函数定义能得到哪些结论？（2）怎样定义周期函数？（3）怎样确定最小正周期？通过探讨，由老师进行归纳总结：由三角函数的定义，可以知道：终边相同的角的同一三角函数的值相等，也就是终边相同的角的正弦函数值相等，即sin(2kπ+x)=sinx,k∈Z；终边相同的角的余弦函数值相等，即cos(2kπ+x)=cosx,k∈Z.对于任意一个角x，每增加的2π整数倍，其正弦函数值、余弦函数值均不变。

所以正弦函数值、余弦函数值均是随角的变化呈周期性变化的。

我们把这种随自变量的变化呈周期性变化的函数叫作周期函数，正弦函数、余弦函数是周期函数，且2kπ（k∈Z，k≠0）为正弦函数、余弦函数的周期。

一般地，对于函数f(x)，如果存在非零实数T，任取定义域内地任意一个值x，都有f(x+T)=f(x),我们就把称它为周期函数，T称为这个函数的周期。

特别注意：若不加特别说明，本书所指的周期均为函数的最小正周期。

【设计意图】通过提问，引出新知，让学生带着问题思考。

二、典例分析.例1. 求下列三角函数值：（1）sin390° ；（2）cos19π6由老师带领学生做题，加深对观念的理解，最后进行点评。