ID3算法实验报告

实验一 ID3算法实现一、实验目的通过编程实现决策树算法，信息增益的计算、数据子集划分、决策树的构建过程。

加深对相关算法的理解过程。

实验类型：验证计划课间：4学时二、实验内容1、分析决策树算法的实现流程；2、分析信息增益的计算、数据子集划分、决策树的构建过程；3、根据算法描述编程实现算法，调试运行；4、对所给数据集进行验算，得到分析结果。

三、实验方法算法描述：以代表训练样本的单个结点开始建树；若样本都在同一个类，则该结点成为树叶，并用该类标记；否则，算法使用信息增益作为启发信息，选择能够最好地将样本分类的属性；对测试属性的每个已知值，创建一个分支，并据此划分样本；算法使用同样的过程，递归形成每个划分上的样本决策树递归划分步骤，当下列条件之一成立时停止：给定结点的所有样本属于同一类；没有剩余属性可以进一步划分样本，在此情况下，采用多数表决进行四、实验步骤1、算法实现过程中需要使用的数据结构描述：Struct{int Attrib_Col; // 当前节点对应属性int Value; // 对应边值Tree_Node* Left_Node; // 子树Tree_Node* Right_Node // 同层其他节点Boolean IsLeaf; // 是否叶子节点int ClassNo; // 对应分类标号}Tree_Node;2、整体算法流程主程序：InputData();T=Build_ID3(Data,Record_No, Num_Attrib);OutputRule(T);释放内存;3、相关子函数：3.1、 InputData(){输入属性集大小Num_Attrib;输入样本数Num_Record;分配内存Data[Num_Record][Num_Attrib];输入样本数据Data[Num_Record][Num_Attrib]；获取类别数C(从最后一列中得到);}3.2、Build_ID3(Data,Record_No, Num_Attrib){Int Class_Distribute[C];If (Record_No==0) { return Null }N=new tree_node();计算Data中各类的分布情况存入Class_Distribute Temp_Num_Attrib=0;For (i=0;i<Num_Attrib;i++)If (Data[0][i]>=0) Temp_Num_Attrib++;If Temp_Num_Attrib==0{N->ClassNo=最多的类；N->IsLeaf=TRUE;N->Left_Node=NULL;N->Right_Node=NULL;Return N;}If Class_Distribute中仅一类的分布大于0{N->ClassNo=该类；N->IsLeaf=TRUE;N->Left_Node=NULL;N->Right_Node=NULL;Return N;}InforGain=0;CurrentCol=-1;For i=0;i<Num_Attrib-1;i++){TempGain=Compute_InforGain(Data,Record_No,I,Num_Attrib); If (InforGain<TempGain){ InforGain=TempGain; CurrentCol=I;}}N->Attrib_Col=CurrentCol;//记录CurrentCol所对应的不同值放入DiferentValue[]；I=0;Value_No=-1;While i<Record_No {Flag=false;For (k=0;k<Value_No;k++)if (DiferentValu[k]=Data[i][CurrentCol]) flag=true;if (flag==false){Value_No++;DiferentValue[Value_No]=Data[i][CurrentCol] } I++;}SubData=以Data大小申请内存空间；For (i=0;i<Value_No;i++){k=-1;for (j=0;j<Record_No-1;j++)if (Data[j][CurrentCol]==DiferentValu[i]){k=k++;For(int i1=0;i1<Num_Attrib;i1++)If (i1<>CurrentCol)SubData[k][i1]=Data[j][i1];Else SubData[k][i1]=-1;}N->Attrib_Col=CurrentCol;N->Value=DiferentValu[i];N->Isleaf=false;N->ClassNo=0;N->Left_Node=Build_ID3(SubData,k+1, Num_Attrib);N->Right_Node=new Tree_Node;N=N->Right_Node;}}3.3、计算信息增益Compute_InforGain(Data,Record_No, Col_No, Num_Attrib) {Int DifferentValue[MaxDifferentValue];Int Total_DifferentValue;Int s[ClassNo][MaxDifferentValue];s=0;// 数组清0;Total_DifferentValue=-1;For (i=0;i<Record_No;i++){J=GetPosition(DifferentValue,Total_DifferentValue,Data[i][Col_no]);If (j<0) {Total_DifferentValue++;DifferentValue[Total_DifferentValue]=Data[i][Col_no];J=Total_DifferentValue;}S[Data[i][Num_Attrib-1]][j]++;}Total_I=0;For (i=0;i<ClassNo;i++){Sum=0;For(j=0;j<Record_No;j++) if Data[j][Num_Attrib-1]==i sum++; Total_I=Compute_PI(Sum/Record_No);}EA=0;For (i=0;i<Total_DifferentValue;i++);{ temp=0;sj=0; //sj是数据子集中属于类j的样本个数；For (j=0;j<ClassNO;j++)sj+=s[j][i];For (j=0;j<ClassNO;j++)EA+=sj/Record_No*Compute_PI(s[j][i]/sj);}Return total_I-EA;}3.4、得到某数字在数组中的位置GetPosition(Data, DataSize,Value){For (i=0;i<DataSize;i++) if (Data[i]=value) return I;Return -1;}3.5、计算Pi*LogPiFloat Compute_PI(float pi){If pi<=0 then return 0;If pi>=1 then return 0;Return 0-pi*log2(pi);}五、实验报告要求1、用C语言实现上述相关算法（可选择利用matlab函数实现）2、实验操作步骤和实验结果，实验中出现的问题和解决方法。

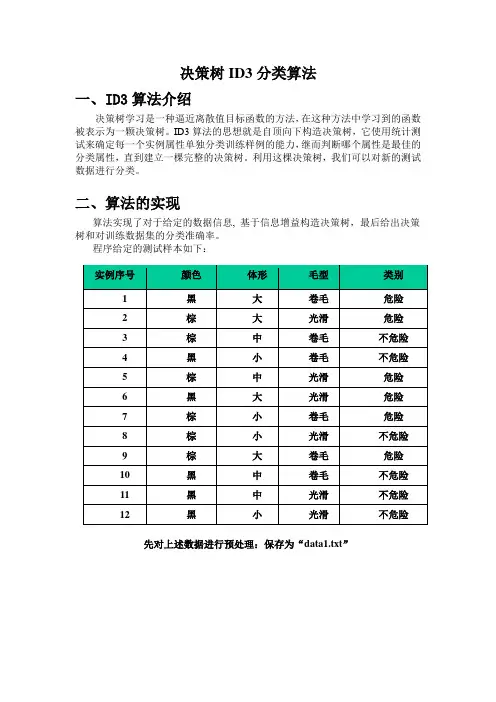
决策树ID3分类算法一、ID3算法介绍决策树学习是一种逼近离散值目标函数的方法，在这种方法中学习到的函数被表示为一颗决策树。

ID3算法的思想就是自顶向下构造决策树，它使用统计测试来确定每一个实例属性单独分类训练样例的能力，继而判断哪个属性是最佳的分类属性，直到建立一棵完整的决策树。

利用这棵决策树，我们可以对新的测试数据进行分类。

二、算法的实现算法实现了对于给定的数据信息, 基于信息增益构造决策树，最后给出决策树和对训练数据集的分类准确率。

程序给定的测试样本如下：实例序号颜色体形毛型类别1黑大卷毛危险2棕大光滑危险3棕中卷毛不危险4黑小卷毛不危险5棕中光滑危险6黑大光滑危险7棕小卷毛危险8棕小光滑不危险9棕大卷毛危险10黑中卷毛不危险11黑中光滑不危险12黑小光滑不危险先对上述数据进行预处理：保存为“data1.txt”再运行程序，读入数据，输出分析过程和决策规则：中间还有一些过程，为了节约资源，不复制过来了，下面是决策规则：根据该规则，树形图如下：三、程序代码及其部分注释其中最核心的部分：void Generate_decision_tree(Tree_Node * & root,vector<int> Samples, vector<int> attribute_list,int class_id)该函数由给定的训练数据产生一棵判定树。

完整代码：#include <stdio.h>#include <iostream>#include <vector>#include <math.h>#include <string.h>using namespace std;typedef struct tnode{char tdata[100];}tnode;typedef struct Tree_Node{char name[100];bool isLeaf; //标记是否叶子节点vector<tnode> att_list;//属性名称列表vector<Tree_Node * > child_list;}Tree_Node,* pTreeNpde;typedef struct dnode{vector<tnode>row;}dnode;typedef struct D_Node{vector<dnode>DB;vector<tnode> attr_name;tnode class_name;}D_Node;D_Node G_DB;pTreeNpde Root = NULL;typedef struct FreeQNode{char name[100];int count;vector<int> Set_ID;}FreeQNode;typedef struct FreeQNodeDouble{char name[100];int count;vector<int> row_id;vector<FreeQNode> classes;//存放分类属性列表及相应的出现次数}FreeQNodeDouble;typedef struct attr_node{int attr_id;vector<tnode> attr_name;vector<int> count_list;}attr_node;vector<attr_node> G_Attr_List;typedef struct binNode{char name[100];int count;vector<int> Set_ID;struct binNode * lchild;struct binNode * rchild;}binNode;typedef struct binNodeDouble{char name[100];int count;vector<int> row_id;struct binNodeDouble * lchild;struct binNodeDouble * rchild;vector<FreeQNode> classes;}binNodeDouble;void insert_tree(binNode * & r, char str[100]){if (NULL == r){binNode * node = new binNode;strcpy(node->name,str);node->count = 1;//printf("[%s,%d]\n",node->name,node->count);node->lchild = node->rchild = NULL;r = node;}else{if (strcmp(r->name,str) == 0){r->count ++;}else if (strcmp(r->name,str) < 0){insert_tree(r->lchild,str);}else{insert_tree(r->rchild,str);}}}void delete_bin_tree(binNode *& r){if (r != NULL){delete_bin_tree(r->lchild);delete_bin_tree(r->rchild);delete(r);r = NULL;}}void Bin_tree_inorder(binNode * r,vector<FreeQNode> & Fq) {if (r != NULL){Bin_tree_inorder(r->lchild,Fq);FreeQNode ft;//printf("%s,%d\n",r->name,r->count);strcpy(,r->name);ft.count = r->count;for (int i= 0;i < r->Set_ID.size();i++){ft.Set_ID.push_back(r->Set_ID[i]); //保存子集对应的ID号}Fq.push_back(ft); //此处少了这条语句，造成结果无法返回Bin_tree_inorder(r->rchild,Fq);}}void Get_attr(binNode * r,attr_node & attr){if (r != NULL){Get_attr(r->lchild,attr);tnode t;strcpy(t.tdata,r->name);//printf("%s,%d\n",r->name,r->count);attr.attr_name.push_back(t);attr.count_list.push_back(r->count);//保存出现次数Get_attr(r->rchild,attr);}}void insert_tree_double(binNodeDouble *& r, int DB_ID,char attr_name[100],char class_name[100]){if (NULL == r){binNodeDouble * node = new binNodeDouble;strcpy(node->name,attr_name);node->count = 1;node->row_id.push_back(DB_ID);node->lchild = node->rchild = NULL;FreeQNode fq;strcpy(,class_name);fq.count = 1;fq.Set_ID.push_back(DB_ID); //保存子集所对应的ID号node->classes.push_back(fq);r= node;}else{if (strcmp(r->name,attr_name) == 0){r->count ++;r->row_id.push_back(DB_ID);//这里也需要保存相应的ID号bool found = false;for (int i = 0; i< r->classes.size();i++){if (strcmp(r->classes[i].name,class_name) == 0){r->classes[i].count ++;r->classes[i].Set_ID.push_back(DB_ID);//保存子集对应的ID号found = true; //发现相同的变量名，计数器增1,break; //并退出循环}}if (!found){FreeQNode fq;strcpy(,class_name);fq.count = 1;fq.Set_ID.push_back(DB_ID);//保存子集所对应的ID号r->classes.push_back(fq);}}else if (strcmp(r->name,attr_name) < 0){insert_tree_double(r->lchild,DB_ID,attr_name,class_name);}else{insert_tree_double(r->rchild,DB_ID,attr_name,class_name);}}void delete_bin_tree_double(binNodeDouble *& r){if (r != NULL){delete_bin_tree_double(r->lchild);delete_bin_tree_double(r->rchild);delete(r);r = NULL;}}void Bin_tree_inorder_double(binNodeDouble *& r,vector<FreeQNodeDouble> &Fq){if (r != NULL){Bin_tree_inorder_double(r->lchild,Fq);FreeQNodeDouble ft;strcpy(,r->name); //保存候属性的名称ft.count = r->count;for (int k = 0;k< r->row_id.size();k++){ft.row_id.push_back(r->row_id[k]);}//printf("doubleTree. %s,%d\n",r->name,r->count);for (int i = 0;i< r->classes.size();i++){FreeQNode fq;strcpy(,r->classes[i].name);fq.count = r->classes[i].count;for (int j = 0;j < r->classes[i].Set_ID.size();j++){fq.Set_ID.push_back( r->classes[i].Set_ID[j]); //保存子集对应的ID号}ft.classes.push_back(fq);}Fq.push_back(ft);ft.classes.erase(ft.classes.begin(),ft.classes.end());//使用完，必须清空Bin_tree_inorder_double(r->rchild,Fq);}}void getFqI(vector<int> S,int class_id,vector<FreeQNode> & Fq){binNode * root = NULL;for (int i = 0;i< S.size();i++){insert_tree(root,G_DB.DB[S[i]].row[class_id].tdata);}Bin_tree_inorder(root,Fq);delete_bin_tree(root);}void getFqIA(vector<int> S,int attr_id,int class_id,vector<FreeQNodeDouble> & Fq){binNodeDouble * root = NULL;for (int i = 0;i< S.size();i++){insert_tree_double(root,S[i],G_DB.DB[S[i]].row[attr_id].tdata,G_DB.DB[S[i]].row[class_id] .tdata);}Bin_tree_inorder_double(root,Fq);delete_bin_tree_double(root);}void readdata(char *filename){char str[1000];FILE * fp;fp = fopen(filename,"r");fgets(str,1000,fp);int len = strlen(str);int attr_no = 0; //属性个数int row_num = 0;if (str != NULL){row_num = 1;}for (int i = 0;i< len;i++){if (str[i] == '\t'){attr_no ++;}}attr_no ++;//最后一个是回车，整个属性值+1printf("%d\n",attr_no);while(fgets(str,1000,fp) != NULL){row_num ++; //统计行数}fclose(fp);fopen(filename,"r");tnode t;for (i = 0;i<attr_no;i++){fscanf(fp,"%s",t.tdata);G_DB.attr_name.push_back(t);printf("%s\n",t.tdata);}strcpy(G_DB.class_name.tdata,G_DB.attr_name[attr_no-1].tdata); for (int j = 1;j< row_num;j++){dnode dt;tnode temp;for (int i = 0;i<attr_no;i++){fscanf(fp,"%s",temp.tdata);dt.row.push_back(temp);}G_DB.DB.push_back(dt);dt.row.erase(dt.row.begin(),dt.row.end());}printf("%d\n",G_DB.DB.size());for (i = 0;i< G_DB.DB.size();i++){for (int j = 0;j< G_DB.DB[i].row.size();j++){printf("%s\t",G_DB.DB[i].row[j].tdata);}printf("\n");}}double Fnc_I(vector<int> S,int class_id){//给定一个子集，计算其按照class_id所对应的分类属性进行分类时的期望I// printf("called Fnc_I(%d)\n ",class_id);vector<FreeQNode> Fq;getFqI(S,class_id,Fq); //调用getFqI获取按照Class_id为分类标准的分类结果,当Fq中为一条数据时，则子集S都属于一个分类//否则，从中找到出现此时最大的，作为返回结果// printf("begin to compute I \n");double total = 0;for (int i = 0;i< Fq.size();i++){total += Fq[i].count;// printf("%s,%d\n",Fq[i].name,Fq[i].count);}double result = 0;if (0 == total){return 0;}for (i = 0;i< Fq.size();i++){double p = Fq[i].count/total;result += -1*(p * log(p)/log(2));}// printf("FNC_I return\n\n");return result;}double Fnc_IA(vector<int> S,int attr_id,int class_id,vector<FreeQNodeDouble> & Fq) {//给定一个子集，计算其按照class_id所对应的分类属性进行分类时的期望I getFqIA(S,attr_id,class_id,Fq);double total = 0;for (int i = 0;i< Fq.size();i++){total += Fq[i].count;}double result = 0;if (0 == total){return 0;}bool pr= false;for (i = 0;i< Fq.size();i++){double stotal = Fq[i].count;double sresult = 0;if (pr) printf("[%s,%d]\n",Fq[i].name,Fq[i].count);for (int j = 0;j < Fq[i].classes.size();j++){if (pr) printf("%s,%d\n",Fq[i].classes[j].name,Fq[i].classes[j].count);for (int k = 0;k < Fq[i].classes[j].count;k++){// printf("%d\t",Fq[i].classes[j].Set_ID[k]+1);}//printf("\n");double sp = Fq[i].classes[j].count/stotal; //计算子集的频率sresult += -1*(sp*log(sp)/log(2));}result += (stotal/total) * sresult;}if (pr) printf("\n");return result;}int SelectBestAttribute(vector<int> Samples,vector<int> attribute_list,int class_id) {//输入训练数据集Samples，候选属性列表attribute_list//分类属性标记class_id//返回best_attributedouble fi = Fnc_I(Samples,5);// printf("%lf\n",fi);double IA = 999999999;int best_attrib = -1;for (int i = 0;i < attribute_list.size();i++){vector<FreeQNodeDouble> fqd;double tfa = Fnc_IA(Samples,attribute_list[i],class_id,fqd);// printf("%d, FIA = %lf\n",i,tfa);if (IA > tfa){IA = tfa;best_attrib = i;}}//printf("%lf\n",IA);printf("gain(%d) = %lf - %lf = %lf\n",best_attrib,fi,IA,fi - IA);return attribute_list[best_attrib];}void fnc_getattr(vector<int> Samples,int att_id,attr_node &at){binNode * root = NULL;for (int i = 0;i< Samples.size();i++){insert_tree(root,G_DB.DB[Samples[i]].row[att_id].tdata);}Get_attr(root,at);delete_bin_tree(root);}void get_class_num_and_name(vector<int> Samples,int class_id,int & class_num,tnode & class_name){attr_node at;binNode * root = NULL;for (int i = 0;i< Samples.size();i++){insert_tree(root,G_DB.DB[Samples[i]].row[class_id].tdata);}Get_attr(root,at);delete_bin_tree(root);//printf("att_size = %d\n",at.attr_name.size());class_num = at.attr_name.size();int num = 0;int id = 0;if (1 == class_num){strcpy(class_name.tdata,at.attr_name[0].tdata);}else{for (int j = 0;j < at.attr_name.size();j++ ){if (at.count_list[j] > num){num = at.count_list[j];id = j;}}}strcpy(class_name.tdata,at.attr_name[id].tdata);//保存最普通的类名}void getAllTheAttribute(vector<int> Samples,vector<int> attribute_list,int class_id){printf("all the attribute are:\n");for (int i = 0;i < attribute_list.size();i++){attr_node at;at.attr_id = attribute_list[i];fnc_getattr(Samples,attribute_list[i],at);G_Attr_List.push_back(at);}for (i = 0;i <G_Attr_List.size();i++){printf("%d\n",G_Attr_List[i].attr_id);for (int j = 0;j< G_Attr_List[i].attr_name.size();j++){printf("%s\t",G_Attr_List[i].attr_name[j].tdata);}printf("\n");}}void Generate_decision_tree(Tree_Node * & root,vector<int> Samples, vector<int>attribute_list,int class_id){/*算法：Generate_decision_tree(samples, attribute)。

规则 ｌ ：如 果 Ｏ ｔ ｏ ＝ ｕ ｎ ， Ｈ ｍ ｄｔ＝ ｕ ｏｋ Ｓ ｎ ｙ 且 ｕ ｉｉ ｌ ｙ
Ｎ ｒａ， ｏｍ ｌ则适合 打球 ； 规 则 ２ 如 果 Ｏ ｔｏ ＝ ｕｎ ， Ｈ ｍｉｉ ＝ ： ｕｏｋ Ｓｎｙ 且 ｕ ｄｔ ｌ ｙ Ｈｇ ， 不适合打球 ； ｉ 则 ｈ 规则３ 如果Ｏ ｔｏ＝ ｖｒａｔ则适合 打球 ； ： ｕｏｋ Ｏ ｅ ｓ ｌ ｃ ， 规 则４ 如 果 Ｏ ｔｏ ＝ ａｎ 且 Ｗｉｄ Ｗｅｋ ： ｕｌ ｋ Ｒ ｉ， ｏ ｎ＝ ａ， 则适 合打球 ； 规则５如果 ， ｕ ｏｋＲ ｉ， ： Ｏ ｔｏ＝ ａ 且ＷｉｄＳｒｎ ， ｌ ｎ ｎ＝ｔ ｇ ｏ 则不适 合打球 ． 本文 首先研 究 了一个 属性 的某 几个属 性值 并 的权熵 之 和与该 属性单 个属 性值 的权熵 之 和 Ｎ 的关 系 ， 出了如 下结论 ： 得 一个 属性 的某几 个属
其中属性的熵定义为该属性单个属性值的权熵之和在生成树的过程中每个结点只有一个属性值权熵相同的属性值看作一个属性值其优点是采用自顶向下不回溯的策略搜索全部的属性空间其建立决策树的算法简单难度小分类速度快
２０ 年 １ ０８ Ｏ月
保 定 学 院 学 报
Ｊ ＯＵＲＮＡＬ ＯＦ ＢＡＯＤＩ ＮＧ ＵＮＩ ＶＥＲＳ ＴＹ Ｉ
权平均值 ， 即
Ａ ） 等 ． 一
而以／ 重 为根进行分类所得到的信息增益为
ｇ ｉ（ ＝ｐ，， Ｅ Ａ） ａ Ａ） （ ） （ ． ｎ ｎ－
个好的分类属性将使信息增益增大． ３ Ｉ 选择使 ｎＡ） Ｄ （ 具有最大的属 值对应的厂 个子集 递归调用上述生成过程生成子节点．
信息熵原理１ 选择信息熵最小的属性作为分类 ７ １ ， 属性 ， 递归地拓展决策树的分枝 ， 完成决策树的

ID3算法的优化朱琳;杨杨【摘要】随着硬件设备的普及，促使信息技术和移动互联网的快速发展，人们已经告别了信息匮乏的时期，而进入到了信息过载的时期。

人们试图用搜索功能搜索出自己想要的信息，如今已是非常困难，怎样从海量的数据中筛选出有价值的信息是信息提供者和信息需求者都要面对的挑战。

本文对数据分类中的 ID3算法的基本概念和原理以及其构造过程进行了详细阐述，针对 ID3算法倾向于选择取值较多的属性的缺点，引进属性阈值和信息增益率两个概念。

弥补ID3算法属性选择标准的不足，来实现新的属性选择标准，对原有ID3算法进行改进。

通过实验对改进前后的算法进行了比较，实验表明，改进后的算法提高了分类准确度。

%With the popularization of hardware equipment, prompting the rapid development of information tech-nology and mobile Internet, people have already bid farewell to the period of lack of information, and entered the period of information overload. People try to use the search function to search out the information they want, and now it is very difficult, how to filter out from the mass of valuable information is information providers and information needs of those who have to face the challenge. In this paper, the basic concept and principle of ID3 algorithm in data classifica-tion and its construction process are expounded. In view of the shortcomings of ID3 algorithm which tend to choose more attributes, the two concepts of attribute threshold and information gain rate are introduced. Make up for the defi-ciency of attribute selection standard of ID3 algorithm to realize the new attributeselection standard and improve the original ID3 algorithm. Experiments show that the improved algorithm improves the classification accuracy.【期刊名称】《软件》【年(卷),期】2016(037)012【总页数】4页(P89-92)【关键词】数据挖掘;ID3算法;信息增益;信息增益率;分类【作者】朱琳;杨杨【作者单位】北京邮电大学，北京 100876;北京邮电大学，北京 100876【正文语种】中文【中图分类】TP311.13在解决分类问题时，使用次数最多、范围最广的算法是决策树算法。

id3算法实验报告篇一：ID3算法实验报告一、实验原理决策树通过把实例从根节点排列到某个叶子节点来分类实例，叶子节点即为实例所属的分类。

树上的每一个节点说明了对实例的某个属性的测试，并且该节点的每一个后继分支对应于该属性的一个可能值，例如下图。

构造好的决策树的关键在于如何选择好的逻辑判断或属性。

对于同样一组例子，可以有很多决策树能符合这组例子。

人们研究出，一般情况下或具有较大概率地说，树越小则树的预测能力越强。

要构造尽可能小的决策树，关键在于选择恰当的逻辑判断或属性。

由于构造最小的树是NP-难问题，因此只能采取用启发式策略选择好的逻辑判断或属性。

用信息增益度量期望熵最低，来选择分类属性。

公式为ID3算法创建树的Root结点如果Examples都为正，那么返回label=+中的单结点Root 如果Examples都为反，那么返回lable=-单结点树Root如果Attributes为空，那么返回单节点树Root，lable=Examples中最普遍的目标属性值否则开始A 目标属性值 lable=Examples中最普遍的否则在这个新分支下加一个子树ID3(example-vi,target-attribute,attributes-|A|) 结束返回 Root二、算法实现训练数据存放在Data.txt 中第一行为训练样本数量和每个样本中属性的数量第二行为每个属性取值的数量之后n行为所有样本节点数据结构struct DTNode{int name; //用 1,2,3...表示选择的属性，0表示不用分类，即叶节点int data[D_MAX+1]; //表示此节点包含的数据,data[i]=1,表示包含二维数组data[][]中的第i条数据int leaf;//leaf=1 正例叶节点；leaf=2 反例叶节点；leaf=0不是节点 int c; //c=1 正类；c=0 反类DTNode *child[P+1];//按属性值的个数建立子树};定义函数void Read_data() //从数据文件Data.txt中读入训练数据DT_pointer Create_DT(DT_pointer Tree,int name,int value)//创建决策树 int chose(int *da)//选择分类属性float Gain(int *da,int p) //计算以p属性分类的期望熵float Entropy(int *da) //计算数据的熵int test_leaf(int *da) //测试节点属性void Out_DT(DT_pointer Tree) //用线性表形式输出建立的决策树int Class(int *da) //对输入的测试样本分类全局变量FILE *fp;int p_num; //属性的数量int pi[P_MAX+1]; //每个属性有几种取值int d_num;//数据的数量int data[P_MAX+1][D_MAX+1];//存储训练数据三、程序不足1.、默认训练数据是正确的，对是否发生错误不予考虑2、没有考虑训练数据可以包含缺少属性值的实例3、只能分正反两类四、程序源码#include#include#include#include#include#define P_MAX 10#define D_MAX 50#define P 5//一条数据包括所有属性的取值（1,2,3...）和分类的值（0或1） FILE *fp;int p_num; //属性的数量int pi[P_MAX+1]; //每个属性有几种取值int d_num;//数据的数量int data[P_MAX+1][D_MAX+1];//存储训练数据//定义结点类型struct DTNode{int name; //此节点分类属性的名称int data[D_MAX+1]; //表示此节点包含的数据int leaf; //leaf=1 正例叶节点；leaf=2 反例叶节点；叶节点int c; //c=1 正类；c=0 反类DTNode *child[P+1];//按属性值的个数建立子树};typedef struct DTNode *DT_pointer;DT_pointer DT = NULL;int root = 0;int test_leaf(int *da) leaf=0不是int i;int a,b;a = 0;// a=0表示没有0类 a=1表示有0类 for(i = 1; i {if(*(da+i) ==1 && data[i][0] == 0){a = 1;break;}}b = 0;//b=0表示没有1类 b=1表示有1类 for(i = 1;i {if(*(da+i) == 1 && data[i][0] == 1){break;}}if(a == 0 && b == 1)return 1;//是1叶节点else if(a == 1 && b == 0)return 2;//是0叶节点else if(a == 0 && b == 0)return 2;//此节点无数据elsereturn 0;//不是叶节点}int test_c(int a) //给叶节点附属性值{if(a == 1)return 1;elsereturn 0;}float Entropy(int *da) //计算数据的熵{篇二：ID3算法实验报告装订线：ID3算法分析与实现学院xxxxxxxxxxxxxxxxxxxx 专业 xxxxxxxxxxxxxxxx 学号xxxxxxxxxxx 姓名 xxxx 指导教师 xxxxXX年x月xx日题目ID3算法分析与实现摘要:决策树是对数据进行分类，以此达到预测的目的。

ID3算法范文ID3算法是一种决策树学习算法，用于在给定数据集中进行分类。

它根据信息论的概念选择最佳的特征来划分数据集，以产生一个有助于分类的决策树模型。

通过理解ID3算法的原理和基本步骤，我们能够更好地理解决策树学习算法的工作原理。

ID3算法基于信息熵的概念，信息熵是衡量数据集的无序程度的度量。

信息熵越高，表示数据集越无序，越难以进行分类。

ID3算法的目标是找到能够最大程度地降低数据集无序程度的特征，将数据集划分为尽可能相似的子集。

算法的基本步骤如下：1.计算整个数据集的信息熵。

首先，需要计算数据集中各个类别的频率，然后使用信息熵公式来计算整个数据集的信息熵。

2.对于每个特征，计算它的信息增益。

信息增益表示使用特征划分数据集后，整个数据集无序程度减少的程度。

信息增益越大，表示该特征对于数据集的分类具有更大的贡献。

信息增益可以通过计算数据集划分后各个子集的信息熵以及它们的权重来计算。

3.选择信息增益最大的特征作为当前节点的划分特征。

选取信息增益最大的特征，意味着该特征能够对数据集进行更好的划分，以便进行更准确的分类。

4.根据选择的划分特征，将数据集划分为几个子集。

每个子集包含特定特征取值的数据样本。

如果属性的取值是离散的，将根据不同的取值来创建子集；如果属性的取值是连续的，可以根据不同的划分点来创建子集。

5.对于每个子集，如果该子集中所有样本都属于同一类别，则将该子集作为叶节点，标记为该类别。

否则，递归地重复步骤2-5，直到所有子集都属于同一类别或者没有更多的可用特征。

ID3算法的优点是简单且易于实现，它适用于处理具有离散属性的问题。

然而，ID3算法也存在一些缺点。

首先，ID3算法倾向于选择具有更多取值的特征作为划分特征，这可能导致过度拟合的问题。

其次，ID3算法无法处理缺失数据和连续属性，需要进行额外的处理。

此外，ID3算法对于噪声和异常值也比较敏感，可能导致不准确的分类结果。

为了弥补ID3算法的不足，后续的决策树学习算法，如C4.5和CART，进行了改进。

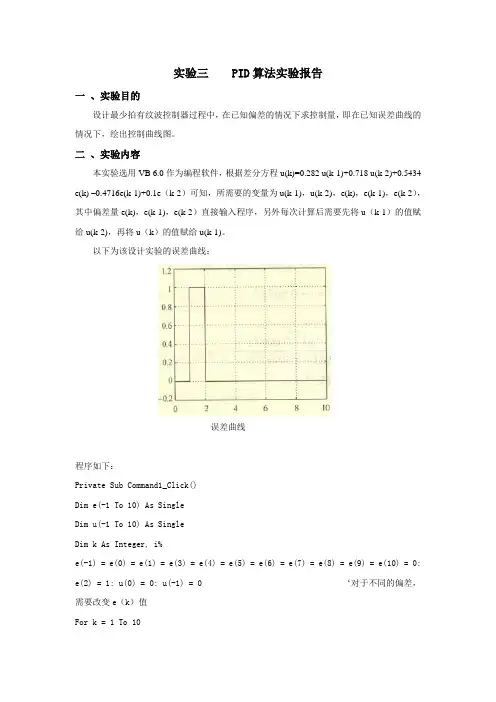
实验三 PID算法实验报告一、实验目的设计最少拍有纹波控制器过程中，在已知偏差的情况下求控制量，即在已知误差曲线的情况下，绘出控制曲线图。

二、实验内容本实验选用VB 6.0作为编程软件，根据差分方程u(k)=0.282 u(k-1)+0.718 u(k-2)+0.5434 e(k) –0.4716e(k-1)+0.1e（k-2）可知，所需要的变量为u(k-1)，u(k-2)，e(k)，e(k-1)，e(k-2），其中偏差量e(k)，e(k-1)，e(k-2）直接输入程序，另外每次计算后需要先将u（k-1）的值赋给u(k-2)，再将u（k）的值赋给u(k-1)。

以下为该设计实验的误差曲线：误差曲线程序如下：Private Sub Command1_Click()Dim e(-1 To 10) As SingleDim u(-1 To 10) As SingleDim k As Integer, i%e(-1) = e(0) = e(1) = e(3) = e(4) = e(5) = e(6) = e(7) = e(8) = e(9) = e(10) = 0: e(2) = 1: u(0) = 0: u(-1) = 0 ‘对于不同的偏差，需要改变e（k）值For k = 1 To 10u(k) = 0.282 * u(k - 1) + 0.718 * u(k - 2) + 0.5434 * e(k) - 0.4716 * e(k - 1) + 0.1 * e(k - 2)Print "u(" & k & ") = "; u(k)Next kEnd Sub三、实验数据e（k）分别等于[0，1，0，0，0，0，0，0，0，0]，结果如下：u（1）= 0u（2）= 0.5434u（3）= - 0.3184u（4）= 0.4004u（5）= - 0.1157u（6）= 0.2549u（7）= - 0.1119u（8）= 0.1798u（9）= 0.0427u（10）= 0.1412以下为求得的控制曲线：控制曲线。

题目： ID3算法分析与实现学 院 xxxxxxxxxxxxxxxxxxxx专 业 xxxxxxxxxxxxxxxx学 号 xxxxxxxxxxx姓 名 xxxx指导教师 xxxx2015年x 月xx 日装订线ID3算法分析与实现摘要:决策树是对数据进行分类，以此达到预测的目的。

该决策树方法先根据训练集数据形成决策树，如果该树不能对所有对象给出正确的分类，那么选择一些例外加入到训练集数据中，重复该过程一直到形成正确的决策集。

决策树代表着决策集的树形结构。

先上问题吧，我们统计了14天的气象数据(指标包括outlook，temperature，humidity，windy)，并已知这些天气是否打球(play)。

如果给出新一天的气象指标数据:sunny,cool,high,TRUE，判断一下会不会去打球。

这个问题当然可以用朴素贝叶斯法求解，分别计算在给定天气条件下打球和不打球的概率，选概率大者作为推测结果。

现在我们使用ID3归纳决策树的方法来求解该问题。

预备知识：信息熵熵是无序性（或不确定性）的度量指标。

假如事件A的全概率划分是（A1,A2,...,An），每部分发生的概率是(p1,p2,...,pn)，那信息熵定义为：通常以2为底数，所以信息熵的单位是bit。

补充两个对数去处公式：ID3算法构造树的基本想法是随着树深度的增加，节点的熵迅速地降低。

熵降低的速度越快越好，这样我们有望得到一棵高度最矮的决策树。

在没有给定任何天气信息时，根据历史数据，我们只知道新的一天打球的概率是9/14，不打的概率是5/14。

此时的熵为：属性有4个：outlook，temperature，humidity，windy。

我们首先要决定哪个属性作树的根节点。

对每项指标分别统计：在不同的取值下打球和不打球的次数。

下面我们计算当已知变量outlook的值时，信息熵为多少。

outlook=sunny时，2/5的概率打球，3/5的概率不打球。

算法的取值偏向缺陷有所克服 。 3 实验结果 表 1给出了测试数据样本集 ,其中属于 M 和 N 类的样本实例个数分别
为 9个和 6个 。 表 1 样本数据
( 1. 1)
其中 pi是任意一个记录属于类别 Ci的概率 ,用 Si / S估计 。容易看出 , 数据集 S的总熵在划分之前是属于不同类别的记录的信息量的加权平均 。
中国校外教育 计算机教学
改进的 ID3算法
◆张保华
(江苏常州工程职业技术学院 ,江苏 常州 )
ID3算法采用自顶向下贪婪搜索遍历可能的决策树空间 ,针对该算法所存在的属性取值偏向问题及只对较小的数据集有效的缺 点 ,给出基于属性权值与信息增益的综合改进策略 。实验结果表明 ,改进后的效果明显有效于传统的算法 。
图 1 改进前决策树
(下转第 499页 )
504 08 /2009
中国校外教育 体育与艺术
演唱通俗歌曲应注意的问题
◆鲁宏国
(黑龙江省大庆市教师进修学院 ,黑龙江 大庆市 )
专业歌手唱通俗歌曲 ,他们有很多以前都是唱美声或民族的歌手 ,但为什么唱起通俗歌曲时却不如业余歌手呢 ? 好的歌手演唱 声音要有特点 ,演唱要有风格 ,适当调整运用好共鸣 ,多听 ,多看 ,用真情来演唱 。
一 、切忌过分强调字正腔圆 由于专业歌手长期的声音训练 ,美声的技能技巧很熟练 ,在唱通俗歌 曲时 ,不自觉地就表现出来 ,让大家听起来有种一会是通俗演唱 ,一会又是 美声演唱 ,给人不舒服感 ,这使整个歌曲的表现受到了影响 。 如歌曲《那片海 》开始部分 : “告诉我这个夜会不会有我 ……”是叙述部分 ,在唱时吐字就在唇和齿 之间 ,不要过于打开去强调腔圆 ,那样就会生硬 ,无味道 。 二 、切忌过于挡气 流行歌曲有一个最普遍使用的方法 ,即“气声唱法 ”,就是声带不完全 闭合来唱 ,这往往让专业歌手唱起来有些不适应 ,因为美声中是要完全闭 合来唱的 ,不是漏气来唱的 。因此 ,专业歌手要练习稍微挡气来唱 ,不要过 于闭合来唱 ,会收到好的效果 。如歌曲《听海 》“我的心是蓝色的 ……”这 段都要用气声来唱 。这样 ,才能把主人公的那种内心空虚感表达出来 。 三 、切忌过于强调音的明亮 只有用心来唱歌的人 ,才会真正地打动人心。歌者在演唱时不要故意去 做声音 ,有的歌曲可能因情感需要用一些方法来增加色彩 ,但也不要过了 ,要 不留痕迹地给人一种真诚感 ,才能打动人。学过声乐的人往往会在演唱中只 注意声音而忽略了情感的真与质朴 ,观众听起来不会被感动 ,我感觉毛阿敏 在唱《绿叶对根的情谊 》时 ,她的声音朴实 ,没有过多的滑腔 ,但却给人以质 朴、真诚 ,没有故意去做什么声音 ,但听起来却流畅 、高亢、感人。 四 、恰当发挥优势 有美声基础的人 ,在演唱一些高难度歌曲时占有一定的优势 ,歌者需 要展示发挥优势时把美声的声音方法用上 。 如《一个真实的故事 》最后“啊 ……”字就要用方法来唱 ,因为它的最

I D3算法原理及应用-CAL-FENGHAI.-(YICAI)-Company One1ID3算法的应用研究摘要决策树算法是数据挖掘领域的核心分类算法之一,其中ID3算法是最为经典的决策树算法。

ID3算法理论清晰、使用简单、学习能力较强,且构造的决策树平均深度较小,分类速度较快,特别适合处理大规模的学习问题,目前已得到广泛应用。

本文对ID3算法进行了详细的描述,介绍了其算法的基本原理、发展近况、及其具体运用。

引言分类技术是一种根据输入数据集建立分类模型的系统方法。

分类技术一般是用一种学习算法确定分类模型，该模型可以很好地拟合输入数据中类标号和属性集之间的联系。

依据学习算法可以建立能够准确地预测未知样本类标号的模型。

分类方法的实例包括：决策树分类法、基于规则的分类法、神经网络、支持向量级、朴素贝叶斯分类方法等。

相对于其他几种算法而言，ID3算法理论清晰，算法简单，是很有实用价值的实例学习算法，计算时间是例子个数、特征属性个数、节点个数属性之积的线性函数，总预测准确率较高，针对属性选择问题，是决策树学习方法中最具影响和最为典型的算法。

因此本文将详细介绍该算法。

算法基本原理在ID3决策树归纳方法中，通常是使用信息增益方法来帮助确定生成每个节点时所应采用的合适属性。

这样就可以选择具有最高信息增益（熵减少的程度最大）的属性最为当前节点的测试属性，以便对之后划分的训练样本子集进行分类所需要的信息最小，也就是说，利用该属性进行当前（节点所含）样本集合划分，将会使得所产生的样本子集中的“不同类别的混合程度”降为最低。

因此，采用这样一种信息论方法将有效减少对象分来所需要的次数，从而确保所产生的决策树最为简单。

设E = F1 ×F2 ×…×Fn 是n 维有穷向量空间,其中j F 是有穷离散符号集, E 中的元素e = <1V ,2V ,…,n V >叫做例子,其中j V ∈j F , j = 1 ,2 , …, n 。

By Yang Ying
Supervisor: Prof. Chai Xin
November 2011
原创性声明
本人郑重声明：所呈交的学位论文，是本人在导师指导下，进行研究工作所取得的成 果。除文中已经注明引用的内容外，本学位论文不包含任何他人或集体已经发表的作品内 容，也不包含本人为获得其他学位而使用过的材料。对本论文所涉及的研究工作做出贡献 的其他个人或集体，均已在文中以明确方式标明。本学位论文原创性声明的法律责任由本 人承担。
第二章 决策树理论及 ID3 算法局限性分析........................................................................... 5
§ 2-1 决策树理论分析................................................................................................................................. 5 2-1-1 关于决策树 ................................................................................................................................... 5 2-1-2 决策树生成过程 ........................................................................................................................... 6 2-1-3 由决策树抽取分类规则 ................................................................................................................ 7 § 2-2 决策树 ID3 算法分析 ........................................................................................................................ 9 2-2-1 关于信息论 .................................................................................................................................... 9 2-2-2 ID3 算法主要部分 ....................................................................................................................... 10 2-2-3 ID3 算法的不足之处 ................................................................................................................... 12 2-2-4 ID3 算法改进与优化的思路 ....................................................................................................... 12 § 2-3 本章小结........................................................................................................................................... 12

竭诚为您提供优质文档/双击可除id3算法实验报告篇一：实验二-决策树实验-实验报告决策树实验一、实验原理决策树是一个类似于流程图的树结构，其中每个内部结点表示在一个属性上的测试，每个分支代表一个测试输入，而每个树叶结点代表类或类分布。

数的最顶层结点是根结点。

一棵典型的决策树如图1所示。

它表示概念buys_computer，它预测顾客是否可能购买计算机。

内部结点用矩形表示，而树叶结点用椭圆表示。

为了对未知的样本分类，样本的属性值在决策树上测试。

决策树从根到叶结点的一条路径就对应着一条合取规则，因此决策树容易转化成分类规则。

图1ID3算法：■决策树中每一个非叶结点对应着一个非类别属性，树枝代表这个属性的值。

一个叶结点代表从树根到叶结点之间的路径对应的记录所属的类别属性值。

■每一个非叶结点都将与属性中具有最大信息量的非类别属性相关联。

■采用信息增益来选择能够最好地将样本分类的属性。

信息增益基于信息论中熵的概念。

ID3总是选择具有最高信息增益（或最大熵压缩）的属性作为当前结点的测试属性。

该属性使得对结果划分中的样本分类所需的信息量最小，并反映划分的最小随机性或“不纯性”。

二、算法伪代码算法Decision_Tree(data,Attributename)输入由离散值属性描述的训练样本集data;候选属性集合Attributename。

输出一棵决策树。

（1）创建节点n；（2）Ifsamples都在同一类c中then（3）返回n作为叶节点，以类c标记；（4）Ifattribute_list为空then（5）返回n作为叶节点，以samples中最普遍的类标记；//多数表决（6）选择attribute_list中具有最高信息增益的属性test_attribute;（7）以test_attribute标记节点n；（8）Foreachtest_attribute的已知值v//划分samples （9）由节点n分出一个对应test_attribute=v的分支；（10令sv为samples中test_attribute=v的样本集合；//一个划分块（11）Ifsv为空then（12）加上一个叶节点，以samples中最普遍的类标记；（13）else加入一个由Decision_Tree(sv,attribute_list-test_attribute)返回节点值。

决策树ID3算法的实现与改进决策树ID3算法的实现与改进⼀、项⽬介绍决策树（Decision Tree）是⽤于分类和预测的主要技术，它着眼于从⼀组⽆规则的事例推理出决策树表⽰形式的分类规则，采⽤⾃顶向下的递归⽅式，在决策树的内部节点进⾏属性值的⽐较，并根据不同属性判断从该节点向下分⽀，在决策树的叶节点得到结论。

因此，从根节点到叶节点就对应着⼀条合理规则，整棵树就对应着⼀组表达式规则。

基于决策树算法的⼀个最⼤的优点是它在学习过程中不需要使⽤者了解很多背景知识，只要训练事例能够⽤属性即结论的⽅式表达出来，就能使⽤该算法进⾏学习。

本项⽬使⽤Java语⾔在Eclipse⼯作平台进⾏开发，实现了ID3算法构建决策树的过程，并对所⽣成的决策树进⾏规则分析。

ID3算法往往会偏袒属性值数⽬较多的属性，这⼀弊端使得该算法在实际分类应⽤中会出现趋向于抛弃⼩数据量的数据元素，然⽽属性值数⽬较多的属性却不总是最优的属性。

例如：在研究影响⼤学⽣成绩的各种因素时，⽤传统的ID3算法确定“学⽣的年龄”为应⾸先判断的属性，但实际教学中⽼师认为这个属性在判断⼤学⽣成绩时并没有那么重要；在销售市场，销售量分析需要对某些少量的元素组有⾜够的重视，⽽ID3算法则会忽视这些影响销售量分析的重要属性。

针对ID3算法偏向于选择取值较多但实际中并不总是最优的属性作为测试属性的缺点，本项⽬对ID3算法进⾏了改进，即在计算信息熵时⼈为地引⼊权值，来区分不同信息属性的依赖度。

此权值是⼀个模糊的概念，它的⼤⼩可由决策者根据先验知识或领域知识来确定每⼀属性的取值（权值越⼩，则属性的重要性就越⾼）。

引⼊权值即在决策树训练过程中，⽣成和修改决策树的实例集之外的所有影响决策树规则⽣成和选择的因素，从⽽避免出现所选属性与现实⽆关或偏⼤数据量的问题。

在本项⽬中，给出了⼀个使⽤信息增益进⾏决策树归纳的例⼦，并通过实验对改进前后的ID3算法进⾏了对⽐分析。

⼆、算法描述决策树ID3算法就是由J. Ross Quilan在1986年⾸次提出的。

基于ID3算法的决策树分类技术研究一、引言决策树是一种常用的分类和回归算法，在数据挖掘领域具有广泛的应用。

其中，基于ID3算法的决策树分类技术是最早、最经典的决策树算法之一、ID3（Iterative Dichotomiser 3）算法主要用于处理离散型数据，并通过信息熵来选择最优的分类属性。

本文将重点研究基于ID3算法的决策树分类技术，探讨其原理、算法流程和应用。

二、ID3算法原理对于一个给定的样本集合D，其包含n个正例和m个反例。

假设样本集D中正例和反例比例分别为p+和p-，则样本集D的信息熵为：E(D) = -p+log2(p+) - p- log2(p-)根据信息熵，我们可以计算出当样本集合D根据一些属性a划分后的信息熵。

假设属性a有k个取值{a1,a2,...,ak}，其中样本集D中第i个取值为Dv(i)，则属性a的信息熵E(D,a)为：E(D,a) = (Dv1/D) E(Dv1) + (Dv2/D) E(Dv2) + ... + (Dvk/D)E(Dvk)其中，E(Dv(i))表示样本集Dv(i)的信息熵。

根据信息熵的定义，我们可以计算出属性a的信息熵减少量，即信息增益。

属性a的信息增益为：Gain(D,a) = E(D) - E(D,a)在ID3算法中，我们选择具有最大信息增益的属性作为划分属性，将样本集划分为多个子集，然后对每个子集递归地应用ID3算法，构造决策树。

三、ID3算法流程（1）输入为训练样本集D和属性集A，输出为决策树T。

（2）若样本集D中所有实例都属于同一类Ck，则生成叶节点，返回T。

（3）若属性集A为空集，则根据样本集D中实例最多的类别生成叶节点，并返回T。

（4）计算属性集A中每个属性的信息增益，选择信息增益最大的属性作为划分属性。

（5）根据划分属性的取值将样本集D划分为多个子集，对每个子集递归地应用上述步骤，构造决策树。

四、应用与改进ID3算法常用于决策支持系统和数据挖掘工具中。

id3算法原理范文ID3算法（Iterative Dichotomiser 3）是一种用于决策树的生成算法。

它使用信息增益来确定每个属性的重要性，并根据信息增益选择最佳的属性来划分数据。

ID3算法在决策树的生成过程中，递归地划分数据集，直到达到叶节点或无法找到新的属性进行划分。

ID3算法的核心原理是基于信息论中的信息增益。

信息增益表示在已知一些属性之后，熵的减少量。

熵是表示数据的不确定性的度量，在决策树中，我们希望通过属性的划分来最大限度地减少数据的不确定性。

因此，我们选择具有最大信息增益的属性作为划分属性。

决策树的生成过程可以通过以下步骤概括：1.计算数据集的初始熵：计算数据集中每个类别的样本数量，并计算数据集的熵。

熵的计算公式为：$H(S) = - \sum_{i=1}^{n}p_i \log_2{p_i}$其中，$p_i$表示类别i在数据集中的比例。

2.对每个属性计算信息增益：遍历属性集合中的每个属性，对每个属性计算其对数据集的划分后的信息增益。

信息增益的计算公式为：$Gain(S, A) = H(S) - \sum_{v=1}^{V}\frac{，S_v，}{，S，}H(S_v)$其中，$S_v$表示经过属性A划分后得到的子集，$V$表示属性A的取值个数，$，S_v，$表示子集$S_v$的大小。

3.选择具有最大信息增益的属性作为划分属性：选择信息增益最大的属性作为当前节点的划分属性。

4.根据划分属性划分数据集：根据划分属性的不同取值对数据集进行划分，生成对应的子节点。

5.对于每个子节点，递归地重复步骤1-4，直到达到叶节点或无法找到新的属性进行划分。

ID3算法有一些需要注意的问题：1.属性选择的偏向：ID3算法倾向于选择具有较多取值的属性，因为具有较多取值的属性有更多的划分可能性。

这可能导致对于具有大量取值的属性的过度匹配。

2.处理缺失值和连续值属性：ID3算法不能直接处理缺失值和连续值属性。

《决策树ID3算法的改进研究》篇一一、引言决策树算法是一种常用的机器学习算法，广泛应用于分类问题。

ID3（Iterative Dichotomiser 3）算法作为决策树算法的一种，以其简单、直观的特点在数据挖掘和机器学习中得到了广泛的应用。

然而，随着数据集的复杂性和规模的增加，ID3算法在处理某些问题时存在一些局限性。

本文旨在研究ID3算法的不足，并提出相应的改进措施，以提高算法的准确性和效率。

二、ID3算法概述ID3算法是一种决策树学习算法，它采用信息增益作为选择划分属性的标准。

算法从根节点开始，对数据集进行训练和学习，根据信息增益选择最优划分属性，将数据集划分为子集，然后递归地对子集进行划分，直到满足停止条件为止。

ID3算法具有简单易懂、计算量小、易于实现等优点。

三、ID3算法的不足虽然ID3算法在许多问题上表现良好，但在处理一些复杂的数据集时，仍存在一些不足。

主要问题包括：1. 对噪声数据敏感：ID3算法在选择划分属性时，容易受到噪声数据的影响，导致划分不准确。

2. 倾向于选择取值较多的属性：当某个属性取值较多时，其信息增益往往较大，导致ID3算法倾向于选择该属性进行划分，这可能导致过拟合。

3. 处理连续属性能力有限：ID3算法主要针对离散属性进行划分，对于连续属性的处理能力有限。

四、改进措施针对ID3算法的不足，本文提出以下改进措施：1. 引入噪声过滤机制：在划分属性前，对数据进行噪声过滤，降低噪声数据对划分结果的影响。

可以通过设置阈值、聚类等方法实现。

2. 属性选择策略优化：在选择划分属性时，引入属性之间的相关性分析，避免选择取值较多且与目标属性相关性较小的属性。

同时，可以采用基于代价复杂度的剪枝策略，对决策树进行后剪枝，以降低过拟合的风险。

3. 扩展处理连续属性的能力：针对连续属性，可以采用离散化处理方法，将连续属性转换为离散属性。

同时，可以引入基于距离的划分方法，以更好地处理连续属性的划分问题。

决策树算法实验报告哈尔滨工业大学数据挖掘理论与算法实验报告(2022年度秋季学期)课程编码 S1300019C 授课教师高宏学生姓名赵天意学号 14S101018学院电气工程及自动化学院一、实验内容使用ID3算法设计实现决策树二、实验设计给定特征是离散的1组实例，设计并实现决策树算法，对实例建立决策树，观察决策树是否正确。

三、实验环境及测试数据实验环境：Windows7操作系统，Python2.7 IDLE 测试数据：样本 outlook temperature Humidity 1 sunny hot High 2 sunny hot High 3 overcast hot High4 rainy mild High5 rainy cool normal6 rainy cool normal7 overcast cool normal8 sunny mild High9 sunny cool normal 10 rainy mild normal 11 sunny mild normal 12 overcast mild High 13 overcast hot normal 14 rainy mild high windy FALSE TRUE FALSE FALSE FALSE TRUE TRUE FALSE FALSE FALSE TRUE TRUE FALSE TRUE play no no yes yes yes no yes no yes yes yes yes yes no 四、实验过程编写决策树程序，输出决策树，输入实例，输出预测类别五、实验结果样本建立的决策树与对所有样本的预测六、遇到的困难及解决方法、心得体会建树过程中用到了递归思想，递归建树。

1/ 1。