凸轮机构的压力角

机械原理复习题凸轮机构及其设计I.填空题1凸轮机构中的压力角是凸轮与从动件接触点处的正压力方向和从动件上力作用点处的速度方向所夹的锐角。

2凸轮机构中，使凸轮与从动件保持接触的方法有力封闭法和几何封闭法（形封闭法）两种。

3在回程过程中，对凸轮机构的压力角加以限制的原因是为减小从动件产生过大的加速度引起的冲击。

4在推程过程中，对凸轮机构的压力角加以限制的原因是提高机械效率、改善受力情况。

5在直动滚子从动件盘形凸轮机构中，凸轮的理论廓线与实际廓线间的关系是法向距离为滚子半径的等距曲线6凸轮机构中，从动件根据其端部结构型式，一般有尖顶从动件、滚子从动件、平底从动件等三种型式。

7设计滚子从动件盘形凸轮机构时，滚子中心的轨迹称为凸轮的理论廓线；与滚子相包络的凸轮廓线称为实际廓线。

8盘形凸轮的基圆半径是理论轮廓曲线上距凸轮转动中心的最小向径。

9根据图示的ϕϕ-22dd s运动线图，可判断从动件的推程运动是__(1)等加速等减速运动规律(2)从动件的回程运动是简谐运动规律。

10从动件作等速运动的凸轮机构中，其位移线图是斜直线，速度线图是平行于凸轮转角坐标轴的直线。

11当初步设计直动尖顶从动件盘形凸轮机构中发现有自锁现象时，可采用增大基圆半径、采用偏置从动件、在满足工作要求的前提下，选择不同的从动件的运动规律等办法来解决。

12在设计滚子从动件盘形凸轮轮廓曲线中，若出现滚子半径大于理论廓线上的最小曲率半径时，会发生从动件运动失真现象。

此时，可采用加大凸轮基圆半径或减小滚子半径方法避免从动件的运动失真。

13用图解法设计滚子从动件盘形凸轮轮廓时，在由理论轮廓曲线求实际轮廓曲线的过程中，若实际轮廓曲线出现尖点或交叉现象，则与滚子半径的选择有关。

14在设计滚子从动件盘形凸轮机构时，选择滚子半径的条件是滚子半径小于凸轮理论轮廓曲线上的最小曲率半径。

15在偏置直动从动件盘形凸轮机构中，当凸轮逆时针方向转动时，为减小机构压力角，应使从动件导路位置偏置于凸轮回转中心的右侧。

凸轮机构基本参数的设计前节所先容的几何法和解析法设计凸轮轮廓曲线，其基圆半径r0、直动从动件的偏距e或摆动从动件与凸轮的中心距a、滚子半径rT等基本参数都是预先给定的。

本节将从凸轮机构的传动效率、运动是否失真、结构是否紧凑等方面讨论上述参数的确定方法。

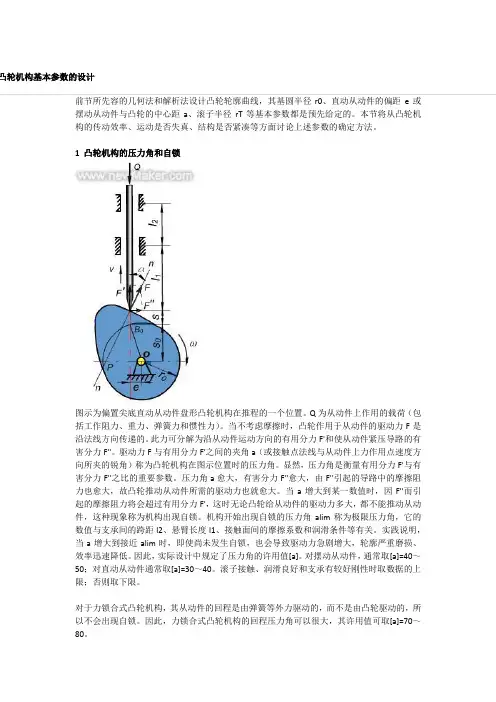
1 凸轮机构的压力角和自锁图示为偏置尖底直动从动件盘形凸轮机构在推程的一个位置。

Q为从动件上作用的载荷（包括工作阻力、重力、弹簧力和惯性力）。

当不考虑摩擦时，凸轮作用于从动件的驱动力F是沿法线方向传递的。

此力可分解为沿从动件运动方向的有用分力F'和使从动件紧压导路的有害分力F''。

驱动力F与有用分力F'之间的夹角a（或接触点法线与从动件上力作用点速度方向所夹的锐角）称为凸轮机构在图示位置时的压力角。

显然，压力角是衡量有用分力F'与有害分力F''之比的重要参数。

压力角a愈大，有害分力F''愈大，由F''引起的导路中的摩擦阻力也愈大，故凸轮推动从动件所需的驱动力也就愈大。

当a增大到某一数值时，因F''而引起的摩擦阻力将会超过有用分力F'，这时无论凸轮给从动件的驱动力多大，都不能推动从动件，这种现象称为机构出现自锁。

机构开始出现自锁的压力角alim称为极限压力角，它的数值与支承间的跨距l2、悬臂长度l1、接触面间的摩擦系数和润滑条件等有关。

实践说明，当a增大到接近alim时，即使尚未发生自锁，也会导致驱动力急剧增大，轮廓严重磨损、效率迅速降低。

因此，实际设计中规定了压力角的许用值[a]。

对摆动从动件，通常取[a]=40～50；对直动从动件通常取[a]=30～40。

滚子接触、润滑良好和支承有较好刚性时取数据的上限；否则取下限。

对于力锁合式凸轮机构，其从动件的回程是由弹簧等外力驱动的，而不是由凸轮驱动的，所以不会出现自锁。

因此，力锁合式凸轮机构的回程压力角可以很大，其许用值可取[a]=70～80。

第四节 凸轮机构基本尺寸设计无论是作图法还是解析法，在设计凸轮廓线前，除了需要根据工作要求选定从动件的运动规律外，还需要确定凸轮机构的一些基本参数，如基圆半径b r 、偏距e 、滚子半径r r 等。

一般来讲，这些参数的选择除了应保证从动件能够准确地实现预期的运动规律外，还应当使机构具有良好的受力状况和紧凑的结构。

本节讨论凸轮机构基本尺寸设计的原则和方法。

一、移动滚子从动件盘形凸轮机构1. 压力角同连杆机构一样，压力角也是衡量凸轮机构传力特性好坏的一个重要参数。

所谓凸轮机构的压力角，是指在不计摩擦的情况下，凸轮对从动件作用力的方向线与从动件上力作用点的速度方向之间所夹的锐角。

对于图4-22所示的移动滚子从动件盘形凸轮机构来说，过滚子中心所作理论廓线的法线nn 与从动件运动方向之间的夹角α就是压力角。

（1）压力角与作用力的关系 由图4-22可以看出，凸轮对从动件的作用力F 可以分解成两个分力，即沿着从动件运动方向的分力F '和垂直于运动方向的分力F ''。

只有前者是推动从动件克服载荷的有效分力，而后者将增大从动件与导路间的摩擦，它是一种有害分力。

压力角α越大，有害分力越大。

当压力角α增大到某一数值时，有害分力所引起的摩擦阻力将大于有效分力F '，这时无论凸轮给从动件的作用力有多大，都不能推动从动件运动，即机构将发生自锁。

因此为减小侧向推力，避免自锁，压力角α应越小越好。

图4-22 凸轮机构的压力角（2）压力角与机构尺寸的关系 设计凸轮时，除了应使机构具有良好的受力状况外，还希望机构结构紧凑。

而凸轮尺寸的大小取决于凸轮基圆半径的大小。

在实现相同运动规律的情况下，基圆半径越大，凸轮的尺寸也越大。

因此，要获得轻便紧凑的凸轮机构，就应当使基圆半径尽可能地小。

但是基圆半径的大小又和凸轮机构的压力角有直接的关系。

下面以图4-22为例来说明这种关系。

图中，过滚子中心B 所作理论廓线的法线nn 与过凸轮轴心0A 所作从动件导路的垂线交于P 点，由瞬心定义可知，该点即为凸轮与从动件在此位置时的瞬心，且ϕωd ds v P A ==0。

图解法求凸轮机构的压力角作者：汪银华来源：《中国机械》2013年第20期摘要：凸轮机构的压力角随凸轮轮廓曲线的变化而变化，随着压力角的增大，从动杆件上的有效作用力愈小。

它反映了机构的传力特性。

故设计凸轮轮廓时，必须将凸轮机构的压力角控制在许用压力角以内。

关键词：凸轮压力角反转法从动杆导路由机构压力角的定义知，凸轮机构压力角指凸轮对从动杆件的作用力F与从动件接触点处速度V的方向间所夹的锐角α。

如图1所示，为对心直动尖顶从动件凸轮机构的压力角。

其图示方法的要点是，从动件直线运动的方向线始终通过凸轮回转中心O。

那么偏心凸轮机构呢？下面具体讨论图2所示偏心凸轮轮廓上任意点A处压力角的作图表示方法。

由于从动杆的导路不通过凸轮回转中心O，那么在凸轮转动过程中，明确从动件相对凸轮转动轴心运动的轨迹，就成为作图的关键。

因为从动件直动的轨迹正是其速度方向所在。

该要点可由反转法原理得知：根据相对运动原理，设想凸轮不动，从动件随导路以角速度—ω绕轴O转动，同时在导路中按预定规律作往复直线运动。

如图3。

很明显，在这种反转的复合运动中，从动件和导路的运动轨迹始终与转动轴心O存在一个偏心距e。

也即从动件运动的速度方向始终与凸轮转动轴心保持偏心距e。

下面作图表示凸轮上点A的压力角α见图4。

⑴以O圆心、偏心距e为半径作圆；⑵过凸轮轮廓上任意点A作e圆的切线，即为从动件及导路所在的相对位置，也即从动件速度V的方向所在；⑶过A点作凸轮轮廓切线，其法线方向为从动件所受力F的方向；⑷F与V所夹锐角，就是凸轮A点处的压力角α。

参考资料：《机械设计基础》张京辉主编，西安电子科技大学出版社。

《机械设计基础》李国斌主编，机械工业出版社，《机械原理》张世民主编，中央广播电视大学出版社，。

机械原理大作业凸轮机构有关公式凸轮机构是机械传动中常见的一种机构，具有转动曲线的特点，可以将驱动轴的转动运动通过凸轮的滚动轮廓来实现对从动件的相应动作控制。

在凸轮机构的设计和分析中，有一些与凸轮曲线有关的公式是十分重要的。

一、凸轮曲线方程凸轮曲线是指凸轮的滚动轮廓，可以通过数学方法来表示。

常见的凸轮曲线方程有圆弧、椭圆、正弦曲线等。

其中，最常用的是圆弧和直线的组合，这种凸轮曲线被称为简谐凸轮曲线。

简谐凸轮曲线方程可以表示为：y = r (1 - cos(θ - θ0))其中，r为凸轮半径，θ为凸轮角度，θ0为凸轮曲线的初相位差。

凸轮在其中一角度θ的位置的坐标可以通过此公式计算得出。

二、凸轮曲线的导数和导数变化率在凸轮机构的设计和分析中，对凸轮曲线的导数和导数变化率也有相当重要的影响。

凸轮的导数表示了凸轮曲线的斜率，而导数的变化率表示了凸轮曲线的曲率。

凸轮曲线的导数可以表示为：dy/dθ = r sin(θ - θ0)凸轮曲线的导数变化率可以表示为：d²y/dθ² = r cos(θ - θ0)通过对凸轮的导数和导数变化率的计算和分析，可以确定从动件的运动状态和速度变化情况，进而进行凸轮机构的设计和优化。

三、凸轮压力和压力角在凸轮机构中，凸轮和从动件之间存在着压力作用。

对于凸轮的任何一个位置，凸轮所施加的压力可以通过力的分解计算得出，并且可以利用凸轮的转角来表示。

凸轮的压力可以表示为：F = P * r * cos(θ - θ0)其中，P为压力系数，r为凸轮半径，θ为凸轮角度，θ0为凸轮曲线的初相位差。

凸轮的压力角可以表示为：φ = atan(dy/dθ)其中，dy/dθ为凸轮曲线的导数。

凸轮的压力角可以用来描述凸轮的主动件施加力的方向和作用范围，对凸轮机构的设计和分析具有指导意义。

以上是凸轮机构常见的几个重要的公式，通过这些公式可以计算和分析凸轮机构的运动学和动力学性能，为凸轮机构的设计和优化提供指导。

简述凸轮机构基圆半径和压力角的关系
半径确定：转轴中心到凸轮廓线最近点的距离加上滚子半径就是基圆半径了。

在其他
条件不变的情况下，基圆半径越小，压力角越大。

基圆半径过小，压力角会超过许用值而
使机构效率太低甚至发生自锁。

因此实际设计中，只能在保证凸轮轮廓的最大压力角不超
过许用值的前提下，考虑减小凸轮的尺寸。

一、基圆半径
通常就是指凸轮的理论廓线的最轻半径。

基圆半径也就是凸轮设计的一个关键参数，
它对凸轮机构的结构尺寸、体积、重量、受力状况和工作性能等都存有关键影响。

二、半径确定
在设计凸轮机构时，凸轮的基圆半径获得越大，所设计的机构越紧凑型。

但是，基圆
半径过大可以引发压力角减小，以致机构工作情况转好，在其他条件维持不变的情况下，
基圆半径越大，压力角越大。

基圆半径过大，压力角会少于许用值而使机构效率太低甚至
出现自锁。

因此实际设计中，就可以在确保凸轮轮廓的最小压力角不少于许用值的前提下，考量增大凸轮的尺寸。

三、凸轮机构影响
凸轮的一个关键尺寸要素就是凸轮的基圆半径。

它不仅同意着推杆尖端的初始边线，
而且对凸轮的尺寸大小及凸轮机构的受力状态都存有直接影响。

四、与最小半径
凸轮的基圆半径不一定就是凸轮的最轻半径。

因为凸轮的最轻半径就是根据确保凸轮
轮廓线上的最小压力角不少于许用压力角的条件去确认的。

但在确认基圆半径时，还要考
量其它条件，所以最后做出的凸轮基圆半径不一定就是最轻半径。

偏心圆盘凸轮机构最小压力角偏心圆盘凸轮机构是一种常见的传动机构，广泛应用于各种机械设备中。

在设计和分析这种机构时，一个重要的参数是压力角。

压力角是指凸轮上接触点的切线与接触线之间的夹角，它直接影响着机构的传动效率和运动平稳性。

本文将重点讨论偏心圆盘凸轮机构中最小压力角的问题。

我们需要明确偏心圆盘凸轮机构的结构特点。

该机构由一个偏心圆盘和一个跟随器组成。

偏心圆盘的轴心与跟随器的轴心不重合，它们之间的距离称为偏心距。

偏心圆盘上有一个或多个凸起的部分，称为凸轮。

当偏心圆盘旋转时，凸轮会推动跟随器做往复运动，实现传动功能。

在偏心圆盘凸轮机构中，最小压力角是指所有接触点中压力角最小的值。

在实际应用中，我们希望最小压力角尽可能小，以减小接触点的滑动和摩擦，提高传动效率和机构的寿命。

因此，最小压力角的分析和设计至关重要。

为了确定最小压力角，我们需要考虑凸轮的轮廓形状和运动规律。

常见的凸轮形状包括圆弧形、抛物线形、渐开线形等。

不同形状的凸轮对应着不同的运动规律和压力角变化特点。

在实际设计中，我们可以根据具体的要求和条件选择最合适的凸轮形状。

以圆弧形凸轮为例，我们可以通过几何推导和运动学分析来确定最小压力角。

假设凸轮的圆弧半径为R，偏心距为e，跟随器的半径为r。

当凸轮旋转一个角度θ时，跟随器的往复运动距离为s。

根据几何关系和运动学原理，我们可以得到几个关键的参数关系。

根据几何关系，凸轮的圆弧长度L和旋转角度θ满足以下关系：L = Rθ然后，根据凸轮和跟随器的接触条件，可以得到几何关系式：Rcos(α) + e - rcos(β) = 0Rsin(α) - rsin(β) = s其中，α和β分别表示凸轮上接触点和跟随器上接触点的角度。

接下来，我们可以通过对上述几个方程求导，得到压力角的表达式。

根据求导的结果，我们可以发现，压力角的大小与凸轮的圆弧半径、偏心距以及跟随器的半径等参数有关。

为了使最小压力角尽可能小，我们可以通过合理选择这些参数来优化设计。

凸轮机构推程中的最大压力角《凸轮机构推程中的最大压力角》哎呀，你一听“凸轮机构推程中的最大压力角”这个名字，是不是就觉得好复杂、好难懂呀？我一开始也是这么想的呢。

我先给你讲讲凸轮机构是啥吧。

凸轮机构就像是一个小魔法装置，在好多机器里都能看到它的身影。

你看那汽车发动机里呀，就有凸轮机构在默默地工作。

它就像一个小指挥家，指挥着其他零件什么时候该动，动多少呢。

这个凸轮呀，就像一个有着奇怪形状的小轮子，它一转呀，就能让和它接触的推杆或者其他部件按照它的节奏运动。

这就好比我们跳舞的时候，有个领舞的人，他做什么动作，后面跟着的舞者就得跟着做相应的动作一样。

那这个推程又是啥呢？简单来说，就是推杆在凸轮的推动下开始上升或者向某个方向移动的这个过程。

就像我们坐电梯，电梯从一楼开始往上升的这个过程，就有点像凸轮机构里的推程呢。

现在咱们要说到这个最大压力角啦。

这个压力角呀，可有点像我们在生活中遇到的阻力一样。

想象一下，你在推一个很重的箱子。

如果这个箱子是正对着你，你推起来就比较轻松，但是如果这个箱子有点歪，你推起来就会觉得更费力。

这个压力角在凸轮机构里就有点像这个箱子歪的程度。

当这个压力角越大的时候，就意味着推杆在运动的时候遇到的“阻力”就越大。

我再给你举个例子吧。

就像我们骑自行车的时候，如果路面很平坦，那我们骑起来就很轻松，就像压力角比较小的时候。

可是如果路面有很多小石子，而且是那种斜着的小石子，我们骑车的时候就会觉得很费劲，这个时候就有点像压力角变大了。

那这个最大压力角到底有什么影响呢？我来给你说说我和我同学讨论这个问题的时候的情况吧。

我跟我同学小明说：“你说这个最大压力角是不是只要存在就会让凸轮机构不好好工作呀？”小明就回答我：“哎呀，也不是啦。

不过如果这个最大压力角太大的话，那可就麻烦了。

”我就很好奇地问：“为啥呢？”小明就说：“你想啊，要是压力角太大，推杆可能就不能按照我们想要的速度和方向运动了。

就像我们想要一支笔直直地画一条线，可是如果有很大的干扰，就像这个大压力角，那这支笔可能就会画出歪歪扭扭的线，这样机器做出来的东西可能就不精确啦。

偏置凸轮机构最大压力角位置1. 什么是偏置凸轮机构说起偏置凸轮机构，哎呀，那可是机械世界里的“明星”！就像是一场精彩的演出，舞台上那个跳跃的主角，给人们带来了无尽的惊喜和欢笑。

偏置凸轮，顾名思义，就是那种有点“偏心”的凸轮，和它的姐妹们（对，都是凸轮哦）不太一样，它总是有点“另类”，喜欢走自己的路，形成那种独特的运动轨迹。

这玩意儿在机器里可有它的妙用，尤其是在那些需要传递运动和力量的地方，嘿，抓住了就是一桩好事！1.1 为什么我们要关注最大压力角位置？那么，聊到这里，大家可能心里会嘀咕，最大压力角位置又是个啥？其实，不瞒你说，这个位置就像是偏置凸轮一场精彩演出的高兴部分，咳咳，压力角就是指那种力的方向那个角度。

当这个的时候，机器的运转可谓如行云流水，顺畅得不要不要的！而一旦超过这个最优角度，哎呀呀，后果可就不堪设想，机械摩擦、能耗增加，甚至可能导致机器的“崩溃”，真是说起来让人心痛不已啊。

1.2 如何找到这个位置？好吧，找这个最大压力角位置可不是随便瞎转转就行的哦！这就像我们去旅行一样，得有个好地图，才能找到那条风景最美的路。

通过计算，这个压力角的位置通常和凸轮的几何形状、运动规律密切相关。

想象一下，就像在广场上跳舞的孩子，转身的一刹那，如果姿势不对，就容易摔跤，偏偏这摔跤一出，吓得大家心都提到嗓子眼。

但只要掌握技巧，我们就能轻松优雅地舞动起来，得到最佳的运动效果，真是太妙了！2. 最大压力角位置的影响因素像一场足球比赛，想赢得胜利必须关注每一个环节。

偏置凸轮机构的最大压力角位置受很多因素的影响呢。

2.1 凸轮曲线的形状首先，咱们得先聊聊这个凸轮的形状，形状就像是决定了你去哪儿吃饭，决定了结果的好坏。

不一样的形状，不一样的运动轨迹，有时甚至会让你的机器陷入“思考”的尴尬境地。

就像在街边找小吃，有时一不留神就错过了排队的机会，考验你的眼力和选择眼光呀！2.2 材料特性接下来就是材料的特性，这可是影响最大压力角位置的重要因素！材料的硬度、强度、韧性，都会直接影响凸轮的工作性能。

压力角与凸轮机构尺寸的关系《压力角与凸轮机构尺寸的关系》
嘿，大家好呀！今天咱来聊聊压力角和凸轮机构尺寸的关系，这可真是个有意思的事儿呢！
我记得有一次啊，我在工厂里看到那些巨大的机器在运作。

其中就有个凸轮机构，那家伙，看着就挺神奇的。

当时我就特别好奇，凑过去仔细观察。

我就看着那个凸轮在那转呀转的，带动着其他零件一起动。

我就在想，这压力角和凸轮机构尺寸到底有啥关系呢？
咱就说这压力角吧，如果它太大了，那可就像一个人背着特别重的东西，走起来就特别费劲，凸轮机构运作起来也不顺畅呀。

而凸轮机构的尺寸呢，要是不合理，就好比一个人的手脚比例不协调，那行动起来肯定也怪怪的。

就好像一个大凸轮配个小零件，或者反过来，那能协调工作吗？肯定不行呀！
然后我就一直盯着那个凸轮机构看呀看，越看越觉得这两者的关系真的很重要。

如果不注意它们之间的关系，这机器说不定哪天就出故障啦。

哎呀呀，经过那次在工厂的观察，我可算是深刻体会到了压力角与凸轮机构尺寸的关系有多密切啦！这真不是随便说说的事儿呀，就像生活中的很多事情一样，都得搭配得恰到好处才行呢！好啦，就说到这儿吧，希望大家也能明白这个有趣的关系哟！。