多体系统动力学压缩建模(覃正著)思维导图
- 格式:xmin
- 大小:4.85 KB
- 文档页数:1

多体动力学(Adams/Car2007)摘要Adams/Car中多体系统的位置、姿态、运动及受力分析。
目录1 矢量 (3)1.1 矢量的定义和符号 (3)1.2 矢量的基本运算 (3)1.3 单位矢量的定义和符号 (4)1.4 零矢量的定义和符号 (4)1.5 平移规定 (4)2 坐标系 (6)2.1 坐标系的定义 (6)2.2 坐标系的分类 (6)2.3 I marker和J marker (6)3 矢量的坐标阵和坐标方阵 (7)4 方向余弦矩阵 (8)5 欧拉角 (11)6 描述车身姿态的3-2-1转角 (15)7 几个位置和姿态函数 (16)7.1 中心位置函数(LOC_CENTERED) (17)7.2 线上位置函数(LOC_ALONG_LINE) (18)7.3 轴上位置函数(LOC_ON_AXIS) (18)7.4 相对位置函数(LOC_RELATIVE_TO) (19)7.5 相对姿态函数(ORI_RELATIVE_TO) (20)7.6 平面姿态函数(ORI_IN_PLANE) (20)7.7 轴在线姿态函数(ORI_ALONG_AXIS) (21)7.8 轴定位姿态函数(ORI_ALIGN_AXIS) (22)8 力(Forces) (24)8.1 弹簧力(Springs) (24)8.2 阻尼力(Dampers) (25)8.3 轮胎力(Tires) (25)8.4 限位块(Bumpstops & Reboundstops) (25)8.5 橡胶衬套(Bushings) (27)9 约束(Joints) (30)9.1 滑移铰(Translational) (31)9.2 旋转铰(Revolute) (33)9.3 圆柱铰(Cylindrical) (35)9.4 球铰(Spherical) (36)9.5 平面铰(Planar) (38)9.6 固定铰(Fixed) (38)9.7 点在线约束(Inline) (39)9.8 点在面约束(Inplane) (39)9.9 姿态约束(Orientation) (40)9.10 平行约束(Parallel_axes) (40)9.11 垂直约束(Perpendicular) (40)9.12 虎克铰(Hooke) (42)9.13 万向节(Universal) (45)9.14 等速万向节(Convel) (47)9.15 关联约束(Coupler) (49)10 悬架试验台(MDI_SUSPENSION_TESTRIG) (50)11 悬架仿真试验多体系统(mdi_front_vehicle) (50)12 悬架仿真试验(Suspension Analysis) (51)12.1 平行轮跳试验(Parallel Wheel Travel Analysis) (51)12.2 反向轮跳试验(Opposite Wheel Travel Analysis) (52)12.3 单轮跳试验(Single Wheel Travel Analysis) (52)12.4 侧倾试验(Roll & Vertical Force Analysis) (53)12.5 转向试验(Steering Analysis) (53)12.6 静载试验(Static Load Analysis) (54)12.7 车轮轮廓试验(Wheel Envelope Analysis) (54)13 悬架仿真试验多体系统的静力学方程 (55)14 柔度矩阵(Compliance Matrix) (56)15 悬架仿真试验输出的特性参数(Output of Suspension Analysis) (58)参考文献 (62)附录一参数及变量定义表 (62)1 矢量我们所处理的物理量绝大部分是矢量,所以矢量的运算是本课程的基础内容。

四类基本模型1 优化模型1.1 数学规划模型线性规划、整数线性规划、非线性规划、多目标规划、动态规划。
1.2 微分方程组模型阻滞增长模型、SARS 传播模型。
1.3 图论与网络优化问题最短路径问题、网络最大流问题、最小费用最大流问题、最小生成树问题(MST)、旅行商问题(TSP)、图的着色问题。
1.4 概率模型决策模型、随机存储模型、随机人口模型、报童问题、Marko v 链模型。
1.5 组合优化经典问题● 多维背包问题(MKP)背包问题:n 个物品,对物品i ,体积为i w ,背包容量为W 。
如何将尽可能多的物品装入背包。
多维背包问题:n 个物品,对物品i ,价值为i p ,体积为i w ,背包容量为W 。
如何选取物品装入背包,是背包中物品的总价值最大。
多维背包问题在实际中的应用有:资源分配、货物装载和存储分配等问题。
该问题属于NP 难问题。
● 二维指派问题(QAP)工作指派问题:n 个工作可以由个工人分n 别完成。
工人完成工i 作的时间为j ij d 。
如何安排使总工作时间最小。
二维指派问题(常以机器布局问题为例):n 台机器要布置在个地方n ,机器与之间i k 的物流量为ik f ,位置与之间j l 的距离为jl d ,如何布置使费用最小。
二维指派问题在实际中的应用有:校园建筑物的布局、医院科室的安排、成组技术中加工中心的组成问题等。
● 旅行商问题(TSP)旅行商问题:有n 个城市,城市与之间i j 的距离为ij d ,找一条经过n 个城市的巡回(每个城市经过且只经过一次,最后回到出发点),使得总路程最小。
● 车辆路径问题(VRP)车辆路径问题(也称车辆计划):已知个客户n 的位置坐标和货物需求,在可供使用车辆数量及运载能力条件的约束下,每辆车都从起点出发,完成若干客户点的运送任务后再回到起点,要求以最少的车辆数、最小的车辆总行程完成货物的派送任务。

多体系统动力学建模方法我折腾了好久多体系统动力学建模方法,总算找到点门道。
说实话,这事儿我一开始也是瞎摸索。
我最初就是按照书上的基本理论,一个劲儿地堆砌公式。
比如,那种牛顿- 欧拉法,我就知道找每个物体的力和力矩平衡方程。
我当时觉得只要把每个物体的受力分析清楚,列出一堆方程就大功告成了。
结果呢,我一计算就发现问题一大堆。
我记得我做一个简单的双摆模型时,按照那种死板的公式计算,得到的结果和实际模拟完全不一样。
后来我才意识到我忽略了一些约束条件。
多体系统当中,各个物体之间的连接关系可是个大关键,就好像一群人拉着手跳舞,你不能只看每个人怎么动,还要看手拉在什么位置、怎么用力拉。
这就类比于多体系统中的约束,像铰链约束,那可不是简单写个力的关系就行的。
后来我又试着用拉格朗日法。
这种方法刚开始理解起来可费劲了,因为它得从系统的能量角度去分析。
但是一旦掌握了,觉得还有点意思。
我觉得这个方法就像是从更高的地方俯瞰整个系统,我不用一个个去分析力的平衡了,看整个系统的能量怎么转变。
不过这里面的广义坐标啥的可不好选,得花时间研究研究什么样的坐标能让我的计算更简单。
再到后来,我学习到了多体系统软件来建模,像Adams软件。
一开始我就跟着教程走,随便画几个刚体、设置几种约束就想得到准确结果。
错得那叫一个离谱啊。
我慢慢懂了,设置参数的时候一定要跟实际物理情况相符合,比如说摩擦系数,我一开始是瞎估计的,后来我才发现必须得好好测量或者参考相关资料里相近材料的值。
还有就是关于模型的简化。
有时候我总想着把所有细节都包进去,结果把自己弄得晕头转向。
就像盖房子,你不需要把每粒沙子怎么排列都考虑进去,有些不重要的小部件或者小影响因素,适当简化掉能让建模轻松很多。
要是再去尝试多体系统建模,我就建议多看看实际的系统,把关键的东西提炼出来。
比如那种机械臂,你要清楚是哪些关节最重要,从实际的运动中找灵感来构建模型,可别光顾着套公式了。
不确定的地方就多做几个简单的测试模型,一点点摸清楚那些原理。


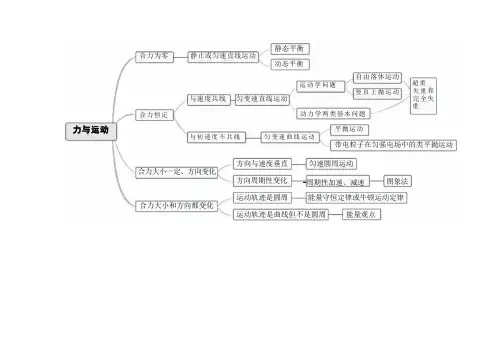
静态平衡合力为零静止或匀速直线运动动态平衡自由落体运动运动学问题超重竖直上抛运动失重和与速度共线匀变速直线运动完全失重合力恒定动力学两类基本问题力与运动平抛运动与初速度不共线匀变速曲线运动带电粒子在匀强电场中的类平抛运动方向与速度垂直匀速圆周运动合力大小一定、方向变化方向周期性变化-周期性加速、减速图象法运动轨迹是圆周能量守恒定律或牛顿运动定律合力大小和方向都变化运动轨迹是曲线但不是圆周能量观点匀速直线运动(F 合=0)直线运动小球压缩弹簧雨滴下落至收尾速度粒子在交变电场中运动匀变速直线运动(F吝恒定)x-t图象v-1图象基本公式常用推论与F 关系v=vo+atx=Vot+ ar²v²-v²=2ax△x=aT²力的运算F=ma自由落体运动竖直上抛运动刹车问题斜面上物体的运动合成法正交分解法非匀变速直线运动(F+ 变化)图象描述条件Fa 与v 不 共 线研究方法运动的合成与分解F ·方向与轨迹关系Fa 指向轨迹的凹侧恒力初速度u 与F△垂 直u 方向的匀速直线运动 合力方向的匀变速直线运动合力恒定特例初速度x 与F 合不共线水平方向以ucos θ做匀速直线运动 竖直方向做匀变速直线运动圆周运动位移分解 速度分解 加速度分解斜抛运动(类斜抛运动)平抛运动 (类平抛运动)曲 线 运 动特点特点分解分解运动描述实例线速度:v=△tAs△0角速度:w=At周期TT=频率f向心加速度:a=向心力:F=ma水平面内的圆周运动模型竖直面内的圆周运动模型v=wrw)π1f4π²T²F=汽车转弯、火车转弯、圆锥摆绳模型,最高点vmm=√gr杆模型,最高点vmin=0v²m-rmw²rm4π²r²=w²r=rT'-圆周运动能量观点标量矢量动量观点能量功W=Flcos a平均功率F= W瞬时功率P=Fucos α机车启动动能定理,W,=△E机械能守恒定律功能关系能量守恒动量定理Ft=mv₂-mv缓冲问题连续体问题电磁感应中的电荷量问题动量守恒定律mi2₁+m₂=m₁v′+m₂₂'碰撞爆炸反冲弹性碰撞非弹性碰撞完全非弹性碰撞动量p=mu-冲量l=FtT力在空间力在时间效果积累效果积累能量与动量力学三大观点常见过程动力学观点能量观点动量观点常见模型匀变速直线运动平抛运动圆周运动一般的曲线运动滑块、滑板斜面弹簧传送带碰撞性质作用电场强度(E= ,E=k Q ,E= d U ),电场线 电势(φ: 9E . ,U=4A-4s,W=qU), 等势面平衡带电粒子在对电荷:F=qE 加速匀强电场中偏转对导体:静电感应(静电平衡、静电屏蔽)电容(定义式C= 决定式C= E,S )4πkd'电场与磁场性质作用带电粒子在电、 磁场中的运动磁感应强度 B= F (I ⊥B)L对通电导线: F=BIL(I ⊥B)对运动电荷:F=quB(v ⊥B) ①仅受电场力②仅受洛伦兹力 ③在复合场中运动 ①直线运动② 类平抛运动 ③圆周运动 ④一般曲线运动应用实例 ①示波管 ②直线加速器 ③速度选择器 ④磁流体发电机 ⑤电磁流量计 ⑥霍尔元件 ⑦质谱仪 ⑧回旋加速器v//B,F=0,做匀速直线运动u⊥B,F=quB,做匀速圆周运动带电粒子在 匀强磁场中带电粒子的受力情况带电粒子的运动性质磁感线,磁通量φ=BSQ U' 磁场电场合力为零合力方向与速度方向在同一直线上合力指向轨迹凹侧速度偏转角:,v6%侧移距离:y=yo+l'tanPIfu某一位置,牛顿第二定律 某一过程,动能定理匀速直线运动 变速直线运动曲线运动规律:牛顿 运动定律或 动能定理 带电粒子在电场中的运动运动的 分解类平抛 运动圆周运动常见磁场磁场的描述磁场对电流的作用磁场对运动电荷的作用匀强磁场条形磁铁的磁场通电直导线周围的磁场通电圆环周围的磁场磁感线磁感应强度安培力洛伦兹力提供向心万大小、方向大小F=BIL(I⊥B)方向左手定则方向-大小F=quB(v⊥B)mi匀速圆R= qB周运动T=qB安培定则2πm磁场在电 场中在组合场 中的运动 (不计重力)在磁 场中计重 力在叠加场中的运动不计 应 重力 用般曲线运动v//E,匀变速直线运动⊥E, 类平抛运动v//B,匀速直线运动v⊥B.匀速圆周运动匀速直线运动 qE 、mg 、quB 平 衡匀速圆周运动 速度选择器质谱仪回旋加速器 磁流体发电机电磁流量计 霍尔元件功能关系注意两个过程的 衔接,前一过程 的末速度是下一 过程的初速度aE=mg,auB 提供向心力quB=mr 电:子复场 的 动 带粒在合中运Aφ电源直流电路用电器电路产 生 交变电流(正、余弦) 描述输送感应电流方向的判定: 楞次定律、右手定则电 磁 感 应感应电动势的大小:E=n²△,E Lv总功率:P=EI输出功率:P=U 内耗功率:P=I²r直流电路的动态分析 含容直流电路的分析 电路故障的分析电路中的能量转化部分电路欧姆定律l=闭合电路欧姆定律l= UR ER+r 电阻:R=p; S T电功: W=uit电热: Q=FRt交流电“四值” 周期、频率变压器远距离输电基本关系制约关系运用牛顿运动定律分析导体棒切割磁感线问题运用动量定理、动量守恒定律分析导体在导轨 上的运动问题运用能量守恒定律分析电磁感应问题运用电磁感应与欧姆定律的有关知识分析图象场、路结合问题 电路与电磁感应探究型实验验证型实验实验仪器实验方法测量做直线运动物体的瞬时速度探究弹簧弹力与形变量的关系探究加速度与物体受力、物体质量的关系探究平抛运动的特点探究向心力大小与半径、角速度、质量的关系探究两个互成角度的力的合成规律验证机械能守恒定律验证动量守恒定律长度测量仪器刻度尺、游标卡尺、螺旋测微器时间测量仪器打点计时器、秒表(不估读)数字计时器(光电门)等效法控制变量法倍增法力学实验探究型实验测量型实验测量仪器读数观察电容器的充、放电现象探究影响感应电流方向的因素探究变压器原、副线圈电压与匝数的关系测量金属丝的电阻率测量电源的电动势和内阻用多用电表测量电学中的物理量电压表、电流表、欧姆表、电阻箱电表的改装电学实验描述方法回复力特点简谐运动共振受迫振动实验:用单摆测量重力加速度的大小描述方法形成条件干涉、衍射波速、波长和频率(周期)的关系光的折射全反射sin C= 1光的干涉薄膜干涉光的衍射光的偏振实验:测量玻璃的折射率实验:用双缝干涉实验测量光的波长麦克斯韦电磁场理论电磁波的产生机械振动机械波光学电磁波机械振动与机械波光电磁波n分子直径数量级为10-*”m.阿伏加德罗常数 扩散现象、布朗运动引力、斥力同时存在分子力表现为引力和斥力的合力 温度是分子平 均动能的标志各向异性晶体各向同性液体玻意耳定律(等温):p.V=p ₂V 查理定律(等容):Pi P:T T 盖一吕萨克定律(等压):V VTT p ₁V p ₂V ₂理想气体状态方程:T T热力学第一定律△U=W+Q热力学第二定律(两种表述)用油膜法估测油酸分子的大小探究等温情况下一定质量气体压强与体积的关系分子动理论固体和液体气体实验定律热力学定律实验分子力- 内能单晶体多晶体分子动能 分子势能非晶体热学固体原子核式结构能级玻尔理论跃迁,hv=E-E(m>n)天然放射现象、三种射线、原子核的组成:中子、质子衰变核反应 电荷数守恒、裂变 质量数守恒聚变核力 (比)结合能 质量亏损,核能,△E=△mc²极限频率最大初动能 E ₁=hv-W ₀饱和光电流 光的强度电子的干涉和衍射h λ=p光子能量ε=hv光电效应物质波原子结构原子物理α粒子散射实验近代物理人工核转变波粒二象性遏止电压原子核。

兰州理工大学李有堂编著机械系统动力学第7章连续系统的振动7.1 引言实际的物理系统都是由弹性体组成的系统,通常为连续系统。
离散系统是连续系统的近似模型,当其近似程度不能满足实际要求时,必须增加模型的自由度,或者采用连续模型。
连续模型是离散模型自由度无限增加时的极限。
连续系统是具有无限多个自由度的系统。
主要讨论可以获得精确解的问题。
弦的横向振动、杆的纵向振动和扭转振动、梁的弯曲振动7.2 弦的横向振动⏹弦:只能承受拉力,而抵抗弯曲及压缩的能力很弱。
⏹钢索、电线、电缆和皮带等柔性体构件⏹假设:材料是均匀连续和各向同性的;材料变形在弹性范围,服从虎克定律;运动是微幅的如图所示为一段长度为l 、两端固定的弦的横向振动的模型,f (x ,t )是作用在弦上的载荷密度,弦的线密度为ρ。
T ——弦上的张力,近似为常量;——时刻t 张力T 与x 轴的夹角 ——时刻t 弦上x 处的横向位移量(,)x t (,)y x t沿y 方向的运动微分方程为22(,)sin (,)sin (,)y x t T x dx t T x t dx t θθρ∂+-=∂对于微幅振动sin tan yxθθθ∂≈≈≈∂(,)(,)x dx t x t dxxθθθ∂+=+∂2222(,)(,)y x t y x t T x tρ∂∂=∂∂T αρ=22222(,)(,)y x t y x t x tα∂∂=∂∂弦的振动微分方程◆ 是一个偏微分方程◆ 对离散系统,运动是一种“同步运动”◆ 弹性体系统即连续系统也应为同步运动,同时达到极大值,同时过零点,因而整个弦的形状在振动中保持不变◆ 弦上各点随时间变化的位移可以分解为两部分的乘积22222(,)(,)y x t y x t x tα∂∂=∂∂(,)()()y x t Y x t Φ=分离变量确定整条弦线在空间的形状,与时间无关,弦的振型函数确定弦上各点位移随时间的变化规律,与空间坐标无关,弦的振动方式✓当 达到极值时,弦上各点位移同时达到极值 ✓当 为零时,弦上各点同时回到平衡位置()t Φ()t Φ(,)()()y x t Y x t Φ=x x Y t Φx t x y ∂∂=∂∂)()(),(2222)()(),(xx Y t Φx t x y ∂∂=∂∂t t Φx Y t t x y ∂∂=∂∂)()(),(2222)()(),(tt Φx Y t t x y ∂∂=∂∂方程左边仅为空间坐标的函数,右边仅为时间的函数,左右两边要保持相等,只有一种可能,就是两边均等于一个常数22222()1()()()Y x t Y x x t tαΦΦ∂∂=∂∂22222(,)(,)y x t y x t x tα∂∂=∂∂222222)()(1)()(n tt Φt Φx x Y x Y ωα-=∂∂=∂∂222()()0n t t tΦωΦ∂+=∂2222()()0n Y x Y x x ωα∂+=∂()sin()n t C t Φωϕ=+()sin cos n nY x A x B xωωαα=+弦的主振型是谐波曲线 (,)()()y x t Y x t Φ=()sin()n t C t Φωϕ=+()sin cos n nY x A x B xωωαα=+12(,)(sin cos )sin()n n n y x t C x C x t ωωωϕαα=++弦的运动规律是正弦曲线C 1、C 2、ωn 、为待定系数 ωn 、C 2——两个端点的边界条件确定、C 1——振动的初始条件确定 )sin(cos sin ),(ϕωαωαω+⎪⎭⎫ ⎝⎛+=t x B x A C t x y n n n ϕϕ弦的两端固定,其边界条件为(0,)(,)0y t y l t ==弦的两端固定,其边界条件为12(,)(sin cos )sin()n nn y x t C x C x t ωωωϕαα=++210, sin 0n lC C ωα==sin 0n l ωα=n lk ωπα=弦振动的特征方程,即频率方程nk k k Tl lαππωρ==第k 阶固有频率✓连续系统固有频率的取值和离散系统固有频率的取值一样,只取某几个特定的数值。

《思维导图画册》-(七年级)第一讲《走近科学》知识思维体系科学画册•你相信吗?空调的发明居然沾了印刷机的光说起对盛夏湿热的体验,人们大多会用酷暑难耐来形容!多亏有了空调相伴,才使人们摆脱了暑热之苦。
然而,空调最初并不是为人类研发的。
1902年,世界上第一个空调系统诞生了,但它是按照印刷机的“体验”进行设计的。
说起空调的发明,有一个人不能不提,他就是美国工程师及发明家威利斯·开利(Willis Haviland Carrier,1876年-1950年)。
由于他是现代空调系统的发明者,因此被誉为是“空调之父”。
那么,空调是怎样发明出来的呢?人类又是如何享用到这个伟大发明的呢?知冷知热的印刷机1901年,开利毕业于康奈尔大学,并获得机械工程硕士学位。
他入职的第一份工作是在一家锻造公司担任供暖工程师。
第二年,他接手的第一个任务就是处理纽约市沙克特威廉印刷厂的温度和湿度问题。
“空调之父”——威利斯·开利原来,这家印刷厂是锻造公司的客户单位。
这家印刷厂在生产中遇到了一个大难题,由于空气温度和湿度的变化,使得纸张的伸缩不定,这样就导致了油墨对位不准,自然就无法生产出清晰的印刷品了。
于是,这家印刷厂就求助于关联公司了。
印刷也是一个细活,对环境条件的要求也是十分苛刻的。
比如,对室内温度和湿度都是有要求的,一般冬季要保持在21℃,夏季要保持在27℃,全年相对湿度要保持在55%。
威利斯·开利对于只有26岁的开利来说,这个问题无疑是一个巨大的挑战。
不过,开利是个聪明人。
他很快就找到了问题的症结所在,原来都是湿热波动惹的“祸”。
但是,要想用机器装置来解决这个问题还是要付出努力的。
大雾让他茅塞顿开开利的一次经历开阔了他的思路。
有一天的傍晚,开利在某火车站等火车的时候,那弥漫天空的大雾启发了他,使得他对温度、湿度和露点之间的关系有了更深刻的认识。
说起雾,可以说是无人不晓,然而,真正能从大雾中捕捉灵感的人并不多。

分布式供能系统建模优化能流逻辑思维图详解摘要:针对复杂分布式供能系统DES/CCHP建模优化中把不同子系统的目标函数形式上加合成为系统目标函数但因其相互间并不存在关联而无法求解的问题,给出了表述DES/CCHP与其各个子系统的能流关系的逻辑思维图,指出了DES/CCHP包括蒸汽动力、区域供冷、区域供暖、生活热水、可再生能源发电、工业余热利用、智能微电网、天然气微网及LNG物流、氢能等9个子系统,提出了采用分解协调优化的策略和方法;首先对拓扑结构、设备参数、各种变量之间有可描述关系的各子系统分别建模和优化求解;然后在各个子系统之间多次迭代协调优化,电力是最主要的协调变量;进而指出上图是物理模型和能流模型的集成,但也蕴含着多种功能层次模型;只有在多种运行/营销层次工况初步优化结果的基础上才能建立设计/决策层次模型,并反复迭代才能获得优化结果。
强调优化的直接目标是经济性,最高能效目标来自基于科学用能原理所选择的子系统拓扑结构和参数,碳排放最少的目标则取决于能效和一次能源的构成。
上述方法已用于多个天然气DES/CCHP工程的规划和建设,有重要的科学意义和实用前景。
关键词:分布式供能系统;建模优化;能流图;分解协调;运性/设计建模迭代随着能源互联网研究工作的逐步深入,作为能源互联网基本单元的分布式供能系统(以下简称DES/CCHP)建模优化的研究越来越多。
而伴随着一次能源逐步向可再生能源转型,“多能互补”一词也开始大量应用。
在部分DES/CCHP研究提出的目标函数中,“多能互补”表现为多种一次能源转换的子系统目标函数的简单加和。
这是一种简单化、概念化的思维陷阱。
因为把实际上不存在相互关联的子项加和起来的目标函数,无论用什么方法都是得不到解的。
笔者已是耄耋之年,没有条件再协同年轻的研究生一起开展严谨、深入的研究工作。
愿把基于近40年从事能量系统集成建模优化和上百个工业和建筑物节能工程项目的实践而获得的对于DES/CCHP建模优化的逻辑思维,奉献给学术界,以助一臂之力。