如何正确运用因子分析法进行综合评价

因子分析在企业财务能力综合分析与评价中的应用摘要：企业财务能力评价问题往往因涉及众多指标而变得复杂，文章采用多元统计中的因子分析法来解决这一问题。

以多元统计理论为手段运用SPSS统计软件，结合二十一家工业企业进行因子分析法的实例研究，旨在说明因子分析法在企业财务能力综合分析评价中的应用。

关键词：因子分析；财务能力；综合评价企业的财务能力是企业正常运转的根本前提，也是企业形成有效竞争力的必要条件。

运用会计信息对企业财务绩效进行评价，对促进企业加强监督管理，优化企业财务状况具有重要意义，使企业在激烈的市场竞争中立于不败之地。

企业财务能力的评价指标体系中涉及众多财务指标，不但在一定程度上增加了问题分析的复杂性，而且反映的信息在一定程度上也存在重复；同时，在多指标综合评价方法中传统方法对于权重的设置还往往带有一定的主观随机性。

为避免上诉问题，文章采用因子分析法对企业的财务能力进行综合分析与评价。

1 因子分析法的基本原理因子分析法是把一些具有错综复杂关系的变量归结为少数几个综合因子的一种多变量统计分析方法。

其具体思想是根据相关性大小把原始变量分组，每组变量代表一个基本结构，称之为公共因子。

评价总体有n个样本，每个样品观测量为p个指标，则其模型为：Xi=ai1F1+ ai2F2+…+aimFm+?着i （i=1，2，…，p）其中，X1，X2，…，Xp使均值为零、方差为1的标准化变量；F1，F2，…，Fm主因子（m<p）；?着i为特殊因子；aij称为因子负荷，揭示了第i个变量在第j个主因子上的相对重要性。

在因子分析过程中，还可以用变量的观测值的线性表达式来计算各主因子的得分以及综合因子的得分值。

本文求解过程借助SPSS13.0统计分析软件来进行。

2 财务能力的综合分析与评价2.1 样本及变量指标的选取本文选取15个指标以构成一个比较完备的指标体系进行分析，X1~X15分别为：资产负债率、已获利息倍数、流动比率、速动比率、总资产周转率、应收账款周转率、固定资产周转率、存货周转率、销售收入增长率、销售利润增长率、总资产增长率、总资产报酬率、净资产收益率、销售利润率、成本费用利润率。

毕业论文中如何正确运用相关性分析和因子分析在毕业论文中，正确运用相关性分析和因子分析是非常重要的。

相关性分析是一种用于确定变量之间关系的统计方法，而因子分析则是用于确定潜在因素的方法。

本文将探讨如何正确运用这两种分析方法，并提供几个例子来说明它们在毕业论文中的应用。

第一部分：相关性分析相关性分析是通过计算变量之间的相关系数来确定它们之间关系的一种方法。

相关系数的范围从-1到+1，-1表示完全负相关，+1表示完全正相关，0表示没有相关性。

在毕业论文中，相关性分析可以用于研究两个或多个变量之间的关系。

例如，在教育领域的研究中，一个研究者可能对学生的成绩和参与课外活动之间的关系感兴趣。

通过进行相关性分析，可以确定这两个变量之间的关系强度和方向。

在运用相关性分析时，研究者需要注意以下几点：1. 确定要分析的变量：在进行分析之前，需要明确要研究的变量。

在上述例子中，研究者需要确定他们要分析的是学生的成绩和参与课外活动。

2. 收集数据：研究者需要收集相关的数据，例如学生的成绩和他们的课外活动参与情况。

数据可以通过问卷调查、观察或其他方法获得。

3. 计算相关系数：通过计算相关系数，研究者可以确定变量之间的相关性。

常用的相关系数有皮尔逊相关系数和斯皮尔曼相关系数。

皮尔逊相关系数适用于连续变量，而斯皮尔曼相关系数适用于有序变量。

举个例子，研究者收集了100名学生的成绩和他们的课外活动参与情况。

通过计算皮尔逊相关系数，研究者发现成绩和课外活动参与之间存在正相关关系，相关系数为0.7，说明两者之间的关系较为密切。

第二部分：因子分析因子分析是一种用于确定潜在因素的方法。

在毕业论文中，因子分析可以用于确定一组变量背后的共同因素。

它可以帮助研究者简化数据集，并找到隐藏的模式和关联。

在运用因子分析时，研究者需要注意以下几点：1. 确定要进行因子分析的变量：在进行因子分析之前，需要明确要进行分析的变量。

例如，在心理学研究中，研究者可能想要确定一组变量（如压力水平、焦虑水平和抑郁水平）背后的共同因素。

因子分析在企业财务能力综合分析与评价中的应用【摘要】企业的财务能力对于企业的经营和发展至关重要。

因子分析是一种多元统计方法，可以帮助企业从多个维度评价财务能力。

本文通过对因子分析在企业财务能力综合分析与评价中的应用进行研究，探讨了因子分析模型的构建和优势，以及通过案例分析展示了其在实际场景中的应用效果。

研究发现，因子分析可以更全面地评价企业的财务能力，为企业提供更有针对性的改进建议。

未来的研究可以进一步探讨因子分析在不同行业和不同规模企业中的适用性，并结合其他方法进行深入研究。

因子分析在企业财务能力综合分析与评价中的应用效果显著，可以为企业提供更准确的决策支持。

结论部分将总结研究成果，并展望未来的研究方向。

【关键词】企业财务能力、因子分析、综合分析、评价、模型构建、优势、案例分析、效果、未来研究方向、总结。

1. 引言1.1 背景介绍企业财务能力的评估在企业管理中占据着重要的地位。

通过对企业的财务能力进行评估，可以帮助企业管理者更好地了解企业的财务状况，及时发现存在的问题并采取有效措施加以改进。

在如今竞争激烈的市场环境下，企业需要具备强大的财务能力才能在市场中立于不败之地。

本文将重点研究因子分析在企业财务能力综合分析与评价中的应用。

将介绍企业财务能力的重要性，然后详细探讨因子分析在企业财务能力评价中的应用以及模型构建方法。

接着分析因子分析在企业财务能力综合分析中的优势，并通过实际案例对因子分析的应用效果进行验证。

希望通过本文的研究，可以为企业财务能力的评价提供更科学准确的方法和思路。

1.2 研究意义企业财务能力是企业财务健康状况的重要指标，直接关系到企业的盈利能力、清偿能力、发展潜力等方面。

对企业的财务能力进行综合评价，有助于企业管理者了解企业的财务状况，及时发现问题并采取有效措施进行调整，提高企业的竞争力和持续发展能力。

研究企业财务能力的综合分析与评价具有重要的意义。

利用因子分析技术对企业的财务能力进行评价有助于从多个指标中提取出影响财务能力的关键因素，降低评价指标的维度，更加全面客观地反映企业财务状况。

因子分析在学生成绩综合评价中的应用作者：张永福赵洪章穆扬来源：《现代电子技术》2008年第06期摘要：在教学管理中，需要科学合理地对学生成绩进行综合评价。

目前，应用较多的如简单相加法和标准分法都存在各种缺点。

运用主成分分析的方法对学生成绩进行因子分析，并通过分析的结果做出一个综合评价，这样可以比较有效地解决其他分析方法存在的问题。

通过对学生在校期间各科成绩进行因子分析的具体实例研究，找出影响学生知识和能力的主要方面因子，并据此对学生成绩做出一个客观、综合的评价。

关键词：因子分析；各科成绩；综合评价；实例分析中图分类号：TP391；O212 文献标识码：B 文章编号：1004-373X(2008)06-137-04Application of Factor Analysis to Comprehensive Evaluation on Students′ GradeZHANG Yongfu ZHAO Hongzhang MU Yang2(1.School of Astronautics，Northwestern Polytechnical University，Xi′an，710072，China；2.School of Educational Experimentation，Northwestern Polytechnical University，Xi′an，710072，China)Abstract：We need to have a comprehensive evaluation on the students′ grade scien tifically and reasonably in the field of teaching management.At present，the methods which are mostly used in the aspect include simple addition and standard marks which both have their own limitations.Making use of the method of factor analysis in evaluati ng the students′ grade by using the principal component analysis can give us a more comprehensive evaluation from the analytical results than before-mentioned methods.In this paper，we find out the primary factors which can have an influence on the students′ knowledge and ability by studying on an example and then make an objective and comprehensive assessment on the students′ grade.Keywords：factor analysis；grade of various subjects；comprehensive evaluation；example analysis1 引言在各大专院校中经常遇到评定各类奖学金，择优分配，推荐研究生等问题。

利用因子分析方法对重庆市各区县经济发展状况的评价在衡量一个地区的经济发展状况时，并不能仅仅简单比较一两项指标数据，特别是现在社会经济各行业错综交汇，更应该从社会经济发展的各方面综合考察，从而描述社会经济的现状，找出存在的问题及其影响因素，为地区经济发展提高政策制定依据。

我对重庆市40个区市县的经济情况进行分析，根据各区县市的数据（见附页），并按经济综合实力评价各区市县的地位和发展状况。

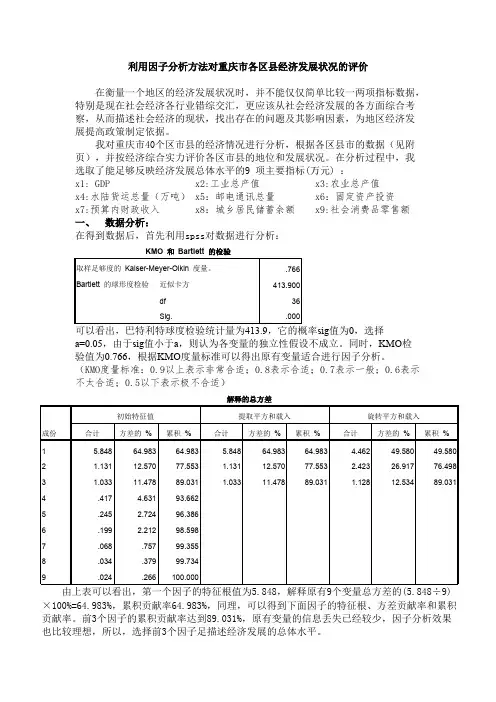
在分析过程中，我选取了能足够反映经济发展总体水平的9 项主要指标(万元) ：x1: GDP x2:工业总产值 x3:农业总产值x4:水陆货运总量（万吨） x5：邮电通讯总量 x6：固定资产投资x7:预算内财政收入 x8：城乡居民储蓄余额 x9:社会消费品零售额一、数据分析：sig值为0，选择a=0.05，由于sig值小于a，则认为各变量的独立性假设不成立。

同时，KMO检验值为0.766，根据KMO度量标准可以得出原有变量适合进行因子分析。

（KMO度量标准：0.9以上表示非常合适；0.8表示合适；0.7表示一般；0.6表示个因子的特征根很高，对解释变量原有的贡献最大，第三个以后的因子特征根3个因子是合适的。

80%甚至90%以上，说明提取的因子已经包含了原始变量的大部分信息，因子提取的效果比较理想。

采用主成分法计算因子载荷矩阵A ，根据因子载荷矩阵可以说明各因子在各变量上的载荷，即影响程度。

由于初始的因子载荷矩阵系数不是太明显，为了使因子载荷矩阵中系数向0-1 分化，对初始因子载荷矩阵进行方差最大旋转，旋转后的因子载荷矩阵如下表所示：邮电通讯总量=0.975F1+0F2+0F3社会消费品零售总额=0.902F1+0.336F2+0F3城乡居民储蓄存款余额=0.828F1+0.311F2+0F3地方财政预算内收=0.815F1+0.451F2+0.119F3GDP=0.707F1+0.608F2+0.273F3固定资产投资=0.660F1+0.651F2+0.165F3水陆货物周转量=0.631F1+0.525F2+0F3工业总产值=0.123F1+0.967F2-0.103F3农业总产值=0F1+0F2+0.993F3由表中可以看出，第一公因子在除工业总产值和农业总产值外，在其它变量上都有较大的载荷，主要表现为除工农业外的各经济指标的综合影响，可将其定义为经济发展的综合实力因子；第二公因子在工业总产值上有很大载荷，体现了工业在经济发展中的作用，定义为工业发展影响因子；同理，第三公因子在农业总产值上有很大载荷，定义为农业发展影响因子。

因子分析在教育质量评价中的实际案例分析教育质量评价是教育管理中非常重要的一个环节，它可以帮助学校和教育机构了解教学质量的现状，找出存在的问题，并制定改进措施。

因子分析是一种多变量统计方法，可以帮助我们理解变量之间的内在结构，并找出潜在的因子。

在教育质量评价中，因子分析可以帮助我们识别影响学校教学质量的关键因素，从而有针对性地改进教育质量。

下面，我们通过一个实际案例来探讨因子分析在教育质量评价中的应用。

案例背景某市教育局想要对该市中小学的教育质量进行评价，并且希望通过评价结果找出存在的问题，为学校的改进提供科学依据。

为了达到这一目的，教育局决定对学校的教学质量、教师水平、学生综合素质等方面进行评价，以期找出影响教学质量的关键因素，并制定相应的改进措施。

数据收集教育局首先收集了相关数据，包括学校的师生比、师资水平、学生素质等多个变量。

这些数据既包括客观指标，如教师的学历、学生的考试成绩，也包括主观指标，如教师对学校教学环境的满意度、学生对学校教学质量的评价等。

因子分析在收集完数据后，教育局委托统计专家对数据进行了因子分析。

通过因子分析，专家发现在所收集的变量中，存在一些内在的联系，例如教师的学历、教学经验和对教学环境的满意度之间存在一定的关联。

通过因子分析，专家将这些变量归纳整合，得到了几个潜在的因子，如“教师水平”、“学校教学环境”等。

结果解读通过因子分析后，教育局得到了一些关键的结论。

首先，教师的学历、教学经验和对教学环境的满意度等因素构成了“教师水平”这一因子，这表明学校可以通过提升教师的学历和经验，改善教学环境来提高教学质量。

其次，学生的综合素质、学校的学习氛围等因素构成了“学校教学环境”这一因子，这表明学校可以通过加强学生的综合素质培养，营造良好的学习氛围来提高教学质量。

改进建议基于因子分析的结果，教育局提出了一系列的改进建议。

针对“教师水平”这一因子，教育局建议学校加强教师的培训和发展，提升教师的专业水平和教学能力；针对“学校教学环境”这一因子，教育局建议学校重视学生的综合素质培养，加强学校管理，营造良好的学习氛围。

SPSS数据分析，基于因子分析学生成绩综合评价因子分析在成绩综合评价中的应用成绩可以是多方面的，包括在校大学生的考试成绩、高考生的入学成绩、公务员考试的笔试（面试）成绩、公司员工或政府官员的测评考核成绩等，本节以学生的考试成绩为例，利用因子分析进行对考核对象的综合评价。

学生成绩能反映学生掌握知识和各种能力的程度，综合得分是评价一个学生学习好坏、评定奖学金和评先评优等工作中最重要的一个指标，也是择优推荐就业很主要的参考因素。

因此，合理的、公平的、科学的对学生成绩做出综合评价显得格外重要。

因子分析概念因子分析是多元统计的重要分析方法之一，其基本思想是根据相关性大小对变量进行分组，使得同组内的变量之间相关性较高，不同组的变量之间相关性较低，每组变量代表了一个基本结构，因子分析中将之称为公共因子。

因子分析在教育学、社会经济学、心理学等领域都有广泛的应用价值。

数据来源SPSS操作依次单击菜单“分析—降维—因子”执行因子分析过程，选取变量。

点击“描述”按钮，依次选系数、显著性水平、KMO 和巴特利特球形度检验，点击继续，返回主菜单。

单击“提取”按钮，勾选“碎石图”，其他选项默认，选择主成份法进行因子提取。

单击“继续”按钮返回主面板。

单击旋转按钮，单击选中最大方差法单选框，表示采用方差最大旋转法进行因子旋转。

单击继续按钮返回主面板。

单击得分按钮，勾选底部的显示因子得分系数矩阵复选框。

单击继续按钮返回主面板。

设置完毕后，点击确定，生成结果。

结果分析KMO检验和Bartlett球形检验。

如图22-11所示，KMO检验研究变量间的偏相关性，计算偏相关时控制了其他因素的影响，所以比简单相关系数要小，一般KMO统计量大于0.9时效果最佳，0.7以上可以接受，0.5以下不宜作因子分析，本例KMO取值0.857进一步印证了作因子分析的必要性。

Bartlett球形检验统计量的Sig值小于0.01，由此否定相关矩阵为单位阵的零假设，即认为各变量之间存在显著的相关性，这与从相关矩阵得出的结论致。

浅谈因子分析方法在多指标综合评价中的运用因子分析方法是一种统计分析方法，主要用于研究多个变量之间的关系，其基本思想是将多个变量通过线性组合进行综合评价。

因子分析方法在多指标综合评价中的运用，可以帮助我们识别出具有代表性的综合指标，从而简化评价过程，提高评价准确性。

首先，因子分析方法在多指标综合评价中的应用可以帮助我们减少指标冗余。

在评价过程中，可能存在大量指标，但很多指标之间可能存在高度相关性。

通过因子分析，我们可以找到一些潜在因子来代表这些相关性，从而减少指标数量，简化评价模型。

这不仅可以节约评价成本，还可以提高评价效率。

另外，因子分析方法可以帮助我们确定主导因素和评价指标的权重。

在多指标综合评价中，不同指标对于评价结果的贡献是不同的。

通过因子分析，我们可以确定各个因子的权重，并进一步计算出各个指标的权重。

这有助于我们合理地设置各个指标的权重，避免主观随意性，提高评价结果的科学性和客观性。

此外，因子分析方法还可以帮助我们解决指标间的共线性问题。

在多指标综合评价中，指标之间可能存在高度相关性，导致评价结果不准确。

通过因子分析，我们可以将这些相关性较高的指标进行合并，生成新的综合指标，从而避免共线性问题对评价结果的影响。

最后，因子分析方法还可以帮助我们进行评价结果的解释和解读。

通过因子分析，我们可以得到各个因子的得分和权重，从而更好地解释评价结果的形成机制。

这有助于我们深入理解评价对象的特征和潜在问题，为进一步改进和优化提供依据。

总之，因子分析方法在多指标综合评价中的运用可以帮助我们简化评价过程，减少指标冗余，理清指标之间的内在关系，确定主导因素和指标的权重，解决指标共线性问题，以及解释评价结果的形成机制。

因此，合理运用因子分析方法可以提高多指标综合评价的科学性和客观性，为决策提供有效的支持。

《应用统计分析》----题目2题目2 数据data2是某医院3年中各月的数据，包括门诊人次、出院人数、病床利用率和周转次数、平均住院天数、治愈或好转率、病死率、诊断符合率、抢救成功率。

采用因子分析法探讨综合评价指标。

一、因子分析法因子分析是主成分分析的推广和发展，也是利用降维方法进行统计分析的一种多元统计方法。

它是一种将多变量化简的技术，其目的是分解原始变量，从中归纳出潜在的“类别”，相关性较强的指标归为一类，不同类间变量的相关性则降低。

每一类变量代表了一个“共同因子”，即一种内在结构,因子分析就是要寻找该结构。

因子分析有一个默认的前提条件就是各变量间必须有相关性，否则，各变量间没有共享信息，就不应当有公因子需要提取，自然也谈不上使用该方法。

具体在该条件的判断上，除了根据专业知识来估计外，还可以使用KMO统计量和Bartlett’s 球形检验加以判定。

二、操作步骤1.导入数据依次单击“文件—打开—数据文件”命令，打开如图1所示的对话框。

图1 导入数据2.因子分析（1）依次单击“分析—降维—因子分析”命令，如图2所示。

打开图3所示的“因子分析”主对话框。

图2 因子分析菜单（a ）选入变量前（b ）选入变量后图3 “因子分析”主对话框（2）在图3（a ）所示的对话框中选中左边的变量，单击按钮，将其选入到左边的列表框中（如图3a 所示）。

（3）单击“描述”按钮，弹出“因子分析：描述统计”对话框，如图4所示，在“统计量”选项组中选取“原始分析结果”；在“相关矩阵”中选取“系数”和“KMO和Bartlett”。

设置完毕后，单击“继续”按钮，确认操作。

图4 “因子分析：描述”对话框图5 “因子分析：抽取”对话框（4）单击“抽取”按钮，得到如图5所示的“因子分析：抽取”对话框。

选择“方法”为“主成分”；在“分析”选项组选择“相关性矩阵”；在“输出”选项组选择“未旋转的因子解”和“碎石图”；在“提取”选项组中将“因子的固定数量：”设置为4；将“最大收敛性迭代次数：”设置为25.（5）单击“旋转”按钮，得到如图6所示的“因子分析：旋转”对话框。

因子分析法在会计专业大学生综合评定中的应用作者：艾雪来源：《当代教育理论与实践》 2016年第6期艾雪（沈阳农业大学经济管理学院，辽宁沈阳１１０８６６）摘要：大学生成绩评定结果除了对于学生有反馈和激励的双重作用之外，还能对教师的教学效果起到诊断、调节和强化的作用。

对实践性强的会计专业而言，现行的成绩综合评定方法存在一定缺陷。

采用因子分析法对１０７名同年级会计专业本科生的主要课程成绩进行分析和检验发现，因子分析法能更客观地分析会计专业学生能力缺失的具体方面，为教师授课的提升及学生能力弥补提供针对性，从而快捷有效地提高教学效果。

关键词：因子分析法；会计专业；成绩评定中图分类号：Ｇ６４２．１文献标志码：Ａ文章编号：１６７４－５８８４（２０１６）０６－００５９－０４大学生成绩评定结果对于学生有反馈和激励的双重作用［１］。

既往的成绩反馈的是学生的学业成果。

对于成绩优异的学生，可以激发其学习积极性，增强自信心，萌发学习成功的感受；对于成绩差强人意的学生，可以通过改进学习方法、提高学习效率、增加学习时间等方式提高成绩。

由此，成绩优异或成绩欠佳的学生都可以通过成绩评定培养积极的学习心态，促进大学生在生理、心理等方面的进步，促使学生整体素质的提高。

学生成绩评价结果还能反馈教师的教学效果，起到诊断、调节和强化的作用。

诊断作用是指学生的成绩分布能有效地反映学生对课程知识点掌握的情况，甄别普遍性的学生掌握良好的知识点以及掌握欠佳的知识点；针对学生集中出现问题的某些知识点，在下一轮教学中，有针对性地引导学生或改进教学方法则是教师对成绩评定结果的调节；强化作用则是针对学生掌握普遍良好、教学方法得当的知识点的授课方式可以在以后的教学中加以发扬。

通过以上三个方面的作用，可以促使教师有目的地完善授课效果，提高学生的培养质量，使之更加符合培养目标和社会需求。

目前在高校实际应用中，对大学生成绩进行综合评价的方法有很多，如原始分求和模型、平均学分成绩模型、平均学分积等模型［２］。

因子分析在企业绩效评价中的应用指南企业绩效评价一直是管理者们关注的焦点之一。

有效的绩效评价可以帮助企业更好地了解自身的发展状况，发现问题并加以改进，从而提高竞争力。

而因子分析作为一种多变量统计分析方法，可以在企业绩效评价中发挥重要作用。

本文将探讨因子分析在企业绩效评价中的应用指南。

一、因子分析的基本原理首先，我们需要了解因子分析的基本原理。

因子分析是一种通过变量之间的相关关系来识别共同因素的统计方法。

在企业绩效评价中，我们通常会收集一系列指标来衡量企业的绩效，例如营业收入、利润率、市场份额等。

这些指标之间存在着一定的相关性，因子分析可以帮助我们找到这些指标背后的共同因素，从而更全面地评价企业的绩效。

二、确定评价指标在进行因子分析之前，我们需要明确企业绩效评价的指标。

这些指标应该具有代表性，能够全面反映企业的绩效情况。

同时，指标之间应该存在一定的相关性，这样才能够进行因子分析。

在确定指标时，可以参考行业标准或者是参照相关研究成果，确保指标的科学性和可靠性。

三、数据收集和整理在开始因子分析之前，我们需要进行数据的收集和整理工作。

这包括对所选指标的数据进行收集和整理，确保数据的准确性和完整性。

对于缺失数据或异常数据，需要进行处理和修正，以确保数据的可靠性。

四、因子提取和旋转在进行因子分析时，首先需要进行因子提取。

因子提取是通过数学方法，将原始的多个指标转化为少数几个共同因素。

常用的因子提取方法包括主成分分析法和最大方差法。

在因子提取之后，还需要进行因子旋转，以便更好地解释因子的含义和解释力。

五、因子得分计算完成因子提取和旋转之后，我们需要计算每个因子的得分。

因子得分是通过对原始指标进行加权得到的，可以反映每个因子在企业绩效中的重要程度。

同时，得分还可以帮助我们比较不同企业之间的绩效情况，从而更好地指导管理决策。

六、因子分析结果的解释和应用最后，我们需要对因子分析的结果进行解释和应用。

通过因子分析，我们可以得到不同因子的得分和权重，从而更全面地评价企业的绩效。