山东省诸城市桃林镇2017届中考数学压轴题专项汇编专题16对角互补模型

全等与相似模型-对角互补模型全等三角形与相似三角形在中考数学几何模块中占据着重要地位。

相似三角形与其它知识点结合以综合题的形式呈现，其变化很多，难度大，是中考的常考题型。

如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到该类问题就信心更足了．本专题就对角互补模型进行梳理及对应试题分析，方便掌握。

模型1、旋转中的对角互补模型对角互补模型概念：对角互补模型特指四边形中，存在一对对角互补，而且有一组邻边相等的几何模型。

思想方法：解决此类问题常用的辅助线画法主要有两种：①过顶点做双垂线，构造全等三角形；②进行旋转的构造，构造手拉手全等。

常见的对角互补模型含90°-90°对角互补模型、120°-60°对角互补模型、2α-(180°-2α)对角互补模型。

1)“共斜边等腰直角三角形+直角三角形”模型(异侧型)条件：如图，已知∠AOB=∠DCE=90°，OC平分∠AOB.结论：①CD=CE，②OD+OE=2OC，③S ODCE=S△COE+S△COD=12OC2.2)“斜边等腰直角三角形+直角三角形”模型(同侧型)条件：如图，已知∠DCE的一边与AO的延长线交于点D，∠AOB=∠DCE=90°，OC平分∠AOB.结论：①CD=CE，②OE-OD=2OC，③S△COE-S△COD=12OC2.3)“等边三角形对120°模型”(1)条件：如图，已知∠AOB=2∠DCE=120°，OC平分∠AOB.结论：①CD=CE，②OD+OE=OC，③S△COD+S△COE=34OC2.4)“等边三角形对120°模型”(2)条件：如图，已知∠AOB=2∠DCE=120°，OC平分∠AOB，∠DCE的一边与BO的延长线交于点D，结论：①CD=CE，②OD-OE=OC，③S△COD-S△COE=34OC2.5)“120°等腰三角形对60°模型”条件：△ABC是等腰三角形，且∠BAC=120°，∠BPC=60°。

专题16 对角互补模型破解策略1．全等型之“90°”如图，∠AOB ＝∠DCE ＝90°，OC 平分∠AOB ，则A O BDCE（1）CD ＝CE ； （2）OD ＋OE ＝2OC ； （3）212OCD OCE S S OC ∆∆+=． 证明 方法一：如图，过点C 分别作CM ⊥OA ，CN ⊥OB ，垂足分别为M ，N ． 由角平分线的性质可得CM ＝CN ，∠MCN ＝90°．所以∠MCD ＝∠NCE ，从而△MCD ≌△NCE （ASA ），故CD ＝CE ．易证四边形MONC 为正方形． 所以OD ＋OE ＝OD ＋ON ＋NE ＝2ON ＝2O C ．所以2212OCD OCE MONC S S S ON OC ∆∆+===正方形． 方法二：如图，过C 作CF ⊥OC ，交OB 于点F ．易证∠DOC ＝∠EFC ＝45°，CO ＝CF ，∠DCO ＝∠ECF ． 所以△DCO ≌△ECF （ASA ） 所以CD ＝CE ，OD ＝FE ， 可得OD ＋OE ＝OF ＝2OC ．所以212OCD OCE OCF S S S OC ∆∆∆+==．【拓展】如图，当∠DCE 的一边与AO 的延长线交于点D 时，则：NM A OBD CE FA OBDCEB AECO D（1）CD ＝CE ； （2）OE －OD ＝2OC ； （3）212OCE OCD S S OC ∆∆-=． 如图，证明同上．FDO CEAB NM DO CEA B2．全等型之“120”如图，∠AOB ＝2∠DCE ＝120°，OC 平分∠AOB ，则：OBECDA（1）CD ＝CE ；（2）OD ＋OE ＝OC ； （3）234OCD OCE S S ∆∆+=． 证明 方法一：如图，过点C 分别作CM ⊥OA ，CN ⊥OB ，垂足分别为M ，N ． 所以232OCD OCE ONC S S S ∆∆∆+==易证△MCD ≌△NCE （ASA ），所以CD ＝CE ，OD ＋OE ＝2ON ＝O C ．NMA D CE BOF AD CEBO方法二：如图，以CO 为一边作∠FCO ＝60°，交OB 于点F ，则△OCF 为等边三角形． 易证△DCO ≌△ECF （ASA ）．所以CD ＝CE ，OD ＋OE ＝OF ＝OC ， ∴S △OCD ＋S △OCE ＝S △OCF ＝43OC 2 【拓展】如图，当∠DCE 的一边与BO 的延长线交于点E 时，则： （1）CD ＝CE ；（2）OD －OE ＝OC ；（3）S △OCD －S △OCE ＝43OC 2 如图，证明同上．EO BA CDN M EO BA CDF EO BA CD3、全等型之“任意角”如图，∠AOB ＝2α，∠DCE ＝180°－2α，OC 平分∠AOB ，则：（1）CD ＝CE ；（2）OD ＋OE ＝2OC ·cos α；（3）S △ODC ＋S △OEC ＝OC 2·sin αcos αEOBA CD证明：方法一：如图，过点C 分别作CM ⊥OA ，CN ⊥OB ，垂足分别为M ，N易证△MCD ≌△NCE （ASA ）∴CD ＝CE ，OD ＋OE ＝2ON ＝2OC ·cos α∴S △ODC ＋S △OEC ＝2S △ONC ＝OC 2·sin αcos α方法二：如图，以CO 为一边作∠FCO ＝180°－2α，交OB 于点F ．MN E O AC D易证△DCO≌△ECF（ASA）∴CD＝CE，OD＋OE＝OF＝2OC·cosα∴S△ODC＋S△OEC＝S△OCF＝OC 2·sinαcosα【拓展】如图，当∠DCE的一边与BO的延长线交于点E时，则：（1）CD＝CE；（2）OD－OE＝2OC·cosα；（3）S△ODC－S△OEC＝OC 2·sinαcosα如图，证明同上4、相似性之“90°”如图，∠AOB＝∠DCE＝90°，∠COB＝α，则CE＝CD·tanα方法一：如图，过点C分别作CM⊥OA，CN⊥OB，垂足分别为M、N易证△MCD∽△NCE，∴αtan===CMCNCDCEMDNE，即CE＝CD·tanα方法二：如图，过点C作CF⊥OC，交OB于点F．易证△DCO ∽△ECF ，∴αtan ===COCFCD CE OD FE ，即CE ＝CD ·tan α 方法三：如图，连接DE ．易证D 、O 、E 、C 四点共圆∴∠CDE ＝∠COE ＝α，故CE ＝CD ·tan α【拓展】如图，当∠DCE 的一边与AO 的延长线交于点D 时，则CE ＝CD ·tan αEOBD CA如图，证明同上．M N EO BDCAF EOBDCAEO BDCA例题讲解例1、已知△ABC 是⊙O 的内接三角形，AB ＝AC ，在∠BAC 所对弧BC 上任取一点D ，连接AD ，BD ，C D ．（1）如图1，若∠BAC ＝120°，那么BD ＋CD 与AD 之间的数量关系是什么？ （2）如图2，若∠BAC ＝α，那么BD ＋CD 与AD 之间的数量关系是什么？图1O BCD图2A OBCD解：（1）BD ＋CD ＝3AD图3F EO BCD如图3，过点A 分别向∠BDC 的两边作垂线，垂足分别为E 、F ． 由题意可得∠ADB ＝∠ADC ＝30°DA OCE易证△AEB ≌△AFC ∴BD ＋CD ＝2DE ＝3AD⑵BD ＋CD ＝2AD sin2α． 如图4，作∠EAD ＝∠BAC ，交DB 的延长线于点E ．则△EBA ≌△DCA ，所以BE ＝CD ，AE ＝A D ．作AF ⊥DE 于点F ，则∠FAD ＝2α．所以BD ＋CD ＝DE ＝2DF ＝2AD sin 2α． 例2如图1，将一个直角三角板的直角顶点P 放在正方形ABCD 的对角线BD 上滑动，并使其一条直角边始终经过点A ，另一条直角边与BC 相交于点F ． ⑴求证：PA ＝PE ；⑵如图2，将⑴中的正方形变为矩形，其余不变，且AD ＝10，CD ＝8，求AP ：PE 的值； ⑶如图3，在⑵的条件下，当P 滑动到BD 的延长线上时，AP ：PE 的值是否发生变化？解：⑴如图4，过点P 分别作PM ⊥AB ，PN ⊥BC ，垂足分别为M ，N ．则PM ＝PN ，∠MPN ＝90°，由已知条件可得∠APE ＝90°，所以∠APM ＝∠EPN ，所以△APM ≌△EPN ． 故AP ＝PE ．⑵如图5，过点P 分别作PM ⊥AB ，PN ⊥BC ，垂足分别为M ，N ．则PM ∥AD ，PN ∥C D ． 所以△BPM ∽△BDA ，△BNP ∽△BC D ．可得PM BP PN AD BD CD ==，所以54PM AD PN CD ==．易证△APM ∽△EPN ，所以54AP PM PE PN ==． 图4A DPBE CN M图3ADBEP FC ADBPCE 图2ADPBE C 图1DFBEOC图4⑶AP ：PF 的值不变．[如图，理由同⑵]进阶训练1．如图，四边形ABCD 被对角线BD 分为等腰Rt △ABD 和Rt △CBD ，其中∠BAD 和∠BCD 都是直角，另一条对角线AC 的长度为2，则四边形ABCD 的面积为_________．答案：四边形ABCD 的面积为2． 【提示】易证A 、B 、C 、D 四点共圆，则∠BCA ＝∠BDA ＝∠ABD ＝∠ACD ，由“全等型之‘90°’”的结论可得S 四边形ABCD ＝12AC 2＝2．2．在△ABC 中，AB ＝AC ，∠A ＝60°，D 是BC 边的中点，∠EDF ＝120°，DE 与AB 边相交于点E ，DF 与AC 边（或AC 边的延长线）相交于点F ．⑴如图1，DF 与AC 边相交于点F ，求证：BE ＋CF ＝12AB ； ⑵如图2，将图1中的∠EDF 绕点D 顺时针旋转一定的角度，使DF 与AC 边的延长线交于点F ，作DN ⊥AC 于点N ，若DN ＝FN ，求证：BE ＋CF ＝3（BE －CF ）．答案：略．第1题图1AEFAEFC D BN 第1题图2AB CD第1题图图6ADBEP FC M N 图5A DBPCE N M【提示】⑴过点D 作DG ∥AC 交AB 于点G ，证△DEG ≌△DFC ，从而BE ＋CF ＝BE ＋EG ＝BG ＝12A B ．⑵过点D 作DG ∥AC 交AB 于点G ，同⑴可得BE －CF ＝12AB ＝DC ＝3，延长AB 至点H ，使得BH ＝CF ，则DH ＝DF ＝DE ，从而BE ＋CF ＝HE ＝2DE ＝2×2DN ＝2DN ，所以BE ＋CF ＝3（BE －CF ）．3．在菱形ABCD 中，两条对角线AC ，BD 相交于点O ，∠MON ＋∠BCD ＝180°，∠MON 绕点O 旋转，射线OM 交BC 于点E ，射线ON 交CD 于点F ，连结EF ． ⑴如图1，当∠ABC ＝90°时，△OEF 的形状是____；⑵如图2，当∠ABC ＝60°时，请判断△OEF 的形状，并说明理由；⑶如图3，在⑴的条件下，将∠MON 的顶点移动到AO 的中点O '处，∠MO 'N 绕点O '旋转，仍满足∠MO 'N ＋∠BCD ＝180°，射线O 'M 交直线BC 于点E ，射线O 'N 交直线CD 于点F ，当BC＝4，且'98O EF ABCD S S 四边形时，求CE 的长．答案：⑴等腰直角三角形；⑵△OEF 是等边三角形；⑶线段CE 的长为33或33． 【提示】⑵由“全等型之‘120°’”的结论可得OE ＝OF ．⑶两种情况，如图：第3题图1 ADBCOME F N ABC DOF E MN第3题图2AOO ' 第3题图3第1题答图2A E FC DB NHG第1题答图1 AEFG'第3题答图。

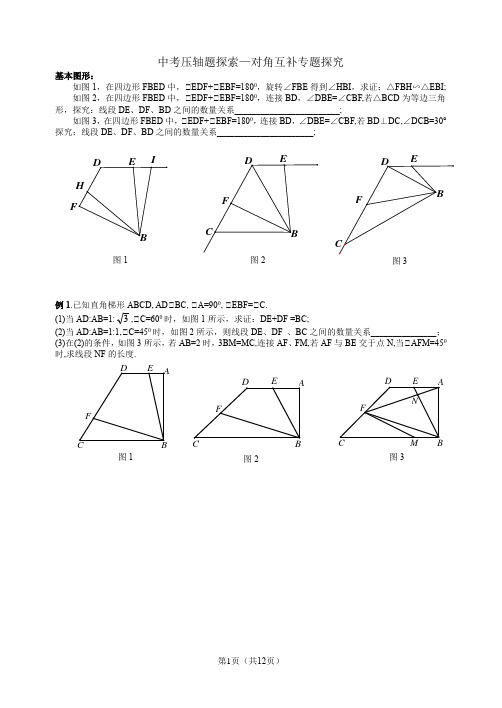
中考压轴题探索—对角互补专题探究基本图形：如图1，在四边形FBED 中，∠EDF+∠EBF=1800，旋转∠FBE 得到∠HBI ，求证：△FBH ∽△EBI; 如图2，在四边形FBED 中，∠EDF+∠EBF=1800，连接BD ，∠DBE=∠CBF,若△BCD 为等边三角 形，探究：线段DE 、DF 、BD 之间的数量关系________________________;如图3，在四边形FBED 中，∠EDF+∠EBF=1800，连接BD ，∠DBE=∠CBF,若BD ⊥DC,∠DCB=30° 探究：线段DE 、DF 、BD 之间的数量关系______________________;例1.已知直角梯形ABCD, AD∠BC, ∠A=900, ∠EBF=∠C.(1)当AD:AB=1:3,∠C=600时，如图1所示，求证：DE+DF =BC;(2)当AD:AB=1:1,∠C=450时，如图2所示，则线段DE 、DF 、BC 之间的数量关系_______________； (3)在(2)的条件，如图3所示，若AB=2时，3BM=MC,连接AF 、FM,若AF 与BE 交于点N,当∠AFM=450时,求线段NF 的长度.FA B C D E 图2 N M F A B D C E 图3 F A B D C E 图1 D B C F E 图2 BD C FE 图3 DBFE I H 图1变式训练：1.已知直角梯形ABCD ，AD∠BC,AD=3AB,∠A=900,∠C=600,DH∠BC 于H,P 为BC 上一点，作∠EPF=600,此角的两边分别交AD 于E, 交CD 于F.(1).如图1，当点P 在点B 处时，求证：2 AE+CF=2CH;(2).如图2，当点P 在点H 处时，线段 AE 、CF 、CH 的数量关系为____________________; (3).在（2）的条件下，连接FB 、EF,FB 与FH 交于点K,若AB=32,EF=21,求线段FK 的长度.2.已知平行四边形ABCD, ∠C=60°，点E 、F 分别为AD 、CD 上两点∠EBF=∠C. (1).如图1，当AB=BC 时，求证：CF+AE=BC ； (2).如图2，当AB=76BC 时，线段：CF 、AE 、BC 三者之间有何数量关系_______________; (3)在(2)的条件下如图3，若AB=6,连接EC 与BF 交于M,当∠BEM 为等边三角形时，求线段FM 的长.(P)H A F D B C E 图1 F D C B A E 图1 图3 (P)K E H AD BC F 图2 (P)E H AD B C F 图2F D A E 图3 M F D C B A E例2.已知：∠ABC 中，∠ACB=900, ∠B=300 ,点P 为边AB 上的一点, ∠EPF=900,PF 与边AC 交于点F,PE 与边BC 交于点E. 设AP:PB=k (1)如图1，当k =31时，则： AF+ _____ BE=21AB;(2).如图2，当k =1时，线段AF 、BE 、AB 的数量关系为___________________;(3).在(2)的条件下，如图3，连接CP,EF 交于点K,将FP 沿着EF 对称，对称后与CP 交于点M ,连接ME,若AC=3,当ME∠FP 时，求tan∠CEM 的值.K图3 M F C P A B E图2 F CE图1 E C F变式训练：1.等边∠ABC 中，BH 为AC 边上的高，点P 为AB 边中点，∠EPF=900,此角的两边与AC 边交于点F,与高BH 交于点E.(1)如图1，求证: FH+3BE=21AB; (2)如图2，则线段FH 、BE 、AB 之间满足的关系式为____________;(3)如图3，在(2)的条件下，连接EF ，直线EF 与BC 交于点N ，将FN 沿着FP 对称，对称后与AB 交于点M,若AC=34,AM:BM=1:3,时，求BN 长度.图1 E P H B C A F 图2 EH CF 图3N MEPHBA F中考压轴题探索—对角互补专题探究（二）1.（遗漏了某个条件）直线m ∥n ，点A 、B 分别在直线m 、n 上，且点A 在点B 的右侧.点P 在直线m 上，AP=13AB,连接BP,以PB 为一边在PB 右侧作等边△BPC ，连接AC.过点P 作PD ⊥n 于点D.(1)当点P 在A 的右侧时（如图1），求证：BD=58AC(2)当点P 在A 的左侧时（如图2），线段BD 与AC 之间的数量关系为_______________. (3)在(2)的条件下，设PD 交AB 于点N ，PC 交AB 于点M （如图3）.若△PBC 的面积为7√34，求线段MN 的长.nmDCP BA图1nmCDP BA图2nmCDP BA 图32.如图，直线y= -33kx+4k (k ＞0)与x 轴交于B,与y 轴交于D,点O 与点C 是关于直线BD 对称，连接BC,若AC=34. (1)求k 的值；(2)点P 为OB 的中点，动点E 从点B 出发，每秒1单位速度沿BH 向点H 运动，过点P 做P E 的垂线交AC 于点F,当点F 与点O 重合时点E 停止运动. 设运动时间为t 秒，△PHF 面积为S ，写出S 与t 点函数关系式，并直接写出自变量t 的取值范围． (3)连接PH,是否存在t 值，使得tan ∠FPH=73，若存在请求t 值，若不存在，说明理由.中考压轴题探索—对角互补专题探究（三）例1．已知：四边形ABCD中，AD∥BC，AB=AD=DC，∠BAD=∠ADC，点E在CD边上运动(点E 与C、D两点不重合)，△AEP为直角三角形，∠AEP=90°，∠P=30°，过点E作EM∥BC交AF 于点M．(1)若∠BAD=120°(如图1)，求证：BF+DE=EM；(2)若∠BAD=90°(如图2)，则线段BF、DE、EM的数量关系为_____________.(3)在(1)的条件下，若AD：BF=3：2，EM=7，求CE的长．变式训练：1.已知：矩形ABCD 中ADK AB，点E 、F 分别在CD 、CB 上运动，且EAFa （角α为锐角）,过E作EM ∥BC 交AF 于点M,探究BF 、DE 、ME 之间的数量关系为_______________________________.(1) 当K=3，=45°时，___________________________. (2) 当K=3，=60°时，___________________________. (3) 当K=3，=30°时，___________________________.2.如图：已知四过形ABCD 中ADK AB、∠DAB=∠BCD=90°，点E 、F 分别在CD 、CB 上运动，且EAF a（角α为锐角）,过E 作EM ∥BC 交AF 于点M ，探究BF 、DE 、ME 之间的数量关系为_______________.BE中考压轴题探索—对角互补专题探究（四）例2.已知:四边形ABCD ，AB=AD ，∠B=∠D=90°,∠EAF=30°,过F 作FM ∥BC 交AE 于M . （1）当∠BAD=60°时(如图1所示)，求证︰BE+FD=FM ；（2）当∠BAD=90°时(如图2所示)，则线段BE ，DF,FM 的数量关系为_______________； （3）在（1）的条件下(如图3所示)，连接DB 交AE 于点G ，交AF 于点K ，交MF 于点N ，若BG:DK=3:5，FM=14时，KN 的长.M F CA BD E 图1 M D A C F 图2图3 GN K MFC A B DE变式训练：1．已知四边形ABCD 中，AD ∥BC ，AB=DC ，∠BAD=∠ADC ，点F 在CD 边上运动(点E 与C 、D 两点不重合)（1）若∠BAD=90°(如图l)，AD=2AB ，∠EAF=450，求证：DF+2BE=FG（2）若∠BAD=150°(如图2)，AB=AD, ∠EAF=300,则DF 、BE 、FG 的数量关系为 . （3）在（1）的条件下（如图3）DF=4AB=6,直线AF 交直线BG 于点H ，求GH 的长.2.已知：四边形ABCD 中，A D ∥BC,AB=CD=kAD,∠BAD=∠ADC,点E 在CD 边上运动（点E 与C 、D 两点不重合），将AE 绕点A 顺时针旋转30°后与BC 边交于点F ，过点E 作EM ∥BC 交AF 于点M. （1）若k=1, ∠BAD=120°(如图1)，求证:DE+BF=12ME. （2）若k=12, ∠BAD=90°(如图2)，则线段DE 、BF 、ME 的数量关系为 . （3）在（1）的条件下，若CE=2，AE=27,求ME 的长.图3 H G C A DB E F GCD A BEF 图1G D A C B E F 图2 图2MFE图1MEF中考压轴题探索—对角互补专题探究（五）例3.如图1，正方形ABCD中，P为边BC延长线上的一点，E为DP的中点，DP的垂直平分线交边DC 于M，交边BC于Q，交边AB的延长线于N.（1）求证DP=MN;（2）若PC：PB=1:3，那么线段QE与QN的数量关系为______________________;（3）如图2，连接BD、MP，绕着点P旋转∠CPM，角的两边分别交边AB、AD于点H、K，交边CD 于点R，当四边形DBQM的面积为24，MR：RC=1：2时，求.变式训练：1.已知：在正方形ABCD 中，P 为直线AD 上一点，连接BP,以BP 为底边作等腰直角三角形△PBE, 连接AE.（1）如图1，当点P 在线段AD 上时，求证：AE;（2）如图2, 当点P 在线段DA 的延长线上时，线段AB 、AP 、AE 的数量关系是 （3）在（2）的条件下，过点A 作AF ∥PE,AF 交BC 的延长线于F,过点C 作∠DCF 的平分线，交AF 于点H,若AB=4,四边形PBEA 的面积为5，求线段CH 的长.2.已知等边三角形ABC ，点D 为BC 的中点，∠NDM=120°两边分别交直线AC 、AB 分别于点M 、N. （1）如图1，求证：MC=21AB+BN ； （2）如图2，线段MC 、AB 、BN 的数量关系是；（3）在（2）的条件下，将∠NDM 的两边DM 、DN 分别反向延长，交AB 、AC 的延长线分别于点E 、F ，连接EF 若BN=1，CM=2，求EF 的长；图1图2图3B B 图2。

专题 15角含半角模型破题策略1．等腰直角三角形角含半角如图，在△ ABC中， AB＝ AC，∠ BAC＝90°，点 D， E在 BC上且∠ DAE＝45°（1）△BAE∽△ADE∽△CDA22 2（2）BD＋CE＝DE．A45°CBD E证明（ 1）易得∠ADC＝∠B＋∠BAD＝∠EAB，因此△ BAE∽△ ADE∽△ CD A．（2）方法一（旋转法）：如图1，将△ABD绕点A逆时针旋转90°获得△ACF，连接EF．A45° FCBD E则∠ EAF＝∠ EAD＝45°， AF＝AD，因此△ ADE∽△ FAE （SAS ）．因此 DE＝EF．而 CF＝ BD，∠ FCE＝∠ FCA＋∠ ACE＝90°，因此 BD＋CE＝ CF＋ CE＝EF＝ DE．方法二（翻折法）：如图2，作点B对于AD 的对称点F，连接AF， DF，EF．A45°CBD EF由于∠ BAD＋∠ EAC＝∠ DAF＋∠ EAF，又由于∠ BAD＝∠ DAF，则∠ FAE＝∠ CAE， AF＝ AB＝ AC，因此△ FAE∽△ CAE（SAS）．因此 EF＝E C．而 DF ＝ BD ，∠ DFE ＝∠ AFD ＋∠ AFE ＝90°，22222因此 BD ＋ EC ＝ FD ＋ EF ＝ DE ．【拓展】 ①如图， 在△ ABC 中，AB ＝ AC ，∠ BAC ＝90°， 点 222延伸线上，且∠ DAE ＝45°，则 BD ＋ CE ＝ DE ．D 在 BC 上，点 E在 BC的 ABD CE能够经过旋转、翻折的方法来证明，如图：FAAFBDCEBDCE②将等腰直角三角形变为随意的等腰三角形：如图，在△ABC 中， AB ＝ AC ，点D ，E 在BC 上，且∠ DAE＝1∠ BAC ，则以BD ，DE ，EC 为三边长的三角形有一个内角度数为180°2－∠ BA C ．ABD EC能够经过旋转、翻折的方法将BD ， DE ， EC 转移到一个三角形中，如图：AAFBDECBDECF2．正方形角含半角如图 1，在正方形ABCD中，点E，F 分别在边BC， CD上，∠ EAF＝45°，连接 EF，则：B A B ABH A45°45°E EEGC FD C F D CFD图1 图 2 图 3（1）EF＝BE＋DF;（2）如图 2，过点A作AG⊥EF于点G，则AG＝AD;（3）如图 3，连接BD交AE于点H，连接FH．则FH⊥AE．（1）如图 4，将△ABE绕点A逆时针旋转 90°获得△ADI证明．B AEC FD I图 4则∠ IAF＝∠ EAF＝45°， AI ＝ AE，因此△ AEF∽△ AIF（ SAS），因此 EF＝ IF ＝ DI＋ DF＝ BE＋ DF．（2）由于△AEF∽△AIF，AG⊥EF，AD⊥IF，因此 AG＝ A D．（3）由∠HAF＝∠HDF＝45°可得A，D，F，H四点共圆，进而∠ AHF＝180°－∠ ADF＝90°，即 FH⊥ AE．【拓展】①如图，在正方形 ABCD中，点 E，F 分别在边 CB， DC 的延伸线上，∠ EAF＝45°，连接EF，则 EF＝ DF－ BE．EABF C D能够经过旋转的方法来证明. 如图:EABFC G D②如图，在一组邻边相等、对角互补的四边形ABCD 中， AB =AD ，∠ BAD +∠ C =180 °，点 E ，F 分别在 BC 、 CD 上，∠ EAF = 1∠ BAD ，连接 EF ，则 EF=BE+DF.2BAECFD能够经过旋转的方法来证明. 如图:BAECFDG例题解说例1 如图 1，点 E 、F 分别在正方形 ABCD 的边 BC 、 CD 上，∠ EAF ＝ 45° .（ 1） 试判断 、 FD 之间的数目关系 .BE 、EF（ 2） 如图 2，在四边形 ABCD 中，∠ BAD ≠ 90°， AB ＝ AD ．∠ B ＋∠ D ＝ 180°，点 E 、F 分别在、 上，则当∠EAF 与∠BAD 知足关系时，仍BC CD有 EF ＝ BE ＋ FD .（ 3）如图 3．在某公园的同一水平面上，四条通道围成四边形ABCD .已知 AB ＝ AD＝ 80m ，∠ B ＝ 60°，∠ ADC ＝ 120°，∠ BAD ＝ 150°，道路 BC ，CD 上分别有景点E ， F ，且 AE ⊥ AD ． DF ＝ 40（ 3 －1） m ．现要在 E 、F 之间修一条笔挺的道路，求这条道路 EF 的长．（ 结果取整数，参照数据： 2 ＝ 1.41 ， 3 ＝ 1.73 ）A DFADDAFFB EC B ECBEC图 1图 2图3解： （ 1）由“正方形内含半角 模型”可得 EF ＝ BE ＋ FD ． （2）∠ BAD ＝ 2∠ EAF ，原因以下：如图 4，延伸 CD 至点 G ，使得 DG ＝ BE ．连接 AG. 易证△ ABE ≌△ ADG （SAS ） . 因此 AE ＝ AG ，即 EF ＝ BE ＋ DF ＝ DG ＋ DF ＝GF .进而证得△ AEF ≌△ AGF （ SSS ）．因此∠ EAF ＝ ∠ GAF ＝ 1 ∠ EAG ＝ 1∠ BAD .22AGHGDFDFABEC图 4BCE图 5（ 3）如图 5，将△ ABE 绕点 A 逆时针旋转 1 50 °至△ ADG ．连接AF ．由题意可得∠ BAE ＝ 60°因此△ ABE 和△ ADG 均为等腰直角三角形 .过点 A 作 AH ⊥ DG 于点 H ．则DH ＝ 1AD ＝ 40m ， AH ＝3AD ＝ 403 m.2 2而 DF ＝ 40（ 3 － 1） m.因此∠ EAF ＝∠ GAF ＝45° . 可得△ EAF ≌△ GAF （SAS ）．因此 EF ＝ GF ＝80m+40（ 3 － l ） m ≈109. 2m.例 2 如图，正方形ABCD 的边长为 a ，BM 、 DN 分别均分正方形的两个外角，且知足∠ MAN＝ 45°．连接 MC 、 NC 、 MN ．（ 1）与△ ABM 相像的三角形是， BM DN ＝（用含有 a 的代数式表示） ；（ 2）求∠ MCN 的度数；（ 3）请你猜想线段BM、DN和 MN之间的等量关系，并证明你的结论. ADB NCM解：（ 1）△NDA，a2 .（ 2）由（ 1）可得BM AB，AD ND因此BM DC．BC DN易证∠ CBM＝∠ NDC＝45°，因此△ BCM∽△ DNC．则∠ BCM＝∠ DNC，因此∠MCN =360°一∠BCD一∠BCM一∠DCN＝270°－（∠DNC+∠DCN）＝270°－（ 180°－∠DNC）＝135°．（3）BM2DN 2MN 2，证明以下：如图，将△ ADN绕点 A顺时针旋转90°，获得△ABE，连接EM.易得 AE＝AN.∠ MAE＝∠ MAN＝45°，∠ EBM＝90°，因此△ A ME≌△ AMN.（SAS）.则 ME＝ MN．在 Rt △BME中，BM2 BE2 EM 2因此BM2 DN 2 EM 2 .ADBCNEM倒 3 如图，在四边形ABCD中， AD∥ BC，∠ BCD＝90°， AB＝BC＋ AD，∠ DAC＝45°， E 为上一点，且∠＝ 45°. 若＝4，求△的面积 .CD BAE CD ABEB CEA D图1解：如图1．过点A作CB的垂线，交CB的延伸线于点F.由∠ DAC=45°，∠ ADC＝90°，可得 AD＝ CD.因此四边形ADCF为正方形.进而 AF＝ FC＝4．令 BC＝ m，则 AB＝4＋ m， BF＝4－ m．2 2在 Rt △AFB中，有 16＋（ 4 －m）一（ 4＋m）如图 2．将△ADE绕点A逆时针旋转90°至△AFG.易证△ AGH≌△ AEB．令 DE＝ n，则 CE＝4－ n， BE＝ BG＝3＋n在 Rt △BCE中，有1+（ 4－n）2＝（ 3＋n）2，解得n＝4 .因此 BG＝25.7 7 1AF BG 50进而SABE SABG .2 7G F B CEA D图 2进阶训练1.如图，等边△ ABC的边长为1，D是△ ABC外一点且∠ BDC＝120°，BD＝ CD，∠ MDN＝60°，求△AMN的周长．ANM BCD△ AMN 的周长是 2【提示】如图，延伸AC 至点 ，使得CE ＝ ，连接DE. 先证△≌△ ，再证△MDNEBMBMDCED≌△ EDN 即可 .ANMBCDE2．如图， 在正方形 ABCD 中，连接 BD ，E 、F 是边 BC ，CD 上的点， △CEF 的周长是正方形 ABCD 周长的一半， AE 、 AF 分别与 BD 交于 M 、 N ，试判断线段 BM 、 DN 和 MN 之间的数目关系，并 证明．ADNFMBEC解： 2＋2＝2．BM DN MN【提示 】由△ CEF 周长是正方形 ABCD 周长的一半，想到“正方形角含半角”，进而旋转构造协助线解决问题（如图1），证△ AEF ≌△ AGF ，得∠ MAN ＝ 1∠ BAD ＝ 4，而后，再由“等腰2直角三角形含半角”（如图2）即可证得．GH GADADNNFFMMBE CBEC图1图23．如图，在△ ABC 中，∠ ACB ＝90°，点 D 在边 AB 上， DE ⊥ BC 于点 E ，且 DE ＝ BC ，点 F 在边 AC 上，连接 BF 交 DE 于点 G ，若∠ DBF ＝45°， DG ＝27，BE ＝ 3，求 CF 的长．5ADGBE解： CF ＝12．5【提示 】如图，将 DE 向左平移至 BH ，连接 HD 并延伸交 AC 于点 I ，则四边形 HBCI 为正方形． 将△ BHD 绕点 B 顺时针旋转 90°至△ BCJ ，则点 J 在 AC 的延伸线上． 连结 DF ，由“正方形角含半角模型”可得 DF ＝ DH ＋ CF ，∠ DFB ＝∠ JFB ＝∠ DGF ，所以 DF ＝ DG ，进而求得CF 的长．F CAHDIGFCBEJ。

对角互补模型破解策略1．全等型之“90°”如图，∠AOB ＝∠DCE ＝90°，OC 平分∠AOB ，则（1）CD ＝CE ； （2）OD ＋OEOC ； （3）212OCD OCE S S OC ∆∆+=． 证明 方法一：如图，过点C 分别作CM ⊥OA ，CN ⊥OB ，垂足分别为M ，N ． 由角平分线的性质可得CM ＝CN ，∠MCN ＝90°． 所以∠MCD ＝∠NCE ， 从而△MCD ≌△NCE （ASA ）， 故CD ＝CE ．易证四边形MONC 为正方形．所以OD ＋OE ＝OD ＋ON ＋NE ＝2ON．所以2212OCD OCE MONC S S S ON OC ∆∆+===正方形． 方法二：如图，过C 作CF ⊥OC ，交OB 于点F ． 易证∠DOC ＝∠EFC ＝45°，CO ＝CF ，∠DCO ＝∠ECF ．所以△DCO ≌△ECF （ASA ）所以CD ＝CE ，OD ＝FE ， 可得OD ＋OE ＝OF． 所以212OCD OCE OCF S S S OC ∆∆∆+==．A O BDCE【拓展】如图，当∠DCE 的一边与AO 的延长线交于点D 时，则：（1）CD ＝CE ； （2）OE －ODOC ； （3）212OCE OCD S S OC ∆∆-=． 如图，证明同上．2．全等型之“120”如图，∠AOB ＝2∠DCE ＝120°，OC 平分∠AOB ，则：（1）CD ＝CE ； （2）OD ＋OE ＝OC ； （3）2OCD OCE S S ∆∆+=． 证明 方法一：如图，过点C 分别作CM ⊥OA ，CN ⊥OB ，垂足分别为M ，N ．所以22OCD OCE ONC S S S ∆∆∆+==易证△MCD ≌△NCE （ASA ），B AECODOBECDA所以CD ＝CE ，OD ＋OE ＝2ON ＝OC ．方法二：如图，以CO 为一边作∠FCO ＝60°，交OB 于点F ，则△OCF 为等边三角形． 易证△DCO ≌△ECF （ASA ）． 所以CD ＝CE ，OD ＋OE ＝OF ＝OC ， ∴S △OCD ＋S △OCE ＝S △OCF ＝43OC 2【拓展】如图，当∠DCE 的一边与BO 的延长线交于点E 时，则： （1）CD ＝CE ；（2）OD －OE ＝OC ；（3）S △OCD －S △OCE ＝43OC 2如图，证明同上．3、全等型之“任意角”如图，∠AOB ＝2α，∠DCE ＝180°－2α，OC 平分∠AOB ，则：（1）CD ＝CE ；（2）OD ＋OE ＝2OC ·cos α；（3）S △ODC ＋S △OEC ＝OC 2·sin αcos α证明：方法一：如图，过点C 分别作CM ⊥OA ，CN ⊥OB ，垂足分别为M ，N易证△MCD ≌△NCE （ASA ）∴CD ＝CE ，OD ＋OE ＝2ON ＝2OC ·cos α ∴S △ODC ＋S △OEC ＝2S △ONC ＝OC 2·sin αcos α方法二：如图，以CO 为一边作∠FCO ＝180°－2α，交OB 于点F ．易证△DCO ≌△ECF （ASA ）∴CD ＝CE ，OD ＋OE ＝OF ＝2OC ·cos α ∴S △ODC ＋S △OEC ＝S △OCF ＝OC 2·sin αcos α【拓展】如图，当∠DCE 的一边与BO 的延长线交于点E 时，则：（1）CD ＝CE ；（2）OD －OE ＝2OC ·cos α；（3）S △ODC －S △OEC ＝OC 2·sin αcos α如图，证明同上4、相似性之“90°”如图，∠AOB ＝∠DCE ＝90°，∠COB ＝α，则CE ＝CD ·tan α方法一：如图，过点C 分别作CM ⊥OA ，CN ⊥OB ，垂足分别为M 、N易证△MCD ∽△NCE ，∴αtan ===CMCNCD CE MD NE ，即CE ＝CD ·tan α 方法二：如图，过点C 作CF ⊥OC ，交OB 于点F ．易证△DCO ∽△ECF ，∴αtan ===COCFCD CE OD FE ，即CE ＝CD ·tan α 方法三：如图，连接DE ．易证D 、O 、E 、C 四点共圆∴∠CDE ＝∠COE ＝α，故CE ＝CD ·tan α【拓展】如图，当∠DCE 的一边与AO 的延长线交于点D 时，则CE ＝CD ·tan α如图，证明同上．例题讲解例1、已知△ABC 是⊙O 的内接三角形，AB ＝AC ，在∠BAC 所对弧BC 上任取一点D ，连接AD ，BD ，CD ． （1）如图1，若∠BAC ＝120°，那么BD ＋CD 与AD 之间的数量关系是什么？ （2）如图2，若∠BAC ＝α，那么BD ＋CD 与AD 之间的数量关系是什么？解：（1）BD ＋CD ＝3AD如图3，过点A 分别向∠BDC 的两边作垂线，垂足分别为E 、F ． 由题意可得∠ADB ＝∠ADC ＝30° 易证△AEB ≌△AFC ∴BD ＋CD ＝2DE ＝3AD ⑵BD ＋CD ＝2ADsin2α． 如图4，作∠EAD ＝∠BAC ，交DB 的延长线于点E ．则△EBA ≌△DCA ，所以BE ＝CD ，AE ＝AD ． 作AF ⊥DE 于点F ，则∠FAD ＝2α．所以BD ＋CD ＝DE ＝2DF ＝2AD sin2α．图1AO BCD图2A OBCD图3F EAO BC D DFBEOA C图4例2如图1，将一个直角三角板的直角顶点P 放在正方形ABCD 的对角线BD 上滑动，并使其一条直角边始终经过点A ，另一条直角边与BC 相交于点F ． ⑴求证：PA ＝PE ；⑵如图2，将⑴中的正方形变为矩形，其余不变，且AD ＝10，CD ＝8，求AP ：PE 的值； ⑶如图3，在⑵的条件下，当P 滑动到BD 的延长线上时，AP ：PE 的值是否发生变化？解：⑴如图4，过点P 分别作PM ⊥AB ，PN ⊥BC ，垂足分别为M ，N ．则PM ＝PN ，∠MPN ＝90°，由已知条件可得∠APE ＝90°，所以∠APM ＝∠EPN ，所以△APM ≌△EPN ． 故AP ＝PE ．⑵如图5，过点P 分别作PM ⊥AB ，PN ⊥BC ，垂足分别为M ，N ．则PM ∥AD ，PN ∥CD ． 所以△BPM ∽△BDA ，△BNP ∽△BCD ．可得PM BP PN AD BD CD ==，所以54PM AD PN CD ==．易证△APM ∽△EPN ，所以54AP PM PE PN ==．⑶AP ：PF 的值不变．[如图，理由同⑵]图3ADBEP FC ADBPCE 图2ADPBE C 图1图4A DPBE CN M图5A DBPCE N M图6ADBEP FC M N进阶训练1．如图，四边形ABCD 被对角线BD 分为等腰Rt △ABD 和Rt △CBD ，其中∠BAD 和∠BCD 都是直角，另一条对角线AC 的长度为2，则四边形ABCD 的面积为_________．答案：四边形ABCD 的面积为2．【提示】易证A 、B 、C 、D 四点共圆，则∠BCA ＝∠BDA ＝∠ABD ＝∠ACD ，由“全等型之‘90°’”的结论可得S 四边形ABCD ＝12AC 2＝2．2．在△ABC 中，AB ＝AC ，∠A ＝60°，D 是BC 边的中点，∠EDF ＝120°，DE 与AB 边相交于点E ，DF 与AC 边（或AC 边的延长线）相交于点F ．⑴如图1，DF 与AC 边相交于点F ，求证：BE ＋CF ＝12AB ； ⑵如图2，将图1中的∠EDF 绕点D 顺时针旋转一定的角度，使DF 与AC 边的延长线交于点F ，作DN ⊥AC 于点N ，若DN ＝FN ，求证：BE ＋CF ＝3（BE －CF ）． 答案：略．【提示】⑴过点D 作DG ∥AC 交AB 于点G ，证△DEG ≌△DFC ，从而BE ＋CF ＝BE ＋EG ＝BG ＝12AB ． AB CD第1题图第1题图1AEFCD BAEFC D BN 第1题图2⑵过点D 作DG ∥AC 交AB 于点G ，同⑴可得BE －CF ＝12AB ＝DC ＝23DN ，延长AB 至点H ，使得BH ＝CF ，则DH ＝DF ＝DE ，从而BE ＋CF ＝HE ＝2DE ＝2×2DN ＝2DN ，所以BE ＋CF ＝3（BE －CF ）．3．在菱形ABCD 中，两条对角线AC ，BD 相交于点O ，∠MON ＋∠BCD ＝180°，∠MON 绕点O 旋转，射线OM 交BC 于点E ，射线ON 交CD 于点F ，连结EF ． ⑴如图1，当∠ABC ＝90°时，△OEF 的形状是____；⑵如图2，当∠ABC ＝60°时，请判断△OEF 的形状，并说明理由；⑶如图3，在⑴的条件下，将∠MON 的顶点移动到AO 的中点O'处，∠MO'N 绕点O'旋转，仍满足∠MO'N ＋∠BCD ＝180°，射线O'M 交直线BC 于点E ，射线O'N 交直线CD 于点F ，当BC ＝4，且'98O EF ABCDS SV 四边形时，求CE 的长．答案：⑴等腰直角三角形；⑵△OEF 是等边三角形；⑶线段CE 的长为33＋3或33－3． 【提示】⑵由“全等型之‘120°’”的结论可得OE ＝OF ．⑶两种情况，如图：第1题答图1 AEFC D BG 第1题答图2A EFC DB NHG第3题图1 ADBCOME F N ABC DOF E MN第3题图2ADBCOO ' 第3题图3第3题答图 AD BC OO 'F NE ME ' M 'F ' N '。

中考数学考前专题复习对角互补模型学校:___________姓名：___________班级：___________考生__________评卷人得分一、解答题1．如图，在Rt ABC中，AC＝BC，∠ACB＝90°，点O在线段AB上（点O不与点A，B重合），且OB＝kOA，点M是AC延长线上的一点，作射线OM，将射线OM绕点O逆时针旋转90°，交射线CB于点N．（1）如图1，当k＝1时，判断线段OM与ON的数量关系，并说明理由；（2）如图2，当k＞1时，判断线段OM与ON的数量关系（用含k的式子表示），并证明；（3）点P在射线BC上，若∠BON＝15°，PN＝kAM（k≠1），且CMAC＜312，请直接写出NCPC的值（用含k的式子表示）．2．（1）特例感知：如图1，已知在Rt ABC中，∠BAC＝90°，AB＝AC，取BC边上中点D，连接AD，点E为AB边上一点，连接DE，作DF∠DE交AC于点F，求证：BE ＝AF；（2）探索发现：如图2，已知在Rt ABC中，∠BAC＝90°，AB＝AC＝3，取BC边上中点D，连接AD，点E为BA延长线上一点，AE＝1，连接DE，作DF∠DE交AC延长线于点F，求AF的长；（3）类比迁移：如图3，已知在ABC中，∠BAC＝120°，AB＝AC＝4，取BC边上中点D，连接AD，点E为射线BA上一点（不与点A、点B重合），连接DE，将射线DE绕点D顺时针旋转30°交射线CA于点F，当AE＝4AF时，求AF的长．3．（1）如图，Rt ABC中，∠A＝90°，AB＝AC，D为BC中点，E、F分别为AB、AC 上的动点，且∠EDF＝90°．求证：DE＝DF；（2）如图2，Rt ABC中，∠BAC＝90°，AC＝4，AB＝3，AD∠BC，∠EDF＝90°．∠求证：DF•DA＝DB•DE；∠求EF的最小值．4．如图，矩形ABCD中，AB＝4，BC＝6，E为线段AD上一动点，连接CE，过点B 作BF∠CE，交射线CD于点F，垂足为P．(1)求证：CED∠BCF；(2)当F为CD的中点时，求tan∠BAP的值；(3)若ABP为等腰三角形时，直接写出DE的长．5．我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”（1）概念理解：请你根据上述定义举一个等邻角四边形的例子；（2）问题探究；如图1，在等邻角四边形ABCD中，∠DAB=∠ABC，AD，BC的中垂线恰好交于AB 边上一点P，连结AC，BD，试探究AC与BD的数量关系，并说明理由；（3）应用拓展；如图2，在Rt∠ABC与Rt∠ABD中，∠C=∠D=90°，BC=BD=3，AB=5，将Rt∠ABD 绕着点A顺时针旋转角α（0°＜∠α＜∠BAC）得到Rt∠AB′D′（如图3），当凸四边形AD′BC为等邻角四边形时，求出它的面积．参考答案：1．（1）OM＝ON，见解析；（2）ON＝k•OM，见解析；（3）131NC kPC k+=-【解析】【分析】（1）作OD∠AM，OE∠BC，证明∠DOM∠∠EON；（2）作OD∠AM，OE∠BC，证明∠DOM∠∠EON；（3）设AC＝BC＝a，解Rt∠EON和斜∠AOM，用含,a k的代数式分别表示,,NC PN再利用比例的性质可得答案．【详解】解：（1）OM＝ON，如图1，作OD∠AM于D，OE∠CB于E，∠∠ADO＝∠MDO＝∠CEO＝∠OEN＝90°，∠∠DOE＝90°，∠AC＝BC，∠ACB＝90°，∠∠A＝∠ABC＝45°，在Rt∠AOD中，2sin2OD OA A OA=∠=，同理：OE＝22OB，∠OA＝OB，∠OD＝OE，∠∠DOE＝90°，∠∠DOM＋∠MOE＝90°，∠∠MON＝90°，∠∠EON＋∠MOE＝90°，∠∠DOM＝∠EON，在Rt∠DOM和Rt∠EON中，MDO NEOOD OEDOM EON∠=∠⎧⎪=⎨⎪∠=∠⎩，∠∠DOM∠∠EON（ASA），∠OM＝ON．（2）如图2，作OD∠AM于D，OE∠BC于E，由（1）知：OD＝22OA，OE＝22OB，∠1OD OAOE OB k==，由（1）知：∠DOM＝∠EON，∠MDO＝∠NEO＝90°，∠∠DOM∠∠EON，∠1OM ODON OE k==，∠ON＝k•OM．（3）如图3，设AC＝BC＝a，∠AB＝2a，∠OB ＝k •OA ，∠OB ＝2•1k k +a ，OA ＝2•11k +a ， ∠OE ＝22OB ＝1k k +a ， ∠∠N ＝∠ABC ﹣∠BON ＝45°﹣15°＝30°，∠EN ＝tan OE N ∠＝3OE ＝3•1k k +a ， ∠CE ＝OD ＝22OA ＝11k +a ， ∠NC ＝CE ＋EN ＝11k +a ＋3•1k k +a ， 由（2）知：1OM OA ON OB k==，∠DOM ∠∠EON ， ∠∠AMO ＝∠N ＝30°∠1AM PN k =， ∠OM AM ON PN=， ∠∠PON ∠∠AOM ，∠∠P ＝∠A ＝45°，∠PE ＝OE ＝1k k +a ， ∠PN ＝PE ＋EN ＝1k k +a ＋3•1k k +a ， 设AD ＝OD ＝x ，∠DM ＝3x ，由AD ＋DM ＝AC ＋CM 得，（3＋1）x ＝AC ＋CM ，∠x ＝312-（AC ＋CM ）＜312-（AC ＋312-AC ）＝12AC ， ∠k ＞1 ∠1313113311k a a NC k k k k k PN k k a a k k ++++==++++， 31,13PN PC NC PC k k NC NC NC k++∴==+=+1,13PC kNC k-∴=+∠131NC kPC k+=-．【点睛】本题考查了三角形全等和相似，以及解直角三角形，解决问题的关键是作OD∠AC，OE∠BC；本题的难点是条件312CMAC-＜得出k＞1．2．（1）见解析；（2）4；（3）5212-或3132-+或3132+【解析】【分析】（1）证明∠BDE∠∠ADF（ASA），根据全等三角形的性质即可得到BE＝AF；（2）方法同（1），利用全等三角形的性质解决问题；（3）证明∠EBD∠∠DCF，推出BE BDCD CF=，设AF＝m，则AE＝4m，分三种情形，分别构建方程求解即可．【详解】（1）证明：如图1中，∠∠ABC中，∠BAC＝90°，AB＝AC，AD是高，∠BD＝CD＝AD12=BC，∠B＝∠C＝45°，∠BAD＝∠CAD12=∠BAC＝45°，∠DF∠DE，∠∠EDF＝∠ADB＝90°，∠∠BDE＝∠ADF＝90°﹣∠ADE，在△BDE和△ADF中，45BDE ADFBD ADB CAD∠=∠⎧⎪=⎨⎪∠=∠=︒⎩，∠∠BDE ∠∠ADF （ASA ），∠BE ＝AF ；（2）解：如图2中，由（1）知，BD ＝CD ＝AD ，∠B ＝∠C ＝∠BAD ＝∠CAD ＝45°，∠∠EDF ＝∠ADB ＝90°，∠∠BDE ＝∠ADF ＝90°+∠ADE ，在△BDE 和△ADF 中，45BDE ADF BD AD B CAD ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ∠∠BDE ∠∠ADF （ASA ），∠BE ＝AF ，∠AB ＝3，AE ＝1，∠BE ＝AB +AE ＝4，∠AF ＝4；（3）解：如图3中，∠AB ＝AC ，BD ＝CD ，∠AD ∠BC ，∠BAD ＝∠CAD 12=∠BAC ＝60°， ∠BD ＝CD ＝AB •sin 60°＝23，∠AE ＝4AF ，∠可以假设AF＝m，则AE＝4m，BE＝4﹣4m，CF＝4﹣m，∠∠EDC＝∠EDF+∠FDC＝∠B+∠BED，∠EDF＝∠B＝30°，∠∠FDC＝∠BED，∠∠B＝∠C，∠∠EBD∠∠DCF，∠BE BD CD CF=，∠4423423mm-=-，整理得，m2﹣5m+1＝0，解得m5212-=或5212+（舍弃），经检验，m5212-=是分式方程的解．当点F在CA的延长线上时，CF＝4+m，由△EBD∠∠DCF，可得BE BD CD CF=，∠4423423mm-=+，解得，m3132-+=或3132--（舍弃），经检验，m3132-+=是分式方程的解．当点E在射线BA上时，BE＝4+4m，∠∠EBD∠∠DCF，∠BE BD CD CF=，∠4423423mm +=-解得，m3132+=或3132-（舍弃），经检验，m3132+=是分式方程的解．综上所述，满足条件的AF的值为5212-或3132-+或3132+．【点睛】本题属于几何变换综合题，考查了全等三角形的判定与性质、相似三角形的判定与性质，等腰直角三角形的判定与性质等知识；熟练掌握等腰直角三角形的判定与性质，证明三角形全等是解题的关键，学会用分类讨论的思想思考问题，属于中考常考题型．3．（1）见解析；（2）∠见解析；∠125【解析】【分析】（1）连接AD，根据等腰三角形的性质可得∠ADE＝∠BDF，从而得到∠BDF∠∠ADE，即可求证；（2）∠先证得∠BDF＝∠ADE，∠B＝∠DAE，可证得∠BDF∠∠ADE，即可求证；∠连接EF，根据勾股定理可得BC=5，根据三角形的面积可得AD125AB ACBC⋅==，从而得到DC165=，再由∠ADB∠∠CAB，可得BD ABAD AC=，再根据BD DFAD DE=，可得到DF ABDE AC=，从而得到∠EDF∠∠CAB，进而得到EF54DE=，可得到当DE最小时，EF取最小值，即可求解．【详解】证明：（1）如图1，连接AD，∠AB＝AC，∠BAC＝90°，BD＝CD，∠AD∠BC，AD＝BD＝DC，∠B＝∠DAE＝45°，∠∠ADB＝∠EDF＝90°，∠∠ADB﹣∠ADF＝∠EDF﹣∠ADF，即∠ADE＝∠BDF，在∠BDF和∠ADE中，B DAEBD ADBDF ADE∠=∠⎧⎪=⎨⎪∠=∠⎩，∠∠BDF∠∠ADE（ASA），∠DE＝DF；（2）∠证明：∠AD∠BC，∠∠ADB＝90°，∠∠ADB＝∠EDF，∠∠ADB﹣∠ADF＝∠EDF﹣∠ADF，即∠BDF＝∠ADE，∠∠BAD+∠DAE＝90°，∠BAD+∠B＝90°，∠∠B＝∠DAE，∠∠BDF∠∠ADE，∠BD DFAD DE=，∠DF•DA＝DB•DE；∠解：如图2，连接EF，在Rt△ABC中，∠BAC＝90°，AC＝4，AB＝3，则BC22AB AC=+=5，∠AD125AB ACBC⋅==，由勾股定理得：DC22165AC AD=-=，∠∠B＝∠B，∠ADB＝∠CAB=90°，∠∠ADB∠∠CAB，∠DB ADAB AC=，∠BD ABAD AC=，由∠可知，BD DFAD DE=，∠DF AB DE AC=， ∠∠EDF ＝∠CAB ＝90°，∠∠EDF ∠∠CAB ，∠EF DE BC AC =，即54EF DE =， ∠EF 54DE =， 当DE 最小时，EF 取最小值，当DE ∠AC 时，DE 最小，此时，DE 12164855425AD DC AC ⨯⋅===， ∠EF 的最小值为：485122545⨯=． 【点睛】本题主要考查了等腰三角形的性质，全等三角形和相似三角形的判定和性质，勾股定理等知识，熟练掌握等腰三角形的性质，全等三角形和相似三角形的判定和性质是解题的关键．4．(1)见解析(2)2711 (3)625-或3或25【解析】【分析】（1）由矩形的四个角都是直角和BF CE ⊥可推出CED ∆和BCF ∆有两组对应角相等，从而证明CED BCF ∆∆∽ ；（2）过点P 作GH CD ⊥于点G ，交AB 于点H ，由四边形BCGH 是矩形，由勾股定理求出BF 的长，再由相似三角形对应边成比例求出PH 、BH 的长，从而求出AH 的长，即可求得tan BAP ∠的值；（3）ABP ∆ 为等腰三角形分为三种情况，按不同情况分类讨论，添加辅助线构造相似三角形，求出DE 的长．(1)∠四边形ABCD 是矩形，BF CE⊥，90BPC︒∴∠=，90.DCE BCP CBF︒∴∠=-∠=∠，CED BCF∴∆∆∽．(2)如图1，过点P作GH CD⊥于点,G，交AB于点H，4CD AB==，122DCF C=∴=，6BC=，2222640BF=+=，40210BF∴==；cosBP BCCBFBC BF==∠，2BP BF CB⋅∴=，22106BP∴=，解得9105=BP，90HBC BCG CGH︒∠=∠=∠=，∠四边形BCGH是矩形，90,//PHA PHB GH BC︒∴∠=∠=，BPH FBC∴∠=∠，cosPH BCFBCBP BF∴==∠，91021065PH∴=⨯，解得275PH=，sinBH CFFBCBP BF==∠，BBF H BP CF⋅=⋅∴，91021025BH∴=⨯，解得95BH=，911455AH∴=-=，272751tan.11115PHBAPAH∴∠===(3)当PA PB=时，如图2，作PH AB⊥于点H，则AH＝BH，90,//BHP BAC AD BC︒∠=∠=，APH D BC∴∥∥，1EP AHCP BH∴==，EP CP∴=，BF CE⊥，6BE BC∴==，∠AE226425=-=，∠DE＝625-；当P A ＝AB 时，如图3，作AM ∠BP 于点M ，则12BM PM BP ==， cos BP BC CBF BC BF==∠， 22636BC BF F BP BF B ===∴， 1182B B P BFM =∴= //AB CD ，ABM F ∴∠=∠，cos BM CF F AB BF∴==∠， 184CF BF EF∴=， ∠整理得CF 92=， 90DCE BCP CBF ︒∠=-∠=∠，tan DE CF CBF CD BC∴==∠， 94236CD CF BC DE ⨯⋅=∴==；当BP ＝AB ＝4时，如图4，则226425PC =-=，,90,DEC PCB EDC CPB CD AB BP ︒∠=∠∠=∠===，()CDE BPC AAS ∴∆∆≌，25DE PC ∴==．综上所述，DE 的长为625-或3或25．【点睛】此题重点考查矩形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识与方法，解题的关键是正确地作出所需要的辅助线，解第（3）题时要分类讨论，求出所有符合条件的结果，此题难度较大，属于考试压轴题．5．（1）矩形或正方形；（2）AC=BD ，理由见解析；（3）10417 或12﹣372． 【解析】【分析】（1）矩形或正方形邻角相等，满足“等邻角四边形”条件；（2）AC=BD ，理由为：连接PD ，PC ，如图1所示，根据PE 、PF 分别为AD 、BC 的垂直平分线，得到两对角相等，利用等角对等角得到两对角相等，进而确定出∠APC=∠DPB ，利用SAS 得到三角形ACB 与三角形DPB 全等，利用全等三角形对应边相等即可得证；（3）分两种情况考虑：（i ）当∠AD′B=∠D′BC 时，延长AD′，CB 交于点E ，如图3（i ）所示，由S 四边形ACBD′=S △ACE ﹣S △BED′，求出四边形ACBD′面积；（ii ）当∠D′BC=∠ACB=90°时，过点D′作D′E∠AC 于点E ，如图3（ii ）所示，由S 四边形ACBD′=S △AED′+S 矩形ECBD′，求出四边形ACBD′面积即可．【详解】（1）矩形或正方形；（2）AC=BD，理由为：连接PD，PC，如图1所示：∠PE是AD的垂直平分线，PF是BC的垂直平分线，∠PA=PD，PC=PB，∠∠PAD=∠PDA，∠PBC=∠PCB，∠∠DPB=2∠PAD，∠APC=2∠PBC，即∠PAD=∠PBC，∠∠APC=∠DPB，∠∠APC∠∠DPB（SAS），∠AC=BD；（3）分两种情况考虑：（i）当∠AD′B=∠D′BC时，延长AD′，CB交于点E，如图3（i）所示，∠∠ED′B=∠EBD′，∠EB=ED′，设EB=ED′=x，由勾股定理得：42+（3+x）2=（4+x）2，解得：x=4.5，过点D′作D′F∠CE于F，∠D′F∠AC，∠∠ED′F∠∠EAC，∠D F ED AC AE''=，即4.544 4.5D F'=+，解得：D′F=36 17，∠S△ACE=12AC×EC=12×4×（3+4.5）=15；S△BED′=12BE×D′F=12×4.5×3617=8117，则S四边形ACBD′=S△ACE﹣S△BED′=15﹣8117=10417；（ii）当∠D′BC=∠ACB=90°时，过点D′作D′E∠AC于点E，如图3（ii）所示，∠四边形ECBD′是矩形，∠ED′=BC=3，在Rt∠AED′中，根据勾股定理得：AE=7，∠S△AED′=12AE×ED′=12×7×3=372，S矩形ECBD′=CE×CB=（4﹣7）×3=12﹣37，则S四边形ACBD′=S△AED′+S矩形ECBD′=372+12﹣37=12﹣372．【点睛】此题是四边形综合题，主要考查了“等邻角四边形”的理解，三角形，四边形的内角和定理，角平分线的意义，勾股定理，旋转的性质，相似三角形的性质和判定，理解“等邻角四边形”的定义是解本题的关键，分类讨论是解本题的难点，是一道中考常考题．。

专题17 一线三等角模型破解策略在直线AB 上有一点P ，以A ，B ，P 为顶点的∠1，∠2，∠3相等，∠1，∠2的一条边在直线AB 上，另一条边在AB 同侧,∠3两边所在的直线分别交∠1，∠2非公共边所在的直线于点C ，D ．1．当点P 在线段AB 上，且∠3两边在AB 同侧时． （1）如图，若∠1为直角，则有△ACP ∽△BP D ．321DBPAC（2）如图,若∠1为锐角，则有△ACP ∽△BP D ．3CDBPA证明：∵∠DPB ＝180°－∠3－∠CPA ，∠C ＝180°－∠1－∠CPA ,而∠1＝∠3 ∴∠C ＝∠DPB ,∵∠1＝∠2，∴△ACP ∽△BPD(3）如图，若∠1为钝角,则有△ACP ∽△BP D ．231DBPAC2．当点P 在AB 或BA 的延长线上,且∠3两边在AB 同侧时． 如图,则有△ACP ∽△BP D ．321CPDBA证明：∵∠DPB ＝180°－∠3－∠CPA ,∠C ＝180°－∠1－∠CPA ，而∠1＝∠3 ∴∠C ＝∠DPB ，∵∠1＝∠2＝∠PBD ，∴△ACP ∽△BPD3．当点P 在AB 或BA 的延长线上,且∠3两边在AB 异侧时． 如图，则有△ACP ∽△BP D ．321CDBAP证明：∵∠C ＝∠1－∠CPB ,∠BPD ＝∠3－∠CPB ，而∠1＝∠3 ∴∠C ＝∠BP D ．∵∠1＝∠2,∴∠PAC ＝∠DBP ．∴△ACP ∽△BP D ． 例题讲解例1：已知：∠EDF 的顶点D 在△ABC 的边AB 所在直线上（不与点A ,B 重合）．DE 交AC 所在直线于点M ，DF 交BC 所在直线于点N ．记△ADM 的面积为S 1,△BND 的面积为S 2． (1)如图1，当△ABC 是等边三角形，∠EDF ＝∠A 时，若AB ＝6，AD ＝4，求S 1S 2的值； （2）当△ABC 是等腰三角形时,设∠B ＝∠A ＝∠EDF ＝α． ①如图2，当点D 在线段AB 上运动时，设AD ＝a ,BD ＝b ,求S 1S 2的表达式(结果用a ，b 和a的三角函数表示）．②如图3，当点D 在BA 的延长线上运动时，设AD ＝a ,BD ＝b ，直接写出S 1S 2的表达式．NFC ME BDAF NM E BDACFN DABEM C图1 图2 图3解:（1）如图4，分别过点M ,N 作AB 的垂线，垂足分别为G ,H ．H G ADBE MC FN则S 1S 2＝12MG AD12NH BD ＝14AD AM sin A BD BN sinB ．由题意可知∠A ＝∠B ＝60º，所以sin A ＝sin B ＝32． 由“一线三等角模型”可知△AMD ∽△BDN ． ∴AM ADBD BN=，从而AM BN ＝AD BD ＝8，∴S 1S 2＝12．（2）①如图5，分别过点M ，N 作AB 的垂线,垂足分别为G ,H ．HG CADBE M N F则S 1S 2＝12MGAD12NH BD ＝14AD AM sin A BD BN sinB ．由“一线三等角模型"可得△AMD ∽△BDN ， 所以AM ADBD BN=，从而AM BN ＝AD BD ＝ab ，所以S 1S 2＝14a ²b ²sin ²a ;②如图6,分别过点M ，N 作AB 的垂线，垂足分别为G ,H ．HGCM EBA DN F则S 1S 2＝12MGAD12NH BD ＝14AD AM sin A BD BN sinB ．由“一线三等角模型”可得△AMD ∽△BDN ， 所以AM ADBD BN，从而AM BN ＝AD BD ＝ab ，所以S 1S 2＝14a ²b ²sin ²a ；例2:如图,在等腰三角形ABC 中,∠BAC ＝120°，AB ＝AC ＝2，点D 是BC 边上的一个动点(不与B 、C 重合)，在AC 上取一点E ,使∠ADE ＝30°．（1）设BD ＝x ，AE ＝y ,求y 关于x 的函数关系式并写出自变量x 的取值范围； （2）当△ADE 是等腰三角形时，求AE 的长．ECD B A解（1）∵△ABC 是等腰三角形，且∠BAC ＝120°, ∴∠ABD ＝∠ACB ＝30°， ∴∠ABD ＝∠ADE ＝30°,∵∠ADC ＝∠ADE ＋∠EDC ＝∠ABD ＋∠DAB ， ∴∠EDC ＝∠DAB ， ∴△ABD ∽△DCE ；∵AB ＝AC ＝2，∠BAC ＝120°， 过A 作AF ⊥BC 于F ， ∴∠AFB ＝90°，∵AB ＝2，∠ABF ＝30°， ∴AF ＝12AB ＝1， ∴BF＝ ∴BC ＝2BF＝则DC＝x ，EC ＝2－y ∵△ABD ∽△DCE ， ∴AB DCBD CE =，∴2x化简得:2122y x =+(0x <<．ECDBA（2）①当AD ＝DE 时，如图2， △ABD ≌△DCE ，则AB ＝CD ，即2＝x ，x＝2,代入2122y x =+ 解得：y＝4-即AE＝4- ②当AE ＝ED 时，如图，∠EAD ＝∠EDA ＝30°,∠AED ＝120°，所以∠DEC＝60°，∠EDC＝90°则ED＝12EC,即y＝12(2－y）解得y＝23，即AE＝23；③当AD＝AE时,有∠AED－∠EDA＝30°,∠EAD＝120°此时点D和点B重合,与题目不符，此情况不存在．所以当△是ADE等腰三角形时，AE＝4－23或AE＝23AB CE进阶训练1．如图,在△ABC中，AB＝AC，点E在BC边上移动（不与点B，C重台）．满足∠DEF＝∠B，且点D，F．分别在边AB，AC上．当点E移动到BC的中点时，求证：FE平分∠DF C．DFA1．略【提示】由题意可得∠B＝∠DEF＝∠C．由“一线三等角模型”可得△BDE∽△CEF，可得BECF＝DEEF．而BE＝CE·所以CECF＝DEEF，从而△DEF∽ECF．所以∠DEF＝∠EFC，即FE平分∠DF C．2． 如图，在等边△ABC 中，点D ，E 分别在AB ，BC 边上，AD ＝2BE ＝6．将DE 绕点E 顺时针旋转60°，得到EF ．取EF 的中点G ，连结AG ．延长CF 交AG 于点H ．若2AH＝5HG ，求BD 的长．GH FDCBA2．BD ＝9．【提示】如图,过点F 作FI ∥AC 交BC 于点I ．则∠FIE ＝∠ACB ＝∠AB C ．易证△DBE ≌△E IF ,则IF ＝BE ，IE ＝BD ，所以BC ＋BE ＝AD ，即IC ＝BE ＝IF ，则∠ACH ＝ ∠BCH ＝30°．延长CH 变AB 于点J ,则CJ ⊥AB ，．A ＝ BJ 分别过点G ,E 作AB 的垂线段，垂足为K ，L ，·则KL ＝KJ ·AJ JK＝AH HG ＝52，所以AJ ：JK ：KL ：BL ＝5：2：2：l ．因为BE ＝3，∠LEB ＝ 30°,所以BL ＝1．5．AB ＝15．所以BD ＝9．L K J IBCDF H G尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

专题4 图形的分割与拼接破解策略把一个几何图形按某种要求分成几个图形，就叫做图形的分割；反过来，按一定的要求也可以把几个图形拼接成一个完美的图形，就叫做图形的拼接．通常，我们会将一个或多个图形先分割，再拼接成一种指定的图形． 常见的图形的分割与拼接有： 1．三角形分割成两个等腰三角形 （1）已知：Rt△ABC ，∠BAC ＝90°． 作法：取斜边BC 的中点D ，连结A D ． 结论：△DAB 和△DAC 是等腰三角形．D AB C（2）已知：△ABC ，∠BAC ≥∠B ，∠C ＝2∠B ．作法：在边BC 上作一点D ，使得点D 在AB 的垂直平分线上，连结A D ． 结论：△DAB 和△DAC 是等腰三角形．DCB A（3）已知：△ABC ，∠ACB ＝3∠B．作法：在边AB 上作一点D ，使得点D 在BC 的垂直平分线上，连结C D ． 结论：△DBC 和△CAD 是等腰三角形．ABDC2．三角形分割成多个等腰三角形（1）已知：任意等腰△ABC ，AB ＝A C ． ①作法：一条垂线＋两条斜边中线．结论：△EAD ，△FAD ，△EBD ，△FCD 均为等腰三角形．ABFCED②作法：一条角平分线＋两条平行线．结论：△AFD ，△FBD ，△EBD ，△DEC 均为等腰三角形．DECF BA③作法：两条角平分线＋一条平行线．结论：△AEF ，△EBD ，△FCD ，△DBC 均为等腰三角形．ABF CE D（2）已知：等腰△ABC ，∠B ＝∠C ＝36°．作法：在BC 上取两点D ，E ，使得其分别在AB ，AC 的垂直平分线上，连结AD ，AE ．结论：△DAB ，△ADE ，△EAC 均为含36°内角的等腰三角形，所以可以无限分等腰三角形．36°36°ABCDE（3）已知：等腰△ABC ，AB ＝AC ，∠A ＝36°． 作法：作∠ABC 的平分线BD ，交AC 于点D ．结论：△DAB ，△BCD 均为含36°内角的等腰三角形，所以可以无限分等腰三角形．AB 36°DC（4）已知：任意△AB C ．作法：一条垂线＋两条斜边中线．结论：△EAD ，△FAD ，△EBD ，△FCD 均为等腰三角形．AB CDEF3．三角形的剪拼（1）剪拼成直角三角形．作法：取AB ，AC 的中点D ，E ；过D 作BC 的垂线，垂足为点F ；过点A 作BC 的平行线，分别交直线DF ，EF 于点G ，H ． 结论：△FGH 为直角三角形．D HG EFCB A（2）剪拼成等腰三角形． 作法：取AB 、AC 的中点D 、E ，连结DE 的垂直平分线FG 交BC 于点G ;过点A 作BC 的平分线，分别交直线GD 、GE 于点H 、I 结论：△GHI 为等腰三角形F GIHD EC BA（3）剪拼成平行四边形．作法：取BC 、AC 的中点D 、E ，分别过点A 作BC 的平行线，交直线DE 于点F ． 结论：四边形ABDF 为平行四边形．EFDCBA（4） 剪拼成矩形．①作法：取AB 、AC 的中点D 、E ，分别过点D 、E 作BC 的垂线，垂足为F 、G ．过点A 作BC 的平行线，分别交直线FD 、GE 于点H 、I ． 结论：四边形HFGI 为矩形．I H ED GAB C②作法：取AB 、AC 的中点D 、E ，分别过点B 、C 作直线DE 的垂线，垂足为F 、G ． 结论：四边形FBCG 为矩形．F G ED CBA③作法：取BC 、AC 的中点D 、E ，过点A 作BC 的平行线，交直线DE 于点F ;分别过点A 、F 作BC 的垂线，垂足为G 、H结论：四边形AGHF 为矩形（先将△ABC 剪拼成平行四边形ABDF ，再将平行四边形剪拼成矩形AGHF ）EFH D G CB A（5）剪拼成正方形（三角形一边上的高是该边长的一半）．①作法：取BC 、AC 的中点D 、E ，过点A 作BC 的平行线，交直线DE 于点F ，分别过A 、F 作BC 的垂线，垂足为G 、H ． 结论：四边形AGHF 为正方形．ABC GDHFE②作法：取AB 、AC 的中点D 、E ，分别过点D 、E 作BC 的垂线，垂足为F 、G ;过点A 作BC 的平行线，分别交直线FD 、GE 于点H 、I 结论：四边形HFGI 为正方形CB AFGD EH I（6）剪拼成等腰梯形．作法：作AD ＝AB 交BC 于点D ，取AC 的中点E ，过点E 作AD 的平行线，交BC 于点F ，过点A 作BC 的平行线，交直线FE 于点G ． 结论：四边形AGFB 为等腰梯形．GFDECBA4．矩形的剪拼（1）剪拼成直角三角形作法：取AD 中点E ，连结CE 并延长，交直线AB 于点F ． 结论：△FBC 是直角三角形．FEDCB A（2）剪拼成等腰三角形①作法：延长CD 至点E ，使得DE ＝CD ，连结AC 、AE ． 结论：△ACE 为等腰三角形，其中AC ＝AEA CDE②作法：取AB 、CD 、AD 的中点E 、F 、G ，连结GE 、GF 并延长，分别交直线BC 于点H 、I 结论：△GHI 为等腰三角形，其中GH ＝GIIHGA BCD E F③作法：取AD 的中点E ，向矩形外作AD 的垂线EF ，使得EF ＝AB ，连结FB 、FC 结论：△FBC 为等腰三角形，其中FB ＝FCAB CDEF④作法：取BC 、CD 、AD 的中点E 、F 、G ，连结FE 、FG 并延长，分别交直线AB 于H 、L 结论：△FHI 为等腰三角形，其中FH ＝FI（3）剪拼成菱形．作法：取BC 的中点E ，向矩形外作BC 的垂线EG ，使得EG ＝AB ，取AD 的中点F ，连结BG 、GC 、CF 、F B ．结论：四边形BGCF 为菱形GABCDEF（4）剪拼成正方形作法：延长CB 至点E ，使得BE ＝AB ，以EC 为直径作圆，交BA 的延长线于点F;在BC 上取一点G ，使得BG ＝BF ，过点F 作BF 的垂线，过点G 作BG 的垂线，两线交于点H 结论：四边形BGHF 为正方形5．正方形的剪拼（1）两个正方形剪拼成一个正方形作法：连结AE ，过点A 作AI 丄AE 交CB 的延长线于点I ;分别以E ，I;为圆心AE 长为半径画弧，交于点H ，连结HI 、HE ． 结论：四边形AEHI 为正方形NHLGFEDC BA（2）一个正方形剪拼成两个正方形作法：以B 为端点在正方形ABCD 内部作射线，分别过A 、C 、D 作射线的垂线，垂足分别为E 、F 、G ，再分别过点A 、C 作DG 的垂线，垂足分别为H 、I 结论：四边形AEGH 和四边形CFGI 为正方形．进阶训练1. 在△ABC 中，∠ABC ＝∠ACB ＝63°，如图1，取三边中点，可以把△ABC 分割成四个等腰三角形，请你在图2中，用另外四种不同的方法把△ABC 分割成四个等腰三角形，并标明分割后的四个等腰三角形的底角的度数（如果经过变换后两个图形重合，则视为同一种方法）图2图1C BACB AABCABC C BA答案：2. 小明在研究四边形的相关性质时发现，在不改变面积的条件下，一般梯形很难转化为菱形，但有些特殊的梯形通过分割可以转化为菱形，如图1，已知在等腰梯形ABCD 中，AD ∥BC ，CD ＝2AD ，∠C ＝60°．图2图1CBADDABC（1）果将该梯形分割成几块，然后可以重新拼成菱形，试在图1中画出变化后的图形； （2）在完成上述任务后，他又试着在直角梯形（如图2，AD ∥BC ，CD ＝2AD ，∠C ＝60°）中，将梯形分成几块，拼成新的图形；①它能拼成一个菱形吗？如果能，请画出相应的图形； ②它能拼成一个正方形吗？如果能，请画出相应的图形． 答案：（1）能拼成菱形：CB AD（2）能拼成菱形：DA B C能拼成正五边形DAB C3．下列网格中的六边形ABCDEF是由一个边长为6的正方形剪去左上角一个边长为2的正方形所得，该六边形按一定的方法可剪拼成一个正方形．（1）根据剪拼前后图形的面积关系求出拼成的正方形的边长；（2）如图甲，把六边形ABCDEF沿EH，BG剪成①，②，③三个部分，请在图甲中画出将②，③与①拼成的正方形，然后标出②，③变动后的位置；（3）在图乙中画出一种与图甲不同位置的两条剪裁线，并画出将此六边形剪拼成的正方形．图甲图乙答：（1）（2）如图；（3）如图：。

专题25 全等三角形的存在性破解策略全等三角形的存在性问题的解题策略有：(1 )当有一个三角形固定时(三角形中所有边角为定值) ，另一个三角形会与这个固定的三角形有一个元素相等；再根据全等三角形的判定，禾U用三角函数的知识(画图) 或列方程来求解.(2)当两个三角形都不固定时(三角形中有角或边为变量)，若条件中有一条边对应相等时，就要使夹这条边的两个角对应相等，或其余两条边对应相等；若条件中有一个角对应相等时，就要使夹这个角的两边对应相等，或再找一个角和一条边对应相等.例题讲解例1如图，在平面直角坐标系中，抛物线y= ax2+ bx+ 4与x轴的一个交点为A(- 2, 0),与y 轴的交点为C,对称轴是x= 3,对称轴与x轴交于点B.(1)求抛物线的表达式；(2)若点D在x轴上，在抛物线上是否存在点P,使得△PBC若存在，求点P的坐标；若不存在，请说明理由.(3)若点M在y轴的正半轴上，连结MA过点M作MA的垂线，交抛物线的对称轴于点N.问：是否存在点M使以点M A N为顶点的三角形与△ BAN全等？若存在，求出点M424a -2b 4=0解：(1)由题意可列方程组解得2a427②当AM= NB MN= BA 时,可列方程组:4 m 2 = n 29 (m -n)2 =25(2)显然 OA= 2, OB= 3, OC= 4.所以 BC OB 2 OC 2 =5 = BA . 若^ P BD^ PBC 贝U BD= BC= 5, PD= PC所以D 为抛物线与x 轴的左交点或右交点，点 B P 在CD 的垂直平分线上,①若点D 为抛物线与x 轴的左交点，即与点 A 重合.如图1，取AC 的中点E ,作直线BE 交抛物线于P i （x i , y i ）, F 2 （X 2. y 2）两点. 此时△ RBC^AP i BD △ RBC ^A R BD.由A 、C 两点的坐标可得点 E 的坐标为（一1, 2）. 所以直线BE 的表达式为y = _〔x -.2 22②若D 为抛物线与x 轴的右交点，则点 D 的坐标为（8, 0）.如图2,取CD 的中点F .作直线BF 交抛物线于P 3 (X 3, y s ), P 4 (X 4, , y 4)两点. 此时△ P s BC^AP s BD △ RBC^A P 4 BD.由C D 两点的坐标可得点 F 的坐标为（4, 2）, 所以直线BF 的表达式为y = 2x — 6.联立方程组厂罕6 3 ,解得卜一仆化，广“一色 y--[X -x 4ys--8 2.4i y4--8-2.4i 所以点.P J , R 的坐标分别为(一i + - 4i , — 8 + 2』4i ), ( — i — ■ 4i , — 8— 2 ■- 4i ),综上可得，满足题意的点 P 的坐标为（4 一 26, 「26）, （4+ 26 , 土丄6 ）,2 2(—i + ■■■'4i , — 8 + 2」4i )或(一i — ■- 4i , — 8 — 2>..；4i ).(3) 由题意可设点 M(0 , m ), N(3 , n ),且m >0 ,则 AM= 4+ m i , MN= 9 +( m — n ) 2 , B N = n 2. 而/ AM =Z ABN= 90° , 所以△ AMNf A ABN 全等有两种可能：①当 AM= AB, M = BN 时，所以此时点M 的坐标为（0 ,.2i ）.所以抛物线的表达式为^-1x 22x 4 • 4 21丄-i y 「x +- 联立方程组 2i 2 -y =—— x +—x +4 / 42，解得 y i - 26 ^ 26 ,X2 =4 26-^26 .y 2 二所以点P i , P 2的坐标分别为（ 4 一炉，土亚6 ）. （4 +V26 ,-1 - 26 )2可列方程组4 m 2 =25 9 (m —n)2 二n 2m 2 n 2 =-2i_ _5 N (舍)，3m^2解得 2 ,5所以此时点M 的坐标为（0, 2）.2点E 在OA 上.如图1. 此时DF 丄OA 所以OF=晅。