层次分析结果表
- 格式:ppt
- 大小:398.50 KB
- 文档页数:59

构建风险层次结构通过选取的指标可以看出这是一个多目标的且问题涉及到许多因素,各种因素的作用相互,情况复杂。
依据层次分析法处理这类复杂的问题就需要对所涉及的因素指标进行分析:哪些是需相互比较的;哪些是需相互影响的。
把那些需相互比较的因素归成同一类,构造出一个各因素类之间相互联结的层次结构模型。
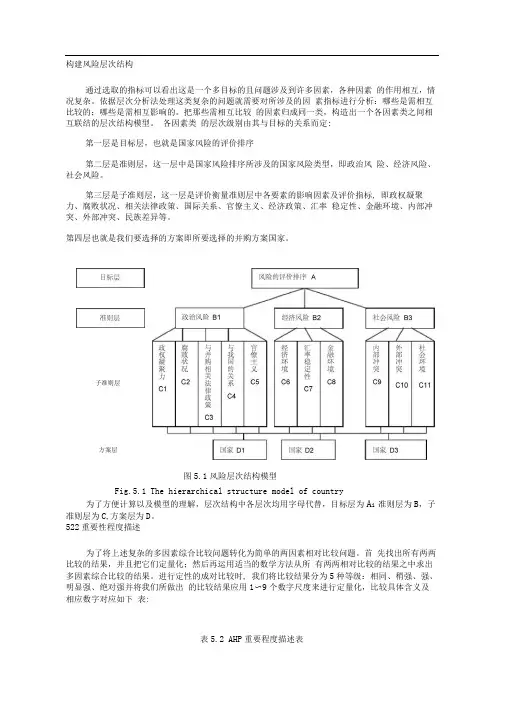
各因素类的层次级别由其与目标的关系而定:第一层是目标层,也就是国家风险的评价排序第二层是准则层,这一层中是国家风险排序所涉及的国家风险类型,即政治风险、经济风险、社会风险。
第三层是子准则层,这一层是评价衡量准则层中各要素的影响因素及评价指标, 即政权凝聚力、腐败状况、相关法律政策、国际关系、官僚主义、经济政策、汇率稳定性、金融环境、内部冲突、外部冲突、民族差异等。
第四层也就是我们要选择的方案即所要选择的并购方案国家。
为了方便计算以及模型的理解,层次结构中各层次均用字母代替,目标层为A i 准则层为B,子准则层为C,方案层为D。
522重要性程度描述为了将上述复杂的多因素综合比较问题转化为简单的两因素相对比较问题。
首先找出所有两两比较的结果,并且把它们定量化;然后再运用适当的数学方法从所有两两相对比较的结果之中求出多因素综合比较的结果。
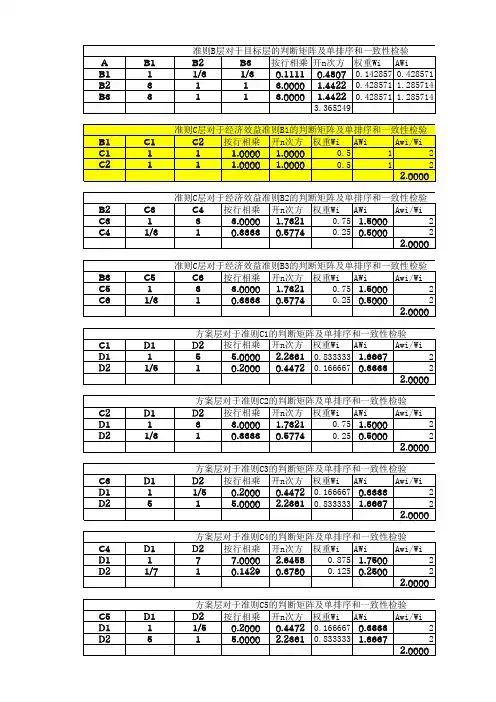
进行定性的成对比较时, 我们将比较结果分为5种等级:相同、稍强、强、明显强、绝对强并将我们所做出的比较结果应用1〜9个数字尺度来进行定量化,比较具体含义及相应数字对应如下表:表5.2 AHP重要程度描述表子准则层方案层图5.1风险层次结构模型Fig.5.1 The hierarchical structure model of countryTable 5.2 Described table of AHP imp orta nt degree定性比较结果数字定量因素1相较于因素2具有相同的重要性 1因素1与因素2相比,前者重要性稍强 3因素1与因素2相比,前者重要性强 5因素1与因素2相比,前者重要性明显强7因素1与因素2相比,前者重要性绝对强9因素1与因素2相比,相对重要性处于上述等级之间2、4、6、8(续表5.2)定性比较结果数字定量因素1与因素2相比,后者的重要性要稍强、强、明显强、1/3、1/5、1/7、绝对强于前者1/9 例如:在准则层中有三个因素政治风险B1、经济风险B2以及社会风险B3,假设如果政治风险B1相较于经济风险B2在风险中的重要性稍强那么就是B1: B2=3:1也就是3。

干部选拔模型摘要如今干部选拔问题已经引起了政府和人民的热切关注,怎样才能选择好的干部已经成为当今社会的焦点问题。
每一位干部都应具有干部应有的良好素质,如:健康状况、业务知识、写作水平、口才、政策水平和工作作风等。
许多单位的选拔标准就用这些属性来衡量。
使用层次分析法对甲、乙、丙三人进行综合评价,并选出最合适的人。
使用MATLAB对程序进行运行以便观察结果。
关键字:层次分析法、MATLAB。
一、问题重述某单位希望从三名同志中选择一名作为干部,选拔的标准用6个属性来衡量:健康状况、业务知识、写作水平、口才、政策水平和工作作风等。
组织部门根据选拔的标准对甲、乙、丙每人进行打分,最终从3人中选择最合适的人。
通过建立数学模型运用层次分析法对闻听进行分析。
二、模型假设1、假设选拔甲、乙、丙时,不考虑其他随机因素,对三人按照选拔标准进行客观的打分。
2、假设三人在选拔时都正常发挥,不考虑其他额外因素,且都不受外界的影响,进行公平的竞争。
3、假设组织部门严格按照部门的流程进行选拔,也不考虑外界因素和影响。
三、符号说明p: 选拔干部的标准的第k个属性;kB: 判断矩阵;: 判断矩阵的特征根;W: 判断矩阵的权向量;CI: 一致性指标;RI:随机一致性指标;CR:一致性比率(用于确定判断矩阵的不一致性的容许范围);四、问题分析对于干部选拔的问题,就是综合分析的最优化问题,也是一个多目标的决策问题,使用层次分析法对甲、乙、丙按照选拔标准进行综合分析,并使用MATLAB 对分析的程序进行运行,观察和分析结果,最终有组织部门根据分析结果从三人中选择最合适的人。
五、建立模型使用层次分析法,先建立层次结构模型,模型分为3层:第一层,为解决问题目的的目标层;第二层,为实现总目标而采取的各种措施和方案的准则层;第三层,用于解决问题的各种措施和方案。
层次结构模型如下用123456,,,,,p p p p p p 分别表示:健康状况、业务水平、写作水平、口才、政策水平、工作作风。




构建风险层次结构通过选取的指标可以看出这是一个多目标的且问题涉及到许多因素,各种因素的作用相互,情况复杂。
依据层次分析法处理这类复杂的问题就需要对所涉及的因素指标进行分析:哪些是需相互比较的;哪些是需相互影响的。
把那些需相互比较的因素归成同一类,构造出一个各因素类之间相互联结的层次结构模型。
各因素类的层次级别由其与目标的关系而定:第一层是目标层,也就是国家风险的评价排序第二层是准则层,这一层中是国家风险排序所涉及的国家风险类型,即政治风险、经济风险、社会风险。
第三层是子准则层,这一层是评价衡量准则层中各要素的影响因素及评价指标,即政权凝聚力、腐败状况、相关法律政策、国际关系、官僚主义、经济政策、汇率稳定性、金融环境、内部冲突、外部冲突、民族差异等。
第四层也就是我们要选择的方案即所要选择的并购方案国家。
图5.1风险层次结构模型Fig.5.1 The hierarchical structure model of country risk为了方便计算以及模型的理解,层次结构中各层次均用字母代替,目标层为iA ,准则层为B i ,子准则层为C i ,方案层为D i 。
5.2.2 重要性程度描述为了将上述复杂的多因素综合比较问题转化为简单的两因素相对比较问题。
首先找出所有两两比较的结果,并且把它们定量化;然后再运用适当的数学方法从所有两两相对比较的结果之中求出多因素综合比较的结果。
进行定性的成对比较时,我们将比较结果分为5种等级:相同、稍强、强、明显强、绝对强并将我们所做出的比较结果应用1~9个数字尺度来进行定量化,比较具体含义及相应数字对应如下表:表5.2 AHP重要程度描述表Table 5.2 Described table of AHP important degree 定性比较结果数字定量因素1相较于因素2具有相同的重要性 1因素1与因素2相比,前者重要性稍强 3因素1与因素2相比,前者重要性强 5因素1与因素2相比,前者重要性明显强7因素1与因素2相比,前者重要性绝对强9因素1与因素2相比,相对重要性处于上述等级之间2、4、6、8(续表5.2)定性比较结果数字定量因素1与因素2相比,后者的重要性要稍强、强、明显强、绝对强于前者1/3、1/5、1/7、1/9例如:在准则层中有三个因素政治风险B1、经济风险B2以及社会风险B3,假设如果政治风险B1相较于经济风险B2在风险中的重要性稍强那么就是B1:B2=3:1也就是3。

层次分析法在报考学校中的应用摘要每年都有大量的高考毕业生面临着择校问题,大部分都没有经验总是会有些茫然失措顾此失彼,据问卷调查可知有一大部分大学生对自己当初的选择不尽如意。
为了减少这种心态下的种种决策失误,所以需要一种可靠的定量的容易操作的,并且具有说服力的方法来作出决策。
本文提出了定性定量相结合的层次分析法步骤,构成了学校满意度的评价指标,根据数据解决问题。
关键词:选学、层次分析法、决策、目标、权向量一、问题的提出刚高考完面临选择学校的学生甲,根据其分数可能被录取的学校有c1甲学校、c2乙学校、c3丙学校、c4丁学校。
如何在填报志愿中对着这四个学校进行排序并选择他比较满意的学校?这是目前需要解决的。
通过研究,最终确定了六个准则作为参照依据,来判断出最适合且让他满意的学校。
准则:B1师资力量B2学校声誉B3就业前景B4录取几率B5食宿条件B6地理位置二、模型的假设1、四个学校相当,各有利弊2、该学生仅在这四个学校中进行选择三、符号说明四、 模型的建立与求解 1、层次结构的建立第一层:目标层,即对可供选择的学校满意度A ;第二层:准则层,即B1师资力量B2学校声誉B3就业前景B4录取几率B5食宿条件B6地理位置第三层:方案层,即c1甲学校、c2乙学校、c3丙学校、c4丁学校 目标层准则层 方案层2、通过相互比较确定个准则对于目标的权重,及各方案对于每一准则的权重,这些权重在人的思维过程中通常是定性的,而在层次分析中则要给出得到权重的定量方法。
综上运用1-9尺度ij a 的含义构造两两比较矩阵并给出RI表1随机一致性指标RI 的数值一致性检验:成对比阵通常不是一致阵,但为了能用它的对应于特征根λ的特征向量作为比较因素的权向量,其不一致程度应在容许范围内即CI=1n n λ--,CR=CIRI<0.1 构造成对比较矩阵和计算权向量 准则层对目标层的成对比矩阵AA=111421/2112421/211/21531/21/41/41/511/31/31/21/21/3311/3222331⎛⎫⎪⎪ ⎪⎪⎪ ⎪⎪⎪⎝⎭方案层对准则层的成对比较阵B1;即B1=方案层对准则层的成对比较阵B2;即B2=方案层对准则层的成对比较阵B3;即B3=方案层对准则层的成对比较阵B4;即B4=方案层对准则层的成对比较阵B5;即B5=12321/2141/21/31/411/41/2241⎛⎫⎪⎪ ⎪⎪⎝⎭115311431/51/411/21/31/321⎛⎫⎪⎪ ⎪⎪⎝⎭11/21/31/7211/21/53211/57551⎛⎫ ⎪ ⎪⎪⎪⎝⎭13541/3121/31/51/211/51/4351⎛⎫⎪ ⎪ ⎪⎪⎝⎭11/231/221511/31/511/62161⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭方案层对准则层的成对比较阵B6;即B6=3、 将方案层对准则层的权重及准则层对目标层的权重进行综合分析并作一致性检验运用matlab 软件求解各成对比阵的最大特征根及对应向量,ω12=[ 0.3876; 0.4519; 0.4025; 0.1099; 0.2093;0.6540]归一化后得作为[0.1750;0.2040;0.1817;0.0496;0.0945;0.2952];λ=6.2620一致性检验; CI= 0.26205=0.0524一致性比率,CR=CI RI =0.05241.24=0.0422<0.1,则一致性检验通过,ω13可以作为权重向量。

1层次分析法首先建立了层次结构模型后,其上下层之间元素的隶属关系就被确定了。
最后需要对每一个层级的所有指标进行两两比照,确定其相对的重要性。
而层次分析通常采用Saaty 标度法来给判断矩阵的元素赋值。
如表1-1所示:表1-1 1~9标度及其含义1/ij a依据表1-1我们可以得到要素层与各方案层的两两判断矩阵ijn nA a ,其次通过以下步骤进行权重的计算以及一致性检验。
〔1〕我们利用方根法求评价因素的权重向量近似值,其计算公式如下:11,(1,2,...,)nni ij j w a i n =⎛⎫== ⎪⎝⎭∏〔2〕对上述利用方根法求解的权重向量按照以下公式做归一化处理,得到最终的权重为:'1,(1,2,...,)ii nik w w i n w===∑〔3〕计算判断矩阵的最大特征值m ax λ。
()max 1=nii iAw nw λ=∑〔4〕一致性检验,由一致性指标:max 1nCI n λ-=-RICI CR =其中,一致性指标CI 越大,这就意味着矩阵的偏离一致性就越大。
反之一致性指标CI 越小,则这就意味着矩阵的偏离一致性就越小。
并且当矩阵的阶数n 越大时,其最大特征值max λ也就会越大,这就可能会导致CI 变得更大,也就意味着矩阵的偏离一致性就越大。
反之,阶数n 越小,最大特征值max λ就会越小,其一致性指标CI 也就越小,则这就意味着矩阵的偏离一致性就越小。
这样的模型并不具有科学性。
因此,矩阵的判断过程便釆用了随机一致性指标,即RI 。
RI 的大小与判断矩阵的阶数n 有关,具体数据如下表1-2所示:表1-2 RI 随机一致性指标假设则说明一次性检验通过,则其对应的特征向量可作为权向量。
指标权重确实定依据前面介绍的层次分析法,对所建立的指标体系中准则层和指标层权重进行计算。
准则层指标权重确定收集专家对评价目标下的准则层指标的基础性的数据,汇总如下表1-3所示,该数据也就是准则层七个指标的判断矩阵。

总结:(1)本次评价的相对重要指标为路网可达性。
(2)为了简便运算,所以忽略了多项指标,导致本次评估不准确。
(3)各项指标的比较赋值缺少相关资料,可能导致最终结果不能得到正确的方案.(4)虽然做作业过程盲点很多,但解决了之后还是感觉收获颇多。
入=1/3(0.731/0.244+0.265/0.088+2.016/0.668)=3.0084一致性检验n=3.RI=0.58CI=(入max-n)/(n-1)=(3.0084-3)/(3-1)=0.0042CR=CI/RI=0.0042/0.58=0.0072<0.1通过一致性检验同理:不同措施对各要素的影响的成对比较矩阵的权重向量分别为W2=(0.25,0.75)T;W2’=(0.2,0.8)T;W2”=(0.17,0.83)T;W31=(0.5,0.5)T;W32=(0.75,0.25)T;W33=(0.17,0.83)T;W34=(0.17,0.83)T,W35=(0.83,0.17)T; W36=(0.83,0.17)T二阶矩阵,全部通过一致性检验层次总排序与检验总排序是指每一个判断矩阵因素针对目标层的相对权重。
这一权重的计算方法采用从上而下的方法,逐层合成。
很明显,第二层的但排序结果就是总排序结果。
已知第二层对目标层的单排序权重为W1=(0.244,0.088,0.668),第三层(指标层)对第二层的单排序权重为W2=(0.25,0.75)T;W2’=(0.2,0.8)T;W2”=(0.17,0.83)T(B) 所以第三层对总目标的总排序为W1.W2=(0.061,0.183,0.0176,0.0704,0.1136,0.5544)对总排序结果进行一致性检验CI=0.061*0+0.183*0+0.0176*0+0.0704*0+0.1136*0+0.5544*0= 0;RI=0,判断矩阵整体一致性是可以接受的W1=0.061*0.5+0.183*0.2+0.0176*0.17+0.0704*0.17+0.1136*0.8 3+0.5544*0.83=0.637;同理W2=0.363,通过堆排序结果分析:建方格式道路网的权重(0.637)大于建环式道路网的权重(0.363),最终方案决定建方格式道路网。
层次分析法层次分析法(Analytic Hierarchy Process ,简称AHP 法)是美国运筹学家、匹兹堡大学教授萨蒂(T. L. Saaty )于20世纪70年代提出的,是一种定性与定量分析相结合的多目标决策分析方法。
它常常被运用于多目标、多准则、多要素、多层次的非结构化的复杂决策问题,特别是战略决策问题的研究,具有十分广泛的实用性,在实际应用中发展较快。
AHP 方法的核心是通过分析复杂系统的有关要素及其相互关系,将系统简化为有序的递阶层次结构,使这些要素归并为不同的层次,在每一层次,可按其上一层的某一准则或要素,对该层要素进行两两相对比较,建立判断矩阵;通过计算判断矩阵的最大特征根及对应的正交特征向量,得出该层要素对于该准则的权重,最后计算出多层次要素对于总体目标的组合权重;依次下去,从而得出不同方案或评估对象的优劣权值,为决策和评选提供依据。
在公共卫生部门的管理工作中,管理目标具有多层次特征,因此,在评估工作中,可应用层次分析方法获得各层次管理指标的权重系数,以满足多层次评估的要求。
AHP 法具体实施步骤如下:(1) 明确问题,建立系统的递阶层次结构。
层次分析法确定各项指标的权重,其基础是完善的指标体系,按照指标体系从上往下逐层地确定各有关指标的权重。
首先把问题条理化、层次化,构造出一个有层次的结构模型。
一个决策系统大体可分为三个层次:(1)最高层(目标层):这一层中只有一个元素,一般它是分析问题的预定目标或理想结果;(2)中间层(准则层):这一层次中包含了为实现目标所涉及的中间环节,它可以由若干层次组成,包括所需考虑的准则、子准则;(3)最低层(方案层):这一层次包括了为实现目标可供选择的各种措施、决策方案等。
本书依据逻辑模型确定的绩效指标体系构造出一个递阶层次结构。
(2) 两两比较,构造成对比较判断矩阵和正互反矩阵。
在确定了比较准则以及备选的方案后,需要比较若干因素对同一目标的影响,从而确定它们在目标中占的比重。
张老师需要购买一辆私家小轿车,他考虑的主要因素有:价格适中,售后比较好,轿车的动力性较好,燃油经济性相对较好。
经过轿车销售商的介绍,他初步选择了甲、乙、丙三款轿车,情况如表5-2所示:表5-2解:用AHP 方法研究解决问题的具体步骤是:第一步:分析和细化具体问题,明确该问题的总目标。
第二步:构建递阶的层次结构模型。
这是AHP 的关键步骤。
通常模型结构分为3层,其中顶层为目标层,中间层为准则层(根据问题的复杂程度,每项准则还可以细分为若干子准则),最底层为方案层。
(1)目标层。
这是最高层次,或称为理想结果层。
如需要,可再分为总目际层,战略目标层,战术目标层以至子战术目标层等;(2)准则层。
第二层次为评价准则或衡量准则,也可为因素层、约束层。
同样,可再分为子准则层、子因素层等;(3)措施层。
第三层次为措施层,或对策层、备择对象(人选、方案)等层,对不同问题可有不同的描述。
同样,可再分为子措施层或子对策层等。
构造一个好的层次结构对于问题的解决极为重要.它决定了分析结果的有效程度。
层次结构建立在决策者(或分析者)对问题全面深入认识的基础之上。
如果在层次的划分和确定层次的支配关系上举棋不定,最好的办法是重新分析问题,打乱原来的结构,重新定义要素并建立新的结构。
第三步:构造判断矩阵,求本层次要素相对于上一层次要素的权重。
建立了递阶层次后,上下层之间元素的隶属关系就被确定了。
假设上一层次的元素k C 作为准则,对下一层次的元素1,,n A A 有支配关系。
在此要在准则k C 下,按其相对重要性对1,,n A A 赋予相应的权重(Weight )。
对于大多数社会经济问题,特别是那些没有统一指标表示而仅靠人的经验判断和估计的问题,往往要通过适当的方法来导出其权重,以给出某种量化指标或直接判断元素之间的重要性。
AHP 中的方法是将本层次的要素A i 和A j (i,j=1,2,…,n )相对于上一层次要素c k (k=1,2,…,m) 按照重要程度进行两两比较,从而得到判断矩阵 A=(a ij )n ×n 。