含有参数的二元一次方程组

专题：含参的二元一次方程组分析：用两个不含参数的二元一次方程重组，求解得参数。

4x y 5 mx ny 3的解和 的解相同，求3x 2y 1 mx ny 1、解的性质例 3 ：已知关于 x,y 二元一次方程组一、同解问题 例 1：已知关于 x,y 二元一次方程组 x y 1 4x ay的解是二元一次方程3 x y 3的解，求 a 的值。

变式 1：已知方程组2x 3y 3x 5y的解适合 x28 ，求 m 的值 .变式 2：已知二元一次方程组4x y 5的解和mx ny 33x 2y mx ny11 的解相同，m,n 的值。

例 2 ：已知二元一次方程组m,n 的值。

4x 3y 7 的解 x,y 的值互为相反数，求 k 的值。

kx (k 1)y 3变式4：若方程组3x y k 1的解x,y满足0 x y 1，求k 的取值范围。

x 3y 3分析：观察方程组和所求式子的结构共性，把二元一次方程组中的参数作整体化处理三、错解问题例4：甲乙两人同时解关于x, y的方程组ax y 3，甲看错了b ，求得的解为2x by 1 的解为x 1，你能求出原题中的a,b 的值吗？y3分析：将解代入没看错的方程看错了方程②中的b，得到方程组的解为x y 54.试计算a2017 ( 110b)2018的值.变式3：已知方程组y 2k3y 1 5k的解x 与y 的和是负数，求k 的取值范围。

变式5：甲、乙两人共同解方程组ax4x5yby152①②，由于甲看错了方程①中的a，得到方程组的解为31；乙1，乙看错了a，求得例5 ：已知3x 7y z 3，求x y4 x 10y z 4z的值。

变式6：已知3x 4y z2x y 8z0，其中xyz2 2 20 ，求x y z的值。

xy yz 2 zx专题：解三元一次方程x yzx yz例 2 ：解 2 34变式 3： 3 4 2x y z 182x 3y z 162x y z 183x y 2z 3 例 4：2x y 3z 11x y z 12例 1 ：解xy2 y 2z 4xz1x 2y 9变式 1：y z 32z x 47变式 2：若 x y 2y z342z x 51，求 x, y,z例 3:y z 26 y1变式 4 ：x y 2z 2x y z 3x z 03x y 2z 3变式 5：2x y 3z 11 x y z 12。

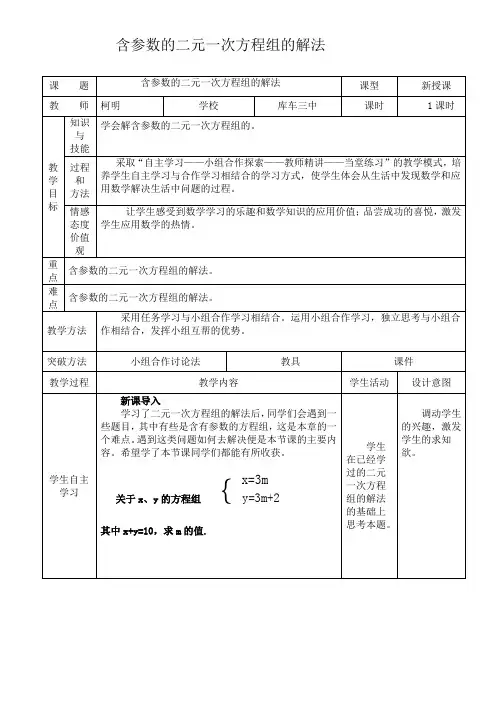
掌握带有参数的二元一次方程组的解法带有参数的二元一次方程组是指方程组中含有参数的二元一次方程。

解决这类方程组的关键在于求出参数的取值范围，并找到满足方程组的解。

下面将详细介绍带有参数的二元一次方程组的解法。

一、带有参数的二元一次方程组的表示形式带有参数的二元一次方程组一般可以表示为：方程组1：$a_1x + b_1y = c_1$$a_2x + b_2y = c_2$其中，$a_1, b_1, c_1, a_2, b_2, c_2$为已知系数，$x, y$为未知数。

二、参数的取值范围为了求解方程组，首先需要确定参数的取值范围。

通常可以通过观察方程来判断参数取值的范围。

例如，如果方程组中含有分母，并要求分母不等于零，那么就需要确定参数不能为使分母为零的值。

三、带有参数的二元一次方程组的解法带有参数的二元一次方程组的解法可以分为以下几种情况：情况一：参数取某个特定值当参数取某个特定值时，方程组就变成了具有确定解的普通二元一次方程组。

根据二元一次方程的解法，解出该方程组，得到解的具体数值。

情况二：参数存在范围当参数存在范围时，需要根据参数的取值范围进行分类讨论。

具体步骤如下：1. 将方程组化简为标准形式，即求出每个方程的标准形式表达式；2. 根据参数的取值范围，将方程组分为不同的情况；3. 分别针对每种情况，解决方程组，并得到解的范围或具体解。

情况三：参数无限制当参数没有明确的取值范围时，需要利用一些性质和技巧，通过代数运算推导出解的性质。

常用的技巧包括代入法、消元法、矩阵法等。

根据具体问题和方程组的特点，选择合适的方法求解。

总之，掌握带有参数的二元一次方程组的解法，首先要明确参数的取值范围，然后根据具体情况选择合适的解法进行求解。

通过逐步分析和计算，可以得出解的范围或具体解。

在实际问题中，带有参数的二元一次方程组的解法能够帮助我们解决更为复杂的数学和实际应用问题。

二元一次方程组的定义及解法知识集结知识元二元一次方程（组）的定义知识讲解1. 二元一次方程的定义：含有两个未知数，且含有未知数的项的次数为1的整式方程叫二元一次方程。

所以满足三个条件：①方程中有且只有两个未知数；②方程中含有未知数的项的次数为1；③方程为整式方程，就是二元一次方程。

注意：主要考查未知数的项的次数为1，方程必须为整式，不能为分式。

例：x=2y.2.二元一次方程组的定义：由几个一次方程组成并且含有两个未知数的方程组，叫二元一次方程组。

注意三条：①方程组中有且只有两个未知数。

②方程组中含有未知数的项的次数为1。

③方程组中每个方程均为整式方程。

注意：二元一次方程组不一定由两个二元一次方程合在一起：①方程可以超过两个；②有的方程可以只有一元。

例题精讲二元一次方程（组）的定义例1.下列方程中，是二元一次方程的是（）.A．8x2+1=y B．y=8x+1C．y=D．xy=1例2.下列方程组中，是二元一次方程组的是（）.C．D．A．B．例3.有下列方程组：（1）（2）（3）（4），其中说法正确的是（）.A．只有（1）、（3）是二元一次方程组B．只有（3）、（4）是二元一次方程组C．只有（4）是二元一次方程组D．只有（2）不是二元一次方程组根据定义求字母的值知识讲解含有参数的二元一次方程组，根据二元一次方程的定义：1.二元的系数不为零。

2.未知数的次数为1。

注意：出现在选择填空题时，可以不用解出方程，可以直接将m,n的值代入验证即可。

例题精讲根据定义求字母的值例1.已知3 =y是二元一次方程，那么k的值是（）.A．2B．3C．1D．0例2.若﹣8 =10是关于x，y的二元一次方程，则m+n=．例3.'若(a-3)x+=9是关于x，y的二元一次方程，求a的值。

'由实际问题抽象出二元一次方程组知识讲解分析实际问题，找出等量关系，列出实际问题.例题精讲由实际问题抽象出二元一次方程组例1.4辆板车和5辆卡车一次能运27吨货，10辆板车和3车卡车一次能运货20吨，设每辆板车每次可运x吨货，每辆卡车每次能运y吨货，则可列方程组（）.A．B．C．D．例2.元旦期间，某服装商场按标价打折销售，小王去该商场买了两件衣服，第一件打6折，第二件打5折，共记230元，付款后，收银员发现两件衣服的标价牌换错了，又找给小王20元，请问两件衣服的原标价各是多少？解：设第一件衣服的原标价为x元，第二件衣服的原标价为y元；由题意可得方程组__________。

设参数法解二元一次方程组
解二元一次方程组是高中数学中最基本的问题之一，也是考研高数中重要的内容之一。

解二元一次方程组的方法有很多，其中最常用的就是设参数法。

设参数法主要是将不确定的未知量设定为一个变量，也就是参数，用参数和其他未知量来构成一组方程，将方程组视为一个整体，解决方程组中的未知量。

例如，解方程组 $x+2y=1$，$2x+4y=2$，我们可以先将y设定为参数，t，即$y=t$，将其代入原方程中，可得$x=1-2t$，即将y代入$x+2y=1$式中，可得$x=1-2t$；将x代入$2x+4y=2$式中，可得 $2(1-2t)+4t=2$，即$t=\frac{1}{2}$。

经过上述步骤，参数t解得出可计算出真正的未知量值：$x=1-2t=1-
2\times{\frac{1}{2}}=\frac{1}{2}$，$y=t=\frac{1}{2}$，从而解得题目的原有的未知量值。

可见，通过设参数法，我们可以解得未知量的值，从而解决二元一次方程组的问题。

总之，设参数法是解决二元一次方程组的非常有效的一种方法，可以解得未知量的正确值，而且易于理解、实施。

它不仅是考研高数中的重要内容，而且也可以在日常生活中不断使用，从而更好地解决实际问题。

方程与不等式之二元一次方程组全集汇编及解析一、选择题1 .二元一次方程3x+y = 7的正整数解有（ ）组.A . 0B . 1C . 2【答案】 C 【解析】【分析】 分别令 x=1 、2进行计算即可得 【详解】 解:方程 3x+y=7， 变形得 :y=7-3x ， 当 x=1 时，y=4;当 x=2 时，y=1,则方程的正整数解有二组 故本题答案应为： C【点睛】 本题考查了二元一次方程的解，给出一个未知数的值求出另一个未知数的值即可2.某家具生产厂生产某种配套桌椅 （一张桌子，两把椅子 ），已知每块板材可制作桌子 1张或椅子 4把，现计划用 120 块这种板材生产一批桌椅 （不考虑板材的损耗，恰好配套 ），设用 x 块板材做椅子，用 y 块板材做桌子，则下列方程组正确的是（）【分析】根据“用 120 块这种板材生产一批桌椅 ”，即可列出一个二元一次方程，根据 “每块板材可做 桌子 1 张或椅子4 把，使得恰好配套，一张桌子两把椅子 ”，列出另一个二元一次方程，即 可得到答案.【详解】解：设用x 块板材做椅子，用y 块板材做桌子， •••用120块这种板材生产一批桌椅，••• x+y=120 ①,生产了 y 张桌子， 4x 把椅子， •••使得恰好配套，1张桌子2把椅子， • 4x=2y ② ， ① 和② 联立得：D .无数x A.2xy 120 4yx B.2y 4x120x C .4x答案】 解析】y 1202yCxD .x120 4yx y 120 4x 2y故选： C. 【点睛】本题考查了由实际问题抽象出二元一次方程组，正确找出等量关系，列出二元一次方程组 是解题的关键.3.若(x+y — 1) 2+|x — y+5| = 0，则 x =( )A .— 2B . 2C . 1【答案】 A【解析】 【分析】 由已知等式，利用非负数的性质列出方程组，求出方程组的解得到 【详解】解得： 故选： 【点睛】 本题主要考查了非负数的性质和二元一次方程组的解法，根据两个非负数的和为零则这两 个数均为零得出方程组是解决此题的的关键 .4.某人购买甲种树苗 12棵，乙种树苗 15棵，共付款 450元，已知甲种树苗比乙种树苗 每棵便宜 3 元，设甲种树苗每棵x 元，乙种树苗每棵 y 元.由题意可列方程组（）【解析】 【分析】根据 购买甲种树苗12棵，乙种树苗15棵，共付款450元”可列方程12x+15y = 450；由甲 种树苗比乙种树苗每棵便宜 3元”可列方程y -x = 3，据此可得.【详解】设甲种树苗每棵x 元，乙种树苗每棵 y 元.解：••• x+y — 1) 2+|x — y+5| = 0,D .— 1x 即可 .A.12x 15y 450 A.x y 312x 15y 450 B.y x 312x 15y 450C .y 3 x【答案】 B 12x 15y 450D .x3y，口土亠 「、计/n 12x 15y 450 由题意可列万程组y x 3故选：B . 【点睛】本题主要考查了由实际问题抽象出二元一次方程组，解题关键是要读懂题目的意思，根据 题目给出的条件，找出合适的等量关系，列出方程组.5. 下列方程组中，是二元一次方程组的是【答案】 【解析】 【分析】根据二元一次方程组的定义进行判断即可. 2,属于二元二次方程组，故本选项错误; B 、 该方程组中含有 3个未知数，属于三元一次方程组，故本选项错误；C 、 该方程组中未知数的最高次数是 2,属于二元二次方程组，故本选项错误；D 、 该方程组符合二元一次方程组的定义，故本选项正确；故选D . 【点睛】本题考查了二元一次方程组的定义，组成二元一次方程组的两个方程应共含有两个未知 数，且未知数的项最高次数都应是一次的整式方程.3x 2y =4① 2x y =2②‘①②得：x-y=2,1则原式=2-2= —.x A . y1 13 2x3x y 5B .2y z 6C. r y 1 5 2xy 1-2 D .2 y 2x 4【详解】解：A 、该方程组中未知数的最高次数是6.已知方程组3x 2y 4，则2x -2y =()1A.-4【答案】A1B.-2C. 2D . 44 故选A.【解析】 【分析】值. 【详解】解：2x+3y-z = 0 ①，x-2y+z = 0 ②， ①+②，得3x+y=0,X 1解得，一— y 3故选D .【点睛】 本题主要考查解三元一次方程组，解答本题的关键是明确题意,【解析】 【分析】 再将其相减即可得解.【详解】 解：•••X m 5① y 3 m ② 由①得, x m 5由②得,y m 3••• x ym 5故选：C【点睛】本题考查了解含参数的二元一次方程组、 解决本题的关键.7.如果 2x 3y z 0,且 x 2y x 0，那么一的值为（yA . 1 【答案】D B- 1c-3将题目中的两个方程相加，即可求得3x+y=0的值，根据 x 与y 的关系代入即可求出求出所求式子的值.5,可得到mx 与y 的关系式是（）A . x y【答案】CB . xC. x yD . x y先解方程组求得以及代数求值的知识点，熟练掌握相关知识点是/.( a+b)( a-b) = (-1+4) x(-1-4) =-15.故选：B . 【点睛】本题考查方程组的解的概念，掌握方程组的解满足方程组中的每一个方程是解题关键.10.为丰富同学们的课余活动，某校计划成立足球和篮球课外兴趣小组，现需购买篮球和 足球若干个，已知购买篮球的数量比足球的数量少1个，篮球的单价为 60元，足球的单价为30元，一共花了 480元，问篮球和足球各买了多少个？设购买篮球 x 个，购买足球y个, 可列方 程组()X y 1X y 1A .60X 30y 480B .60X 30y 480X y 1X y 1C. 30X 60y 480D .30X 60y 480【答案】B 【解析】 【分析】根据购买篮球的数量比足球的数量少1个，篮球的单价为共花了 480元”找到等量关系列出方程即可. 【详解】设购买篮球X 个，购买足球y 个，根据题意可列方程组：X y 160X 30y 480 , 故选：B .9. 若6"I 是关于X 、y 的方程组ax + by =2hx + rty =7的解，则(a+b)(a - b)的值为()B .— 15 A . 15 【答案】B 【解析】 【分析】 把方程组的解代入方程组可得到关于 (a+b )( a-b )的值. 【详解】 解：••• {:二!是关于X 、y 的方程组C. 16 D .— 16 a 、b 的方程组，解方程组可求 a , b ，再代入可求ax + by = 2 砧丽 bx ■^ay = 7的解，60元，足球的单价为 30元,9 7【点睛】本题考查了由实际问题抽象出二元一次方程组的知识，解题的关键是能够找到题目中的等 量关系，难度不大.11.用5个大小相同的小长方形拼成了如图所示的大长方形，若大长方形的周长是 每个小长方形的周长是（）【解析】 【分析】【点睛】本题主要考查二元一次方程组的应用，读懂题意列出方程组是解题的关键.【答案】A 【解析】 【分析】根，即可. 【详解】6X 5y 7m 2 且 x+y=9,3x y 728,则C. 13D . 16设小长方形的长为 方形的周长. X,宽为 y ，根据题意列出方程组，解方程组求出 x,y 的值，进而可求小长【详解】 设小长方形的长为X,宽为 y ，根据题意有 X 2y (3y X X)228解得•••小长方形的周长为（4 2） 故选：A . 12，12.在方程组A . 76x 3x 5y 7m y 72的解中,y 的和等于9,则7m 2的算术平方根为B .D . J 7根据条件得到二元一次方程组X y 3x y，求出X , y 的值，进而求出7m 2的算术平方【答案】A【详解】3xy 9 x 4，解得：，y 7 y 52 = 6x 5y =6X 4+5X 5=49 2的算术平方根为：7.故选A . 【点睛】本题主要考查二元一次方程组的解的意义，掌握解二元一次方程组的方法，是解题的关 键.13.方程5x + 2y =— 9与下列方程构成的方程组的解为yA . X + 2y = 1 C. 5x + 4y =— 3【答案】D 【解析】B . 3x + 2y =— 8 D . 3x — 4y =— 8试题分析：将x 与y 的值代入各项检验即可得到结果.解：方程5x+2y=- 9与下列方程构成的方程组的解为賃二-2的是 3x — 4y=— 8.故选D .点评：此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知 数的值.14.《九章算术》中记载：今有甲乙二人持钱不知其数，甲得乙半而钱五十，乙得甲太半而亦钱五十.问甲乙持钱各几何？ ”其大意是：今有甲、乙两人各带了若干钱 •如果甲得到乙所有钱的一半，那么甲共有钱|50;如果乙得到甲所有钱的三分之二， 甲、乙两人各带了多少钱？设甲带钱为 yXy “ f yx + - = 502x = 50 + -2 A .B .2yC.引 y\ ■D. 2Xy + y = 50y = 50 H - I 3【解析】 【分析】设甲需带钱X ,乙带钱2- = 5Q ,据此列方程组可得. 3 y ,根据题意可得，甲的钱 +乙的钱的一半=50, 乙的钱+甲所有钱的乙带钱为/，根据题意,當【答案】A 那么乙也共有 50|.问 可列方程组为（）y - 北+矿502x— + y =故选：A . 【点睛】本题考查了由实际问题抽象出二元一次方程组，解答本题的关键是读懂题意，设出未知 数，找出合适的等量关系，列出方程组.15.小明在超市帮妈妈买回一袋纸杯，他把纸杯整齐地叠放在一起，如图请你根据图中的 信息，若小明把100个纸杯整齐叠放在一起时，它的高度约是（y【分析】通过观察图形，可知题中有两个等量关系：单独一个纸杯的高度加上 高出单独一个纸杯的高度等于 9，单独一个纸杯的高度加上8个纸杯叠放在一起高出单独一个纸杯的高度等于 14.根据这两个等量关系，可列出方程组，再求解. 【详解】解：设每两个纸杯叠放在一起比单独的一个纸杯增高2x y 9X 1 则，解得7x y 14y 7则 99x+y = 99 X 1+7= 106即把100个纸杯整齐的叠放在一起时的高度约是 106cm .故选：A . 【点睛】本题以实物图形为题目主干，图形形象直观，直接反映了物体的数量关系，这是近年来比 较流行的一种命题形式，主要考查信息的收集、处理能力.本题易错点是误把 9cm 当作3个纸杯的高度，把14cm 当作8个纸杯的高度.116. 一辆汽车从 A 地驶往B 地，前-路段为普通公路，其余路段为咼速公路，已知汽车在3普通公路上行驶的速度为 60km/h ，在高速公路上行驶的速度为100km/h ，汽车从A 地到B解：设甲需带钱X ,乙带钱y ,根据题意, 得: A . 106cm【答案】A 【解析】B . 110cm C. 114cm D . 116cm3个纸杯叠放在一起xcm ,单独一个纸杯的高度为 ycm ,B地一共行驶了2.2h .设普通公路长、高速公路长分别为xkm、ykm，则可列方程组为【答案】c 【解析】 【分析】2x y 60 盍 2.2故答案为：C . 【点睛】本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组 是解题的关键.m 3，的解满足x > y > 0,则m 的取值范围是（）.5m【答案】A【解析】 【分析】2m 1•/x > y > 0,2m 1 m 2解之得m > 2. 故选A.【点睛】x 2y A .x y cc ———2.2B .x602y 100 2.2 2xC.x60盍2.2D .2xx 10060 2-2设普通公路长、高速公路长分别为xkm 、ykm ， 1-，结合汽车从A3的二元一次方程组，此题得解.由普通公路占总路程的地到B 地一共行驶了 2.2h ，即可得出关于 x , y 【详解】设普通公路长、高速公路长分别为 xkm 、ykm ，依题意，得:17.若关于X , y 的方程组x y2x yA . m >2B . m >— 3C.— 3< m < 2 D . m <3 或 m > 2先解方程组用含 【详解】m 的代数式表示出 X 、y 的值，再根据x >y >0列不等式组求解即可.x y m2x y 5m3，得本题考查了二元一次方程组及一元一次不等式组的应用，用含 值是解答本题的关键.18.小颖家离学校1200米，其中有一段为上坡路，另一段为下坡路，她去学校共用了 分钟，假设小颖上坡路的平均速度是【答案】 【解析】 【分析】【详解】•••她去学校共用了 16分钟,【分析】m 的代数式表示出x 、y 的 163千米/小时，下坡路的平均速度是 5千米/小时，若设小颖上坡用了 xmin ，下坡用了 y min ，根据题意可列方程组（3x A .x 5y 1200 y 16 3——x605 —y 60 16 1.23x C.x5y 1.2 y 163一xD605—y 60 161200 根据路程=时间乘以速度得到方程3一 x60—y 1.2，再根据总时间是16分钟即可列出方60 ••• x+y=16,•••小颖家离学校1200 米,3 一x 605 60y1.2，3 一x •- 60 x y5 —y 60 161.2 故选：B. 【点睛】此题考查二 元一次方程组的实际应用，正确理解题意列出方程组，注意时间单位，这是解 题中容易出现错误的地方.19.如果方程组 by ax y的解与方程组5bx 的解相同，贝y a+b 的值为（）ay 2A . - 1【答案】B【解析】 B .C.D . 0bx ay =2 ，得到一个关于by ax = 5整理即可得出 a+b 的值.16cm ,②小长方形的1个长1个宽 4cm ，进而可得到关于 x 、y 的两个方程，可求 得解，从而可得到小长方形的面积. 【详解】设小长方形的长为 X ,宽为y ,如图可知，x 3y x y 解得:x = 4把代入方程组 尸3右两边分别相加，a ,b 的方程组，将方程组的两个方程左x = 4、, 把代入方程组尸3 bx ay =2 by ax =5得：4b 3a =2②,3b 4a =5②①+②，得：7 (a+b ) 则 a+b=1. 故选B . 【点睛】此题主要考查了二元一次方程组的解的定义：一般地, 解，叫做二元一次方程组的解.理解定义是关键.=7,兀一次方程组的两个方程的公共20.如图，在长方形 ABCD 中，放入六个形状、大小相同的小长方形 若AB16cm , EF 4cm ，则一个小长方形的面积为 (3 (即空白的长方形),A . 16cm 2【答案】B 【解析】 【分析】B . 21cm 2C. 24cm 2D . 32 cm 2设长方形的长和宽为未数，根据图示可得两个量关系:①小长方形的1个长3个宽164E所以小长方形的面积 3 7 21 cm2故选B．【点睛】本题考查了二元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．。