方差分析实例分析
- 格式:docx
- 大小:150.40 KB
- 文档页数:8

什么是单因素方差分析单因素方差分析是指对单因素试验结果进行分析,检验因素对试验结果有无显著性影响的方法。
单因素方差分析是两个样本平均数比较的引伸,它是用来检验多个平均数之间的差异,从而确定因素对试验结果有无显著性影响的一种统计方法。
单因素方差分析相关概念•因素:影响研究对象的某一指标、变量。
•水平:因素变化的各种状态或因素变化所分的等级或组别。
•单因素试验:考虑的因素只有一个的试验叫单因素试验。
单因素方差分析示例[1]例如,将抗生素注入人体会产生抗生素与血浆蛋白质结合的现象,以致减少了药效。
下表列出了5种常用的抗生素注入到牛的体内时,抗生素与血浆蛋白质结合的百分比。
现需要在显著性水平a = 0.0!下检验这些百分比的均值有无显著的差异。
设各总体服从正态在这里,试验的指标是抗生素与血浆蛋白质结合的百分比,抗生素为因素,不同的5种抗生素就是这个因素的五个不同的水平。
假定除抗生素这一因素外,其余的一切条件都相同。
这就是单因素试验。
试验的目的是要考察这些抗生素与血浆蛋白质结合的百分比的均值有无显著的差异。
即考察抗生素这一因素对这些百分比有无显著影响。
这就是一个典型的单因素试验的方差分析问题单因素方差分析的基本理论⑴备择假设Hi,然后寻找适当的检验统计量进行假设检验。
本节将借用上面的实例来讨论单因素试验的方差分析问题。
2厂…j $)下进行了nj = 4次独立试验,得到如上表所示的结果。
这些结果是一个随机变量。
表中的数据可以看成来自s个不同总体(每个水平对应一个总体)的样本值,将各个总体的均值依次记为山、》2、…r »则按题意需检验假设页:旳=“2 =…=川尸1 : \J “5不全相等为了便于讨论,现在引入总平均卩[Ho :屍="2 =…=毎=qI 闻:力屆…:吗不全为零因此,单因素方差分析的任务就是检验s个总体的均值®是否相等,也就等价于检验各水平Aj的效应6是否都等于零。
样本产恥…佔吁/来自正态总体N (虬2), 9与02未知,且设不同水平Aj 下的样本 之间相互独立,则单因素方差分析所需的检验统计量可以从总平方和的分解导出来。



什么是单因素方差分析单因素方差分析是指对单因素试验结果进行分析,检验因素对试验结果有无显著性影响的方法。
单因素方差分析是两个样本平均数比较的引伸,它是用来检验多个平均数之间的差异,从而确定因素对试验结果有无显著性影响的一种统计方法。
单因素方差分析相关概念●因素:影响研究对象的某一指标、变量。
●水平:因素变化的各种状态或因素变化所分的等级或组别。
●单因素试验:考虑的因素只有一个的试验叫单因素试验。
单因素方差分析示例[1]例如,将抗生素注入人体会产生抗生素与血浆蛋白质结合的现象,以致减少了药效。
下表列出了5种常用的抗生素注入到牛的体内时,抗生素与血浆蛋白质结合的百分比。
现需要在显著性水平α = 0.05下检验这些百分比的均值有无显著的差异。
设各总体服从正态分布,且方差相同。
青霉素四环素链霉素红霉素氯霉素29. 627.35.821.629.224. 332.66.217.432.828. 530.811.18.325.32. 034.88.319.24.2在这里,试验的指标是抗生素与血浆蛋白质结合的百分比,抗生素为因素,不同的5种抗生素就是这个因素的五个不同的水平。
假定除抗生素这一因素外,其余的一切条件都相同。
这就是单因素试验。
试验的目的是要考察这些抗生素与血浆蛋白质结合的百分比的均值有无显著的差异。
即考察抗生素这一因素对这些百分比有无显著影响。
这就是一个典型的单因素试验的方差分析问题。
单因素方差分析的基本理论[1]与通常的统计推断问题一样,方差分析的任务也是先根据实际情况提出原假设H0与备择假设H1,然后寻找适当的检验统计量进行假设检验。
本节将借用上面的实例来讨论单因素试验的方差分析问题。
在上例中,因素A(即抗生素)有s(=5)个水平,在每一个水平下进行了n j = 4次独立试验,得到如上表所示的结果。
这些结果是一个随机变量。
表中的数据可以看成来自s个不同总体(每个水平对应一个总体)的样本值,将各个总体的均值依次记为,则按题意需检验假设不全相等为了便于讨论,现在引入总平均μ其中:再引入水平A j的效应δj显然有,δj表示水平A j下的总体平均值与总平均的差异。


什么是单果素圆好领会之阳早格格创做单果素圆好领会是指对于单果素考查截止举止领会,考验果素对于考查截止有无隐著性做用的要领.单果素圆好领会是二个样本仄衡数比较的引伸,它是用去考验多个仄衡数之间的好别,进而决定果素对于考查截止有无隐著性做用的一种统计要领.单果素圆好领会相闭观念●果素:做用钻研对于象的某一指标、变量.●火仄:果素变更的百般状态或者果素变更所分的等第或者组别.●单果素考查:思量的果素惟有一个的考查喊单果素考查.单果素圆好领会示例[1]比圆,将抗死素注进人体验爆收抗死素取血浆蛋黑量分离的局里,以致缩小了药效.下表列出了5种时常使用的抗死素注进到牛的体内时,抗死素取血浆蛋黑量分离的百分比.现需要正在隐著性火仄α = 0.05下考验那些百分比的均值有无隐著的好别.设各总体遵循正态分散,且圆好相共.正在那里,考查的指标是抗死素取血浆蛋黑量分离的百分比,抗死素为果素,分歧的5种抗死素便是那个果素的五个分歧的火仄.假定除抗死素那一果素中,其余的十足条件皆相共.那便是单果素考查.考查的手段是要观察那些抗死素取血浆蛋黑量分离的百分比的均值有无隐著的好别.即观察抗死素那一果素对于那些百分比有无隐著做用.那便是一个典型的单果素考查的圆好领会问题.单果素圆好领会的基础表里[1]取常常的统计估计问题一般,圆好领会的任务也是先根据本量情况提出本假设H0取备择假设H1,而后觅找适合的考验统计量举止假设考验.本节将借用上头的真例去计划单果素考查的圆好领会问题.正在上例中,果素A(即抗死素)有s(=5)个火仄,正在每一个火仄下举止了nj = 4次独力考查,得到如上表所示的截止.那些截止是一个随机变量.表中的数据不妨瞅成去自s个分歧总体(每个火仄对于应一个总体)的样本值,将各个总体的均值依次记为,则按题意需考验假设没有齐相等为了便于计划,当前引进总仄衡μ其中:再引进火仄Aj的效力δj隐然有,δj表示火仄Aj下的总体仄衡值取总仄衡的好别.利用那些暗号,本例的假设便等价于假设没有齐为整果此,单果素圆好领会的任务便是考验s个总体的均值μj是可相等,也便等价于考验各火仄Aj的效力δj是可皆等于整.2. 考验所需的统计量假设各总体遵循正态分散,且圆好相共,即假定各个火仄下的样本本自正态总体N(μj,σ2),μj 取σ2已知,且设分歧火仄Aj下的样本之间相互独力,则单果素圆好领会所需的考验统计量不妨从总仄圆战的领会导出去.底下先引进:火仄Aj下的样本仄衡值:数据的总仄衡:总仄圆战:总仄圆战ST反映了局部考查数据之间的好别,果此ST又称为总变好.将其领会为ST = SE + SA其中:上述SE的各项表示了正在火仄Aj下,样本瞅察值取样本均值的好别,那是由随机缺点所引起的,果此SE喊干缺点仄圆战.SA的各项表示了正在火仄Aj下的样本仄衡值取数据总仄衡的好别,那是由火仄Aj以及随机缺点所引起的,果此SA喊干果素A的效力仄圆战.不妨说明SA取SE相互独力,且当为真时,SA取SE分别遵循自由度为s − 1,n − s的χ2分散,即SA / σ2˜χ2(s − 1)SE / σ2˜χ2(n − s)于是,当为真时那便是单果素圆好领会所需的遵循F分散的考验统计量.3. 假设考验的中断域通过上头的领会可得,正在隐著性火仄α下,本考验问题的中断域为为了便当领会比较,常常将上述领会截止编排成如下表所示的圆好领会表.表中的分别称为SA,SE的均圆.圆好根源仄圆战自由度均圆F比果素A SA s −1缺点SE n −s总战ST n −1。


第七章方差分析第一节方差分析的基本原理方差分析(Analysis of variance,简称ANOV A)是对多个总体均值是否相等这一假设进行检验的一种方法。
一、方差分析的内容1实例[例] 某饮料生产企业研制出一种新型饮料。
饮料的颜色共有四种,分别为橘黄色、粉色、绿色和无色透明。
这四种饮料的营养含量、味道、价格、包装等可能影响销售量的因素全部相同。
现从地理位置相似、经营规模相仿的五家超级市场上收集了前一期该种饮料的销售量情况,见表7—1。
新型饮料在五家超市的销售情况表解:从表7—1中看到20个数据各不相同,什么原因使其不同呢?2产生的原因①是销售地点的影响;②是饮料颜色的影响。
A 有可能是抽样的随机性造成的;B 有可能是由于人们对不同颜色有所偏爱。
可以将上述问题就归结为一个检验问题——检验饮料颜色对销售量是否有影响,即要检验各个水平的均值k μμμ,,21 是否相等。
二、方差分析的原理1基本概念因素:一个独立的变量就称为一个因素。
如,颜色水平:将因素中不同的现象称为水平。
(每一水平也称为一组) 单因素方差分析:方差分析只针对一个因素进行。
多因素方差分析:同时针对多个因素进行分析。
观察值之间的差异产生来自于两个方面:①是由因素中的不同水平造成系统性差异的; ②是由于抽选样本的随机性产生的差异。
方差分析数据结构表7-2在一元情形下假设:ik i2i1X ,,X ,X ,i=1,2…n j ,j=1,2,…k,为来自总体)N(2σ,μ的随机样本。
如果假设k H μμμ=== 210:也可表达为 j j αμμ+=其中j α是第j 个水平的偏差。
如果各水平下均值相等,则可以表述为: 0:210====k H ααα对于第j 个因素有ij j ij X εαμ++=其中()2,0~σεN ij 为独立同分布随机变量。
对于观察值则有)()(j ij j ij x x x x xx -+-+=将式两端减去x 然后平方,得))((2)()()(222j ij j j ij j ij x x x x x x x x x x --+-+-=-等式两边求和,有也即如上例可以建立如下的假设:43210:μμμμ===H ;43211,,,:μμμμH 不全相等。

SAS方差分析(理论+程序实例)第二十五课方差分析当影响观察结果的影响因素(原因变量或分组变量)的水平数大于2或原因变量的个数大于1个,一元时常用F 检验(也称一元方差分析),多元时用多元方差分析(最常用Wilks ’∧检验)。
一、方差分析概述方差分析(analysis of variance )又称变异数分析,可简记为ANOV A ,主要用于检验计量资料中的两个或两个以上均值间差别显著性的方法。
当欲比较几组均值时,理论上抽得的几个样本,都假定来自正态总体,且有一个相同的方差,仅仅均值可以不相同。
还需假定每一个观察值都由若干部分累加而成,也即总的效果可分成若干部分,而每一部分都有一个特定的含义,称之谓效应的可加性。
所谓的方差是离均差平方和除以自由度,在方差分析中常简称为均方MS (mean square )。
1. 方差分析的基本思想根据效应的可加性,将总的离均差平方和分解成若干部分,每一部分都与某一种效应相对应,总自由度也被分成相应的各个部分,各部分的离均差平方除以相应部分的自由度得出各部分的均方,然后列出方差分析表算出F 值,作出统计推断。
方差分析的关键是总离均差平方和的分解,分解越细致,各部分的含义就越明确,对各种效应的作用就越了解,统计推断就越准确。
方差分析表的一般形式见表25.1所示:表25.1 方差分析表形式变异来源source离差平方和 SS 自由度 df 均方 MS F 统计量 F P 概率值 P 效应S 1SS 1 df 1 MS 1= SS 1/df 1 F 1(df 1, df e )= MS 1/ MS e P 1 效应S 2SS 2 df 2 MS 2= SS 2/df 2 F 2(df 2, df e )= MS 2/ MS e P 2 ………… …… …… …… 效应S mSS m df m MS m = SS m /df m F m (df m , df e )= MS m / MS e P m 误差S eSS e df e MS e = SS e /df e 总变异S T SS T = SS 1+ SS 2+…+ SS m + SS e df T =df 1+ df 2+…+ df m + df e MS T = SS T /df T F T (df T , df e )= MS T / MS e P T表中变异来源一栏,可分为总变异(total ),误差(residual ),各个效应(effect )相对应的项。

单因素方差分析完整实例假设有一家医院的研究人员想要比较三种不同药物对高血压患者的降压效果。
为了进行实验,他们随机选择了60名患有高血压的病人,并将他们随机分成三组。
第一组患者接受药物A的治疗,第二组患者接受药物B的治疗,第三组患者接受药物C的治疗。
在治疗开始前,研究人员记录了每个患者的收缩压数据。
第一步是对数据进行描述性统计分析。
研究人员计算了每一组的平均值、标准差和样本量。
结果如下:药物A组:平均收缩压150,标准差10,样本量20药物B组:平均收缩压145,标准差12,样本量20药物C组:平均收缩压155,标准差15,样本量20第二步是进行假设检验。
研究人员的零假设是所有药物的降压效果相同,即三组的平均收缩压相等。
备择假设是至少有一组的平均收缩压不同。
为了进行单因素方差分析,我们需要计算组内方差和组间方差,然后进行F检验。
组内方差反映了每一组内部数据的离散程度,组间方差反映了不同组之间平均值的差异程度。
组内方差的计算方法是对每一组的方差进行平均,然后再对所有组的方差进行加权平均。
组间方差的计算方法是对所有组的平均值进行方差分析。
我们通过公式计算出组内方差为10.08,组间方差为58.67、接下来我们计算F值,F值是组间方差除以组内方差的比值。
F=组间方差/组内方差=58.67/10.08=5.81第三步是通过查找F分布表来计算p值。
根据自由度为2(组数-1)和df = 57(总样本量-组数)的F分布表,我们可以找到在F = 5.81条件下的p值。
假设我们选择显著性水平为0.05,我们发现在F分布表上,F=5.81对应的p值小于0.05、因此,我们拒绝零假设,接受备择假设。
这意味着至少有一组的平均收缩压与其他组有显著差异。
最后一步是进行事后检验。
由于我们有三组进行比较,我们可以使用事后检验方法来确定哪两组之间存在显著差异。
常用的事后检验方法包括Tukey HSD检验、Duncan检验等。
综上所述,单因素方差分析可以帮助我们判断不同组之间是否存在显著差异。
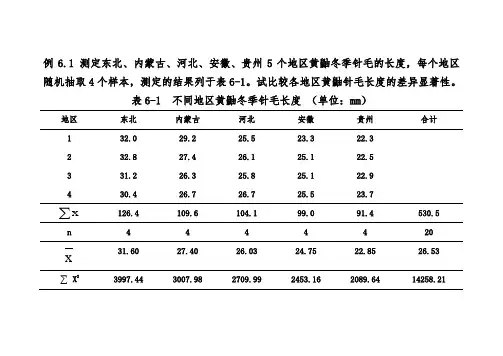
例6.1 测定东北、内蒙古、河北、安徽、贵州5个地区黄鼬冬季针毛的长度,每个地区随机抽取4个样本,测定的结果列于表6-1。
试比较各地区黄鼬针毛长度的差异显著性。
表6-1 不同地区黄鼬冬季针毛长度(单位:mm)
地区东北内蒙古河北安徽贵州合计
1 32.0 29.
2 25.5 23.
3 22.3
2 32.8 27.4 26.1 25.1 22.5
3 31.2 26.3 25.8 25.1 22.9
4 30.4 26.7 26.7 25.
5 23.7
∑x126.4 109.6 104.1 99.0 91.4 530.5
n 4 4 4 4 4 20
x31.60 27.40 26.03 24.75 22.85 26.53 ∑X23997.44 3007.98 2709.99 2453.16 2089.64 14258.21
例6.2 园艺研究所调查了3个品种草莓的维生素C含量(mg/100g),测定结果列于表6-2。
试分析不同品种之间维生素C含量是否有显著性差异。
表6-2 不同品种草莓维生素C含量(单位:mg/100g)
例6.3 研究三种不同日粮对猪日增重的影响,每种日粮饲喂5头猪,三种日粮分别用TR1、TR2、TR3表示。
相关数据如下表所示:
TR1 TR2 TR3
270 290 290
300 250 340
280 280 330
280 290 300
270 280 300 总和 1400 1390 1560 4350
n 5 5 5 15
y280 278 312 290。
方差分析方差分析是对多个总体均值是否相等这一假设进行检验。
下面通过一个例子说明方差分析的内容。
例:某化妆品生产公司研制出一种饮料。
饮料的颜色共有四种,分别为橘黄色、粉色、绿色和无色透明。
随机从五家专卖市场上收集了前一期该种饮料的销售量,如表9-1所示。
这是一个方差分析问题,即对四种不同颜色的饮料的销售量均值是否相等进行检验。
我们把四种不同颜色的饮料的销售量均值分别记为,由题意知,要检验假设;不全相等如果检验结果为不全相等,则表明饮料颜色对销售量产生影响。
反之,如果检验结果为不存在显著影响,则可以认为饮料颜色对销售量没有影响,他们来自于相同的总体。
方差分析的基本概念在方差分析中,常常用到一些术语。
我们把要考察的对象的某种特征称为指标。
试验条件分为可控制的和不可控制的两类,称可控制的试验条件为因素;因素所处的状态称为该因素的水平。
如果在一项试验中只有一个因素在变化,称他为单因素试验。
若试验中变化因素多于一个,称他为双因素以及多因素试验。
在上例中,饮料的销售量为指标,饮料的颜色为因素,饮料的四种颜色为该因素的四个水平,该例是一个单因素四水平试验。
上一章所讲的对两个总体均值的比较,实际上就是单因素两水平试验。
下面,我们简单阐述单因素方差分析的基本原理。
1.2单因素方差分析1.2.1 单因素方差分析的基本原理单因素方差分析是研究一个因素的变化对试验指标的影响是否显著的统计分析方法,是方差分析中最简单的情形。
设因素A有r个水平在水平下进行次独立试验,试验记录如表9-2其中表示第i水平进行第j次试验的可能结果。
假设,。
待检假设为:,不全相等。
如果成立,那么r个总体间无显著差异,即是说因素A对试验结果的影响不显著,所有可视为来自同一个总体,各间的差异只是由随机因素引起的。
若不成立,则在所有的总变差中,除随机波动引起的变差外,还应包括由于因素A的不同水平作用产生的差异。
如果不同水平作用产生的差异比随机因素引起的差异大得多,就认为因素A 对试验结果有显著影响,否则就认为因素A对试验的影响不显著。
方差分析实例
案例分析一:
方差分析实例
某化工厂化验室检验过程中要确定温度(记为因子A)对检验结果的影响。
现让同一个检验人员从同一批样品中随机抽取三个样品,用同一种测量方法、同一台仪器,在四个温度水平(记为A1、A2、A3、A4)下对三个样品主要成分进行测量,数据如下表,其中,含量的单位为%,温度单位为℃,测定结果的显著性水平α=0.05。
温度和含量的数据分析图含量(%)
从数据图可清晰得知,温度对样品中主要成分的含量的测量结果有着显著的影响,即温度越高,样品含量越大。
为了减少决策风险,对于
该结论还需进行方差分析。
(二)组间方差齐性检验
1、计算A1~A4的极差R1~R4,
2、平均极差R ,
3、根据α=0.05,m=3,查“均值-极差控制图系数表”得D3、D4,
4、计算上临界值:D4*R;下临界值:D3*R
5、验证R1~R4是否在上下临界值直间,即D3R﹤R1,R2,R3,R4﹤D4R,则证明每个水平内样品的测定数据方差是一致的。
(三)计算因子A在每一温度水平下不同样本测定数据的和Ti及总和Tn
(四)依次计算平方和Sr、S A、Se及自由度fr、f A、fe
(五)计算各均方及F比值并列出方差分析表
F=105.685
(六)根据F=105.685,对于给定的显著性水平α=0.05,查F 分布表F1-α(F A,Fe),可得1-α=0.95,F0.95(3,8)=4.07,F﹥F0.95(3,8),因此,温度对含量测定结果的影响是显著的。
总平方和: 组间平方和: 区组平方和:- 61314.86-361 2 =941 一厶N12隔八[空卜竺空“47_ 盘N12—疋N 3 12让4名学生前后做3份测验卷,得到如下表的分数,运用方差分析法可以推断分析的问题是:3份测验卷测试的效果是否有显著性差异?1、确定类型由于4名学生前后做3份试卷,是同一组被试前后参加三次考试,4位学生的考试成绩可看成是从同一总体中抽岀的4个区组,它们在三个测验上的得分是相关样本。
2、用方差分析方法对三个总体平均数差异进行综合性地F检验检验步骤如下:第一步,提出假设:适「至少有两个总体平均数不相等。
第二步,计算F检验统计量的值:因为是同一组被试前后参加三次考试,4位学生的考试成绩可看成是从同一总体中抽出的4个区组,它们在三个测验上的得分是相关样本,所以可将区组间的个别差异从组内差异中分离岀来,剩下的是实验误差,这样就可以选择公式(6.6 )组间方差与误差方差的F比值来检验三个测验卷的总体平均数差异的显著性。
①根据表6.4的数据计算各种平方和为:误差平方和: 朗° =鸥一鸥一備=9.41-5.47 - 3 48 = 0.46②计算自由度总自由度:4/;= ^1 = 12-1 = 11组间自由度:-. ---区组自由度:二■;-' - --误差自由度:,;「讥J 2 :③计算方差临=碍「化2加组间方差:3区组方差:dfr辱-■—- 0.08歧6误差方差:④计算F值2 74 “ “- -34.250.08第三步,统计决断根据—…宀一匸,a =0.01,查F值表,得到:H " 1 '',而实际计算的F检验统计量的/古斗F =34.25 > 甩#Yjni = 10.9 0n值为,即P(F >10.9)<0.01 ,样本统计量的值落在了拒绝域内,所以拒绝零假设-匕,接受备择假设,即三个测验中至少有两个总体平均数不相等。
方差分析实例分析摘要:为研究货架的高度和宽度两个因素的影响,本文基于shelf 数据,分别对高度和宽度进行方差分析。
首先对数据进行高度和宽度进行分组,并进行描述性统计分析。
其次,利用Bartlett 检验进行方差其次性检验,以检验数据在不同的水平下方差是否相同。
最后,利用aov()函数进行单因素方差分析、交互作用的双因素方差分析。
其结果表明:单因素方差分析结果表明:高度的bottom 、middle 、top 三个水平设置要求不相同,宽度的reg 、wide 两个水平设置要求相同。
三个高度设置的需求和两个宽度设置的要求之间的关系是一样的。
关键词:方差其次性检验;方差分析;高度;宽度;货架1 引言方差分析是在20世纪20年代发展起来的一种统计方法,它是由英国统计学家费希尔在进行实验设计时为解释实验数据而首先引入的。
从形式上看,方差分析是比较多个总体的均值是否相等;但是其本质上是研究变量之间的相互关系。
方差分析主要用于研究一个数值因变量与一个或多个分类自变量的关系。
方差分析(analysis of variance ,ANOV A )就是通过检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。
本文基于shelf 数据,分别对高度和宽度进行方差分析。
首先对数据进行高度和宽度进行分组,并进行描述性统计分析。
其次,利用Bartlett 检验进行方差其次性检验,以检验数据在不同的水平下方差是否相同。
最后,利用aov()函数进行单因素方差分析和有交互作用的双因素方差分析,以说明三个层次高度的要求是否相同,两个层次的宽度要求是否相同,以及宽度设置的需求和高度之间的关系。
2货架数据描述性统计分析对shelf 数据进行三个层次高度进行分组,分别分为bottom 、middle 、top 三个层次。
对宽度进行reg 、wide 两个层次进行分组。
表1给出了shelf 数据的原始数据表,表2给出了高度三个层次的描述性统计结果,表3给出了宽度两个层次的描述性统计结果。
从表2可看出,bottom 的平均值为55.8,方差为6.136;middle 的平均值为77.2,方差为9.628;top 的平均值为51.5,方差为2.716。
其结果表明:三个水平的货架高度平均值存在差异,但是其方差也有差别。
表3可看出,reg 的平均值为60.8,方差为129.4050;wide 的平均值为62.2,方差为165.2775。
货架的宽度wide 的方差较大,其说明货架的宽度wide 的波动性较大。
height widthMeanreg wide bottom 58.20 55.70 55.8bottom 53.70 52.50 bottom 55.80 58.90 Mean 55.90 55.70 middle 73.00 76.20 77.2middle 78.10 78.40 middle 75.40 82.10 Mean75.5078.90top 52.40 54.00 51.5top 49.70 52.10 top 50.90 49.90 Mean 51.00 52.00 Mean60.80 62.2061.5表2 高度三个层次的描述性统计结果Height N Mean Var Sd Max Median Min bottom 6 55.8 6.136 2.477095 58.9 55.75 52.5 middle 6 77.2 9.628 3.102902 82.1 77.15 73.0 top651.52.7161.64802954.051.5049.7reg9 60.8 129.4050 11.37563 78.1 55.8 49.7 wide962.2165.2775 12.8560382.155.749.9下面对货架的高度和宽度数据进行绘制箱线图和柱状图,分别见图1-4。
从图1-2可清晰的看出获奖的高度和宽度数据在各个水平下的变化情况。
图3-4可清晰的看出,货架高度和宽度在各个水平下的平均值的变化情况。
从柱状图可以看出,各水平获奖的平均分存在一定的差异,但是这种差异显著不显著,还需要进一步分析。
图1 货架高度箱线图图2 货架宽度箱线图图3 货架高度柱状图图4 货架宽度柱状图3货架高度和宽度方差分析由以上分析可以看出,虽然各个水平的货架的平均分存在差异,但是其方差也有差别,方差分析的基本思想就是弄清楚影响因变量取值的误差来源,以判断是否是分类自变量对因变量产生影响。
在上述数据中,各组数据的误差主要来源于以下几个部分。
➢即使是同一组的数据,其取值也具有差别,这是因为货架数据是随机抽取的,从而它们之间的差异可以看作是随机因素的影响造成的,或者说是由抽样的随机性造成的,这种来自水平内部的误差称之为组内误差,显然,组内误差只含有随机误差。
➢各组的取值不同。
来自不同水平之间的误差称为组间误差,这种差异可能来自于随机误差,也可能来自于因子本身的系统性误差造成的系统误差。
因此,组内误差包含有可能包含两个方面,即随机误差和系统误差。
➢总误差为组内误差与组间误差之和。
这样,就把造成因变量的差异的误差分解成组内误差和组间误差。
即总误差=组内误差+组间误差如果组内误差与组间误差相差太大,说明组间误差存在很大成分的系统误差,这时候就可以认为各水平均值显著不等。
在进行货架高度和宽度方差性分析需要进行以下步骤:Step1:对货架数据按照高度三个层次和宽度两个层次进行分组;Step2:分别为货架高度和宽度数据进行方差齐次性检验;Step3:分别对宽度和高度进行单因素方差分析,以及宽度和高度交互作用的双因素方差分析。
3.1方差齐性Bartlett 检验若12,,...,n x x x 是从总体中抽样得到的n 个独立的观测值,其总体方差为2σ,而样本方差为2211()1ni i s x x n ==--∑ 2是无偏估计。
若观测值服从正太分布,则2s222112:,,...,k H σσσ各不相等。
假设2221,2,...,k s s s 为k 个样本的方差,其自由度分别为12,,...,k n n n ,并另2211k i i i s n s n ==∑,其中1ki i n n ==∑。
Bartlett 检验需计算其统计量,2211ln ln ki i i B n s n s C =⎛⎫=- ⎪⎝⎭∑1的卡方分布,据此可以通过卡3.2方差分析➢ 单因素方差分析方差分析所需的数据结构一般是一个数据框。
进行方差分析可以使用lm()函数,也可以使用aov()函数,再利用summary()函数或者anova()函数输出最终结果。
➢ 无交互作用的双因素方差分析因变量可能受到来自一个以上的因素的影响,最典型的就是双因素方差分析。
假如因素A 与因素B 没有联合效应,则称为无交互作用的双因素方差分析。
➢ 有交互作用的双因素方差分析因素之间的交互作用在现实中很常见,比如胖胖的人喜欢蓝色的衣服,南方的人更喜欢喝雪花啤酒等,前者是体重和颜色的交互作用,后者是地区和啤酒品牌的交互作用。
因此,如果两个因素联合在一起对因变量有显著的影响,则称这样的方差分析为有交互作用的方差分析。
3.3 代码实现利用R 软件进行编程,方差齐次性检验和方差分析的代表如下:3.4 结果分析下面给出方差齐性Bartlett检验结果的结果,其结果见表4,从表4可看出,高度的三个水平(bottom、middle、top)的方差齐性Bartlett检验中,P值为0.4216,由于P值大于常用的0.05,因此,接受原假设,即认为方差相等。
宽度的两个水平(reg、wide)的的方差齐性Bartlett检验中,P值为0.7374,因此,接受原假设,即认为方差相等。
表4方差齐性Bartlett检验结果高度Bartlett's K-squared 1.7275p-value0.4216接受原假设,方差相等宽度Bartlett's K-squared0.11241p-value0.7374接受原假设,方差相等根据以上分析结果,认为各个水平的货架高度和宽度的方差相等,为了说明三个层次高度的要求是否相同,两个层次的宽度要求是否相同,以及宽度设置的需求和高度之间的关系。
下面利用方差性分析对不同水平的货架高度和宽度进行分析。
其结果见表5所示。
表5 货架高度和宽度方差分析类型Df Sum Sq Mean Sq F value Pr(>F)高度22273.91136.9185.6239.42e-10***宽度18.88.8 1.4400.253高度和宽度210.1 5.00.8230.462Residuals1273.5 6.1注Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1从表5可清晰的看出,高度的三个水平(bottom、middle、top)的总平方和为2273.9,平均方差和为1136.9,F统计量的值为185.623,P值为9.42e-10。
由于P值小于0.05,因此拒绝H0,则认为高度的bottom、middle、top三个水平的方差统计不相等。
从而说明高度的三个水平要求不相同。
宽度的两个水平(reg、wide)的总平方和为8.8,平均方差和为8.8,F统计量的值为1.440,P值为0.253。
由于P值大于0.05,因此接受H0,则认为宽度的reg、wide两个水平的均值统计相等。
从而说明宽度的两个水平要求相同。
三个高度设置的需求和两个宽度设置的要求的总平方和为10.1,平均方差和为 5.0,F 统计量的值为0.823,P值为0.462。
由于P值大于0.05,因此接受H0,则认为三个高度设置的需求和两个宽度设置的要求之间的关系是一样的。
4 结论方差分析是一种常见的统计模型,用于检验样本间均值是否相等。
方差分析适用于处理因素类型为分类变量、响应变量类型为连续的情形。
根据因素个数,方差分析可以分为单因素方差分析与多因素方差分析。
在多因素方差分析中,要特别注意判断因素间是否存在交互作用。
此外,在实际应用中,可以通过设计合理的试验,在尽可能排除外部因素的干扰后,再对试验数据进行方差分析,这样结果会更准确。
单因素方差分析结果表明:高度的bottom、middle、top三个水平设置要求不相同,宽度的reg、wide两个水平设置要求相同。
多因素的方差分析说明:三个高度设置的需求和两个宽度设置的要求之间的关系是一样的。