下载文档原格式
竭诚为您提供优质文档/双击可除wps表格规划求解篇一：excel规划求解功能操作说明excel规划求解功能操作说明以microsoftexcel20xx为例，说明使用excel的求解线性规划问题功能的使用方法。
一、加载规划求解功能1.点击【工具】按钮，在下拉菜单中选择【加载宏】功能。
2.在弹出的【可加载宏】选项卡中勾选【规划求解】，点击确定按钮。
此时，【工具】下拉菜单中增加规划求解功能，表示加载成功。
二、构造表格excel表格并填入各项数据以教材18页【例题2-8】为例，构造表格如下：1.录入约束条件系数约束条件（1）为5x1+x2-x3+x4=3，则在约束系数的第一行的x1,x2,x3,x4,x5，限制条件，常数b列下分别录入5,1，-1,1,0，=，3如下图所示。
约束系数区的第二行录入约束条件（2）的系数、限制符号及常数b，即-10,6,2,0,1，=，2；约束系数区的第三行录入约束条件（3）（x1≥0）的系数、限制符号及常数b，即1,0,0,0,0，≥，0；约束系数区的第四行录入约束条件（4）（x2≥0）的系数、限制符号及常数b，即0,1,0,0,0，≥，0；约束系数区的第五行录入约束条件（5）（x3≥0）的系数、限制符号及常数b，即0,0,1,0,0，≥，0；约束系数区的第六行录入约束条件（6）（x4≥0）的系数、限制符号及常数b，即0,0,0,1,0，≥，0；约束系数区的第七行录入约束条件（7）（x5≥0）的系数、限制符号及常数b，即0,0,0,0,1，≥，0。
如下图所示。
2.录入目标函数系数目标函数为maxz=4x1-2x2-x3，则在目标函数的x1,x2,x3,x4,x5列下分别录入4，-2，-1,0,0，如下图所示。
3.录入约束条件的计算公式双击约束条件（1）行的“总和”单元格，录入以下内容：“=b3*b12+c3*c12+d3*d12+e3*e12+F3*F12”说明：录入的内容即是约束条件（1）的计算公式，其中“b3*b12”代表5x1;“c3*c12”代表1x2；“d3*d12”代表-1x3；“e3*e12”代表1x4；“F3*F12”代表0x5。
单纯形表法详细讲解
单纯形法是一种求解线性规划问题的数学方法。
以下是其详细步骤：
1. 确定初始基可行解：一般采用取松弛变量的方法来获得初始基可行解，从而得到对应的单位矩阵作为基。
2. 判断是否满足最优解条件：单纯形法从可行域中的一个点开始，判断该顶点是否为最优解。
如果不是，就寻找另一个目标函数值更优的顶点。
3. 迭代优化：通过单纯形表判断出顶点是否为最优解，如果线性规划问题没有最优解，则继续迭代优化，直到找到最优解或确定问题无解。
4. 确定最优解：在单纯形表中，理解其系数矩阵、基、基向量、非基向量和基变量等基本概念，从而确定最优解。
5. 确定换入变量和换出变量：在单纯形表中，如果发现非基变量的系数大于零，则可以通过增加这些变量的值来使目标函数增加。
由于每个变量都大于零，对于某个变量增加是有所限制的，如果该变量过大，由于其他限制条件，会导致其他变量小于零。
因此，应该让该变量一直增大，直到有一个其他变量刚好等于0为止，那么这个变量就被换出基。
6. 进行高斯行变换：使用第4行对各行进行高斯行变换，使得二列第四行中的每个x都变成零，也包括c2。
如需更多关于单纯形法的信息，可以咨询数学专家或查阅相关文献资料。
EXCEL规划求解功能操作说明Excel规划求解功能是Excel内置的解决最优化问题的工具，可用于线性规划、整数规划、非线性规划等诸多领域。
该功能十分便捷灵活，可以帮助用户快速找到问题的最优解。
一、添加求解功能1.打开Excel表格，点击“文件”>“选项”>“加载项”。
2.在弹出的窗口中选择“Excel加载项”>“转到”>“excel加载项”>“管理”。
在“可用的加载项”中勾选“求解器”并关闭窗口。
3.返回Excel表格，在数据选项卡中选择“分析”>“求解”，弹出求解对话框。
二、建立规划模型1.确定目标：需要确定最终要达到的目标或绩效指标，例如最大化利润、最小化成本等。
2.确定决策变量：需要确定影响目标的变量，例如销售量、成本等。
3.建立约束：需要确定影响决策变量的条件，例如材料成本、生产时间等。
注意约束需要用等式、不等式等数学形式表示。
例如，在一个玩具生产厂家的例子中，有以下规划问题：在有限的资源下，最大化玩具的利润。
目标：最大化利润。
决策变量：生产每种玩具的数量。
三、设置求解参数1.目标单元格：选择Excel表格中目标单元格，该单元格包含要优化的方程式。
4.变量单元格必须满足约束：勾选此项，保证变量单元格满足约束条件。
5.求解方法：选择要使用的求解算法，包括线性规划、非线性规划和整数规划等。
1.点击“求解”按钮，系统会自动寻找目标单元格、变量单元格和约束单元格区域。
2.系统执行计算，找到最优解并将其展示在新的单元格区域中。
3.若求解成功，单击“继续”将结果保存在Excel表中。
总之，利用Excel规划求解功能，用户可以通过建立规划模型，设置求解参数和运行求解功能轻轻松松地优化各种最优化问题。
利用Excel求解线性规划问题线性规划问题的求解有很多方法，也有很多工具。
比如常用的Matlab、Lingo，记得参加数学建模的时候就是用的Lingo解决线性规划问题的。
本文主要讲解如何使用Excel求解线性规划问题，Excel本身是没有计算线性规划问题能力的，因此我们首先要加载相应的宏定义。
一、加载宏定义（不同版本的加载方式有所不同）：Excel 2003：单击“工具”菜单，然后单击“加载宏”，选择“规划求解”点击确定。
Excel 2007：方法一：用快捷键。
先按Alt+T，再按I键，即可打开加载宏对话框。
方法二：单击“Office按钮→Excel 选项→加载项”，确保“管理”右侧下拉列表中的选项是“Excel 加载项”，单击“转到”按钮即可。
Excel 2010：直接在功能区中选择“开发工具”选项卡，在“加载项”组中单击“加载项”命令，选择“规划求解”点击确定。
注意：如果功能区中没有“开发工具”选项卡，可以通过自定义功能区来显示“开发工具”选项卡：单击“文件→选项→自定义功能区”，然后在右侧区域中勾选“开发工具”并单击“确定”。
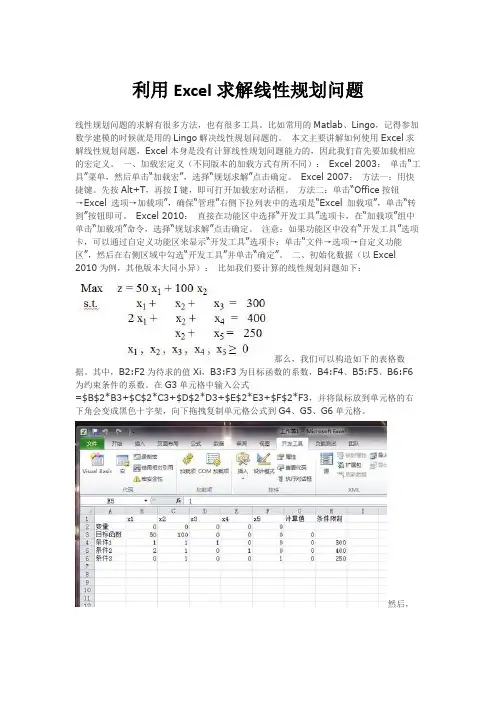
二、初始化数据（以Excel 2010为例，其他版本大同小异）：比如我们要计算的线性规划问题如下：那么，我们可以构造如下的表格数据。
其中，B2:F2为待求的值Xi，B3:F3为目标函数的系数，B4:F4、B5:F5、B6:F6为约束条件的系数。
在G3单元格中输入公式=$B$2*B3+$C$2*C3+$D$2*D3+$E$2*E3+$F$2*F3，并将鼠标放到单元格的右下角会变成黑色十字架，向下拖拽复制单元格公式到G4、G5、G6单元格。
然后，单击“数据”选项卡，单击“规划求解”打开“规划求解参数”对话框。
∙修改“设置目标”为$G$3,即最优解下目标函数的值z所在的单元格。
∙选择是求最大值，还是最小值。
∙“可变单元格”指的是最优解取值变量所在的单元格。
∙“遵守约束”指的是约束条件中对各变量的约束情况。
线性规划问题的两种求解方式线性规划是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支，它是辅助人们进行科学管理的一种数学方法。
线性规划所研究的是：在一定条件下，合理安排人力物力等资源，使经济效果达到最好。
一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题。
解决线性规划问题常用的方法是图解法和单纯性法，而图解法简单方便，但只适用于二维的线性规划问题，单纯性法的优点是可以适用于所有的线性规划问题，缺点是单纯形法中涉及大量不同的算法，为了针对不同的线性规划问题，计算量大，复杂繁琐。
在这个计算机高速发展的阶段，利用Excel建立电子表格模型，并利用它提供的“规划求解”工具，能轻松快捷地求解线性模型的解。
无论利用哪种方法进行求解线性规划问题，首先都需要对线性规划问题建立数学模型，确定目标函数和相应的约束条件，进而进行求解。
从实际问题中建立数学模型一般有以下三个步骤；1、根据所求目标的影响因素找到决策变量；2、由决策变量和所求目标的函数关系确定目标函数；3、由决策变量所受的限制条件确定决策变量所要满足的约束条件。
以下是分别利用单纯形法和Excel表格中的“规划求解”两种方法对例题进行求解的过程。
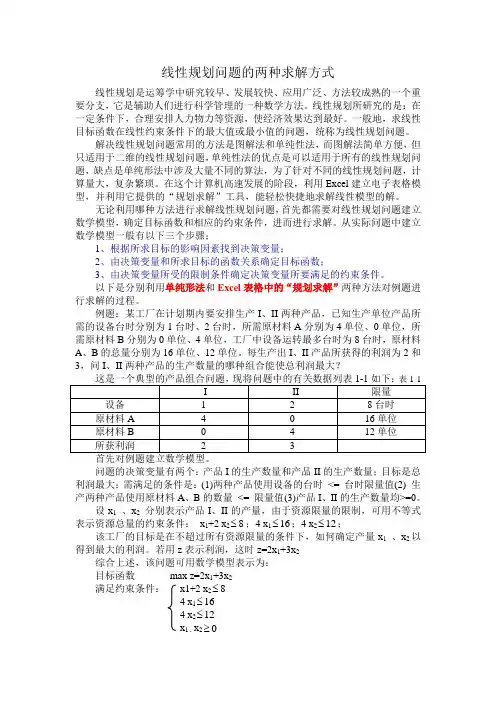
例题：某工厂在计划期内要安排生产I、II两种产品，已知生产单位产品所需的设备台时分别为1台时、2台时，所需原材料A分别为4单位、0单位，所需原材料B分别为0单位、4单位，工厂中设备运转最多台时为8台时，原材料A、B的总量分别为16单位、12单位。
每生产出I、II产品所获得的利润为2和3，问I、II两种产品的生产数量的哪种组合能使总利润最大？问题的决策变量有两个：产品I的生产数量和产品II的生产数量；目标是总利润最大；需满足的条件是：(1)两种产品使用设备的台时<= 台时限量值(2) 生产两种产品使用原材料A、B的数量<= 限量值(3)产品I、II的生产数量均>=0。
表格法解线性规划问题【教学目标】知识目标：理解用表格法解线性规划问题的方法和步骤.能力目标：通过例子详细地介绍了表格法解线性规划问题的过程，并引入了线性规划标准型的概念，归纳总结了表格法解线性规划问题的步骤.【教学重点】理解用表格法解线性规划问题的方法和步骤.【教学难点】理解用表格法解线性规划问题的方法和步骤.【教学设计】1、表格法也称单纯形法，是解线性规划问题的常用方法，使用该方法时，首先要将一般的线性规划问题化为标准型.在教材中给出了化标准型的方法.讲解时一定要注意b≥0以及变量的非负性.2、表格法解线性规划问题的过程，教材中归纳为五个步骤，这实际上是一个算法，可以利用前面介绍过的算法知识来学习.3、初始表格中初始解组的确定是关键，一般可取松弛变量，但当标准型中没有这样的变量满足初始解组的要求时，通常要通过添加人工变量来解决，本教材没有就这方面的问题进行深入讨论（一般的运筹学教材中都可找到该容）.4、表格在转换时（通常称为转轴），教材中提到用加减消元法来转轴.教师可就这部分容作适当的讲解.5、由于通常的表格转换要进行多次，而表头部分是不变的，因此可以将多表格合并起来，具体样式可参见5.5节表5-16.【教学过程】5.3.1线性规划问题的标准形式求线性规划问题的图解法虽然直观简便，但对多于两个变量的情况就不能适用了，对于多于两个决策变量的线性规划问题，可以用什么方法呢？下面介绍一种用表格的方法来求解线性规划问题的解. 表格法是根据单纯形法而专门设计的一种计算表格.单纯形法（Simple Method ）是求解线性规划问题的主要方法，该法由丹赛（Dantzig ）于1947年提出，后经过多次改进而成，是求解线性规划问题的实用算法.由上节的叙述可知，如果线性规划问题的最优解存在，则必定可以在其可行解集合的顶点（极点）中找到．因此，寻求一个最优解就是在其可行域的各个极点中搜索最优点.单纯形法实质上是一个迭代过程，该迭代即是从可行域的一个极点移到另一个近邻的极点，直到判定某一极点为最优解为止. 为使用表格法，首先介绍线性规划问题的标准形式.一般的线性规划问题中目标函数可能是求最大(或最小)值，而线性约束条件中可能是线性方程，也可能是线性不等式，约束条件中约束方程（或不等式）的个数也未必就比决策变量的个数少，这些问题对于线性规划的求解，带来极大的不便，为此，引入下述标准形式：求目标函数最大值 n n x c x c x c x c Z ++++=...m ax 332211 (用和式表示为j j nj x c Z ∑==1max )⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≥=+++=+++=+++0,...,0,0.....................2122112222212111212111n mn mn m m n n n n x x x b x a x a x a b x a x a x a b x a x a x a 满足用和式表示为满足⎪⎩⎪⎨⎧=≥==∑=),,3,2,1(,0),,3,2,1(,1n j x m i b x a j i i ij nj 其中，),,2,1;,,3,2,1(,,n j m i c b a j i ij ==各都是确定的常数，),,2,1(n j x j =是决策变量，Z 是目标函数，ij a 叫做技术系数，i b ≥0（),2,1m i =叫做资源系数，j c 叫做目标函数系数. 特点：1、目标函数为极大化；2、除决策变量的非负约束外，所有的约束条件都是等式，且右端常数均为非负；3、所有决策变量均非负．如果根据实际问题建立起来的线性规划模型不是标准型的，可以用下述方法将它化为标准型.（1）若目标函数是n n x c x c x c x c Z ++++=...m in 332211可令,'z z -=将目标函数转化为)...(max 332211'n n x c x c x c x c Z ++++-= （2）若约束条件不等式中是“≤”,可在不等式左边加上非负变量，将不等式转化为方程.如2126x x +≤180可转化为,18026321=++x x x 其中3x ≥0.这里的3x 叫做松弛变量. 表示没有用完的资源.（3）若约束条件不等式是“≥”，可在不等式左边减去非负变量，将不等式转化为等式方程，如2122x x +≥10可转化为1022421=-+x x x ， 其中，4x ≥0.这里的4x 叫做多余变量，表示不存在的资源.一般地，松弛变量和多余变量的目标函数系数为0.（4）若有一个变量k x 没有非负约束（叫做自由变量），可令s l k x x x -=，其中l x ≥0，s x ≥0. 知识巩固例1 将5.1节问题1中的线性规划问题化为标准型约束条件 ⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+≤+0,0210534001041802621212121x x x x x x x x 求目标函数最大值 212231m ax x x Z +=解 分别对前三个约束条件引入松弛变量543,,x x x ，得标准型：约束条件 ⎪⎪⎩⎪⎪⎨⎧=≥=++=++=++.5,3,2,1,02105340010418026521421321 j x x x x x x x x x x j 求目标函数最大值 212231m ax x x Z +=5.3.2表格法下面我们通过实例来介绍表格法.首先要列出初始表格．为了得到初始表格，我们分几步来说明： 先把标准型中的约束条件方程转换成表格（表5.4）的形式． 如:5.1问题1转化的结果为：⎪⎪⎩⎪⎪⎨⎧=≥=++++=++++=++++.5,,2,1,02100053400001041800026543215432154321 j x x x x x x x x x x x x x x x x j 列成表格为： 表5.4(表格中的列数为变量个数加1，行数为方程个数加1) 从约束方程中，很容易得到，当01=x ，02=x 时，1803=x ，4004=x ，2105=x ，显然这是一组可行解（我们把它叫作初始解组），将其中三个取非0值的变量543,,x x x 列成一列对应地加在上表的最左侧，然后再在所得表的左侧添加一列对应于该初始解组变量的目标函数系数，在表的上侧添加一行对应于各变量的目标函数系数，得如下表：其中在初始解组中的变量必须满足在对应行的约束条件方程中系数为1，而同列其他系数为0，（如果约束条件方程中不满足这要求，可以通过对线性约束条件方程作加减消元法而得到.）再在上表的基础上，增加1行(叫做检验数行j σ)和1列(叫做比值列i θ)得下面形式：按下面的计算公式在表中依次填上检验数行j σ和比值列i θ,其中检验数计算公式,1ij mi i j j a c c ∑=-=σ例如31=j σ，即为1x 所在列的目标函数系数行中的1c 值减去该列系数与第一列初始解组的目标函数系数的对应乘积和，31)304060(311=⨯+⨯+⨯-=σ.选取检验数最大的正数所在列(记作k 列，表中用[ ]表示)然后计算比值i θ．比值的计算公式,0,>=ik ik i i a a b θ，例如61801=θ. 选取最小的i θ值，记所在行为i 行(表中用[ ]表示)，如下表(1=i ） 最后填上目标函数Z 值一格，其中目标函数Z 为第一列B C 与b 所在列对应乘积和． 得下表：这样我们得到了初始表格（表5.7）显然，前面的初始解组并不能产生最优目标函数值，因此，必须要对初始解组中的变量进行替换，以求更好的解.通常，我们按下述方法进行变量的替换：根据上面所选的第k列第i行(如上表中3x所在行和1x所在列，我们将两者的交叉点用( )表示)，对初始解组作调整，将变量k x换入，替代第i行中的初始变量(即表中换入1x，换出3x)，根据表格法的要求，必须同时将换入变量k x在( )中的系数通过加减消元法化为1，且同列其他系数为0，而初始解组中其他未换出变量所在列的系数不变，通常可用加减消元法来求得．下面我们具体来说明表格的转换．框中<A>行除以6得<A/>行；<B>行减<A/>×4得<B/>行；<C>行减<A/>×3得<C/>行(表5.8转换到表5.9)．表5.8表5.9再依次填上检验数行j σ和比值列i θ，得下表(表5.10)．表5.10如果检验数全为非正数，那么，所得解就是最优解．否则，继续按前方法修改可行解，直至不能继续为止．显然，上表中2x 换入，变量5x 换出．转下表(表5.11)．表5.11因为所有的检验数j σ≦0，故当前可行解201=x ，302=x ，03=x ，04=x ，05=x 为最优解，删去松弛变量，即得原线性规划最优解为201=x ，302=x ，最优值为 Z=1280．通过上面的例子，可以归纳一般的表格法的计算步骤如下： 第一步：建立初始表格．第二步：检查：若所有的σj ≤0，则当前可行解即为最优解；否则转入(3)．第三步：检查：若存在σk >0,且a ik ≤0，(i =1,2,…,m )，则无最优解；否则转入(4) ．第四步：选取检验数行中最大的正数所在的列，(记作k 列，表中用[ ]表示)然后计算比值i θ，比值的计算公式0,>=ik ikii a a b θ．选取最小的i θ值，记所在行为i 行(表中用[ ]表示)，确定x k ，将x k 换入，将松弛变量x h 换出，用加减消元法化x k 的系数a ik 为1，且同列其他系数为0．以x k 取代x h 得新表，转入(2). 巩固知识 典型例题例2 用表格法解5.1节中的例1：某工厂用钢与橡胶生产3种产品A 、B 、C ,有关资料如表5.3所示.已知每天可获得100单位的钢和120单位的橡胶，问每天应按排生产A 、B 、C 三种产品各多少，能使总利润最大？试写出问题的线性约束条件和目标函数.表5.3则可得约束条件⎪⎩⎪⎨⎧≥≥≥≤++≤++0,0,012023310032321321321x x x x x x x x x目标函数为321244540m ax x x x Z ++= 解 引入松弛变量54,x x ，得标准型：321244540m ax x x x Z ++=满足 ⎪⎩⎪⎨⎧=≥=+++=+++5,3,2,1,01202331003253214321 j x x x x x x x x x j列初始表格(表5.12)．表5.12因为2σ 为最大正数，转下表(表5.13)．表5.13将1x 换入，5x 换出，得表5.14．表5.14因为所有的检验数j σ≦0，故当前可行解201=x ,202=x ,03=x ，04=x ，05=x 为最优解，删去松弛变量，即得原线性规划最优解为201=x ,202=x ,03=x ，目标函数最优值为 1700=Z .。
