当前位置：文档之家 › 18.2二元线性规划问题的图解法2

18.2二元线性规划问题的图解法2

  • 格式：ppt
  • 大小：403.00 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

线性规划的标准化及图解法 ppt课件

线性规划的标准化及图解法 ppt课件

15
将线性规划化成标准形式
1.若目标函数求极小：
设目标函数为
Min f = c1x1 + c2x2 + … + cnxn 则可以令z ＝ -f
求极大化问题化成求下面的极小化问题. 即
Max z = -c1x1 - c2x2 - … - cnxn
但必须注意，尽管以上两个问题的最优解相 同，但他们最优解的目标函数值 却相差一个符号，即
设A、B型电机各生产x1,x2台，x1,x2称为决策变量。
利润函数600x1+400x2
2x1+3x2 ≤ 100 4x1+2x2 ≤ 120
约束条件
目标函数
2020/12/17
ppt课件
2
精品资料
• 你怎么称呼老师？
• 如果老师最后没有总结一节课的重点的难点，你 是否会认为老师的教学方法需要改进？
在标准形式中，要求右端项必须每一个分 量非负。当某一个右端项为负时，如
• 要求维生素B的含量大于5，有 0.8x1+0.3x2+0.9x3+0.7x4 5
• 要求维生素C的含量大于10，有 1.2x1+0.9x2+0.7x3+1.5x4 10
• 目标是成本最小，有 Min 5x1+6x2+6x3+7x4
2020/12/17
ppt课件
10
线性规划的应用模型
于是可得如下的线性规划的模型：
18
将线性规划化成标准形式
例2.：将以下线性规划问题转化为标准 形式
解：第一个约束引入松弛变量x4, 第二个约束引入剩余变量x5
2020/12/17
ppt课件

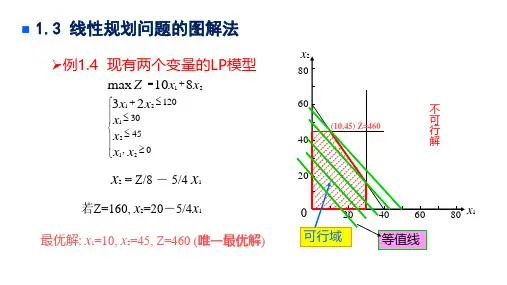
线性规划问题的图解法

线性规划问题的图解法
第二十四页，共51页。
单纯形法的计算(jìsuàn)步骤
单纯形法的思路(sīlù)
找出一个(yī ɡè)初始可行解
4x1
16
可行(kěxíng)域
单纯形法的进一步讨论(tǎolùn)－人工变量法
第四十三页，共51页。
单纯形法的计算(jìsuàn)步骤
是否最优 故人(gùrén)为添加两个单位向量，得到人工变量单纯形法数学模型：
量作为换出变量。
L
min
bi a ik
a ik
0
第二十九页，共51页。
单纯形法的计算(jìsuàn)步骤
③ 用换入变量(biànliàng)xk替换基变量(biànliàng)中的换出变量 (biànliàng)，得到一个新的基。对应新的基可以找出一个新的基可 行解，并相应地可以画出一个新的单纯形表。
： X (1) K和X (2) K
X X (1) (1 ) X (2) (0 1)
则X为顶点(dǐngdiǎn).
(wèntí)
的 几
第四页，共51页。
凸组合(zǔhé)：
意线 义性
规 划 问 题 的 几 何
设X（1) ,..., X (k)是n维向量空间中的k个点,
若存在1,..., k ,且0 i 1, i 1,2,..., k,
A
1 域2 3
D
| E|
45
4 x2 16 x1 + 2x2 8
|||| 6789
x1
第九页，共51页。
❖图解法
目标(mùbiāo)函数 Max Z = 2x1 + 3x2
x2 9—
8—
7—
6—
5—
4—

线性规划问题的图解法

线性规划问题的图解法
这种情况通常称为无“有限最优解” 或“最优 解无界”。
如果一个实际问题抽象成像例1-4这样的线性规 划模型，比如是一个生产计划问题，其经济含义就是 某些资源是无限的，产品的产量可以无限大。此时应 重新检查和修改模型，否则就没有实际意义。
注意，对于无界可行域的情况，也可能有唯一
最优解或无穷多个最优解。
x1 2x2 ≤8 代表一个半平面
其边界: x1+2 x2 =8
x1+2 x2 =8 及x1，x2 ≥0
x2 B
Q4
3
2
x12x28
△ AOB
点A、B 连线AB △A0B
1
A x1
0 1 2345678
经济含义 ？
点A(8,0)：
全部的设备都用来生产Ⅰ产品而不生产Ⅱ 产品,那么Ⅰ产品的最大可能产量为8台,计 算过程为： x1+2×08 x18
maxZ2x13x2
x1 2 x2 ≤ 8
4

4
x1 x2
≤ ≤
16 12
x 1 , x 2 ≥ 0
x2 B 4x1 16
3E F
2
1
4x2 12
C
最优点
x12x28
A
D
x1
0
1 2345 678
结果
有唯一最优解 可行域是一个非空有界区域
讨论 可行域有几种可能 ? 解有几种可能 ?
结果表明，该线性规划有无穷多个 最优解－－线段AB上的所有点都是最优
点，它们都使目标函数取得相同的最大值 Zmax=14。
无界解
maxZx1x2

x
2
1
x
1
x2

线性规划问题的图解法

线性规划问题的图解法
bm 0 1 am ,m 1 amn m
j
0 0 j c j c i a ij
bi 其中： i a kj 0 a kj
单纯形法的计算步骤
例1.8 用单纯形法求下列线性规划的最优解
max Z 3 x1 4 x 2 2 x1 x 2 40 x1 3 x 2 30 x , x 0 1 2
A
0
E
| 5
| 6
| 7
| 8
| 9
x1
图解法
9— 8—
目标函数 Max Z = 2x1 + 3x2
约束条件 x1 + 2x2 8
4x1 16 4x2 12 x1、 x2 0
x2
7—
6— 5—
4x1 16
C 4 x2 16
4 —B
3— 2— 1—
D
| 1 | 2 | 3 | 4
4—
3— 2— 1— 0
x1
图解法
9— 8—
目标函数 Max Z = 2x1 + 3x2
约束条件 x1 + 2x2 8
4x1 16 4x2 12 x1、 x2 0
x2
7—
6— 5—
4x1 16 4 x2 12 x1 + 2x2 8
4—
3— 2— 1— 0
可行域
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
x2
X1 + 1.9X2 = 11.4 (≤)
8=5X1+4X2 此点是唯一最优解 （ 0， 2）
D
43=5X1+4X2
可行域

§18.2二元线性规划问题的图解法(2)

§18.2二元线性规划问题的图解法(2)

时,z的最大值和最小值.
可行域上的最优解
y
A: (5.00, 2.00) B: (1.00, 1.00) C: (1.00, 4.40)
x 4 y 3 1.先 作 出 3 x 5 y 25 x 1 所表示的区域 .
C
5
2.作直线 0 : 2 x y 0 l
（3）求：通过解方程组求出最优解；
（4）答：作出答案。
可行域上的最优解
课后作业
1、课本 2、练习册 P99 习题 T3 P92 解答题 T5
2x+y=300 A 125
300x+900y=112500
C x+2y=250 150 B 250
Hale Waihona Puke Ox答案：当x=0,y=0时，z=300x+900y有最小值0.
当x=0,y=125时，z=300x+900y有最大值112500.
可行域上的最优解
练习2、已知 y x 1 x - 5y 3 5x 3y 15 求z=3x+5y的最大值和最小值。
可行域上的最优解
5x+3y=15 y
y=x+1
5
B(3/2,5/2)
1
X-5y=3
O
-1
1 5
x
A(-2,-1)
Z max 17; Z min 11
可行域上的最优解
小 结
解线性规划问题的步骤：
（1）画：画出线性约束条件所表示的可行域； （2）移：在线性目标函数所表示的一组平行 线中，利用平移的方法找出与可行域有公共 点且纵截距最大或最小的直线；
x-4y+3=0
A B

线性规划问题的图解法

线性规划问题的图解法
第二步：对约束条件加以图解。
第三步：画出目标函数等值线，结合目标函数 的要求求出最优解：最优生产方案。
第四步：最优解带入目标函数，得出最优值。
4
约束条件的图解:
每一个约束不等式在平面直角坐标系中 都代表一个半平面，只要先画出该半平面的 边界，然后确定是哪个半平面。
怎麽画边界
?
怎麽确定 半平面
以第一个约束条件: x1 2x2 ≤8 为例, 说明图解过程。
结果表明，该线性规划有无穷多个 最优解－－线段AB上的所有点都是最优
点，它们都使目标函数取得相同的最大值 Zmax=14。
17
无界解
max Z x1 x2
x12x1x2
x2 ≤
≤ 2
4
x1, x2 ≥ 0
x2
6
4
2 x1
0
1
2
3
4
5
18
如图中可行域是一个无界区域，如阴影区所示。 虚线为目表函数等值线，沿着箭头指的方向平移可 以使目标函数值无限制地增大，但是找不到最优解。
12
max Z 2x1 3x2
x1 2x2 ≤ 8
4 4
x1 x2
≤16 ≤12
x1, x2 ≥ 0
x2 B 4x1 16
3E F
2
1
4x2 12
C
最优点
x1 2x2 8
A
D
x1
0
1 2345 678
13
结果
有唯一最优解 可行域是一个非空有界区域
可行域有几种可能 ? 讨论
解有几种可能 ?
这种情况通常称为无“有限最优解” 或“最优 解无界”。
如果一个实际问题抽象成像例1-4这样的线性规划 模型，比如是一个生产计划问题，其经济含义就是某 些资源是无限的，产品的产量可以无限大。此时应重 新检查和修改模型，否则就没有实际意义。

18.2二元线性规划问题的图解法


练习
渗透数形结 合的思想，培 养学生的观 察能力
2 z x ，这是斜率为 3 3

2 z ，在 y 轴上的截距为 的直线。当 z 变化时， 3 3
可以得到一族互相平行的直线，如图，由于这些直 线的斜率是确定的， 因此只要给定一个点， （例如 （1， 2 ））， 就 能 确 定 一 条 直 线 作业 （y 距
【出现的问题】
1、不根据提示，列出目标函数 【追问】 当 x, y 满足不等式组（1）并且为非负整 数时，Z 的最大值是多少？ 【引导】 把目标函数化成斜截式，引导学生寻找
目标函数的几何意义。
4、归纳总结
（1）这节课学习了哪些知识； （2）学到了哪些思考问题的方法？
9 17 , ）的直线 8 8
所对应的 t 最大. 所以 zmin=3×(-2)+５×(-1)=-11.
zmax=3×
×
9 +5 8
y
17 =14 8
x-y+1=0 9 17 3x+5y=0 ( , ) A 8 8 x-5y-3=0 1 C -1 O x 3 -1 B 5x+3y-15=0
5
教学程序 时间分配
引导学生 设元转化， 实现 了由数到形的 转化， 成功实现 数形结合， 分解 了本节课的难 点
x 2 y 8 4 x 16 得二元一次不等式组： 4 y 12 x0 y0
（2）画出不等式组所表示的平面区域： 如图，图中的阴影部分的整点（坐标为整数的点） 就代表所有可能的日生产安排。 （3）提出新问题： 进一步，若生产一件甲产品获利 2 万元，生产一件 乙产品获利 3 万元，采用哪种生产安排利润最大？ （4）尝试解答： 设生产甲产品 x 件，乙产品 y 件时，工厂获得的利 润为 z,则 z=2x+3y.这样，上述问题就转化为： 当 x,y 满足不等式（1）并且为非负整数时，z 的最大值是多少？ 把 z=2x+3y 变形为 y 总结

18.2 线性规划问题的图解法1


[2(m 3) (m 2) m 2] [2(m 3) 2(m 2) m 2] 0
(2m 3)(m 8) 0
解得 m
3 2
或 m>8
18.2 线性规划问题的图解法
课堂练习 3
P96 3
作业 P99 1，2
取原点（0，0），代入x＋y－9，得：
0＋0－9＝－9＜0
原点在直线x＋y－9=0的左下方，所以直线x＋y－9=0的左下方 的区域就是不等式x＋y －9＜0表示的平面区域．
18.2 线性规划问题的图解法
y 9
x+y-9=0
O
9
x
18.2 线性规划问题的图解法
课堂练习 1
画出下列不等式表示的平面区域： （1）4x－7y － 28＜0
所表示的平面区域。
解:
画直线x+y-12=0(画成实线）
不等式x＋y ≥ 12表示直线x＋y－12＝0上及其右上方的点的集合； 不等式0 ≤ x≤10是夹在直线x＝0和x=10之间的区域（包括直线 x＝0和x=10）
不等式0 ≤ y≤15是夹在直线y＝0和y=15之间的区域（包括直 线y＝0和y=15） y x=10
“实例考察”中生产问题的线性约束条件）
的解集表示的图形又是什么？
18.2 线性规划问题的图解法
在平面直角坐标系中，方程Ax＋By＋C＝0（A，B不全 为0）表示一条直线，它把平面分成两个区域。 二元一次不等式Ax＋By＋C＞0在平面直角坐标系中表示直线
Ax＋By＋C＝0某一侧所有点组成的平面区域。
18.2 线性规划问题的图解法
二、二元一次不等式组的解表示的平面区域
二元一次不等式组的解表示的平面区域是各个不 等式所表示的平面点集的交集，因而是各个不等式所 表示的平面区域的公共部分。

线性规划问题的图解法

不可行解➢例1.4 现有两个变量的LP 模型⎪⎪⎩⎪⎪⎨⎧≥≤≤≤++=0,45301202121212123810max x x x x x x x x Z 020406080x 120406080x 2x2= Z/8 －5/4 x 1可行域若Z=160, x 2=20－5/4x 1(10,45) Z=460等值线最优解:x 1=10, x 2=45, Z=460 (唯一最优解)◼1.3 线性规划问题的图解法图解法不可行解➢若将上例的目标函数改为：x x Z 2321max +=20406080x 120406080x 2x 2= Z/2 －3/2 x1若Z=60, x 2=30－3/2x 1A(10,45) Z=120最优目标值：Z=120最优解为AB 线段上所有点：无穷多组最优解。

约束条件不变，其最优解会发生什么变化？B(30,15) Z=120➢例1.5 某LP 问题的可行域如下图：因约束方程为≤ ，目标为MaxZ ：无解（无界解）约束方程为≥ ：无解（无可行解）⎪⎩⎪⎨⎧≥≥≤−≥≤+−+=0,2)(4)(2max 21212121x x x x x x x x Z➢局限性：仅能求解两个变量的LP问题。

➢直观：有助于了解LP问题求解的原理。

➢重要启示：（1）LP问题的可行域一般是凸多边形，最优解一定在可行域的某个顶点上得到；（2）若在两个顶点上同时得到最优解，则这两顶点连线上的一切点都是该问题的最优解（多组最优解）。

（3）可行域有时无界（4）可行域有时是空集统称为无解。

中职二元线性规划问题的图解法


ABCD
在工作表中输入二元线性 规划问题的各个参数，如 目标函数系数、约束条件 系数和常数项。
Excel将给出最优解、最 优值以及满足约束条件的 解集。
MATLAB求解方法
01
在MATLAB中，使用 “fmincon”函数来求解二元线 性规划问题。
02
输入目标函数系数、约束条件系 数和常数项，以及其他求解参数
资源分配问题的图解法
通过绘制二维平面图，将资源分配问题中的两个决策变量（如医生和床位的数量）在平 面图上表示出来，并根据约束条件和目标函数绘制等效用线或等效用面积，找到最优解。
运输问题
运输问题
在物流和运输领域中，如何合理安排运 输路线和运输量，使得运输成本最低、 运输效率最高。例如，在货物配送中， 如何选择最佳的配送路线和车辆数量， 使得总运输时间和总成本最小。
特点
二元线性规划问题具有明确的目标函 数和约束条件，且目标函数和约束条 件都是线性的，即只包含一次项。
问题的提
实际应用
二元线性规划问题在实际生活中有着广泛的应用，如生产计 划、资源分配、投资组合优化等。
问题形式
给定一组线性约束条件和目标函数，求解两个决策变量的最 优值。
问题的解决方式
解析法
通过代数方法求解二元线性规划问题， 需要一定的数学基础和计算能力。
求解最优解
将最优解位置代入原问题中，求得最优解的值。
分析最优解
根据求得的最优解，分析其对原问题的意义和影 响。
03
二元线性规划问题的实 际应用
生产计划问题
生产计划问题
在生产过程中，需要确定各种产品的生产数量、生产时间和生产成本，以满足市场需求和利润最大化 。二元线性规划可以用来解决这类问题，通过优化生产计划，提高生产效率，降低生产成本。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
max z=5x+4y
3x 4y 250 2x y 100 x 0 y 0
解: 四边形OABC所围成的区域就是该问题的可行域
问题转化为在四边形OABC找一点，
使得目标函数在该点取得最大值。 y
观察z=5x+4y取值的变化规律。
方程5x+4y=c表示一条直线， 当c取不同的值时，得到一组 平行的直线（图中虚线）。
22
x x

y 20 5y 40
x 0
y 0
解: 图中阴影部分是问题的可行域
目标函数在A点取得最小值。
y
2X+y=20
6X+5y=80
A（10，4）是直线 6x+5y=80和直线 2x+5y=40的交点
C 2X+5y=40
o
min z 410 5 4 60
y
o
x
复习：画出不等式表示的平面区域：
⑴ 4x-3y>9
y
o1
-1
4x-3y=9
23
x
-2 -3
说明：划分区域时，找好特殊点，注意不等号。
复习：画出不等式组表示的平面区域：
y≥2x+1
x=2x+1
3 2
1
-2 -1
123
o
x x+2y=4
说明：划分区域时，找好特殊点，注意不等号。
一、课题引入：
问题：max z=5x+4y
3x 4y 250 2x y 100 x 0 y 0
二、线性规划的概念： 目标函数 （线性目标函数）
max z=5x+4y
3x 4y 250 2x y 100 x 0 y 0
线性约 束条件
线性规划：求线性目标函数在线性约束条件下的最 大值或最小值的问题，统称为线性规划问题．
求函数z=x-y在平面区域

y

1

0
x 2 y 2 0
内的取值范围.
例6:
求函数z=x-y在平面区域
x

y

2 1

0 0
内的取值范围.
解: 画出平面区域。
x 2 y 2 0
y
x+2y-2=0
1
x=2 y=1
直线x-y=z往右下方移动时， 直线上的横坐标x随之增大， y随之减小，但-y却增大，故 z值增大。反之z减小。
可行解 ：满足线性约束条 件的解(x，y)叫可行解；
可行域 ：由所有可行解组 成的集合叫做可行域；
可行域
线性规划：求线性目标函数在线性约束条件下的最 大值或最小值的问题，统称为线性规划问题．
可行解 ：满足线性约束条 件的解(x，y)叫可行解；
可行域 ：由所有可行解组 成的集合叫做可行域；
最优解 ：使目标函数取得 最大或最小值的可行解叫 线性规划问题的最优解。
求得： x 30

y

40
max z 530 4 40 310
y
2X+y=100
C B(30,40) 3X+4y=250
x
o
A
所以点心店每天需做甲种馒头30kg,乙种馒头40kg， 才能取得最大润310元。
例5：求解线性规划问题
min z=4x+5y
6x 5y 80
当直线往右上方平移时，直 线上的横坐标x和纵坐标y的 值随之增大，所以对应的z 值也在不断地增大，当移到 四边形OABC的顶点B时，z 取得最大值。
2X+y=100
C B(30,40) 3X+4y=250
x
o
A
5X+4y=c 5X+4y=0
解: 目标函数在B点取得最大值。
B点的坐标可由方程组
3x 4y 250 2x y 100
可行域
在平面直角坐标系中，Ax+By+C=0(A,B不全为0） 表示一条直线，当C取不同的值时，所得的方程表 示不同的直线。这些直线可以看做由直线 Ax+By=0
平移而得到。
y
AX+By=C2
在移动的过程中， z =Ax+By的值是增大还 是减小？
o
x
AX+By=C1 AX+By=0
例4：求18.1例1线性规划问题的解
A(10,4) x
我们用图解的方法得到了二元 线性规划问题的最优解.这种方 法叫做:图解法.
练习: P98 2
解线性规划问题的一般步骤：
第一步：在平面直角坐标系中作出可行 域； 第二步：在可行域内找到最优解所对应 的点； 第三步：解方程的最优解，从而求出目 标函数的最大值或最小值。
例6:
x 2 0
1 2 x 因此函数z=x-y在点A（0，1）
x-y=0
处取得最小值-1,在点B（2，
x-y=z
0）处取得最大值2。
所以 z -1,2
练习:
x 3y 6
求函数z=2x+y在平面区域 x y 6
x 1

y

1
内的取值范围.
作业:
P99：
3，4，5.