统计学中的标准分高考标准分计算课件

标准分计算公式标准分是一种常用的评分方法，它可以将不同的分数转化为统一的标准分，使得不同指标之间具有可比性。

标准分计算公式是根据正态分布的统计原理而来，可以帮助我们更好地理解和比较数据。

在实际应用中，标准分计算公式被广泛应用于各个领域，如教育、人力资源管理、市场营销等。

下面我们将详细介绍标准分的计算公式及其应用。

标准分计算公式的基本原理是将原始分数转化为标准差单位，以便进行比较和分析。

其计算公式如下：Z = (X μ) / σ。

其中，Z代表标准分，X代表原始分数，μ代表样本的均值，σ代表样本的标准差。

通过这个公式，我们可以将原始分数X转化为以均值为零、标准差为1的标准分Z。

这样一来，不同指标之间的得分就可以进行比较和分析了。

标准分计算公式的应用非常广泛。

在教育领域，标准分可以帮助学生和老师更好地理解学生的成绩，并进行横向和纵向的比较。

在人力资源管理中，标准分可以帮助企业对员工的绩效进行评估和比较。

在市场营销领域，标准分可以帮助企业对不同产品的销售情况进行比较分析。

总之，标准分计算公式在实际应用中发挥着重要的作用。

需要注意的是，标准分计算公式虽然可以将不同指标转化为统一的标准分，但在具体应用时需要考虑到一些因素。

首先，样本的均值和标准差需要具有代表性，否则计算出的标准分可能失真。

其次，不同指标之间的可比性需要经过合理的论证和分析，不能简单地依赖标准分进行比较。

最后，标准分只是一种评分方法，不能完全代表指标的全部信息，需要结合实际情况进行综合分析。

在实际操作中，我们可以通过各种统计软件和工具来计算标准分，比如Excel、SPSS等。

这些工具可以帮助我们更快捷、准确地进行标准分的计算和分析，提高工作效率。

综上所述，标准分计算公式是一种重要的评分方法，它可以帮助我们更好地理解和比较数据，发挥着重要的作用。

在实际应用中，我们需要充分理解其计算原理，并结合实际情况进行合理的分析和应用。

希望本文对您有所帮助，谢谢阅读！。

标准分计算公式标准分是一种常用的统计学方法，用于将不同指标的数值进行比较和评价。

在各种考试、评比和排名中，标准分都有着广泛的应用。

标准分计算公式是一种基本的数学工具，掌握好标准分的计算方法对于正确理解和使用统计数据至关重要。

本文将详细介绍标准分的计算公式及其应用。

标准分的概念。

标准分是一种用来衡量某个数值相对于平均值的偏离程度的方法。

它可以将不同指标的数值进行统一的比较和评价，消除了不同指标之间的量纲差异。

标准分的平均值为0，标准差为1，因此可以直观地看出某个数值相对于平均值的偏离程度。

标准分的计算方法可以将原始数据转化为标准化的数据，方便进行比较和分析。

标准分的计算公式。

标准分的计算公式为，Z = (X μ) / σ。

其中，Z表示标准分，X表示原始数据的数值，μ表示原始数据的平均值，σ表示原始数据的标准差。

通过这个公式，我们可以将原始数据转化为标准分，从而进行比较和评价。

标准分的应用。

标准分广泛应用于各种考试和评比中。

在学术考试中，标准分可以将不同科目的成绩进行比较和排名，消除了不同科目难易程度的差异。

在招聘考试中，标准分可以将不同应聘者的成绩进行比较和评价，帮助雇主选择最合适的人才。

在市场调研中，标准分可以将不同产品的销售额进行比较和分析，帮助企业制定营销策略。

标准分的优缺点。

标准分作为一种统计学方法，具有很多优点。

首先，标准分可以消除不同指标之间的量纲差异，方便进行比较和评价。

其次，标准分可以直观地反映出某个数值相对于平均值的偏离程度，帮助人们更好地理解数据。

此外，标准分可以将原始数据转化为标准化的数据，方便进行数学运算和统计分析。

然而，标准分也存在一些局限性。

首先，标准分的计算需要知道原始数据的平均值和标准差，如果原始数据的分布不满足正态分布，标准分的计算结果可能不够准确。

其次，标准分只能反映出某个数值相对于平均值的偏离程度，无法反映出原始数据的绝对数值大小，因此在一些特定情况下可能不够全面。

什么是标准分标准分是一种统计学概念，用于衡量一个数据点相对于整体数据集的位置。

它可以帮助我们理解数据的分布情况，以及某个数据点在整体数据中的相对位置。

标准分的计算方法是将数据点与整体数据的平均值相减，再除以标准差。

标准分的概念在统计学和数据分析中被广泛应用，下面我们将详细介绍标准分的计算方法、意义以及应用场景。

首先，标准分的计算方法是通过以下公式进行计算，Z = (X μ) / σ，其中Z代表标准分，X代表具体的数据点，μ代表整体数据的平均值，σ代表整体数据的标准差。

通过这个公式，我们可以将任意一个数据点转化为其在整体数据中的相对位置，从而进行比较和分析。

其次，标准分的意义在于帮助我们理解数据的分布情况。

通过计算标准分，我们可以知道某个数据点相对于整体数据的位置是偏高还是偏低，从而判断其是否为异常值或者特殊情况。

同时，标准分还可以帮助我们进行不同数据集的比较，因为它将数据点转化为统一的标准单位，消除了不同数据集之间的量纲影响。

此外，标准分在实际应用中有着广泛的场景。

比如在财务分析中，我们可以利用标准分来评估某个公司的财务状况相对于整个行业的水平；在教育评估中，我们可以利用标准分来比较不同学生的成绩表现；在市场营销中，我们可以利用标准分来分析消费者的购买行为等等。

总之，标准分是一种重要的统计学概念，它可以帮助我们理解数据的分布情况，进行数据的比较和分析，以及在实际应用中发挥作用。

通过计算标准分，我们可以更加准确地把握数据的特征和规律，从而做出更加科学的决策和分析。

希望本文能够帮助大家更好地理解标准分的概念和意义，为实际应用提供帮助。

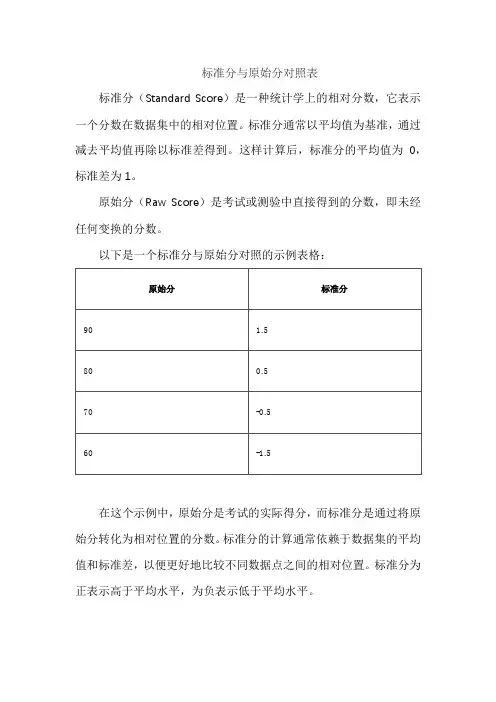
标准分与原始分对照表
标准分（Standard Score）是一种统计学上的相对分数，它表示一个分数在数据集中的相对位置。

标准分通常以平均值为基准，通过减去平均值再除以标准差得到。

这样计算后，标准分的平均值为0，标准差为1。

原始分（Raw Score）是考试或测验中直接得到的分数，即未经任何变换的分数。

以下是一个标准分与原始分对照的示例表格：
在这个示例中，原始分是考试的实际得分，而标准分是通过将原始分转化为相对位置的分数。

标准分的计算通常依赖于数据集的平均值和标准差，以便更好地比较不同数据点之间的相对位置。

标准分为正表示高于平均水平，为负表示低于平均水平。

标准分怎么算
标准分是指根据某种标准确定的分数。

在不同的领域、不同的评价体系中，标准分的计算方法也会有所不同。

接下来，我们将以常见的考试评分为例，介绍标准分的计算方法。

首先，标准分的计算需要依据考试的总分、平均分和标准差。

在统计学中，标准差是一组数据离散程度的度量，它能够反映数据的波动情况。

在考试评分中，标准差可以帮助我们了解考生分数的分布情况，从而确定标准分。

其次，计算标准分的步骤如下：
1. 首先，我们需要计算考试的平均分和标准差。

平均分是所有考生分数的总和除以考生人数，而标准差则需要通过一定的公式进行计算。

2. 接着，我们计算每位考生的标准分。

标准分的计算公式为，标准分 = （考生分数平均分）/标准差。

3. 最后，根据计算出的标准分，我们可以对考生进行排名和评定。

标准分可以帮助我们更客观地评价考生的水平，避免了因为考试难易程度不同而导致的分数偏差。

总的来说，标准分的计算方法可以帮助我们更准确地评价考生的水平，避免了因为考试难易程度不同而导致的分数偏差。

通过对考试成绩的标准化处理，我们能够更公平地对待每一位考生，从而更好地促进教育教学工作的开展。

在实际应用中，标准分的计算方法也可能会因评价体系的不同而有所差异。

因此，在使用标准分进行评价时，我们需要结合具体的评价体系和标准，以确保评价的客观性和公正性。

总之，标准分的计算方法是一种重要的评价工具，它可以帮助我们更客观地评价考生的水平，促进教育教学工作的开展。

希望本文对您有所帮助，谢谢阅读！。

什么是标准分标准分是统计学中常用的一个概念，它是指将原始分数转化为具有特定均值和标准差的分数。

标准分的计算可以帮助我们更好地理解数据的分布情况，进行数据比较和分析。

在实际应用中，标准分也被广泛用于学术研究、心理测量、人才选拔等领域。

本文将从标准分的计算方法、应用场景和意义等方面进行详细介绍。

首先，我们来看一下标准分的计算方法。

标准分的计算是基于原始分数与均值的差异来进行的。

假设我们有一组原始分数数据，首先需要计算这组数据的均值和标准差，然后通过以下公式来计算标准分：\[Z = \frac{X \mu}{\sigma}\]其中，Z代表标准分，X代表原始分数，μ代表均值，σ代表标准差。

通过这个公式，我们可以将原始分数转化为具有均值为0、标准差为1的标准分数，从而进行数据的比较和分析。

接下来，我们来谈谈标准分的应用场景。

标准分在实际应用中有着广泛的应用，特别是在学术研究和心理测量领域。

在学术研究中，标准分常常用于比较不同样本的数据，消除了原始分数的量纲和单位差异，使得数据更具有可比性。

在心理测量中，标准分可以帮助我们更好地理解个体的得分情况，进行人才选拔和评估。

最后，我们来探讨一下标准分的意义。

标准分的计算可以帮助我们更好地理解数据的分布情况，发现数据的规律性和特点。

同时，标准分还可以帮助我们进行数据的比较和分析，发现数据之间的差异和联系。

在实际应用中，标准分的使用可以使数据更具有可比性，更加客观和科学。

综上所述，标准分是一种重要的统计学概念，它通过将原始分数转化为具有特定均值和标准差的分数，帮助我们更好地理解数据的分布情况，进行数据的比较和分析。

在学术研究、心理测量、人才选拔等领域都有着广泛的应用。

通过对标准分的计算方法、应用场景和意义的深入了解，我们可以更好地应用标准分这一工具，进行数据分析和决策。

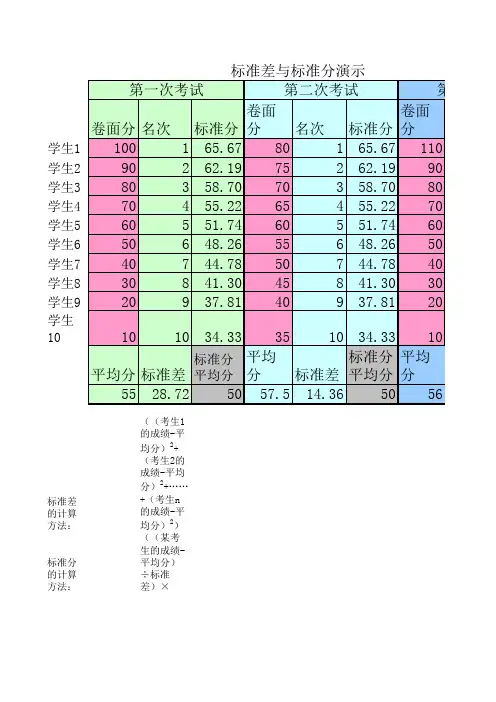
标准分600分比例标准分是指在统计学中用于将不同指标或变量进行比较和评估而转换为标准单位的一种方法。

它的本质是将原始数据转化为相对位置的度量，从而能够在不同的数据间进行比较和分析。

标准分的计算公式是：标准分= (观察值-平均值) /标准差。

其中观察值是指待转换的原始数据，平均值是指同一样本或总体的平均值，标准差是指同一样本或总体的标准差。

标准分的主要作用是消除不同指标或变量之间的度量单位差异，使得不同样本或总体的数据能够在同一比例尺上进行比较和评估。

标准分值通常呈现为以100为平均值，以标准差为单位的分数，即平均值为0，标准差为1。

标准分值高于平均值表示该观察值高于平均水平，标准分值低于平均值则表示该观察值低于平均水平。

标准分也常用于进行人员、学生或考试成绩的评估和比较。

例如，大学的入学考试成绩通常会进行标准化转换，以便于不同地区、不同学校或不同年份的考生之间进行公平的比较和录取。

标准分的优点是能够将不同的指标或变量进行标准化转换，使得数据能够在同一比例尺上进行比较和分析。

同时，标准分能够消除不同指标或变量之间的度量单位差异，使得比较结果更加准确和可靠。

然而，标准分也存在一些局限性。

首先，标准分只是一种相对位置的度量，不能直接反映出观察值的绝对水平。

其次，标准分的计算依赖于样本或总体的平均值和标准差，如果这些统计量不稳定或有所变化，标准分的结果也会发生改变。

总之，标准分是一种常用的统计学方法，用于将不同指标或变量进行比较和评估。

它能够消除不同指标或变量之间的度量单位差异，使得数据在同一比例尺上进行比较和分析。

标准分在人员选拔、考试评估等领域有广泛应用，但同时也需要注意其局限性和应用条件。

标准分计算公式标准分是一种常用的统计分析方法，它可以帮助我们对不同数据进行比较和评估。

在各种考试、测试和评估中，标准分都扮演着重要的角色。

本文将介绍标准分的计算公式，帮助大家更好地理解和运用这一统计方法。

首先，我们来看一下标准分的概念。

标准分是一种将原始分数转化为具有一定标准的分数的方法。

它可以使不同测试或考试的分数具有可比性，也可以帮助我们更直观地理解数据的分布情况。

标准分的计算公式如下：标准分 = (原始分数平均数) / 标准差。

在这个公式中，原始分数是指我们要进行转化的分数，平均数是指所有分数的平均值，标准差是衡量数据分散程度的指标。

通过这个公式，我们可以将原始分数转化为以平均数为中心，标准差为单位的分数，从而进行比较和分析。

接下来，我们来看一个具体的例子，以帮助大家更好地理解标准分的计算方法。

假设某次考试的数学成绩平均分为80分，标准差为10分。

某位学生的数学成绩为75分，我们可以通过标准分计算公式来计算他的标准分：标准分 = (75 80) / 10 = -0.5。

通过计算，我们可以得知这位学生的数学成绩低于平均水平0.5个标准差。

同样地，如果某位学生的数学成绩为90分，他的标准分计算结果为：标准分 = (90 80) / 10 = 1.0。

这表示这位学生的数学成绩高于平均水平1.0个标准差。

通过标准分的计算，我们可以更清晰地了解每位学生的成绩相对于整体水平的位置，有助于更公平地评价他们的表现。

除了帮助我们比较不同个体的成绩，标准分还可以帮助我们分析整体数据的分布情况。

当数据呈正态分布时，标准分可以帮助我们判断数据集中的个体相对于平均水平的位置，以及数据的分散程度。

这对于统计分析和决策制定都具有重要意义。

在实际运用中，标准分还可以帮助我们进行数据的标准化处理，使得不同数据具有可比性。

在招聘、选拔和评估中，标准分常常被用来对不同考生或申请者的成绩进行比较和评价，从而更公平地进行选拔和录取。

标准分数
（1）定义
标准分数：以标准差为单位表示一个原始分数在团体中所处位置的相对位置量数，也叫Z 分数
离平均数有多远，即表示原始分数在平均数以上或以下几个标准差的位置。

X X Z s
-=
（2）性质
①Z 分数无实际单位，是以平均数为参照点，以标准差为单位的一个相对量
②一组原始分数转换得到的Z 分数可正可负，所有原始分数的Z 分数之和为零
③原始数据的Z 分数的标准差为1
④若原始分数呈正态分布，则转换得到的所有Z 分数均值为0，标准差为1的标准正态分布
（3）优点
①可比性——不同性质的成绩，一经转换为标准分数，就可在同一背
景下比较
②可加性——不同性质的原始数据具有相同的参照点，因此可相加
③明确性——知道了标准分数，利用分布寒暑表就能知道其百分等级
④稳定性——转换成标准分数之后，规定了标准差为1，保证了不同性质分数在总分数中权重一样
（4）应用
①比较几个分属性质不同的观测值在各自数据分布中相对位置的高低
②计算不同质的观测值得总合或平均值，以表示在团体中的相对位置
③若标准分数中有小数、负数等不易被人接受的问题，可通过
Z'=aZ+b 的线性公式将其转化成新的分数（如韦氏成人智力量表）文章来源：博仁教育。

标准分的计算标准分也称为标准分数。

标准分的计算方法有两种：公式法和查表法。

一、公式法计算标准分（一）单科标准分的计算某次考试，共有n个考生参加考试（通常将分数为0的考生与未参加考试的考生同等对待，因此与考数n 即分数大于0分的考生数），已知：与考数n，每个考生的原始分数（卷面得分）x i( i = 1, 2, …, n。

x i是第i个考生的得分)。

标准分数（Z分数）的计算公式为：式中，是全部考生原始分的平均值，σ是标准差。

（二）标准分数的性质Z分数是原始数据（原始分数）与平均数（原始分数的平均值）之差除以标准差（原始分数的标准差）所得的商，无单位。

如果原始数据大于平均数则Z值为正；如果原始数据小于平均数则其Z值为负；如果原始数据等于平均数则Z 值为零。

标准分有如下性质：①标准分的分布与原始分的分布相同。

②标准分的平均值是0，标准分的标准差是1。

③原始分转换为标准分是线性变换，不会改变分数的分布形状，也不改变原来分数的位置次序，也就是不改变名次，不改变相对位置，不改变相对距离。

（三）实际使用的标准分数标准分（Z分数）在一般情况下都带小数，而且会出现负值，实际使用时不太方便，所以还要对Z分数进行线性变换：y = a z + b，其中a、b均为常数，根据需要取值，如a取100，b取500，我们就得到了平均分为500，标准差是100的标准分数。

（对于任一学科，每位考生有且仅有一个z分数，相应有一个标准分。

）常用的标准分除了z分数外，还有T分数、CEEB分数、ITED分数、MET 分数等，它们与z分数的关系是：T分数= 10 z + 50CEEB分数= 100 z + 500ITED分数= 5 z + 15MET分数= 12 z + 60两个假设：① z分数的范围：-4<z<4 （或 -5<z>5）②当某个考生的原始分数是0时，相当于该生“没有参加考试”，也就是“没有分数”，此时 z分数的值有三种计算方法：一是直接用公式计算，例如 MET 分数=12；二是指定为-5，即指定 MET分数=0；三是指定为一个大于-5而小于-4的数值，也就是 MET分数指定为一个大于0而小于12的数值，例如：MET分数等于1或10。

讲给语文老师的统计知识：什么是标准分-su的日志-网易博客讲给语文老师的统计知识：什么是标准分默认分类 2010-08-08 20:40:46 阅读79 评论0 字号：大中小订阅一、什么是标准分数？标准分数是一个统计术语，它描述的是某一个分数在团体中所处的位置。

在统计学中，标准分数的计算公式：Z=Xi-XS。

公式中Xi的表示某人实测成绩，在统计学中称为原始分；公式中的X和S表示标准化团体某个学科某次测验的平均分和标准差。

X表示测验分数的集中趋势，用公式X=XiN计算；S表示测验分数的离散程度，用公式S=(Xi-X)2N计算，S的值越大，说明测验分数离散程度越大。

二、标准分数有什么用处？标准分数其实就是以0为平均数，以标准差为单位的位置量数。

一个Z分数表示的是数轴上的一个点，当原始分正好等于平均分时，Z ＝0；当原始分等于X+S时，Z=+1；当原始分等于X+2S时，Z=+2；以此顺延。

同理，当原始分等于X-S时，Z=－1；当原始分等于X-2S 时，Z=－2；以此顺延。

我们可以将某次测验的所有原始分转换为Z 分数，就可以获得数轴上的若干个点，Z值越大，表示所处的位置越靠前，成绩越好。

不同测验的原始分，都可以通过公式，依据本次测验的平均分和标准差，将本次测验的原始分转换为Z分数，用数轴来表示标准分的分布位置。

例如，不同国家的货币，如马克、英镑，它们的数值间因为没有共同的单位是不能直接进行比较和加减的。

只有将它们转换为一个统一的标准，才有可比性。

为了对欧洲各种货币进行这种转换，就出现了欧元。

欧元就相当于标准分，马克、英镑就相当于原始分，而各自的兑换率就相当于标准差。

马克、英镑按照各自的兑换率换算成欧元，就可以进行比较或相加。

同样，对不同学科、不同时间的测验的原始分，也应该进行这样的转换才能进行分数的加减或者比较。

有人认为，各科或每次考试分数的满分都是100分，最低分都是0分，所以各科的考试分数不存在换算的问题。