2008年福建高考数学试题(理科)及答案
- 格式:doc
- 大小:740.00 KB
- 文档页数:11
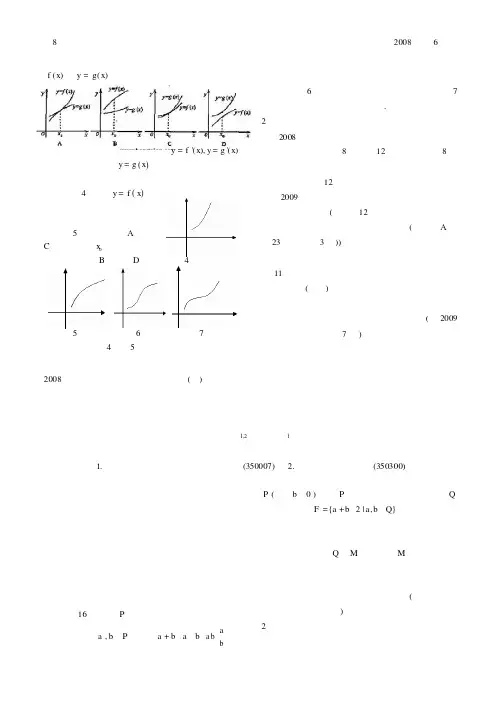
()f x ,()y g x =的图象可能是解析:观察备选项,结合函数'(),'()y f x y g x ==的图象可知:函数()y g x =单调递增,且递增的速度呈现由慢到快的趋势,与之相对应的熟悉的函数图象如图4;函数()y f x =单调递增,且递增的速度呈现由快到慢的趋势,与之相对应的熟悉的函数图象如图5,故可排除A 、C ;又因为在0x 处,斜率相等,可排除B ,故选D .图4图5图6图7评注:对图4、图5函数单调性的考查,在高考屡见不鲜,常见的考查形式是通过图象揭示函数的单调性如图6呈现由慢到快再到慢的递增趋势;图7呈现由快到慢再到快的递增趋势.2思考与商榷2008年高考福建卷对数与形结合的考查整体上是比较到位的,如第8题、第12题的命制:第8题的非封闭可行域的线性规划问题,能很好考查学生的观察能力;第12题的利用导数研究函数单调性问题对2009年的高考复习起着较好的导向作用——重视基础,回归课本(注:第12题所涉及的两种函数模型是常见的重要函数模型,且有本可循(见人教A 版第23页练习第3题)).美中不足的是试卷在考查方式上略显不足,如第11题,题目设置较为陈旧;此外,《普通高中数学课程标准(实验)》新增了“函数零点及二分法”的内容,对数与形的要求比大纲要求略显提高,笔者认为,试卷若能增加以新增内容为背景试题(如2009年高考广东卷理科第7题),那么试卷对于由大纲课程到课标课程的平稳过渡将有更好的指引功能.2008年福建省高考数学理科试卷评析(五)创新意识的考查分析叶诚理1,2柯跃海11.福建师范大学数学与计算机科学学院(350007)2.福建省福清第一中学(350300)数学创新题,是以考生已有的知识为基础,定义一种新知识,或将学科间的知识进行整合,或体现问题的开放性与探究性等.高考数学命题的创新有利于进一步完善试题的选拔功能,促进高中数学课程改革的实施.同时,创新题能有效地避免试题的模式化,检测考生在新的情境中实现知识迁移的能力,从而有效考查考生的创新意识与学习潜能.1试题陈述第16题:设P 是一个数集,且至少含有两个数,若对任意,∈,都有+、、a∈、P (除数0b ≠),则称P 是一个数域.例如有理数集Q是数域;数集{2|,}F a b a b Q =+∈也是数域.有下列命题:①整数集是数域;②若有理数集QM ,则数集M 必为数域;③数域必为无限集;④存在无穷多个数域.其中正确的命题的序号是(把你认为正确命题的序号都写上).2试题背景试题的背景为高等代数中有关数域的概念.即8福建中学数学2008年第6期a b P a b ab a b b如下定义:设P是由一些复数组成的集合.如果P中任意两个数(这两个数可以相同)的和、差、积、商(除数不为零)仍然是P中的数,那么P就称为一个数域.例如:有理数集Q,实数集R,复数集C均为数域.整数集Z就不是数域,因为不是任意两个整数的商都是整数.数域概念的实质是,对于数集P中的任意两个数满足四则运算的封闭性(除数不为零).显然数域中必包含0与1,因为任给数集P中的一个非零的数,本身相减得0,相除得1.3试题解析本题可采用特殊法来解决.①错.例如,1,2Z∈,但1/2Z,故可得出整数集不是数域;②错.例取数集{2}M Q=∪,则满足Q M,接着取2与Q中元素1来验证,发现12M+,故M错;③正确.任给a P∈,由已知条件,则1aPa=∈.用1和自己重复相加,可得全体正整数,而正整数为无限集.由P的任意性,得出P为无限集.④正确.由已知{2|,}F a b a b Q=+∈为数域,则{|,}F a b m a b Q′=+∈,其中m为正素数也为数域,正素数有无穷多个,因而形如,,a b m a b Q+∈的数域也有无限个,即存在无限多个数域.4试题评注本题是将大学教材中的概念下放到高考题中的一次尝试,试题具有一定的难度和区分度,有利于高校选拔人才.本题主要涉及到集合中数集、子集,函数映射等相关概念,检测了学生面对陌生情景,提取有效信息,灵活利用合情推理进行思维正向迁移的能力.解答本题,考生要懂得把新概念转化成熟悉的函数的语言:数域实际上是建立在数集基础上的一种映射f,即任给a、b P∈,:*f a b c,则c P∈(其中*表示加减乘除运算).再将函数语言特殊化,从而解答本题.5思考与商榷纵览全卷,比较突出的创新试题只有一道,作为一份向课标卷过渡的高考卷,创新题的比例略显不足.试卷中的创新试题题实际上来源于大学《高等代数》中有关数域的内容,命题者把大学阶段的基础题“搬”进高考试卷,创新程度稍显不够.事实上,创新题的命制可在内容立意新、情境设置新、设问方式新或题型结构新等方面去考虑,尤其是高等数学与初等数学的“上联下靠”更值得关注.2008年福建省高考数学理科试卷评析(六)应用意识的考查分析邱云1,2李祎11.福建师范大学数学与计算机科学学院(350007)2.福建省宁化第一中学(365400)数学应用意识是指主体主动从数学的角度观察事物、阐述现象、分析问题,用数学的语言、知识、思想方法描述、理解和解决问题的心理倾向性.其具体表现为:将实际问题转化成数学问题,即数学建模能力.应用题是发展学生应用意识的重要载体,是高考考查应用意识的主要方式.1试题分析应用意识考查情况如下:题号分值题型考查知识点试题背景55选择题概率种子发芽75选择题排列、组合人员选派2012解答题概率、期望证书考试例1(第5题)某一批花生种子,如果每1粒发芽的概率为5,那么播下粒种子恰有粒发芽的概2008年第6期福建中学数学94/42。

2008年高考数学福建理科试卷及解答一. 选择题(本大题共12小题,共0分)1. (2008年福建理1)若复数是纯虚数,则实数的值为( )A.1B.2C.1或2D.-12. (2008年福建理2)设集合,,那么“m A”是“m B”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3. (2008年福建理3)设是公比为正数的等比数列,若,则数列前7项的和为()A.63B.64C.127D.1284. (2008年福建理4)函数,若,则的值为( )A.3B.0C.-1D.-25. (2008年福建理5)某一批花生种子,如果每1粒发牙的概率为,那么播下4粒种子恰有2粒发芽的概率是()A. B. C. D.6. (2008年福建理6)如图,在长方体中,AB=BC=2, ,则与平面所成角的正弦值为( )A. B.C. D.7. (2008年福建理7)某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( )A.14B.24C.28D.488. (2008年福建理8)若实数满足,则的取值范围是()A.(0,1)B.C.(1,+)D.9. (2008年福建理9)函数的图象按向量平移后,得到函数的图象,则的值可以为( )A.B. C.-D.-10. (2008年福建理10)在△ABC中,角ABC的对边分别为,若,则角B的值为()A. B. C.或 D.或11. (2008年福建理11)双曲线()的两个焦点为,若P为其上一点,且,则双曲线离心率的取值范围为()A.(1,3)B.C.(3,+)D.12. (2008年福建理12)已知函数的导函数的图象如下图,那么图象可能是()A. B. C. D.二. 填空题(本大题共4小题,共0分)13. (2008年福建理13)若,则______(用数字作答).14. (2008年福建理14)若直线与圆(为参数)没有公共点,则实数的取值范围是__________________.15. (2008年福建理15)若三棱锥的三个侧圆两两垂直,且侧棱长均为,则其外接球的表面积是____.16. (2008年福建理16)设P是一个数集,且至少含有两个数,若对任意,都有(除数),则称P是一个数域.例如有理数集Q是数域;数集也是数域.有下列命题:①整数集是数域;②若有理数集,则数集M必为数域;③数域必为无限集;④存在无穷多个数域.其中正确的命题的序号是________.(把你认为正确的命题的序号填填上)三. 解答题(本大题共6小题,共0分)17. (2008年福建理17)已知向量m=(sinA,cosA),n=,m·n=1,且A为锐角. (Ⅰ)求角A的大小;(Ⅱ)求函数的值域.18. (2008年福建理18)如图,在四棱锥P-ABCD中,则面PAD⊥底面ABCD,侧棱PA=PD =,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.(Ⅰ)求证:PO⊥平面ABCD;(Ⅱ)求异面直线PD与CD所成角的大小;(Ⅲ)线段AD上是否存在点Q,使得它到平面PCD的距离为?若存在,求出的值;若不存在,请说明理由.19. (2008年福建理19)已知函数.(Ⅰ)设是正数组成的数列,前n项和为,其中.若点(n∈N*)在函数的图象上,求证:点也在的图象上;(Ⅱ)求函数在区间内的极值.20. (2008年福建理20)某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试。

2008年福建省高考数学理科试卷评析(二)函数与方程思想的考查分析卢云辉1,2陈清华11.福建师范大学数学与计算机科学学院(350007)2.福建省厦门市松柏中学(361012)1函数与方程思想简述函数思想就是用运动和变化的观点、集合与对应的思想,去分析和研究数学问题中的数量关系,建构函数关系,运用函数的图象或性质去分析、解决问题.方程思想就是以变量间的等量关系为出发点,建立方程(组),通过解方程(组),或者运用方程的性质去分析、解决问题.函数思想与方程思想在中学数学解题中应用广泛,互相依存,互为补充.历年高考试卷对函数与方程思想都予以极大的关注.2试题评析试卷遵循《考试说明》,考查了《考试说明》规定的基本内容,体现了“常规中考能力,基础中显功底”的命题理念.试题中涉及到函数与方程思想有第4、12、14、17、19、21、22题.2.1以函数为中心,注重考查通性通法用函数的形式把数量关系表示出来,运用函数的性质加以研究,也就是从量的变化、联系和发展角度拓宽解题思路.例1(第4题)函数()3sin1()f x x x x R=++∈,若()2f a=则()f a的值为A.3B.0C.1D.2解析:构造函数()()1g x f x==3sinx x+()x R∈,利用()y g x=为奇函数解决问题.选B.评注:本题也可直接利用()()2f a f a+=求解.例2(第12题)已知函数(),()y f x y g x==的导函数的图象如右图,那么函数y=()f x,()y g x=的图象可能是解析:分析函数(),()y f x y g x==的导函数图象可知:在x0处,()y f x=与()y g x=的切线的斜率相等,排除备选项B;在x1(10x x>)处,()y g x=切线的斜率大于()y f x=切线的斜率,排除备选项A;在x2(20x x<)处,()y g x=切线的斜率小于()y f x=切线的斜率,排除备选项C;故选D.评注:由()0g x′′>和()0f x′′<说明()y g x=是凹函数,而()y f x=是凸函数,可排除备选项A与C.以导数为工具研究函数的有关性质,体现了教材改革的新理念,是初等数学与高等数学的衔接点.2.2利用函数方程思想解决数列问题由于数列是一种特殊的函数,而方程、不等式与函数是互相联系的,在一定条件下它们可以互相转化,因此数列问题为函数与方程思想的应用提供了广阔的空间,应用函数与方程思想解决数列问题有独到之处.例3(第19题)已知函数()f x=32123x x+.(I)设{}na是正数组成的数列,前n项和为n S,其中13a=.若点(2,211a a an n n++)(n∈N)在函数()y f x′=的图象上,求证:点(,)n s n也在()y f x′=的图象上;(II)求函数()f x在区间(1,)a a内的极值.解析:(I)由()f x=32123x x+,2008年第6期福建中学数学3所以2'()2f x x x =+,由点(2,211a a a n n n ++)(n ∈N )在函数()y f x ′=的图象上,得12n n a a +=从而求得22n S n n =+,所以2'()2n S f n n n ==+,故点(,)n n S (n ∈N )也在()y f x ′=的图象上.(II)略.评注:本题第(I)问是函数与数列相结合的基础题,把(,)n n S (n ∈N )看成是函数()y f x =上的离散点,使得问题获得解决.例4(第22题)已知函数()ln(1)f x x x =+.(I)求()f x 的单调区间;(II)记()f x 在区间[0,n](n ∈N )上的最小值为b n ,令ln(1)n n a n b =+.(i)如果对一切n ∈N ,不等式2a a n n <+2c a n+恒成立,求实数c 的取值范围;(ii)求证:1313211211224242a a a a a a n a n a a a a a a n+++<+.解析:(I)()f x 的单调递增区间为(1,0);()f x 的单调递减区间为(0,+∞).(II)因为()f x 在区间[0,n](n ∈N )上是减函数,所以b n =()f n =ln(1)n n +,则ln(1)a nb n n n =+=.(i)因为对一切n ∈N ,不等式22ca a n n a n <++恒成立,所以22cn n n <++对于n ∈N 恒成立.则222c n n n<++对于n ∈N 恒成立.考虑函数2()22,[1,)g x x xx x =++∈+∞.因为1122()1(2)(22)2g x xx x ′=++11110122x x x x x++=<=++,所以()g x 在[1,+∞]内是减函数;则当n ∈N 时,()g n 随n 的增大而减小,又因为lim ()1g n n =→∞所以对于一切n ∈N ()g n >1.因此c ≤1,即实数c的取值范围是(∞,1).(ii)略.评注本题(II)第(i)问关键在于将222c n n n<++(n ∈N )恒成立转化为求函数2()22,[1,)g x x xx x =++∈+∞的最小值.2.3利用函数与方程思想解决解析几何问题例5(第14题)若直线340x y m ++=与圆1cos 2sin ()x y θθθ=+=+为参数没有公共点,则实数m 的取值范围是.解析1:将3144y xm=与圆方程2(1)(2)1x y ++=联立消元得223144(1)(2)1xm x ++=,由<0得实数m 的取值范围.解析2:圆心(1,2)到直线340x y m ++=的距离|314(2)|2234m d ×+×+=+,由1d r >=可得答案为(∞,0)∪(10,+∞).评注:将曲线交点个数问题转换成方程有无实根问题,借助判别式的符号得出结论是常用的方法之一;此题若利用圆的几何性质,则可借助圆心到直线的距离与半径的大小关系求解,计算过程更简捷.例6(第21题)椭圆22221x y a b+=(0)a b >>的一个焦点是(1,0)F ,O 为坐标原点.(I)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;(II)设过点F 的直线l 交椭圆于,A B 两点.若直线l 绕点F 任意转动,恒有222||||||OA OB A B +<,求a 的取值范围.解析:(I)布列方程组22232231a b c bc c =+×==解得2,3a b ==.OABFXY4福建中学数学2008年第6期(II)设11(,)A x y ,22(,)B x y .当直线A B 不与x 轴重合时,设直线AB 的方程为1x my =+,代入22221(0)a b x y a b +=>>.由恒有222||||||OA OB A B +<,所以∠A OB 恒为钝角.即OA OB=(,,)f a b m <0.所以2222222a b m aa b b >+对于m R ∈恒成立;即2a 2222220a b b a b m +<<.求出a 的取值范围即可;当直线AB 与x 轴重合恒有222||||||OA OB A B +<成立.问题获得解决.答案为((15)/2,)++∞.评注:解析几何中的许多问题都与方程联系密切.其中涉及交点坐标的问题,若结合二次方程的根与系数关系求解则能化难为易、化繁为简.本题第(Ⅱ)问虽运算量较大,但区分度也较高.3思考与商榷纵观整份试卷,试题立足基础,考查能力,突出选拔功能,尤其注重对思想方法的考查.全卷涉及到函数与与方程思想的分值64分(约占全卷42﹪),为中学数学注重思想方法教学提供良好的导向.但作为大纲试卷与课标试卷过渡期的最后一份高考试卷,若能对函数的零点存在定理或用二分法求方程的近似解作一些考查,将使试卷的过渡承转功能得以更好的体现.第12题备选项C 中,()y g x =与()y f x =的图象相对位置略显模糊,容易导致解读失误,似应加以调整.化归与转化思想是指在解决数学问题时,采用某种手段将问题进行转化,使问题得以解决的数学思想.随着高考试题的命制由知识立意转向能力立意,高考加大了对化归与转化思想的考查.本文从5个方面剖析化归与转化思想在试卷中的体现.,1熟悉化原则对于较复杂的问题,采取必要的手段,使问题逐步变得熟悉、简单、明了,并最终得以解决,这就是“化生为熟”的转化原则.例1(第15题)若三棱锥的三个侧面两两垂直,且侧棱长均为3,其外接球的表面积是________.解析:如图1所示,将三棱锥A BCD “补形”为一个相对应的正方体,把三棱锥的外接球问题转化为熟悉的正方体外接球问题,故填9π.评注:在转化空间图形时,常用平移、等积、割补等方法,使陌生问题熟悉化.例2(第4题)函数3()sin 1f x x x =++()x R ∈,若()2f a =,则()f a 的值为A .3B .0C .-1D .-2解析:由已知函数值()2f a =和待求函数值()f a 的关系,联想到熟悉的函数奇偶性,从而作出如下化归:构造奇函数3()()1sin g x f x x x ==+.进而由()()11g a f a ==及()()1g a g a ==,得()()10f a g a =+=,故选B .2简单化原则将复杂问题化归为简单问题,通过对简单问题的解决,达到解决复杂问题的目的,或获得某种解题的启示和依据.这里的简单,有时还指问题的处理方式或解决方案上的简单.例3(第题)如图,椭圆22(x y +=>2008年福建省高考数学理科试卷评析(三)化归与转化思想的考查分析张夏强1,2陈清华11.福建师范大学数学与计算机科学学院(350007)2.福建省闽清第二中学(350811)2008年第6期福建中学数学5图BD C 212221a b a b 1A。

1.Amdahl提出的计算机系统机构的经典定义是:计算机系统结构是程序员看到的计算机属性,即概念性结构和功能特性。
2.计算机系统中的提高并行性的措施很多,但就其基本思想而言,可以归为3类技术途径,这就是时间重叠、资源重复和资源共享。
3.MIPS的数据寻址方式有立即数寻址和偏移量寻址两种,但通过把0作为偏移量可实现寄存器间接寻址,而把 RO作为基址寄存器可实现16位绝对寻址方式。
4.交叉访问存储器通常有两种地址映像方式:顺序交叉和取模交叉,其中取模交叉方式不仅可以减少体冲突而且可以使用位选择方法来代替在确定体内地址时使用的除法运算。
5.互联网络从拓扑结构上可分为静态互连网络和动态…。
6.根据存储器的分布方式,多处理器计算机有两种基本结构,就是集中式共享存储结构和具有分布的物理存储器结构。
7.在多处理器系统中并行性遇到的挑战,一个是程序中的并行性有限,另一个是相对较高的通信开销。
1.系列机软件必须保证( C )A.向前兼容,并向上兼容B.向前兼容,并向下兼容C.向后兼容,力争向上兼容D.向后兼容,力争向下兼容2.计算机系统结构不包括( C )A.数据表示 B.机器工作状态的定义和切换C.主存速度 D.信息保护3.字串位并是指同时对一个字的所有位进行处理,其并行等级( D )A.不存在并行性 B.较高的并行性C.最高一级的并行性D.已经开始出现并行性4.RISC计算机的指令系统集类型是(C )A.堆栈型 B.累加器型C.寄存器—寄存器型 D.寄存器-存储器型5.关于“一次重叠”说法不正确的是( A )A.仅“执行K”与“分析K+1”重叠B. 应尽量使“分析K+1”与“执行K”时间相等C. “分析K”完后立即开始“执行K”D. 只需一套指令分析部件和一套执行部件6.在Cache存储器中常用的地址映象方式是( C )A.全相联映 B.页表法映象C.组相联映象 D.段页表映象7.块冲突概率最高的Cache地址映象方式是( A )A.直接 B.组相联 C.段相联 D.全相联8.设8个处理器编号分别为0,1,2,…,7用Cube2 (交换函数中的C2)互联函数时,第3号处理机与第( D )号处理机相联。

2008年普通高等学校招生全国统一考试(全国卷2)数学(供理科考生使用)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至4页,考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷(选择题共60分)参考公式:如果事件A B ,互斥,那么球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ,相互独立,那么 其中R 表示球的半径()()()P A B P A P B =球的体积公式如果事件A 在一次试验中发生的概率是P ,那么 34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率()(1)(012)k k n kn n P k C P p k n -=-=,,,,其中R 表示球的半径一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}3|0|31x M x x N x x x +⎧⎫==<=-⎨⎬-⎩⎭,≤,则集合{}|1x x ≥=( ) A .M N B .M NC .()M MN ðD .()M MN ð2.135(21)lim(21)x n n n →∞++++-=+( )A .14B .12C .1D .23.圆221x y +=与直线2y kx =+没有..公共点的充要条件是( )A .(k ∈B .((2)k ∈-+,∞C .(k ∈D .((3)k ∈-+,∞4.复数11212i i +-+-的虚部是( ) A .15i B .15 C .15i -D .15-5.已知O ,A ,B 是平面上的三个点,直线AB 上有一点C ,满足20AC CB +=,则OC =( ) A .2OA OB -B .2OA OB -+C .2133OA OB - D .1233OA OB -+6.设P 为曲线C :223y x x =++上的点,且曲线C 在点P 处切线倾斜角的取值范围为04π⎡⎤⎢⎥⎣⎦,,则点P横坐标的取值范围为( )A .112⎡⎤--⎢⎥⎣⎦,B .[]10-,C .[]01,D .112⎡⎤⎢⎥⎣⎦,7.4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( )A .13B .12C .23D .348.将函数21x y =+的图象按向量a 平移得到函数12x y +=的图象,则( )A .(11)=--,aB .(11)=-,aC .(11)=,aD .(11)=-,a 9.一生产过程有4道工序,每道工序需要安排一人照看.现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人中安排1人,则不同的安排方案共有( )A .24种B .36种C .48种D .72种 10.已知点P 是抛物线22y x =上的一个动点,则点P 到点(0,2)的距离与P 到该抛物线准线的距离之和的最小值为( )AB .3CD .9211.在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别为棱AA 1,CC 1的中点,则在空间中与三条直线A 1D 1、EF 、CD 都相交的直线( )A .不存在B .有且只有两条C .有且只有三条D .有无数条 12.设()f x 是连续的偶函数,且当x >0时()f x 是单调函数,则满足3()4x f x f x +⎛⎫=⎪+⎝⎭的所有x 之和为( ) A .3-B .3C .8-D .8第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分.13.函数100xx x y e x +<⎧=⎨⎩,,,≥的反函数是__________. 14.在体积为的球的表面上有A ,B ,C 三点,AB =1,BCA ,C,则球心到平面ABC 的距离为_________.15.已知231(1)nx x x x ⎛⎫+++ ⎪⎝⎭的展开式中没有..常数项,n ∈*N ,且2≤n ≤8,则n =______. 16.已知()sin (0)363f x x f f ωωπππ⎛⎫⎛⎫⎛⎫=+>= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,且()f x 在区间63ππ⎛⎫⎪⎝⎭,有最小值,无最大值,则ω=__________.三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分) 在ABC △中,内角A B C ,,对边的边长分别是a b c ,,,已知2c =,3C π=. (Ⅰ)若ABC △a b ,;(Ⅱ)若sin sin()2sin 2C B A A +-=,求ABC △的面积.18.(本小题满分12分)(Ⅰ)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;(Ⅱ)已知每吨该商品的销售利润为2千元,ξ表示该种商品两周销售利润的和(单位:千元).若以上述频率作为概率,且各周的销售量相互独立,求ξ的分布列和数学期望.19.(本小题满分12分)如图,在棱长为1的正方体ABCD A B C D ''''-中,AP=BQ=b (0<b <1),截面PQEF ∥A D ',截面PQGH ∥AD '.(Ⅰ)证明:平面PQEF 和平面PQGH 互相垂直; (Ⅱ)证明:截面PQEF 和截面PQGH 面积之和是定值,并求出这个值;(Ⅲ)若D E '与平面PQEF 所成的角为45,求D E '与平 面PQGH 所成角的正弦值. 20.(本小题满分12分)在直角坐标系xOy 中,点P 到两点(0,(0的距离之和等于4,设点P 的轨迹为C ,直线1y kx =+与C 交于A ,B 两点.(Ⅰ)写出C 的方程;(Ⅱ)若OA ⊥OB ,求k 的值;A BCDE FP Q H A ' B 'C 'D 'G(Ⅲ)若点A 在第一象限,证明:当k >0时,恒有|OA |>|OB |. 21.(本小题满分12分)在数列||n a ,||n b 中,a 1=2,b 1=4,且1n n n a b a +,,成等差数列,11n n n b a b ++,,成等比数列(n ∈*N ) (Ⅰ)求a 2,a 3,a 4及b 2,b 3,b 4,由此猜测||n a ,||n b 的通项公式,并证明你的结论; (Ⅱ)证明:1122111512n n a b a b a b +++<+++….22.(本小题满分14分) 设函数ln ()ln ln(1)1xf x x x x=-+++. (Ⅰ)求f (x )的单调区间和极值;(Ⅱ)是否存在实数a ,使得关于x 的不等式()f x a ≥的解集为(0,+∞)?若存在,求a 的取值范围;若不存在,试说明理由.2008年普通高等学校招生全国统一考试(辽宁卷) 数学(供理科考生使用)试题参考答案和评分参考说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分.一、选择题:本题考查基本知识和基本运算.每小题5分,共60分. 1.D 2.B 3.C 4.B 5.A 6.A 7.C 8.A 9.B 10.A 11.D 12.C 二、填空题:本题考查基本知识和基本运算.每小题4分,满分16分. 13.11ln 1.x x y x x -<⎧=⎨⎩,,, ≥14.3215.516.143三、解答题17.本小题主要考查三角形的边角关系,三角函数公式等基础知识,考查综合应用三角函数有关知识的能力.满分12分.解:(Ⅰ)由余弦定理及已知条件得,224a b ab +-=, 又因为ABC △1sin 2ab C =4ab =. ······················· 4分 联立方程组2244a b ab ab ⎧+-=⎨=⎩,,解得2a =,2b =. ·············································· 6分(Ⅱ)由题意得sin()sin()4sin cos B A B A A A ++-=,即sin cos 2sin cos B A A A =, ········································································ 8分 当cos 0A =时,2A π=,6B π=,a =b =, 当cos 0A ≠时,得sin 2sin B A =,由正弦定理得2b a =,联立方程组2242a b ab b a ⎧+-=⎨=⎩,,解得a =b =所以ABC △的面积1sin 2S ab C ==······················································ 12分18.本小题主要考查频率、概率、数学期望等基础知识,考查运用概率知识解决实际问题的能力.满分12分. 解:(Ⅰ)周销售量为2吨,3吨和4吨的频率分别为0.2,0.5和0.3. ····················· 3分 (Ⅱ)ξ的可能值为8,10,12,14,16,且 P (ξ=8)=0.22=0.04, P (ξ=10)=2×0.2×0.5=0.2, P (ξ=12)=0.52+2×0.2×0.3=0.37, P (ξ=14)=2×0.5×0.3=0.3, P (ξ=16)=0.32=0.09.ξ的分布列为·················································································· 9分E ξ=8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4(千元) ···························· 12分 19.本小题主要考查空间中的线面关系,面面关系,解三角形等基础知识,考查空间想象能力与逻辑思维能力。

2008年普通高等学校招生全国统一考试(福建卷)数 学(理工类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)若复数2(32)(1)a a a i -++-是纯虚数,则实数a 的值为A.1B.2C.1或2D.-1解:由2320a a -+=得12a =或,且101a a -≠≠得2a ∴=(纯虚数一定要使虚部不为0) (2)设集合{|0}1xA x x =<-,{|03}B x x =<<,那么“m ∈A ”是“m ∈B ”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件解:由01xx <-得01x <<,可知“m A ∈”是“m B ∈”的充分而不必要条件 (3)设{a n }是公比为正数的等比数列,若151,16a a ==,则数列{}n a 前7项的和为A.63B.64C.127D.128解:由151,16a a ==及{a n }是公比为正数得公比2q =,所以771212712S -==- (4)函数3()sin 1()f x x x x R =++∈,若()2f a =,则()f a -的值为A.3B.0C.-1D.-2解:3()1sin f x x x -=+为奇函数,又()2f a =∴()11f a -=故()11f a --=-即()0f a -=.(5)某一批花生种子,如果每1粒发牙的概率为45,那么播下4粒种子恰有2粒发芽的概率是 A.16625B.96625C. 192625D. 256625解:独立重复实验4(4,)5B ,22244196(2)55625P k C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭A(6)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为B.C.D.解:连11A C 与11B D 交与O 点,再连BO,则1OBC ∠为BC 1与平面BB 1D 1D所成角.111OC COS OBC BC ∠=,1OC =,1BC =1COS OBC ∴∠== (7)某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48解:6人中选4人的方案4615C =种,没有女生的方案只有一种,所以满足要求的方案总数有14种 (8)若实数x 、y 满足100x y x -+≤⎧⎨>⎩ 则yx 的取值范围是A.(0,1)B.(]0,1C.(1,+∞)D.[)1,+∞解:由已知1y x ≥+,111y x x x x +==+,又0x >,故yx的取值范围是(1,)+∞(9)函数()cos ()f x x x R =∈的图象按向量(,0)m 平移后,得到函数'()y f x =-的图象, 则m 的值可以为A.2πB.πC.-πD.- 2π解:()sin y f x x '=-=,而()cos ()f x x x R =∈的图象按向量(,0)m 平移后得到cos()y x m =-,所以cos()sin x m x -=,故m可以为2π. (10)在△ABC 中,角ABC 的对边分别为a 、b 、c ,若222(a +c -b ,则角B 的值为A.6π B.3π C.6π或56πD.3π或23π解: 由222(a +c -b 3ac 得222(a +c -b )3cos = 22sin Bac B即3cos cos = 2sin B B B3sin B ∴,又在△中所以B 为3π或23π(11)双曲线22221x y a b-=(a >0,b >0)的两个焦点为F 1、F 2,若P 为其上一点,且|PF 1|=2|PF 2|,则双曲线离心率的取值范围为A.(1,3)B.(]1,3C.(3,+∞)D.[)3,+∞解:如图,设2PF m =,12(0)F PF θθπ∠=<≤,当P 在右顶点处θπ=,222(2)4cos 254cos 2m m m c e a θθ+-===-∵1cos 1θ-<≤,∴(]1,3e ∈另外也可用三角形的两边和大于第三边,及两边差小于第三边,但要注意前者可以取到等号成立,因为可以三点一线. 也可用焦半径公式确定a 与c 的关系。

2008年高考北京理科数学详解一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知全集U =R ,集合{}|23A x x =-≤≤,{}|14B x x x =<->或,那么集合()U A B ð等于( )A .{}|24x x -<≤B .{}|34x x x 或≤≥C .{}|21x x -<-≤D .{}|13x x -≤≤【标准答案】: D【试题分析】: C U B=[-1, 4],()U A B ð={}|13x x -≤≤ 【高考考点】:集合【易错提醒】: 补集求错【备考提示】: 高考基本得分点 2.若0.52a =,πlog 3b =,22πlo g sin5c =,则( )A .a b c >>B .b a c >>C .c a b >>D .b c a >> 【标准答案】: A【试题分析】:利用估值法知a 大于1,b 在0与1之间,c 小于0. 【高考考点】: 函数的映射关系,函数的图像。
【易错提醒】: 估值出现错误。
【备考提示】: 大小比较也是高考较常见的题型,希望引起注意。
3.“函数()()f x x ∈R 存在反函数”是“函数()f x 在R 上为增函数”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【标准答案】: B【试题分析】: 函数()()f x x ∈R 存在反函数,至少还有可能函数()f x 在R 上为减函数,充分条件不成立;而必有条件显然成立。
【高考考点】: 充要条件,反函数,映射关系,函数单调性。
【易错提醒】: 单调性与一一对应之间的关系不清楚 【备考提示】: 平时注意数形结合训练。
4.若点P 到直线1x =-的距离比它到点(20),的距离小1,则点P 的轨迹为( ) A .圆 B .椭圆 C .双曲线 D .抛物线【标准答案】: D【试题分析】: 把P 到直线1x =-向左平移一个单位,两个距离就相等了,它就是抛物线的定义。

稳中求新、突出能力、多题把关——08年福建高考数学试卷评析浦城一中徐转贵一、整体评价:2008年福建高考数学试题从整体看,贯彻了“总体保持稳定,深化能力立意,积极改革创新”的指导思想,试题在保持连续稳定继承历年特点的同时,又注重了改革创新;试卷既注重了对基础知识的重点考查(1-11题、13-15题、17-18题、19-22题的第一问),也注重了对能力的考查(12题、16题、19-22题的第二问)。
从考生的反映来看,试题总体难度适中,且最后两道大题的第二问,考查有一定的深度,有较好的区分度和效度,有利于高校选拔;试卷坚持重点内容重点考查,注重在“知识的交叉处”命题,且注重对常规数学思想方法以及通性、通法的考查,注重创新意识、应用能力的考查,全卷稳中求新,新中求活,活中凸显能力。
1、试卷结构保持稳定:今年的数学试题与往年的试题在题量上、题型分布上仍保持不变,各种题型个数及分布没有太大的发生变化(只是应用题移到20题位置,后移一位),选择题仍为12道,60分;填空题仍为4道,分值为16分;解答题仍为6道,分值为74分。
2、注重数学应用和创新意识的考查:08年高考数学题的一个变化是将前几年19题的应用题放到了第四道大题(第20题),它要求考生应理论联系实际,综合应用所学数学知识、思想和方法,通过一定的推理逻辑分析对问题做出符合实际的分类判断,它考查学生数学建模的能力,既考查从数学的角度观察、思考和分析实际问题的能力,又考查相关知识及技能的理解和掌握程度,从而有效地考查学生综合素质。
3、拉大文理科的差别:今年的试题文理科完全相同的试题只有6道,完全不同的题有8道题,其它为姐妹题,比往年拉大了文理科的试题差距,兼顾了我省文科考生的实际状况,做到文理起点不同,终点相同的目标。
4、在知识的交汇点处命制试题,体现能力立意:试题强调了知识间的内在联系,注重各部分知识的综合性,注重在知识网络的交汇点处设计试题。
试题大都涉及到两个或两个以上章节的知识点,比较典型的是第17题为三角向量二次函数的交汇,第19题为函数与数列的交汇、第21题为解析几何向量不等式的交汇,第22题是函数导数与数列的综合等等。

2008年全国统一高考数学试卷(理科)(全国卷Ⅰ)一、选择题(共12小题,每小题5分,满分60分)1.(5分)函数的定义域为()A.{x|x≥0}B.{x|x≥1}C.{x|x≥1}∪{0}D.{x|0≤x≤1} 2.(5分)掷一个骰子,向上一面的点数大于2且小于5的概率为p1,拋两枚硬币,正面均朝上的概率为p2,则()A.p1<p2 B.p1>p2 C.p1=p2D.不能确定3.(5分)在△ABC中,=,=.若点D满足=2,则=()A.B.C.D.4.(5分)设a∈R,且(a+i)2i为正实数,则a=()A.2 B.1 C.0 D.﹣15.(5分)已知等差数列{a n}满足a2+a4=4,a3+a5=10,则它的前10项的和S10=()A.138 B.135 C.95 D.236.(5分)若函数y=f(x)的图象与函数y=ln的图象关于直线y=x 对称,则f(x)=()A.e2x﹣2B.e2x C.e2x+1D.e2x+27.(5分)设曲线在点(3,2)处的切线与直线ax+y+1=0垂直,则a=()A.2 B.C.D.﹣28.(5分)为得到函数的图象,只需将函数y=sin2x的图象()A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位9.(5分)设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式<0的解集为()A.(﹣1,0)∪(1,+∞)B.(﹣∞,﹣1)∪(0,1)C.(﹣∞,﹣1)∪(1,+∞)D.(﹣1,0)∪(0,1)10.(5分)若直线=1与圆x2+y2=1有公共点,则()A.a2+b2≤1 B.a2+b2≥1 C. D.11.(5分)已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,则AB1与底面ABC所成角的正弦值等于()A.B. C. D.12.(5分)如图,一环形花坛分成A,B,C,D四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为()A.96 B.84 C.60 D.48二、填空题(共4小题,每小题5分,满分20分)13.(5分)若x,y满足约束条件,则z=2x﹣y的最大值为.14.(5分)已知抛物线y=ax2﹣1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为.15.(5分)在△ABC中,AB=BC,.若以A,B为焦点的椭圆经过点C,则该椭圆的离心率e=.16.(5分)等边三角形ABC与正方形ABDE有一公共边AB,二面角C﹣AB﹣D的余弦值为,M,N分别是AC,BC的中点,则EM,AN 所成角的余弦值等于.三、解答题(共6小题,满分74分)17.(10分)设△ABC的内角A,B,C所对的边长分别为a,b,c,且acosB﹣bcosA=c.(Ⅰ)求的值;(Ⅱ)求tan(A﹣B)的最大值.18.(12分)四棱锥A﹣BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,,AB=AC.(Ⅰ)证明:AD⊥CE;(Ⅱ)设CE与平面ABE所成的角为45°,求二面角C﹣AD﹣E的大小.19.(12分)已知函数f(x)=﹣x2+ax+1﹣lnx.(Ⅰ)当a=3时,求函数f(x)的单调递增区间;(Ⅱ)若f(x)在区间(0,)上是减函数,求实数a的取值范围.20.(12分)已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方法:方案甲:逐个化验,直到能确定患病动物为止.方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;(Ⅱ)ξ表示依方案乙所需化验次数,求ξ的期望.21.(12分)双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.已知||、||、||成等差数列,且与同向.(Ⅰ)求双曲线的离心率;(Ⅱ)设AB被双曲线所截得的线段的长为4,求双曲线的方程.22.(12分)设函数f(x)=x﹣xlnx.数列{a n}满足0<a1<1,a n+1=f (a n).(Ⅰ)证明:函数f(x)在区间(0,1)是增函数;(Ⅱ)证明:a n<a n+1<1;(Ⅲ)设b∈(a1,1),整数.证明:a k+1>b.2008年全国统一高考数学试卷(理科)(全国卷Ⅰ)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)(2008•全国卷Ⅰ)函数的定义域为()A.{x|x≥0}B.{x|x≥1}C.{x|x≥1}∪{0}D.{x|0≤x≤1}【分析】偶次开方的被开方数一定非负.x(x﹣1)≥0,x≥0,解关于x的不等式组,即为函数的定义域.【解答】解:由x(x﹣1)≥0,得x≥1,或x≤0.又因为x≥0,所以x≥1,或x=0;所以函数的定义域为{x|x≥1}∪{0}故选C.2.(5分)(2008•全国卷Ⅰ)掷一个骰子,向上一面的点数大于2且小于5的概率为p1,拋两枚硬币,正面均朝上的概率为p2,则()A.p1<p2 B.p1>p2 C.p1=p2D.不能确定【分析】计算出各种情况的概率,然后比较即可.【解答】解:大于2小于5的数有2个数,∴p1==;投掷一次正面朝上的概率为,两次正面朝上的概率为p2=×=,∵>,∴p1>p2.故选B.3.(5分)(2008•全国卷Ⅰ)在△ABC中,=,=.若点D满足=2,则=()A.B.C.D.【分析】把向量用一组向量来表示,做法是从要求向量的起点出发,尽量沿着已知向量,走到要求向量的终点,把整个过程写下来,即为所求.本题也可以根据D点把BC分成一比二的两部分入手.【解答】解:∵由,∴,∴.故选A4.(5分)(2008•全国卷Ⅰ)设a∈R,且(a+i)2i为正实数,则a=()A.2 B.1 C.0 D.﹣1【分析】注意到a+bi(a,b∈R)为正实数的充要条件是a>0,b=0 【解答】解:(a+i)2i=(a2+2ai﹣1)i=﹣2a+(a2﹣1)i>0,a=﹣1.故选D.5.(5分)(2008•全国卷Ⅰ)已知等差数列{a n}满足a2+a4=4,a3+a5=10,则它的前10项的和S10=()A.138 B.135 C.95 D.23【分析】本题考查的知识点是等差数列的性质,及等差数列前n项和,根据a2+a4=4,a3+a5=10我们构造关于基本量(首项及公差)的方程组,解方程组求出基本量(首项及公差),进而代入前n项和公式,即可求解.【解答】解:∵(a3+a5)﹣(a2+a4)=2d=6,∴d=3,a1=﹣4,∴S10=10a1+=95.故选C6.(5分)(2008•全国卷Ⅰ)若函数y=f(x)的图象与函数y=ln的图象关于直线y=x对称,则f(x)=()A.e2x﹣2B.e2x C.e2x+1D.e2x+2【分析】由函数y=f(x)的图象与函数y=ln的图象关于直线y=x 对称知这两个函数互为反函数,故只要求出函数y=f(x)的反函数即可,欲求原函数的反函数,即从原函数y=ln中反解出x,后再进行x,y互换,即得反函数的解析式.【解答】解:∵,∴,∴x=(e y﹣1)2=e2y﹣2,改写为:y=e2x﹣2∴答案为A.7.(5分)(2008•全国卷Ⅰ)设曲线在点(3,2)处的切线与直线ax+y+1=0垂直,则a=()A.2 B.C.D.﹣2【分析】(1)求出已知函数y在点(3,2)处的斜率;(2)利用两条直线互相垂直,斜率之间的关系k1•k2=﹣1,求出未知数a.【解答】解:∵y=∴y′=﹣∵x=3∴y′=﹣即切线斜率为﹣∵切线与直线ax+y+1=0垂直∴直线ax+y+1=0的斜率为﹣a.∴﹣•(﹣a)=﹣1得a=﹣2故选D.8.(5分)(2008•全国卷Ⅰ)为得到函数的图象,只需将函数y=sin2x的图象()A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位【分析】先根据诱导公式将函数化为正弦的形式,再根据左加右减的原则进行平移即可得到答案.【解答】解:∵,只需将函数y=sin2x的图象向左平移个单位得到函数的图象.故选A.9.(5分)(2008•全国卷Ⅰ)设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式<0的解集为()A.(﹣1,0)∪(1,+∞)B.(﹣∞,﹣1)∪(0,1)C.(﹣∞,﹣1)∪(1,+∞)D.(﹣1,0)∪(0,1)【分析】首先利用奇函数定义与得出x与f(x)异号,然后由奇函数定义求出f(﹣1)=﹣f(1)=0,最后结合f(x)的单调性解出答案.【解答】解:由奇函数f(x)可知,即x与f (x)异号,而f(1)=0,则f(﹣1)=﹣f(1)=0,又f(x)在(0,+∞)上为增函数,则奇函数f(x)在(﹣∞,0)上也为增函数,当0<x<1时,f(x)<f(1)=0,得<0,满足;当x>1时,f(x)>f(1)=0,得>0,不满足,舍去;当﹣1<x<0时,f(x)>f(﹣1)=0,得<0,满足;当x<﹣1时,f(x)<f(﹣1)=0,得>0,不满足,舍去;所以x的取值范围是﹣1<x<0或0<x<1.故选D.10.(5分)(2008•全国卷Ⅰ)若直线=1与圆x2+y2=1有公共点,则()A.a2+b2≤1 B.a2+b2≥1 C. D.【分析】用圆心到直线的距离小于或等于半径,可以得到结果.【解答】解:直线与圆有公共点,即直线与圆相切或相交得:d≤r ,∴故选D.11.(5分)(2008•全国卷Ⅰ)已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,则AB1与底面ABC所成角的正弦值等于()A.B. C. D.【分析】法一:由题意可知三棱锥A1﹣ABC为正四面体,设棱长为2,求出AB1及三棱锥的高,由线面角的定义可求出答案;法二:先求出点A1到底面的距离A1D的长度,即知点B1到底面的距离B1E的长度,再求出AE的长度,在直角三角形AEB1中求AB1与底面ABC所成角的正切,再由同角三角函数的关系求出其正弦.【解答】解:(法一)因为三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,设为D,所以三棱锥A1﹣ABC为正四面体,设棱长为2,则△AA1B1是顶角为120°等腰三角形,所以AB1=2×2×sin60°=2,A1D==,所以AB1与底面ABC所成角的正弦值为==;(法二)由题意不妨令棱长为2,点B1到底面的距离是B1E,如图,A1在底面ABC内的射影为△ABC的中心,设为D,故DA=,由勾股定理得A1D==故B1E=,如图作A1S⊥AB于中点S,易得A1S=,所以AB1==2,所以AB1与底面ABC所成角的正弦值sin∠B1AE==.故选B.12.(5分)(2008•全国卷Ⅰ)如图,一环形花坛分成A,B,C,D四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为()A.96 B.84 C.60 D.48【分析】这道题比起前几年出的高考题要简单些,只要分类清楚没有问题,分为三类:分别种两种花、三种花、四种花,分这三类来列出结果.【解答】解:分三类:种两种花有A42种种法;种三种花有2A43种种法;种四种花有A44种种法.共有A42+2A43+A44=84.故选B二、填空题(共4小题,每小题5分,满分20分)13.(5分)(2008•全国卷Ⅰ)若x,y满足约束条件,则z=2x﹣y的最大值为9.【分析】首先作出可行域,再作出直线l0:y=2x,将l0平移与可行域有公共点,直线y=2x﹣z在y轴上的截距最小时,z有最大值,求出此时直线y=2x﹣z经过的可行域内的点的坐标,代入z=2x﹣y中即可.【解答】解:如图,作出可行域,作出直线l0:y=2x,将l0平移至过点A处时,函数z=2x﹣y有最大值9.14.(5分)(2008•全国卷Ⅰ)已知抛物线y=ax2﹣1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为2.【分析】先根据抛物线y=ax2﹣1的焦点坐标为坐标原点,求得a,得到抛物线方程,进而可知与坐标轴的交点的坐标,进而可得答案.【解答】解:由抛物线y=ax2﹣1的焦点坐标为坐标原点得,,则与坐标轴的交点为(0,﹣1),(﹣2,0),(2,0),则以这三点围成的三角形的面积为故答案为215.(5分)(2008•全国卷Ⅰ)在△ABC中,AB=BC,.若以A,B为焦点的椭圆经过点C,则该椭圆的离心率e=.【分析】设AB=BC=1,,则,由此可知,从而求出该椭圆的离心率.【解答】解:设AB=BC=1,,则,∴,.答案:.16.(5分)(2008•全国卷Ⅰ)等边三角形ABC与正方形ABDE有一公共边AB,二面角C﹣AB﹣D的余弦值为,M,N分别是AC,BC 的中点,则EM,AN所成角的余弦值等于.【分析】先找出二面角的平面角,建立边之间的等量关系,再利用向量法将所求异面直线用基底表示,然后利用向量的所成角公式求出所成角即可.【解答】解:设AB=2,作CO⊥面ABDE,OH⊥AB,则CH⊥AB,∠CHO为二面角C﹣AB﹣D的平面角,结合等边三角形ABC与正方形ABDE可知此四棱锥为正四棱锥,则,=故EM,AN所成角的余弦值故答案为:三、解答题(共6小题,满分74分)17.(10分)(2008•全国卷Ⅰ)设△ABC的内角A,B,C所对的边长分别为a,b,c,且acosB﹣bcosA=c.(Ⅰ)求的值;(Ⅱ)求tan(A﹣B)的最大值.【分析】本题考查的知识点是正弦定理及两角和与差的正切函数,(Ⅰ)由正弦定理的边角互化,我们可将已知中,进行转化得到sinAcosB=4cosAsinB,再利用弦化切的方法即可求的值.(Ⅱ)由(Ⅰ)的结论,结合角A,B,C为△ABC的内角,我们易得tanA=4tanB>0,则tan(A﹣B)可化为,再结合基本不等式即可得到tan(A﹣B)的最大值.【解答】解:(Ⅰ)在△ABC中,,由正弦定理得即sinAcosB=4cosAsinB,则;(Ⅱ)由得tanA=4tanB>0当且仅当时,等号成立,故当时,tan(A﹣B)的最大值为.18.(12分)(2008•全国卷Ⅰ)四棱锥A﹣BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,,AB=AC.(Ⅰ)证明:AD⊥CE;(Ⅱ)设CE与平面ABE所成的角为45°,求二面角C﹣AD﹣E的大小.【分析】(1)取BC中点F,证明CE⊥面ADF,通过证明线面垂直来达到证明线线垂直的目的.(2)在面AED内过点E作AD的垂线,垂足为G,由(1)知,CE⊥AD,则∠CGE即为所求二面角的平面角,△CGE中,使用余弦定理求出此角的大小.【解答】解:(1)取BC中点F,连接DF交CE于点O,∵AB=AC,∴AF⊥BC.又面ABC⊥面BCDE,∴AF⊥面BCDE,∴AF⊥CE.再根据,可得∠CED=∠FDC.又∠CDE=90°,∴∠OED+∠ODE=90°,∴∠DOE=90°,即CE⊥DF,∴CE⊥面ADF,∴CE⊥AD.(2)在面ACD内过C点作AD的垂线,垂足为G.∵CG⊥AD,CE⊥AD,∴AD⊥面CEG,∴EG⊥AD,则∠CGE即为所求二面角的平面角.作CH⊥AB,H为垂足.∵平面ABC⊥平面BCDE,矩形BCDE中,BE⊥BC,故BE⊥平面ABC,CH⊂平面ABC,故BE⊥CH,而AB∩BE=B,故CH⊥平面ABE,∴∠CEH=45°为CE与平面ABE所成的角.∵CE=,∴CH=EH=.直角三角形CBH中,利用勾股定理求得BH===1,∴AH=AB﹣BH=AC﹣1;直角三角形ACH中,由勾股定理求得AC2=CH2+AH2=3+(AC﹣1)2,∴AB=AC=2.由面ABC⊥面BCDE,矩形BCDE中CD⊥CB,可得CD⊥面ABC,故△ACD为直角三角形,AD===,故CG===,DG==,,又,则,∴,即二面角C﹣AD﹣E的大小.19.(12分)(2010•大纲版Ⅱ)已知函数f(x)=﹣x2+ax+1﹣lnx.(Ⅰ)当a=3时,求函数f(x)的单调递增区间;(Ⅱ)若f(x)在区间(0,)上是减函数,求实数a的取值范围.【分析】(1)求单调区间,先求导,令导函数大于等于0即可.(2)已知f(x)在区间(0,)上是减函数,即f′(x)≤0在区间(0,)上恒成立,然后用分离参数求最值即可.【解答】解:(Ⅰ)当a=3时,f(x)=﹣x2+3x+1﹣lnx∴解f′(x)>0,即:2x2﹣3x+1<0函数f(x)的单调递增区间是.(Ⅱ)f′(x)=﹣2x+a﹣,∵f(x)在上为减函数,∴x∈时﹣2x+a﹣≤0恒成立.即a≤2x+恒成立.设,则∵x∈时,>4,∴g′(x)<0,∴g(x)在上递减,∴g(x)>g()=3,∴a≤3.20.(12分)(2008•全国卷Ⅰ)已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方法:方案甲:逐个化验,直到能确定患病动物为止.方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;(Ⅱ)ξ表示依方案乙所需化验次数,求ξ的期望.【分析】(1)由题意得到这两种方案的化验次数,算出在各个次数下的概率,写出化验次数的分布列,求出方案甲所需化验次数不少于依方案乙所需化验次数的概率.(2)根据上一问乙的化验次数的分布列,利用期望计算公式得到结果.【解答】解:(Ⅰ)若乙验两次时,有两种可能:①先验三只结果为阳性,再从中逐个验时,恰好一次验中概率为:②先验三只结果为阴性,再从其它两只中验出阳性(无论第二次试验中有没有,均可以在第二次结束),∴乙只用两次的概率为.若乙验三次时,只有一种可能:先验三只结果为阳性,再从中逐个验时,恰好二次验中概率为在三次验出时概率为∴甲种方案的次数不少于乙种次数的概率为:(Ⅱ)ξ表示依方案乙所需化验次数,∴ξ的期望为Eξ=2×0.6+3×0.4=2.4.21.(12分)(2008•全国卷Ⅰ)双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.已知||、||、||成等差数列,且与同向.(Ⅰ)求双曲线的离心率;(Ⅱ)设AB被双曲线所截得的线段的长为4,求双曲线的方程.【分析】(1)由2个向量同向,得到渐近线的夹角范围,求出离心率的范围,再用勾股定理得出直角三角形的2个直角边的长度比,联想到渐近线的夹角,求出渐近线的斜率,进而求出离心率.(2)利用第(1)的结论,设出双曲线的方程,将AB方程代入,运用根与系数的关系及弦长公式,求出待定系数,即可求出双曲线方程.【解答】解:(1)设双曲线方程为,由,同向,∴渐近线的倾斜角为(0,),∴渐近线斜率为:,∴.∵||、||、||成等差数列,∴|OB|+|OA|=2|AB|,∴|AB|2=(|OB|﹣|OA|)(|OB|+|OA|)=(|OB|﹣|OA|)•2|AB|,∴,∴,可得:,而在直角三角形OAB中,注意到三角形OAF也为直角三角形,即tan∠AOB=,而由对称性可知:OA的斜率为k=tan,∴,∴2k2+3k﹣2=0,∴;∴,∴,∴.(2)由第(1)知,a=2b,可设双曲线方程为﹣=1,∴c=b.由于AB的倾斜角为+∠AOB,故AB的斜率为tan(+∠AOB )=﹣cot(∠AOB)=﹣2,∴AB的直线方程为y=﹣2(x﹣b),代入双曲线方程得:15x2﹣32bx+84b2=0,∴x1+x2=,x1•x2=,∴4=•=•,即16=﹣112b2,∴b2=9,所求双曲线方程为:﹣=1.22.(12分)(2008•全国卷Ⅰ)设函数f(x)=x﹣xlnx.数列{a n}满足0<a1<1,a n+1=f(a n).(Ⅰ)证明:函数f(x)在区间(0,1)是增函数;(Ⅱ)证明:a n<a n+1<1;(Ⅲ)设b∈(a1,1),整数.证明:a k+1>b.【分析】(1)首先求出函数的导数,然后令f′(x)=0,解出函数的极值点,最后根据导数判断函数在区间(0,1)上的单调性,从而进行证明.(2)由题意数列{a n}满足0<a1<1,a n+1=f(a n),求出a n+1=a n﹣a n lna n,然后利用归纳法进行证明;=f(a n)可得a k+1=a k﹣b﹣a k,然后(3)由题意f(x)=x﹣xlnx,a n+1进行讨论求解.【解答】解:(Ⅰ)证明:∵f(x)=x﹣xlnx,∴f′(x)=﹣lnx,当x∈(0,1)时,f′(x)=﹣lnx>0故函数f(x)在区间(0,1)上是增函数;(Ⅱ)证明:(用数学归纳法)(i)当n=1时,0<a1<1,a1lna1<0,a2=f(a1)=a1﹣a1lna1>a1,∵函数f(x)在区间(0,1)是增函数且函数f(x)在x=1处连续,∴f(x)在区间(0,1]是增函数,a2=f(a1)=a1﹣a1lna1<1,即a1<a2<1成立,(ⅱ)假设当x=k(k∈N+)时,a k<a k+1<1成立,即0<a1≤a k<a k+1<1,那么当n=k+1时,由f(x)在区间(0,1]是增函数,0<a1≤a k<a k+1<1,得f(a k)<f(a k+1)<f(1),=f(a n),而a n+1则a k=f(a k),a k+2=f(a k+1),a k+1<a k+2<1,+1也就是说当n=k+1时,a n<a n+1<1也成立,根据(ⅰ)、(ⅱ)可得对任意的正整数n,a n<a n+1<1恒成立.=f(a n)可得(Ⅲ)证明:由f(x)=x﹣xlnx,a n+1a k+1=a k﹣a k lna k=,1)若存在某i≤k2,满足a i≤b3,则由(Ⅱ)知:a k+1﹣b<a i﹣b≥04,2)若对任意i≤k6,都有a i>b,则a k+1=a k﹣a k lna k==≥a1﹣b1﹣ka1ln=0,即a k>b成立.+1。
编者按:2008年福建省高考倍受关注,原因在于这是“大纲课程”的最后一次高考,承载着由“大纲试卷”向“课标试卷”平稳过渡的导向任务,人们希望从这份试卷中得到启发,为明年“课标课程”的第一次高考而未雨绸缪.基于同样的原因,本刊特邀部分专家从不同的视角对2008年福建省高考数学理科试卷进行评析.2008年福建省高考数学理科试卷评析(一)试卷的总体分析与思考方碧贞1,2柯跃海1陈清华11福建师范大学数学与计算机科学学院(350007)2福建省仙游第一中学(351200)1试卷分析1.1试卷题量与分值分布分析与2004-2007年福建省自行命题的数学高考试卷一致,2008年福建省高考数学理科试卷设置了22题试题.其中,第1-12题为选择题,每题5分;第13-16题为填空题,每题4分;第17-22题为解答题,17-21题每题12分,22题14分.全卷满分150分.1.2考查内容分布分析表一:内容考查分布表章节题号1.集合与简易逻辑22.函数4、12、17、19、223.数列3、19、224.三角函数4、9、10、175.平面向量9、17、216.不等式2、8、227.直线和圆的方程148.圆锥曲线的方程11、219.直线、平面、简单几何体6、15、1810.排列、组合与二项式定理7、1311.概率、概率与统计5、2012.导数及其应用9、12、19、2213.极限2214.复数115.新知学与用16表一列举的数据表明,试卷保持了前四年试卷的风格,重视在知识网络的交汇处设置试题,既注重全面考查基础知识又突出考查主干内容,各知识版块的考查与前四年试卷的相应部分保持相对稳定,所考查内容的分布较为合理.1.3考查基本数学思想的分布分析表二:基本数学思想考查分布表数学思想题号1.函数与方程思想4、12、14、17、19、21、222.化归与转化思想4、7、8、10、15、18、213.数与形结合思想2、8、9、11、12、14、19、214.分类与整合思想1、7、19、20、21表二列举的数据表明,试卷加大了数学思想的考查力度,以数学知识为素材全面考查了最基本的数学思想,体现了高考命题关注从数学学科的整体意义和思想价值立意、注重通性通法、淡化特殊技巧的理念,对中学数学教学有着较好的导向作用.1.4考查数学能力的分布分析表三:数学能力考查分布表数学能力题号1.运算能力除9、12外2.空间想象能力6、15、183.应用意识5、7、204.创新意识16表三列举的数据表明,试卷以数学知识为依托,以问题为载体,较为全面考查各种能力.试卷侧重考查考生理解和应用、尤其是综合和灵活应用知识的能力,较好地发挥了试卷的选拔功能.2试卷评价2.1总体评价试卷以教育部年颁发的《全日制普通高级2008年第6期福建中学数学12002中学数学教学大纲》、教育部考试中心颁发的《2008年普通高等学校招生全国统一考试大纲》及福建省教育厅颁发的《2008年福建省高考数学科考试说明》为依据.试卷结构与前四年的试卷结构基本保持一致,试卷注重对基础知识、基本技能的考查,同时突出考查主干知识,适度考查了实际应用能力和创新能力.试卷中难、中、易试题比例较恰当,整体难度适中,与往年相比,难度基本持平.比较符合我省高中数学教学的实际.2.2特点剖析2.2.1注重基础,突出重点试卷紧扣《考试大纲》,重视对中学数学基础知识、基本技能和基本方法的考查.试题突出通性通法.选择题第(1)-(11)题,填空题第(13)-(15)题,解答题第(17)、(18)、(20)题等,都是以考查基础知识、基本方法为主的题目,并且贴近教材,符合中学教学实际.试卷对中学数学主干内容作了重点考查.函数、导数及其应用、三角函数、不等式、数列、平面向量、立体几何、解析几何、概率与概率统计等内容在试卷中占有较大的比重.2.2.2重视对能力与素质的考查,注重考查综合运用能力试题注重对思维能力、运算能力、空间想象能力以及对知识的综合运用能力的考查.第(18)、(19)、(21)、(22)题都突出考查运算能力(特别是对字母符号的计算要求较高).第(18)题既可以通过空间线面关系解答,也可以通过建立空间直角坐标系解答,考查了空间想象能力、逻辑推理能力.第(16)题是一道信息阅读题,通过引入“数域”的概念,考查了学习新知识、应用新知识的能力.2.2.3重视对数学思想方法的考查试卷在考查基础知识、基本技能的同时,重视数学思想和方法的考查.其中对函数与方程思想、化归与转化思想、数与形结合思想以及分类与整合思想的考查力度更大.2.2.4部分试题有新意试卷中部分试题有新意,对知识的理解以及知识和能力的综合运用要求较高.第(12)题以图象考查原函数与导函数之间的关系,由于设置了两个函数,使得知识背景与知识应用的新颖度大为提高;第(16)题的背景新颖,是初等数学与高等数学的交汇点.2.3逐题分析2.3.1选择题第1-11题为常规题,考生可以较为顺利地完成解答.第12题考查导数与原函数的关系,读图、识图、用图是关键,试题具有一定的思维灵活性.2.3.2填空题第13-14题为常规题.第16题为创新题,考查高等代数的一个概念:数域.其解答要求考生具有一定的数学能力与数学思想内涵,此题起点高、落点低,问题情景较有新意.2.3.3解答题第17、18、20题属于常规题,运算量适中.其它解答题的“入口”较宽,“出口”较窄,于考生而言具有一定的挑战性.第19题对考生的理解能力和运算能力有较高的要求,部分学生会因此影响后续的解题.第21题的第(Ⅱ)小题运算量比较大,难度较高;第22题考查导数,尤其第(Ⅱ)、(Ⅲ)小题考查不等式的证明,综合性较强,对考生思维深度的要求较高.3建议与商榷纵观整份试卷,无论是从试题的难度、还是从考试内容的分布看,都较为符合福建省中学数学教学的实际,对中学数学的教学有一定的导向作用.但也存在一些值得进一步商榷的问题.(1)试题的创新程度似应进一步提高,考生学习潜能的考查稍嫌不足.(2)单纯以概率知识的简单应用来考查考生的应用意识,其信度似应作进一步探讨.(3)第(12)题中图形的精确性似有进一步提高的必要.(4)解析几何问题似应加大对几何特性的考查,淡化对数式运算的考查.(5)解答题的计算量似应考虑适当控制.(6)试卷的过渡作用不甚明显,“课标课程”相关理念的渗透程度似应稍微加大.2福建中学数学2008年第6期。
编者按:2009年福建省将进行“课标课程”的第一次高考.本刊特邀部分专家从不同的视角对全国高考“课标课程”数学理科试卷进行评析,以期为2009年福建省“课标课程”高考的复习迎考提供借鉴.2008年高考数学课标课程理科试卷评析(一)“算法”试题的分析与思考张夏强1,2陈清华11福建师范大学数学与计算机科学学院(350007)2福建省闽清第二中学(350811)算法作为《普通高中数学课程标准(实验)》(以下简称《课标》)背景下数学必修课程的新增内容,反映了时代的特点,同时也体现了中国数学课程的特色.《课标》指出:学生可以在感受算法思想的基础上,体验程序框图在解决实际问题中的作用,发展有条理地进行思考和表达的能力,提高逻辑思维能力.2008年,江苏加入了以广东、山东、海南和宁夏等四省(区)领头的课标课程高考行列,本文以这五省(区)高考数学理科试卷中的算法试题为例,就算法的考查展开分析,并提出若干思考.1算法试题概况年份题序题型设计方式考查知识2007年第6题选择题补充判断语句人数求和2008年第9题填空题读程序写结果整除问题2007年第10题选择题读程序写结果数列求和2008年第13题填空题读程序写结果数列求和2007年第5题选择题读程序写结果数列求和2008年第5题选择题补充判断语句比较大小江苏卷2008年第7题填空题读程序写结果数列求和广东卷(理)山东卷(理)海南与宁夏卷(理)由上表可见,2007年,广东、山东、海南与宁夏四省(区)都把算法试题定位为容易题,以选择题的形式进行考查.从试题设计方式上看,广东卷的试题给出了缺损判断条件的循环结构流程图,要求学生补充完整;山东卷、海南与宁夏卷的试题则都是给出了程序,要求学生读程序写结果.2008年,除海南与宁夏卷仍然将算法试题定位为容易题、以选择题的形式进行考查外,广东、山东和江苏都以填空题的形式考查算法,这在一定程度上提高了试题难度.从试题设计方式上看,海南与宁夏卷的试题给出了缺损判断条件的循环结构流程图,要求学生补充完整;广东卷、山东卷和江苏卷的试题则都是给出了程序,要求学生读程序写结果.由上表还可以看出,2007年与2008年两次“课标课程”高考的算法试题主要都是以循环结构解决数列求和问题为背景,考查学生是否真正领会算法的思想.2算法试题评析从2007年、2008年高考试题可以看出,算法与函数、不等式、数列、统计等传统知识交汇融合、贯通一体,形成了背景新颖、联系广泛、结构精巧的综合题,考查学生对构造性数学意义的理解,展现课标课程背景下高考命题的新视角、新理念.2.1用算法描述统计问题例1(2008年高考江苏理科卷第7题)某地区为了解70~80岁老人的日平均睡眠时间(单位:h),随机选择了50位老人进行调查.下表是这50位老人日睡眠时间的频率分布表.序号(i )分组(睡眠时间)组中值(i G )频数(人数)频率(i F )1[4,5) 4.560.122[5,6) 5.5100.203[6,7) 6.5200.404[7,8)7.5100.205[8,9)8.540.08在上述统计数据的分析中,一部分计算算法流程图,则输出的S 的值是.解析:该程序图解决的问题是统计50位老人的平均睡眠时间,计算可得51 6.42i i i S G F ===∑,故填6.42.评注:在算法教学中,体会算法思想并能根据算法思想解决实际问题是重要的教学目标之一.2007年高考广东卷算法试题以条形统计图为知识背景,本题与开始S ←0输入G i ,F ii ←1S ←S +G i F ii ≥5i ←i +1NY输出S 结束2008年第7期福建中学数学11i i =+之有异曲同工之处——以频率分布表为铺垫,命题角度新颖,考查学生运用算法思想解决实际问题的能力.2.2用算法描述数列问题例2(2008年高考山东理科卷第13题)执行右边的程序框图,若p =0.8,则输出的n =.解析:该程序图解决的问题是求出满足()S n ≥p 的最小正整数n ,其中()S n 是一个等比数列前n 项和,通过求解112nn i==∑()0.8S n p ≥=可得n ≥4,填4.评注:本题将算法与数列等内容有机地联系起来,立意新、角度好,体现应用最朴素的素材目的.本题以循环结构流程图的形式给出了等比数列求和的算法,把握循环的出口(控制条件)是解决问题的关键、考查了考生对循环结构、终止条件的理解及估算能力.2.3用算法描述不等式问题例3(2008年高考海南与宁夏理科卷第5题)右面的程序框图,如果输入三个实数a b c 、、,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的()A.c x >B.x c >C.c b> D.b c>解析:该程序图表示求三个数a b c 、、中最大数的一个算法,类比与第一个判断框的判断语句,容易得到第二个判断框的判断语句为c x >,故选A .评注:在不完整的程序框图中,填补一些条件或内容,是高考考查算法知识的重要题型,此类试题要求考生要有比较扎实的算法初步基本知识,以及综合分析问题和解决问题的能力,对考生要求相对较高.2.4用算法描述整除性问题例4(2008年高考广东理科卷第9题)阅读图3的程序框图,若输入4m =,6n =,则输出a =,i =.(注:框图中的赋值符号“=”也可以写成“←”或“:=”)解析:要结束程序的运行,就必须借助n 整除a 的条件,由于m 同时也整除a ,所以a 的最小值应为m 和n 的最小公倍数12,亦即此时有3i =.填12,3.评注:算法与整除性问题的整合在教材中体现为:应用“辗转相除法”和“更相减损法”求最大公约数.考查学生是否“结合具体数学实例,体验程序框图在解决问题中的应用”.把算法植根于数学的其它知识模块,是《课标》的要求,也是命题的一个重要方向.3思考与商榷随着教学实践的推进,人们对算法的认识将进一步加深,考查的方式将会向多样化、灵活化方向发展.以下根据对2008年高考算法试题的研读,结合对《课标》算法知识定位的理解,对高考算法试题的命制趋势提出几点看法:(1)题型设置趋于多样化,不仅有填空、选择题,还会有解答题,考查学生“通过模仿、操作、探索,学习设计程序框图来表达解决问题的过程”.(2)设计方式不仅有补充判断语句、读程序写结果,也可向“循环体的设计”上命题,考查学生是否掌握循环结构的实质.(3)近两年高考考查算法知识以数的累加为主,今后的命题应该也会考虑数的累乘问题的考查.(4)逐步加大与函数、数列、不等式、三角、概率统计等其它知识点的交汇,考查学生的知识整合能力.(5)问题背景设置向新颖化发展,以算法为载体的创新题必将成为高考试题中的一大亮点.a m i=×2福建中学数学2008年第7期。
2008年普通高等学校招生全国统一考试(江西卷)理科数学一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.在复平面内,复数z =sin 2+i cos 2对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限2.定义集合运算:A *B ={z |z =xy ,x ∈A ,y ∈B }.设A ={1,2},B ={0,2},则集合A *B 的所有元素之和为A .0B .2C .3D .6 3.若函数y =f (x )的值域是[21,3],则函数F (x )=f (x )+)(1x f 的值域是A .[21,3] B .[2,310] C .[25,310] D .[3,310] 4.123lim1--+→x x x =A .21 B .0 C .-21D .不存在 5.在数列{}n a 中,12a =, 11ln(1)n n a a n+=++,则n a =A .2ln n +B .2(1)ln n n +-C .2ln n n +D .1ln n n ++ 6.函数tan sin tan sin y x x x x =+--在区间3(,)22ππ内的图象是7.已知1F 、2F 是椭圆的两个焦点,满足120MF MF ⋅=的点M 总在椭圆内部,则椭圆离心率的取值范围是A .(0,1)B .1(0,]2 C. D. 8.(1+3x )6(1+41x)10展开式中的常数项为ABCDA .1B .46C .4245D .42469.已知实数1a 、2a 和有理数1b 、2b ,若210a a <<,210b b <<,且12121=+=+b b a a ,则下列代数式中值最大的是 ( )、A 2121b b a a + 、B 2211b a b a + 、C 1221b a b a + 、D 2110.连结球面上两点的线段称为球的弦.半径为4的球的两条弦AB 、CD 的长度分别等于27、43,M 、N 分别为AB 、CD 的中点,每条弦的两端都在球面上运动,有下列四个命题:①弦AB 、CD 可能相交于点M ;②弦AB 、CD 可能相交于点N ;③MN 的最大值为5;④MN 的最小值为l .其中真命题的个数为A .1个B .2个C .3个D .4个11.电子钟一天显示的时间是从00∶00到23∶59,每一时刻都由四个数字组成,则一天中任一时刻显示的四个数字之和为23的概率为 A .1801 B .2881 C .3601 D .4801 12.已知函数f (x )=2mx 2-2(4-m )x +l ,g (x )=mx ,若对于任一实数x ,f (x )与g (x )的值至少有一个为正数,则实数m 的取值范围是A .(0,2)B .(0,8)C .(2,8)D .(-∞,0)二.填空题:本大题共4小题,每小题4分,共16分.请把答案填在答题卡上.13.直角坐标平面内三点A(1,2)、B(3,-2)、C(9,7),若E 、F 为线段BC 的三等分点,则²= . 14.不等式132+-x x ≤21的解集为 . 15.过抛物线x 2=2py (p >0)的焦点F 作倾斜角为30°的直线,与抛物线分别交于A 、B 两点(点A 在y 轴左侧),则FBAF= . 16.如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a 升水时,水面恰好经过正四棱锥的顶点P .如果将容器倒置,水面也恰好过点P (图2).有下列四个命题: A .正四棱锥的高等于正四棱柱高的一半B .将容器侧面水平放置时,水面也恰好过点PC .任意摆放该容器,当水面静止时,水面都恰好 经过点PD .若往容器内再注入a 升水,则容器恰好能装满其中真命题的代号是 .(写出所有真命题的代号) .三.解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)在△ABC 中.a 、b 、c 分别为角A 、B 、C 所对的边长,a =23,tan2B A ++tan 2C =4,sin B sin C =cos 22A.求A 、B 及b 、c . 18.(本小题满分12分)因冰雪灾害,某柑桔基地果林严重受损,为此有关专家提出两种拯救果树的方案,每种方案都需分两年实施.若实施方案一,预计第一年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4;第二年可以使柑桔产量为第一年产量的1.25倍、1.0倍的概率分别是0.5、0.5.若实施方案二,预计第一年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5;第二年可以使柑桔产量为第一年产量的1.2倍、1.0倍的概率分别是0.4、0.6.实施每种方案第一年与第二年相互独立,令ξi (i =1,2)表示方案i 实施两年后柑桔产量达到灾前产量的倍数. (1)写出ξ1、ξ2的分布列;(2)实施哪种方案,两年后柑桔产量超过灾前产量的概率更大?(3)不管哪种方案,如果实施两年后柑桔产量达不到、恰好达到、超过灾前产量,预计利润分别为10万元、15万元、20万元.问实施哪种方案的平均利润更大?19.(本小题满分12分)数列{}n a 为等差数列,n a 为正整数,其前n 项和为n S ,数列{}n b 为等比数列,且113,1a b ==,数列{}n a b 是公比为64的等比数列,2264b S =.(1)求,n n a b ;(2)求证1211134n S S S +++< . 20.(本小题满分12分)正三棱锥O -ABC 的三条侧棱OA 、OB 、OC 两两垂直,且长度均为2.E 、F 分别是AB 、AC 的中点,H 是EF 的中点,过EF 的一个平面与侧棱OA 、OB 、OC 或其延长线分别相交于A 1、B 1、C 1,已知OA 1=23. (1)证明:B 1C 1⊥平面OAH ;(2)求二面角O -A 1B 1-C 1的大小.21.(本小题满分12分)设点P (x 0,y 0) 在直线x =m ( y ≠±m ,0<m <1)上,过点P 作双曲线搿x 2-y 2=1的两条切线PA 、PB ,切点为A 、B ,定点M(m1,0). (1)过点A 作直线x -y =0的垂线,垂足为N ,试求△AMN 的重心G 所在的曲线方程;(2)求证:A 、M 、B 三点共线.1C 1A22.(本小题满分14分) 已知函数f (x )=x+11+a+11+8+ax ax,x ∈(0,+∞).(1)当a =8时,求f (x )的单调区间; (2)对任意正数a ,证明:l <f (x )<2.2008年普通高等学校招生全国统一考试(江西卷)理科数学参考答案1.D .因sin 20,cos 20><所以sin 2cos2z i =+对应的点在第四象限, 2.D .因*{0,2,4}A B =3.B .令()t f x =,则1[,3]2t ∈,110()[2,]3F x t t =+∈ 4.A.11x x →→=1 =1=2x →5. A . 211ln(1)1a a =++,321ln(1)2a a =++,…,11ln(1)1n n a a n -=++- 1234ln()()()()2ln 1231n na a n n ⇒=+=+-6.D. 函数2tan ,tan sin tan sin tan sin 2sin ,tan sin x x x y x x x x x x x <⎧=+--=⎨≥⎩当时当时7.C .由题知,垂足的轨迹为以焦距为直径的圆,则2222212c b c b a c e <⇒<=-⇒<又(0,1)e ∈,所以1(0,)2e ∈8.D . 常数项为346861061014246C C C C ++=9. A. 22121212121()()222a ab b a a b b +++≤+=112212************()()()()()0a b a b a b a b a a b a a b a a b b +-+=-+-=--≥ 11221221()a b a b a b a b +≥+12121122112112221()()2()a a b b a b a b a b a b a b a b =++=+++≤+112212a b a b +≥10.C . 解:①③④正确,②错误。
2008年普通高等学校夏季招生考试数学理工农医类(全国Ⅰ) 本试卷分第I 卷(选择题)和第I I卷(非选择题)两部分.第I 卷1至2页,第II 卷3至9页.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷考生注意:ﻩ1.答题前,考生在答题卡上务必用0.5毫米黑色墨水签字笔将自己的姓名、准考证号、填写清楚 ,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效.......... 3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.参考公式:如果事件A B ,互斥,那么 ﻩﻩﻩﻩ 球的表面积公式()()()P A B P A P B +=+ﻩ ﻩﻩﻩ 24πS R =ﻩ如果事件A B ,相互独立,那么ﻩ ﻩﻩﻩ其中R 表示球的半径ﻩ()()()P A B P A P B = ﻩﻩ球的体积公式 如果事件A 在一次试验中发生的概率是P ,那么34π3V R = ﻩn 次独立重复试验中恰好发生k 次的概率ﻩ 其中R 表示球的半径()(1)(01,2)k k n k n n P k C P P k n -=-=,,,一、选择题1.函数y ( )A.{}|0x x ≥ﻩB.{}|1x x ≥ C.{}{}|10x x ≥ ﻩD.{}|01x x ≤≤ 2.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t 的函数,其图像可能是( )3.在ABC △中,AB =c ,AC =b .若点D 满足2BD DC =,则AD =( )A .B .C .D .A.2133+b c ﻩB .5233-c b ﻩ C.2133-b c ﻩﻩﻩD.1233+b c 4.设a ∈R ,且2()a i i +为正实数,则a =( )A.2ﻩﻩB .1 ﻩC .0ﻩﻩD .1-5.已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( )A.138ﻩﻩB .135ﻩﻩC.95ﻩ D.236.若函数(1)y f x =-的图像与函数ln 1y =的图像关于直线y x =对称,则()f x =( )A.21x e - B.2x e ﻩ C .21x e + ﻩD.22x e +7.设曲线11x y x +=-在点(32),处的切线与直线10ax y ++=垂直,则a =( ) A.2 ﻩB.12 ﻩC.12-ﻩ D.2- 8.为得到函数πcos 23y x ⎛⎫=+⎪⎝⎭的图像,只需将函数sin 2y x =的图像( ) A .向左平移5π12个长度单位 ﻩB.向右平移5π12个长度单位 C.向左平移5π6个长度单位 ﻩ D.向右平移5π6个长度单位 9.设奇函数()f x 在(0)+∞,上为增函数,且(1)0f =,则不等式()()0f x f x x --<的解集为( )A.(10)(1)-+∞,,B.(1)(01)-∞-,,C.(1)(1)-∞-+∞,, ﻩD .(10)(01)-,, 10.若直线1x y a b+=通过点(cos sin )M αα,,则( ) A .221a b +≤ﻩ B.221a b +≥ﻩﻩC.22111a b +≤ D .22111a b+≥ 11.已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( )A .13ﻩﻩB.3 ﻩ C .3 ﻩD .2312.如图,一环形花坛分成A B C D ,,,四块,现有4种不同的花供选种,要求在每块里种1种。
2008年福建高考数学试题(理科)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)若复数(a 2-3a +2)+(a-1)i 是纯虚数,则实数a 的值为 A.1B.2C.1或2D.-1(2)设集合A={x |1xx -<0},B={x |0<x <3},那么“m ∈A ”是“m ∈B ”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件(3)设{a n }是公比为正数的等比数列,若a 1=1,a 5=16,则数列{a n }前7项的和为 A.63B.64C.127D.128(4)函数f (x )=x 3+sin x +1(x ∈R ),若f (a )=2,则f (-a )的值为 A.3B.0C.-1D.-2(5)某一批花生种子,如果每1粒发牙的概率为45,那么播下4粒种子恰有2粒发芽的概率是 A.16625B.96625C. 192625D. 256625(6)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为 A.63B.265C.155D.105(7)某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为 A.14B.24C.28D.48(8)若实数x 、y 满足100x y x -+≤⎧⎨>⎩,则yx 的取值范围是A.(0,1)B.(]0,1C.(1,+∞)D.[)1,+∞(9)函数f (x )=cos x (x ∈R )的图象按向量(m,0) 平移后,得到函数y =-f ′(x )的图象,则m 的值可以为A.2πB.πC.-πD.-2π (10)在△ABC 中,角ABC 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =3ac ,则角B 的值为A.6π B.3π C.6π或56πD.3π或23π(11)又曲线22221x y a b==(a >0,b >0)的两个焦点为F 1、F 2,若P 为其上一点,且|PF 1|=2|PF 2|,则双曲线离心率的取值范围为 A.(1,3)B.(]1,3C.(3,+∞)D.[)3,+∞(12)已知函数y =f (x ),y =g (x )的导函数的图象如下图,那么y =f (x ),y =g (x )的图象可能是第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置. (13)若(x -2)5=a 5x 5+a 4x 4+a 3x 3+a 2x 2+a 1x +a 0,则a 1+a 2+a 3+a 4+a 5=__________.(用数字作答) x =1+cos θ(14)若直线3x+4y+m=0与圆 y =-2+sin θ(θ为参数)没有公共点,则实数m 的取值范围是 .(153,则其外接球的表面积是 . (16)设P 是一个数集,且至少含有两个数,若对任意a 、b ∈R ,都有a +b 、a -b , ab 、ab∈P (除数b ≠0),则称P 是一个数域.例如有理数集Q 是数域;数集{}2,F a b b Q =+∈也是数域。
有下列命题:①整数集是数域;②若有理数集Q M ⊆,则数集M 必为数域;③数域必为无限集; ④存在无穷多个数域.其中正确的命题的序号是 .(把你认为正确的命题的序号填填上)三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分)已知向量m =(sin A ,cos A ),n =3,1)-,m ·n =1,且A 为锐角.(Ⅰ)求角A 的大小;(Ⅱ)求函数()cos 24cos sin ()f x x A x x R =+∈的值域.(18)(本小题满分12分)如图,在四棱锥P-ABCD 中,则面PAD ⊥底面ABCD ,侧棱PA =PD =2,底面ABCD 为直角梯形,其中BC ∥AD ,AB ⊥AD ,AD =2AB =2BC =2,O 为AD 中点.(Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求异面直线PB 与CD 所成角的大小;(Ⅲ)线段AD 上是否存在点Q ,使得它到平面PCD 3AQQD的值;若不存在,请说明理由.(19)(本小题满分12分)已知函数321()23f x x x =+-. (Ⅰ)设{a n }是正数组成的数列,前n 项和为S n ,其中a 1=3.若点211(,2)n n n a a a ++-(n ∈N*)在函数y =f ′(x )的图象上,求证:点(n ,S n )也在y =f ′(x )的图象上; (Ⅱ)求函数f (x )在区间(a -1,a )内的极值. (20)(本小题满分12分)某项考试按科目A 、科目B 依次进行,只有当科目A 成绩合格时,才可继续参加科 目B 的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证 书.现某人参加这项考试,科目A 每次考试成绩合格的概率均为23,科目B 每次考试 成绩合格的概率均为12.假设各次考试成绩合格与否均互不影响. (Ⅰ)求他不需要补考就可获得证书的概率;(Ⅱ)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为ξ,求ξ的数学期望E ξ.(21)(本小题满分12分)如图、椭圆22221(0)x y ab a b+=的一个焦点是F (1,0),O为坐标原点.(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;(Ⅱ)设过点F 的直线l 交椭圆于A 、B 两点.若直线l 绕点F 任意转动,值有222OA OBAB +,求a 的取值范围.(22)(本小题满分14分)已知函数f (x )=ln(1+x )-x (Ⅰ)求f (x )的单调区间;(Ⅱ)记f (x )在区间[]0,n (n ∈N*)上的最小值为b n 令a n =ln(1+n )-b n . (i )如果对一切n 22nn n a a a ++-c 的取值范围; (ii )求证: 131321122424221 1.n n na a a a a a a a a a a a a -++++2008年福建高考数学试题(理科)参考答案一、选择题:本大题考查基本概念和基本运算.每小题5分,满分60分.(1)B (2)A (3)C (4)B (5)B (6)D (7)A (8)C (9)A (10)D (11)B (12)D 二、填空题:本大题考查基础知识和基本运算.每小题4分,满分16分. (13)31(14)(,0)(10,)-∞⋃+∞(15)9π(16)③④三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.(17)本小题主要考查平面向量的数量积计算、三角函数的基本公式、三角恒等变换、一元二次函数的最值等基本知识,考查运算能力.满分12分. 解:(Ⅰ)由题意得3sin cos 1,m n A A =-=12sin()1,sin().662A A ππ-=-=由A 为锐角得,.663A A πππ-==(Ⅱ)由(Ⅰ)知1cos ,2A =所以2213()cos 22sin 12sin 2sin 2(sin ).22f x x x x s x =+=-+=--+因为x ∈R ,所以[]sin 1,1x ∈-,因此,当1sin 2x =时,f (x )有最大值32.当sin x =-1时,f (x )有最小值-3,所以所求函数f (x )的值域是33,2⎡⎤-⎢⎥⎣⎦.(18)本小题主要考查直线与平面的位置关系、异面直线所成角、点到平面的距离等基本知识,考查空间想象能力、逻辑思维能力和运算能力.满分12分.解法一:(Ⅰ)证明:在△PAD 中PA =PD ,O 为AD 中点,所以PO ⊥AD ,又侧面PAD ⊥底面ABCD ,平面PAD ⋂平面ABCD =AD , PO ⊂平面PAD , 所以PO ⊥平面ABCD .(Ⅱ)连结BO ,在直角梯形ABCD 中、BC ∥AD ,AD =2AB =2BC , 有OD ∥BC 且OD =BC ,所以四边形OBCD 是平行四边形, 所以OB ∥DC .由(Ⅰ)知,PO ⊥OB ,∠PBO 为锐角, 所以∠PBO 是异面直线PB 与CD 所成的角.因为AD =2AB =2BC =2,在Rt △AOB 中,AB =1,AO =1, 所以OB =2,在Rt △POA 中,因为AP =2,AO =1,所以OP =1,在Rt △PBO 中,tan ∠PBO =122,arctan .222PG PBO BC ==∠= 所以异面直线PB 与CD 所成的角是2arctan2. (Ⅲ)假设存在点Q ,使得它到平面PCD 的距离为32. 设QD =x ,则12DQC S x ∆=,由(Ⅱ)得CD =OB =2, 在Rt △POC 中, 222,PC OC OP =+= 所以PC =CD =DP , 233(2),42PCD S ∆== 由V p-DQC =V Q-PCD ,得2,所以存在点Q 满足题意,此时13AQ QD =. 解法二:(Ⅰ)同解法一.(Ⅱ)以O 为坐标原点,OC OD OP 、、的方向分别为x 轴、y 轴、z 轴的正方向,建立空间直角坐标系O-xyz ,依题意,易得A (0,-1,0),B (1,-1,0),C (1,0,0),D (0,1,0), P (0,0,1),所以110111CDPB ---=(,,),=(,,). 所以异面直线PB 与CD 所成的角是arccos63,(Ⅲ)假设存在点Q ,使得它到平面PCD的距离为2, 由(Ⅱ)知(1,0,1),(1,1,0).CP CD =-=-设平面PCD 的法向量为n =(x 0,y 0,z 0).则0,0,n CP n CD ⎧=⎪⎨=⎪⎩所以00000,0,x z x y -+=⎧⎨-+=⎩即000x y z ==,取x 0=1,得平面PCD 的一个法向量为n =(1,1,1). 设(0,,0)(11),(1,,0),Q y yCQ y -≤≤=-由32CQ n n=,得2=解y =-12或y =52(舍去), 此时13,22AQ QD ==,所以存在点Q 满足题意,此时13AQ QD =. (19)本小题主要考查函数极值、等差数列等基本知识,考查分类与整合、转化与化归等数学思想方法,考查分析问题和解决问题的能力.满分12分. (Ⅰ)证明:因为321()2,3f x x x =+-所以f ′(x )=x 2+2x , 由点211(,2)(N )n n n a a a n +++-∈在函数y =f ′(x )的图象上, 又0(N ),n a n +>∈所以11()(2)0,n n n n a a a a -+---=所以2(1)32=22n n n S n n n -=+⨯+,又因为f ′(n )=n 2+2n ,所以()n S f n '=, 故点(,)n n S 也在函数y=f ′(x )的图象上. (Ⅱ)解:2()2(2)f x x x x x '=+=+, 由()0,f x '=得02x x ==-或.当x 变化时,()f x '﹑()f x 的变化情况如下表: 注意到(1)12a a --=<,从而①当212,21,()(2)3a a a f x f -<-<-<<--=-即时的极大值为,此时()f x 无极小值; ②当10,01,()a a a f x -<<<<即时的极小值为(0)2f =-,此时()f x 无极大值;③当2101,()a a a f x ≤--≤≤≥或或时既无极大值又无极小值.(20)本小题主要考查概率的基本知识与分类思想,考查运用数学知识分析问题/解愉问题的能力.满分12分.解:设“科目A 第一次考试合格”为事件A ,“科目A 补考合格”为事件A 2;“科目B 第一次考试合格”为事件B 1,“科目B 补考合格”为事件B 2.(Ⅰ)不需要补考就获得证书的事件为A 1·B 1,注意到A 1与B 1相互独立, 则1111211()()()323P A B P A P B =⨯=⨯=. 答:该考生不需要补考就获得证书的概率为13. (Ⅱ)由已知得,ξ=2,3,4,注意到各事件之间的独立性与互斥性,可得1112(2)()()P P A B P A A ξ==+2111114.3233399=⨯+⨯=+= 112112122(3)()()()P P A B B P A B B P A A B ξ==++2112111211114,3223223326693=⨯⨯+⨯⨯+⨯⨯=++= 12221212(4)()()P P A A B B P A A B B ξ==+12111211111,3322332218189=⨯⨯⨯+⨯⨯⨯=+= 故4418234.9993E ξ=⨯+⨯+⨯=答:该考生参加考试次数的数学期望为83.(21)本小题主要考查直线与椭圆的位置关系、不等式的解法等基本知识,考查分类与整合思想,考查运算能力和综合解题能力.满分12分.解法一:(Ⅰ)设M ,N 为短轴的两个三等分点, 因为△MNF 为正三角形, 所以32OF MN =, 即1=32, 3.23bb 解得= 2214,a b =+=因此,椭圆方程为221.43x y += (Ⅱ)设1122(,),(,).A x y B x y (ⅰ)当直线 AB 与x 轴重合时,2222222222,4(1),.OA OB a AB a a OA OB AB +==>+<因此,恒有(ⅱ)当直线AB 不与x 轴重合时,设直线AB 的方程为:22221,1,x y x my a b=++=代入整理得22222222()20,a b m y b my b a b +++-=所以222212122222222,b m b a b y y y y a b m a b m -+==++因为恒有222OA OB AB +<,所以∠AOB 恒为钝角. 即11221212(,)(,)0OA OB x y x y x x y y ==+<恒成立.2121212121212(1)(1)(1)()1x x y y my my y y m y y m y y +=+++=++++2222222222222222222222(1)()210.m b a b b m a b m a b m m a b b a b a a b m +-=-+++-+-+=<+又a 2+b 2m 2>0,所以-m 2a 2b 2+b 2-a 2b 2+a 2<0对m ∈R 恒成立, 即a 2b 2m 2> a 2 -a 2b 2+b 2对m ∈R 恒成立.当m ∈R 时,a 2b 2m 2最小值为0,所以a 2- a 2b 2+b 2<0. a 2<a 2b 2- b 2, a 2<( a 2-1)b 2= b 4,因为a >0,b >0,所以a <b 2,即a 2-a -1>0, 解得a或a(舍去),即a, 综合(i )(ii),a,+∞). 解法二:(Ⅰ)同解法一,(Ⅱ)解:(i )当直线l 垂直于x 轴时,x =1代入22222221(1)1,A y b a y a b a -+===1.因为恒有|OA |2+|OB |2<|AB |2,2(1+y A 2)<4 y A 2, y A 2>1,即21a a->1,解得a >12+或a <12(舍去),即a >12+. (ii )当直线l 不垂直于x 轴时,设A (x 1,y 1), B (x 2,y 2).设直线AB 的方程为y =k (x -1)代入22221,x y a b+=得(b 2+a 2k 2)x 2-2a 2k 2x + a 2 k 2- a 2 b 2=0,故x 1+x 2=222222222222222,.a k a k a b x x b a k b a k-=++因为恒有|OA |2+|OB |2<|AB |2,所以x 21+y 21+ x 22+ y 22<( x 2-x 1)2+(y 2-y 1)2, 得x 1x 2+ y 1y 2<0恒成立.x 1x 2+ y 1y 2= x 1x 2+k 2(x 1-1) (x 2-1)=(1+k 2) x 1x 2-k 2(x 1+x 2)+ k 2=(1+k 2)2222222222222222222222222()a k a b a k a a b b k a b k k b a k b a k b a k --+--+=+++.由题意得(a 2- a 2 b 2+b 2)k 2- a 2 b 2<0对k ∈R 恒成立.①当a 2- a 2 b 2+b 2>0时,不合题意;②当a 2- a 2 b 2+b 2=0时,a =12+; ③当a 2- a 2 b 2+b 2<0时,a 2- a 2(a 2-1)+ (a 2-1)<0,a 4- 3a 2 +1>0,解得a 2a 2a ,因此a ≥.综合(i )(ii ),a ,+∞). (22)本小题主要考查函数的单调性、最值、不等式、数列等基本知识,考查运用导数研究函数性质的方法,考查分析问题和解决问题的能力,满分14分. 解法一:(I )因为f(x)=ln(1+x )-x ,所以函数定义域为(-1,+∞),且f/(x)=11x +-1=1x x-+. 由f ’(x )>0得-1<x <0,f (x )的单调递增区间为(-1,0); 由f ’(x )<0得x >0,f (x )的单调递增区间为(0,+∞). (II)因为f (x )在[0,n]上是减函数,所以b n =f (n )=ln(1+n )-n , 则a n =ln(1+n )-b n =ln(1+n )-ln(1+n )+n =n .(i)==>1.=又1x ==,因此c <1,即实数c 的取值范围是(-∞,1). (II )由(i< 因为[135(21)246(2)n n ⋅⋅⋅⋅-⋅⋅⋅⋅⋅]2=3222133557(21)(21)11,246(2)2121n n n n n ⋅⋅⋅-+=⋅⋅⋅⋅⋅++<所以135(21)246(2)n n -<1∈N *),则113135(21)224246(2)n n -+++<1313211222422 1.n nna a a a a a a a a a a a a -++=+++即<1(n ∈N *)解法二:(Ⅰ)同解法一.(Ⅱ)因为f (x )在[]0,n 上是减函数,所以()ln(1),n b f n n n ==+- 则ln(1)ln(1)ln(1).n n a n bn n n n =+-=+-++= (i 2n a +-n ∈N*恒成立.2n +-对n ∈N*恒成立.则2cn+-n ∈N*恒成立.设()2g n n =+n ∈N*,则c <g (n )对n ∈N*恒成立. 考虑[)()21,.g x x x =+∈+∞因为12211()1(2)?(22)1121x g x x x x x -+=-++=-+′=0,第11页所以[)()1,g x +∞在内是减函数;则当n ∈N*时,g (n )随n 的增大而减小,又因为42lim ()lim(2x x x x g n n →∞→∞+=+-== 1. 所以对一切*N ,() 1.n g n ∈>因此c ≤1,即实数c 的取值范围是(-∞,1]. (ⅱ) 由(ⅰ)<下面用数学归纳法证明不等式135(21)N ).246(2)n nn +-<∈ ①当n =1时,左边=12,左边<右边.不等式成立. ②假设当n=k 时,不等式成立.即135(21)246(2)k k -< 当n=k +1时,32122321222122212121)22(2642)12(12531++++=++=++++⋯+⋯••••••k k k k k k k k k k k k k <)()-( =,1)1(2132132148243824++=++++++•k k k k k k k <即n =k +1时,不等式成立综合①、②得,不等式*)N (121)2(642)12(531∈+⋯-⋯••••••••n n n n <成立. 所以1212)2(642)12(531--+⋯-⋯••••••••n n n n < )2(642)12(531423121n n ••••••••••⋯-⋯⋯+++ .112123513-+=-⋯n n +=-+-<即*)N (1212421231423121∈-⋯⋯⋯+++-n a a a a a a a a a a a a a n nn <+.。