下载文档原格式
第二章2-2解：由P gh ρ=得h 水 =Pg ρ水=3350101109.8⨯⨯⨯=5.1m 335010=3.21.6109.8Ph m gρ⨯==⨯⨯四氯化碳四氯化碳 335010=0.37513.6109.8Ph m g ρ⨯==⨯⨯水银水银2-3 解：（1）体积弹性模量 /dpEv d ρρ=+在重力场中流体的压强形式为：dpg dzρ=- d dp gdz Evρρρ∴=-=两边积分，带入边界条件：00,0,z p ρρ===0lnEvp Ev Ev ghρ∴=- 11222212.5*160N F *40000NF L L s F s ==⎛⎫=== ⎪⎝⎭题解：有杠杆原理知：F 所以： 6、如题2-6图所示，封闭容器中盛有ρ=800kg/3m的油，1300h mm =，油下面为水，2500h mm =，测压管中水银液位读数400hmm =，求封闭容器中油面上的压强p 的大小。
解：12g 0p h gh gh ρρρ++-=油水水银12g p gh h gh ρρρ=--水银油水333313.6109.840010109.8500100.8--=⨯⨯⨯⨯-⨯⨯⨯-⨯=44.6110pa ⨯2-7：解：（1）、2224F gh s 10009.81001010101098Nρ--==⨯⨯⨯⨯⨯=2）m 121216G [s h h s h ]1000199109.81.95g Nρ-=⨯⨯=⨯⨯⨯=（-）+02h（3）因为在21h h -处谁对容器有向上的压力2-8，解：由同一液面压强相等可列：(0)()gh sin /6p(0)1239.21/^3p p h l kn m θθπ===∴=液2-9 解：设A 点距左U 形管测压计水银页面高度为H 则B 点距右U 型管测压计水银高度为H+hB A B h gh g H h gh gh gh m ag ρρρρρρA P -P -+P P -P =-=-⨯⨯P 水水水水则（+）=则（）=（13600-1000）9.80.3=370442.10，解：选取右侧U 形管汞柱高作为等压面，有：1132()m B P g h h gh gh gh p ρρρρ++-+=+酒汞汞水B p 42.7410pa =-⨯2-11解:左边液面压强与右边液面压强相等知，.66g .66.89g .82g .8211g ⨯+-⨯=⨯+-⨯未知水未知水）（）（ρρρρ解得333102.31m kg 103.85⨯=⋅⨯=-未知ρ3m kg -⋅2-12 解：设左支管液面到另一液体分界面的距离为1h ，右支管为2h ，则有：1112222P gh P gh gh ρρρ+=++或121122121221()()P P g h h ghP P gh gh ghρρρρρρ-=--+-=-+=-得 1221()P P h gρρ-=-2-13解：gh P gh ρρ+=水水银P=gh gh ρρ∴-水银水127400.07891.8F PS N∴==⨯=2-14解：以闸门与液面交点为O 点，沿闸门向下方向建立坐标S ，取微元ds ，在面积bds 内，液体压力对链轴取矩()()0.2sin600.2dM ghbds s g s sdsρρ=-+=-+ 所以)0sin 600.2Mgb s sds ρ=-+Q对链轴取矩)cos600.2Q M Q =由力矩平衡得 0Q M M +=化简)1.*1.9320.302Q -=得 26778Q N=()()D 33352.151y y *1132***2*4121232,8832**10*10*12*89.6*10xcC c xc cD c I y sI b a y s d y F g h s ρ=+==========题解：依题意知又即:*16、一个很长的铅垂壁面吧海水和淡水隔开，海水深7m ；试确定淡水多深时壁面所受液体作用力合力为零。
严新华主编《水力学（修订本）》教材（科技文献出版社2001年版）部分习题参考答案第一章 习题答案1-1 水的运动粘性系数s m /10006.126-⨯=ν；空气的动力粘性系数s Pa ⋅⨯=-51081.1μ。
1-2 活塞移动速度s m V /49.0=。
1-3 动力粘性系数s Pa ⋅=151.0μ。
1-4 2/5.11m N =τ。
1-5 阻力矩m N M ⋅=6.39。
第二章 习题答案2-1（a ）图中2/6.68m KN p A =；绝对压强2/93.169m KN p A='。
（b ）图中22/4.29,0,/6.19m KN p p m KN p A B C -===；绝对压强222/93.71,/33.101,/93.120m KN p m KN p m KN p AB C ='='='。
2-2 20/4900m N p -=；液面真空值20/4900m N p V =。
2-3（1）2/54.115m KN p A ='；2/47.17m KN p A =。
（2）压力表读数m h m KN p M 213.1,/63.92==。
2-4 A 点表压强2/8.9m KN p A -=；液面空气真空度2/6.19m KN p V =。
2-5 m H 40.0=。
2-6 cm h 1284=。
2-7 O H 84.172mmh V =。
2-8 ①2/22.185m KN p p B A =-；②2/42.175m KN p p B A =-。
2-9 ⑴21/86.1m KN p p B A -=-为油时：ρ；⑵21/784.0m KN p p B A -=-为空气时：ρ。
2-10 ⎪⎭⎫⎝⎛-='b a 1ρρ；gH b a p p BA ρ=-。
2-11 241/1084.118m N p ⨯=。
2-12 )/3.101(/84.37822m KN p m KN p a =='取：。
第三、四章 流体动力学基础习题及答案3-8已知流速场u x =xy 2, 313y u y =-, u z =xy, 试求：（1）点（1，2，3）的加速度；（2）是几维流动；（3）是恒定流还是非恒定流；（4）是均匀流还是非均匀流？解：（1）411633x x x x x x y z u u u u a u u u xy t x y z ∂∂∂∂=+++==∂∂∂∂25333213313233312163. 06m/s y y z x y a y u y a yu xu xy xy xy a =-===+=-====（2）二元流动 （3）恒定流（4）非均匀流41xy 33-11已知平面流动速度分布为x y 2222cxu u x ycy x y =-=++，， 其中c 为常数。
求流线方程并画出若干条流线。
解：2222-xdx=ydyx ydx dydx dy cy cx u u x y x y =⇒-=⇒++积分得流线方程：x 2+y 2=c方向由流场中的u x 、u y 确定——逆时针3-17下列两个流动，哪个有旋？哪个无旋？哪个有角变形？哪个无角变形？(1)u x =－ay,u y =ax,u z =0 （2）z 2222,,0,a c x ycy cxu u u x y x y =-==++式中的、为常数。
z 2222,,0,a c x y cy cxu u u x y x y =-==++式中的、为常数。
解：（1）110 ()()22yx x y z u u a a a xy ωωω∂∂===-=+=∂∂有旋流动 xy 11()()0 22y x xy zx u u a a x y εεε∂∂=+=-==∂∂ 无角变形 (2)222222222222222222211()2()2()22()()12()2()0 0 2()y x z x y u u x y c cx x y c cy x y x y x y c x y c x y x y ωωω∂⎡⎤∂+-+-=-=+⎢⎥∂∂++⎣⎦⎡⎤+-+====⎢⎥+⎣⎦无旋流动2222xy 22222112()()()022()()y x u u c x y c x y x y x y x y ε∂⎡⎤∂---=+==-≠⎢⎥∂∂++⎣⎦ 有角变形4—7变直径管段AB ，d A =0.2m,d B =0.4m ，高差△h=1.5m ，测得p A =30kPa ，p B =40kPa ，B 点处断面平均流速v B =1.5m/s ，试判断水在管中的流动方向。
习题一 场论和张量代数(习题一中黑体符号代表矢量)1．(一)用哈密顿符号法证明：rot n n n n n n n n n n n n n nC C ⨯=-⨯∇⨯=-⨯∇⨯=-∇⋅+⋅∇=-∇⋅+⋅∇()()()()()()C 12因为n 为单位向量，n n ⋅=1，故 ∇⋅=()n n 0，于是rot n n n n ⨯=⋅∇(). 注意： 将rot n n ⨯写成rot n n n n ⨯=∇⨯⨯()是不正确的。
右端表示矢量][)(pk q jpqijk x n n ∂∂εε.直接写rot n n n n n n n n ⨯=-⨯∇⨯=-∇⋅+⋅∇()()()尽管也能给出证明，但由第二步(反用混合积公式)到第三步却是错误的，一定要引入辅助矢量n C 才能进行正确的推导。
(二)张量表示法证明：()()1()()2n n n ijk jmnk jik jmn k im kn km in k m m mk i k k k k i k in n nn n n x x x n n n n n n x x x εεεεδδδδ∂∂∂⨯==-=--∂∂∂∂∂∂⋅=-+=-+⋅∇=⋅∇∂∂∂rot n n n n n n2．(一)哈密顿符号法：grad(a n a n n a n a ⋅=∇⋅=⨯∇⨯+⋅∇)()()()； rot(a n a n n a n a ⨯=∇⨯⨯=⋅∇-∇⋅)()()().于是n a n a n n n a n a n n a a a ⋅⋅-⨯=⋅⨯∇⨯+∇⋅=⋅∇⋅=∇⋅=[()()][()()]()grad rot div(二)张量表示法：()()[grad()rot()]()j j j p k i ijk i j ijk kpq q i j i j j p j ii j ip jq iq jp q i j j i j i j a n a a n n n n x x x x a a a a n n n n n n x x x x εεεδδδδ⎛⎫⎛⎫∂∂∂∂⨯⋅⋅-⨯=-=- ⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎡⎤∂∂∂∂=--=-⎢⎥∂∂∂∂⎢⎥⎣⎦a n n a n a n div j i j ji i ja n x a Q n n Q x ⎡⎤∂+⎢⎥∂⎢⎥⎣⎦∂=+=+∂ a其中()0j j i i i jji j j i ij i ja a a aQ n n n n n n n x x x x ∂∂∂∂=-=-=∂∂∂∂(进行j i ,指标互换)，证毕。
习题二2.1 设质量力222222f ()()()y yz z z zx x x xy y =++++++++i j k 在此力场中，正压流体和斜压流体是否可以保持静止？说明原因。
解：22(22)(22)()0f y z i z x j x xy y k ∇⨯=-+-+++≠333333()2222220f f y z z x x y ⋅∇⨯=-+-+-=固正压流体不能保持静止，斜压流体可以保持静止。
2.2 在自由面以下10m 深处，水的绝对压力和表压分别是多少？假定水的密度为1000kg 3m -,大气压为101kpa 。
解： 表压为：10p p p gh ρ=-==1000*9.81=98100pa. 绝对压力为：10p p p =+=98100+101000=199100pa.2.3 正立方体水箱内空间每边长0.6m,水箱上面装有一根长30m 的垂直水管，内径为25mm,水管下端与水箱内部上表面齐平，箱底是水平的。
若水箱和管装满水（密度为1000kg 3m -），试计算：（1）作用在箱底的静水压力；（2）作用在承箱台面上的力。
解： （1）p gh ρ==1000*9.8*（30+0.6）=300186pa (2) F gv ρ==1000*9.8*(0.216+0.015)=2264N.2.4 如题图2.4所示，大气压力为a p =100kN 2m -,底部A 点出绝对压力为130kN 2m -,问压力计B 和压力计C 所显示的表压各是多少？解：C 表显示：1c A p p gh ρ=-=130-9.81*1=120.43kN 2m -B 表显示：2B A p p gh ρ=-=100+9.81*1*3=139.43kN 2m -2.5 倾斜式微压计由贮液杯和倾斜管组成，如题图2.5所示，贮液杯内自由面上的压力为大气压力a p ，斜管接待测压力p(<a p ),若p=a p 时斜管中液柱读数为0a ，试证明 00()(1)sin sin a sp p g a a s ραα-=-+式中，a 为测压时斜管中液柱的读数；s 为斜管的横截面积；0s 为贮液杯的横截面积；α为斜管的倾斜角。
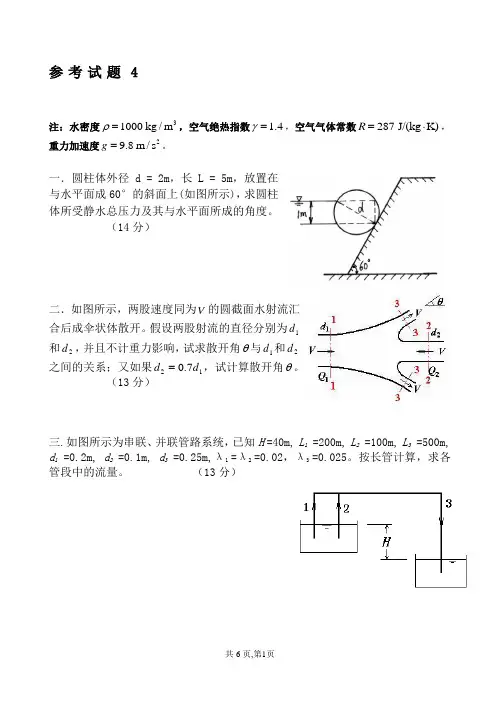
参考试题4注：水密度31000kg /m ρ=，空气绝热指数 1.4γ=，空气气体常数287 J/(kg K)R =⋅，重力加速度29.8m/s g =。
一．圆柱体外径d = 2m ，长L = 5m ，放置在与水平面成60°的斜面上(如图所示)，求圆柱体所受静水总压力及其与水平面所成的角度。
（14分）二．如图所示，两股速度同为V 的圆截面水射流汇合后成伞状体散开。
假设两股射流的直径分别为1d 和2d ，并且不计重力影响，试求散开角θ与1d 和2d 之间的关系；又如果127.0d d =，试计算散开角θ。
（13分）三.如图所示为串联、并联管路系统，已知H =40m, L 1 =200m, L 2 =100m, L 3 =500m, d 1 =0.2m, d 2 =0.1m, d 3 =0.25m,λ 1 =λ 2 =0.02，λ 3 =0.025。
按长管计算，求各管段中的流量。
（13分）四.将一个沿x 轴正方向，速度15 m/s V =的直线均匀流与一个位于坐标原点的点涡叠加，已知在叠加后的势流中点(0, 1)是驻点，试求点涡的强度Γ。
(13分)五.长 1.22 m l =，宽1.22 m b =的平板沿长度方向顺流放置在空气气流中，气流速度 3.05m/s U =，空气运动粘度20.149cm /s ν=，密度31.2kg/m ρ=。
假设边界层临界雷诺数5510xc Re =⨯，试计算平板双面的总摩擦阻力D F 。
（10分）提示：层流边界层和湍流边界层的摩擦阻力系数分别为1/21.328L f l C Re -=，1/50.074T f lC Re -=六.如图所示，密度为ρ，动力粘度为μ的流体在相距h 的大平板之间做定常运动，板与水平面的夹角为θ 。
假设上板运动速度为1U ，下板运动速度为2U ，流体中压强沿x 方向不变，试在图示坐标系下导出流体速度分布的表达式。
（13分） 提示：平面定常流动的N-S 方程为22221x u u p u u u v f x y x x y μρρ⎛⎫∂∂∂∂∂+=-++ ⎪∂∂∂∂∂⎝⎭22221y v v p v v u v f x y y x y μρρ⎛⎫∂∂∂∂∂+=-++ ⎪∂∂∂∂∂⎝⎭七．滞止温度0296 K T =，滞止压强50410 Pa p =⨯的超声速空气流进入拉伐尔（缩放）喷管，喷管最小截面积220 cm A *=，假设管内无激波，流动等熵，出口截面马赫数Ma = 0.52。
