2018版 江苏高考预测试题(一)

2018年江苏高考模拟卷（一）（含答案及详解）一、语言文字运用(15分)1．依次填入下列各句横线处的成语，最恰当的一组是（ 3分）①在义工联盟中，他不仅是发起人、带头者，更是义工精神的实践者、坚守者，时时处处都，亲力亲为。

②不管日方如何、绞尽脑汁、变换手法宣传自己的错误立场，都改变不了钓鱼岛属于中国这一基本事实。

③他地寻求国画艺术的发展道路，多方探索，力求变化创新，在挥毫泼墨中抒发画家丰富的思想感情。

A．处心积虑苦心孤诣殚精竭虑 B．处心积虑殚精竭虑苦心孤诣C．殚精竭虑处心积虑苦心孤诣 D．苦心孤诣殚精竭虑处心积虑2．下列各句中，没有语病的一句是（ 3分）A．通过海丝之路走向海外的潮汕人，在一杯功夫茶之后，美美地回味那“九曲回肠、心旷神怡”，故乡的一草一木也由此映人眼帘。

B．新《广告法》规范了原《广告法》存在的一些问题，解决了公众反映比较强烈的一些广告乱象，在制度层面更加完善、健全、合理。

C．造成“提笔忘字”的因素很多，但不可否认，造成“能识不能写”这一尴尬局面的主要原因是触屏操控和电子输入方式导致的。

D．阳光学校继承了《中庸》“天命之谓性，率性之谓道，修道之谓教”这一教育思想，于2014年提出了“率性教育”的理念。

3．下列各句表达得体的一项是( 3分 )A．王明肯定李昊的写作水平：“您的文章写得真好，本世纪散文百家，您必能忝列其中。

”B．张磊过生日，接受朋友的礼物：“既然你这么客气，又这么真诚，那我就笑纳了。

”C．刘娟在纪念抗战胜利70周年活动中，采访抗日女英雄时问：“老奶奶，请问您芳龄。

”D．75岁高龄的前院长说：“好吧，既然诸位如此客气，那么这件事就由老朽做主了！”4. 填入下面一段文字横线处的语句，最恰当的一句是（ 3分）人们只知道噪声影响听力，其实噪声还影响视力。

试验表明：当噪声强度达到90分贝时。

人的视觉细胞敏感性下降，识别弱光反应时间延长；噪声达到95分贝时，有40％的人瞳孔放大，视力模糊；而噪声达到115分贝时，多数人的眼球对光亮度的适应都有不同程度的减弱。

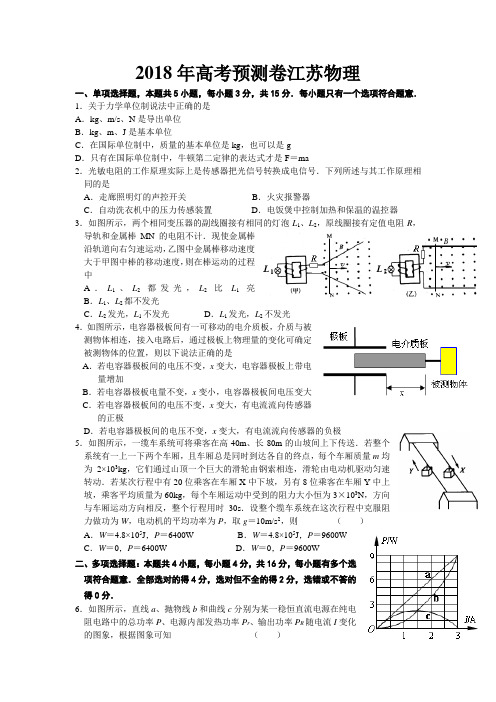
2018年高考预测卷江苏物理一、单项选择题，本题共5小题，每小题3分，共15分．每小题只有一个选项符合题意． 1．关于力学单位制说法中正确的是 A ．kg 、m/s 、N 是导出单位 B ．kg 、m 、J 是基本单位C ．在国际单位制中，质量的基本单位是kg ，也可以是gD ．只有在国际单位制中，牛顿第二定律的表达式才是F ＝ma2．光敏电阻的工作原理实际上是传感器把光信号转换成电信号．下列所述与其工作原理相同的是 A ．走廊照明灯的声控开关 B ．火灾报警器C ．自动洗衣机中的压力传感装置D ．电饭煲中控制加热和保温的温控器3．如图所示，两个相同变压器的副线圈接有相同的灯泡L 1、L 2，原线圈接有定值电阻R ，导轨和金属棒MN 的电阻不计．现使金属棒沿轨道向右匀速运动，乙图中金属棒移动速度大于甲图中棒的移动速度，则在棒运动的过程中A ．L 1、L 2都发光，L 2比L 1亮B ．L 1、L 2都不发光C ．L 2发光，L 1不发光D ．L 1发光，L 2不发光 4．如图所示，电容器极板间有一可移动的电介质板，介质与被测物体相连，接入电路后，通过极板上物理量的变化可确定被测物体的位置，则以下说法正确的是A ．若电容器极板间的电压不变，x 变大，电容器极板上带电量增加B ．若电容器极板电量不变，x 变小，电容器极板间电压变大C ．若电容器极板间的电压不变，x 变大，有电流流向传感器的正极D ．若电容器极板间的电压不变，x 变大，有电流流向传感器的负极5．如图所示，一缆车系统可将乘客在高40m 、长80m 的山坡间上下传送．若整个系统有一上一下两个车厢，且车厢总是同时到达各自的终点，每个车厢质量m 均为2×103kg ，它们通过山顶一个巨大的滑轮由钢索相连，滑轮由电动机驱动匀速转动．若某次行程中有20位乘客在车厢X 中下坡，另有8位乘客在车厢Y 中上坡，乘客平均质量为60kg ，每个车厢运动中受到的阻力大小恒为3×103N ，方向与车厢运动方向相反，整个行程用时30s ．设整个缆车系统在这次行程中克服阻力做功为W ，电动机的平均功率为P ，取g ＝10m/s 2，则 （ ） A ．W ＝4.8×105J ，P ＝6400W B ．W ＝4.8×105J ，P ＝9600W C ．W ＝0，P ＝6400W D ．W ＝0，P ＝9600W 二、多项选择题：本题共4小题，每小题4分，共16分，每小题有多个选项符合题意．全部选对的得4分，选对但不全的得2分，选错或不答的得0分．6．如图所示，直线a 、抛物线b 和曲线c 分别为某一稳恒直流电源在纯电阻电路中的总功率P 、电源内部发热功率P r 、输出功率P R 随电流I 变化的图象，根据图象可知 （ ）BA ．电源的电动势为9V ，内阻为3ΩB ．电源的电动势为3V ，内阻为1ΩC ．图象中任意电流值对应的P 、P r 、P R 间的关系为P >P r +P RD ．电路中总电阻为2Ω时，外电阻上消耗的功率最大且为2.25W7．太阳内部不断进行着核聚变反应，使其质量不断减小．很久以前和现在相比，以下判断正确的是 A ．地球绕太阳运动的速度大 B ．地球绕太阳运动的周期大 C ．地球绕太阳运动的角速度大 D ．地球绕太阳运动的半径大8．如图所示，质量分别为m 1、m 2的两个物块间用一轻弹簧连接，放在倾角为θ的粗糙斜面上，物块与斜面间的动摩擦因数均为μ．平行于斜面、大小为F 的拉力作用在m 1上，使m 1、m 2一起向上作匀加速运动，斜面始终静止在水平地面上，则 （ ） A ．弹簧的弹力为212m F m m + B ．弹簧的弹力为212m F m m +＋μm 2g sin θC ．地面对斜面的摩擦力水平向左D ．地面对斜面的摩擦力水平向右9．如图所示，质量为m 、带电量为＋q 的三个相同的带电小球A 、B 、C ，从同一高度以初速度v 0水平抛出，B 球处于竖直向下的匀强磁场中，C 球处于垂直纸面向里的匀强电场中，它们落地的时间分别为t A 、t B 、t C ，落地时的速度大小分别为v A 、v B 、v C ，则以下判断正确的是（ ）A．t A =t B =t C B ．t A =t C <t B C ．v B <v A <v C D ．v A =v B <v C三、简答题．本题共3题，共计44分．把答案填在答题卡相应的横线上或按题目要求作答．第10、11题为必做题，第12题为选修3－4、3－3模块试题．10．（10分）听说水果也能做电池，某兴趣小组的同学用一个柠檬做成电池．他们猜想水果电池内阻可能较大，从而设计了一个如图所示电路来测定该柠檬电池的电动势和内电阻．实验中他们多次改变电阻箱的电阻值，记录下电阻箱的阻值及相应的电流计示数，并算出电流的倒数，将数据填在如下的表格中．（1）利用图像法处理数据可以减小实验误差．在讨论作图方案时，甲同学认为应作R-I 图，而乙同学认为应该作IR 1-图，你认为哪个同学的想法更科学？____（填“甲”或“乙”），其简单理由是： ． （2）按照（1）中你选择的方案，在给出的坐标纸上作出图象．（3）利用你作出的图象，可求出该柠檬电池的电动势为 V ，内阻为 Ω． （4）完成实验后，该兴趣小组的同学初步得出了水果作为电池不实用的物理原因是：． EB11．（10分）某同学利用透明直尺和光电计时器来验证机械能守恒定律，实验的简易示意图如下，当有不透光物体从光电门间通过时，光电计时器就可以显示物体的挡光时间.所用的西瓯XDS-007光电门传感器可测的最短时间为0.01ms.将挡光效果好、宽度为d ＝3.8×10－3m的黑色磁带贴在透明直尺上，从一定高度由静止释放，并使其竖直通过光电门.某同学测得各段黑色磁带通过光电门的时间△t i与图中所示的高度差△h i，并将部分数据进行了处理，结果如下表所示。

2018年高考押题卷（1）【江苏卷】数学试题一、填空题：（本大题共14个小题，每小题5分，共70分，将答案填在答题纸上）1．设集合{}1,0,1A =-，{}0,1,2,3B =，则AB =【命题意图】本题考查集合交集的概念等基础知识，意在考查学生的基本运算能力． 【答案】{}0,1 【解析】A B {}1,0,1=-{}0,1,2,3={}0,1.2.已知23(,,ia bi ab R ii +=+∈为虚数单位)，则a b +=【命题意图】本题考查复数的运算，复数概念等基础知识，意在考查学生的基本运算能力． 【答案】1【解析】23323,2, 1.ia bi i a bi ab a b i +=+⇒-=+⇒==-+=3. 已知一个圆锥的母线长为2，侧面展开是半圆，则该圆锥的体积为【命题意图】本题考查圆锥体积、圆锥展开图等基础知识，意在考查基本运算能力．4. 袋子里有两个不同的红球和两个不同的白球，从中任取两个球，则这两个球颜色相同的概率为【命题意图】本题考查古典概型概率基础知识，意在考查学生的基本运算能力和逻辑推理能力.【答案】1 3【解析】从中4个球中任取两个球共有6种基本事件，其中两个球颜色相同包含两种基本事件，故概率为21 = 63.5. 下图是一个算法流程图，则输出的x的值是【命题意图】本题考查算法流程图、简单的不等式运算基础知识，意在考查基本概念，以及基本运算能力． 【答案】59.【解析】第一次循环：3,7x y ==，第二次循环：13,33x y ==，第三次循环：59,151x y ==，结束循环，输出59.x = 6.已知双曲线22221(0)x y a b a b -=>>的一个焦点为(3,0)，直线10x y --=与双曲线右支有交点，则当双曲线离心率最小时双曲线方程为 【命题意图】本小题主要考查双曲线的离心率，双曲线标准方程等基础知识，意在考查分析问题的能力、基本运算能力．【答案】22154x y -=7.若实数,x y 满足约束条件22,1,1,x y x y x y -⎧⎪--⎨⎪+⎩≤≥≥则目标函数2z x y =+的最小值为【命题意图】本题考查线性规划求最值基础知识，意在考查学生的基本运算能力．【答案】1【解析】可行域为ABC ∆及其内部，其中(3,4),(1,0),(0,1),A B C 直线2z x y =+过点(0,1)C 时取最小值1.8. 设等比数列{}n a 的前n 项和为n S ，若,63,763==S S 则=++987a a a 【命题意图】本题考查等比数列的性质及求和等基础知识，意在考查分析能力及基本运算能力． 【答案】448.【解析】由题意得1237a a a ++=，45663756a a a ++=-=，所以789568448a a a ++=⨯=9. 将函数()sin y x x x =+?¡的图像向左平移()0m m >个单位长度后，所得的图像关于y 轴对称，则m 的最小值是【命题意图】本题考查三角函数图像与性质等基础知识，意在考查基本运算能力.【答案】6π10.若实数,x y 满足0x y >>，且22log log 1x y +=，则22x y x y+-的最小值为【命题意图】本题考查基本不等式求最值基础知识，意在考查分析问题和解决问题能力以及运算求解能力． 【答案】4 【解析】因为22log log 12x y xy +=⇒=，所以222()24()4,x y x y xy x y x y x y x y+-+==-+≥---当且仅当时2,2x y xy -==，即11x y ==-22x y x y+-的最小值为4.11. 若函数()ln |31|f x x =-在定义域的某个子区间(1,1)k k -+上不具有单调性，则实数k 的取值范围为【命题意图】本题考查函数的图象和性质的综合运用等基础知识，意在考查分析问题的能力、基本运算能力及推理能力．【答案】)35,34[]32,1( --. 【解析】函数()y f x =的图象如图，11013k k -<<+≤或121133k k ≤-<<+，解得213k -<≤-或4533k ≤<.12.已知实数,,a b c 满足222a b c +=，0c ≠，则2ba c -的取值范围为【命题意图】本题考查三角函数最值等基础知识，意在考查学生分析能力及基本运算能力．【答案】[13. 已知圆22:2C xy +=，直线:240l x y +-=，点00(,)P x y 在直线l 上．若存在圆C 上的点Q ，使得45OPQ ∠=（O 为坐标原点），则0x 的取值范围为【命题意图】本题考查正弦定理、直线与圆的位置关系基础知识，意在考查运用数形结合思想、分析问题和解决问题的能力、基本运算能力及推理能力．【答案】8[0,]5【解析】在OPQ ∆中，设α=∠OQP ，由正弦定理，得αsin 45sin 0OPOQ =，即αsin 222OP =，得2sin 2≤=αOP ，即2)22(202≤-+x x ，解得5800≤≤x .14. 已知函数2()f x ax =，若存在两条过点(1,2)P -且相互垂直的直线与函数()f x 的图像都没有公共点，则实数a 的取值范围为【命题意图】本题考查函数与方程、函数图像与性质基础知识，意在考查分析问题、解决问题的能力、基本运算能力及推理能力．【答案】1(,)8+∞二、解答题 （本大题共6小题，共90分．解答应写出文字说明、证明过程或演算步骤．）15. （本小题满分14分）已知(cos ,sin ),(cos ,sin )a b ααββ==． （1）若67πβα=-，求a b ⋅的值； （2）若4,58a b πα⋅==，且⎪⎭⎫⎝⎛-∈-0,2πβα，求tan()αβ+的值．【命题意图】本题考查平面向量的数量积、两角和与差的三角函数、同角三角函数关系式等基础知识，意在考查分析问题和解决问题的能力、基本运算能力．16. （本小题满分14分）如图，在正三棱锥111ABC A B C -中，E ，F 分别为1BB ，AC 的中点.（1）求证：//BF 平面1A EC ；（2）求证：平面1A EC ⊥平面11ACC A .【命题意图】本题考查线面平行及面面垂直的判定定理等基础知识，意在考查空间想象能力、分析问题和解决问题的能力、推理论证能力.【解析】（1）连接1AC 交1AC 于点O ，连接OF ，F为AC 中点，∴111//=2OF CC OF CC 且，E 为1BB 中点，∴111//=2BE CC BE CC 且，∴//=BE OF BE OF且，∴四边形BEOF是平行四边形， ………4分∴//BF OE ，又BF ⊄平面1A EC ，OE ⊂平面1A EC ，∴//BF 平面1A EC (7)分17. （本小题满分14分）如图，两座建筑物AB ，CD 的底部都在同一个水平面上，且均与水平面垂直，它们的高度分别是9m 和15m ，从建筑物AB 的顶部A 看建筑物CD 的张角45CAD ∠=． （1）求BC 的长度；（2）在线段BC 上取一点P(点P 与点B ，C 不重合)，从点P 看这两座建筑物的张角分别为APB α∠=，DPC β∠=，问点P 在何处时，tan()αβ+最小？【命题意图】本题考查解三角形、两角和的正切公式、基本不等式的应用等基础知识，意在考查学生转化与化归能力，分析问题和解决问题的能力，以及运算推理能力．【解析】(1)如图作AN CD ⊥ 于N ．因为m CD m AB CD AB 15,9,//==, 所以m NC m DN 9,6==. 设AN x DAN θ∠＝，＝ ，因为45=∠CAD ,所以θ-=∠45CAN .在Rt ANC∆和Rt AND∆ 中，因为069tan ,tan(45-)=x x θθ=，………………………4分所以()91tan 451tan tan xθθθ-∴︒+＝－＝,化简整理得215540x x －－＝ ，解之得12)183(x x ＝，＝－舍去 ．所以BC的长度是18 m． ………………………7分(2)设BP t ＝ ，所以915PC=18-t,tan =,tan =18t t αβ- (9)分 则BCADP(第17题图)tan tan 661tan t 9151(an 145277227827)18t t t tan t t t t t αβαβαβ++----+++--++＋＝＝＝-＝- ………14分63013502)27(1350)27(=≥+++t t,当且仅当1350t+27=27t +，即时，()tan αβ＋ 取最小值． ……15分 答：P在距离B点m)27615(- 时,()tan αβ＋ 最小． ………………………16分 18. （本小题满分16分）已知椭圆C :22221(0)x y a b a b +=>>, 经过点P(1,，离心率是.（1）求椭圆C 的方程；（2） 设直线l 与椭圆C 交于,A B 两点，且以AB 为直径的圆过椭圆右顶点M ，求证：直线l 恒过定点．【命题意图】本题考查椭圆的标准方程与简单几何性质，直线与圆锥曲线的位置关系等基础知识，意在考查基本的运算能力、分析问题和解决问题的能力．将①②代入③，得 225161204m m k -+=+，解得65m =或2m =（舍）．综上，直线l 经过定点6(,0).5…………………14分19. （本小题满分16分）已知函数()xf x e =，2()1(,)g x ax bx a b R =++∈.[学科网 ]（1）若0a ≠，则a ，b 满足什么条件时，曲线()y f x =与()y g x =在0x =处总有相同的切线？ （2）当1a =时，求函数()()()g x h x f x =的单调减区间；（3）当0a =时，若()()f x g x ≥对任意的x R ∈恒成立，求b 的取值的集合. 【命题意图】本小题主要考查利用导数求切线方程，利用导数求单调区间及最值，不等式恒成立等基础知识，考查学生转化与化归能力、综合分析问题和解决问题的能力以及运算求解能力．（2）由1a =，21()xx bx h x e ++=，∴2(2)1()x x b x b h x e -+-+-'=， ∴2(2)1(1)((1))()x x x b x b x x b h x e e -+-+----'==-，………7分由()0h x '=，得11x =，21x b =-，∴当0b >时，函数()y h x =的减区间为(,1)b -∞-，(1,)+∞；当0b =时，函数()y h x =的减区间为(,)-∞+∞；当0b <时，函数()y h x =的减区间为(,1)-∞，(1,)b -+∞. ………10分 （3）由1a =，则()()()1xx f x g x ebx ϕ=-=--，∴()x x e b ϕ'=-，①当0b ≤时，()0x ϕ'≥，函数()x ϕ在R 上单调递增， 又(0)0ϕ=，∴ (,0)x ∈-∞时，()0x ϕ<，与函数()()f x g x ≥矛盾， (12)分②当0b >时，()0x ϕ'>，ln x b >；()0x ϕ'<，ln x b <，∴函数()x ϕ在(,ln )b -∞单调递减；(ln ,)b +∞单调递增，20. （本小题满分16分）等差数列{}na 的前n 项和为nS ，已知12a=，622S =.（1）求nS ；（2）若从{}na 中抽取一个公比为q 的等比数列{}nk a ，其中11k=，且12n k k k <<<，*n k N ∈.①当q 取最小值时，求{}nk 的通项公式；②若关于*()n n N ∈的不等式16n n S k +>有解，试求q 的值. 【命题意图】本题考查等差数列和等比数列综合应用，等差数列前n 项和公式，数列单调性等基础知识，意在考查学生灵活运用基本量进行探索求解、推理分析能力．【解析】（1）设等差数列的公差为d ，则611665222S a d =+⋅⋅=，解得23d =，……2分所以(5)3n n n S +=.………4分（2）①因为数列}{n a 是正项递增等差数列，所以数列}{nk a 的公比1>q ，若22=k ，则由382=a ，得3412==a a q ，此时932)34(223=⋅=k a ，由)2(32932+=n ，解得*310N n ∉=，所以22>k ，同理32>k ；……6分若42=k ，则由44=a ，得2=q ，此时122-⋅=n k n a ，另一方面，2(2)3n k n a k =+，所以2(2)23n n k +=，即1322n nk -=⨯-， ………8分所以对任何正整数n ，n k a 是数列}{n a 的第2231-⋅-n 项．所以最小的公比2=q ．所以2231-⋅=-n n k ． ………10分附加题部分21.【选做题】（本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．）A．【选修4—1几何证明选讲】（本小题满分10分）如图，△ABC 内接于⊙O，点D在OC的延长线上，AD与⊙O相切，割线DM 与⊙O相交于点M，N，若∠B=30°，AC=1，求DMDN【命题意图】本题主要考查切割线定理等基础知识，意在考查学生平面几何推理证明和逻辑思维能力.xy ，B．【选修4—2：矩阵与变换】（本小题满分10分）已知曲线C：1若矩阵M ⎥=⎥⎥⎦对应的变换将曲线C变为曲线C '，求曲线C '的方程.【命题意图】本题考查矩阵与向量乘积、相关点法求轨迹方程等基础知识，意在考查运算求解能力．【解析】设曲线C 一点(,)x y ''对应于曲线C '上一点(,)x y ，∴22x x y y '⎡⎤⎡⎤-⎢⎥⎢⎥⎢⎢⎥⎢⎥⎥=⎢⎥⎢⎥⎥⎢⎥⎢⎥⎥'⎦⎣⎦⎣⎦，∴x y x ''=x y y ''+=， (5)分∴x '=，y '=，∴1x y ''==，∴曲线C '的方程为222y x -=.…10分C.【选修4—4：坐标系与参数方程】（本小题满分10分）在极坐标系下，已知圆O ：cos sin ρθθ=+和直线:sin()42l πρθ-=，（1）求圆O 和直线l 的直角坐标方程；（2）当()0,θπ∈时，求直线l 与圆O 公共点的一个极坐标． 【命题意图】本题主要考查极坐标方程转化为直角坐标方程，直线与曲线位置关系等基本内容. 意在考查转化与化归能力、基本运算能力，方程思想与数形结合思想.D ．【选修4—5：不等式选讲】（本小题满分10分）已知,,a b c 均为正数,证明：2222111()a b c a b c +++++≥【命题意图】本题考查利用均值不等式证明不等式等基础知识，意在考查综合分析问题解决问题以及运算求解能力，逻辑思维能力．【解析】因为a b c，，均为正数，由均值不等式得22223()a b c abc ++≥3，………………2分因为13111()abc a b c-++≥3，所以223111(()abc a b c -++)≥9．…………………………………5分故22222233111(()()a b c abc abc a b c -++++++)≥39． （当且仅当c b a ==时取等号）又32233()9()abc abc -+=≥（当且仅当433=abc 时取等号），所以原不等式成立．…………………………………10分【必做题】（第22题、第23题，每题10分，共20分.解答时应写出文字说明、证明过程或演算步骤） 22. 如图，在空间直角坐标系中，正四棱锥的侧棱长与底边长都为，点M ，N 分别 在PA ，BD上，且13PM BN PA BD ==． （1）求证：MN ⊥AD ；（2）求MN 与平面PAD 所成角的正弦值．【命题意图】本题考查向量数量积，向量垂直，直线与平面所成角等基础知识，意在考查运算求解能力，逻辑思维能力．（2）设平面PAD 的法向量为(,,),n x y z =(3,3,0),(3,0,3),AD AP =--=-由0,0,n AD n AP ⎧⋅=⎪⎨⋅=⎪⎩得330,330.x y x z --=⎧⎨-+=⎩取1,z =得1, 1.x y ==-23. 设集合{}5,4,3,2,1=S ，从S 的所有非空子集中，等可能地取出一个.（1）设S A ⊆，若A x ∈，则A x ∈-6，就称子集A 满足性质p ，求所取出的非空子集满足性质p 的概率；（2）所取出的非空子集的最大元素为ξ，求ξ的分布列和数学期望()ξE .【命题意图】本题考查子集定义及性质、古典概型及离散型随机变量分布列和期望等基础知识，意在考查分析问题和解决问题能力，运算求解能力，逻辑思维能力． 【解析】可列举出集合S的非空子集的个数为：31125=-个.（2分）（1）满足性质p 的非空子集为：{}3，{}5,1，{}4,2，{}5,3,1，{}4,3,2，{}5,4,2,1，{}5,4,3,2,1共7个，所以所取出的非空子集满足性质p 的概率为： 317=p .（6分）（2）ξ的可能值为1，2，3，4，5.（9分）()31129311653184314331223111=⨯+⨯+⨯+⨯+⨯=ξE .（10分）。

2018年普通高等学校招生全国统一考试·冲刺预测卷一（江苏卷）数学Ⅰ一、填空题：本大题共14小题，每小题5分，共计70分，把答案填写在答题卡上相应位置上．．．．．．．．．.1. 已知全集为，集合，，则__________．【答案】【解析】则2. 若复数，则的虚部为__________．【答案】【解析】其虚部为3. 已知各项均为正数的等比数列满足，且，则__________．【答案】18【解析】解得，即，则4. 已知某高级中学，高一、高二、高三学生人数分别为880、860、820，现用分层抽样方法从该校抽调128人，则在高二年级中抽调的人数为__________．【答案】43【解析】由题意可知，在高二年级中抽调的人数为5. 执行如图所示程序框图，输出的为__________．【答案】【解析】第一次循环，第二次循环，第三次循环，第四次循环，第五次循环，第六次循环，，此时不满足条件，输出6. 已知双曲线：，过双曲线的右焦点作的渐近线的垂线，垂足为，延长与轴交于点，且，则双曲线的离心率为__________．【答案】【解析】双曲线：的渐近线方程为，右焦点过与渐近线垂直的直线为由可解得：，在中，令，可得：，整理得：，则即双曲线的离心率为7. 在含甲、乙的6名学生中任选2人去执行一项任务，则甲被选中、乙没有被选中的概率为__________．【答案】【解析】含甲，乙的名学生中任选人有种方法甲被选中，乙没有被选中的方法有种方法则甲被选中、乙没有被选中的概率为8. 已知函数的部分图象如图所示，若，，则__________．【答案】【解析】由函数图象可知函数的周期，又则，则则9. 已知在体积为的圆柱中，，分别是上、下底面直径，且，则三棱锥的体积为__________．【答案】【解析】设上，下底面圆的圆心分别为，，圆的半径为由已知，，则是中点到平面的距离与到平面的距离相等故，设三棱锥的高为则，10. 已知函数（，且），若，则不等式的解集为__________．【答案】【解析】函数，故函数为偶函数当时，，故，函数在上为增函数，由偶函数的性质可知在上为减函数，则或解得，且，则不等式的解集为11. 已知菱形的边长为2，，点、分别在边、上，，.若，，则__________．【答案】【解析】①即②，解得12. 已知关于实数，的不等式组，构成的平面区域为，若，使得，则实数的取值范围是__________．【答案】【解析】作出不等式组的可行域如图所示表示可行域内一点与之间的距离的平方和点到直线的距离为故故实数的取值范围是点睛：本题主要考查的知识点是二元一次不等式组表示的平面区域，考查了学生的数形结合思想和简单的转化思想，属于中档题目，本题的关键是要表示可行域内一点与之间的距离的平方和。

2018年江苏省高三数学预测卷及答案
5
◎试卷使用说明
1、此试卷完全按照2018年江苏高考数学考试说明命题，无超纲内容。

2、此试卷成绩基本可以反映高考时的数学成绩，上下浮动15分左右。

3、若此试卷达120分以上，高考基本可以保底120分；若达85分，只要在下一个阶段继续努力高考可以达96分。

4、此试卷不含理科加试内容。

江苏省2018届高三数学综合检测卷
一、填空题（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．）
1．复数在复平面上对应的点在第象限．
2．某商场有四类食品，其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20 种，从中抽取一个容量为20的样本进行食品安全检测．若采用分层抽样的方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是．
3．已知集合，集合，若命题
“ ”是命题“ ”的充分不必要条，则实
数的取值范围是．
4．如图，直三棱柱ABc-A1B1c1中，AB=1，Bc=2，Ac= ，AA1=3，为线段BB1上的一动点，则当A＋c1最小时，△Ac1的面积为．（第4题）．
5．集合若则．
6．阅读如图所示的程序框，若输入的是100，则输出的变量的值是．。

数学试题 第1页（共6页） 数学试题 第2页（共6页）绝密★启用2018年高考数学原创押题预测卷01（江苏卷）数学（考试时间：120分钟 试卷满分：160分）注意事项：1．本试卷均为非选择题（第1题~第20题，共20题）。

考试结束后，请将本试卷和答题卡一并交回。

2．答题前，请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符。

4．作答试题，必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效。

5．如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗。

一、填空题（本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．） 1．若集合22{|1},{|20}A x x B x x x =<=-=，则AB =_____________．2．若复数z 满足2018i 34i z ⋅=+（其中i 为虚数单位），则||z =_____________．3．对某校学生进行分层抽样调查，在高一、高二、高三三个年级抽取学生数分别为12,13,14.若高一学生有600名，则该校高中三个年级学生总人数为_____________．4．学校开设两节选修课，三名学生从中各自随机选择一节选修课，则三人不同时选同一选修课的概率为_____________．5．若抛物线24y x =的焦点到双曲线22221(0,0)x y a b a b-=>>的渐近线的距离为12，则双曲线的离心率为_____________．6．如图是一个算法的伪代码，则运行结果为_____________．201810While 201822End While Pr int a s I I s s a a a I I s←←←≤←⨯←-←+ 7．已知三棱锥S ABC -中侧棱,,SA SB SC 两两相互垂直，且3,4,5,SA SB SC ===则该三棱锥外接球的表面积为_____________．8．已知等比数列{}n a 中，0n a >，若2342349a a a a a a =++，则3a 的最小值为_____________． 9．已知函数2ππcossin ,[,]44y x x x x =-∈-，则其值域为_____________． 10．在三角形ABC 中，D 为边BC 中点，过C 作CE 垂直AD 于E ，若2CE =，则EB EC ⋅的值为_____________．11．已知PM 垂直直线42()y kx k k R =+-∈于M 点，若(2,0),(3,3)P N --，则线段MN 长度的最大值为_____________．12．若3,(0)m m m ->恰为函数sin()(0,0,0π)y A x A ωϕωϕ=+>><<两个相邻零点，则ϕ=_____________．13．若函数2()|1||1|f x x a x =-+-在[2,2]-上的最大值为6，则正数a 的值为_____________． 14．已知()|21|x f x =-，若方程2()(23)()120f x k f x k -+++=有三个不同的实根，则实数k 的取值范围为_____________．二、解答题（本大题共6小题，共计90分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤） 15．（本小题满分14分）在ABC △中，角A ，B ，C 所对的边分别为,,a b c ，1sin 8A B ==． （1）求cos C 的值；数学试题 第3页（共6页） 数学试题 第4页（共6页）（2）若24ab =，求ABC △的周长．16．（本小题满分14分）如图，在三棱锥P ABC -中，AB PC ⊥，M 是AB 的中点，点N 在棱PC 上，点D 在BN 上，MD ∥ 平面PAC ，平面ABN ⊥平面PMC ，MN 与PC 不垂直． （1）证明：点D 是BN 的中点； （2）证明：CA CB =．17．（本小题满分14分）三个城市,,A B C 恰构成正三角形，现准备在线段AC 之间建一个动车中转站D ，经测算，在,,AD CD BD 三段每单位建设成本比为1：2：4．设,AD B α∠=,,AD CD BD 三段总建设成本为S （万元）．设,AB m =AD 段每单位建设成本为a （万元）． （1）求S 关于α的函数关系式，并指出α的取值范围； （2）确定D 点位置，使得S 最小．18．（本小题满分16分）设1F ，2F 分别为椭圆)0(1:2222>>=+b a by a x E 的左、右焦点，点23,1(P 在椭圆E 上，且点P 和1F 关于y 轴上某点对称． （1）求椭圆E 的方程；（2）过右焦点2F 的直线l 与椭圆相交于A ，B 两点，过点P 且平行于AB 的直线与椭圆交于另一点Q ，问是否存在直线l ，使得四边形PABQ 是平行四边形？若存在，求出l 的方程；若不存在，说明理由．19．（本小题满分16分）已知数列{}n a 的前n 项和为n S ，若12a=，1(1)(1)n n nS n S n n +=+++．（1）求数列{}n a 的通项公式； （2）若11n n n b a a +=，数列{}n b 前n 项和为n T ，求使不等式2018n mT <恒成立时整数m 的最小值； （3）是否存在正整数k {}n a 中的项？20．（本小题满分16分）已知函数()ln f x x =，2()()(0)g x a x x a =->．（1）若曲线()y f x =与()y g x =在1x =处的切线相同，求a 的值； （2）求证：11()()f g a a≤；（3）若方程()()f x g x =有且仅有一解，求a 的值．数学试题 第5页（共6页） 数学试题 第6页（共6页）数学Ⅱ（附加题）（考试时间：30分钟 试卷满分：40分）注意事项：1．本试卷均为非选择题（第21题~第23题）。

2018年江苏省高考数学押题试卷一、填空题（本大题共14小题，每小题5分，共70分．请把答案填写在题中横线上）1．已知集合A={x|x2﹣x﹣2≤0}，集合B={x|1＜x≤3}，则A∪B= ．2．已知a，b∈R，i是虚数单位，若a+i=1﹣bi，则（a+bi）8= ．3．从某班抽取5名学生测量身高（单位：cm），得到的数据为160，162，159，160，159，则该组数据的方差s2= ．4．若双曲线x2+my2=1过点（﹣，2），则该双曲线的虚轴长为．5．根据如图所示的伪代码，可知输出的结果S为．6．在三张奖券中有一、二等奖各一张，另一张无奖，甲乙两人各抽取一张（不放回），两人都中奖的概率为．7．已知函数y=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜π）的图象如图所示，则该函数的解析式是．8．如图，在长方体ABCD﹣A1B1C1D1中，对角线B1D与平面A1BC1交于E点．记四棱锥E﹣A1B1C1D1的体积为V1，长方体ABCD﹣A1B1C1D1的体积为V2，则的值是．9．已知实数x ，y 满足，则的取值范围是 ．10．已知{a n }，{b n }均为等比数列，其前n 项和分别为S n ，T n ，若对任意的n ∈N *，总有=，则= ．11．已知平行四边形ABCD 中．∠BAD=120°，AB=1，AD=2，点P 是线段BC 上的一个动点，则•的取值范围是 ．12．如图，已知椭圆+=1（a ＞b ＞0）上有一个点A ，它关于原点的对称点为B ，点F 为椭圆的右焦点，且满足AF ⊥BF ，当∠ABF=时，椭圆的离心率为 ．13．在斜三角形ABC 中，a ，b ，c 分别是角A ，B ，C 所对的边，若+=，则的最大值为 ．14．对于实数a ，b ，定义运算“□”：a□b=设f （x ）=（x ﹣4）□（x ﹣4），若关于x 的方程|f （x ）﹣m|=1（m ∈R ）恰有四个互不相等的实数根，则实数m 的取值范围是 ．二、解答题（本大题共6小题，共90分．解答时应写出文字说明、证明过程或演算步骤）15．设α为锐角，且cos （α+）=．（1）求cos （）的值；（2）求cos （2α﹣）的值．16．在直三棱柱ABC ﹣A 1B 1C 1中，CA=CB ，AA 1=AB ，D 是AB 的中点（1）求证：BC 1∥平面A 1CD ；（2）若点P 在线段BB 1上，且BP=BB 1，求证：AP ⊥平面A 1CD ．17．如图，直线l 是湖岸线，O 是l 上一点，弧是以O 为圆心的半圆形栈桥，C 为湖岸线l上一观景亭，现规划在湖中建一小岛D ，同时沿线段CD 和DP （点P 在半圆形栈桥上且不与点A ，B 重合）建栈桥，考虑到美观需要，设计方案为DP=DC ，∠CDP=60°且圆弧栈桥BP 在∠CDP 的内部，已知BC=2OB=2（km ），设湖岸BC 与直线栈桥CD ，DP 是圆弧栈桥BP 围成的区域（图中阴影部分）的面积为S （km 2），∠BOP=θ （1）求S 关于θ的函数关系式；（2）试判断S 是否存在最大值，若存在，求出对应的cosθ的值，若不存在，说明理由．18．在平面直角坐标系xOy中，设椭圆（a＞b＞0）的离心率是e，定义直线y=为椭圆的“类准线”，已知椭圆C的“类准线”方程为y=，长轴长为4．（1）求椭圆C的方程；（2）点P在椭圆C的“类准线”上（但不在y轴上），过点P作圆O：x2+y2=3的切线l，过点O且垂直于OP的直线l交于点A，问点A是否在椭圆C上？证明你的结论．19．已知数列{an }满足2an+1=an+an+2+k（n∈N*，k∈R），且a1=2，a3+a5=﹣4．（1）若k=0，求数列{an }的前n项和Sn；（2）若a4=﹣1，求数列{an}的通项公式an．20．已知函数f（x）=e x（x3﹣2x2+（a+4）x﹣2a﹣4），其中a∈R，e为自然对数的底数．（1）关于x的不等式f（x）＜﹣e x在（﹣∞，2）上恒成立，求a的取值范围；（2）讨论函数f（x）极值点的个数．2018年江苏省高考数学押题试卷参考答案与试题解析一、填空题（本大题共14小题，每小题5分，共70分．请把答案填写在题中横线上）1．已知集合A={x|x2﹣x﹣2≤0}，集合B={x|1＜x≤3}，则A∪B= {x|﹣1≤x≤3} ．【考点】1D：并集及其运算．【分析】求解一元二次不等式化简集合A，然后直接利用并集运算得答案．【解答】解：由x2﹣x﹣2≤0，解得﹣1≤x≤2．∴A={x|﹣1≤x≤2}，又集合B={x|1＜x≤3}，∴A∪B={x|﹣1≤x≤3}，故答案为：{x|﹣1≤x≤3}，2．已知a，b∈R，i是虚数单位，若a+i=1﹣bi，则（a+bi）8= 16 ．【考点】A5：复数代数形式的乘除运算．【分析】利用复数相等求得a，b的值，代入（a+bi）8，再由复数代数形式的乘法运算化简得答案．【解答】解：由a+i=1﹣bi，得a=1，b=﹣1，从而（a+bi）8=（1﹣i）8=（﹣2i）4=16．故答案为：16．3．从某班抽取5名学生测量身高（单位：cm），得到的数据为160，162，159，160，159，则该组数据的方差s2= ．【考点】BC：极差、方差与标准差．【分析】求出数据的平均数，从而求出方差即可．【解答】解：数据160，162，159，160，159的平均数是：160，则该组数据的方差s2=（02+22+12+02+12）=，故答案为：．4．若双曲线x2+my2=1过点（﹣，2），则该双曲线的虚轴长为 4 ．【考点】KC：双曲线的简单性质．【分析】根据条件求出双曲线的标准方程即可得到结论．【解答】解：∵双曲线x2+my2=1过点（﹣，2），∴2+4m=1，即4m=﹣1，m=﹣，则双曲线的标准范围为x2﹣=1，则b=2，即双曲线的虚轴长2b=4，故答案为：4．5．根据如图所示的伪代码，可知输出的结果S为205 ．【考点】E5：顺序结构．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是输出满足条件i=2n+1，n∈N，i=i+2≥100时，S=2i+3的值【解答】解：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是输出满足条件i=2n+1，n∈N，i=i+2≥100时，S=2i+3的值，∵i+2=101时，满足条件，∴输出的S值为S=2×101+3=205．故答案为：205．6．在三张奖券中有一、二等奖各一张，另一张无奖，甲乙两人各抽取一张（不放回），两人都中奖的概率为．【考点】C5：互斥事件的概率加法公式．【分析】利用列举法求出甲、乙两人各抽取1张的基本事件的个数和两人都中奖包含的基本事件的个数，由此能求出两人都中奖的概率．【解答】解：设一、二等奖各用A，B表示，另1张无奖用C表示，甲、乙两人各抽取1张的基本事件有AB，AC，BA，BC，CA，CB共6个，其中两人都中奖的有AB，BA共2个，故所求的概率P=．故答案为：．7．已知函数y=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜π）的图象如图所示，则该函数的解析式是y=2sin（x+）．【考点】HK：由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】由图可知，A=2，由点（0，1）在函数的图象上，可得sinφ=，利用五点作图法可解得φ，又点（﹣，0）在函数的图象上，可得﹣ω+=kπ，k∈Z，进而解得ω，从而得解该函数的解析式．【解答】解：∵由图知A=2，y=2sin（ωx+φ），∵点（0，1），在函数的图象上，∴2sinφ=1，解得：sinφ=，∴利用五点作图法可得：φ=，∵点（﹣，0），在函数的图象上，可得：2sin（﹣ω+）=0，∴可得：﹣ω+=kπ，k∈Z，解得：ω=﹣，k∈Z，∵ω＞0，∴当k=0时，ω=，∴y=2sin（x+）．故答案为：y=2sin（x+）．8．如图，在长方体ABCD﹣A1B1C1D1中，对角线B1D与平面A1BC1交于E点．记四棱锥E﹣A1B1C1D1的体积为V1，长方体ABCD﹣A1B1C1D1的体积为V2，则的值是．【考点】LF：棱柱、棱锥、棱台的体积．【分析】连接B1D1∩A1C1=F，证明以E是△A1BC1的重心，那么点E到平面A1B1C1D1的距离是BB1的，利用体积公式，即可得出结论．【解答】解：连接B1D1∩A1C1=F，平面A1BC1∩平面BDD1B1=BF，因为E∈平面A1BC1，E∈平面BDD1B1，所以E∈BF，连接BD，因为F是A1C1的中点，所以BF是中线，又根据B1F平行且等于BD，所以=，所以E是△A1BC1的重心，那么点E到平面A1B1C1D1的距离是BB1的，所以V1=×BB1，而V2=×BB1，所以=．故答案为：．9．已知实数x，y满足，则的取值范围是[1，] ．【考点】7C：简单线性规划．【分析】作出不等式组对应的平面区域，利用直线斜率的几何意义进行求解即可．【解答】解：作出不等式组对应的平面区域，的几何意义是区域内的点到定点D（0，﹣1）的斜率，由图象知，AD的斜率最大，BD的斜率最小，此时最小值为1，由得，即A（1，），此时AD的斜率k==，即1≤≤，故的取值范围是[1，]故答案为：[1，]10．已知{a n }，{b n }均为等比数列，其前n 项和分别为S n ，T n ，若对任意的n ∈N *，总有=，则= 9 ．【考点】8E ：数列的求和．【分析】设{a n }，{b n }的公比分别为q ，q′，利用=，求出q=9，q′=3，可得=3，即可求得结论．【解答】解：设{a n }，{b n }的公比分别为q ，q′，∵=，∴n=1时，a 1=b 1．n=2时，．n=3时，．∴2q ﹣5q′=3，7q′2+7q′﹣q 2﹣q+6=0， 解得：q=9，q′=3，∴．故答案为：9．11．已知平行四边形ABCD中．∠BAD=120°，AB=1，AD=2，点P是线段BC上的一个动点，则•的取值范围是[﹣，2] ．【考点】9R：平面向量数量积的运算．【分析】以为坐标原点，以BC所在的直线为x轴，建立如图所述的直角坐标系，作AE⊥BC，垂足为E，求出A（，），D（，），设点P（x，0），0≤x≤2，根据向量的坐标运算以及向量的数量积的运算得到•=（x﹣）2﹣，根据二次函数的性质即可求出答案．【解答】解：以B为坐标原点，以BC所在的直线为x轴，建立如图所述的直角坐标系，作AE ⊥BC，垂足为E，∵∠BAD=120°，AB=1，AD=2，∴∠ABC=60°，∴AE=，BE=，∴A（，），D（，），∵点P是线段BC上的一个动点，设点P（x，0），0≤x≤2，∴=（x﹣，﹣），=（x﹣，﹣），∴•=（x﹣）（x﹣）+=（x﹣）2﹣，∴当x=时，有最小值，最小值为﹣，当x=0时，有最大值，最大值为2，则•的取值范围为[﹣，2]，故答案为：[﹣，2]．12．如图，已知椭圆+=1（a＞b＞0）上有一个点A，它关于原点的对称点为B，点F为椭圆的右焦点，且满足AF⊥BF，当∠ABF=时，椭圆的离心率为．【考点】K4：椭圆的简单性质．【分析】设椭圆的左焦点为F1，连结AF1，BF1，通过|AB|=|F1F|=2c，所以在Rt△ABF中，|AF|=2csin，|BF|=2ccos，由椭圆定义，转化求解离心率即可．【解答】解：设椭圆的左焦点为F1，连结AF1，BF1，由对称性及AF⊥BF可知，四边形AFBF1是矩形，所以|AB|=|F1F|=2c，所以在Rt△ABF中，|AF|=2csin，|BF|=2ccos，由椭圆定义得：2c（cos+sin）=2a，即：e====．故答案为：．13．在斜三角形ABC中，a，b，c分别是角A，B，C所对的边，若+=，则的最大值为．【考点】HR：余弦定理；HP：正弦定理．【分析】由+=可得， +=，通分化简，根据正弦定理及余弦定理在化简，利用基本不等式的性质求解．【解答】解：由+=可得， +=，即=，∴=，即=，∴sin2C=sinAsinBcosC．根据正弦定理及余弦定理可得，c2=ab•，整理得a2+b2=3c2，∴=≤=，当且仅当a=b时等号成立．故答案为．14．对于实数a，b，定义运算“□”：a□b=设f（x）=（x﹣4）□（x﹣4），若关于x的方程|f（x）﹣m|=1（m∈R）恰有四个互不相等的实数根，则实数m的取值范围是（﹣1，1）∪（2，4）．【考点】54：根的存在性及根的个数判断．【分析】根据新定义得出f（x）的解析式，作出f（x）的函数图象，则f（x）与y=m±1共有4个交点，根据图象列出不等式组解出．【解答】解：解不等式x﹣4≤﹣4得x≥0，f（x）=，画出函数f（x）的大致图象如图所示．因为关于x的方程|f（x）﹣m|=1（m∈R），即f（x）=m±1（m∈R）恰有四个互不相等的实数根，所以两直线y=m±1（m∈R）与曲线y=f（x）共有四个不同的交点，∴或或，解得2＜m＜4或﹣1＜m＜1．故答案为（﹣1，1）∪（2，4）．二、解答题（本大题共6小题，共90分．解答时应写出文字说明、证明过程或演算步骤）15．设α为锐角，且cos（α+）=．（1）求cos（）的值；（2）求cos（2α﹣）的值．【考点】GP：两角和与差的余弦函数．【分析】（1）由已知及同角三角函数基本关系式可求sin（α+），利用诱导公式即可得解cos（）的值．（2）利用诱导公式可求sin（），由2α=（α+）﹣（），利用两角差的余弦函数公式即可计算得解．【解答】（本题满分为14分）解：（1）∵α为锐角，∴α+∈（，）．又cos（α+）=，故sin（α+）=，…4分∴cos（）=cos[﹣（α+）]=sin（α+）=，…6分（2）又sin（）=﹣sin[﹣（α+）]=﹣cos（α+）=﹣，…8分故cos（2α）=cos[（α+）﹣（）]=cos（α+）cos（）﹣sin（α+）sin（）=×﹣×（﹣）=…14分16．在直三棱柱ABC﹣A1B1C1中，CA=CB，AA1=AB，D是AB的中点（1）求证：BC1∥平面A1CD；（2）若点P在线段BB1上，且BP=BB1，求证：AP⊥平面A1CD．【考点】LW：直线与平面垂直的判定；LS：直线与平面平行的判定．【分析】（1）连接AC1，设与CA1交于O点，连接OD，由O为AC1的中点，D是AB的中点，可得OD∥BC1，即可证明BC1∥平面A1CD．（2）法一：设AB=x，则证明△ABP∽△ADA1，可得AP⊥A1D，又由线面垂直的性质可得CD⊥AP，从而可证AP⊥平面A1CD；法二：由题意，取A1B1的中点O，连接OC1，OD，分别以OC1，OA1，OD为x，y，z轴建立空间直角坐标系，设OA1=a，OC1=b，由题意可得各点坐标，可求=（b，﹣a，2），=（0．﹣a，2），=（0，﹣2a，﹣），由•=0，•=0，即可证明AP⊥平面A1CD．【解答】证明：（1）如图，连接AC1，设与CA1交于O点，连接OD∴直三棱柱ABC﹣A1B1C1中，O为AC1的中点，∵D是AB的中点，∴△ABC1中，OD∥BC1，又∵OD⊂平面A1CD，∴BC1∥平面A1CD．（2）法一：由题意，设AB=x，则BP=x，AD=x，A1A=x，由于=，∴△ABP∽△ADA1，可得∠BAP=∠AA1D，∵∠DA1A+∠ADA1=90°，可得：AP⊥A1D，又∵CD⊥AB，CD⊥BB1，可得CD⊥平面ABA1B1，∴CD⊥AP，∴AP⊥平面A1CD．法二：由题意，取A1B1的中点O，连接OC1，OD，分别以OC1，OA1，OD为x，y，z轴建立空间直角坐标系，设OA1=a，OC1=b，则：由题意可得各点坐标为：A1（0，a，0），C（b，0，2a），D（0，0，2），P（0，﹣a，），A（0，a，2），可得： =（b，﹣a，2），=（0．﹣a，2），=（0，﹣2a，﹣），所以：由•=0，可得：AP⊥A1C，由•=0，可得：AP⊥A1D，又：A1 C∩A1D=A1，所以：AP⊥平面A1CD17．如图，直线l是湖岸线，O是l上一点，弧是以O为圆心的半圆形栈桥，C为湖岸线l 上一观景亭，现规划在湖中建一小岛D，同时沿线段CD和DP（点P在半圆形栈桥上且不与点A，B重合）建栈桥，考虑到美观需要，设计方案为DP=DC，∠CDP=60°且圆弧栈桥BP在∠CDP 的内部，已知BC=2OB=2（km），设湖岸BC与直线栈桥CD，DP是圆弧栈桥BP围成的区域（图中阴影部分）的面积为S（km2），∠BOP=θ（1）求S关于θ的函数关系式；（2）试判断S是否存在最大值，若存在，求出对应的cosθ的值，若不存在，说明理由．【考点】HN ：在实际问题中建立三角函数模型．【分析】（1）根据余弦定理和和三角形的面积公式，即可表示函数关系式，（2）存在，存在，S′=（3cosθ+3sinθ﹣1），根据两角和差的余弦公式即可求出．【解答】解：（1）在△COP 中，CP 2=CO 2+OP 2﹣2OC •OPcosθ=10﹣6cosθ，从而△CDP 得面积S △CDP =CP 2=（5﹣3cosθ），又因为△COP 得面积S △COP =OC •OP=sinθ，所以S=S △CDP +S △COP ﹣S 扇形OBP=（3sinθ﹣3cosθ﹣θ）+，0＜θ＜θ0＜π，cosθ0=，当DP 所在的直线与半圆相切时，设θ取的最大值为θ0，此时在△COP 中，OP=1，OC=3，∠CPO=30°，CP==6sinθ0，cosθ0=，（2）存在，S′=（3cosθ+3sinθ﹣1），令S′=0，得sin （θ+）=，当0＜θ＜θ0＜π，S′＞0，所以当θ=θ0时，S 取得最大值，此时cos （θ0+）=﹣，∴cosθ0=cos[（θ0+）﹣]=cos （θ0+）cos+sin （θ0+）sin=18．在平面直角坐标系xOy 中，设椭圆（a ＞b ＞0）的离心率是e ，定义直线y=为椭圆的“类准线”，已知椭圆C 的“类准线”方程为y=，长轴长为4．（1）求椭圆C 的方程；（2）点P 在椭圆C 的“类准线”上（但不在y 轴上），过点P 作圆O ：x 2+y 2=3的切线l ，过点O 且垂直于OP 的直线l 交于点A ，问点A 是否在椭圆C 上？证明你的结论． 【考点】K4：椭圆的简单性质．【分析】（1）由题意列关于a ，b ，c 的方程，联立方程组求得a 2=4，b 2=3，c 2=1，则椭圆方程可求；（2）设P （x 0，2）（x 0≠0），当x 0=时和x 0=﹣时，求出A 的坐标，代入椭圆方程验证知，A 在椭圆上，当x 0≠±时，求出过点O 且垂直于0P 的直线与椭圆的交点，写出该交点与P 点的连线所在直线方程，由原点到直线的距离等于圆的半径说明直线是圆的切线，从而说明点A 在椭圆C 上．【解答】解：（1）由题意得： ==2，2a=4，又a 2=b 2+c 2，联立以上可得： a 2=4，b 2=3，c 2=1．∴椭圆C 的方程为+y 2=1；（2）如图，由（1）可知，椭圆的类准线方程为y=±2，不妨取y=2，设P （x 0，2）（x 0≠0），则k OP =，∴过原点且与OP 垂直的直线方程为y=﹣x ，当x 0=时，过P 点的圆的切线方程为x=，过原点且与OP 垂直的直线方程为y=﹣x ，联立，解得：A （，﹣），代入椭圆方程成立；同理可得，当x 0=﹣时，点A 在椭圆上；当x 0≠±时，联立，解得A 1（，﹣），A 2（﹣，），PA 1所在直线方程为（2+x 0）x ﹣（x 0﹣6）y ﹣x 02﹣12=0．此时原点O到该直线的距离d==，∴说明A点在椭圆C上；同理说明另一种情况的A也在椭圆C上．综上可得，点A在椭圆C上．19．已知数列{an }满足2an+1=an+an+2+k（n∈N*，k∈R），且a1=2，a3+a5=﹣4．（1）若k=0，求数列{an }的前n项和Sn；（2）若a4=﹣1，求数列{an}的通项公式an．【考点】8H：数列递推式；8E：数列的求和．【分析】（1）若k=0，则数列{an }满足2an+1=an+an+2（n∈N*，k∈R），则数列{an}是等差数列，利用等差数列的前n项和公式即可得出．（2）2an+1=an+an+2+k（n∈N*，k∈R），a3+a5=﹣4，a4=﹣1，可得2a4=a3+a5+k，k=2．数列{an}满足2an+1=an+an+2+2，利用递推关系可得：2（an+1﹣an）=（an﹣an﹣1）+（an+2﹣an+1），令bn=an+1﹣an，则2bn =bn﹣1+bn+1．数列{bn}是等差数列，即可得出．【解答】解：（1）若k=0，则数列{an }满足2an+1=an+an+2（n∈N*，k∈R），∴数列{an}是等差数列，设公差为d，∵a1=2，a3+a5=﹣4．∴2×2+6d=﹣4，解得d=．∴Sn=2n×=．（2）2an+1=an+an+2+k（n∈N*，k∈R），a3+a5=﹣4，a4=﹣1，则2a4=a3+a5+k，﹣2=﹣4+k，解得k=2．数列{a n }满足2a n+1=a n +a n+2+2， 当n ≥2时，2a n =a n ﹣1+a n+1+2，相减可得：2（a n+1﹣a n ）=（a n ﹣a n ﹣1）+（a n+2﹣a n+1）， 令b n =a n+1﹣a n ， 则2b n =b n ﹣1+b n+1．∴数列{b n }是等差数列，公差=b 4﹣b 3=（a 5﹣a 4）﹣（a 4﹣a 3）=﹣2． 首项为b 1=a 2﹣a 1，b 2=a 3﹣a 2，b 3=a 4﹣a 3， 由2b 2=b 1+b 3，可得2（a 3﹣a 2）=a 2﹣2﹣1﹣a 3， 解得3（a 3﹣a 2）=﹣3，b 2=a 3﹣a 2=﹣1． ∴b n =b 2+（n ﹣2）（﹣2）=﹣2n+3． ∴a n+1﹣a n =﹣2n+3．∴a n =（a n ﹣a n ﹣1）+（a n ﹣1﹣a n ﹣2）+…+（a 2﹣a 1）+a 1 =[﹣2（n ﹣1）+3]+[﹣2（n ﹣2）+3]+…+（﹣2+3）+2=+2=﹣n 2+4n ﹣1．20．已知函数f （x ）=e x （x 3﹣2x 2+（a+4）x ﹣2a ﹣4），其中a ∈R ，e 为自然对数的底数．（1）关于x 的不等式f （x ）＜﹣e x 在（﹣∞，2）上恒成立，求a 的取值范围； （2）讨论函数f （x ）极值点的个数．【考点】6D ：利用导数研究函数的极值；3R ：函数恒成立问题．【分析】（1）原不等式转化为所以a ＞﹣（x ﹣2）2，根据函数的单调性即可求出a 的范围， （2）先求导，再构造函数，进行分类讨论，利用导数和函数的极值的关系即可判断．【解答】解：（1）由f （x ）＜﹣e x ，得e x （x 3﹣2x 2+（a+4）x ﹣2a ﹣4）＜﹣e x ， 即x 3﹣6x 2+（3a+12）x ﹣6a ﹣8＜0对任意x ∈（﹣∞，2）恒成立， 即（6﹣3x ）a ＞x 3﹣6x 2+12x ﹣8对任意x ∈（﹣∞，2）恒成立，因为x ＜2，所以a ＞=﹣（x ﹣2）2，记g（x）=﹣（x﹣2）2，因为g（x）在（﹣∞，2）上单调递增，且g（2）=0，所以a≥0，即a的取值范围为[0，+∞）；（2）由题意，可得f′（x）=e x（x3﹣x2+ax﹣a），可知f（x）只有一个极值点或有三个极值点．令g（x）=x3﹣x2+ax﹣a，①若f（x）有且仅有一个极值点，则函数g（x）的图象必穿过x轴且只穿过一次，即g（x）为单调递增函数或者g（x）极值同号．（ⅰ）当g（x）为单调递增函数时，g′（x）=x2﹣2x+a≥0在R上恒成立，得a≥1．（ⅱ）当g（x）极值同号时，设x1，x2为极值点，则g（x1）•g（x2）≥0，由g′（x）=x2﹣2x+a=0有解，得a＜1，且x12﹣2x1+a=0，x22﹣2x2+a=0，所以x1+x2=2，x1x2=a，所以g（x1）=x13﹣2x12﹣2+ax1﹣a=x1（2x1﹣a）﹣x1+ax1﹣a=﹣（2x1﹣a）﹣ax1+ax1﹣a= [（a﹣1）x1﹣a]，同理，g（x2）= [（a﹣1）x2﹣a]，所以g（x1）g（x2）= [（a﹣1）x1﹣a]• [（a﹣1）x2﹣a]≥0，化简得（a﹣1）2x1x2﹣a（a﹣1）（x1+x2）+a2≥0，所以（a﹣1）2a﹣2a（a﹣1）+a2≥0，即a≥0，所以0≤a＜1．所以，当a≥0时，f（x）有且仅有一个极值点；②若f（x）有三个极值点，则函数g（x）的图象必穿过x轴且穿过三次，同理可得a＜0．综上，当a≥0时，f（x）有且仅有一个极值点，当a＜0时，f（x）有三个极值点．。

2018年普通高等学校招生全国统一考试（江苏卷）预测2物理第Ⅰ卷（选择题共38分）一、本题共6小题，每小题3分，共18分，在每小题给出的四个选项中只有一个选项是符合题目要求的，选对得3分，有选错或不答的得0分1．原子核自发地放出电子的现象称为β 衰变，开始时科学家曾认为β 衰变中只放出电子，即β 粒子，后来发现，这个过程中，除了放出电子以外，还放出一种叫作“反中微子”的粒子，反中微子不带电，与其他物质的相互作用极弱．下面关于β 衰变的说法中正确的是（）A．静止的原子核发生β 衰变时β 粒子与衰变后的核的运动速度方向一定相反B．原子核发生β 衰变时放出的能量等于β 粒子与衰变后的核的动能之和C．原子核能发生β 衰发，说明原子核内含有电子D．发生β 衰变后的原子核的核子数不变但带电量增加2．人造地球卫星在科研、国防等方面起着不可替代的作用．只要发射的技术高，就能使人造地球卫星（）A．在地球赤道面离地面任意高度的圆轨道上，并且相对于地面永远是静止的B．在与地球赤道共面的圆轨道上做匀速圆周运动，但相对地面不一定是静止C．有可能在地球任一纬度线所决定的平面内，绕地球做匀速圆周运动D．始终在某一经度圈所在的平面内运动，且轨道与该经度圈为同心圆，卫星相对地面静止3．在研究微型电动机的性能时，应用如图2所示的实验电路．当调节滑动变阻器R使电动机停止转动时，电流表和电压表的示数分别为0.50A和2.0V．重新调节R使电动机恢复正常运转，此时电流表和电压表的示数分别为2.0A和24.0V，则这台电动机正确运转时的输出功率为（）图2A．32W B．44W C．47W D．48W4．在电视机的显像管中，电子束的扫描是用磁偏转技术实现的，其扫描原理如图3所示．圆形区域内的偏转磁场方向垂直于圆面，当不加磁场时，电子束将通过O点而打在屏幕的中心M点．为了使屏幕上出现一条以M点为中点的亮线PQ，偏转磁场的磁感应强度B随时间变化的规律应是图4中的（）图3图45．如图5所示，一木块B 放在水平地面上，木块A 放在木板B 的上面，木块A 的右端通过轻质弹簧固定在竖直墙壁上．用力F 向左拉木板B ，使它们以速度v 运动，这时弹簧秤示数为F ．下列说法中正确的是（ ）图5A ．木板B 受到的滑动摩擦力的大小等于F B ．地面受到的滑动摩擦力的大小等于FC ．若木板以2v 的速度运动，木块A 受到的滑动摩擦力的大小等于2FD ．若用力2F 拉木板B ，木块A 受到的滑动摩擦力的大小等于F6．如图5所示，荷质比为e /m 的电子，以速度0v 沿AB 边射入边长为a 的等边三角形的匀强磁场区域中，欲使电子从BC 边穿出，磁感应强度B 的取值为（ ）图5A ．aemv B 03=B ．ae mv B 02=C ．aemv B 03<D ．ae mv B 02<二、本题共5小题，每小题4分，共20分．在每小题给出的四个选项中，有多项是正确的，全部选对的得4分，选不全的得2分，有选错或不答的得0分．7、如图所示，电源电动势为E ，内阻为r ．当开关S 闭合，滑动变阻器的滑片P 位于中点位置时，三个小灯泡L 1、L 2、L 3都正常发光，且亮度相同，则（ ） A ．三个灯泡的额定功率相同 B ．三个灯泡的额定电压相同 C ．三个灯泡的电阻按从大到小排列是L 1、L 3、L 1 D ．当滑片P 稍微向左滑动，灯L 1和L 3变暗，灯L 2变亮8、如图所示电路为演示自感现象的实验电路. 若闭合开关s ，电流达到稳定后通过线圈L 的电流为I 1，通过小灯泡L 2的电流 为I 2，小灯泡L 2处于正常发光状态，则以下说法正确的是（ ） A ．s 闭合的瞬间，L 2灯缓慢变亮，L 1灯立即亮； B ．s 闭合的瞬间，通过线圈L 的电流由零逐渐增大到I 1； C ．s 断开的瞬间，小灯泡L 2中电流由I 1逐渐减为零，方向与I 2相反；D ．s 断开的瞬间，小灯泡L 2中电流由I 2逐渐减为零，方向不变.9、如图所示，一细光束通过玻璃三棱镜折射后分成a 、b 、c 三束单色光，则这三种单色光（ ） A 、频率关系是a v <b v <c vB 、在真空中的传播速度关系是a v <b v <c vC 、通过同一双缝产生的干涉条纹的间距a d <b d <c dD 、通过同一双缝产生的干涉条纹的间距a d >b d >c d10、如图所示，某人正通过定滑轮用不可伸长的轻质细绳将质量为m 的货物提升到高处。

2018年江苏高考数学模拟试题（一）数学Ⅰ 必做题部分一、填空题：本大题共18小题，每小题5分，共计70分．请把答案填写在答．题卡相应位置上．．．．．．．． 1．已知集合{}0,1A =，集合{}1,0,B x =-, 且A B ⊆，则实数x 的值为 ． 1．答案：1，解析：根据子集的定义知x 的值为1．2．已知复数(1)(1)i bi +⋅+为纯虚数，则实数b 的值为 ． 2．答案：1，解析：(1)(1)(1)(1)i bi b b i +⋅+=-++ ，(1)(1)i bi +⋅+是纯虚数，10b ∴-=，且10b +≠ ，1b ∴=．3．一个算法的流程图如下图所示，则输出s 的结果为 ．3．答案：11，解析：第一次循环后，3Y =，第二次循环后，5Y =，第三次循环后，7Y =，⋅⋅⋅，所以输出11Y =．4．如图表示甲、乙两名篮球运动员每场得分情况的茎叶图，则甲、乙得分的中位数分别是,a b ，则a b += ．4．答案：57.5，解析：由茎叶图知甲的中位数为32a =，乙的中位数为25.5a =，．57.5a b ∴+=．5．一口袋中放有质地、大小完全相同的6个球，编号分别为1，2，3，4，5，6，甲先摸出一个球，记下编号，放回后乙再摸一个球，甲、乙两人所摸球的编号不同的概率是 ．5．答案：56，解析：设“编号不相同”为事件B ，则“编号相同”为其对立事件B ，事件B 包含的基本事件为（1，1），（2，2），（3，3），（4，4），（5，5），（6，6），61()366P B ==， 所以 15()1()166P B P B =-=-=，编号不同的概率为56．6．在△ABC 中，角A ，B ，C 所对边分别为a ，b ，c ，且tan 21tan A c Bb+=，则角A 的大小为 ．6．答案：π3，解析：tan 2sin cos 2sin 11tan sin cos sin A c A B C BbB AB+=⇒+=，即sin cos sin cos 2sin sin cos sin B A A B C B AB+=，∴sin()2sin sin cos sin A B C B AB+=， ∴1cos 2A =．∵0πA <<，∴π3A =．7．已知质点P 在半径为10cm圆周运动，角速度是1rad/s ，设(10,0)A 为起始点，记点在y 轴上的射影为M ，则18π秒时点M 的速度cm/s ．7．答案：10，解析：运动t s 后，(10cos ,10sin ),P t t 则M 的位移()10sin S t t =，10cos v S t '∴==，则18π秒时点M 的速度是18cm/s ．瞬时变化率就是导数是解题的关键．8．如图，设椭圆22221(0)x y a b a b+=>>长轴为AB ，短轴为CD ，E 是椭圆弧BD 上的一点，AE 交CD 于K ，CE 交AB 于L ，则22EK EL AK CL ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭的值为 .8．答案：1，解析：利用投影将斜距离之比转化为水平的距离或竖直的距离之比，将线段之比转化为坐标的绝对值之比，体现坐标法解决问题的思想.如图所示，设点00(,)E x y ，过点E 分别向x 、y 轴引垂线，垂足分别为N 、M ，由△MKE ∽△OKA ，故x EK ME AK AO a==，同理0yEL CL b=，则22220022x y EK EL AK CL a b ⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭，又点00(,)E x y 在椭圆上，故有2200221x y a b +=，即221EK EL AK CL ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭. 9．各项均为正数的等比数列{}n a 满足1764,8a a a ==，若函数231012310()f x a x a x a x a x =++++的导数为()f x '，则1()2f '的值为 ． 9．答案：554，解析： 由等比数列的性质知24174a a a ==，又因为各项均为正数，所以42a =．因为68a =，所以112,4q a ==，所以32-=n n a ，又91210()210f x a a x a x '=+++，其通项公式为1n n na x -，将21=x 代入得114n n na x n -=，所以1155()(1210)244f '=+++=．18．已知ABC ∆的三边,,a b c 满足1349c b a ≤≤≤≤≤≤，则ABC ∆的面积S 最大值为 ．18．答案：6，解析： 11sin 34sin 90622S bc A =≤⨯⨯⋅=，当2224,3,b c a b c ===+时，等号取得，即当5,4,3a b c ===时，ABC ∆的面积S 的最大值为6．18．用[]x 表示不超过x 的最大整数．已知()[]f x x x =+的定义域为[1,1)-，则函数()f x 的值域为 ．18．答案：[2,1)[0,1)--，解析：根据[]x 的定义分类讨论．当[1,0)x ∈-时，1y x =-，21y -≤<-；当[0,1)x ∈时，y x =，01y ≤<；所以函数()f x 的值域为[2,1)[0,1)--． 18．已知点G 、H 分别为ABC ∆的重心（三条中线的交点）、垂心（三条高所在直线的交点），若4,6AC AB ==，则HG BC ⋅的值为 ． 18．答案：203-，解析：1()()()3HG BC AG AH BC AG BC AC AB AC AB ⋅=-⋅=⋅=+⋅- 22120()33AC AB =-=-．另解：注意到题中的ABC ∆形状不确定，因此可取特殊情形90ACB ∠=，则点H 即为点A ，由此可迅速得到答案．18．设,x y 是正实数，且1x y +=，则2221x y x y +++的最小值是 ． 18．答案：14，解析：设2x s +=，1y t +=，则4s t +=．所以2221x y x y +++=22(2)(1)41(4)(2)s t s t s t s t --+=-++-+41()()6s t s t =+++-． 41()2s t =+-．因为41141149()()(5)444t s s t s t s t s t +=++=++≥，等号当且仅当4,4t ss t s t =+=取得，84,33s t ==，即当且仅当21,33x y ==时，2221x y x y +++的取得最小值14．18．在棱长为1的正方体1111ABCD A B C D -中，若点P 是棱上一点，则满足12PA PC +=的点P 的个数为 ．18．解析：方法1：利用椭圆的定义．一方面点P 在以1,A C 为焦点，长轴长为2的椭圆上；另一方面，P 可能在AB ，AD ，1AA ，11C B ，11C D ，1C C 上，或者在111111,,,,,BB DD CD A B BC AD 上．因为112BA BC +=>，故点B 在以,A C 为焦点，长轴长为2的椭圆外，所以椭圆必与线段AB 相交，同理在AD ，1AA ，11C B ，11C D ，1C C 上各有一点满足条件． 又若点P 在1BB上，则12PA PC +=>．11D 1故1BB 上不存在满足条件的点P ，同理11111,,,,DD CD A B BC A D 上不存在满足条件的点P ．故满足题设条件的点P 的个数为6．方法2：若P 在AB 上，设AP x =，有12,PA PC x +=+=解得12x =． 故AB 上有一点P （AB 的中点）满足条件．同理在AD ，1AA ，11C B ，11C D ，1C C 上各有一点满足条件．又若点P 在1BB 上，则12PA PC +=>．故1BB 上不存在满足条件的点P ，同理11111,,,,DD CD A B BC A D 上不存在满足条件的点P ．故满足题设条件的点P 的个数为6．二、解答题：（本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤．）18．（本小题满分18分）如图2，点P 在ABC ∆内，23AB CP BC ===, , πP B ∠+∠=，记B α∠=．（1）试用α表示AP 的长；（2）求四边形ABCP 的面积的最大值，并求出此时α的值．18．解：（1）△ABC 与△APC 中，由余弦定理得，22223223cos AC α=+-⨯⨯， ①()222222cos AC AP AP α=+-⋅⋅π-， ②由①②得()24cos 12cos 90 0 AP AP ααα++-=∈π，，，解得34cos AP α=-；（2）()()1123sin 2sin 0 ABC APC S S S AP ααα∆∆=-=⨯⨯-⨯⨯π-∈π, ， 由（1）得4sin cos S αα=⋅2sin2 α=，()0 α∈π，，所以当4απ=时，max 2S =． 18．（本小题满分18分）已知PA ⊥菱形ABCD 所在平面，点E 、F 分别为线段BC 、PA 的中点． （1）求证：BD PC ⊥； （2）求证：BF ∥平面PDE ． 18．证明：（1）PA ⊥平面ABCD ，BD ⊂平面ABCD ，PA BD ∴⊥，又ABCD 是菱形，AC BD ∴⊥， 又,PA AC ⊂平面PAC ，PA AC A =，BD ∴⊥平面PAC ，又PC ⊂平面PAC ， ∴BD PC ⊥．（2）取线段PD 的中点G ，连结,EG FG ，则FG ∥AD ，且12FG AD =，又BE ∥AD ，且12BE AD =，FG ∴∥BE ，FG BE =，∴四边形BEGF 是平行四边形， BF∴∥EG ，又BF ⊄平面PDE ，EG ⊂平面PDE ，BF∴∥平面PDE ．18．（ 本小题满分18分） 某商场分别投入x 万元，经销甲、乙两种商品，可分别获得利润1y 、2y 万元，利润曲线分别为1C ：1=x y m a b ⋅+，2C ：2=y cx ，其中,,,m a b c 都为常数．如图所示：（1）分别求函数1y 、2y 的解析式；高 考 资 源 网（2）若该商场一共投资18万元经销甲、乙两种商品，求该商场所获利润的最小值．（可能要用的数ln 20.7≈）18．解（1）由函数1=x y m a b ⋅+过点525(0,0),(2,),(4,)1616可得 2405162516m b m a b m a b ⎧⎪+=⎪⎪⋅+=⎨⎪⎪⋅+=⎪⎩， 可得2548548a b m ⎧⎪=⎪⎪=-⎨⎪⎪=⎪⎩，15524848x y ∴=⋅- 由函数2=y cx 过点7(3,)4可得712c =，27=12y x ∴ （2）设该商场经销甲商品投入x 万元，乙商品投入12x -万元，该商场所获利润为y 万元则12557573312(12)2484812481248x x y y y x x =+=⋅-+-=⋅-+57577772ln 22248124810129612x x x y '=⋅-=⋅⋅-=⋅-令0y '=可得3x =，（18分）y '在(0,3)单调递增，∴当(0,3),0,x y '∈<y 在(0,3)单调递减，当(3,)0,x y '∈+∞>，y 在(3,)+∞单调递增，当3x =时，利润y 有最小值28748．答：该商场所获利润的最小值28748．18．（本小题满分18分）已知圆221:(1)1C x y ++=和圆222:(4)4C x y -+=． （1）过圆心1C 作倾斜角为θ的直线l 交圆2C 于,A B 两点，且A 为1C B 的中点，求sin θ；（2）过点(,1)P m 引圆2C 的两条割线1l 和2l ，直线1l 和2l 被圆2C 截得的弦的中点分别为,M N .试问过点2,,,P M N C 的圆是否过定点（异于点2C ）？若过定点，求出该定点；若不过定点，说明理由；（3）过圆2C 上任一点00(,)Q x y 作圆1C 的两条切线，设两切线分别与y 轴交于点S 和T ，求线段ST 长度的取值范围．18．解：（1）设直线l 的方程为(1)y k x =+，则圆心2C 到直线l的距离d =设AB 的中点为R，则11123AR AB C R ==== 则2118d =，所以在12Rt C RC ∆中，212sin 520C R d C C θ===． （2）依题意，过点2,,,P M N C 的圆即为以2PC 为直径的圆， 所以(4)()(1)(0)0x x m y y --+--=，即22(4)40x m x m y y -+++-= 整理成关于实数m 的等式22(4)40x m x x y y -+-+-=恒成立则224040x x x y y -=⎧⎨-+-=⎩，所以40x y =⎧⎨=⎩或41x y =⎧⎨=⎩ 即存在定点(4,1).（3）设过00(,)Q x y 的直线与圆1C 切线，则1d ==，即2200()1k kx y k +-=+， 整理成关于k 的方程222000000(2)(22)10x x k y x y k y +-++-=， （☆） 判别式22222000000000(22)4(1)(2)448y x y y x x x y x ∆=+--+=++，所以00k =直线00()y y k x x -=-与y 轴的交点为00(0,)y kx -， 不妨设010(0,)S y k x -，020(0,)T y k x -，则210||ST k k x =-． 而12,k k 是（☆）方程的两根，则2100||ST k k x =-=2200(4)4x y -+=，所以000ST ===．(t t =∈，则251616t ST t t t==++， 考察关于t的函数16()([2,f t t t t=+∈，函数()f t 在区间[]2.4是单调递减，在区间4,⎡⎣上单调递增，所以max (())10f t =，min (())8f t =．所以ST ∈⎦．19．（本小题满分18分）数列{}n a 满足,2,021==a a ,,3,2,1,2sin 4)2cos 1(222 =++=+n n a n a n n ππ （1）求3456,,,a a a a ；（2）设1321k k S a a a -=+++，k k a a a T 242+++= ，分别求,k k S T 关于k 的表达式； （3）设22kk kS W T =+，求使1>k W 的所有k 的值，并说明理由． 19．解：（1）∵2,021==a a ，∴42sin 4)2cos 1(2123=++=ππa a ，422sin 4)22cos 1(2224=++=ππa a ，225333(1cos )4sin 822a a ππ=++=， 226444(1cos )4sin 822a a ππ=++=．（2）当)(12*N k k n ∈-=时，4212sin 4)212cos 1(12212212+=-+-+=--+k k k a k a k a ππ， ∴{}12-k a 是以0为首项，4为公差的等差数列，则)1(412-=-k a k ， 当)(2*N k k n ∈=时，k k k a ka k a 222222222sin 4)22cos 1(=++=+ππ， ∴{}k a 2是以2为首项，2为公比的等比数列，则k k a 22=，∴{}n a 的通项公式为⎪⎩⎪⎨⎧∈=∈-=-=)(2,2)(12),1(2*2*N k k n N k k n n a n n ．)1(2)1(4401231-=-+++=+++=-k k k a a a S k k ，2222212242-=+++=+++=+k k k k a a a T ，（3）112)1(2)1(422-+-=-=+=k k k k k k k k k T S W ， 于是1615,45,23,23,1,0654321======W W W W W W ． 下面证明：当6≥k 时，1<k W ． 事实上，当6≥k 时，-+=-+k k k k k W W 2)1(102)3(2)1(1<-=--kk k k k k ，即k k W W <+1， 又16<W ，∴当6≥k 时，1<k W ． 故满足1>k W 的k 的值为5,4,3．20．（本题满分18分）已知函数||)(3a x ax x f -+=（R a ∈）．（1）是否存在实数a ，使得函数)(x f 在]0,(-∞上单调递减，在),0[+∞上单调递增？请说明理由；（2）若10<<a ，求函数)(x f 在]1,1[-上的最大值；（3）求证：对任意的实数a ，存在0x ，恒有0)(0≠x f ，并求出符合该特征的0x 的取值范围．20．解：（1）当0≠a 时，)()()(33a x a x ax ax ax ax x f ≥<⎩⎨⎧-++-=，令a x ax x g +-=3)(（a x <），a x ax x h -+=3)(（a x >），13)(2-='ax x g ，13)(2+='ax x h ，无论0>a 还是0<a 均不符合要求；（2）若10<<a ，)()()(33a x a x ax ax a x ax x f ≥<⎩⎨⎧-++-=，当a x <时，13)(2-='ax x f ，ax ax x f 31013)(2±=⇒=-='， 当a x >时，13)(2+='ax x f ， ①当310≤<a ，131≥a，此时)(x f 在],1[a -上单调减，在]1,[a 上单调增，则在]1,1[-上1)1()1()(max ==-=f f x f ； ②当33131≤<a ，此时a a ≥31，此时)(x f 在]31,1[a--上单调增， 在],31[a a-上单调减，在]1,[a 上单调增， 由于)1()1()31(f f af =->-， 则在]1,1[-上aa a f x f 3132)31()(max +=-=； ③当1313<<a ，此时a a <31，则此时)(x f 在]31,1[a --上单调增， 在]31,31[a a -上单调减，在],31[a a-上单调增，在]1,[a 上单调P增，则在]1,1[-上aa a f x f 3132)31()(max +=-=； 综合①②③有 当310≤<a 时，1)(max =x f ； 当131<<a 时，aaa a a x f 9323132)(max +=+=． （3） ①当0=a 时，||)(x x f =，方程0||)(==x x f 只有0根；②当0>a 时，方程0||)(3=-+=a x ax x f 没有0根和正根， 当0>a ，0<x 时，a x ax x f +-=3)(， 由方程0)(3=+-=a x ax x f 得13+=x xa ， 则0101033<+⇒⎪⎩⎪⎨⎧>+=<x x x a x ，得1-<x ； ③当0<a 时，方程0||)(3=-+=a x ax x f 没有0根和负根， 当0<a ，0>x 时，a x ax x f -+=3)(， 由方程0)(3=-+=a x ax x f 得13--=x xa ， 则0101033>-⇒⎪⎩⎪⎨⎧<--=>x x x a x ，得1>x ； 综上可知，对任意的实数a ，存在]1,0()0,1[0 -∈x ，恒有0)(0≠x f ．数学附加题21．【选做题】在A 、B 、C 、D 四小题中只能选做2题，每小题18分，共计20说分．请在答题纸指定区域内．．．．．．．．．．作答．明、证明过程或演算步骤．A ．选修4—1：几何证明选讲如图，PA 切⊙O 于点A ，D 为PA 的中点，过点D 割线交⊙O 于B 、C 两点．求证: DPB DCP ∠=∠．A ．证明：因为PA 与圆相切于A ， 所以2DA DB DC =⋅， 因为D 为PA 中点，所以DP =DA ，所以DP 2=DB ·DC ，即PD DB DCPD= ． 因为BDP PDC ∠=∠， 所以BDP ∆∽PDC ∆， 所以DPB DCP ∠=∠． B ．选修4—2：矩阵与变换已知1 0 4 31 2 4 1-⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦B , 求矩阵B .B ．解：设 , a b c d ⎡⎤=⎢⎥⎣⎦B 则1 01 22 2a b a c b d ⎡⎤⎡⎤=⎢⎥⎢⎥++⎣⎦⎣⎦B ， 故4,4,3,3,4 3.24,4, 4 221, 2.a ab b ac c bd d =-=-⎧⎧⎪⎪==-⎡⎤⎪⎪=⎨⎨⎢⎥+==-⎣⎦⎪⎪⎪⎪+=-=-⎩⎩解得故B C ．选修4—4：坐标系与参数方程已知极坐标系的极点在直角坐标系的原点，极轴与x 轴的正半轴重合．曲线C的极坐标方程为2222cos 3sin 3+=ρθρθ，直线l的参数方程为,1x y t⎧=⎪⎨=+⎪⎩(t 为参数，t∈R)．试在曲线C 上求一点M ，使它到直线l 的距离最大． C ．解：曲线C的普通方程是2213x y +=．直线l的普通方程是0x ．设点M的直角坐标是,sin )θθ，则点M 到直线l 的距离是d ==．因为)4+≤πθ，所以当πsin()14θ+=-，即ππ2π(42k k θ+=-∈Z)，即3π2π(4k k θ=-∈Z)时，d 取得最大值．==θθ．综上，点M 的极坐标为7π)6或点M 的直角坐标为(时，该点到直线l的距离最大． D ．选修4—5：不等式选讲 设函数()f x =（1）当5a =-时，求函数()f x 的定义域；（2）若函数()f x 的定义域为R ，试求a 的取值范围． D ．解：（1）由题设知：1250x x ++--≥，如图，在同一坐标系中作出函数12y x x =++-和5y =的图象（如图所示）,知定义域为(][,23,-∞-（2）由题设知，当x R ∈时，恒有120x x a ++-+≥， 即12x x a ++-≥- 由（1）123x x ++-≥，∴3,3a a-≤∴≥-.【必做题】第22题、第23题，每题18分，共计20分．请在答题纸指定区域内．．．．．．．．．．作答．解答应写出文字说明、证明过程或演算步骤． 22．求证：对于任意的正整数n，(2n其中s N *∈. 22．解：由二项式定理可知，121122(22222nn n n n n n n n n C C C C --+=++++,设(2n x==，而若有(2n =,a b N *∈，则(2n ，,a b N *∈，∵(2(21n n⋅=⋅=，∴令,a s s N *=∈，则必有1b s =-． ∴(2n s N *∈．注：本题也可用数学归纳法证明，证明正确的也给相应的分数．23．已知抛物线2:2(0)C y px p =>的焦点为F ，准线为l ，点A 在抛物线C 上，设以F 为圆心，FA 为半径的圆F 交准线l 于,M N 两点． （1）若90MFN ∠=︒，且AMN ∆的面积为24，求p 的值；（2）若,,A F M 三点共线于直线m ，设直线m 与抛物线C 的另一个交点为B ，记A 和B 两点间的距离为()f p ，求()f p 关于p 的表达式．23．解：（1）由对称性可知，MFN ∆为等腰直角三角形，则斜边2MN p =， 且点A 到准线l的距离d FA FM ===．11222AMN S MN d p ∆=⋅=⋅=2p =． （2） 由对称性可设2000(,)(0)2y A y y p >，,02p F ⎛⎫⎪⎝⎭． 由点A ，M 关于点F 对称，得200,2y M p y p ⎛⎫-- ⎪⎝⎭，所以2022y p p p -=-，解得0y，即32p A ⎛⎫⎪⎝⎭．直线m的方程为2p y x ⎫=-⎪⎭，与抛物线方程联列222y pxp y x ⎧=⎪⎨⎫=-⎪⎪⎭⎩得220y py p --=，解得1y，2y p =．所以,6p B p ⎛⎫ ⎪ ⎪⎝⎭．这样8()3f p AB p ===．。