辅助圆专题(课堂PPT)

第二十五讲辅助圆在处理平面几何中的许多问题时，常需要借助于圆的性质，问题才得以解决.而我们需要的圆并不存在(有时题设中没有涉及圆；有时虽然题设涉及圆，但是此圆并不是我们需要用的圆)，这就需要我们利用已知条件，借助图形把需要的实际存在的圆找出来，添补辅助圆的常见方法有：1利用圆的定义添补辅助圆；2.作三角形的外接圆；3•运用四点共圆的判定方法：(1)若一个四边形的一组对角互补，则它的四个顶点共圆.(2)同底同侧张等角的三角形，各顶点共圆.⑶若四边形ABCD的对角线相交于P,且PA・PC=PB • PD,则它的四个顶点共圆.(4)若四边形ABCD的一组对边AB、DC的延长线相交于P,且PA • PB= PC • PD,则它的四个顶点共圆.【例题求解】【例1】如图，直线AB和AC与O O分别相切于B、C, P为圆上一点，P到AB、AC的距离分别为4cm、6cm，那么P到BC的距离为___________________________.思路点拨连DF, EF,寻找PD、PE、PF之间的关系，证明△ PDFPFE,而发现P、D、B、F与P、E、C、F分别共圆，突破角是解题的关键.注：圆具有丰富的性质：(1)圆的对称性；(2)等圆或同圆中不同名称量的转化；(3)与圆相关的角；(4)圆中比例线段.适当发现并添出辅助圆，就为圆的丰富性质的运用创造了条件，由于图形的复杂性，有时在图中并不需画出圆，可谓“图中无圆，心中有圆”【例2】女口图，若PA=PB,Z APB=2 / ACB , AC 与PB 交于点P, 且PB=4, PD=3，贝UAD • DC 等于( )A. 6B. 7C. 12D. 16思路点拨作出以P点为圆心、PA长为半径的圆，为相交弦定理的应用创设了条件.注：到一个定点等距离的几个点在同一个圆上，这是利用圆的定义添辅助圆的最基本方法.【例3】 如图，在厶ABC 中，AB=AC ，任意延长 CA 到P ，再延长AB 到Q ,使AP=BQ ，求证：△ ABC 的外心0与A ，P , Q 四点共圆.思路点拨 先作出△ ABC 的外心0,连P0、0Q ,将问题转化为证明角相等.【例4】 如图，P 是O 0外一点，PA 切O 0于A , PBC 是O 0的割线，AD 丄P0于D .求思路点拨 因所证 比例 线段 不是对 应边，故 不能 通过判 定厶PBD 与△ PCD 相似证 明.PA 2=PD • P0=PB • PC , B 、C 、0、D 共圆，这样连 0B ，就得多对相似三角形，以此达到证明的目的.注：四点共圆既是一类问题， 又是平面几何中一个重要的证明方法， 它和证明三角形全等和 相似三角形有着同等重要的地位， 这是因为，某四点共圆，不但与这四点相联系的条件集中 或转移，而且可直接运•用圆的性质为解题服务.【例5】如图，在△ ABC 中，高 BE 、CF 相交于 H ,且/ BHC=135 ° , G ABC 内的一 点，且 GB=GC ,/ BGC = 3/ A ，连结 HG ,求证：HG 平分/ BHF .思路点拨 经计算可得/ A=45 ° ,△ ABE ,△ BFH 皆为等腰直角三角形，只需证/GHB= / GHF=22.5 ° .由/BGC=3 / A=135证明. 证:PB PC PD _CD注：许多直线形问题借助辅助圆，常能降低问题的难度，使问题获得简解、巧解或新解.学力训练21.如图，正方形ABCD的中心为0,面积为1989cm , P为正方形内一点，且/ OPB=45PA: PB=5 : 14,贝U PB 的长为_______________ .2.如图，在△ABC 中，AB=AC=2 , BC 边上有100个不同的点P i、P2,, P100，记2m i=AP j - BP i P i C(i=1 , 2,, 100),则mt +m2半八-+m1003.设△ ABC三边上的高分别为AD、BE、CF,且其垂心H不与任一顶点重合，则由点B、C、D、E、F、H中某四点可以确定的圆共有（）(第｝JS1)D . 6个A｛第3题）4.如图，已知OA=OB=OC，且/A. ^k 倍B. 是k 倍25 .如图，在等腰梯形ABCD中，AD上，满足条件的/1AOB= k / BOC，则/ ACB 是/1C. 2kD.'kBAC 的(BPC=90°C.AB // CD , AB=998 , CD=1001 ,的点P的个数为（）D .不小于3的整数AD=1999 , 点P在线段6 .如图，AD、A. 37 .如图;&如图,已知求证:BE是锐角三角形的两条高, ABC= 18 , DEC =2 ,D. 34则COSC等于（）1 2B.丄C.-3 3H是厶ABC三条高的交点，连结DF, DE , EF,求证：H是厶DEF的内心.已知△ ABC中，AH是高，AT是角平分线，且TD丄AB , TE丄AC.(1) / AHD= / AHE ;(2)BHBDCHCE｛第7題） 爍&謝｝9 .如图，已知在凸 四边形 ABCDE 中，/ BAE=3 ：• , BC=CD=DE ,且/ BCD= / CDE= 180 _2 ：..求证：/ BAC= / CAD= / DAK ,10.如图，P 是O O 外一点，PA 和PB 是O O 的切线,11.如图，已知点P 是O O 外一点，PS 、PT 是O O 的两条切线，过点P 作O O 的割线PAB , 交O OA 、B 两点，与ST 交于点C .求证：」丄•丄）PC 2 PA PB A AA ,B 为切点，P O 与AB 交于点M , 过M 任作O O 的弦CD .求证: / CPO= / DPO .（第 11【例■求解】 例 1 275 连ZfFP. A ADPF C ^AFPE, ft PF = PD* PE. 011 A BA0ffi,i£iaOApOC .OP’OQ,在△OCF 〒△□&(?申.OC N OA .由 d®，CA = AB^AP-BQ, ^CP-AQ.又叮 OjftAABC 的外心，:・£OCP=ZOAC、丫等H 三角旱的外心必在II 角的平分线上+齐^OAC=ZOAQ,从而£OCP - ZOAQ.得 AOCPK2AOlAQ ，TJaZCPO=ZAQO 故 O,儿f\Q 四点共亂■/ PA 1 = PD PO= PB ・ FG^B,C r O. D 四点共圆， A ^PCD^^POB. 得務■需=題 ①又 △P0CSAM6 帯龙■誌 ② 由①•②得 舌常=祐MS V ZA = 180*-ZBHC=135* ・ZBGC=3ZA = 135\ Z^BH-45* A B,G,C t H 四点并圆，褂■蔓畤竺 =22.产.XZBHF=45*.^ZGHB= yZBHF.tt HG 平5>ZBHR【学力训给】1. 42 隹结OA£乩A”吕・O ・P 四点拄圆，得ZAPB = ZAOB=9Q*2. 400 3, D ,显见疔別应有下列四点共IB1 iAFHE,BFHD t CDHE,AFDC,UFEC,CDFA*. n S. C 将何删特比为直St AB 与以CD 为直径的位■关系 6. B7(井剧由BDHF.CDHE 四越其凰，得= £FDH ・^FCH 工£FDH +DH 为"DE 平分线8. (l)D t E.H 在WAT 为直栓的0U± J»ZAHD=ZATD t ZAHE=ZATE.Jl ；ZATD=Z^TE ，故ZAHD=Z J AHEi {2JR/AAHB 与思A TDB 有公共ffiZB, »AAHBc^ATDB +冷器■等*同理心AHCs&TEC 、得器-笛・由于 丁"亦所冷 ^久連苗 BD.CE.ll] BC- CD= DE^BCD-^CDE= 1B0' - 2a ^CIiD=ZCDB=ZDCE^ZDEC=V . f#^BCD^^CDE, :' ZfiCE=C180D -2a )-& = lB0,-3<l .而££AE H 丸匸 A+E.GE 归圆一同理可证儿乩D 、E 其圆，拽 A,B t C,D»E 共IMJO. OA.fj OA 丄PA"A 阿丄OP, QM • MP = AM 1, MC • MD^ MA * MB = T /・ MD * MC = MO -MP,：,点 <XD 、P 工四点其时収 OC=O 乩 "： ZCPO=ZDPO.DA -L- pn】】・过o 点作OE 丄AB 干E,则—.由切制线定理得、F 卄PA ・PB.^阳・3\设OP 交ST 于D.则OP 丄ST, 由相假形町证,PS 2 * PD * PO ，X PS 1 - PA * PH t Iff ZCDO=- ZCEO= 90'. A C 、EQ 、D 四点 tE 以 OC 为直艮的圆上*"f ・PE=PD* PO ，W PA ・PB = PC* FE-PA 芋月*兀 化简潯点一寺（吉 参考答案 M lbW3。

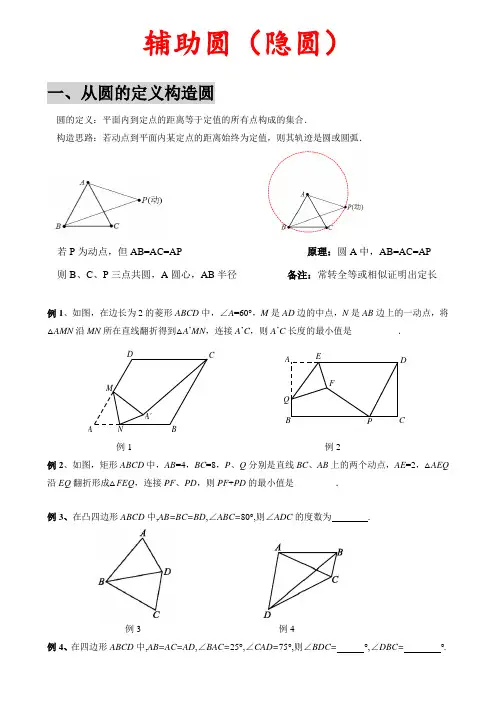
辅助圆（隐圆）一、从圆的定义构造圆圆的定义：平面内到定点的距离等于定值的所有点构成的集合．构造思路：若动点到平面内某定点的距离始终为定值，则其轨迹是圆或圆弧．若P 为动点，但AB=AC=AP 原理：圆A 中，AB=AC=AP 则B 、C 、P 三点共圆，A 圆心，AB 半径 备注：常转全等或相似证明出定长例1、如图，在边长为2的菱形ABCD 中，∠A =60°，M 是AD 边的中点，N 是AB 边上的一动点，将△AMN 沿MN 所在直线翻折得到△A ’MN ，连接A ’C ，则A ’C 长度的最小值是__________．例1 例2例2、如图，矩形ABCD 中，AB =4，BC =8，P 、Q 分别是直线BC 、AB 上的两个动点，AE =2，△AEQ 沿EQ 翻折形成△FEQ ，连接PF 、PD ，则PF +PD 的最小值是_________．例3、在凸四边形ABCD 中,AB=BC=BD ,∠ABC=80°,则∠ADC 的度数为 .例3 例4例4、在四边形ABCD 中,AB=AC=AD ,∠BAC=25°,∠CAD=75°,则∠BDC= °,∠DBC= °.A'NMABCDQABCDEFP二、定边对直角知识回顾：直径所对的圆周角是直角．构造思路：一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧．固定线段AB 所对动角∠C 恒为90° 原理：圆O 中，圆周角为90°所对弦是直径 则A 、B 、C 三点共圆，AB 为直径 备注：常通过互余转换等证明出动角恒为直角图形释义：若AB 是一条定线段，且∠APB =90°，则P 点轨迹是以AB 为直径的圆．例1、如图1，E 、F 是正方形ABCD 的边AD 上的两个动点，满足AE =DF ，连接CF 交BD 于点G ，连接BE 交AG 于点H ，若正方形边长为2，则线段DH 长度的最小值是________．例1 例2 例3例2、如图2，正方形ABCD 的边长为4，动点E 、F 分别从点A 、C 同时出发，以相同的速度分别沿AB 、CD 向终点B 、D 移动，当点E 到达点B 时，运动停止，过点B 作直线EF 的垂线BG ，垂足为点G ，连接AG ，则AG 长的最小值为 ．例3、如图3，正方形ABCD 的边长是4，点E 是AD 边上一动点，连接BE ，过点A 作AF ⊥BE 于点F ，点P 是AD 边上另一动点，则PC +PF 的最小值为________．ABHGAB CD E FGFEDCB A A BCD EFP练习：1、如图1，Rt △ABC 中，AB ⊥BC ，AB =8，BC =4，P 是△ABC 内部的一个动点，且满足∠PAB =∠PBC ，则线段CP 长的最小值是_________．图1 图2 图32、如图2，在Rt △ABC 中，∠ACB =90°，BC =4，AC =10，点D 是AC 上的一个动点，以CD 为直径作圆O ，连接BD 交圆O 于点E ，则AE 的最小值为_________．3、如图3，已知圆C 的半径为3，圆外一定点O 满足OC =5，点P 为圆C 上一动点，经过点O 的直线l 上有两点A 、B ，且OA =OB ，∠APB =90°，l 不经过点C ，则AB 的最小值为________．三、定边对定角在“定边对直角”问题中，依据“直径所对的圆周角是直角”，关键性在于寻找定边、直角，而根据圆周角定理：同圆或等圆中，同弧或等弧所对的圆周角都相．定边必不可少，而直角则可一般为定角．例如，AB 为定值，∠P 为定角，则A 点轨迹是一个圆．当然，∠P 度数也是特殊角，比如30°、45°、60°、120°，下分别作对应的轨迹圆．PABCBl若∠P =30°，以AB 为边，同侧构造等边三角形AOB ，O 即为圆心．若∠P =45°，以AB 为斜边，同侧构造等腰直角三角形AOB ，O 即为圆心．若∠P =60°，以AB 为底，同侧构造顶角为120°的等腰三角形AOB ，O 即为圆心若∠P =120°，以AB 为底，异侧为边构造顶角为120°的等腰三角形AOB ，O 即为圆心．例1、如图1，△ABC 为等边三角形，AB =3，若P 为△ABC 内一动点，且满足∠PAB =∠ACP ，则线段PB 长度的最小值为_________．图1 图2 图3例2、如图2，等边△ABC 边长为2，E 、F 分别是BC 、CA 上两个动点，且BE =CF ，连接AE 、BF ，交点为P 点，则CP 的最小值为________．例3、如图3，AB 是圆O 的直径，M 、N 是弧AB （异于A 、B ）上两点，C 是弧MN 上一动点，∠ACB的角平分线交圆O 于点D ，∠BAC 的平分线交CD 于点E ，当点C 从点M 运动到点N 时，则C 、E 两点的运动路径长的比是_______．ABCPEFCBAPAB四、四点共圆1、四点共圆模型①若动角∠A+动角∠C=180° 原理：圆内接四边形对角互补 则A 、B 、C 、D 四点共圆 备注：点A 与点C 在线段AB 异侧2、四点共圆模型②固定线段AB 所对同侧动角∠P=∠C 原理：弦AB 所对同侧圆周角恒相等 则A 、B 、C 、P 四点共圆 备注：点P 与点C 需在线段AB 同侧例１、如图，AD 、BE 、CF 为△ABC 的三条高，H 为垂线，问： （1）图中有多少组四点共圆？ （2）求证：∠ADF ＝∠ADE ．变式：如图， BE.CF 为△ABC 的高，且交于点H,连接AH 并延长交于BC 于点D,求证：AD ⊥BC.例3、如图，E是正方形ABCD的边AB上的一点，过点E作DE的垂线交∠ABC的外角平分线于点F，求证：FE=DE.。