角度大小比较

锐角直角与钝角的判定锐角、直角与钝角的判定角度是几何学中的重要概念，而锐角、直角和钝角是角度种类中的三种基本分类。

在几何学中，正确判定角度的类型对于解决各种问题和计算具有重要意义。

本文将详细讨论锐角、直角和钝角的判定方法，并举例说明。

一、锐角的判定锐角是指角度小于90度的角。

我们可以通过以下两种方法来判定一个角是否为锐角。

方法一：角度大小判定法给定一个角ABC，首先需要测量角的大小。

使用量角器或直尺等工具，将角ABC的两边放置在工具上，然后读取角度数值。

如果所测得的角度小于90度，则可以确定该角为锐角。

例如，当我们测量一个角，读数为75度，那么可以断定该角是锐角。

方法二：角度比较法如果给出一个三角形ABC，并已知三个内角A、B和C的度数，可以通过比较角度大小来判定是否存在锐角。

例如，如果三角形ABC的内角A=40度，内角B=80度，内角C=60度，我们可以发现内角B的度数大于90度，因此可以得出结论：角B不是锐角。

二、直角的判定直角是指角度恰好为90度的角。

下面是两种判定直角的方法。

方法一：度数判定法给定一个角，通过测量角度大小并判断是否恰好为90度，可以确定该角是否为直角。

例如，当我们测量一个角，读数为90度，那么可以推断该角是直角。

方法二：垂直判定法当我们面临一条直线和另一条与之垂直的直线时，可以判断两条直线之间形成了直角。

例如，当一条直线与另一条垂直相交时，我们可以确定所形成的角度为直角。

三、钝角的判定钝角是指角度大于90度但小于180度的角。

我们可以通过以下两种方法来判定一个角是否为钝角。

方法一：度数判定法给定一个角，通过测量角度大小并判断是否大于90度但小于180度，可以确定该角是否为钝角。

例如，当我们测量一个角，读数为120度，那么可以断定该角是钝角。

方法二：角度比较法如果给出一个三角形ABC，并已知三个内角A、B和C的度数，可以通过比较角度大小来判定是否存在钝角。

例如，如果三角形ABC的内角A=100度，内角B=120度，内角C=40度，我们可以发现内角B的度数大于90度且小于180度，因此可以得出结论：角B是钝角。

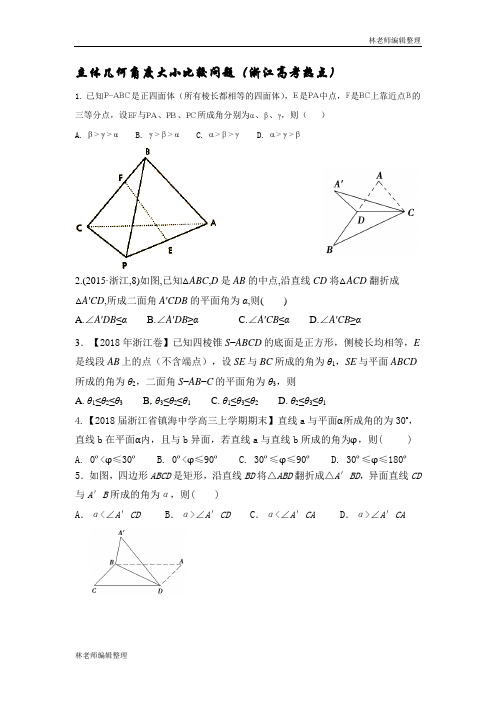
立体几何角度大小比较问题（浙江高考热点）1.已知是正四面体（所有棱长都相等的四面体），是中点，是上靠近点的三等分点，设与、、所成角分别为、、，则（）A. B. C. D.2.(2015·浙江,8)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD翻折成△A′CD,所成二面角A′CDB的平面角为α,则()A.∠A′DB≤αB.∠A′DB≥αC.∠A′CB≤αD.∠A′CB≥α3．【2018年浙江卷】已知四棱锥S−ABCD的底面是正方形，侧棱长均相等，E 是线段AB上的点（不含端点），设SE与BC所成的角为θ1，SE与平面ABCD 所成的角为θ2，二面角S−AB−C的平面角为θ3，则A. θ1≤θ2≤θ3B. θ3≤θ2≤θ1C. θ1≤θ3≤θ2D. θ2≤θ3≤θ14.【2018届浙江省镇海中学高三上学期期末】直线a与平面α所成角的为30o，直线b在平面α内，且与b异面，若直线a与直线b所成的角为φ，则( ) A. 0º<φ≤30º B. 0º<φ≤90º C. 30º≤φ≤90º D. 30º≤φ≤180º5．如图，四边形ABCD是矩形，沿直线BD将△ABD翻折成△A′BD，异面直线CD 与A′B所成的角为α，则( )A．α<∠A′CD B．α>∠A′CD C．α<∠A′CA D．α>∠A′CA6. 已知得内角所对的边分别为，且，点在所在平面上的投影恰好是的重心，设平面与底面所成的锐二面角分别为，则A.B.C.D.7. 已知三棱锥 S －ABC 的底面 ABC 为正三角形， SA ＜SB ＜SC ，平面 SBC ， SCA ， SAB 与平面 ABC 所成的锐二面角分别为 α1， α2， α3，则（ ）A. α1＜α2B. α1＞α2C. α2＜α3D. α2＞α38. 在三棱锥中，平面，，分别是的中点，，且.设与所成角为，与平面所成角为，二面角为，则（ ）A.B. C.D.9. 如图，正四面体A BCD -， P 是棱CD 上的动点，设CP tCD =（()01t ∈，），分别记AP 与BC ， BD 所成角为α， β，则（ ）A. αβ≥B. αβ≤C. 当102t ⎛⎤∈ ⎥⎝⎦，时， αβ≥D. 当102t ⎛⎤∈ ⎥⎝⎦，时，αβ≤10，已知两个平面βα,和三条直线b a m ,,，若m =βα ，α⊂a 且m a ⊥，β⊂b ，设α和β所成的一个二面角的大小为1θ，直线a 和平面β所成的角的大小为2θ，直线b a ,所成的角的大小为3θ，则A ．321θθθ≥=B ．213θθθ=≥C ．31θθ≥，32θθ≥D ．21θθ≥，23θθ≥11.已知在矩形ABCD 中，AD =，沿直线BD 将ABD ∆ 折成'A BD ∆，使得点'A 在平面BCD 上的射影在BCD ∆内（不含边界），设二面角'A BD C --的大小为θ，直线','A D A C 与平面BCD 所成的角分别为,αβ，则（ ）第13题图D 'COBAA ．αθβ<<B ．βθα<< C. βαθ<< D ．αβθ<< 12. 如图,二面角α-l -β中,P ∈l ,射线PA ,PB 分别在平面α, β内,点A 在平面β内的射影恰好是点B ,设二面角α-l -β、PA 与平面β所成的角、PB 与平面α所成的角的大小分别为,,δϕθ,则（ ）A ．δϕθ≥≥ B. δθϕ≥≥ C. ϕδθ≥≥ D. θδϕ≥≥13．如图， 矩形ABCD 中，1,2AB BC ==，将ADC ∆沿对角线AC 翻折至AD C '∆，使顶点D '在平面ABC 的投影O 恰好落在边BC 上，连结BD '．设二面角D AB C '--，D AC B '--，B AD C '--大小分别为,,αβγ，则（ ）A ．αβγ+>B ．αβγ+=C ．γαβ+>D ．γβα+>14,（2017·浙江卷） 如图，已知正四面体D - ABC (所有棱长均相等的三棱锥)，P ，Q ，R 分别为AB ，BC ，CA 上的点，AP ＝PB ，BQ QC ＝CRRA ＝2，分别记二面角D - PR- Q ，D - PQ - R ，D - QR - P 的平面角为α，β，γ，则( )A．γ＜α＜β B ．α＜γ＜β C ．α＜β＜γ D ．β＜γ＜α15. 如图，在中，，，为的中点.将沿着翻折至，使得，则的取值不可能．．．为（ ） A. B. C. D.。

角的比较与运算教案教学目标•了解角的比较与运算的基本概念•掌握角的大小比较和角度的四则运算•能够灵活运用所学知识解决与角度大小、运算相关的问题教学重点•角的比较与大小•角的四则运算教学难点•能够灵活运用所学知识解决实际问题教学过程1. 角的基本概念回顾•恢复学生对角的概念的理解，包括角的定义、顶点、边、度数等。

2. 角的比较与大小•从涉及角大小的实例出发，让学生探究角的大小的比较方法。

自己找寻或者提供材料，让学生辨认出哪一个角是锐角，哪一个是直角等，并判断它们之间的大小关系。

3. 角的四则运算1.加法：将相邻的角分别以其顶点为原点，共线边为X轴，分别标记刻度，然后相加。

–举例说明：•60度 + 30度 = 90度2.减法：将被减角和减角以其顶点为原点，共线边为X轴，分别标记刻度，然后相减。

其实，可翻折角进行建模，然后应用加法原则进行运算。

–举例说明：•180度 - 60度 = 120度3.乘法：不同角度之间的乘法，能够应用余弦公式进行计算。

–举例说明：•cos(60度) * cos(30度) = (1/2) * √(3)/24.除法：只能应用余弦公式进行计算，即除以某一角的余弦值来使角度相除。

–举例说明：•cos(60度) / cos(30度) = 1/√(3)4. 实际应用•联系实际应用场景，例如使用角的比较与运算解决一个三角形问题；或者试着去解决以下问题：–一段铁棒，一端是x度，另一端是y度，在中间钳制一把夹子，勾出了z度，问夹子的大小是多少度？教学总结•总结角的比较与运算的基本概念与方法•强调实际应用，让学生掌握角的比较与运算的解决实践问题的方法参考资料•《初中数学》•《初中数学知识同步课程》。

小学二年级数学角度大小练习题1. 角度的概念和表示方法在数学中，角度是描述两条射线之间的夹角的概念。

我们可以使用度数来表示角度大小。

一个完整的圆可以被分为360度，而一个直角的角度大小为90度。

通常，我们使用角标来表示角度，比如∠ABC。

2. 角度的比较现在，我们来练习一些角度的比较题目。

请根据题目中给出的图形和信息，判断下列各对角度的大小关系，并用符号“>”、“<”或“=”填空。

a) ∠ABC ______ ∠DEFb) ∠JKL ______ ∠MNOc) ∠PQR ______ ∠STU3. 角度大小的计算接下来，我们来计算一些角度的具体数值。

根据题目中给出的信息，求解下列各角的具体度数。

a) 在一个直角三角形ABC中，∠B的角度大小为30度，求解∠A和∠C的度数。

b) 在一个等腰三角形DEF中，∠E的角度大小为50度，求解∠D和∠F的度数。

c) 在一个平行四边形GHIJ中，∠G的角度大小为100度，求解∠H、∠I和∠J的度数。

4. 角度的分类角度可以根据其大小来进行分类。

根据度数的范围，我们可以将角度分为锐角、直角、钝角和平角。

a) 根据下列各个度数的范围，判断它们属于哪一类角，并将答案填入括号中。

i) 60度（）ii) 90度（）iii) 120度（）iv) 180度（）b) 根据下列各个角的大小关系，填入括号中的符号“<”、“>”或“=”。

i) 直角 ______ 钝角ii) 平角 ______ 锐角iii) 直角 ______ 平角5. 角度的应用角度的概念在现实生活中有广泛的应用。

请结合下列题目中给出的实例，来解答相关问题。

a) 格林老师在教室墙上贴了一幅旗帜，旗帜底部边缘与地面的夹角大小为40度，帮助格林老师计算旗帜所占据的角度范围。

b) 小明使用一个角度仪测量他家花园中两片叶子的夹角，角度仪显示的数值为135度。

请问这两片叶子之间的夹角属于什么类别？6. 总结通过本次练习，我们加深了对小学二年级数学中角度大小的理解。

化学键键角大小比较化学键是化合物中原子间的相互作用力，通过这种力，原子之间形成了化学键。

化学键的键角是指化学键的两端原子所形成的角度大小。

化学键的键角大小对于化合物的结构和性质具有重要的影响，下面我们就来比较一下不同类型化学键的键角大小。

1. 共价键共价键是由两个或多个原子共用一对电子而形成的化学键。

共价键的键角受到原子间的排斥力和吸引力的影响，因此键角大小取决于原子间的电子云密度和原子大小。

在共价键中，单键的键角一般在100-110°之间，双键的键角约为120°，而三键的键角则约为180°。

例如，H2O分子中氢原子与氧原子形成的单键键角为104.5°，C2H4分子中碳原子与碳原子之间的双键键角为120°。

2. 离子键离子键是由正负离子之间的静电作用力形成的化学键。

离子键的键角大小受到离子半径大小和离子的电荷数目的影响。

一般来说，离子键的键角较小，通常在90°左右。

例如，NaCl晶体中，Na+和Cl-离子之间的键角为90°。

3. 金属键金属键是由金属原子之间共享电子形成的化学键。

金属键的键角大小主要受到金属原子的大小、电子云密度和晶格结构的影响。

一般来说，金属键的键角较大，通常在120°以上。

例如，铜原子之间形成的金属键的键角为135°左右。

4. 氢键氢键是由氢原子与电负性较强的原子（如氮、氧、氟）之间形成的静电作用力形成的化学键。

氢键的键角大小主要受到氢键中氢原子、电负性较强的原子和周围原子的排列方式的影响。

一般来说，氢键的键角较小，通常在180°以下。

例如，DNA双螺旋结构中，氢键的键角约为180°。

不同类型的化学键的键角大小存在差异，这种差异对于化合物的结构和性质具有重要的影响。

了解不同类型化学键的键角大小，对于理解化学反应和化学物质的性质具有重要意义。