电路基础课后习题答案集

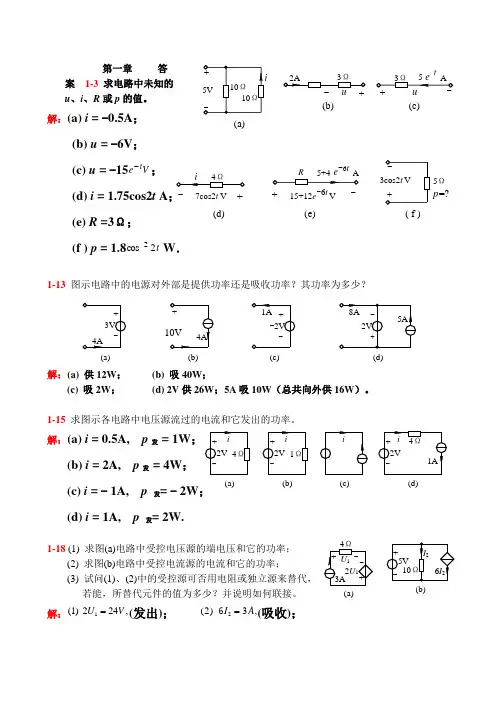
第一章 答案 1-3 求电路中未知的u 、i 、R 或p 的值。

解：(a) i = -0.5A ；(b) u = -6V ； (c) u = -15e V t -； (d) i = 1.75cos2t A ； (e) R =3Ω； (f ) p = 1.8cos 22t W ．1-13 图示电路中的电源对外部是提供功率还是吸收功率？其功率为多少？解：(a) 供12W ； (b) 吸40W ；(c) 吸2W ；(d) 2V 供26W ；5A 吸10W （总共向外供16W ）。

1-15 求图示各电路中电压源流过的电流和它发出的功率。

解：(a) i = 0.5A,p 发 = 1W(b) i = 2A, p 发 = 4W ；(c) i = - 1A, p 发= - 2W ； (d) i = 1A, p发= 2W.1-18 (1) 求图(a)电路中受控电压源的端电压和它的功率；(2) 求图(b)电路中受控电流源的电流和它的功率；(3) 试问(1)、(2)中的受控源可否用电阻或独立源来替代，若能，所替代元件的值为多少？并说明如何联接。

解：(),1241 2U V =(发出)；(),232 6I A =(吸收)；(a)5Ω7cos2t V +- R-6t 15+12e V+ -(d) (e) ( f )-6t p =?-t (b) (c)(a) (b)(c)(d)(b)(c)(d)(a)(b)(a)(3) 图(a)中的VCVS 可用下正上负的24V 电压源替代； 图(b)中的CCCS 可用3A ↓的电流源或(5/3)Ω的电阻替代。

1-19 试用虚断路和虚短路的概念求图示两电路中的 i 1 、i 2 及u 0 的表达式。

解：(a) i 1 = 0，u 0 = U S ，i 2 = U S /L (b) i 1 = i 2 = U S /R 1 ，u 0 = - R f U S /R 1 .1-22 求图示各电路中的u ab ，设端口a 、b 均为开路。

电流源发出的功率
P iS u 3A 32V 3A 96W
答案 1.12 解：
4V 1A , u 1 2A 2V 4 受控电压源发出的功率 i
P CCVS 3i 2A 31A 2A 6W
受控电流源发出的功率
PVCCS 4V 0.25u 4V 0.25u 4V 0.25S 2V=-2W
i3 5A 7A 2A
节点③: i4 7A 3A 10A 节点②: i5 i3 i4 8A 对回路列 KVL 方程得： 回路 l1 ： u1 i3 10 i5 8 44V 回路 l2 ：
u2 i4 15 i5 8 214V
答案 1.1 解：图示电路电流的参考方向是从 a 指向 b。当时间 t<2s 时电流从 a 流向 b, 与参考方向相同，电流为正值；当 t>2s 时电流从 b 流向 a，与参考方向相反，电 流为负值。所以电流 i 的数学表达式为
2A t 2s i -3A t 2s
答案 1.2 解：当 t 0 时
8V 2A 4 对节点列 KCL 方程 节点①： i3
i2 3A 0.5A 2.5A
节点②：
i1 i2 i3 2.5A 2A 4.5A
对回路 l 列 KVL 方程：
10 i2 5 3A u 8V
得
u 32V 电压源发出的功率
P US 8V i1 8V 4.5A 36W
答案 1.6 解：各元件电压电流的参考方向如图所示。 元件 1 消耗功率为: p1 u1i1 10V 2A 20W 对回路 l 列 KVL 方程得 u2 u1 u4 10V-5V 5V 元件 2 消耗功率为: p2 u2i1 5V 2A 10W 元件 3 消耗功率为: p3 u3i3 u4i3 5V (3)A 15W 对节点①列 KCL 方程 i4 i1 i3 1A 元件 4 消耗功率为: p4 u4i4 5W 答案 1.7 解：对节点列 KCL 方程 节点①:

习题22.1在图2.18所示的电路中，求各理想电流源的端电压、功率及各电阻上消耗的功率。

解答：由节点方程得I3=I2-I1=1A，U1=I3R1=1A×20Ω=20V，U2=U1+I2R2=20V+2A×10Ω=40V，P1= U1I1=20V×1A=20W，P2=-U2I2=-80W，电阻上的功率P R1=20V×1A=20W，P R2=20V×2A=40W。

2.2求图2.19所示电路中各支路电流，并计算理想电流源的电压Ｕ１。

已知Ｉ１＝３Ａ，Ｒ２＝１２Ω，Ｒ３＝８Ω，Ｒ４＝１２Ω，Ｒ５＝６Ω。

电压和电流的参考方向如图中所示。

解答：节点方程I1+I2+I3=0，I3=I4+I5，网孔方程I2R2=I3R3+I4R4，I4R4=I5R5，联立上述方程得I2=I3=-1.5A，I4=-0.5A，I5=-1A，U1=I2R2=-1.5A×12Ω=-18V。

2.3试用支路电流法求图2.20所示电路中各支路电流，并求三个电源的输出功率和负载电阻ＲＬ上的取用功率。

解答：节点方程I1+I2+10=I，网孔方程0.8I1+116=0.4I2+120，0.8I1+4I=120，联立三方程得I1=75/8A，I2=35/4A，I=225/8A，三个电源的输出功率分别为1125W，1015W，1125W；负载电阻上的取用功率为3164.0625W。

2.4用网孔电流法求解习题2.3。

解答：将电流源与负载电阻的位置互换形成三个网孔，网孔参考电流方向均为顺时针方向，网孔电流方程如下1.2I A-0.4I B=120-116，4.4I B-0.4I A-4I C=116，I C=-10A，解得I A=75/8A，I B=145/8A，于是I1=I A=75/8A，I2=I B-I A=35/4A，I=I B-I C=225/8A。

2.5图2.21所示电路，网孔电流如图中所标，试列写可用来求解该电路的网孔方程。

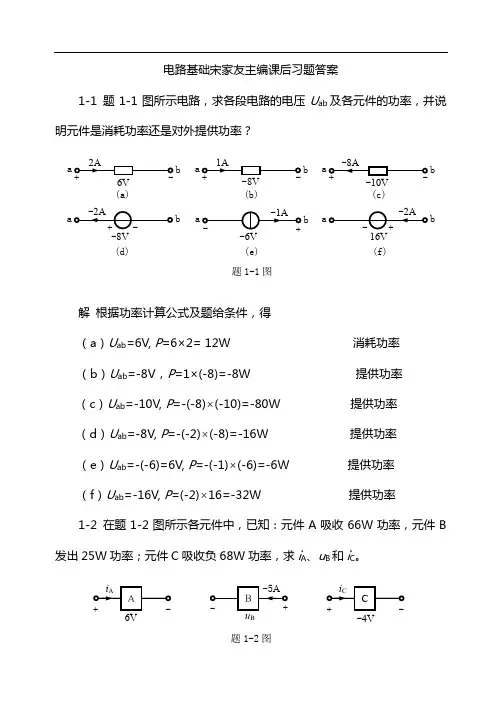
电路基础宋家友主编课后习题答案1-1 题1-1图所示电路，求各段电路的电压U ab 及各元件的功率，并说明元件是消耗功率还是对外提供功率？解 根据功率计算公式及题给条件，得（a ）U ab =6V, P =6×2= 12W 消耗功率 （b ）U ab =-8V ，P =1×(-8)=-8W 提供功率 （c ）U ab =-10V, P =-(-8)⨯(-10)=-80W 提供功率 （d ）U ab =-8V, P =-(-2)⨯(-8)=-16W 提供功率 （e ）U ab =-(-6)=6V, P =-(-1)⨯(-6)=-6W 提供功率 （f ）U ab =-16V, P =(-2)⨯16=-32W 提供功率1-2 在题1-2图所示各元件中，已知：元件A 吸收66W 功率，元件B 发出25W 功率；元件C 吸收负68W 功率，求i A 、u B 和i C 。

(a)(b)(d) (e) (f)a 6V- +b 2A a-8V - +b 1A a -10V- + b-8A(c)a -8V - +b -2A a 16V -+ b-2Aa -6V - +b -1A 题1-1图题1-2图6V +-i A ＡuB +-Ｂ-5A -4V +-i CC解 根据题意，对元件A ，有P A =6i A =66, i A =666=11A 对元件B ，有P B =-5u B =-25, u B =525--=5V 对元件C ，有P C =-4i C =-68, i C =468--=17A 1-3 题1-3图所示电路中，5个元件代表电源或负载。

通过实验测量得知：I 1=-2A ，I 2=3A ，I 3=5A ，U 1=70V ，U 2=-45V ，U 3=30V ，U 4=-40V ，U 5=-15V 。

（１）试指出各电流的实际方向和各电压的实际极性？ （２）判断那些元件是电源；那些元件是负载？ （３）计算各元件的功率，验证功率平衡？解（1）图中虚线箭头为各支路电流的实际方向、 极性为各元件电压的实际极性。

第1章章后习题解析1.1 一只“100Ω、100 W”的电阻与120 V电源相串联，至少要串入多大的电阻 R才能使该电阻正常工作？电阻R上消耗的功率又为多少？解：电阻允许通过的最大电流为1100100'===RPI A所以应有1120100=+R，由此可解得：Ω=-=201001120R电阻R上消耗的功率为P=12×20=20W1.2 图1.27（a）、（b）电路中，若让I=0.6A，R=？图1.27（c）、（d）电路中，若让U=0.6V，R=？解：(a)图电路中，3Ω电阻中通过的电流为Iˊ=2－0.6=1.4AR与3Ω电阻相并联，端电压相同且为U=1.4×3=4.2V所以R=4.2÷0.6=7Ω(b)图电路中，3Ω电阻中通过的电流为Iˊ=3÷3=1AR与3Ω电阻相并联，端电压相同，因此R=3÷0.6=5Ω(c)图电路中，R与3Ω电阻相串联，通过的电流相同，因此R=0.6÷2=0.3Ω(d)图电路中，3Ω电阻两端的电压为Uˊ=3－0.6=2.4VR与3Ω电阻相串联，通过的电流相同且为I=2.4÷3=0.8A所以R=0.6÷0.8=0.75Ω1.3 两个额定值分别是“110V，40W”“110V，100W”的灯泡，能否串联后接到220V的电源上使用？如果两只灯泡的额定功率相同时又如何？解：两个额定电压值相同、额定功率不等的灯泡，其灯丝电阻是不同的，“110V，40W”灯泡的灯丝电阻为：Ω===5.302401102240PUR;“110V，100W”灯泡的灯丝电阻为：Ω===12110011022100PUR，若串联后接在220V的电源上时，其通过两灯泡的电流相同，且为：52.01215.302220≈+=I A，因此40W灯泡两端实际所加电压为：3.1575.30252.040=⨯=U V，显然这个电压超过了灯泡的额定值，而100 W灯泡两端实际所加电压为：U100=0.52×121=62.92V，其实际电压低于额定值而不能正常工作，因此，这两个功率不相等的灯泡是不能串联后接到220V电源ΩΩ图1.27 习题1.2电路图上使用的。

电路第四版课后习题答案第一章：电路基础1. 确定电路中各元件的电压和电流。

- 根据基尔霍夫电压定律和电流定律，我们可以列出方程组来求解未知的电压和电流值。

2. 计算电路的等效电阻。

- 使用串联和并联电阻的计算公式，可以求出电路的等效电阻。

3. 应用欧姆定律解决实际问题。

- 根据欧姆定律 \( V = IR \)，可以计算出电路中的电压或电流。

第二章：直流电路分析1. 使用节点电压法分析电路。

- 选择一个参考节点，然后对其他节点应用基尔霍夫电流定律，列出方程组并求解。

2. 使用网孔电流法分析电路。

- 选择电路中的网孔，对每个网孔应用基尔霍夫电压定律，列出方程组并求解。

3. 应用叠加定理解决复杂电路问题。

- 将复杂电路分解为简单的子电路，然后应用叠加定理计算总的电压或电流。

第三章：交流电路分析1. 计算交流电路的瞬时值、有效值和平均值。

- 根据交流信号的表达式，可以计算出不同参数。

2. 使用相量法分析交流电路。

- 将交流信号转换为复数形式，然后使用复数运算来简化电路分析。

3. 计算RLC串联电路的频率响应。

- 根据电路的阻抗，可以分析电路在不同频率下的响应。

第四章：半导体器件1. 分析二极管电路。

- 根据二极管的伏安特性，可以分析电路中的电流和电压。

2. 使用晶体管放大电路。

- 分析晶体管的共发射极、共基极和共集电极放大电路，并计算放大倍数。

3. 应用场效应管进行电路设计。

- 根据场效应管的特性，设计满足特定要求的电路。

第五章：数字逻辑电路1. 理解逻辑门的工作原理。

- 描述不同逻辑门（如与门、或门、非门等）的逻辑功能和电路实现。

2. 使用布尔代数简化逻辑表达式。

- 应用布尔代数的规则来简化复杂的逻辑表达式。

3. 设计组合逻辑电路。

- 根据给定的逻辑功能，设计出相应的组合逻辑电路。

第六章：模拟集成电路1. 分析运算放大器电路。

- 根据运算放大器的特性，分析电路的增益、输入和输出关系。

2. 设计滤波器电路。

第一章 思考题与习题
第一章 思考题与习题
1.1. 半导体材料都有哪些特性？为什么电子有源器件都是由半导体材料制成 的？
1.2. 为什么二极管具有单向导电特性？如何用万用表判断二极管的好坏？
1.3. 为什么不能将两个二极管背靠背地连接起来构成一个三极管？
1.4. 二极管的交、直流等效电阻有何区别？它们与通常电阻有什么不同？
(b) uo
t
(a)
(c)
图 P2-3
2.13 设如图 P2-4(a)所示的放大电路，Rb=200k，RC=2k，UD=0.7V，β＝100， VCC=12V，VBB=2.7V，各电容值足够大，输入、输出特性曲线分别如图 P2-4(c)、 (d)所示，试 1. 计算印静态工作点，画出负载线 2. 画出中频交流等效电路 3. 设输入电压 ui 如图 P2-4(b)所示，试用图解法画出输出 uo 的波形 4. 输出主要产生何种失真，如何改善
(b) 1. D1、D2 均反向导通，Uo = UZ2＋UZ1 ＝ 9.6 V 2. 反向不导通，Uo = 6V
3. Uo = 3V
(c) 1. D1、D2 均正向导通，Uo = UD＋UD ＝ 1.4 V
2. Uo = UD＋UD ＝ 1.4 V
3. Uo = UD＋UD ＝ 1.4 V
(d) 1. D2 反向导通，D1 不导通， Uo = 3.3 V
D1
u1
u1
5V
0
u2
＋
t
D2 R uo
u2
5V
0
t
图 P1-4(a)
图 P1-4(b)
解： u0
4.7V
0
t
1.13.如图 P1-5 所示电路，设二极管为理 想二极管(导通电压 UD=0，击穿电压 UBR=∞ )，试画出输出 uo 的波形。

电路与信号分析基础课后练习题含答案
题目
1.在具有线性元器件的电路中，输入电压和电流的比值被称为什么？
2.对于一个简单电路，V S表示输入电压，R表示电阻，I表示通过
电路的电流。

写出满足欧姆定律的等式，并画出电路图。

3.在电路中添加电阻会发生什么情况？
4.我们如何分析一个具有多个电阻的电路？
5.什么是瞬态行为？
6.当一个直流电源连到电路上，电路表现出什么行为？
7.在交流电路中，什么是频率响应？
8.在降噪方面，什么是低通滤波器？
答案
1.阻抗 (Impedance): 在具有线性元器件的电路中，输入电压和电流的
比值被称为阻抗。

2.V S=IR, 其中V S表示输入电压，I表示通过电路的电流，R表
示电阻。

电路图如下：
电路图
电路图
3.电路中添加电阻会降低电信号的强度，导致信号在电路中流动时减弱。

4.分析具有多个电阻的电路的方法是应用基尔霍夫的电流和电压定律，来解决电路中的未知量。

5.瞬态行为指电路中的短暂行为，指在电路中出现瞬时响应的行为模式。

6.当一个直流电源连接到电路中，电路中的元件会保持电流和电压的恒定状态，这种状态会持续到电源断电为止。

7.在交流电路中，频率响应是指当输入信号的频率发生变化时，电路的输出信号会如何变化的特性。

8.低通滤波器是一种设计用于消除电路中高频噪声的电路，它会过滤掉输入信号中高于某个频率的信号。

因此，低通滤波器被广泛用于音频和其他信号处理应用。

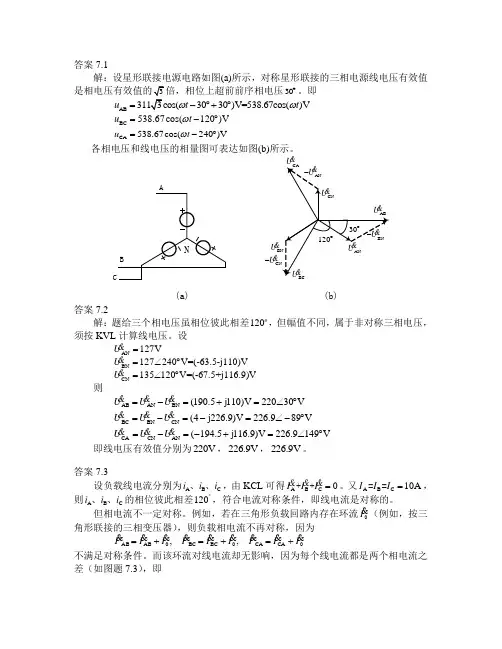
答案7.1解：设星形联接电源电路如图(a)所示，对称星形联接的三相电源线电压有效值30︒。

即AB 3030)V=538.67cos()V u t t ωω=-︒+︒BC 538.67cos(120)V u t ω=-︒ C A 538.67cos(240)Vu t ω=-︒各相电压和线电压的相量图可表达如图(b)所示。

ABCN(a) U (b)C U -答案7.2解：题给三个相电压虽相位彼此相差120 ，但幅值不同，属于非对称三相电压，须按KVL 计算线电压。

设AN 127V U = BN 127240V =(-63.5-j110)V U =∠︒ C N135120V =(-67.5+j116.9)V U =∠︒ 则A B A N BN BC BN C N C A C N A N(190.5j110)V 22030V (4j226.9)V 226.989V (194.5j116.9)V 226.9149V U U U U U U U U U =-=+=∠︒=-=-=∠-︒=-=-+=∠︒即线电压有效值分别为220V ，226.9V ，226.9V 。

答案7.3设负载线电流分别为A B C i i i 、、，由KCL 可得A B C 0I I I = ++。

又A B C 10A I I I ===，则A B C i i i 、、的相位彼此相差120︒，符合电流对称条件，即线电流是对称的。

但相电流不一定对称。

例如，若在三角形负载回路内存在环流0I （例如，按三角形联接的三相变压器），则负载相电流不再对称，因为0CA CA 0BC BC 0AB AB ',','I I I I I I I I I +=+=+= 不满足对称条件。

而该环流对线电流却无影响，因为每个线电流都是两个相电流之差（如图题7.3），即BCCA BC CA C AB BC AB BC B CA AB CA AB A '','',''I I I I I I I I I I I I I I I -=-=-=-=-=-=AB C图 题7.3如已知负载对称，则相电流也是对称的，每相电流为77.53/10≈A 。

答案10.1解：0<t时，电容处于开路，故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得：V 20)0()0(==-+C C u u换路后一瞬间，两电阻为串联，总电压为)0(+C u 。

所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得：m A5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解：0<t时电容处于开路，电感处于短路，Ω3电阻与Ω6电阻相并联，所以A3)363685(V45)0(=Ω+⨯++=-i，A 2)0(366)0(=⨯+=--i i LV 24)0(8)0(=⨯=--i u C由换路定律得：V24)0()0(==-+C C u u ，A 2)0()0(==-+L L i i由KVL 得开关电压：V8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u答案10.3解：0<t 时电容处于开路，0=i ，受控源源电压04=i ，所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C>t 时，求等效电阻的电路如图(b)所示。

等效电阻Ω=++-==5)36(4i ii i i u R 时间常数s 1.0i ==C R τ0>t 后电路为零输入响应，故电容电压为：V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为：V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4 解：<t 时电感处于短路，故A 3A 9363)0(=⨯+=-L i ，由换路定律得： A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。

(b)等效电阻Ω=+⨯+=836366i R ，时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应，故电感电流为 A e 3e )0()(2/t t L L i t i --+==τ)0(≥t电感电压V e 24d d )(21t Lti Lt u --==)0(>t Ω3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为：W3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解：由换路定律得0)0()0(==-+L L i i ，达到稳态时电感处于短路，故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。

3.7 把L=51mH的线圈（其电阻极小，可忽略不计），接在电压为220V、频率为 50Hz的交流电路中，要求：（1）绘出电路图；（2）求出电流I的有效值；（3） 求出XL。
解：（1）绘出电路图如右图所示； （2）电流有效值为
U 220 103
I
13.75
L 314 51
（3）线圈感抗为
解：根据电路图可画出相量示意图如图所示，由相量图中的电压三角形又可 导出阻抗三角形，由阻抗三角形可得
XC

1
C

10 6 314 0.1

31847
tg 30 X C R
R X C 31847 55165 tg 30 0.5773
4.5 已知RLC串联电路的参数为R=20Ω，L=0.1H，C=30μF，当信号频率分别为 50Hz、1000Hz时，电路的复阻抗各为多少？两个频率下电路的性质如何？
解：（1）电流表A的读数即电路中总电流，即
I 52 (20 25)2 7.07
（2）频率提高一倍时，感抗增大一倍而使得通过电感的电流减半，即A2读 数为10A；容抗则减半而使通过电容的电流加倍，即A3读数为50A。所以总 电流表A的读数为
I 52 (10 50)2 40.3
0 L
1500
计算结果表明，当并谐电路中再并入一个电阻时，电路的品质因数降低，选择性变差
5.10 一个R=13.7Ω，L=0.25mH的电感线圈，与C=100pF的电容器分别接成串 联和并联谐振电路，求谐振频率和两种谐振情况下电路呈现的阻抗。
解：①串联谐振时，电路的谐振频率为
1
10 6
f 0 2
R 2 (0.22 (2.5 52 5) 7.1

题12.1图示电路，设)(),(21R R L u f i f i ==ψ。

以q 及ψ为状态变量列出状态方程，并讨论所得方程是自治的还是非自治的。

图题12.1解：分别对节点①和右边回路列KCL 与KVL 方程：C q u u i i q i CL L R C C /===--==ψ将各元件方程代入上式得非线性状态方程：Cq C q f f q /)/()(21=--=ψψ方程中不明显含有时间变量t ，因此是自治的。

题12.2图示电路，设)(),(222111q f u q f u ==，列出状态方程。

4R R 图题12.2解：分别对节点①、②列KCL 方程： 节点①：=1i 321S 1/)(R u u i q --= 节点②：=2i 423212//)(R u R u u q --= 将)(),(222111q f u q f u == 代入上述方程，整理得状态方程：⎩⎨⎧+-=++-=)/())((/)(/)(/)(4343223112S3223111R R R R q f R q f q i R q f R q f q 题12.3在图示电路中电容的电荷与电压关系为)(111q f u =，电感的磁链电流关系为)(222ψf i =。

试列出电路的状态方程。

1u u 图题12.3解：分别对节点①列KCL 方程和图示回路列KVL 方程得：⎩⎨⎧-=-=(2) (1) /323321u u R u i q S ψ3u 为非状态变量，须消去。

由节点①的KCL 方程得：0413332432=-++-=++-R u u R u i i i i 解得()([)/()(224114332413f R q f R R R i R u u +=++=将)(111q f u =、)(222ψf i = 及3u 代入式(1)、(2)整理得：⎩⎨⎧++-+-=+++-=S u R R R R f R R R q f R R R f R R q f q )/()()/()()/()()/()(4343224331124332243111ψψψ 题12.4图示电路，设)sin(,S 3t u a i ωβ==ψ，试分别写出用前向欧拉法、后向欧拉法和梯形法计算响应)(t ψ的迭代公式，步长为h 。

习题参考答案习题11-11-1．．（1）（a ）图，u 和i 参考方向是非关联参考方向；（b ）图，u 和i 参考方向是关联参考方向。

参考方向。

（2）（a ）图，u 的实际方向与参考方向相同，i 的实际方向与参考方向相反。

（b ）图，u 的实际方向与参考方向相反，i 的实际方向与参考方向相同。

的实际方向与参考方向相同。

（3）（a ）图，8=p W ，吸收功率；（b ）图，24-=p W ，发出功率。

，发出功率。

1-21-2．．030)24()4(24=+-+-++-=åp ，功率平衡。

，功率平衡。

1-31-3．．（a ）图，01R i u u s +-=；（b ）图，02R i u u s -=1-41-4．．022233311=+-+++-S S S U R I U R I R I U1-51-5．．120W1-61-6．不能，实际电压将超过额定电压；可以。

．不能，实际电压将超过额定电压；可以。

．不能，实际电压将超过额定电压；可以。

1-71-7．．(a)W =1R ；(b)W =2R1-81-8．．（1）0=U V ，0=I A ；（2）3100=U V ，310=I A ；（3）25=U V ，5.2=I A （该题中已知条件中“W =10L R ”有误，应当改为“W =10R ”）1-91-9．．5=aV V ，=bV 1V 1V。

1-101-10．．5条支路，条支路，33个结点。

个结点。

a a 、b 两点间电流电压都等于零。

两点间电流电压都等于零。

1-111-11．．=aI 11A 11A，，=bI -6A -6A，，=cI -11A -11A。

1-121-12．．31-=IA 、2I =5.22A =5.22A、、3I =2.22A =2.22A。

1-131-13．开关断开时．开关断开时．开关断开时,,6=AV V ，6-=BV V 。

闭合时，8=AV V ，0=BV V 。

+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ，列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示，试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向，
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2

2-37. –2 ; 4 . 2-38 11/2 ※ 第三章 3-1. 44V;–1+9=8V; 6+ 9=15V; sin t +0.2 e – t V. 3-2. 155V. 3-3. 190mA. 3-4. 1.8 倍. 3-5. 左供 52W, 右供 78W. 3-6. 1Ω; 1A; 0.75A. 3-7. 3A; 1.33mA; 1.5mA; 2/3A; 2A. 3-8. 20V, –75.38V. 3-8(习题册)：0.2Ω 3-9(习题册)：2W 3-9. –1A; 2A; 1A. 3-10. 5V, 20Ω; –2V, 4Ω. 3-12. 4.6Ω. 3-13. 2V; 0.5A. 3-14. 10V, 5kΩ. 3-15. 3-16.22.5V 3-17. 4/3Ω, 75W; 4/3Ω, 4.69W. 3-18. 3Ω, 529/12W.; 1Ω, 2.25W. 3-19 3-20. 50Ω. 3-21. 0.2A. 3-22. 1A. 3-23. 1.6V. 3-24. 4A; 3-25. 23.6V; 5A,10V. 3-26. 3-27 4V 3-28. ※ 第四章 o o o 4-1. 141.1V, 100V, 50Hz, 0.02s,0 , –120 ; 120 . o o o 4-2. 7.07/0 A, 1/–45 A, 18.75/–40.9 A. 4-3. U m 3 , 7.75mA . 4-4. 10/53.13oA, 10/126.87oA, 10/–126.87oA, 10/–53.13 A；各瞬时表达式略。 4-5. 67.08V, 30V, 25V; 12V, 0, 12V, 0; 0, 0, 12V. 4-6. 7.07A; 10A, 50A. 4-7. 173.2Ω. 4-8. 4Ω, 1.5H. 4-9.11V 4-10. 5Ω, 0.1F. o o 4-11. 5A; 20/–53.13 Ω, 0.05/53.13 S.

输入端口电流为零的条件可知
iC iR
又由运算放大器输入端口电压为零的条件可知
iR
uR R
ui R
, uo
uC
故
uo
1 C
t
iC ( )d
1 C
0
iC
(
)d
1 C
t 0
iC
(
)d
1 C
t
0 iC ( )d uC (0)
1 RC
t
0 ui ( )d uC (0)
答案 5.5 解：取电容、电感上的电压、电流为关联参考方向，如图所示。由运算放大器
i C du du dt dt
将式(1)代入，可得
1A 0 t 1s i(t) 0 1s t 2s
1A 2s t 3s
i(t) 的变化规律如图(d)所示。
i/A 1
o
1
2
3
t/s
-1
图 (d)
(2)在关联参考方向下，电容上电压与电流关系又可表示为
u(t) 1
t
i( )d
C
由 KVL 方程得
uS u i 1 (2t 4)V
答案 5.7 解：设各元件电压、电流取关联参考方向，由 KVL 得
uR uC uL uL 0
即
iC R uC
(1 ) L diC dt
0
(1)
将
iC
C
duC dt
2e2tA
代入(1)式得
2e2t e2t (1 ) 4e2t 0
i(t) 1
0 u( )d 1
1
1.5d
1
t
(1)d
L
L0
L1
i(0) 1.5 1 (1 t) 0.5 0.5

How many coulombs are represented by these amounts of electrons:(a) (b)1710482.6×181024.1×(c) (d)191046.2×2010628.1×Chapter 1, Solution 1(a) q = 6.482x1017 x [-1.602x10-19 C] = -0.10384 C(b) q = 1. 24x1018 x [-1.602x10-19 C] = -0.19865 C(c) q = 2.46x1019 x [-1.602x10-19 C] = -3.941 C(d) q = 1.628x1020 x [-1.602x10-19 C] = -26.08 CChapter 1, Problem 2.Determine the current flowing through an element if the charge flow is given by(a)()()mC 83+=t t q (b)()C 2)482t-t (t q +=(c) ()()nC e 5e 3t q t 2-t −−=(d) ()pC t sin 10 120t q π=(e)()C t 50cos 204μt e t q −=Chapter 1, Solution 2(a) i = dq/dt = 3 mA(b) i = dq/dt = (16t + 4) A(c) i = dq/dt = (-3e -t + 10e -2t ) nA(d) i=dq/dt = 1200120ππcos t pA(e) i =dq/dt =−+−e t t t 48050100050(cos sin ) A μPROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsFind the charge q (t ) flowing through a device if the current is:(a)()()C 10 A,3==q t i (b) 0)0(,mA )52()(=+=q t t i(c) C 2(0) A,)6/10cos(20)(μμπ=+=q t t i(d)()0(0) A,40sin 1030==−q t e t i tChapter 1, Solution 3(a) C 1)(3t +=+=∫q(0)i(t)dt q(t)(b) mC 5t)(t 2+=++=∫q(v)dt s)(2t q(t)(c) ()q(t)20 cos 10t /6q(0)(2sin(10/6)1)C t ππμ=++=++∫ (d) C 40t) sin 0.12t (0.16cos40e 30t -+−=−+=+=∫ t)cos 40-t 40sin 30(1600900e 10q(0)t 40sin 10e q(t)-30t30t-Chapter 1, Problem 4.A current of 3.2 A flows through a conductor. Calculate how much charge passes through any cross-section of the conductor in 20 seconds.Chapter 1, Solution 4q = it = 3.2 x 20 = 64 CChapter 1, Problem 5.Determine the total charge transferred over the time interval of 0 ≤ t ≤ 10s when1()2i t t = A.Chapter 1, Solution 5102010125 C 024t q idt tdt ====∫∫ PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsThe charge entering a certain element is shown in Fig. 1.23. Find the current at:(a) t = 1 ms (b) t = 6 ms (c) t = 10 msFigure 1.23Chapter 1, Solution 6(a) At t = 1ms, ===280dt dq i 40 A (b) At t = 6ms, ==dtdq i 0 A (c) At t = 10ms, ===480dt dq i –20 APROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsThe charge flowing in a wire is plotted in Fig. 1.24. Sketch the correspondingcurrent.Figure 1.24Chapter 1, Solution 7⎢⎢⎢⎣⎡<<<<<<==8t 6 25A,6t 2 25A,-2t 0 A,25dt dq iwhich is sketched below:PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsThe current flowing past a point in a device is shown in Fig. 1.25. Calculate the total charge through the point.Figure 1.25Chapter 1, Solution 8C 15μ1102110idt q =×+×==∫PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsThe current through an element is shown in Fig. 1.26. Determine the total charge that passed through the element at:(a) t = 1 s (b) t = 3 s (c) t = 5 sFigure 1.26Chapter 1, Solution 9(a) C 10===∫∫10dt 10idt q (b) C5.2255.7151521510110idt q 30=++=×+⎟⎠⎞⎜⎝⎛×−+×==∫ (c) C 30=++==∫101010idt q 5Chapter 1, Problem 10.A lightning bolt with 8 kA strikes an object for 15 μ s. How much charge isdeposited on the object?Chapter 1, Solution 10q = it = 8x103x15x10-6 = 120 mCPROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsChapter 1, Problem 11.A rechargeable flashlight battery is capable of delivering 85 mA for about 12 h. How much charge can it release at that rate? If its terminals voltage is 1.2 V, how much energy can the battery deliver?Chapter 1, Solution 11q= it = 85 x10-3 x 12 x 60 x 60 = 3,672 CE = pt = ivt = qv = 3672 x1.2 = 4406.4 JChapter 1, Problem 12.If the current flowing through an element is given by()⎪⎪⎩⎪⎪⎨⎧><<<<<<=15s t 0,15st 10 A, 12-10s t 6 A,186s t 0 A,3t t iPlot the charge stored in the element over 0 < t < 20s.Chapter 1, Solution 12For 0 < t < 6s, assuming q(0) = 0,q t idt q tdt t t t()().=+=+=∫∫03015020At t=6, q(6) = 1.5(6)2 = 54For 6 < t < 10s,PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators 4q t idt q dt t t t()()=+=+=−∫∫6185418566At t=10, q(10) = 180 – 54 = 126For 10<t<15s,q t idt q dt t t t()()()=+=−+=−+∫∫1012126122461010At t=15, q(15) = -12x15 + 246 = 66For 15<t<20s,PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators 66q t dt q t()()=+=∫01515Thus,q t t t t ().,=−−+⎧⎨⎪⎪⎩⎪⎪15185412246662C,0 <t <6s C, 6 <t <10s C, 10 < t < 15s C 15 <t <20sThe plot of the charge is shown below.The charge entering the positive terminal of an element is10sin 4 mC q t π=while the voltage across the element (plus to minus) is2cos 4 V v t π=(a) Find the power delivered to the element at t = 0.3 s(b) Calculate the energy delivered to the element between 0 and 0.6s.Chapter 1, Solution 13(a) 40cos 4 mA dq i t dtππ== 280cos 4 mW p vi t ππ==At t=0.3s, 280cos (40.3)164.5 mW p x ππ==(b) 0.60.620080cos 440[1cos8] mJ W pdt tdt t dt ππππ===+∫∫∫0.61400.6sin 878.34 mJ 08W t πππ⎡⎤=+=⎢⎥⎣⎦PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsThe voltage v across a device and the current I through it are()()()A 110 V, 2cos 55.0t e t i t t v −−==Calculate:(a) the total charge in the device at t = 1 s(b) the power consumed by the device at t = 1 s.Chapter 1, Solution 14(a) ()()()C 2.131=−+=+===∫∫2e 21102e t 10dt e -110idt q 0.5-10.5t -100.5t -(b) p(t) = v(t)i(t)p(1) = 5cos2 ⋅ 10(1- e -0.5) = (-2.081)(3.935)= -8.188 WChapter 1, Problem 15.The current entering the positive terminal of a device is ()A 32t e t i −= and the voltage across the device is .()V / 5dt di t v =(a) Find the charge delivered to the device between t = 0 and t = 2 s.(b) Calculate the power absorbed.(c) Determine the energy absorbed in 3 s.Chapter 1, Solution 15 (a) ()=−−=−===∫∫1e 5.1e 23dt 3e idt q 4-202t 202t-1.4725 C (b)W e 90)(t 4−−==−=−==vi p e 305e 6dt di 5v 2t -2t (c) J 22.5−=−−===∫∫304t -304t -e 490dt e -90pdt w PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsFigure 1.27 shows the current through and the voltage across a device. (a) Sketch the power delivered to the device for t >0. (b) Find the total energy absorbed by thedevice for the period of 0< t < 4s.0 2 4 t(s)Figure 1.27 For Prob. 1.16.PROPRIETARY MATERIAL. © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators(a)30 mA, 0 < t <2()120-30t mA, 2 < t<4t i t ⎧=⎨⎩5 V, 0 < t <2()-5 V, 2 < t<4v t ⎧=⎨⎩150 mW, 0 < t <2()-600+150t mW, 2 < t<4t p t ⎧=⎨⎩ which is sketched below.PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No partof this Manual may be displayed, reproduced or distributed in any form or by any means, without the priorwritten permission of the publisher, or used beyond the limited distribution to teachers and educators(b) From the graph of p,40 J W pdt ==∫Figure 1.28 shows a circuit with five elements. IfW, 30 W, 45 W, 60 W, 2055421===−=p p p pcalculate the power p 3 received or delivered by element 3.Figure 1.28Chapter 1, Solution 17Σ p = 0 → -205 + 60 + 45 + 30 + p 3 = 0p 3 = 205 – 135 = 70 WThus element 3 receives 70 W.PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsFind the power absorbed by each of the elements in Fig. 1.29.Figure 1.29Chapter 1, Solution 18p1 = 30(-10) = -300 Wp2 = 10(10) = 100 Wp3 = 20(14) = 280 Wp4 = 8(-4) = -32 Wp5 = 12(-4) = -48 WPROPRIETARY MATERIAL. © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsChapter 1, Problem 19.Find I in the network of Fig. 1.30.V 4 A PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No partof this Manual may be displayed, reproduced or distributed in any form or by any means, without the priorwritten permission of the publisher, or used beyond the limited distribution to teachers and educatorsFigure 1.30 For Prob. 1.19.Chapter 1, Solution 19I = 4 –1 = 3 AOr using power conservation,9x4 = 1x9 + 3I + 6I = 9 + 9I4 = 1 + I or I = 3 AChapter 1, Problem 20.Find V 0 in the circuit of Fig. 1.31.Figure 1.31Chapter 1, Solution 20Since Σ p = 0-30×6 + 6×12 + 3V 0 + 28 + 28×2 - 3×10 = 072 + 84 + 3V 0 = 210 or 3V 0 = 54V 0 = 18 VChapter 1, Problem 21.A 60-W, incandescent bulb operates at 120 V. How many electrons and coulombs flow through the bulb in one day?Chapter 1, Solution 21600.5 A 120p p vi i v =⎯⎯→=== q = it = 0.5x24x60x60 = 43200 C18236.2410 2.69610 electrons e N qx x x ==PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsChapter 1, Problem 22.A lightning bolt strikes an airplane with 30 kA for 2 ms. How many coulombs of charge are deposited on the plane?Chapter 1, Solution 2233301021060 C q it x x x −===Chapter 1, Problem 23.A 1.8-kW electric heater takes 15 min to boil a quantity of water. If this is done once a day and power costs 10 cents per kWh, what is the cost of its operation for 30 days?Chapter 1, Solution 23W = pt = 1.8x(15/60) x30 kWh = 13.5kWhC = 10cents x13.5 = $1.35Chapter 1, Problem 24.A utility company charges 8.5 cents/kWh. If a consumer operates a 40-W light bulb continuously for one day, how much is the consumer charged?Chapter 1, Solution 24W = pt = 40 x24 Wh = 0.96 kWhC = 8.5 cents x0.96 = 8.16 centsChapter 1, Problem 25.A 1.2-kW toaster takes roughly 4 minutes to heat four slices of bread. Find the cost of operating the toaster once per day for 1 month (30 days). Assume energy costs 9 cents/kWh.Chapter 1, Solution 25cents 21.6 cents/kWh 930hr 604 kW 1.2 Cost =×××= PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsA flashlight battery has a rating of 0.8 ampere-hours (Ah) and a lifetime of 10 hours.(a) How much current can it deliver?(b) How much power can it give if its terminal voltage is 6 V?(c) How much energy is stored in the battery in kWh?Chapter 1, Solution 26(a) mA 80.=⋅=10hh A 80i (b) p = vi = 6 × 0.08 = 0.48 W(c) w = pt = 0.48 × 10 Wh = 0.0048 kWhChapter 1, Problem 27.A constant current of 3 A for 4 hours is required to charge an automotive battery. If the terminal voltage is 10 + t /2 V, where t is in hours,(a) how much charge is transported as a result of the charging?(b) how much energy is expended?(c) how much does the charging cost? Assume electricity costs 9 cents/kWh.Chapter 1, Solution 27∫∫=××====×==kC 43.2 36004 3 T 33dt idt q 36004 4h T Let (a)T 0[]kJ 475.2...)((=××+×=⎟⎟⎠⎞⎜⎜⎝⎛+=⎟⎠⎞⎜⎝⎛+===×∫∫∫36001625036004033600250103dt 3600t 50103vidt pdt W b)36004020T 0t t Tcents 1.188(=×===cent 9kWh 3600475.2 Cost Ws)(J kWs, 475.2W c) PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsA 30-W incandescent lamp is connected to a 120-V source and is left burningcontinuously in an otherwise dark staircase. Determine:(a) the current through the lamp,(b) the cost of operating the light for one non-leap year if electricity costs 12 centsper kWh.Chapter 1, Solution 28A 0.25===12030 (a)V P i$31.54(=×==××==262.8 $0.12Cost kWh 262.8Wh 2436530pt W b)Chapter 1, Problem 29.An electric stove with four burners and an oven is used in preparing a meal as follows.Burner 1: 20 minutes Burner 2: 40 minutesBurner 3: 15 minutes Burner 4: 45 minutesOven: 30 minutesIf each burner is rated at 1.2 kW and the oven at 1.8 kW, and electricity costs 12 cents per kWh, calculate the cost of electricity used in preparing the meal.Chapter 1, Solution 29cents39.6.=×==+=⎟⎠⎞⎜⎝⎛++++== 3.3 cents 12Cost kWh 3.30.92.4hr 6030kW 1.8hr 6045)1540(20kW 21pt wPROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsPROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsReliant Energy (the electric company in Houston, Texas) charges customers as follows:Monthly charge $6First 250 kWh @ $0.02/kWhAll additional kWh @ $0.07/kWhIf a customer uses 1,218 kWh in one month, how much will Reliant Energy charge?Chapter 1, Solution 30Monthly charge = $6First 250 kWh @ $0.02/kWh = $5Remaining 968 kWh @ $0.07/kWh= $67.76Total = $78.76Chapter 1, Problem 31.In a household, a 120-W PC is run for 4 hours/day, while a 60-W bulb runs for 8hours/day. If the utility company charges $0.12/kWh, calculate how much the household pays per year on the PC and the bulb.Chapter 1, Solution 31Total energy consumed = 365(120x4 + 60x8) WCost = $0.12x365x960/1000 = $42.05Chapter 1, Problem 32.A telephone wire has a current of 20 μ A flowing through it. How long does it take for a charge of 15 C to pass through the wire?Chapter 1, Solution 32i = 20 µAq = 15 Ct = q/i = 15/(20x10-6) = 750x103 hrsA lightning bolt carried a current of 2 kA and lasted for 3 ms. How many coulombs of charge were contained in the lightning bolt?Chapter 1, Solution 33C 61032000idt q dtdq i 3=××==→=−∫Chapter 1, Problem 34.Figure 1.32 shows the power consumption of a certain household in one day.Calculate: (a) the total energy consumed in kWh, (b) the average power per hour.Figure 1.32Chapter 1, Solution 34(a) Energy = = 200 x 6 + 800 x 2 + 200 x 10 + 1200 x 4 + 200 x 2 pt ∑ = 10 kWh(b) Average power = 10,000/24 = 416.7 WPROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsThe graph in Fig. 1.33 represents the power drawn by an industrial plant between 8:00 and 8:30 A.M. Calculate the total energy in MWh consumed by the plant.Figure 1.33Chapter 1, Solution 35energy = (5x5 + 4x5 + 3x5 + 8x5 + 4x10)/60 = 2.333 MWhrChapter 1, Problem 36.A battery may be rated in ampere-hours (Ah). A lead-acid battery is rated at 160 Ah.(a) What is the maximum current it can supply for 40 h?(b) How many days will it last if it is discharged at 1 mA?Chapter 1, Solution 36days 6,667,(A 4====⋅=day/ 24h h 0001600.001A 160Ah t b)40h A 160i (a)PROPRIETARY MATERIAL . © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educatorsA 12-V battery requires a total charge of 40 ampere-hours during recharging. Howmany joules are supplied to the battery?Chapter 1, Solution 37W = pt = vit = 12x 40x 60x60 = 1.728 MJChapter 1, Problem 38.How much energy does a 10-hp motor deliver in 30 minutes? Assume that 1 horsepower = 746 W.Chapter 1, Solution 38P = 10 hp = 7460 WW = pt = 7460 × 30 × 60 J = 13.43 × 106 JChapter 1, Problem 39.A 600-W TV receiver is turned on for 4 hours with nobody watching it. If electricity costs 10 cents/kWh, how much money is wasted?Chapter 1, Solution 39W = pt = 600x4 = 2.4 kWhC = 10cents x2.4 = 24 centsPROPRIETARY MATERIAL. © 2007 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators。