光学镜头理论基础

光学镜头参数详解
摘要：
I.光学镜头概述
- 定义与作用
II.光学镜头的主要参数
- 焦距
- 相对孔径与光圈数
- 视场角与像面尺寸
- 分辨率
- 景深
- 工作距离
- 相机接口
III.光学镜头的选择与应用
- 选择光学镜头的考虑因素
- 光学镜头的应用领域
IV.结论
正文：
I.光学镜头概述
光学镜头是一种用于将光线聚焦在一点上的光学器件，通常由多个透镜组成。

它广泛应用于各种光学设备和仪器中，如照相机、望远镜、显微镜等。

光学镜头的主要作用是将来自物体的光线聚焦在成像传感器或眼睛上，从而产生
清晰的图像。

II.光学镜头的主要参数
1.焦距
焦距是指从光学镜头的中心点到焦点的距离。

它决定了像与实际物体之间的比例。

镜头焦距越长，成像越大。

2.相对孔径与光圈数（f）
相对孔径是指镜头的有效孔径与焦距的比值，主要影响像面的照度。

镜头发展史1. 引言镜头作为摄影和电影制作中不可或缺的装备，对于影像的质量和效果起着至关重要的作用。

本文将从早期简单的透镜到现代复杂的镜头技术，探讨镜头发展的历史。

2. 早期光学原理早在公元前4世纪，古希腊数学家欧几里得就研究了光线传播的规律，并提出了透镜和反射器的概念。

然而，在光学领域真正有重大突破的是17世纪初期。

3. 透镜与望远镜在17世纪初，荷兰科学家哈雷尔·斯内尔斯发明了最早的单片凸透镜，成为人类历史上第一个可放大物体并观察的装置。

此后，伽利略·伽利雷将两片透镜组合在一起，发明了望远镜，并用于天文观测。

4. 单反相机与复合透镜系统19世纪初，法国物理学家约瑟夫·尼斯福尔·尼埃普斯发明了世界上第一台单反相机。

这种相机利用复合透镜系统，实现了对焦和成像的功能，为后来相机的发展奠定了基础。

5. 菲涅耳透镜与广角镜头19世纪中叶，法国物理学家奥古斯丁·菲涅耳发明了菲涅耳透镜。

相比传统的凸透镜，菲涅耳透镜更轻薄，并且可以减少光线损失。

同时，随着照相术的发展，广角镜头也开始被广泛使用。

6. 镀膜技术与色差校正20世纪初，德国化学家卡尔·齐塞尔开发出了镀膜技术。

通过在透镜表面涂上一层膜，可以减少反射和散射光线，提高光学系统的透明度和成像质量。

同时，色差问题也成为一个亟待解决的难题。

爱尔兰物理学家约瑟夫·普拉克特提出了使用多片玻璃组合的方法来校正色差。

7. 镜头设计与光学计算随着镜头的功能和要求越来越高，光学计算成为一个必不可少的环节。

20世纪中叶，美国物理学家道格拉斯·哈特里开发了第一套用于计算光学系统参数的方法，并在此基础上建立了镜头设计的理论。

这一突破使得镜头设计变得更加科学化和精确。

8. 自动对焦与变焦镜头20世纪70年代，自动对焦技术开始应用于相机镜头。

通过使用传感器和电机，相机可以自动调整镜头位置以实现对焦。

而在80年代，变焦镜头开始流行起来。

相机镜头原理
相机镜头原理是指在摄影过程中，通过光学镜头使得光线能够聚焦在感光元件（例如胶片或图像传感器）上的方法。

镜头有助于控制光线的入射角度和路径，从而实现对景物的清晰成像。

镜头的基本构造通常包括凸透镜和凹透镜，它们根据其形状和位置不同发挥着不同的作用。

凸透镜可以使光线汇聚到一个焦点上，从而形成清晰的图像。

凹透镜则与凸透镜相反，它使光线发散，导致成像模糊。

在相机中，镜头位于相机机身和感光元件之间。

当光线通过镜头进入相机时，它会经过折射和散射的过程。

这些过程受到镜头的形状、材料和光线的入射角度等参数的影响。

在镜头中，光线的折射是通过改变光线的入射角度来实现的。

折射的程度由镜头的曲率和折射率决定。

镜头的曲率越大，折射角度越大，光线聚焦的焦距越短。

当光线通过镜头并聚焦在感光元件上时，清晰的图像就被记录下来。

这是因为光线通过镜头被聚焦成散射程度最小的形式，从而形成尖锐的轮廓和清晰的细节。

不同类型的镜头，如广角镜头、长焦镜头和变焦镜头等，通过改变镜头设计和元件的排列，能够实现不同的拍摄效果和功能。

总之，相机镜头的原理基于光学原理和几何光学，通过控制光
线的折射和散射，使得光线能够聚焦在感光元件上，从而实现清晰、准确的图像记录。

光学基础理论一. 光学基本定律1.光直线传播定律2.光独立传播定律3.光反射定律I**= - I I –入射角I**-- 反射角4.光折射定律n Sin I = n*Sin I* I –入射角I*-- 折射角n-- 折射率(入射空间) n*--折射率(折射空间)n = C/V C –光在真空中的速度V--光在介质中的速度二. 全反射在特定条件下,光线在界面能全部反射回去,这叫光的全反射.临界角: Sin I m=n*/n I m--临界角当入射角大于临界角时,产生全反射.全反射的用途:1.棱镜2.光纤三. 球面与球面系统-1-由二个球面组成一个透镜,一个或多个透镜组成一个镜头, 多个镜头和其它光学元件组成一个光学系统.四. 与镜头和透镜相关的基本参数1.焦距(EFL)A.物方焦距( f ): 由前主面到前焦点的距离.B.像方焦距( f*): 由后主面到后焦点的距离.Q—前主面Q’---后主面H---前主点H’---后主点F---前焦点F’---后焦点U---物方孔径角U’---像方孔径角焦距公式: f*=h/tgU* f =h/tgU在镜头或透镜中有一对垂轴放大率为+1的二个平面Q和Q’.2.后截距(BFL)A.由镜头或光学系统最后一面到像面的距离为光学后截距(BFL).B.由下座端部到像面的距离为机械后截距(BFL*)BFL>BFL*-2-3.F/NO (F数)F/NO=f*/D入 f *---焦距(EFL)D入---入瞳直径入瞳为光栏经其前方光学系统所成的像.举例:4.半视角(FOV/2)(ω)[视场角(FOV)(2ω)]物镜在其接收元件上成像的空间范围称为视场角.其一半为半视角.Y’ = f*tgωY’---像的大小f*---焦距(EFL)-3-5.畸变量(DIST)在视场角较大或者很大时,所产生的像变形称为畸变.DIST=[Y’-Y0’/Y0’]×100%Y’—实际像高Y0’---理想像高6.相对照度(REL)是指像面边缘照度和中心照度之比.REL = E’W/E E--像面中心照度E’W--像面边缘照度E=1/4×πKL(2a/f*)2E’W=K1E×Cos4ω’K—透过率L---物体位置2a/f*---相对孔径(F/NO倒数) K1---渐晕系数7.光学总长(TOTR)是指由镜头第一面到像面的距离.-4-五. 波长与颜色1.波长光以波动形式向前传播,光波是电磁波,是电场和磁场的振动,其振动强度有周期性变化. 光的传播用正曲线描述,如图:λ---波长a---振幅π---圆周率t---时间u = a Sin[2π(t/T –X/λ)]T—周期T=1/ƒƒ—频率X---为t时间沿X轴振动的位置。

摄像机基础知识介绍摄像机基础知识介绍摄像机常用专业术语解释大汇总1) 什么是镜头的焦距？——(难度:中等)答：从光学原理来讲焦距就是从焦点到透镜中心的距离。

即焦距长度。

如"f=8-24mm，"，就是指镜头的焦距长度为8-24mm2) CCTV的含义是什么？——(难度:中等)答：CCTV 是英文Closed Circuit T elevision的缩写，意思是闭路电视监控系统3) 焦距长短与成像大小、视角大小有什么关系？——(难度:容易) 答：焦距长短与成像大小成正比，焦距越长成像越大，焦距越短成像越小。

镜头焦距长短与视角大小成反比，焦距越长视角越小，焦距越短视角越大。

3) 什么是镜头F值？——(难度:容易)答：F 值即指镜头之明亮度。

镜头规格中所显示＜最大口径比1:1.2＞之＜1.2＞即为F值。

F值越小表示镜头之明亮度越高。

F值每缩小一级距，明亮度即增加两倍。

镜头之射入光量与光束之断面积[镜头的有效口径[D]的平方]成比例，因此影像明亮度为F值平方之反比。

由此推算，F值每缩小一级距，明亮度即增加两倍。

4) 什么是镜头的光圈？——(难度:容易)答：光圈的功能就如同我们人类眼睛的虹蟆，主要用来调整摄像机的进光量，F表示镜头的孔径，较小的F值表示较大的光圈5) 什么是景深？——(难度:容易)答：当某一物体聚焦清晰时，从该物体前面的某一段距离到其后面的某一段距离内的所有景物也都当清晰的。

焦点相当清晰的这段从前到后的距离就叫做景深6) 什么是广角镜头？（Wide Angle）——(难度:容易)答：广角镜头因焦距非常短，所以投射到底片上的景物就变小了扩阔镜头拍摄角度，除可拍摄更多景物，更能在狭窄的环境下拍摄出宽阔角度的影像。

视角90度以上，观察范围较大，近处图像有变形。

7) 什么是长焦镜头？——(难度:容易)答：视角20度以内，焦距可达几十毫米或上百毫米8) 什么是变焦镜头？——(难度:容易)答：镜头焦距连续可变，焦距可以从广角变到长焦，焦距越长成像越大。

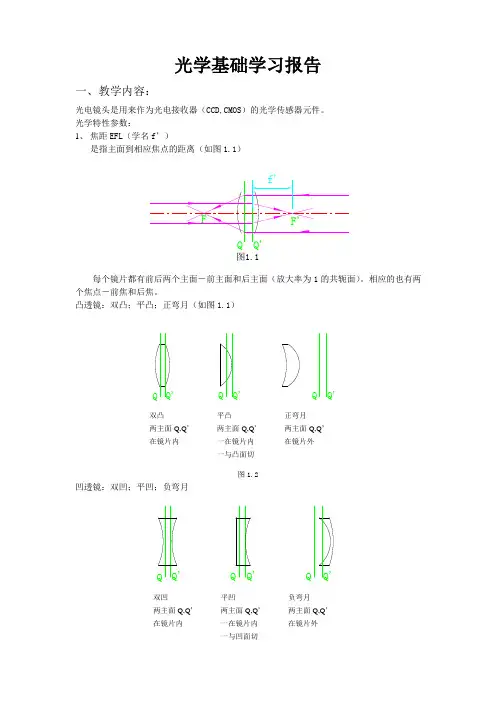
光学基础学习报告一、教学内容：光电镜头是用来作为光电接收器（CCD,CMOS）的光学传感器元件。

光学特性参数：1、焦距EFL（学名f’）是指主面到相应焦点的距离（如图1.1）图1.1每个镜片都有前后两个主面－前主面和后主面（放大率为1的共轭面）。

相应的也有两个焦点－前焦和后焦。

凸透镜：双凸；平凸；正弯月（如图1.1）图1.2凹透镜：双凹；平凹；负弯月图1.3折射率实际反映的是光在物质中传播速度与真空中速度的比值关系。

薄透镜：)]1()1[()1('121R R n f -⨯-==Φ Φ—透镜光焦距；f ’—焦距； n —折射率；R 1,R 2－两球面曲率半径厚透镜：21221)1()]1()1[()1('1R nR dn R R n f -+-⨯-==Φ d －中心厚度干涉仪与光距座可以量测f ’,R1,R2,d →利用上述的公式可以计算出n 值，从而来确定所用材料。

A 、 EFL 增加，TOTR （光学总长）增加；要降低TOTR 就必须降低EFL ，但EFL 降低，像高就要降低B 、 EFL 与某些象差相关C 、 EFL 上升将使F/NO 增大D 、 EFL ，FOV （视场角）和IMA （像高）三者间有关系tanFOV ⨯=EFL IMA －铁三角关系EFL 的增大（减小）会使像高变大（小），为了保持像高，就必须要增大（减小）FOV ，然而FOV 的增大会使得REL （相对照度）的数值增大。

2、 BFL 后焦距（学名后截距）图2.13、 F 数（F/NO ）Df NO F '/=f ’－FELD 入－入瞳直径入瞳为光阑经其前方光学镜片所成的像，反映进入光学系统的光线 A 、 与MTF 相关，F/NO ↑，则MTF ↑；反之下降 B 、 与景深相关，F/NO ↑，则景深↑，反之下降 C 、 与象差相关，F/NO ↑，则象差↓，反之增加D、与光通量相关，F/NO↑，则光通量↓，反之增加对于光电镜头，F/NO最大在2.8～3.5之间（经验值）允许有±5%的误差，在物方有照明时，F数可根据照明的照度情况来增大4、视场角FOV（2ω），半视场角FOC/2（ω）物镜在其接收元件上成像的空间范围称为视场角。

薄透镜成像理论及应用引言：薄透镜是光学中常见的元件之一，它的成像原理和应用广泛。

本文将介绍薄透镜的成像理论，以及它在实际应用中的一些案例。

一、薄透镜成像理论薄透镜成像理论是光学中的基础知识之一。

薄透镜是指其厚度相比于其曲率半径来说非常薄的透镜。

根据薄透镜成像理论，光线通过透镜时会发生折射，并在另一侧形成一个成像。

1.1 透镜的焦距透镜的焦距是薄透镜成像理论中重要的概念之一。

焦距是指光线经过透镜后会汇聚到的点或者看似汇聚的点。

对于凸透镜来说，焦距是正的，而对于凹透镜来说，焦距是负的。

1.2 透镜成像公式透镜成像公式是薄透镜成像理论中的核心公式。

它描述了物体与成像之间的关系。

根据透镜成像公式，可以计算出物体的位置、成像的位置以及成像的放大倍数等信息。

1.3 光线追迹法光线追迹法是薄透镜成像理论中常用的方法之一。

通过绘制光线的路径，可以直观地了解透镜的成像原理。

光线追迹法可以帮助我们理解透镜的工作原理，并预测成像的效果。

二、薄透镜的应用薄透镜不仅在理论研究中有重要作用，还在实际应用中得到了广泛的应用。

下面将介绍薄透镜在光学仪器、眼镜和摄影等方面的应用。

2.1 光学仪器薄透镜在光学仪器中有着重要的应用。

例如，显微镜和望远镜中的物镜和目镜都是由薄透镜组成的。

薄透镜的成像原理使得光学仪器能够放大远处的物体，使其能够清晰可见。

2.2 眼镜薄透镜在眼镜中的应用是人们熟知的。

近视眼和远视眼患者可以通过佩戴适当的薄透镜眼镜来矫正视力。

薄透镜的成像原理使得眼镜能够将光线正确地聚焦在视网膜上，从而改善视力。

2.3 摄影薄透镜在摄影中也有重要的应用。

相机中的镜头就是由薄透镜组成的。

薄透镜的成像原理使得相机能够捕捉到清晰的图像。

此外，透镜的不同焦距可以实现不同的拍摄效果，如广角、望远等。

结论：薄透镜成像理论是光学中的重要内容，通过了解薄透镜的成像原理，可以更好地理解光学现象。

薄透镜在实际应用中有着广泛的应用，包括光学仪器、眼镜和摄影等领域。