下载文档原格式
基于matlab的四杆机构运动分析一、四杆机构基本概念四杆机构是一种通过变换连杆长度，改变机构运动形态的机械系统。
四杆机构通常由固定连杆、推动连杆、连接杆和工作连杆四个连杆组成，其中固定连杆和推动连杆固定不动，连接杆和工作连杆则沿固定轴线的方向做平动或旋转运动。
四杆机构的基本构造如下图所示：四杆机构的四个连杆的长度和构造参数，以及驱动机构的运动决定了机构的运动特性。
在进行四杆机构运动分析时，需要通过求解运动学关系式和动力学方程，得到连杆的运动规律和力学特性。
二、四杆机构运动学分析1.运动学基本方程四杆机构的运动学分析基本方程是连杆长度变化的定理，即:l₁²+l₂²-2l₁l₂cosθ₂=l₃²+l₄²-2l₃l₄cosθ₄其中，l₁，l₂分别为固定连杆和推动连杆长度；l₃，l₄分别为连接杆和工作连杆长度；θ₂，θ₄分别为推动连杆和工作连杆的夹角。
2.运动学求解方法根据四杆机构运动学基本方程，可以求解机构中任意连杆的角度和位置，从而分析机构运动规律。
在matlab程序中，运动分析可以采用分析法或图解法。
分析法通常采用向量法或坐标法，即将四杆机构中各连杆和运动副的运动量表示为向量或坐标，然后根据连杆长度变化的定理，求解四个未知角度θ₁、θ₂、θ₃、θ₄。
图解法则先通过画图确定机构的运动规律，在图上求解连杆的角度。
比如可以采用伯格（Bourgeois）图法或恰普利恩（Chaplygin）图法等。
四杆机构动力学分析基本方程包括平衡方程和力平衡方程。
平衡方程：当四杆机构处于平衡状态时，连杆的受力关系可以表示为：ΣF=0其中ΣF为各连杆受力的合力。
ΣF=m×a其中，m为每个连杆的质量，a为连杆的加速度。
四杆机构动力学求解方法以matlab为工具，可借助matlab的求解器完成求解。
具体可以利用matlab的优化工具箱、控制工具箱和系统动态学工具箱等，来实现机构模型的动态模拟、仿真和优化设计。
基于Matlab的机构运动分析教学实践1. 引言机构运动分析是机械设计中的重要环节之一，其研究涉及运动学和动力学等多专业知识。
对于机械工程专业的学生而言，学习机构运动分析并进行相关实践，可有效提高其综合素质和能力，为其未来工作打下坚实基础。
本文主要介绍基于Matlab的机构运动分析教学实践，探讨如何通过实践来巩固和深化相关知识，并为机械专业学生提供一定的参考。
2. 实践内容2.1 实验要求本次实践以单平面机构为例，要求学生使用Matlab软件对其结构和运动学特性进行分析，并绘制相关曲线图。
具体要求包括：1.根据机构结构，计算机构的连杆长度、摆动角度等运动参数。
2.使用Matlab编程，绘制机构的位置分析图和速度分析图。
3.对机构运动学分析结果进行总结，分析机构的运动特性和运动规律。
2.2 实验过程在实践过程中，学生首先需要了解单平面机构的构造和运动规律，掌握机构运动学计算的方法和Matlab编程技能。
接着，学生应根据实验要求设计程序，并输入对应参数，运行程序后绘制各种曲线图。
最后，学生应对实验结果进行总结和分析，深化对机构运动学的理解。
2.3 实验成果对于单平面机构的位置分析图和速度分析图，学生应绘制出各连杆的运动轨迹和速度曲线，并对其进行标注解释。
通过对实验结果的深入分析，学生能够更好地理解机构运动学的基本概念和运动规律，为今后从事与机械设计相关工作打下坚实基础。
3. 实践心得通过本次实践，笔者深刻认识到机构运动分析是机械设计中的重要环节之一，也是机械工程专业核心知识点之一。
学生应尽早掌握基本概念和计算方法，并通过实践来加深对机构运动规律的理解。
Matlab 软件在机构运动分析中具有广泛的应用价值，学生应熟练掌握其编程技能，以更有效地完成实验任务。
4. 结论通过本文的介绍，我们可以了解到基于Matlab的机构运动分析教学实践的相关内容和要求。
学生应通过实践来深化对机构运动学的理解，并为今后从事与机械设计相关工作打下坚实基础。
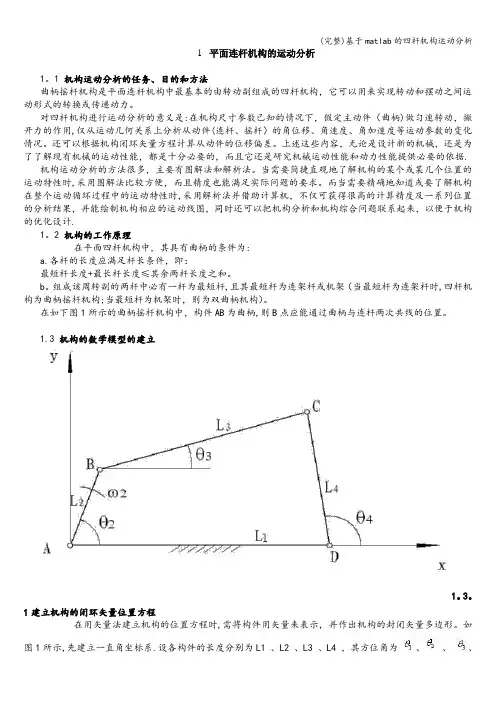
1平面连杆机构的运动分析1。
1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构，它可以用来实现转动和摆动之间运动形式的转换或传递动力。
对四杆机构进行运动分析的意义是:在机构尺寸参数已知的情况下，假定主动件（曲柄)做匀速转动，撇开力的作用,仅从运动几何关系上分析从动件(连杆、摇杆）的角位移、角速度、角加速度等运动参数的变化情况。
还可以根据机构闭环矢量方程计算从动件的位移偏差。
上述这些内容，无论是设计新的机械，还是为了了解现有机械的运动性能，都是十分必要的，而且它还是研究机械运动性能和动力性能提供必要的依据.机构运动分析的方法很多，主要有图解法和解析法。
当需要简捷直观地了解机构的某个或某几个位置的运动特性时,采用图解法比较方便，而且精度也能满足实际问题的要求。
而当需要精确地知道或要了解机构在整个运动循环过程中的运动特性时,采用解析法并借助计算机，不仅可获得很高的计算精度及一系列位置的分析结果，并能绘制机构相应的运动线图，同时还可以把机构分析和机构综合问题联系起来，以便于机构的优化设计.1。
2 机构的工作原理在平面四杆机构中，其具有曲柄的条件为:a.各杆的长度应满足杆长条件，即：最短杆长度+最长杆长度≤其余两杆长度之和。
b。
组成该周转副的两杆中必有一杆为最短杆,且其最短杆为连架杆或机架（当最短杆为连架杆时,四杆机构为曲柄摇杆机构;当最短杆为机架时，则为双曲柄机构）。
在如下图1所示的曲柄摇杆机构中，构件AB为曲柄,则B点应能通过曲柄与连杆两次共线的位置。
1.3 机构的数学模型的建立1。
3。
1建立机构的闭环矢量位置方程在用矢量法建立机构的位置方程时,需将构件用矢量来表示，并作出机构的封闭矢量多边形。
如图1所示,先建立一直角坐标系.设各构件的长度分别为L1 、L2 、L3 、L4 ，其方位角为、、、.以各杆矢量组成一个封闭矢量多边形，即ABCDA。
其个矢量之和必等于零。
基于MATLAB/Solidworks COSMOSMotion的平面连杆机构动力学分析07208517王锡霖4-23在图示的正弦机构中,已知l AB =100 mm,h1=120 mm,h2 =80 mm,W1 =10 rad/s(常数)，滑块2和构件3的重量分别为G2 =40 N和G3 =100 N,质心S2 和S3 的位置如图所示，加于构件3上的生产阻力Fr=400 N，构件1的重力和惯性力略去不计。
试用解析法求机构在Φ1=60°、150°、220°位置时各运动副反力和需加于。
构件1上的平衡力偶Mb分别对三个构件进行受力分析如图：构件3受力图构件2受力图构件1受力图（1）滑块2：V S2 =L AB W1 ①a s2 = L AB W12②构件3：S=L AB sinΦ1 ③V3=L AB W1 COSΦ1 ④a3=-L AB W12 sinΦ1 ⑤(2)确定惯性力：F12=m2as2=(G2/g)LABW12 ⑥F13=m3a3=(G3/g)LABW12sinΦ1 ⑦(3)各构件的平衡方程：构件3：∑Fy=0,FR23 =Fr-F13∑Fx=0,FR4’=FR4∑MS3 =0,FR4=FR23LAcosΦ1/h2构件2：∑Fx=0,FR12x=F12cosΦ1∑Fy=0,FR12y=FR32-F12sinΦ1构件1：∑Fx=0,FR41x=FR12x∑Fy=0,FR41y=FR12y∑MA =0,Mb=FR32LABcosΦ1总共有八个方程，八个未知数。
归纳出一元八次方程矩阵：1 0 0 0 0 0 0 0 FR23 Fr-F130 1 -1 0 0 0 0 0 FR4’ 0-LAB COSΦ1/h20 1 0 0 0 0 0 FR40 0 0 1 0 0 0 0 FR12x = F12cosΦ1-1 0 0 0 1 0 0 0 FR12y -F12sinΦ10 0 0 -1 0 1 0 0 FR41x 00 0 0 0 -1 0 1 0 FR41y 0-LABCOSΦ1 0 0 0 0 0 0 1 Mb 0 AX=B进而可得：X=A\B。
二连杆正逆运动学求解matlab二连杆是机械系统中常见的一种连杆机构，由两个相互连接的连杆组成。
在机械工程中，正逆运动学是研究连杆运动的重要内容之一。
本文将使用Matlab来求解二连杆的正逆运动学问题。
正逆运动学是机械工程中的两个基本问题，正运动学问题是已知连杆的几何参数和运动关系，求解连杆末端的位置和速度；逆运动学问题则是已知连杆末端的位置和速度，求解连杆的几何参数和运动关系。
我们需要定义二连杆的几何参数，包括连杆的长度和初始位置。
假设连杆1的长度为L1，连杆2的长度为L2，连杆1的初始位置为(0,0)，连杆2的初始位置与连杆1的末端相连。
我们需要求解的是连杆2末端的位置和速度。
对于正运动学问题，我们可以根据连杆的几何关系和运动关系，通过几何推导来求解连杆末端的位置。
在Matlab中，我们可以使用向量和矩阵运算来实现这一过程。
我们可以根据连杆的几何关系，利用三角函数来求解连杆2末端的位置。
假设连杆1与x轴的夹角为θ1，连杆2与连杆1的夹角为θ2，则连杆2末端的位置可以表示为：x = L1*cos(θ1) + L2*cos(θ1+θ2)y = L1*sin(θ1) + L2*sin(θ1+θ2)其中，x和y分别表示连杆2末端的x坐标和y坐标。
接下来，我们可以根据连杆的运动关系，求解连杆的速度。
假设连杆1的角速度为ω1，连杆2的角速度为ω2，则连杆2末端的速度可以表示为：v_x = -L1*ω1*sin(θ1) - L2*(ω1+ω2)*sin(θ1+θ2)v_y = L1*ω1*cos(θ1) + L2*(ω1+ω2)*cos(θ1+θ2)其中，v_x和v_y分别表示连杆2末端的x方向和y方向的速度。
对于逆运动学问题，我们可以先根据连杆末端的位置，通过几何推导来求解连杆的几何参数。
然后，根据连杆末端的速度，通过运动学关系来求解连杆的角速度。
在Matlab中，我们可以使用符号计算工具箱来求解逆运动学问题。
基于matlab的平面四连杆机构设计以及该机构的运动仿真分析摘要四连杆机构因其结构方便灵活,能够传递动力并实现多种运动形式而被广泛应用于各个领域,因此对其进行运动分析具有重要的意义。
传统的分析方法主要应用几何综合法和解析综合法,几何综合法简单直观,但是精确度较低;解析法精确度较高,但是计算工作量大。
随着计算机辅助数值解法的发展,特别是MATLAB软件的引入,解析法已经得到了广泛的应用。
对于四连杆的运动分析，若应用MATLAB 则需要大量的编程，因此我们引入proe软件，我们不仅可以在此软件中建立实物图，而且还可以对其进行运动仿真并对其运动分析。
在设计四连杆时，我们利用解析综合法建立数学模型，再根据数学模型在MATLAB中编程可以求得其他杆件的长度。
针对范例中所求得的各连杆的长度，我们在proe软件中画出其三维图（如图4）并在proe软件中进行仿真分析得出CB,的角加速度的变化，从而得到CB,两接触处所受到的力是成周期性变化的，可以看出CB,两点处的疲劳断裂，我们提B,两点处极易疲劳断裂，针对C出了在设计四连杆中的一些建议。
关键字：解析法 MATLAB 软件 proe 软件 运动仿真建立用解析法设计平面四杆机构模型对于问题中所给出的连架杆AB 的三个位置与连架杆CD 的三个位置相对应，即三组对应位置为：332211,,,,,ψϕψϕψϕ，其中他们对应的值分别为： 52,45,82,90,112,135，为了便于写代数式，可作出AB 与CD 对应的关系，其图如下：图—2 AB 与CD 三个位置对应的关系通过上图我们可以通过建立平面直角坐标系并利用解析法来求解，其直角坐标系图如下：φααi θi φi图—3 平面机构直角坐标系通过建立直角坐标系OXY ，如上图所示，其中0α与0φ为AB 杆与CD 杆的初始角，各杆件的长度分别用矢量d c b a ,,,,表示，将各矢量分别在X 轴与Y 轴上投影的方程为⎩⎨⎧=++=+)sin(*)sin(*)sin(*)cos(*)cos(*)cos(*φθαφθαc b a c d b a在上述的方程中我们可以消除θ，从而可以得到α与φ之间的关系如下：)cos(2)cos(2)cos(2)(2222αφαφab ac cd b d c a +-=+-++ (1) 为便于化简以及matlab 编程我们可以令：⎪⎪⎪⎩⎪⎪⎪⎨⎧==-++=c d H a d H ac b d c a H 32222212 (2) 通过将（2）式代入（1）式中则可以化简得到如下等式： )cos()cos()cos(321αφαφH H H +-=+ （3）我们可以通过（3）式将两连架杆对应的位置带入（3）式中，我们可以得到如下方程：⎪⎩⎪⎨⎧+-=++-=++-=+)cos()cos()cos()cos()cos()cos()cos()cos()cos(333332123222211311121ϕψϕψϕψϕψϕψϕψH H H H H H H H H （4） 联立（4）方程组我们可以求得321,,H H H ，再根据（2）中的条件以及所给定的机架d 的长度，我们可以求出其它杆件的长度为：⎪⎪⎪⎩⎪⎪⎪⎨⎧-++===1222322acH d c a b H d c H d a （5）四连杆设计范例：在日常生活中，我们经常看到消防门总能自动关上，其实它是利用四连杆机构与弹簧组成的。
构件上点的运动分析函数文件（m文件）格式：function [ 输出参数] = 函数名（输入参数）p_crank.m function [p_Nx,p_Ny]=p_crank(Ax,Ay,theta,phi,l1)v_crank.m function [v_Nx,v_Ny]=v_crank(l1,v_Ax,v_Ay,omiga,theta,phi)a_crank.m function [a_Nx,a_Ny]=a_crank(l1,a_Ax,a_Ay,alpha,omiga,theta,phi)函数中的符号说明函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）p_RRR.m function [cx,cy,theta2,theta3]=p_RRR(bx,by,dx,dy,l2,l3,m)v_RRR.m function [vcx,vcy,omiga2,omiga3]=v_RRR(vbx,vby,vdx,vdy,cx,cy,bx,by,dx,dy)a_RRR.m function [acx,acy,alpha2,alpha3]=a_RRR(abx,aby,adx,ady,cx,cy,bx,by,dx,dy,omiga2,omiga3)函数中的符号说明m =1 m = -1RRR Ⅱ级杆组运动分析函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）p_RRP.m function [cx,cy,sr,theta2]=p_RRP(bx,by,px,py,theta3,l2,m)v_RRP.m function [vcx,vcy,vr,omiga2]=v_RRP(bx,by,cx,cy,vbx,vby,vpx,vpy,theta2,theta3,l2,sr,omiga3) a_RRP.m function [acx,acy,ar,alpha2]=a_RRP(bx,by,cx,cy,px,py,abx,aby,apx,apy,theta3,vr,omiga2,omiga3,alpha3)函数中的符号说明1 1∠BCP < 90︒，∠BC 'P > 90︒，m =1RRP Ⅱ级杆组运动分析函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）p_RPR.m function [dx,dy,sr,theta3]=p_RPR(bx,by,cx,cy,e,l3,m)v_RPR.m function [vdx,vdy,omiga3,vr]=v_RPR(bx,by,cx,cy,dx,dy,vcx,vcy,vbx,vby,theta3) a_RPR.m function [adx,ady,alpha3,ar]=a_RPR(bx,by,cx,cy,dx,dy,acx,acy,abx,aby,vr,omiga3,theta3)RPR Ⅱ级杆组运动分析实线位置，m =1 虚线位置，m = -1函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）F_RRR.m function [R12x,R12y,R23x,R23y,R34x,R34y]=F_RRR(bxy,cxy,dxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,as2,as3,alpha2,alpha3)RRR Ⅱ级杆组力分析R 23xF 2R F 3xR 23函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）F_RRP.m function [R12x,R12y,R23x,R23y,R34x,R34y,lcn]=F_RRP(bxy,cxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,theta3,as2,as3,alpha2,alph3)RRP Ⅱ级杆组力分析R 34函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）F_RPR.m function [R12x,R12y,R23x,R23y,R35x,R35y,lcn]=F_RRP(bxy,cxy,dxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,R34,theta3,as2,as3,alpha3)RPR Ⅱ级杆组力分析238. 作用有平衡力的构件力分析作用有平衡力的构件力分析函数文件（m文件）格式：function [ 输出参数] = 函数名（输入参数）F_Bar.m function [R01x,R01y,Mb]=F_Bar(axy,bxy,s1,m1,Js1,M1,F1,R12,as1,alpha1)函数中的符号说明9. 平面连杆机构运动分析算例例1图示曲柄摇杆机构，已知l 1=150mm ，l 2=220mm ，l 3=250mm ，l 4=300mm ，曲柄以n 1=100r/min 逆时针匀速转动，分析该机构的运动。
在MATLAB环境下开发平面连杆机构运动分析系统摘要建立了铰链四杆机构运动分析的数学模型 ,以MATLAB程序设计语言为平台 ,将参数化设计与交互式相结合 ,设计了铰链四杆机构分析软件 ,该软件具有方便用户的良好界面 ,并给出界面设计程序 ,从而使机构分析更加方便、快捷、直观和形象.设计者只需输入参数就可得到分析结果 ,再将运行结果与设计要求相比较 ,对怎样修改设计做出决策.它为四杆机构设计提供了一种实用的软件与方法.关键词：平面四杆机构，MATLAB软件，运动分析，分析THE DEVELOPMENT OF SYSTEM FOR ANALYSIS OF MOTION IN PLANE FOUR BAR MECHANISM BASED ONMATLAB SOFTWAREAbstractA mathematical model of motion analysis was established in planefour - linkage , and analytical software was developed. The software adopted Matlab as a design language. It combined parametric design with interactive design and as input parameters was imported and the devisers can make decision - making of modification by the comparing analytical result with design demand. It provides an applied software and method for linkage.Key words:Plane Four Bar Mechanism, MATLAB, Analysis of Motion, Analyze目录1 绪论 (1)2 平面连杆机构的设计分析 (4)2.1平面四连杆机构的运动分析 (4)2.2 机构的数学模型的建立 (4)2.2.1 建立机构的闭环矢量位臵方程 (5)2.2.2 求解方法 (7)3 基于MATLAB程序设计 (8)3.1 程序流程 (8)3.2M文件编写 (8)3.3程序运行结果输出 (12)4 基于MATLAB图形界面设计 (23)4.1界面设计 (23)4.2代码设计 (24)5 结论.......................................................................................... 错误！未定义书签。
一、课程设计容及要求：1．对连杆机构运动工作原理及运动参数有一定理解2．掌握MATLAB基本命令3．了解MATLAB编程的基本知识，并能编写简单M文件4．了解MATLAB图形界面设计的基本知识5．课程设计说明书：应阐述整个课程设计容，要突出重点和特色，图文并茂，文字通畅。
应有目录、摘要及关键词、正文、参考文献等容，字数一般不少于6000字。
二、主要参考资料有关复杂刀具参数计算及结构设计、机械制造工艺与设备的手册与图册。
三、课程设计进度安排指导教师（签名）：时间：教研室主任(签名)：时间：院长（签名）：时间：目录1平面连杆机构的运动分析 (1)1.1 机构运动分析的任务、目的和方法 (1)1.2 机构的工作原理 (1)1.3 机构的数学模型的建立 (1)1.3.1建立机构的闭环矢量位置方程 (1)1.3.2求解方法 (2)2 基于MATLAB程序设计 (4)2.1 程序流程图 (4)2.2 M文件编写 (6)2.3 程序运行结果输出 (7)3 基于MATLAB图形界面设计 (11)3.1界面设计 (11)3.2代码设计 (12)4 小结 (17)参考文献 (18)1平面连杆机构的运动分析1.1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构，它可以用来实现转动和摆动之间运动形式的转换或传递动力。
对四杆机构进行运动分析的意义是：在机构尺寸参数已知的情况下，假定主动件（曲柄）做匀速转动，撇开力的作用，仅从运动几何关系上分析从动件（连杆、摇杆）的角位移、角速度、角加速度等运动参数的变化情况。
还可以根据机构闭环矢量方程计算从动件的位移偏差。
上述这些容，无论是设计新的机械，还是为了了解现有机械的运动性能，都是十分必要的，而且它还是研究机械运动性能和动力性能提供必要的依据。
机构运动分析的方法很多，主要有图解法和解析法。
当需要简捷直观地了解机构的某个或某几个位置的运动特性时，采用图解法比较方便，而且精度也能满足实际问题的要求。
matlab 中m 文件里面的参数-概述说明以及解释1.引言1.1 概述概述部分：参数在Matlab中的M文件中起着重要的作用，它们是用来传递数值、变量或是一些特定的设置给函数或脚本的。
通过使用参数，我们可以为M 文件提供灵活性和可重用性，使得代码更加可配置和可扩展。
在M文件中，参数通常用来控制特定的行为或计算过程。
通过在函数或脚本定义时声明参数，并在调用函数或执行脚本时提供相应的数值或变量，我们可以根据实际需求来调整程序的行为。
参数的设置可以灵活地改变程序的输出结果，提高了代码的可定制性和适用性。
在本文中，我们将详细介绍M文件中参数的定义和使用方法。
我们将探讨参数的常见用法和技巧，包括参数的类型、默认值的设定以及参数的传递方式等。
此外，我们还将探讨一些参数的优化与应用，以帮助读者理解参数在M文件中的重要性和使用价值。
通过对M文件中参数的深入研究，我们能够更好地理解和使用Matlab的函数和脚本。
参数的合理设置不仅能够提高代码的执行效率和准确性，也能够使代码更易读、易维护和易扩展。
因此，理解参数在M文件中的作用和用法对于编写高效、优质的Matlab代码至关重要。
在下一节中，我们将详细介绍M文件及其作用，以帮助读者更好地理解参数在M文件中的使用环境和背景。
请继续阅读下一节内容。
文章结构部分的内容如下：1.2 文章结构本篇文章主要围绕着matlab 中m 文件中的参数展开讨论。
文章分为引言、正文和结论三个部分。
在引言部分，我们首先对文章的主题进行了概述，说明了本文将要讨论的问题和目的。
接着介绍了文章的结构，明确了各个部分的内容和顺序。
最后，对整篇文章进行了总结，给出了一个简要的概括。
在正文部分，我们详细讨论了matlab 中的M 文件及其作用。
我们解释了M 文件的含义和作用，介绍了其在matlab 编程中的重要性。
然后，我们重点关注了M 文件中的参数定义，解释了参数的概念和用途。
接着我们详细阐述了在M 文件中参数的使用方法，包括如何定义参数、如何传递参数以及如何在程序中使用参数。
第三章四連桿之MATLAB程式第三章中之四連桿分析可以參考相關資料。
本節則針對四連桿之動作程式加以說明。
目前所設計之程式有f4bar.m、drawlinks.m、fb_angle_limits.m、drawlimits.m 等四個程式，茲分別說明如下：圖一、四連桿之關係位置及各桿名稱一、f4bar函數：f4bar函數之呼叫格式如下：function [values,form] = f4bar(r,theta1,theta2,td2,tdd2,sigma,driver)輸入變數：.r(1:4) = 各桿之長度，r(1)為固定桿，其餘分別為曲桿、結合桿及被動桿。
.theta1 = 第一桿之水平角，或為四連桿之架構角，以角度表示。
.theta2 = 驅動桿之水平夾角，以角度表示。
一般為曲桿角，但若為結合桿驅動，則為結合桿之水平夾角。
.td2 = 驅動桿(第二桿或第三桿)之角速度(rad/sec)。
.tdd2 = 驅動桿(第二桿或第三桿)之角加速度(rad/sec^2)。
.sigma = +1 or -1. 組合模式，負值表示閉合型，正值為分支型，但有時需視實際情況而定。
.driver = 0 (驅動桿為第二桿); 1 (驅動桿為第三桿)輸出變數：.form = 組合狀態，0 ：表示無法組合；1：可以正確組合.values = 輸出矩陣，其大小為 4 X 7，各行之資料分配如下：其中第一行之連桿位置向量，屬於單桿的位置向量。
第二行為各桿之水平夾角，第三及第四行為各桿之角度速度及角加速度。
第五至七行則為P點與Q點之速度與加速度量，第五行為向量，第六行為絕對量，第七行為夾角。
值得一提的是第一行、三行、四行及五行之向量表示法屬於複數之型式。
故若要得到其絕對值僅需在MATLAB指令檔中，以abs()這一個函數指令即可求得，而以函數angle()則可求得其夾角，雖然第二行與第七行之輸出亦有相對應之夾角。
例一：為第二桿為驅動桿[val,form]=f4bar([3 2 4 2],0,60,10,0,-1,0)val = Columns 1 through 33 0 01 + 1.7321i 60 103.8682 - 1.0182i -14.7465.40781.8682 + 0.71389i 20.913 16.549 Columns 4 through 60 1 + 1.7321i 20 1.8682 + 0.71389i 2-127.58 173.21 - 100i 200-236.27 364.19 - 953.09i 1020.3 Column 76020.913-30-69.087form = 1 (表示可以組合)本例中，有框線者表示其為輸入值。
格式：格式：，格式：3x8. 作用有平衡力的构件力分析9. 平面连杆机构运动分析算例例1图示曲柄摇杆机构，已知l 1=150mm ，l 2=220mm ，l 3=250mm% % % % 绘制运动线图 theta1=theta1*180/pi; figure(1) subplot(3,1,1);plot(theta1,cx,'-',theta1,cy,':r'),grid on xlabel('曲柄转角( ° )');ylabel('位移(mm/s)'); legend('C 点x 方向位移','C 点y 方向位移');subplot(3,1,2);plot(theta1,vcx,'-',theta1,vcy,':r'),grid onxlabel('曲柄转角( ° )');ylabel('速度(mm/s)');legend('C点x方向速度','C点y方向速度');subplot(3,1,3);plot(theta1,acx,'-',theta1,acy,':r'),grid onxlabel('曲柄转角( ° )');ylabel('加速度(mm/s^2)'); legend('C点x方向加速度','C点y方向加速度'); figure(2)subplot(2,1,1);plot(theta1,theta3*180/pi),grid onxlabel('曲柄转角( ° )');ylabel('摇杆角位移( ° )'); subplot(2,1,2);plot(theta1,omiga3),grid onxlabel('曲柄转角( ° )');ylabel('摇杆角速度(rad/s)'); subplot(2,1,3);plot(theta1,alpha3),grid onxlabel('曲柄转角( ° )');ylabel('摇杆角加速度(/rad/s^2)');例2 图示曲柄滑块机构，已知l 1=150mm ，l 2=150mm ，e =25mm ，曲柄以n 1=955r/min 逆时针匀速转动，分析该机构的运动。
主程序% 曲柄滑块机构运动分析 clc,clearl1=50;% 曲柄长度 l2=150;% 连杆长度 e=25;% 偏距 n=955;% 曲柄转速m=1;% RRP II 级杆组装配模式系数omiga1=2*pi*n/60;alpha1=0;% 曲柄角速度、角加速度ax=0;ay=e;vax=0;vay=0;aax=0;aay=0;% A 点位置、速度、及速度 px=0;py=0;% 滑块导路上一定点（选为O 点）的坐标 vpx=0;vpy=0;apx=0;apy=0;% 滑块导路上一定点的速度、加速度 theta3=0;omiga3=0;alpha3=0;% 滑块导路角位置、角速度、角加速度 phi=0;% 曲柄的结构参数theta1=0:30:360;% 曲柄转角(每隔10°计算一次) theta1=theta1*pi/180;% 调用crank 函数，计算B 点运动参数 [bx,by]=p_crank(ax,ay,theta1,phi,l1);[vbx,vby]=v_crank(l1,vax,vay,omiga1,theta1,phi); [abx,aby]=a_crank(l1,aax,aay,alpha1,omiga1,theta1,phi); % 调用RRP 函数，计算BC 杆和滑块的运动参数 [cx,cy,sr,theta2]=p_RRP(bx,by,px,py,theta3,l2,m);[vcx,vcy,vr,omiga2]=v_RRP(bx,by,cx,cy,vbx,vby,vpx,vpy,theta2,theta3,l2,sr,omiga3); [acx,acy,ar,alpha2]=a_RRP(bx,by,cx,cy,px,py,abx,aby,apx,apy,theta3,vr,omiga2,omiga3,alpha3); % 绘制运动线图crankx=l1.*cos(theta1);cranky=e+l1.*sin(theta1); theta1=theta1*180/pi; figure(1) subplot(3,1,1); plot(theta1,cx,'r'),grid onxlabel('曲柄转角( ° )');ylabel('滑块位移(mm/s)');曲柄滑块机构subplot(3,1,2);plot(theta1,vcx,'r'),grid onxlabel('曲柄转角( °)');ylabel('滑块速度(mm/s)'); subplot(3,1,3);plot(theta1,acx,'r'),grid onxlabel('曲柄转角( °)');ylabel('滑块加速度(mm/s^2)');例3=840mmlCDe=0;%%%%plot(theta1,theta3*180/pi,'r'),grid onxlabel('曲柄转角( ° )');ylabel('摇杆角位移( ° )');subplot(3,1,2);plot(theta1,omiga3,'r'),grid onxlabel('曲柄转角( ° )');ylabel('摇杆角速度(rad/s)');subplot(3,1,3);plot(theta1,alpha3,'r'),grid onxlabel('曲柄转角( ° )');ylabel('摇杆角加速度(rad/s^2)');例4 图示六杆机构，已知l AB =80mm ，l BC =260mm ，l DE =400mmH 2=170mm 滑块5% e=0;% % % % [ex,ey]=p_crank(dx,dy,theta3,phi2,l31);[vex,vey]=v_crank(l31,vdx,vdy,omiga3,theta3,phi2); [aex,aey]=a_crank(l31,adx,ady,alpha3,omiga3,theta3,phi2); % 调用RRP 函数，计算F 点运动参数 [fx,fy,sr,theta4]=p_RRP(ex,ey,px,py,theta5,l4,m2);[vfx,vfy,vr,omiga4]=v_RRP(ex,ey,fx,fy,vex,vey,vpx,vpy,theta4,theta5,l4,sr,omiga5); [afx,afy,ar,alpha4]=a_RRP(ex,ey,fx,fy,px,py,aex,aey,apx,apy,theta4,vr,omiga4,omiga5,alpha5);% 绘制运动线图theta1=theta1*180/pi;subplot(3,1,1);plot(theta1,sr,'r'),grid onxlabel('曲柄转角( ° )');ylabel('滑块5位移(mm)'); subplot(3,1,2);plot(theta1,vr,'r'),grid onxlabel('曲柄转角( ° )');ylabel('滑块5速度(mm/s)'); subplot(3,1,3);plot(theta1,ar,'r'),grid onxlabel('曲柄转角( ° )');ylabel('滑块5加速度(mm/s^2)');10.平面连杆机构力分析算例H=0.65 m构件质量m4构件1%e=0;%omiga1=pi*n1/30;alpha1=0;% 曲柄角速度、角加速度% 曲柄AB的运动参数theta1=0:10:360; 曲柄转角(每隔10°计算一次)theta1=theta1*pi/180;% 调用crank函数，计算B点运动参数[bx,by]=p_crank(ax,ay,theta1,phi,lab);[vbx,vby]=v_crank(lab,vax,vay,omiga1,theta1,phi);[abx,aby]=a_crank(lab,aax,aay,alpha1,omiga1,theta1,phi);% 调用RPR函数，计算CD杆和D点运动参数[dx,dy,sr3,theta3]=p_RPR(cx,cy,bx,by,e,lcd,m1);[vdx,vdy,omiga3,vr3]=v_RPR(cx,cy,bx,by,dx,dy,vbx,vby,vcx,vcy,theta3);[adx,ady,alpha3,ar3]=a_RPR(cx,cy,bx,by,dx,dy,abx,aby,acx,acy,vr3,omiga3,theta3);% 调用RRP函数，计算E点运动参数[ex,ey,sr,theta4]=p_RRP(dx,dy,px,py,theta5,lde,m2);[vex,vey,vr,omiga4]=v_RRP(dx,dy,ex,ey,vdx,vdy,vpx,vpy,theta4,theta5,lde,sr,omiga5); [aex,aey,ar,alpha4]=a_RRP(dx,dy,ex,ey,px,py,adx,ady,apx,apy,theta5,vr,omiga4,omiga5,alpha5); % 调用crank函数，计算CD杆和DE杆质心点的运动参数[s3x,s3y]=p_crank(dx,dy,theta3,phi,lcd/2);[vs3x,vs3y]=v_crank(lcd/2,vcx,vcy,omiga3,theta3,phi);[as3x,as3y]=a_crank(lcd/2,acx,acy,alpha3,omiga3,theta3,phi);[s4x,s4y]=p_crank(dx,dy,theta4,phi,lcd/2);[vs4x,vs4y]=v_crank(lcd/2,vdx,vdy,omiga4,theta4,phi);[as4x,as4y]=a_crank(lcd/2,adx,ady,alpha4,omiga4,theta4,phi);% 力参数m1=0;m2=0;m3=20;m4=15;m5=62;% 各构件质量Js1=0;Js2=0;Js3=0.11;Js4=0.18;Js5=0;% 各构件绕其质心的转动惯量M1=0;M2=0;M3=0;M4=0;M5=0;% 作用于构件1、2、3、4、5的主矩F1=[0,0];F2=[0,0];F3=[0,0];F4=[0,0];% 作用于构件1、2、3、4的主矢fr=110;fr5=(omiga3>0)*fr;% 生产阻力for i=1:length(theta1)F5=[fr5(i),0];% 作用于构件5的主矢% 力分析% 调用RRP II级杆组力分析函数，计算运动副D、E中的约束反力[R34x(i),R34y(i),R45x(i),R45y(i),R56x(i),R56y(i),lcn]=F_RRP([dx(i),dy(i)],[ex(i),ey(i)],...[s4x(i),s4y(i)],[ex(i),ey(i)],m4,m5,Js4,Js5,M4,M5,F4,F5,theta5,...[as4x(i),as4y(i)],[aex(i),aey(i)],alpha4(i),alpha5);% 调用RPR II级杆组力分析函数，计算运动副B、C中的约束反力[R12x(i),R12y(i),R23x(i),R23y(i),R36x(i),R36y(i),lcn(i)]=F_RPR([cx,cy],[bx(i),by(i)],...[dx(i),dy(i)],[bx(i),by(i)],[s3x(i),s3y(i)],m2,m3,Js2,Js3,M2,M3,F2,F3,...[R34x(i),R34y(i)],theta3(i),[abx(i),aby(i)],[as3x(i),as3y(i)],alpha3(i));% 调用单杆力分析函数，计算运动副A中的约束反力及平衡力矩[R16x(i),R16y(i),Mb(i)]=F_Bar([ax,ay],[bx(i),by(i)],s1,m1,Js1,M1,F1,...[R12x(i),R12y(i)],as1,alpha1);endtheta1=theta1*180/pi;figure(1)subplot(3,1,1)plot(theta1,sr),grid onxlabel('曲柄转角（°）');ylabel('滑块位移（m）');subplot(3,1,2)plot(theta1,vr),grid onxlabel('曲柄转角（°）');ylabel('滑块速度（m/s）');subplot(3,1,3)plot(theta1,ar),grid onxlabel('曲柄转角（°）');ylabel('滑块加速度（m/s^2）');figure(2)plot(theta1,Mb),grid onxlabel('曲柄转角（°）');ylabel('平衡力矩（N.m）');。
