人教版七年级数学下册第六章实数知识点汇总(最新整理)

人教版七年级下册第六章实数知识点
实数是数学中最基本的概念之一，是指可以用数字表示的所有数。

实数由有理数和无理数两部分组成。

有理数是可以表示成两个整数之比的数，包括整数、分数、小数等，而无理数则不能表示成有理数的形式，如圆周率π、自然对数的底数e等。

在七年级数学下册第六章中，我们将学习实数的相关知识，包括实数的分类、实数的运算、实数的比较等。

一、实数的分类
1.有理数：有理数包括正整数、负整数、零、正分数、负分数和整数。

2.无理数：无理数是不能表示成有理数的形式的数，它们包括无限不循环小数和根号下无理数等。

二、实数的运算
1.加法：实数的加法满足交换律、结合律和分配律。

2.减法：实数的减法可以转化成加法，即a-b=a+(-b)。

3.乘法：实数的乘法满足交换律、结合律和分配律。

4.除法：实数的除法可以转化成乘法，即a÷b=a×(1/b)，其中b≠0。

5.乘方：实数的乘方表示数的自我乘积，即a的n次幂表示为an。

三、实数的比较
1.正数比较大小：正数比较大小时，数值越大的数越大。

2.负数比较大小：负数比较大小时，数值越小的数越大。

3.正数和负数比较大小：正数比负数大。

4.零和正数、负数比较大小：零比负数大，比正数小。

5.一般实数比较大小：需要将实数转化成同一种形式再比较大小。

以上就是七年级数学下册第六章实数知识点的简单介绍，希望对大家有所帮助。

在学习实数时，我们需要多做练习，多思考，才能真正掌握实数的相关知识。

第六章 实数主要知识点6.1 平方根1、平方根（1）平方根的定义：如果一个数x 的平方等于a ，那么这个数x 就叫做a 的平方根．即：如果a x =2，那么x 叫做a 的平方根．（2）开平方的定义：求一个数的平方根的运算，叫做开平方．开平方运算的被开方数必须是非负数才有意义。

（3）平方与开平方互为逆运算：±3的平方等于9，9的平方根是±3（4）一个正数有两个平方根，即正数进行开平方运算有两个结果；一个负数没有平方根，即负数不能进行开平方运算；0的平方根是0.（5）符号：正数a 的正的平方根可用a 表示，a 也是a 的算术平方根；正数a 的负的平方根可用-a 表示．（6）a x =2 <—> a x ±=a 是x 的平方 x 的平方是ax 是a 的平方根(除0外，x 的值一正一负互为相反数)a 的平方根是x(除0外，x 的值一正一负互为相反数)2、算术平方根（1）算术平方根的定义： 一般地，如果一个正数x 的平方等于a ，即a x =2，那么这个正数x 叫做a 的算术平方根．a 的算术平方根记为a ，读作“根号a”，a 叫做被开方数．规定：0的算术平方根是0.也就是，在等式a x =2 (x≥0)中，规定a x =。

（2）a 的结果有两种情况：当a 是完全平方数时，a 是一个有限数；当a 不是一个完全平方数时，a 是一个无限不循环小数。

（3）当被开方数扩大时，它的算术平方根也扩大；当被开方数缩小时与它的算术平方根也缩小。

（4）夹值法及估计一个（无理）数的大小（5）a x =2 (x≥0) <—> a x =a 是x 的平方 x 的平方是ax 是a 的算术平方根(x 的取值为非负数) a 的算术平方根是x(x 的取值为非负数)（6）正数和零的算术平方根都只有一个，零的算术平方根是零。

a （a ≥0） 0≥a==a a 2 ；注意a 的双重非负性：-a （a <0） a ≥0（7）平方根和算术平方根两者既有区别又有联系：区别在于正数的平方根有两个，而它的算术平方根只有一个；联系在于正数的正平方根就是它的算术平方根，而正数的负平方根是它的算术平方根的相反数。

人教版七年级数学下册第六章实数知识点汇总【知识点一】实数的分类1、按定义分类： 2.按性质符号分类：注：0既不是正数也不是负数.【知识点二】实数的相关概念1.相反数(1)代数意义：只有符号不同的两个数，我们说其中一个是另一个的相反数． 0 的相反数是 0.(2)几何意义：在数轴上原点的两侧，与原点距离相等的两个点表示的两个数互为相反数，或数轴上，互为相反数的两个数所对应的点关于原点对称 .(3) 互为相反数的两个数之和等于0.a、 b 互为相反数a+b=0.2.绝对值|a| ≥0．3.倒数（ 1） 0 没有倒数 (2) 乘积是 1 的两个数互为倒数． a、 b 互为倒数 .▲▲ 平方根【知识要点】1.算术平方根：正数 a 的正的平方根叫做 a 的算术平方根，记作“a”。

2.如果 x2=a，则 x 叫做 a 的平方根，记作“± a”（a称为被开方数）。

3. 正数的平方根有两个，它们互为相反数；0 的平方根是0；负数没有平方根。

4.平方根和算术平方根的区别与联系：区别：正数的平方根有两个，而它的算术平方根只有一个。

联系：（ 1）被开方数必须都为非负数；（ 2）正数的负平方根是它的算术平方根的相反数，根据它的算术平方根可以立即写出它的负平方根。

（ 3）0 的算术平方根与平方根同为 0。

5.如果 x3=a，则 x 叫做 a 的立方根，记作“3 a”（ a 称为被开方数）。

6.正数有一个正的立方根； 0 的立方根是 0；负数有一个负的立方根。

7.求一个数的平方根（立方根）的运算叫开平方（开立方）。

8.立方根与平方根的区别：一个数只有一个立方根，并且符号与这个数一致；只有正数和0有平方根，负数没有平方根，正数的平方根有 2 个，并且互为相反数，0 的平方根只有一个且为0.9.一般来说，被开放数扩大（或缩小）n 倍，算术平方根扩大（或缩小） n 倍，例如25 5, 2500 50.10.平方表：（自行完成）222221 = 6 =11 =16 =21 =22=72=122=172=222=32=82=132=182=232=42=92=142=192=242=52=102=152=202=252=题型规律总结：1、平方根是其本身的数是0；算术平方根是其本身的数是0 和 1；立方根是其本身的数是0 和±1。

人教版七年级数学下册第六章实数知识点汇总【知识点一】实数的分类 1、按定义分类： 2.按性质符号分类：注：0既不是正数也不是负数.【知识点二】实数的相关概念1.相反数(1)代数意义：只有符号不同的两个数，我们说其中一个是另一个的相反数．0的相反数是0.(2)几何意义：在数轴上原点的两侧，与原点距离相等的两个点表示的两个数互为相反数，或数轴上，互为相反数的两个数所对应的点关于原点对称.(3)互为相反数的两个数之和等于0.a、b互为相反数a+b=0.2.绝对值|a|≥0．3.倒数（1）0没有倒数(2)乘积是1的两个数互为倒数．a、b互为倒数.▲▲平方根【知识要点】1.算术平方根：正数a的正的平方根叫做a的算术平方根，记作“a”。

2. 如果x2=a，则x叫做a的平方根，记作“±a”（a称为被开方数）。

3. 正数的平方根有两个，它们互为相反数；0的平方根是0；负数没有平方根。

4. 平方根和算术平方根的区别与联系：区别：正数的平方根有两个，而它的算术平方根只有一个。

联系：（1）被开方数必须都为非负数；（2）正数的负平方根是它的算术平方根的相反数，根据它的算术平方根可以立即写出它的负平方根。

（3）0的算术平方根与平方根同为0。

5. 如果x3=a，则x叫做a的立方根，记作“3a”（a称为被开方数）。

6. 正数有一个正的立方根；0的立方根是0；负数有一个负的立方根。

7. 求一个数的平方根（立方根）的运算叫开平方（开立方）。

8.立方根与平方根的区别：一个数只有一个立方根，并且符号与这个数一致；只有正数和0有平方根，负数没有平方根，正数的平方根有2个，并且互为相反数，0的平方根只有一个且为0.9. 一般来说，被开放数扩大（或缩小）n倍，算术平方根扩大（或缩小）n倍，例如502500,525==.10.平方表：（自行完成）____________________________________________________________________________________________________题型规律总结：1、平方根是其本身的数是0；算术平方根是其本身的数是0和1；立方根是其本身的数是0和±1。

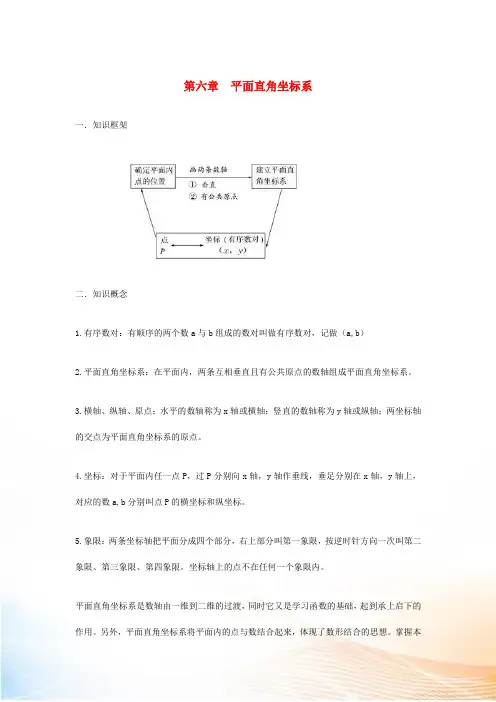
第六章平面直角坐标系
一．知识框架
二．知识概念
1.有序数对：有顺序的两个数a与b组成的数对叫做有序数对，记做（a,b）
2.平面直角坐标系：在平面内，两条互相垂直且有公共原点的数轴组成平面直角坐标系。

3.横轴、纵轴、原点：水平的数轴称为x轴或横轴；竖直的数轴称为y轴或纵轴；两坐标轴的交点为平面直角坐标系的原点。

4.坐标：对于平面内任一点P，过P分别向x轴，y轴作垂线，垂足分别在x轴，y轴上，对应的数a,b分别叫点P的横坐标和纵坐标。

5.象限：两条坐标轴把平面分成四个部分，右上部分叫第一象限，按逆时针方向一次叫第二象限、第三象限、第四象限。

坐标轴上的点不在任何一个象限内。

平面直角坐标系是数轴由一维到二维的过渡，同时它又是学习函数的基础，起到承上启下的作用。

另外，平面直角坐标系将平面内的点与数结合起来，体现了数形结合的思想。

掌握本
节内容对以后学习和生活有着积极的意义。

教师在讲授本章内容时应多从实际情形出发，通过对平面上的点的位置确定发展学生创新能力和应用意识。

第六章实数【知识点一】实数的分类1、按定义分类:【知识点二】实数的相关概念1・相反数(1) 代数意义：只有符号不同的两个数，我们说其中一个是另一个 的相反数。

0的相反数是Q 。

(2) 几何意义：在数轴上原点的两侧，与原点距离相箋的两个点表 示的两个数互为相反数，或数轴上，互为相反数的两个数所对应 的点关于原点对称。

(3) 互为相反数的两个数之和等于0。

若a 、b 互为相反数，则 a+b=0。

2.绝对值 |a|>0o 正数的绝对值等于它本身,负数的绝对值等于它的相反数,0的绝对值等于Q 。

3•倒数(1)0没有倒数(2)乘积是1的两个数互为倒数。

若a 、 有理数 厂正有理数L 负有理数 厂正无理数 L负无理数有限小数和无限循坏小数无限不循环小数 2、按性质符号分类: 厂正有理数 正实数三0 I 正无理数注：0既不是止数也不是负数.负实数 负有理数 负无理数b互为倒数则ab=l o4•平方根(1)如果一个数的平方等于a,这个数就叫做a的平方根.一个正数有两个平方根,它们互为相反数;0有一个平方根,它是0本身；负数没有平方根.a(a>0)的平方根记作土侖。

(2)—个正数a的正的平方根，叫做a的算术平方根。

0的算术平方根是0。

a(a>0)的算术平方根记作返。

5 •立方根如果x3=a,那么x叫做a的立方根.一个正数有二个正的立方根；一个负数有二个鱼的立方根；零的立方根是雯.a的立方根记作需。

如果两个被开方数互为相反数，则它们的立方根也互为相反数，反之亦然。

即有畅"扬。

【知识点三】实数与数轴数轴定义：规定了原点,正方向和单位长度的直线叫做数轴, 数轴的三要素缺一不可。

【知识点四】实数大小的比较1.对于数轴上的任意两个点，靠生边的点所表示的数较大。

2.正数都大于0,负数都小于0,两个正数，绝对值较大的那个正数大；两个负数，绝对值大的反而小.3•无理数的比较大小：对于开平方，被开方数越大，它的算术平方根越大。

人教版七年级下册第六章实数知识点在人教版七年级下册数学教材中，第六章是实数。

实数是数学中的基本概念之一，是包含有理数和无理数的数系。

在此章节中，我们将学习实数的定义、性质、大小比较、绝对值等基本概念，为以后的数学学习打下坚实的基础。

以下是本章的知识点和拓展内容：1. 实数的定义：实数是包括有理数和无理数的数系。

其中，有理数是可以表示为两个整数的比例，无理数则不能表示为有理数。

2. 实数的表示：实数可以用小数、分数、百分数等多种方式表示。

3. 科学计数法：科学计数法是一种用于表示极大数或极小数的方法，能够简化计算和阅读。

例如，1.23×10^5表示为123000，0.00005表示为5×10^-5。

4. 实数的大小比较：在实数中，有理数和无理数之间没有大小比较。

但是，有理数之间和无理数之间可以通过大小比较符号进行比较。

5. 绝对值：绝对值表示一个数的距离原点的距离，用符号“|x|”表示。

例如，|3|=3，|-5|=5。

绝对值有以下性质：①|a|≥0，且|a|=0当且仅当a=0；②|ab|=|a|×|b|；③|a+b|≤|a|+|b|。

6. 实数的运算：实数的运算包括加、减、乘、除等。

其中，加法和乘法满足交换律、结合律和分配律，减法和除法不满足交换律和结合律。

7. 小数的进位和舍位：小数进位和舍位是数学中的常见概念。

在小数的运算中，需要注意正确的进位和舍位方法。

以上是本章的基础知识点和拓展内容。

实数是数学中的基本概念之一，是学习高中数学的必备基础。

通过本章的学习，可以帮助学生建立正确的实数观念和解决实际问题的能力。

七年级数学（下）期末考前知识点总结（2）第六章 实数1.平方根的定义：定义：如果一个数的平方等于a ，这个数就叫做a 的平方根（或二次方根）。

即：如果x 2=a ，那么x 就叫做a 的平方根。

平方根的表示法：一个正数a 的正的平方根，用符号“a ±”表示，读作“正负根号a ”；正数a 的负平方根，表示为－a ，读作“负根号a ”。

正数、零、负数的平方根：正数a 的平方根有两个，它们互为相反数，可以表示为±a ；零的平方根有一个，仍是零；负数没有平方根；2.算术平方根：（1）定义：一个正数a 的正的平方根，叫做a 的算术平方根，记作a ；0的算术平方根是0（2）对a 的理解：①()2a =a ；②a ≥0（3）对记号a ，－a ，±a 的理解： ①a 表示非负数（a ≥0）； ②－a 表示a （a ≥0）的算术平方根的相反数； ③±a 表示a （a ≥0）的平方根； ④a <0时，a ，－a ，±a 都没有意义。

3. 立方根的概念：满足a x 3=的x 的值叫做a 的立方根2. 立方根的表示：数的立方根表示为，读作“三次根”或“立方根号”或“的立方根”a a a a a 3其中a 是被开方数，3是根指数说明：这里的根指数3不能省略，而平方根中的根指数一般省略不写。

3. 弄清立方根与平方根的区别与联系：区别：（1）定义不同：如果，那么叫做的平方根x a x a 2=，如果，那么叫做的立方根x a x a 3=（2）个数不同：一个正数有两个平方根，它们互为相反数， 而一个正数的立方根只有一个，且同样为正数（3）表示方法不同：正数的平方根表示为a a ±，正数的立方根表示为a a 3（4）取值范围不同：任何数都有立方根，并且有唯一的与其自身符号相同的立方根，但只有非负数才有平方根，负数没有平方根（5）逆运算不同：平方与开平方互为逆运算，立方与开立方互为逆运算联系：零的平方根与立方根都是零本身4. 立方根的性质：一个正数只有一个正的立方根；负数有一个负的立方根；零的立方根为零5. 开立方的概念：求一个数a 的立方根的运算叫做开立方，亦可以这样定义：求立方根号a ，叫做对a 开立方6. 用计算器求立方根：跟用计算器求平方根的方法一样，先阅读说明书，再根据说明书中所指明的步骤具体操作。

七年级下册数学第6章知识点归纳
【篇一：七年级下册数学第6章知识点归纳】
第六章实数一、知识定义： 1.算术平方根：正数a 的正的平方根叫做a 的算术平方根，记作“ 叫做a的平方根，记作“ 正数的平方根有两个，它们互为相反数（即和为0）；0的平方根是0；负数没有平方根。

平方根和算术平方根的区别与联系：区别：正数的平方根有两个，而它的算术平方根只有一个。

联系：（1）被开方数必须都为非负数；（2）正数的负平方根是它的算术平方根的相反数，根据它的算术平方根可以立即写出它的负平方根。

（3）0 的算术平方根与平方根同为0。

叫做a的立方根，记作“ 正数有一个正的立方根；0的立方根是0；负数有一个负的立方根。

——歌德96、君子赠人以言，庶人赠人以财。

——荀况97、受惠的人，必须把那恩惠常藏心底，但是施恩的人则不可记住它。

- 和1。

每一个正数都有两个互为相反数的平方根，其中正的那个是算术平方根；任何一个数都有唯一一个立方根，这个立方根的符号与原数相同。

有意义的条件是a0。

3、公式：( 取任何数）。

4、区分( 5、非负数的重要性质：若几个非负数之和等于0，则每一个非负数都为0（此性质应用很广，务必掌握）。

6、判断无理数的三种形式：（1）开方开不尽的数（2）无限不循环小数，（3）含有
【篇二：七年级下册数学第6章知识点归纳】。

人教版七年级下册第六章实数知识点
实数是数学中非常重要的一个概念，其涉及到数学中的各个领域。

在七年级下册的第六章中，我们主要学习了实数的相关知识。

1. 实数的概念
实数是指所有可以表示成有限小数、无限循环小数或无限不循环小数的数。

简单来说，实数包括整数、分数、小数、无理数等。

2. 实数的分类
根据实数的性质，可以将实数分为有理数和无理数两类。

有理数是可以表示成分数形式的实数，包括整数、分数和循环小数。

无理数是不能表示成分数形式的实数，例如根号2、π等。

3. 实数的运算
实数的运算包括加、减、乘、除四种基本运算。

对于任意两个实数a和b，它们的和、差、积、商分别为：
a+b，a-b，ab，a÷b（b≠0）
此外还有实数的乘方运算，即a的n次方（n为正整数），表示a 连乘n次的结果。

4. 实数的比较
实数之间可以进行大小比较。

对于任意两个实数a和b，若a>b，则a称为大于b，b称为小于a。

若a=b，则a与b相等。

若a<b，则a称为小于b，b称为大于a。

5. 实数的表示
实数可以用数轴上的点表示。

数轴是一条直线，上面的每个点都
与一个实数一一对应。

数轴上的原点表示0，向右表示正数，向左表示负数。

以上就是七年级下册第六章实数的相关知识点。

实数是数学中非常基础的概念，掌握好实数的相关知识对于后续的学习非常重要。

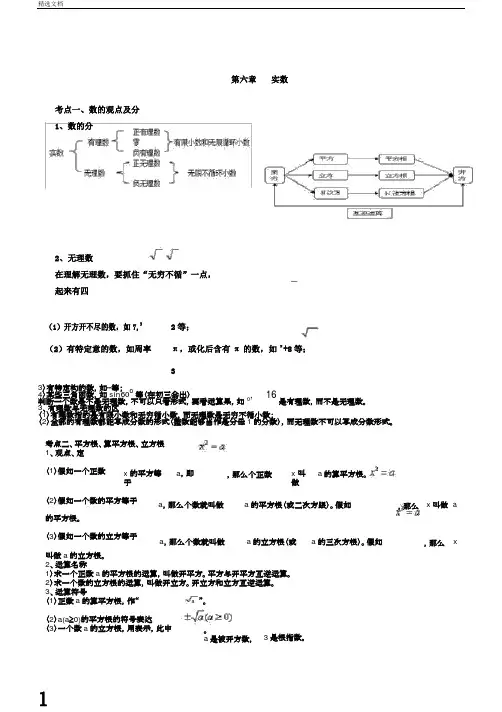
第六章实数考点一、数的观点及分1、数的分2、无理数在理解无理数，要抓住“无穷不循”一点，起来有四（1）开方开不尽的数，如7,32等；（2）有特定意的数，如周率π，或化后含有π的数，如π+8等；33）有特定构的数，如⋯等；4）某些三角函数，如sin60o等（在初三会出）判断一个数是不是无理数，不可以只看形式，要看运算果，如0,16是有理数，而不是无理数。

3、有理数与无理数的区（1）有理数指的是有限小数和无穷循小数，而无理数是无穷不循小数；（2）全部的有理数都能写成分数的形式（整数能够当作是分母1的分数），而无理数不可以写成分数形式。

考点二、平方根、算平方根、立方根1、观点、定（1）假如一个正数x的平方等于a，即，那么个正数x叫做a的算平方根。

（2）假如一个数的平方等于a，那么个数就叫做a的平方根（或二次方跟）。

假如，那么x叫做a 的平方根。

（3）假如一个数的立方等于a，那么个数就叫做a的立方根（或a的三次方根）。

假如，那么x 叫做a的立方根。

2、运算名称1）求一个正数a的平方根的运算，叫做开平方。

平方与开平方互逆运算。

2）求一个数的立方根的运算，叫做开立方。

开立方和立方互逆运算。

3、运算符号（1）正数a的算平方根，作“a”。

（2）a(a≥0)的平方根的符号表达（3）一个数a的立方根，用表示，此中。

a是被开方数，3是根指数。

4、运算公式4、开方规律小结（1）若a≥0，则a的平方根是a，a的算术平方根a；正数的平方根有两个，它们互为相反数，其中正的那个叫它的算术平方根；0的平方根和算术平方根都是0；负数没有平方根。

实数都有立方根，一个数的立方根有且只有一个，而且它的符号与被开方数的符号同样。

正数的立方根是正数，负数的立方根是负数，0的立方根是0。

（2）若a<0a为随意实数，则a的立方根是。

，则a没有平方根和算术平方根；若（3）正数的两个平方根互为相反数，两个互为相反数的实数的立方根也互为相反数。

1 实数 第6章 实数知识点
1．有理数，无理数概念：
有理数：任何有限小数和无限循环小数都是有理数。

无理数：无限不循环小数叫做无理数。

2．平方根和算术平方根的概念及其性质：
（1）概念：如果2x a =，那么x 是a
的平方根，记作：
a 的算术平方根。

（2）性质：①当a ≥0
0；当a
无意义；
②2＝a
a =。

（3）开平方：求一个数a 的平方根的运算，叫做开平方，期中a 叫做被开方数。

3．立方根的概念及其性质：
（1）概念：若3x a =，那么x 是a
（2
a =；
②3a =；
＝
（3）开立方：求一个数a 的立方根的运算，叫做开立方，期中a 叫做被开方数。

4．实数的概念及其分类：
（1）概念：实数是有理数和无理数的统称；
（2）分类：
a 按定义分
⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧无限不循环小数负无理数正无理数无理数数有限小数或无限循环小负分数负整数负有理数零正分数正整数正有理数有理数实数
b 按大小分:
⎪⎩
⎪⎨⎧负实数零正实数
在数轴上表示的两个实数,右边的数总比左边的数大.
5．与实数有关的概念：在实数范围内，相反数，倒数，绝对值的意义与有理数范围内的意义完全一致；在实数范围内，有理数的运算法则和运算律同样成立。

每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点都表示一个实数，即实数和数轴上的点是一一对应的。

因此，数轴正好可以被实数填满。

6．算术平方根的运算律：（a ≥0，b ≥0）；（a ≥0，b ＞0）
=。

人教版七年级数学下册第六章实数知识点汇总-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN人教版七年级数学下册第六章实数知识点汇总【知识点一】实数的分类1、按定义分类： 2.按性质符号分类：注：0既不是正数也不是负数. 【知识点二】实数的相关概念1.相反数(1)代数意义：只有符号不同的两个数，我们说其中一个是另一个的相反数．0的相反数是0.(2)几何意义：在数轴上原点的两侧，与原点距离相等的两个点表示的两个数互为相反数，或数轴上，互为相反数的两个数所对应的点关于原点对称.(3)互为相反数的两个数之和等于0.a、b互为相反数 a+b=0.2.绝对值|a|≥0．3.倒数（1）0没有倒数(2)乘积是1的两个数互为倒数．a、b互为倒数 .▲▲平方根【知识要点】1.算术平方根：正数a的正的平方根叫做a的算术平方根，记作“a”。

2. 如果x2=a，则x叫做a的平方根，记作“±a”（a称为被开方数）。

3. 正数的平方根有两个，它们互为相反数；0的平方根是0；负数没有平方根。

4. 平方根和算术平方根的区别与联系：区别：正数的平方根有两个，而它的算术平方根只有一个。

联系：（1）被开方数必须都为非负数；（2）正数的负平方根是它的算术平方根的相反数，根据它的算术平方根可以立即写出它的负平方根。

（3）0的算术平方根与平方根同为0。

5. 如果x3=a，则x叫做a的立方根，记作“a”（a称为被开方数）。

6. 正数有一个正的立方根；0的立方根是0；负数有一个负的立方根。

27. 求一个数的平方根（立方根）的运算叫开平方（开立方）。

8. 立方根与平方根的区别：一个数只有一个立方根，并且符号与这个数一致；只有正数和0有平方根，负数没有平方根，正数的平方根有2个，并且互为相反数，0的平方根只有一个且为0.9. 一般来说，被开放数扩大（或缩小）n倍，算术平方根扩大（或缩小）n倍，例如502500,525==.10.平方表：（自行完成）题型规律总结：1、平方根是其本身的数是0；算术平方根是其本身的数是0和1；立方根是其本身的数是0和±1。

初一数学知识点第六章 实数 知识点归纳一、实数的概念及分类 （3分）1、实数的分类 正有理数 有理数 零 有限小数和无限循环小数实数 负有理数正无理数无理数 无限不循环小数负无理数整数包括正整数、零、负整数。

正整数又叫自然数。

正整数、零、负整数、正分数、负分数统称为有理数。

2、无理数在理解无理数时，要抓住“无限不循环”这一时之，归纳起来有四类：（1）开方开不尽的数，如32,7等；（2）有特定结构的数，如0.1010010001…等；（3）有特定意义的数，如圆周率π，或化简后含有π的数，如3π+8等； 3. 实数与数轴上点的关系：实数与数轴上的点就是一一对应的，即每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点都是表示一个实数。

与有理数一样，对于数轴上的任意两个点，右边的点所表示的实数总比左边的点表示的实数大二、实数的倒数、相反数和绝对值 （3分）1、相反数从数轴上看，互为相反数的两个数所对应的点关于原点对称，如果a 与b 互为相反数，则有a+b=0，a=—b ，反之亦成立。

2、绝对值一个数的绝对值就是表示这个数的点与原点的距离，|a|≥0。

零的绝对值时它本身，若|a|=a ，则a ≥0；若|a|=-a ，则a ≤0。

正数大于零，负数小于零，正数大于一切负数，两个负数，绝对值大的反而小。

3、倒数如果a 与b 互为倒数，则有ab=1，反之亦成立。

倒数等于本身的数是1和-1。

零没有倒数。

4、 无限小数是有理数（×） 无限小数是无理数（×）有理数是无限小数（×） 无理数是无限小数（√）数轴上的点都可以用有理数表示（×） 有理数都可以由数轴上的点表示（√）数轴上的点都可以用无理数表示（×） 无理数都可以由数轴上的点表示（√）数轴上的点都可以用实数表示（√） 实数都可以由数轴上的点表示（√）三、平方根、算数平方根和立方根1、平方根如果一个数的平方等于a ，那么这个数就叫做a 的平方根（或二次方跟）。

人教版七年级数学下册第六章实数知识点汇总【知识点一】实数的分类1、按定义分类:2、按性质符号分类: 注:0既不就是正数也不就是负数、【知识点二】实数的相关概念1、相反数(1)代数意义:只有符号不同的两个数,我们说其中一个就是另一个的相反数.0的相反数就是0、(2)几何意义:在数轴上原点的两侧,与原点距离相等的两个点表示的两个数互为相反数,或数轴上,互为相反数的两个数所对应的点关于原点对称、(3)互为相反数的两个数之与等于0、a、b互为相反数a+b=0、2、绝对值|a|≥0.3、倒数(1)0没有倒数(2)乘积就是1的两个数互为倒数.a、b互为倒数、▲▲平方根【知识要点】1、算术平方根:正数a的正的平方根叫做a的算术平方根,记作“a”。

2、如果x2=a,则x叫做a的平方根,记作“±a”(a称为被开方数)。

3、正数的平方根有两个,它们互为相反数;0的平方根就是0;负数没有平方根。

4、平方根与算术平方根的区别与联系:区别:正数的平方根有两个,而它的算术平方根只有一个。

联系:(1)被开方数必须都为非负数;(2)正数的负平方根就是它的算术平方根的相反数,根据它的算术平方根可以立即写出它的负平方根。

(3)0的算术平方根与平方根同为0。

5、如果x3=a,则x叫做a的立方根,记作“3a”(a称为被开方数)。

6、正数有一个正的立方根;0的立方根就是0;负数有一个负的立方根。

7、求一个数的平方根(立方根)的运算叫开平方(开立方)。

8、立方根与平方根的区别:一个数只有一个立方根,并且符号与这个数一致;只有正数与0有平方根,负数没有平方根,正数的平方根有2个,并且互为相反数,0的平方根只有一个且为0、9、一般来说,被开放数扩大(或缩小)n倍,算术平方根扩大(或缩小)n 倍,例如502500,525==、10、平方表:(自行完成)题型规律总结:1、平方根就是其本身的数就是0;算术平方根就是其本身的数就是0与1;立方根就是其本身的数就是0与±1。

七年级下册数学第六章知识点总结七年级下册数学第六章知识点总结一、实数的概念及分类1、实数的分类正有理数有理数零有限小数和无限循环小数负有理数正无理数无理数无限不循环小数负无理数整数包括正整数、零、负整数。

正整数又叫自然数。

正整数、零、负整数、正分数、负分数统称为有理数。

2、无理数在理解无理数时，要抓住“无限不循环〞这一时之，归纳起来有四类：(1)开方开不尽的数，如7,2等;π(2)有特定意义的数，如圆周率π，或化简后含有π的数，如+8等; 3(3)有特定结构的数，如0.101101…等;二、实数的倒数、相反数和绝对值1、相反数实数与它的相反数时一对数(只有符号不同的两个数叫做互为相反数，零的相反数是零)，从数轴上看，互为相反数的两个数所对应的点关于原点对称，如果a与b互为相反数，则有a+b=0，a=—b，反之亦成立。

2、绝对值一个数的绝对值就是表示这个数的点与原点的距离，|a|≥0.零的绝对值时它本身，也可看成它的相反数，若|a|=a，则a≥0;若|a|=-a，则a≤0.正数大于零，负数小于零，正数大于一切负数，两个负数，绝对值大的反而小。

3、倒数如果a与b互为倒数，则有ab=1，反之亦成立。

倒数等于本身的数是1和-1.零没有倒数。

4. 实数与数轴上点的关系：每一个无理数都可以用数轴上的一个点表示出来，数轴上的点有些表示有理数，有些表示无理数，实数与数轴上的点就是一一对应的，即每一个实数都可以用数轴上的一个点来表示;反过来，数轴上的每一个点都是表示一个实数。

三、平方根、算数平方根和立方根1、平方根(1)平方根的定义：如果一个数x的平方等于a，那么这个数x 就叫做a的平方根.即：如果a，那么x叫做a的平方根.x2(2)开平方的定义：求一个数的平方根的运算，叫做开平方.开平方运算的被开方数必须是非负数才有意义。

33的平方等于9，9的平方根是(3)平方与开平方互为逆运算：(4)一个正数有两个平方根，即正数进行开平方运算有两个结果;一个负数没有平方根，即负数不能进行开平方运算(5)符号：正数a的正的平方根可用表示，也是a的算术平方根;正数a的负的平方根可用-表示.a2(6)x xa是x的平方 x的平方是ax是a的平方根 a的平方根是x2、算术平方根a，那么这个正数(1)算术平方根的定义：一般地，如果一个正数x的平方等于a，即x2x叫做a的算术平方根.a的算术平方根记为，读作“根号a〞，a叫做被开方数.规定：0的算术平方根是0.。