正交试验设计方法 讲义及举例
- 格式:doc
- 大小:181.50 KB
- 文档页数:10



正交试验设计方法讲义及举例第5章 正交试验设计方法5.1 试验设计方法概述试验设计是数理统计学的一个重要的分支。
多数数理统计方法主要用于分析已经得到的数据,而试验设计却是用于决定数据收集的方法。
试验设计方法主要讨论如何合理地安排试验以及试验所得的数据如何分析等。
例5-1 某化工厂想提高某化工产品的质量和产量,对工艺中三个主要因素各按三个水平进行试验(见表5-1)。
试验的目的是为提高合格产品的产量,寻求最适宜的操作条件。
对此实例该如何进行试验方案的设计呢?很容易想到的是全面搭配法方案(如图5-1所示):此方案数据点分布的均匀性极好,因素和水平的搭配十分全面,唯一的缺点是实验次数多达33=27次(指数3代表3个因素,底数3代表每因素有3个水平)。
因素、水平数愈多,则实验次数就愈多,例如,做一个6因素3水平的试验,就需36=729次实验,显然难以做到。
因此需要寻找一种合适的试验设计方法。
试验设计方法常用的术语定义如下。
试验指标:指作为试验研究过程的因变量,常为试验结果特征的量(如得率、纯度等)。
例1的试验指标为合格产品的产量。
因素:指作试验研究过程的自变量,常常是造成试验指标按某种规律发生变化的那些原因。
如例1的温度、压力、碱的用量。
水平:指试验中因素所处的具体状态或情况,又称为等级。
如例1的温度有3个水平。
温度用T 表示,下标1、2、3表示因素的不同水平,分别记为T 1、T 2、T 3。
常用的试验设计方法有:正交试验设计法、均匀试验设计法、单纯形优化法、双水平单纯形优化法、回归正交设计法、序贯试验设计法等。
可供选择的试验方法很多,各种试验设计方法都有其一定的特点。
所面对的任务与要解决的问题不同,选择的试验设计方法也应有所不同。
由于篇幅的限制,我们只讨论正交试验设计方法。
5.2 正交试验设计方法的优点和特点用正交表安排多因素试验的方法,称为正交试验设计法。
其特点为:①完成试验要求所需的实验次数少。


多因素优化试验设计—正交试验法上一章我们介绍了单因素优化试验设计方法。
但是在实际生产和科学试验中,往往有多个因素同时影响结果,在这种情况下采用单因素试验方法就难以满足要求。
本章将介绍在多因素寻优试验中,用尽量少的试验尽快获得最优结果的科学试验方法。
第一节正交试验设计正交试验法,就是在多因素优化试验中,利用数理统计学与正交性原理,从大量的试验点中挑选有代表性和典型性的试验点,应用“正交表”科学合理地安排试验,从而用尽量少的试验得到最优的试验结果的一种试验设计方法。
例3-2-1 已知碳、硅、锰含量影响铸铁的力学性能,我们把这三种元素分别用A、B、C表示。
我们根据生产经验将三种元素分别选两种含量(见表3-2-1),分别表示为A1、A2、B1、B2、C1、C2。
现在我们研究这三种元素两种含量如何组合,铸铁的性能最优。
表3-2-1 铸铁性能试验参数在例3-2-1中,我们称碳硅锰含量为因素,其两种含量称为水平,这个试验就是三因素二水平试验。
如果按照普通的方法将三个因素的两个水平分别搭配进行试验,需要进行8次试验,如图3-2-1长方体的8个顶点所示。
显然这是十分繁琐的。
如果试验的因素和水平更多,那么试验量将更加惊人。
但是在正交试验中,如果三个因素之间没有交互作用,我们只要选择其中的以下4个试验(图3-2-1中红点所示)A1B1C1、A1B2C2、A2B1C2、A2B2C1就可以代替全部8个试验。
图3-2-1 正交试验点示意图这是为什么呢?仔细观察图3-2-1可以发现,在长方体的六个面上,每个面都有两个试验点。
而在长方体的12个边上,每个边上都有1个试验点。
进一步观察4个试验点,可以发现,每个因素的各个水平参加试验的次数一样多,都是二次。
各个数据对,如(A1,B1)、(A1,B2)、(A2,B1)、(A2,B2)、(B1,C1)、(B2,C2)、(B1,C2)、(B2,C1)、(A1,C1)、…、(A2,C1)出现的次数也一样多,都是1次。


正交试验设计法一、定义:正交试验设计法就是利用正交表来合理安排多因素试验的一种方法。
二、常用术语1、指标:指标就是试验要考察的效果。
常用X、Y、Z……来表示。
▼定量指标:能够用数量来表示的试验指标,如重量、尺寸、温度。
▼定性指标:不能用数量来表示的试验指标,如颜色、味道、外观。
●定性指标量化:可用打分法、分等法。
2、因素:因素是指对试验指标可能产生影响的原因。
因素是在试验中应当加以考察的重点内容。
一般用大写字母A、B、C……来表示。
3、水平(位级):位级是指因素在试验中所处的状态或条件。
常用阿拉伯数字1、2、3……来表示。
如: A1、A2、A3、B1、B2、B3。
三、正交表 (已设计好的标准化表格,是进行正试验法的基本工具)1、日本型正交表:由日本质量管理专家田口玄一博士创立。
该正交试验设计法,除需试验的因素外,还要研究分析因素与因素之间的交互作用,一起上列,对试验结果的分析用方差分析等方法,过程较复杂。
2、中国型正交表是由以我国张千里教授为首的中国专家所创立。
它不考虑因素之间的交互作用,而将其交互作用融于试验之中,对试验结果的分析采用极差分析法,简单的用“看一看”与“算一算”相结合的分析、简单、易行、同样能得到满意的结论,是一种实用的试验方法,很适合现场应用。
四、正交表的特点:1、均衡分散性:每一列中各种字码出现的次数相同,保证试验条件均衡地分散在配合完全的位级组合之中,因而代表性强,容易出现好条件。
2、整齐可比性:任意两列中全部有序数字对出现次数都是相同的。
保证了在各个位级的效果之中,最大限度地排除了其他因素的干扰,能最有效地进行比较,作出展望。
五、用中国型正交表安排试验的步骤 1、明确试验目的 2、确定考察指标 3、挑因素、选位级,制定因素位级表 ①挑因素的原则: ▼分析影响指标的各种因素,排除: 不可控因素 对指标影响不大的因素 已掌握得好的因素(让其固定在适当位置上) ▼选对指标可能影响大,又无把握的因素。

正交试验设计方法讲义及举例正交试验设计方法是一种多因素试验设计方法,它能够有效地减少试验所需的样本数量,提高试验结果的精确性和可靠性。
正交试验设计方法是在已知因素水平的情况下选择对试验结果影响最大的因素进行研究的一种方法。
以下是正交试验设计方法的讲义及举例:一、正交试验设计方法的原理及步骤:1.原理:正交试验设计方法通过选择适当的正交表,将多个因素的不同水平组合进行排列,使各因素的变化对试验结果影响均匀化,从而获得准确可靠的试验结果。
2.步骤:a.确定试验因素及其水平:根据试验目的确定需要研究的因素及其水平。
b.选择正交表:根据试验因素的个数和水平确定适用的正交表,正交表能够保证试验结果的均匀性和可靠性。
c.设计试验方案:根据选择的正交表,将试验因素的水平进行组合,获得试验方案。
d.进行试验:按照试验方案进行实际试验。
e.分析试验结果:对试验结果进行统计分析,获得对试验因素的影响程度及其交互作用等信息。
f.微调试验方案:根据试验结果微调试验方案,迭代优化试验过程。
二、正交试验设计方法的优点:1.降低样本数量:正交试验设计方法能够通过对试验水平的排列组合,使试验因素的水平均匀分布,从而减少试验所需的样本数量。
2.提高试验效率:正交试验设计方法能够在有限样本量下获得更多的试验信息,提高试验效率。
3.确保结果可靠:正交试验设计方法通过保证试验因素的均匀分布,减少人为因素的干扰,从而保证试验结果的可靠性和准确性。
4.揭示因素交互作用:正交试验设计方法能够揭示因素之间的交互作用,进一步优化设计过程。
三、正交试验设计方法的举例:例如,公司要研究一种新的洗发水对头发柔顺度的影响,试验主要包括3个因素:洗发水品牌(A、B、C)、洗发水用量(X、Y、Z)和洗发水停留时间(T1、T2、T3)。
根据正交试验设计方法,按照以下步骤进行设计:1.选择正交表:根据3个因素和各因素的水平,选择适用的正交表,如L9正交表。
2.设计试验方案:根据L9正交表,将3个因素的水平进行组合,得到9个试验方案,每个方案分别测试一种组合情况。

正交实验设计方法讲义和实例课堂讲稿和正交试验设计方法示例第5章正交试验设计方法5.1试验设计方法概述试验设计是数理统计的一个重要分支。
大多数数理统计方法主要用于分析获得的数据,而实验设计用于确定数据收集方法。
测试设计方法主要讨论如何合理安排测试以及如何分析测试数据。
例5-大多数数学统计方法主要用于分析获得的数据,而实验设计用于确定数据收集方法。
测试设计方法主要讨论如何合理安排测试以及如何分析测试数据。
示例5:该方案中数据点的分布非常均匀,因子和级别的匹配非常全面。
唯一的缺点是实验的数量多达33=27(指数3代表3个因素,基数3代表每个因素的3个水平)。
因素和水平越多,实验就越多。
例如,做一个6因素3水平的实验需要36=729个实验,这显然很难做到。
因此,有必要找到一种合适的测试设计方法。
图5-1总体布置方案试验设计方法中常用术语定义如下。
测试指数: 指数量(如产量、纯度等。
)作为测试研究过程的因变量,这通常是测试结果的特征。
例1的测试指标是合格产品的产量。
因素:它指的是实验研究过程中使用的自变量,这往往是实验指标按照一定规律变化的原因。
例如,实施例1中使用的温度、压力和碱量。
级别:指测试中因素的具体状态或情况,也称为等级。
例如,实施例1中的温度有3个等级。
温度用t表示,下标1、2和3表示不同水平的因素,分别标记为t1、T2、T3 .常见的测试设计方法包括:正交试验设计法、均匀试验设计法、单纯形优化法、双层单纯形优化法、回归正交设计法、序贯试验设计法等。
有许多测试方法可供选择,各种测试设计方法都有一定的特点。
面临的任务不同于要解决的问题,选择的测试设计方法也应该不同。
由于空间限制,我们将只讨论正交设计方法。
5.2正交试验设计方法的优点和特点用正交表安排多因素试验的方法称为正交试验设计方法。
其特征在于:①完成测试要求所需的实验数量很少。
(2)数据点的分布非常均匀。
③相关极差分析法、方差分析法和回归分析法可以用来分析检验结果,得出许多有价值的结论。

正交设计举例正交设计是一种研究多因素多水平的设计方法,它根据正交性从全面试验中挑选出部分有代表性的点进行试验。
这些代表性的点具备了“均匀分散,齐整可比”的特点,是一种高效率、快速、经济的实验设计方法。
以下是正交设计的一个具体例子:假设某建筑材料研究院想要研究如何提高粉煤灰砖的抗折强度。
在这个试验中,有三个因素可能会影响抗折强度,分别是成型用水量、碾压时间和每次碾压的料重。
每个因素都有三个水平,例如成型用水量可以是9%、10%、11%,碾压时间可以是8min、10min、12min,每次碾压的料重可以是330kg、360kg、400kg。
如果进行全面试验,需要进行3^3=27种组合的实验,且尚未考虑每一组合的重复数。
但是,如果采用正交设计,可以选择一个三因素三水平的正交表,例如L9(3^4),只需要进行9次试验。
这9次试验将涵盖所有因素的所有水平,而且每个因素的每个水平都会与其他因素的每个水平组合一次,且仅组合一次。
具体的试验方案可以如下安排:试验1:成型用水量9%、碾压时间8min、每次碾压的料重330kg试验2:成型用水量9%、碾压时间10min、每次碾压的料重360kg试验3:成型用水量9%、碾压时间12min、每次碾压的料重400kg试验4:成型用水量10%、碾压时间8min、每次碾压的料重360kg试验5:成型用水量10%、碾压时间10min、每次碾压的料重400kg试验6:成型用水量10%、碾压时间12min、每次碾压的料重330kg试验7:成型用水量11%、碾压时间8min、每次碾压的料重400kg试验8:成型用水量11%、碾压时间10min、每次碾压的料重330kg试验9:成型用水量11%、碾压时间12min、每次碾压的料重360kg通过这9次试验,可以找出影响抗折强度的最优组合。
这种方法大大减少了试验次数,提高了效率,而且能够得到全面试验的效果。
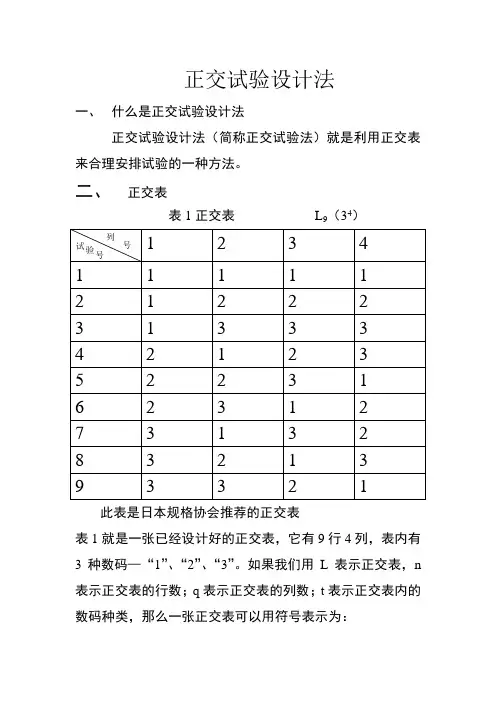
正交试验设计法一、什么是正交试验设计法正交试验设计法(简称正交试验法)就是利用正交表来合理安排试验的一种方法。
二、正交表表1正交表L9(34)此表是日本规格协会推荐的正交表表1就是一张已经设计好的正交表,它有9行4列,表内有3种数码—“1”、“2”、“3”。
如果我们用L表示正交表,n 表示正交表的行数;q表示正交表的列数;t表示正交表内的数码种类,那么一张正交表可以用符号表示为:例如:L9(34)正交表,最多可以安排4个因素做试验,每个因素可取3个水平,共有9种试验方案,这显然大大减少了试验方案是数量,因为如果安排4因素3水平的全搭配试验必须有34=81次试验方案才行。
三、正交表的优点多:可以考虑多因素,多指标。
快:试验周期短,见效快。
好;可以找到最佳方案。
省:试验次数少。
假如:考虑十三个因素,三水平的试验。
用L27(313)安排只要做27次试验。
而进行全面试验时,则要做313=1594323次试验,如果每天做10次试验,也要做436.8年之久方可做完.四、正交试验表的种类分两类:一类是水平数相同的正交表,即正交表中每一列所包含的代表水平的数码是一样的。
例如:L4(23)、L8(27)、L9(34)等等。
另一类是水平数不同的正交表,例如:L8(41×24)、L18(21×37)、L18(61×36)、L16(42×212)L32(49×24)。
L8(41×24)L16(42×212)四:常用正交试验设计与分析步骤1、明确试验目的2、确定考察指标3、挑因素选水平4、设计试验方案5、实施试验方案6、试验结论分析7、验证试验8、结论与建议例:设计纸飞机试验1、试验目的:找到一组飞行距离最远的纸飞机设计参数。
2、考察指标Y——纸飞机飞行距离。
3、挑因素选水平分析:影响Y的重要因素A:材料B:尺寸C:抛出力D:抛出角度根据实际情况每个因素取3个水平制定因素水平表因素水平表4、设计试验方案由因素水平表可以清楚的看出,这是一项4因素3水平的试验,必须有3种数码的正交表中找到合适的表安排此项试验,这类表试验次数最少的是L9(34)表于是就选L9(34)正交表安排试验方案。
用正交法测定几种因素对蔗糖酶活力的影响目的要求1.初步掌握正交实验设计方法的使用2.求出蔗糖酶的最适温度和最适pH值实验原理酶的催化作用是在一定条件下进行的,它受多种因素的影响,如:底物浓度、酶浓度、溶液的pH值和离子浓度、温度、抑制剂和激活剂等都能影响催化反应的速度。
通常是在其他因素恒定的条件下,通过对某因素在一系列变化条件下的酶活性测定,求得该因素对酶活力的影响,这是单因素的简单比较法。
本实验用正交法测定温度、pH值、底物浓度和酶浓度四种因素对蔗糖酶活性的影响,这是多因素(≥3)的实验方法。
正交法是通过正交表安排多因素实验,利用统计数学原理进行数据分析的一种科学方法,它符合“以尽量少的试验,获得足够的、有效的信息”的实验设计原则。
正交试验法的程序为下列八个步骤:(1)确定试验目的。
实验目的是多种多样的,如找出产品质量指标的最佳组合、确定最佳工艺条件等。
本实验的目的是为了提高酶的反应速度,提高酶的活力。
(2)选择质量特性指标。
应选择能提高或改进的质量特性及因素效应。
对于本实验来说就是产物(葡萄糖)生成量的多少。
(3)选定相关因素。
即选择和确定可能对实验结果或质量特性值有影响的那些因素,可人为控制与调节的因素,如温度、pH等。
这些因素之间有相互独立性。
(4)确定水平。
水平,又称位级,是因素的一个给定值或一种特定的措施,或一种特定的状态。
水平也就是因素变化的各种状态。
在确定水平时,应考虑选择范围、水平数和水平位置。
如本实验的温度水平可以选择20℃、30 ℃、50 ℃三个水平。
(5)选用正交表。
应从因素数、水平数以及有无重点因素需要强化考察等各方面综合考虑选用正交表。
一般情况下,首先根据水平数选用2或3系列表,然后,以容纳试验因素数,选用实验次数最少的正交表。
如有重点考察的因素,则根据其多考察的水平数,选混合型正交表。
(6)配列因素水平,制定实验方案。
按随机原则,把因素配列于选用的正交表中,制定实验的顺序、时间等,即制定实验具体方案。
正交试验设计方法讲义及举例第5章正交试验设计方法5.1 试验设计方法概述试验设计是数理统计学的一个重要的分支。
多数数理统计方法主要用于分析已经得到的数据,而试验设计却是用于决定数据收集的方法。
试验设计方法主要讨论如何合理地安排试验以及试验所得的数据如何分析等。
例5-1某化工厂想提高某化工产品的质量和产量,对工艺中三个主要因素各按三个水平进行试验(见表5-1)。
试验的目的是为提高合格产品的产量,寻求最适宜的操作条件。
对此实例该如何进行试验方案的设计呢?很容易想到的是全面搭配法方案(如图5-1所示):此方案数据点分布的均匀性极好,因素和水平的搭配十分全面,唯一的缺点是实验次数多达33=27次(指数3代表3个因素,底数3代表每因素有3个水平)。
因素、水平数愈多,则实验次数就愈多,例如,做一个6因素3水平的试验,就需36=729次实验,显然难以做到。
因此需要寻找一种合适的试验设计方法。
试验设计方法常用的术语定义如下。
试验指标:指作为试验研究过程的因变量,常为试验结果特征的量(如得率、纯度等)。
例1的试验指标为合格产品的产量。
因素:指作试验研究过程的自变量,常常是造成试验指标按某种规律发生变化的那些原因。
如例1的温度、压力、碱的用量。
水平:指试验中因素所处的具体状态或情况,又称为等级。
如例1的温度有3个水平。
温度用T表示,下标1、2、3表示因素的不同水平,分别记为T1、T2、T3。
表5-1 因素水平水平因素温度℃压力Pa 加碱量kg符号T p m123T1 (80 )T2(100)T3(120)p1(5.0)p2(6.0)p3(7.0)m 1(2.0)m2(2.5)m3(3.0)图5-1 全面搭配法方案常用的试验设计方法有:正交试验设计法、均匀试验设计法、单纯形优化法、双水平单纯形优化法、回归正交设计法、序贯试验设计法等。
可供选择的试验方法很多,各种试验设计方法都有其一定的特点。
所面对的任务与要解决的问题不同,选择的试验设计方法也应有所不同。
由于篇幅的限制,我们只讨论正交试验设计方法。
5.2 正交试验设计方法的优点和特点用正交表安排多因素试验的方法,称为正交试验设计法。
其特点为:①完成试验要求所需的实验次数少。
②数据点的分布很均匀。
③可用相应的极差分析方法、方差分析方法、回归分析方法等对试验结果进行分析,引出许多有价值的结论。
从例1可看出,采用全面搭配法方案,需做27次实验。
那么采用简单比较法方案又如何呢?先固定T1和p1,只改变m,观察因素m不同水平的影响,做了如图2-2(1)所示的三次实验,发现m=m2时的实验效果最好(好的用□表示),合格产品的产量最高,因此认为在后面的实验中因素m应取m2水平。
固定T1和m2,改变p的三次实验如图5-2(2)所示,发现p=p3时的实验效果最好,因此认为因素p应取p3水平。
固定p3和m2,改变T 的三次实验如图5-2(3)所示,发现因素T 宜取T2水平。
因此可以引出结论:为提高合格产品的产量,最适宜的操作条件为T2p3m2。
与全面搭配法方案相比,简单比较法方案的优点是实验的次数少,只需做9次实验。
但必须指出,简单比较法方案的试验结果是不可靠的。
因为,①在改变m值(或p值,或T值)的三次实验中,说m2(或p3或T2)水平最好是有条件的。
在T≠T1,p≠p1时,m2水平不是最好的可能性是有的。
②在改变m的三次实验中,固定T=T2,p=p3应该说也是可以的,是随意的,故在此方案中数据点的分布的均匀性是毫无保障的。
③用这种方法比较条件好坏时,只是对单个的试验数据进行数值上的简单比较,不能排除必然存在的试验数据误差的干扰。
运用正交试验设计方法,不仅兼有上述两个方案的优点,而且实验次数少,数据点分布均匀,结论的可靠性较好。
正交试验设计方法是用正交表来安排试验的。
对于例1适用的正交表是L9(34),其试验安排见表5-2。
所有的正交表与L9(34)正交表一样,都具有以下两个特点:(1)在每一列中,各个不同的数字出现的次数相同。
在表L9(34)中,每一列有三个水平,水平1、2、3都是各出现3次。
(2)表中任意两列并列在一起形成若干个数字对,不同数字对出现的次数也都相同。
图5-2 简单比较法方案在表L9(34)中,任意两列并列在一起形成的数字对共有9个:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),每一个数字对各出现一次。
表5-2 试验安排表这两个特点称为正交性。
正是由于正交表具有上述特点,就保证了用正交表安排的试验方案中因素水平是均衡搭配的,数据点的分布是均匀的。
因素、水平数愈多,运用正交试验设计方法,愈发能显示出它的优越性,如上述提到的6因素3水平试验,用全面搭配方案需729次,若用正交表L27(313)来安排,则只需做27次试验。
在化工生产中,因素之间常有交互作用。
如果上述的因素T的数值和水平发生变化时,试验指标随因素p变化的规律也发生变化,或反过来,因素p的数值和水平发生变化时,试验指标随因素T变化的规律也发生变化。
这种情况称为因素T、p间有交互作用,记为T×p 。
5.3 正交表使用正交设计方法进行试验方案的设计,就必须用到正交表。
正交表请查阅有关参考书。
5.3.1 各列水平数均相同的正交表各列水平数均相同的正交表,也称单一水平正交表。
这类正交表名称的写法举例如下:各列水平均为2的常用正交表有:L4(23),L8(27),L12(211),L16(215),L20(219),L32(231)。
各列水平数均为3的常用正交表有:L9(34),L27(313)。
各列水平数均为4的常用正交表有:L16(45)各列水平数均为3的常用正交表有:L25(56)5.3.2 混合水平正交表各列水平数不相同的正交表,叫混合水平正交表,下面就是一个混合水平正交表名称的写法:L 8(41×24)常简写为L 8(4×24)。
此混合水平正交表含有1 个4水平列,4个2水平列,共有1+4=5列。
5.3.3 选择正交表的基本原则一般都是先确定试验的因素、水平和交互作用,后选择适用的L表。
在确定因素的水平数时,主要因素宜多安排几个水平,次要因素可少安排几个水平。
(1)先看水平数。
若各因素全是2水平,就选用L(2*)表;若各因素全是3水平,就选L(3*)表。
若各因素的水平数不相同,就选择适用的混合水平表。
(2)每一个交互作用在正交表中应占一列或二列。
要看所选的正交表是否足够大,能否容纳得下所考虑的因素和交互作用。
为了对试验结果进行方差分析或回归分析,还必须至少留一个空白列,作为“误差”列,在极差分析中要作为“其他因素”列处理。
(3)要看试验精度的要求。
若要求高,则宜取实验次数多的L表。
(4)若试验费用很昂贵,或试验的经费很有限,或人力和时间都比较紧张,则不宜选实验次数太多的L表。
(5)按原来考虑的因素、水平和交互作用去选择正交表,若无正好适用的正交表可选,简便且可行的办法是适当修改原定的水平数。
(6)对某因素或某交互作用的影响是否确实存在没有把握的情况下,选择L表时常为该选大表还是选小表而犹豫。
若条件许可,应尽量选用大表,让影响存在的可能性较大的因素和交互作用各占适当的列。
某因素或某交互作用的影响是否真的存在,留到方差分析进行显著性检验时再做结论。
这样既可以减少试验的工作量,又不致于漏掉重要的信息。
5.3.4 正交表的表头设计所谓表头设计,就是确定试验所考虑的因素和交互作用,在正交表中该放在哪一列的问题。
(1)有交互作用时,表头设计则必须严格地按规定办事。
因篇幅限制,此处不讨论,请查阅有关书籍。
(2)若试验不考虑交互作用,则表头设计可以是任意的。
如在例5-1中,对L 9(3 4)表头设计,表5-3所列的各种方案都是可用的。
但是正交表的构造是组合数学问题,必须满足5.2中所述的特点。
对试验之初不考虑交互作用而选用较大的正交表,空列较多时,最好仍与有交互作用时一样,按规定进行表头设计。
只不过将有交互作用的列先视为空列,待试验结束后再加以判定。
5.4 正交试验的操作方法(1)分区组。
对于一批试验,如果要使用几台不同的机器,或要使用几种原料来进行,为了防止机器或原料的不同而带来误差,从而干扰试验的分析,可在开始做实验之前,用L 表中未排因素和交互作用的一个空白列来安排机器或原料。
与此类似,若试验指标的检验需要几个人(或几台机器)来做,为了消除不同人(或仪器)检验的水平不同给试验分析带来干扰,也可采用在L表中用一空白列来安排的办法。
这样一种作法叫做分区组法。
(2)因素水平表排列顺序的随机化。
如在例5-1中,每个因素的水平序号从小到大时,因素的数值总是按由小到大或由大到小的顺序排列。
按正交表做试验时,所有的1水平要碰在一起,而这种极端的情况有时是不希望出现的,有时也没有实际意义。
因此在排列因素水平表时,最好不要简单地按因素数值由小到大或由大到小的顺序排列。
从理论上讲,最好能使用一种叫做随机化的方法。
所谓随机化就是采用抽签或查随机数值表的办法,来决定排列的别有顺序。
(3)试验进行的次序没必要完全按照正交表上试验号码的顺序。
为减少试验中由于先后实验操作熟练的程度不匀带来的误差干扰,理论上推荐用抽签的办法来决定试验的次序。
(4)在确定每一个实验的实验条件时,只需考虑所确定的几个因素和分区组该如何取值,而不要(其实也无法)考虑交互作用列和误差列怎么办的问题。
交互作用列和误差列的取值问题由实验本身的客观规律来确定,它们对指标影响的大小在方差分析时给出。
(5)做实验时,要力求严格控制实验条件。
这个问题在因素各水平下的数值差别不大时更为重要。
例如,例5-1中的因素(加碱量)m的三个水平:m1=2.0,m2=2.5,m3=3.0,在以m=m2=2.5为条件的某一个实验中,就必须严格认真地让m2=2.5。
若因为粗心和不负责任,造成m2=2.2或造成m2=3.0,那就将使整个试验失去正交试验设计方法的特点,使极差和方差分析方法的应用丧失了必要的前提条件,因而得不到正确的试验结果。
5.5 正交试验结果分析方法正交试验方法之所以能得到科技工作者的重视并在实践中得到广泛的应用,其原因不仅在于能使试验的次数减少,而且能够用相应的方法对试验结果进行分析并引出许多有价值的结论。
因此,有正交试验法进行实验,如果不对试验结果进行认真的分析,并引出应该引出的结论,那就失去用正交试验法的意义和价值。
5.5.1 极差分析方法下面以表5-4为例讨论L4(23)正交试验结果的极差分析方法。
极差指的是各列中各水平对应的试验指标平均值的最大值与最小值之差。
从表5-4的计算结果可知,用极差法分析正交试验结果可引出以下几个结论:(1)在试验范围内,各列对试验指标的影响从大到小的排队。