只有逻辑斯谛方程
- 格式:ppt
- 大小:160.00 KB
- 文档页数:11


关于逻辑斯谛方程关于逻辑斯谛方程000摘要:逻辑斯谛方程即微分方程:dN/dt=rN(K-N)/K。
当一个物种迁入到一个新生态系统中后,其数量会发生变化。
假设该物种的起始数量小于环境的最大容纳量,则数量会增长。
该物种在此生态系统中有天敌、食物、空间等资源也不足(非理想环境),则增长函数满足逻辑斯谛方程,图像呈S形,此方程是描述在资源有限的条件下种群增长规律的一个最佳数学模型。
在以下内容中将具体介绍逻辑斯谛方程的原理、生态学意义及其应用。
关键词:逻辑斯谛方程;原理;生态学意义;应用1 前言1938年一位比利时的数学家Verhulst首先将营养关系反映到种群数学模型方面,是它首先导出了后来被广泛称为逻辑斯谛的方程。
但在当时并没有引起大家的注意,直到1920年两位美国人口学家Pearl和Reed在研究美国人口问题时,再次提出这个方程,才开始流行,故现在文献中通常称之为Verhulst-Pearl阻碍方程。
其所以又称为逻辑斯谛方程是因为其有某种逻辑推理的含义。
按现在的用语来说,它是一个说理模型,实际上是反映营养对种群增长的一种线性限制关系的说理模型。
1963年,洛伦兹发现确定性系统的随机性为,并且发现了这种随机行为对初值的敏感性。
1975年,美籍华人学者李天岩和数学家约克发表“周期中蕴含着混沌”的著名文章,揭示从有序到混沌的演化过程。
这些内容都包含在逻辑斯谛差分方程中。
1976年R.梅在英国《自然》杂志上发表了研究逻辑斯谛方程的成果—《表现非常复杂的动力学的简单数学模型》,引起学术界极大关注,内容已远远超越了生态学领域,揭示出逻辑斯谛方程深处蕴藏的丰富内涵。
2 逻辑斯谛方程的原理在种群增长早期阶段,种群大小N很小,N/K值也很小,因此1-N/K接近于1,所以抑制效应可以忽略不计,种群增长实质上为r/N,成几何增长。
然而,当N变大时,抑制效应增加,直到当N=K时,(1-N/K)变成了(1-K/K),等于0,这时种群的增长为零,种群达到了一个稳定的大小不变的平衡状态。


§4 从倍周期分定走向混沌4-1 逻辑斯谛(Logistic )映射我们将以一个非常简单的数学模型来加以说明从倍周期分定走向混沌现象。
该模型称为有限环境中无世代交替昆虫生息繁衍模型。
若昆虫不加以条件控制,每年增加λ倍,我们将一年作为一代,把第几代的虫日记为,则有:i N o i i i N N N 11++==λλ (4-1)i N ,1>λ增长很快,发生“虫口爆炸”,但虫口太多则会由于争夺有限食物和生存空间,以及由于接触传染导致疾病曼延,使虫口数目减少,它正比于,假定虫口环境允许的最大虫口为,并令2i N o N oii N N x =,则该模型由一个迭代方程表示: 21i i i N N N λλ−=+即为:)1(1i i i x x x −=+λ (4-2)其中:]4,0[],1,0[∈∈λi x 。
(4-2)式就是有名的逻辑斯谛映射。
4-2 倍周期分歧走向混沌借助于对这一非线性迭代方程进行迭代计算,我们可以清楚地看到非线性系统通过倍周期分岔进入混沌状态的途径。
(一)迭代过程迭代过程可以用图解来表示。
图4-1中的水平轴表示,竖直轴表示,抛物线表示(4-2)式右端的迭代函数。
45º线表示n x 1+n x n n x x =+1的关系。
由水平轴上的初始点作竖直线,找到与抛物线的交点,A 的纵坐标就是。
由点)0,(0x R ),(10x x A 1x),(10x x A 作水平直线,求它与45º线的交点,经B 点再作竖直线,求得与抛物线的交点,这样就得到了。
仿此做法可得到所迭代点。
),(11x x B ),(21x x 2x 从任何初始值出发迭代时,一般有个暂态过程。
但我们关心的不是暂态过程,而是这所趋向的终态集。
终态集的情况与控制参数λ有很大关系。
增加λ值就意味着增加系统的非线性的程度。
改变λ值,不仅仅改变了终态的量,而且也改变了终态的质。
它所影响的不仅仅是终态所包含的定态的个数和大小,而且也影响到终态究竟会不会达到稳定。

逻辑斯蒂回归基本原理最近在研究逻辑斯蒂回归,发现了一些有趣的原理,今天来和大家聊聊。
你知道吗?生活中有很多情况就像是逻辑斯蒂回归的实例呢。
就像我们预测一个人会不会买某件商品。
假设我们考虑两个因素,一个是这个人的收入,另一个是这个商品是不是很流行。
一般来说,收入高的人可能更有能力买东西,流行的东西也更容易被购买。
但这个关系又不是绝对的,不是说收入高就肯定会买,流行就所有人都会买。
逻辑斯蒂回归的基本原理其实就是想找到一种数学上的关系,来描述这种可能性。
从专业角度来说,逻辑斯蒂回归是一种广义的线性回归模型,它的响应变量(我们要预测的结果,例如会不会买东西,1代表会,0代表不会)是一种分类变量。
我们把输入的各种特征(像前面说的收入和商品流行程度等)通过特定的函数计算,这个函数就像是一个魔法变换器。
打个比方吧,这个过程就好比是把各种乱七八糟的食材(输入特征)放进一个神奇的搅拌机(逻辑斯蒂函数),最后得出一个蛋糕(预测的结果:买或者不买)。
这个搅拌机的运作原理是特殊的,它要保证最后产出的结果在0到1之间,这个数值就表示会买这个商品的概率。
有意思的是,这个模型是怎么达到对结果良好预测的呢?这就要说到模型中的系数了。
就像刚刚那个例子里,收入和商品流行程度对购买结果的影响程度是不一样的,这个影响程度就是通过系数来体现的。
不一样的系数就像是烹饪里不同食材放的量不一样,某个食材(特征)多放点(系数大),可能对最后的蛋糕(结果)影响就大一些。
老实说,我一开始也不明白为什么不直接用线性回归就好了。
后来才知道,线性回归得到的结果可能是任意实数,但我们这里预测的是某个事件发生的概率,概率只能在0到1之间,所以这就是逻辑斯蒂回归存在的意义之一。
实际应用案例超级多,就比如说银行会根据客户的收入、信用记录这些资料(特征),采用逻辑斯蒂回归来预测这个客户会不会违约(一种分类结果)。
这样银行就可以提前做好应对措施,降低风险。
在应用逻辑斯蒂回归的时候也有一些注意事项。

逻辑斯谛方程是一个一阶非线性常微分方程,可分离变量求通解。
具体求解步骤如下:
1. 确定方程的形式:逻辑斯谛方程即微分方程dN/dt=rN(K-N)/K,其中N为种群个体总数,t为时间,r为种群增长潜力指数,K为环境最大容纳量。
2. 对方程进行分离变量:将方程改写为dN/dt=rN(1-N/K)。
3. 对分离后的方程进行求解:通过求解这个微分方程,可以得到种群数量的变化规律。
请注意,以上步骤仅适用于一般的逻辑斯谛方程求解,具体的求解过程可能因方程的具体形式和参数而有所不同。



§4 从倍周期分定走向混沌4-1 逻辑斯谛(Logistic )映射我们将以一个非常简单的数学模型来加以说明从倍周期分定走向混沌现象。
该模型称为有限环境中无世代交替昆虫生息繁衍模型。
若昆虫不加以条件控制,每年增加λ倍,我们将一年作为一代,把第几代的虫日记为,则有:i N o i i i N N N 11++==λλ (4-1)i N ,1>λ增长很快,发生“虫口爆炸”,但虫口太多则会由于争夺有限食物和生存空间,以及由于接触传染导致疾病曼延,使虫口数目减少,它正比于,假定虫口环境允许的最大虫口为,并令2i N o N oii N N x =,则该模型由一个迭代方程表示: 21i i i N N N λλ−=+即为:)1(1i i i x x x −=+λ (4-2)其中:]4,0[],1,0[∈∈λi x 。
(4-2)式就是有名的逻辑斯谛映射。
4-2 倍周期分歧走向混沌借助于对这一非线性迭代方程进行迭代计算,我们可以清楚地看到非线性系统通过倍周期分岔进入混沌状态的途径。
(一)迭代过程迭代过程可以用图解来表示。
图4-1中的水平轴表示,竖直轴表示,抛物线表示(4-2)式右端的迭代函数。
45º线表示n x 1+n x n n x x =+1的关系。
由水平轴上的初始点作竖直线,找到与抛物线的交点,A 的纵坐标就是。
由点)0,(0x R ),(10x x A 1x),(10x x A 作水平直线,求它与45º线的交点,经B 点再作竖直线,求得与抛物线的交点,这样就得到了。
仿此做法可得到所迭代点。
),(11x x B ),(21x x 2x 从任何初始值出发迭代时,一般有个暂态过程。
但我们关心的不是暂态过程,而是这所趋向的终态集。
终态集的情况与控制参数λ有很大关系。
增加λ值就意味着增加系统的非线性的程度。
改变λ值,不仅仅改变了终态的量,而且也改变了终态的质。
它所影响的不仅仅是终态所包含的定态的个数和大小,而且也影响到终态究竟会不会达到稳定。

逻辑斯谛三点法证明
逻辑斯谛三点法是一种数学证明方法,通过该方法可以证明给定命题的真假性。
下面是逻辑斯谛三点法证明的步骤:
1、建立命题:首先要明确需要证明的命题是什么,例如“命题A为真”或“命题B为假”。
2、取反命题:假设命题的反命题为真,即“命题A为假”或“命题B为真”。
这一步是利用反证法的思想,假设反命题为真,然后通过推理得出矛盾,从而证明原始命题为真。
3、推导矛盾:利用前提条件和已知事实,通过逻辑推理推导出矛盾的结论。
这个步骤需要使用逻辑规则和定理,如排中律、推理法则等,逐步推导出矛盾的结论。
4、得出结论:由于通过推导得出了矛盾的结论,根据推理的正确性,可以得出原始命题的真假性。
如果矛盾的结论是不可能的,则原始命题为真。
如果矛盾的结论是必然发生的,则原始命题为假。
需要注意的是,在使用逻辑斯谛三点法证明命题的时候,要注意正确使用逻辑规则和定理,并确保推导的每一步都是严谨和正确的。
同时,有些命题可能需要额外的信息或者前提条件才能使用逻辑斯谛三点法进行证明。
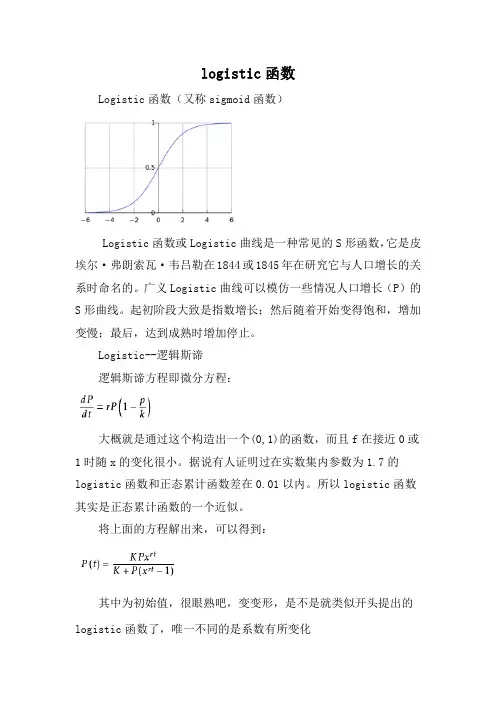
logistic函数
Logistic函数(又称sigmoid函数)
Logistic函数或Logistic曲线是一种常见的S形函数,它是皮埃尔·弗朗索瓦·韦吕勒在1844或1845年在研究它与人口增长的关系时命名的。
广义Logistic曲线可以模仿一些情况人口增长(P)的S形曲线。
起初阶段大致是指数增长;然后随着开始变得饱和,增加变慢;最后,达到成熟时增加停止。
Logistic--逻辑斯谛
逻辑斯谛方程即微分方程:
大概就是通过这个构造出一个(0,1)的函数,而且f在接近0或1时随x的变化很小。
据说有人证明过在实数集内参数为1.7的logistic函数和正态累计函数差在0.01以内。
所以logistic函数其实是正态累计函数的一个近似。
将上面的方程解出来,可以得到:
其中为初始值,很眼熟吧,变变形,是不是就类似开头提出的logistic函数了,唯一不同的是系数有所变化。
逻辑斯蒂公式曲线
逻辑斯蒂曲线是一条描述种群增长或消亡的数学曲线,它的形状呈现为S形。
在逻辑斯蒂曲线中,种群数量的变化表现为一个S形的曲线图,其中种群数量随着时间的变化先以指数方式增长,然后逐渐趋于稳定。
逻辑斯蒂公式的数学表达式为:N(t)=K/(1+e^(-r(t-t0))),其中N(t)表示在时间t的种群数量,K表示环境容量,r表示种群增长率,t0表示种群达到最大值的时间。
逻辑斯蒂曲线的形状是由逻辑斯蒂参数决定的,包括环境容量K 和种群增长率r。
当种群数量接近环境容量K时,种群增长速度会逐渐减缓,最终趋于稳定。
逻辑斯蒂曲线可以用来描述多种生物学现象,例如种群数量的变化、疾病的传播、生态系统的平衡等。
在生态学和生物多样性保护领域中,逻辑斯蒂曲线被广泛应用于预测物种数量的变化和制定保护策略。
广义逻辑斯谛分布广义逻辑斯谛分布(Generalized Logistic Distribution,GLD)是一种概率分布模型,在统计学中广泛应用于描述随机变量的分布情况。
它是逻辑斯谛分布(Logistic Distribution)的扩展,可以用作连续型随机变量的概率分布函数。
GLD的形式非常简洁,只有两个参数,分别为位置参数和尺度参数。
GLD的概率密度函数可以表示为:f(x) = a / (b + c * exp(-d(x-m)))其中,a、b、c、d、m都是GLD的参数。
a表示高度,b表示左侧的渐进值,c表示右侧的渐进值,d是斜率,m是中心点位置。
GLD可以用于许多实际应用场景,例如:1.生物学:GLD可以用于描述细胞增殖率、光合作用的光强等生物学现象。
2.金融学:GLD可以用于描述收益分布、股票价格变动等金融现象,尤其是在风险管理中。
3.工程学:GLD可以用于描述水位、能耗等工程现象。
4.医学:GLD可以用于描述疾病的发病率、死亡率等医学现象。
5.环境科学:GLD可以用于描述河流流量、土地利用变化等环境现象。
与逻辑斯谛分布相比,GLD的优势在于灵活性更强,因此可以更好地拟合不同类型的数据。
同时,GLD也具有极好的数学性质,比如具有良好的可微性和可积性等,因此在建立概率模型时非常有用。
在实际应用中,GLD的参数通常需要通过数据拟合来确定。
通常使用最大似然法(maximum likelihood,ML)或最大后验估计(maximum a posteriori,MAP)等方法来确定GLD的参数。
总之,广义逻辑斯谛分布是一种非常重要的概率模型,具有广泛的应用价值。
无论在科研、工程、金融、医学等领域中,GLD都可以作为一种可信赖的分布模型,用于描述不同类型的随机变量的分布情况。
逻辑斯蒂4参数求导1. 引言逻辑斯蒂回归(Logistic Regression)是一种常用的分类算法,其通过对数据进行建模,预测样本所属的类别。
逻辑斯蒂回归的模型参数可以通过最大似然估计来求解,其中包括4个参数:截距项(intercept)、斜率项(slope)、方差项(variance)和偏差项(bias)。
本文将详细介绍逻辑斯蒂回归的4个参数求导过程。
2. 逻辑斯蒂回归模型逻辑斯蒂回归模型是一种广义线性模型(Generalized Linear Model),用于解决二分类问题。
模型的输出是一个概率值,表示样本属于某一类别的概率。
该概率值通过逻辑斯蒂函数(Logistic Function)进行转换,公式如下:P(y=1|x)=11+e−(β0+β1x)其中,P(y=1|x)表示样本属于类别1的概率,β0表示截距项,β1表示斜率项,x 表示样本的特征。
3. 模型参数求解逻辑斯蒂回归模型的参数可以通过最大似然估计来求解。
最大似然估计的目标是找到一组参数,使得样本观测到的概率最大。
对于逻辑斯蒂回归模型,最大似然函数可以表示为:L(β0,β1)=∏Pni=1(y i=1|x i)y i⋅(1−P(y i=1|x i))1−y i其中,n表示样本的数量,y i表示样本的真实类别,x i表示样本的特征。
为了方便计算,通常对上述最大似然函数取对数,得到对数似然函数:logL(β0,β1)=∑(y i logP(y i=1|x i)+(1−y i)log(1−P(y i=1|x i)))ni=1最大似然估计的目标是最大化对数似然函数,即求解下面的优化问题:maxβ0,β1logL(β0,β1)为了求解上述优化问题,需要对对数似然函数求导。
4. 参数求导过程4.1. 对截距项求导对于截距项β0,我们需要求解∂logL∂β0。
首先,我们可以计算∂P(y=1|x)∂β0:∂P(y=1|x)∂β0=∂∂β0(11+e−(β0+β1x))=−e−(β0+β1x)(1+e−(β0+β1x))2接下来,我们可以计算∂logL∂β0:∂logL∂β0=∑(y i1P(y i=1|x i)∂P(y i=1|x i)∂β0−(1−y i)11−P(y i=1|x i)∂P(y i=1|x i)∂β0)ni=1将上述两个式子代入,可得:∂logL∂β0=∑(y i1P(y i=1|x i)(−e−(β0+β1x i)(1+e−(β0+β1x i))2)n i=1−(1−y i)11−P(y i=1|x i)(e−(β0+β1x i)(1+e−(β0+β1x i))2))化简上述式子,可以得到对截距项求导的表达式。
姓名 班级 学号 同组者 科目 生态学实验 题目 种群在资源有限环境中的逻辑斯蒂增长 组别 *****种群在资源有限环境中的逻辑斯蒂增长【实验目的】1. 认识到环境资源是有限的,任何种群数量的动态变化都受到环境条件的制约。
2. 加深对逻辑斯蒂增长模型的理解与认识,深刻领会该模型中生物学特性参数r 与环境因子参数——生态学特性参数K 的重要作用。
3. 学会如何通过实验估计出r 、K 两个参数和进行曲线拟合的方法。
【实验原理】逻辑斯蒂方程增长是种群在资源有限环境下连续增长的一种最简单形式,又称为阻滞增长。
种群在有限环境下的增长曲线是S 型的,它具有两个特点:(1)S 型增长曲线有一个上渐近线,即S 型增长曲线逐渐接近于某一个特定的最大值,但不会超过这个最大值的水平,此值即为种群生存的最大环境容纳量,通常用K 表示。
当种群大小达到K 值的时候,将不再增长。
(2)S 型曲线是逐渐变化的,平滑的,不是骤然变化的。
逻辑斯蒂增长的数学模型:)(K N K rN dt dN -= 或 )1(K NrN dt dN -= 式中:dtdN——种群在单位时间内的增长率;N ——种群大小; t ——时间;r ——种群的瞬间增长率; K ——环境容纳量; (KN-1)——“剩余空间”,即种群还可以继续利用的增长空间。
逻辑斯蒂增长模型的积分式:rta e KN -+=1式中:a ——常数;e ——常数,自然对数的底。
【实验器材】 坐标纸、笔 【操作步骤】1.老师给出草履虫培养的种群数目,将下面的表格填好。
姓名 班级 学号 同组者 科目 生态学实验 题目 种群在资源有限环境中的逻辑斯蒂增长 组别 *****2.将7天内的草履虫种群大小数据,标定在以时间为横坐标、草履虫种群数量为纵坐标的平面坐标系中,从得到的散点图中不仅可以看出草履虫种群大小随时间的变化规律,还可以得到此环境下可以容纳草履虫的最大环境容纳量K 。
通常从平衡点以后,选取最大的一个N ,以防止在计算)(NNK In -的过程中真数出现负值。