一-2命题逻辑等值演算(精选)

13
联结词与复合命题( 联结词与复合命题(续)
3.析取式与析取联结词“∨” 析取式与析取联结词“ 析取式与析取联结词 为二命题， 称作p与 定义 设 p,q为二命题，复合命题“p或q”称作 与q 为二命题 复合命题“ 或 称作 析取式，记作p∨ ， 称作析取联结词 析取联结词， 的析取式，记作 ∨q，∨称作析取联结词，并规 为假当且仅当p与 同时为假 同时为假. 定p∨q为假当且仅当 与q同时为假 ∨ 为假当且仅当 例 将下列命题符号化 (1) 2或4是素数 是素数. 或 是素数 (2) 2或3是素数 是素数. 或 是素数 (3) 4或6是素数 是素数. 或 是素数 (4) 小元元只能拿一个苹果或一个梨 小元元只能拿一个苹果或一个梨. (5) 王晓红生于 王晓红生于1975年或 年或1976年. 年或 年
14
是素数, 是素数, 是素数 是素数, 是素数 是素数, 解 令 p:2是素数 q:3是素数 r:4是素数 s:6是素数, 是素数 是素数 均为相容或. 则 (1), (2), (3) 均为相容或. 分别符号化为: 分别符号化为: p∨r , p∨q, r∨s, ∨ ∨ ∨ 它们的真值分别为 1, 1, 0. 而 (4), (5) 为排斥或 为排斥或. 小元元拿一个苹果， 小元元拿一个梨 小元元拿一个梨， 令 t :小元元拿一个苹果，u:小元元拿一个梨， 小元元拿一个苹果 则 (4) 符号化为 (t∧¬u) ∨(¬t∧u). ∧ ¬∧ 王晓红生于1975年,w:王晓红生于 令v :王晓红生于 王晓红生于 年 :王晓红生于1976年, 年 则 (5) 既可符号化为 (v∧¬w)∨(¬v∧w), 又可 ∧ ∨¬ ∧ 符号化为 v∨w , 为什么 ∨ 为什么?
19
例 求下列复合命题的真值 (1) 2 + 2 ＝ 4 当且仅当 3 + 3 ＝ 6. (2) 2 + 2 ＝ 4 当且仅当 3 是偶数 是偶数. (3) 2 + 2 ＝ 4 当且仅当 太阳从东方升起 太阳从东方升起. (4) 2 + 2 ＝ 4 当且仅当 美国位于非洲. 美国位于非洲. (5) 函数 f (x) 在x0 可导的充要条件是它在 x0 连续. 连续 它们的真值分别为 1，0，1，0，0. ， ， ， ，

名称
M0 M1 M2 M3
20
实例
由三个命题变项 p, q, r 形成的极小项与极大项.
极小项
公式
成真赋值 名称
p q r 0 0 0 m0
p q r 0 0 1 m1
p q r 0 1 0 m2
p q r 0 1 1 m3
p q r 1 0 0 m4
p q r 1 0 1 m5
p q r 1 1 0 m6
p(qr) (pq) r p(qr) 不与 (pq) r 等值
2
等值式例题
例1 判断下列各组公式是否等值: (1) p(qr) 与 (pq) r
p q r qr p(qr) pq (pq)r
000 1
1
001 1
1
010 0
1
011 1
1
100 1
1
101 1
1Hale Waihona Puke 110 00111 1
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
1
1
结论: p(qr) (pq) r
3
等值式例题
(2) p(qr) 与 (pq) r
p q r qr p(qr)
000 1
1
001 1
1
010 0
1
011 1
1
100 1
1
101 1
1
110 0
0
111 1
1
pq (pq)r
1
0
1
1
1
0
1
1
0
1
0

第二章作业评分要求：1. 每小题6分: 结果正确1分; 方法格式正确3分; 计算过程2分. 合计48分2. 给出每小题得分(注意: 写出扣分理由)3. 总得分在采分点1处正确设置.一. 证明下面等值式(真值表法, 解逻辑方程法, 等值演算法, 三种方法每种方法至少使用一次):说明证1. p ⇔(p ∧q)∨(p ∧¬q)解逻辑方程法设 p ↔((p ∧q)∨(p ∧¬q)) =0, 分两种情况讨论:⎩⎨⎧=⌝∧∨∧=0)()(1)1(q p q p p 或者 ⎩⎨⎧=⌝∧∨∧=1)()(0)2(q p q p p (1)(2)两种情况均无解, 从而, p ↔(p ∧q)∨(p ∧¬q)无成假赋值, 为永真式. 等值演算法(p ∧q)∨(p ∧¬q)⇔ p ∧(q ∨¬q)∧对∨的分配率⇔ p ∧1 排中律⇔ p 同一律 真值表法2. (p→q)∧(p→r)⇔p→(q∧r)等值演算法(p→q)∧(p→r)⇔ (¬p∨q)∧(¬p∨r)蕴含等值式⇔¬p∨(q∧r)析取对合取的分配律⇔ p→(q∧r)蕴含等值式3. ¬(p↔q)⇔(p∨q)∧¬(p∧q)等值演算法¬(p↔q)⇔¬( (p→q)∧(q→p) )等价等值式⇔¬( (¬p∨q)∧(¬q∨p) )蕴含等值式⇔¬( (¬p∧¬q)∨(p∧q) )合取对析取分配律, 矛盾律, 同一律⇔ (p∨q)∧¬(p∧q)德摩根律4. (p∧¬q)∨(¬p∧q)⇔(p∨q)∧¬(p∧q)等值演算法(p∧¬q)∨(¬p∧q)⇔ (p∨q)∧¬(p∧q)析取对合取分配律, 排中律, 同一律说明: 用真值表法和解逻辑方程法证明相当于证明为永真式.等值演算法证明时每一步后面最好注明理由以加深印象, 熟练后可以不写. 由于等值演算法证明具有较强的技巧性, 平时应注意总结心得.二. 求下列公式的主析取范式与主合取范式(等值演算法与用成真赋值或成假赋值求解都至少使用一次):1.2.3.4.1. (¬p→q)→(¬q∨p)解(¬p→q)→(¬q∨p)⇔ (p∨q)→(¬q∨p)蕴含等值式⇔ (¬p∧¬q)∨(¬q∨p)蕴含等值式, 德摩根律⇔ (¬p∧¬q)∨¬q ∨ p结合律⇔ p∨¬q吸收律, 交换律⇔ M1因此, 该式的主析取范式为m0∨m2∨m32. (¬p→q)∧(q∧r)解逻辑方程法设 (¬p→q)∧(q∧r) =1, 则¬p→q=1且 q∧r=1,解得q=1, r=1, p=0 或者 q=1, r=1, p=1, 从而所求主析取范式为 m3∨m7, 主合取范式为M0∧M1∧M2∧M4∧M5∧M6等值演算法(¬p→q)∧(q∧r)(p q)(q r) 蕴含等值式(p q r)(q r) 对分配律, 幂等律(p q r) (p q r)(p q r) 同一律, 矛盾律, 对分配律m7 m3主合取范式为M0∧M1∧M2∧M4∧M5∧M63. (p↔q)→r解逻辑方程法设 (p↔q)→r =0, 解得 p=q=1, r=0 或者 p=q=0, r=0, 从而所求主合取范式为M0∧M6, 主析取范式为m1∨m2∨m3∨m4∨m5∨m7等值演算法(p↔q)→r((p q)(q p))r 等价等值式((p q)(q p))r 蕴含等值式(p q)(q p)r 德摩根律, 蕴含等值式的否定(参见PPT)(p q r)(q p r) 对分配律, 矛盾律, 同一律M0 M6主析取范式为m1∨m2∨m3∨m4∨m5∨m74. (p→q)∧(q→r)解等值演算法(p→q)∧(q→r)(p q)(q r) 蕴含等值式(p q)(p r)(q r) 对分配律, 矛盾律, 同一律(p q r)(p q r) (p q r)(p q r)(p q r)(p q r)m1 m0 m3 m7主合取范式为M2 M4 M5 M6.解逻辑方程法设 (p q) (q r) = 1, 则p q =1 且 q r =1.前者解得: p=0, q=0; 或者 p=0, q=1; 或者 p=1, q=1.后者解得: q=0, r=0; 或者 q=0, r=1; 或者 q=1, r=1.综上可得成真赋值为 000, 001, 011, 111, 从而主析取范式为m0m1m3m7, 主合取范式为M2 M4 M5 M6.真值表法公式 (p q) (q r) 真值表如下:p q r(p q) (qr)00010011010001111000101011001111013724 M5 M6.。

课堂练习
证明： (P → Q) (R → Q) = (P ∨ R) → Q
等值演算旳应用－1
利用基本旳等价关系，化简下列电路图
P
P QR
PR
Q
R
P QS
PS
S
T
& ≥1
≥1 &
&
解：上述电路图可描述为： （1）((P∧Q∧R)∨(P∧Q∧S))∧((P∧R)∨(P∧S)) （2）((P∧Q∧R)∨(P∨Q∨S))∧(P∧S∧T)
1
101 1
1
110 0
0
111 1
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
1
1
结论: p(qr) (pq) r
7
等值式例题
(2) p(qr) 与 (pq) r
p q r qr p(qr)
000 1
1
001 1
1
010 0
1
011 1
1
100 1
1
101 1
1
110 0
0
111 1
1
pq (pq)r
1
0
1
同一律
A0A. A1A
排中律
AA1
矛盾律
AA0
蕴涵等值式
ABAB
等价等值式
AB(AB)(BA)
假言易位
ABBA
等价否定等值式 ABAB
归谬论
(AB)(AB) A
尤其提醒：必须牢记这16组等值式，这是继续学习旳基础
11
命题与集合之间旳关系
能够将命题公式G，H了解为某总体论域上全部使命題為真 旳解釋旳集合，而要求G∧H为两集合旳公共部分（交集）， G∨H为两集合旳全部（并集），┐G为总体论域中G旳补集， 将命题中旳真值“1”了解为集合中旳总体论域（全集）， 将命题中旳真值“0”了解为集合中旳空集，则有：

A,B代表任意 的命题公式
摩根律 : (AB) = AB，
(AB) = AB
吸收律: A(AB) = A, A(AB) = A
零律:
AT = T, AF = F
同一律: AF = A, AT = A
TA = A， T A = A，
补余律: AA = T， AA = F，
等值公式
2. 常用等值公式
公式A的子公式置换后，A化为公式B，必有A = B
n 等值演算
n 由已知的等值公式推演出新的等值公式的过程 n 如已知: AA = A
则: BAA = BA
n 等值演算的基础： (1) 等值关系的性质：自反、对称、传递 (2) 基本的等值式 (3) 置换规则
三个重要的等值式
P Q = P Q P Q = (P Q) ( P Q )
C
P∧Q
FF
T
T
F
T
P∧Q
FT
T
T
F
F
TF
F
F
T
T
P∧Q
TT
T
F
F 任意
2.3 命题公式与真值表的关系
按真值表列出命题公式的方法
从F来列出
如下表中B为F有二种可能
所以，B的命题公式形式为：□ ∧ □
而取F相应的P、Q解释分别为： P∨Q 、 P∨ Q
所以，B=(P∨Q)∧(P∨Q ) 同理，A= P∨Q
按真值表列出命题公式的方法
从T来列出
如下表中A为T有三种可能
所以，A的命题公式形式为：□∨ □ ∨□ 而取T相应的P、Q解释分别为： P∧Q、P∧Q、 P∧Q
所以，A=(P∧Q) ∨(P∧Q) ∨(P∧Q)

类似的讨论可知，若Ai是含n个命题变项的简单合取式，且 Ai为矛盾式，则Ai中必同时含某个命题变项及它的否定式， 反之亦然。
2.2 析取范式和合取范式
定理2.1 (1)一个简单析取式是重言式当且仅当它同时含有某个命题
变项及它的否定式。 (2)一个简单合取式是矛盾式当且仅当它同时含有某个命题
变项及它的否定式。 定义2.3 (1)由有限个简单合取式构成的析取式称为析取范式
A∨1 1,A∧0 0 A∨0 A，A∧1 A A∨┐A 1 A∧┐A 0 A→B ┐A∨B AB (A→B)∧(B→A) A→B ┐B→┐A AB ┐A┐B (A→B)∧(A→┐B) ┐A
对偶原理
一个逻辑等值式，如果只含有┐、∨、∧、0、1 那么同时
把∨和∧互换 把0和1互换 得到的还是等值式。
(A∨B)∨C A∨(B∨C) (A∧B)∧C A∧(B∧C)
A∨(B∧C) (A∨B)∧(A∨C) （∨对∧的分配律）
A∧(B∨C) (A∧B)∨(A∧C) （∧对∨的分配律）
┐(A∨B) ┐A∧┐B ┐(A∧B) ┐A∨┐B
A∨(A∧B) A，A∧(A∨B) A
基本等值式
8.零律 9.同一律 10.排中律 11.矛盾律 12.蕴涵等值式 13.等价等值式 14.假言易位 15.等价否定等值式 16.归谬论
例2.5 解答
(1) (p→q)∧p→q
(┐p∨q)∧p→q
（蕴涵等值式）
┐((┐p∨q)∧p)∨q
（蕴涵等值式）
(┐(┐p∨q)∨┐p)∨q
（德摩根律）
((p∧┐q)∨┐p)∨q
（德摩根律）
((p∨┐p)∧(┐q∨┐p))∨q （分配律）
(1∧(┐q∨┐p))∨q

6/2/2013 9:02 PM Discrete Math. , Chen Chen 15
例2.6
CHAPTER TWO
例2.6 在某次研讨会的休息时间，3名与会者根据王教授的口音 对他是哪个省市的人进行了判断： 甲说王教授不是苏州人，是上海人。
乙说王教授不是上海人，是苏州人。 丙说王教授不是上海人，也不是杭州人。 听完3人的判断，王教授笑着说，他们3人中有一人说得全对， 有一人说对了一半，有一人说得全不对。试用逻辑演算法分析 王教授到底是哪里的人？ 解： 设命题 p, q, r分别表示 ： 王教授是苏州、上海、杭州人。 则p, q, r中必有一个真命题，两个假命题。要通过逻辑演算将 真命题找出来。 设： 甲的判断为： A1= ┐p∧q; 乙的判断为：A2= p∧┐q; 丙的 判断为：A3= ┐q∧r。
等值式模式
CHAPTER TWO
当命题公式中变项较多时，用上述方法判断两个公式是否 等值计算量很大。为此，人们将一组经检验为正确的等值式作 为等值式模式，通过公式间的等值演算来判断两公式是否等值。 常用的等值式模式如下：
1.双重否定律：A⇔ ┐(┐A) 2.幂等律：A⇔A∨A, A⇔A∧A
3.交换律: A∨B⇔B∨A, A∧B⇔B∧A 4.结合律: (A∨B)∨C⇔A∨(B∨C), (A∧B)∧C⇔A∧(B∧C) 5.分配律：A∨(B∧C)⇔(A∨B)∧(A∨C) (∨对∧的分配律)
⇔ ┐(┐p∨q)∨r (蕴含等值式，置换规则） ⇔ (p∧┐q)∨r (德摩根律，置换规则）
⇔(p∨r)∧(┐q∨r)(分配律，置换规则） 为简便起见, 以后凡用到置换规则时, 均不必标出。
6/2/2013 9:02 PM Discrete Math. , Chen Chen 10

2.1.1 等值的定义

给定两个命题公式A和B, 而P1…Pn是出现于A和B中的 所有命题变项, 那么公式A和B共有2n个解释, 若对其 中的任一解释, 公式A和B的真值都相等, 就称A和B是 等值的(或等价的)。记作A = B或AB 显然，可以根据真值表来判明任何两个公式是否是等 值的

ቤተ መጻሕፍቲ ባይዱ1: 证明(P∧P)∨Q = Q
第二章 命题逻辑的等值和推理演算



推理形式和推理演算是数理逻辑研究的基本内容 推理形式是由前提和结论经蕴涵词联结而成的 推理过程是从前提出发，根据所规定的规则来推 导出结论的过程 重言式是重要的逻辑规律，正确的推理形式、等 值式都是重言式


本章对命题等值和推理演算进行讨论，是以语义 的观点进行的非形式的描述，不仅直观且容易理 解，也便于实际问题的逻辑描述和推理。 严格的形式化的讨论见第三章所建立的公理系统。
2.1 等值定理

若把初等数学里的＋、－、×、÷等运算符看作是数 与数之间的联结词，那么由这些联结词所表达的代数 式之间，可建立许多等值式如下： x2－y2 = (x＋y)(x－y) (x＋y)2 = x2＋2xy＋y2 sin2x＋cos2x = 1 ……
在命题逻辑里也同样可建立一些重要的 等值式
证明: 画出(P∧P)∨Q与Q的真值表可看出等式 是成立的。
例2: 证明P∨P = Q∨Q

证明: 画出P∨P, Q∨Q的真值表, 可看出它 们是等值的, 而且它们都是重言式。
说明

从例1、2还可说明, 两个公式等值并不一定要 求它们一定含有相同的命题变项


若仅在等式一端的公式里有变项P出现, 那么等式 两端的公式其真值均与P无关。 例1中公式(P∧P)∨Q与Q的真值都同P无关 例2中P∨P, Q∨Q都是重言式, 它们的真值也都 与P、Q无关。

命题公式等值演算命题公式等值演算（Propositional Formula Equivalence）是数理逻辑领域中的一个重要概念和技巧。

本文将介绍命题公式等值演算的基本思想和常用方法，并通过一些例子来详细说明。

一、命题公式等值关系的定义在逻辑学和计算机科学中，命题公式是由包含命题变量、逻辑运算符和括号构成的表达式。

而命题公式等值关系则是指两个命题公式具有相同的真值。

换句话说，当且仅当两个命题公式在每一个赋值下具有相同的真值时，它们才是等值的。

例如，对于命题变量p和q，表达式(p∧q)∨(¬p∧¬q)和(p∨¬q)∧(¬p∨q)是等值的，因为它们在每一个赋值下的真值相同。

二、命题公式等值演算的基本规则命题公式等值演算是通过一系列基本规则来推导等值式的过程。

下面是一些常用的基本规则：1. 交换律：p∧q ≡ q∧p，p∨q ≡ q∨p2. 结合律：(p∧q)∧r ≡ p∧(q∧r)，(p∨q)∨r ≡ p∨(q∨r)3. 分配律：p∧(q∨r) ≡ (p∧q)∨(p∧r)，p∨(q∧r) ≡ (p∨q)∧(p∨r)4. 吸收律：p∧(p∨q) ≡ p，p∨(p∧q) ≡ p5. 否定律：p∨¬p ≡ T，p∧¬p ≡ F6. 德摩根定律：¬(p∧q) ≡ ¬p∨¬q，¬(p∨q) ≡ ¬p∧¬q7. 双重否定律：¬(¬p) ≡ p三、命题公式等值演算的应用命题公式等值演算是数理逻辑中的一项基础技术，可以应用于证明命题的等价关系、简化复杂的命题公式以及构造等价的命题公式等领域。

1. 证明等价关系通过命题公式等值演算，可以证明两个命题公式之间的等价关系。

例如，要证明(p∨q)∧(¬p∨q) ≡ q，可以使用分配律、交换律和吸收律等基本规则进行推导。

2. 简化命题公式当给定一个复杂的命题公式时，可以利用命题公式等值演算的基本规则来简化它，使得它更加易于理解和计算。

mi(Mi)称为极小项(极大项)的名称。且有mi Mi ,
Mi mi。
例 2 由p, q两个命题变项形成的极小项与极大项
例 3 p, q, r三个命题变项形成的极小项与极大项
三、主范式
1、主析取范式：由极小项构成的析取范式。
2、主合取范式：由极大项构成的合取范式。
3、主范式：主析取范式与主合取范式统称为主范式。
值。
方法三 用等值演算先化简两个公式，再观察.
例3用等值演算法判断下列公式的类型
(1) q(pq)
解： q(pq)
q(pq) （蕴涵等值式）
q(pq)
（德摩根律）
p(qq)
（交换律，结合律）
p0
（矛盾律）
0
（零律）
由最后一步可知，该式为矛盾式.
(pq)r
（否定号内移——德摩根律）
这一步已为析取范式（两个简单合取式构成）
继续： (pq)r
(pr)(qr) （对分配律）
得到合取范式（由两个简单析取式构成）。
二、极小项与极大项
1、定义 在含有n个命题变项的简单合取式(简单析取式)中，若每个命题变项（或它的
否定式）均以文字的形式出现且仅出现一次，称这样的简单合取式(简单析取式)为极
离散数学
第二章 命题逻辑等值演算
|
第二章 命题逻辑等值演算
一、等值式
1、等值式：设A，B是命题公式，且AB为重言式,则称A与B是等值的，记作AB。
说明 ：1）符号不是联结符，只是一种记法。
2）若A与B的真值表相同（真值表法），则AB；否则A
B。
3）判断公式等值的方法——利用已知的等值式通过代换得到新的等值式。
五、主范式的应用

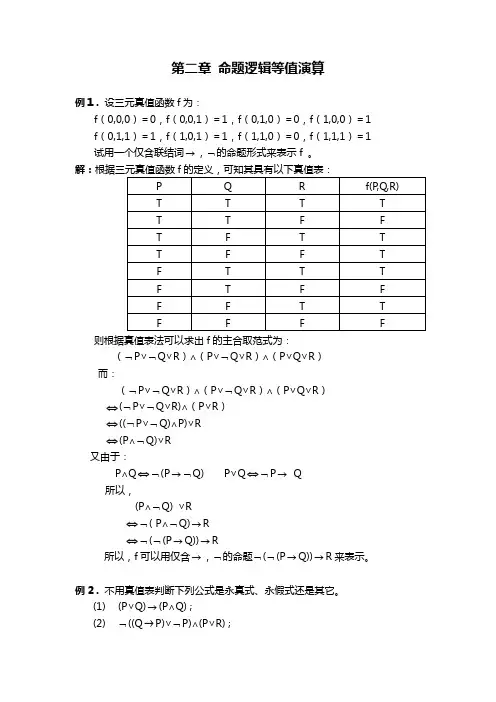
第二章命题逻辑等值演算例1 . 设三元真值函数f为：f（0,0,0）＝0，f（0,0,1）＝1，f（0,1,0）＝0，f（1,0,0）＝1 f（0,1,1）＝1，f（1,0,1）＝1，f（1,1,0）＝0，f（1,1,1）＝1 试用一个仅含联结词→，⌝的命题形式来表示f 。

解：则根据真值表法可以求出f的主合取范式为：（⌝P∨⌝Q∨R）∧（P∨⌝Q∨R）∧（P∨Q∨R）而：（⌝P∨⌝Q∨R）∧（P∨⌝Q∨R）∧（P∨Q∨R）⇔(⌝P∨⌝Q∨R)∧（P∨R）⇔((⌝P∨⌝Q)∧P)∨R⇔(P∧⌝Q)∨R又由于：P∧Q⇔⌝(P→⌝Q) P∨Q⇔⌝P→Q所以，(P∧⌝Q) ∨R⇔⌝( P∧⌝Q)→R⇔⌝(⌝(P→Q))→R所以，f可以用仅含→，⌝的命题⌝(⌝(P→Q))→R来表示。

例2 . 不用真值表判断下列公式是永真式、永假式还是其它。

(1)(P∨Q)→(P∧Q) ;(2)⌝((Q→P)∨⌝P)∧(P∨R) ;(3)((⌝P∨Q)→R)→((P∨⌝Q)∨R) .解：（1）(P∨Q)→(P∧Q) ⇔⌝(P∨Q)∨(P∧Q) ⇔(⌝P∧⌝Q)∨(P∧Q) 所以，(P∨Q)→(P∧Q)既非永真式也非永假式。

（2）⌝((Q→P)∨⌝P)∧(P∨R) ⇔⌝((⌝Q∨P)∨⌝P)∧(P∨R)⇔⌝T∧(P∨R) ⇔F∧(P∨R) ⇔F所以，⌝((Q→P)∨⌝P)∧(P∨R)为永假式。

（3）((⌝P∨Q)→R)→((P∨⌝Q)∨R) ⇔(⌝(⌝P∨Q)∨R)→((P∨⌝Q)∨R) ⇔((P∨⌝Q)∨R)→((P∨⌝Q)∨R) ⇔T所以，((⌝P∨Q)→R)→((P∨⌝Q)∨R)为永真式。

例3 .证明下列等价式。

（1）(P→Q)∧(P→R) ⇔P→Q∧R ;（2）P∧Q∧(⌝P∨⌝Q) ⇔⌝P∧⌝Q∧(P∨Q) .解：说明: 这两道题看似麻烦，但是如果不采用直接推导的方法，而是利用范式或是左右夹击推导的方法，会起到事半功倍的效果。

再如 ┑p ∨ q 既是p →q的析取范式又是它的的合取范式
如果公式的范式不唯一则对于将公式按等值进行分类的利用价值就不高
p q (p → q)∧(q→p) (p∧q)∨(┓p∧┓q)
00
1
1
01
0
0
10
0
0
11
1
1
（0,0）与（1,1）为公式的成真赋值。 （0,1）与（1,0）为公式的成假赋值
命题公式的分类（根据公式在赋值下的真值情况进行分类） 1）若命题公式在它的各种赋值下取值均为真,则称命题公式是重言
式或永真式。 2）若命题公式在它的各种赋值下取值均为假,则称命题公式是矛盾
2
如：┐Q∧（Ｐ→Q） → ┐P
4
分析1：若要得出：当设 A为真，B为
假的情况不会出现，
5
那么A →B 为永真式。
6
可证明：设前件为真
7
分析2： 还可以从设 B为假，推出A
为真的情况不会出现（A为假），
9
证明： 设后件为假
8
那么A →B 为永真式。
1 0
(（Ｐ→Q）∧( Q→R)) →(Ｐ→R)
不同真值表的公式 1）当命题变元确定后，通过五个连接词及其命题变元可以构成 无数个不 同表现形式的命题公式。 问题：这些不同形式的命题公式的真值表是否都不相同？ 先看变元仅有两个p,q 那么关于这两个变元的公式的赋值仅有4组
（┐p ∨ q）∧（┐q∨┐p∨r）∧┐q
是含三个简单析取式的合取范式．
2、性质：
1)一个析取范式是矛盾式当且仅当它的每个简单合取式都是矛盾式
2)一个合取范式是重言式当且仅当它的每个简单析取式都是重言式
┐p ∧ P ∨ ┐ q∧ q ⇔ 0 ∨ 0 ⇔ 0

1命题逻辑的等值演算这一讲讨论命题公式之间的等值关系，其中一些重要的等值关系将用于对命题公式进行等值运算和设计推理规则。

1. 等值式定义1.1 若命题公式A 和B 是恒等的布尔代数式，即在任何赋值下二者的值总相等，则称二者是等值的，记为A B A B ≡⇔或者称为等值式。

注意，等值式不是逻辑公式，而是逻辑学的公式。

显然，A ≡B 当且仅当A B ↔是永真公式。

等值关系的性质：（1） 自反性：对任何公式A ，都有 A A ≡。

（2） 对称性：若 A B ≡，则 B A ≡。

（3） 传递性：若 A B ≡且若 B C ≡，则 A C ≡。

例1.2 试证明下列等值式。

a a ⌝⌝≡证明：当a =1时，左式=101⌝⌝=⌝==右式。

当a =0时，左式=010⌝⌝=⌝==右式。

因此，左式恒等于右式。

依定义，该等值式成立。

例1.3试证明下列等值式。

()()() a b c a b a c ∧∨≡∧∨∧证明：当a =1时，左式=b c ∨，右式=b c ∨，两边相等。

当a =0时，左式=0，右式=0，两边相等。

因此，该等值式成立。

2上述两例中的证明方法可以称为代数分析法。

还有一种演算方法，可以将将左式等值地变形为右式。

这种保持公式真值的演算称为等值演算。

2. 等值演算规则：替换等值演算是将当前公式中的某个子公式替换为与之等值的公式。

替换在课本中称为置换，与抽象代数中的置换（permutation ）是不同的概念。

替换的定义如下。

定义3.1 设[] A Φ是一个命题公式，A 是出现在其中某处的一个子公式。

若用另外一个公式B 替换[] A Φ中的A ，则可得一个新公式，记为[] A Φ。

我们称这种公式变形为替换（replacement ）。

注意，这里A 是指[] A Φ中某一处出现的子公式，不是[] A Φ中所有与A 相同的子公式。

例如，将()()p q p r ⌝⌝→∨⌝⌝→中第二次出现的子公式p ⌝⌝替换为p ，得()()p q p r ⌝⌝→∨→定理3.2（替换原理）若 A B ≡，则[][] A B Φ≡Φ。

如果将真值1，0 看做是数，则每一个解释对应一 个n位二进制数。 假设使极小项m取1值的解释对应的二进制数为i， 今后将m记为mi。
例:
对p，q，r而言，pqr是极小项 解释{p，q，r}使该极小项取1值，解释{p，q， r} 对应的二进制数是2 (010) 于是pqr记为m2
例：
(p(qr))s (p(qr))s p(qr)s p(qr)s …………….
式)
(ps)(qr) (psq)(psr)
( 析取范
…… (合取范式)
主范式
定义2. 4 设p1,…,pn是n个不同原子，一个简单合取式如果 恰好包含所有这n个原子或其否定，且其排列顺序与 p1,…,pn的顺序一致，则称此简单合取式为关于p1,…,pn的 一个极小项。 显然，共有2n个不同的极小项。 例如: 对原子 p，q，r 而言， pqr，pqr，pqr 都是 极小项，但是，p，pq不是极小项， 对原子p，q而言,pq是极小项。
例
判断公式 (pq)(qr)(rp)是否永假? 解： (pq)(qr)(rp) (pq)(qr)(rp) ((pq)(qq)(pr)(qr))(rp) (pqr)(qqr)(prr)(q rr)(pqp)(qqp)(prp) (qrp) 故公式(pq)(qr)(rp)不是永假的。
命题公式和真值表的关系
从0来列写
B (…) ∧ (…)
由1列写的方式进行转化： B (…)∨ (…) B (…) ∧ (…) (…) 写成析取式，表示一种 B 值为假的情况。如 p=1，q=0 时为假，
(…) 写成p ∧q， (…)写成 p ∨ q
1值取p形式
定理
对于任意公式G，存在唯一一个与G等值的主析取 范式。

等值演算的应用举例
证明两个公式等值 (p→q)→r (p∨r)∧(┐q∨r)
解答
(p→q)→r (┐p∨q)→r ┐(┐p∨q)∨r (p∧┐q)∨r
（蕴含等值式、置换规则） （蕴含等值式、置换规则） （德摩根律、置换规则）
(p∨r)∧(┐q∨r) （分配律、置换规则） 也可以从右边开始演算
• 两公式什么时候代表了同一个命题呢？ • 抽象地看，它们的真假取值完全相同时 即代表了相同的命题。 • 设公式A,B共同含有n个命题变项，若A 与B有相同的真值表，则说明在2n个赋值 的每个赋值下，A与B的真值都相同。于 是等价式AB应为重言式。
等值的定义及说明
定义1.10 设A,B是两个命题公式，若A,B构成的 等价式AB为重言式，则称A与B是等值的，记 作 AB。 不能写成=，逻辑演算与数学演算不同。
• 这些具体的等值式都被称为原来的等值式模式的 代入实例。 • 由已知的等值式推演出另外一些等值式的过程为 等值演算。 • 置换规则 设Φ(A)是含公式A的命题公式，Φ(B)是 用公式B置换了Φ(A)中所有的A后得到的命题公 式，若BA，则Φ(B)Φ(A)。
关于等值演算的说明
• 等值演算的基础 – 等值关系的性质： 自反性：AA。 对称性：若AB，则BA。 传递性：若AB且BC，则AC。 – 基本的等值式 – 置换规则 • 等值演算的应用 – 证明两个公式等值 – 判断公式类型 – 解判定问题
8.零律 9.同一律 10.排中律 11.矛盾律 12.蕴涵等值式 13.等价等值式 14.假言易位 15.等价否定等值式 16.归谬论
A∨1 1,A∧0 0 A∨0 A，A∧1 A A∨┐A 1 A∧┐A 0 A→B ┐A∨B AB (A→B)∧(B→A) A→B ┐B→┐A AB ┐A┐B (A→B)∧(A→┐B) ┐A