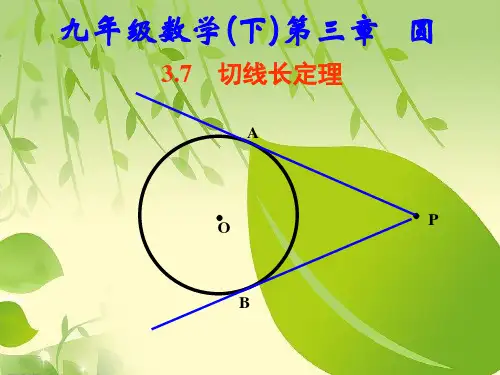
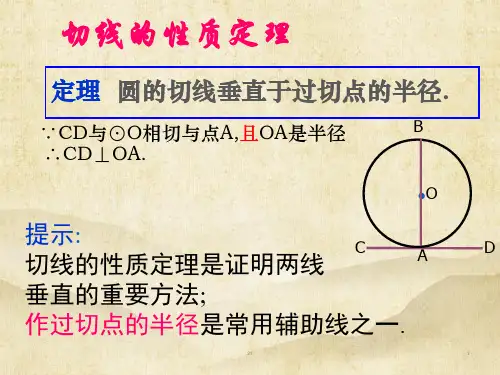
﹡7 切线长定理
【基础梳理】 1.切线长定义 过圆外一点作圆的切线,这点和切点之间的_线__段__长__叫做 这点到圆的切线长.
2.切线长定理
切线长定理 文字叙述 过圆外一点画圆的两条切线,它们的切线长_相__等__.
如图,∵AB,AC都是圆O的切线,切点 符号语言 分别是点B、点C.
∴AB=_A_C_
∴由勾股定理得,2OA2=OP2, 即OA2=8,∴OA=2 2 .即半径长为2 2 .
【微点拨】 切线长定理中的一二三 如图,PA,PB与☉O相切,切点分别是A,B,则此 图中包含信息有: 1.一条角平分线:即PO平分∠APB且平分∠AOB. 2.两个等腰三角形:△PAB,△AOB是等腰三角形. 3.三个垂直:即OA⊥PA,OB⊥PB,PO⊥AB.
知识点二 切线长定理的应用 【示范题2】如图,边长为1的正方形ABCD的边AB是☉O 的直径,CF是☉O的切线,E为切点,F点在AD上,BE是☉O 的弦,求△CDF的面积.
【备选例题】如图,PA,PB是☉O的切线,A, B为切点,AC是☉O的直径,∠P=60°. (1)求∠BAC的度数. (2)当OA=2时,求AB的长.
知识点一 切线长定理 【示范题1】如图,PA切☉O于A,PB切☉O于B,∠APB= 90°,OP=4,求☉O的半径.
【思路点拨】先判断四边形OAPB为正方形,再由勾股定 理求得圆的半径. 【自主解答】∵PA切☉O于B=90°,OA=OB,∴四边形OAPB为正方形, ∴AO=AP,∵OP=4,
【解析】(1)∵PA,PB是☉O的切线, ∴AP=BP. ∵∠P=60°, ∴∠PAB=60°, ∵AC是☉O的直径, ∴∠PAC=90°, ∴∠BAC=90°-60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°, ∴OP=4. 由勾股定理得:AP=2 3 . ∵AP=BP,∠APB=60°, ∴△APB是等边三角形, ∴AB=AP=2 3 .