判断推理常用公式

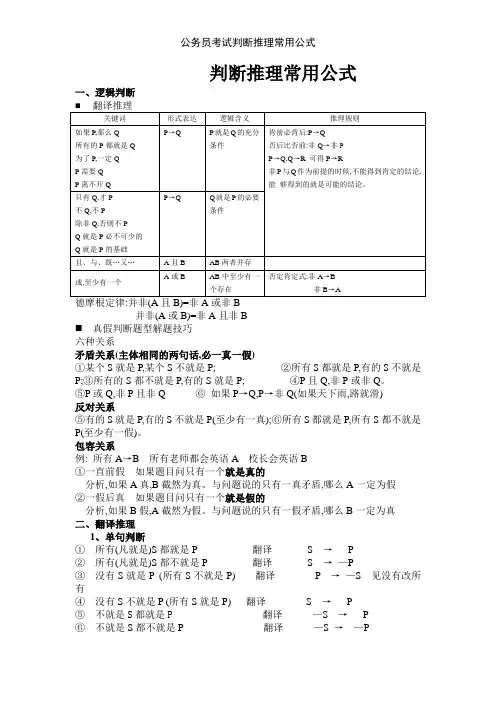
判断推理常用公式一、逻辑判断并非(A或B)=非A且非B⏹真假判断题型解题技巧六种关系矛盾关系(主体相同的两句话,必一真一假)①某个S就是P,某个S不就是P; ②所有S都就是P,有的S不就是P;③所有的S都不就是P,有的S就是P; ④P且Q,非P或非Q。

⑤P或Q,非P且非Q⑥如果P→Q,P→非Q(如果天下雨,路就滑)反对关系⑤有的S就是P,有的S不就是P(至少有一真);⑥所有S都就是P,所有S都不就是P(至少有一假)。

包容关系例: 所有A→B 所有老师都会英语A 校长会英语B①一直前假如果题目问只有一个就是真的分析,如果A真,B截然为真。

与问题说的只有一真矛盾,哪么A一定为假②一假后真如果题目问只有一个就是假的分析,如果B假,A截然为假。

与问题说的只有一假矛盾,哪么B一定为真二、翻译推理1、单句判断①所有(凡就是)S都就是P 翻译S →P②所有(凡就是)S都不就是P 翻译S →—P③没有S就是P (所有S不就是P) 翻译P →—S 见没有改所有④没有S不就是P (所有S就是P) 翻译S →P⑤不就是S都就是P 翻译—S →P⑥不就是S都不就是P 翻译—S →—P2、否定关系1、并非所有A都就是B 等价于有的A不就是B(并非所有换成有的,就是换不就是)2、并非有的A就是B 等价于所有A都不就是B(并非有的换成所有,就是换成不就是)3、等价关系1、所有的A都不就是B 等价于所有的B都不就是A2、有的A就是B 等价于有的B就是啊五个解题步骤①符号化;②找关系(六种关系);③推知其余项真假;④根据其余项真假,得出真实情况;⑤带回“矛盾或反对”项,判断其真假。

排列组合题型1、选项信息充分,运用排除法,2、选项不处分,找推理起点:信息最大优先,特殊信息优先■削弱题型方法:１、否因削弱已知因果推理主线:因→果否因削弱:强调原因不成立或起不到作用。

2、她因已知推理主线:因→果她因削弱:强调存在别的原因会导致该结果,或者导致不了该结果。

逻辑命题与推理必然性推理（演绎推理）：对当关系推理、三段论、复合命题推理、关系推理和模态推理可能性推理：归纳推理（枚举归纳、科学归纳）、类比推理命题直言命题的种类：（AEIOae）⑴全称肯定命题：所有S是P（SAP）⑵全称否定命题：所有S不是P（SEP）⑶特称肯定命题：有的S是P（SIP）⑷特称否定命题：有的S不是P（SOP）⑸单称肯定命题：某个S是P（SaP）⑹单称否定命题：某个S不是P（SeP）直言命题间的真假对当关系：矛盾关系、（上）反对关系、（下）反对关系、从属关系矛盾关系：具有矛盾关系的两个命题之间不能同真同假。

主要有三组：SAP与SOP之间。

“所有同学考试都几个了”与“有些同学考试不及格”SEP与SIP之间。

“所有同学考试不及格”与“有些同学考试及格”SaP与SeP之间。

“张三考试及格”与“张三考试不及格”上反对关系：具有上反对关系的两个命题不能同真（必有一假），但是可以同假。

即要么一个是假的，要么都是假的。

存在于SAP与SEP、SAP与SeP、SEP与SaP之间。

下反对关系：具有下反对关系的两个命题不能同假（必有一真），但是可以同真。

即要么一个是真的，要么两个都是真的。

存在于SIP与SOP、SeP与SIP、SaP与SOP之间。

从属关系（可推出关系）：存在于SAP与SIP、SEP与SOP、SAP与SaP、SEP与SeP、SaP与SIP、SeP与SOP六种直言命题之间存在的对当关系可以用一个六角图形来表示，“逻辑方阵图”SAP SEPSaP SePSIP SOP直言命题的真假包含关系全同关系、真包含于关系、真包含关系、交叉关系、全异关系复合命题：负命题、联言命题、选言命题、假言命题负命题的一般公式：并非P联言命题公式：p并且q “并且、…和…、既…又…、不但…而且、虽然…但是…”选言命题：相容的选言命题、不相容的选言命题相容的选言命题公式：p或者q“或、或者…或者…、也许…也许…、可能…可能…”【一个相容的选言命题是真的，只有一个选言支是真的即可。

逻辑命题与推理之青柳念文创作必定性推理（演绎推理）：对当关系推理、三段论、复合命题推理、关系推理和模态推理能够性推理：归纳推理（列举归纳、迷信归纳）、类比推理命题直言命题的种类：（AEIOae）⑴全称必定命题：所有S是P（SAP）⑵全称否定命题：所有S不是P（SEP）⑶特称必定命题：有的S是P（SIP）⑷特称否定命题：有的S不是P（SOP）⑸单称必定命题：某个S是P（SaP）⑹单称否定命题：某个S不是P（SeP）直言命题间的真假对当关系：抵触关系、（上）反对关系、（下）反对关系、从属关系抵触关系：具有抵触关系的两个命题之间不克不及同真同假.主要有三组：SAP与SOP之间.“所有同学测验都几个了”与“有些同学测验不及格”SEP与SIP之间.“所有同学测验不及格”与“有些同学测验及格”SaP与SeP之间.“张三测验及格”与“张三测验不及格”上反对关系：具有上反对关系的两个命题不克不及同真（必有一假），但是可以同假.即要么一个是假的，要么都是假的.存在于SAP与SEP、SAP与SeP、SEP与SaP之间.下反对关系：具有下反对关系的两个命题不克不及同假（必有一真），但是可以同真.即要么一个是真的，要么两个都是真的.存在于SIP与SOP、SeP与SIP、SaP与SOP之间.从属关系（可推出关系）：存在于SAP与SIP、SEP与SOP、SAP与SaP、SEP与SeP、SaP与SIP、SeP与SOP六种直言命题之间存在的对当关系可以用一个六角图形来暗示，“逻辑方阵图”SAP SEPSaP SePSIP SOP直言命题的真假包含关系全同关系、真包含于关系、真包含关系、交叉关系、全异关系合同关系真包含于关系真包含关系交叉关系全异关系SAP 真真假假假SEP 假假假真真SIP 真真真真假SOP 假假真真真复合命题：负命题、联言命题、选言命题、假言命题负命题的一般公式：并不是P联言命题公式：p而且q “而且、…和…、既…又…、不单…而且、虽然…但是…”选言命题：相容的选言命题、不相容的选言命题相容的选言命题公式：p或者q“或、或者…或者…、也许…也许…、能够…能够…”【一个相容的选言命题是真的，只有一个选言支是真的即可.只有当全部选言支都假时，相容的选言命题才是假的】不相容选言命题公式：要么p要么q“要么…要么…、不是…就是…、或者…或者…二者必居其一、或者…或者…二者不成兼得”【一个不相容的选言命题是真的，有且只有一个选言支是真的.当选言支全真或全假时，此命题为假】假言命题：充分条件假言命题、需要条件假言命题、充要条件假言命题充分条件假言命题公式：如果p，那末q“如果…就…、有…就有…、倘若…就…、哪里有…哪里有…、一旦…就…、假若…、只要…就…”【有前件必定有后件.如果有前件却没有后件，这个充分条件假言命题就是假的.因此，对于一个充分条件的假言命题来讲，只有当其前件真而后件假时，命题才假.】需要条件假言命题公式：只有p，才q“没有…就没有…、不…不…、除非…不…、除非…才…”【没有前件必定没有后件.如果没有前件也有后件，这个需要假言命题为假.对于一个需要条件的假言命题来讲，只有当其前件假而后件真时，命题才假.】充要条件假言命题公式：当且仅当p，才q【有前件必定有后件，没有前件必定没有后件.充要条件假言命题在前件与后件等值即前件真而且后件真，或者前件假而且后件假时，命题为真，在前件与后件不等值即前真后假，或前假后真时，命题为假】充分条件与需要条件之间可以相互转化：如果p，那末q＝＝＝只有q，才p只有p，才q，＝＝＝如果q，那末p模态命题：反映事物存在或发展的必定性或能够性的命题.模态命题包含“必定”、“能够”等模态词.必定必定命题：必定P必定否定命题：必定非P能够必定命题：能够p能够否定命题：能够非P四者之间的关系如下：模态方阵必定P 必定非P能够P 能够非P推理1、直言命题的变形推理：换质推理、换位推理⑴换质推理也就是改变谓项.“是”或者“不是”除了改变联项外，同时还需要把结论中的谓项变成前提谓项的抵触概念.“所有S是P”可以换质为“所有S不是非P”“所有S不是P”可以换质为“所有S是非P”“有些S是P”可以换质为“有些S不是非P”“有些S不是P”可以换质为“有些S是非P”⑵换位推理就是改变前提中主项与谓项的位置.除了交换主项与谓项的位置外，还需要注意的是在前提中不周延的词项在结论中也不克不及周延.“所有S是P”换位为“有些P是S”“所有S不是P”换位为“所有P不是S”“有些S是P”换位为“有些P是S”注意：“有些S不是P”不克不及换位为“有些P不是S”2、联言推理：分解式与组合式分解式就是由前提中一个联言命题为真，推出其任一支命题为真的联言命题.组合式就是由前提中一些支命题为真推出这些支命题所组成的联言命题为真的联言推理.3、选言推理：相容的选言推理与不相容的选言推理相容的选言推理规则：（只有一种有效的推理形式，即否定必定式）否定一部分选言支，就要必定另外一部分选言支；必定一部分选言支，不克不及因此而否定另外一部分选言支；不相容的选言推理规则：（否定必定式、必定否定式）否定除了一个选言支以外的其余选言支，就要必定阿谁没有被否定的选言支；必定一个选言支，就要否定其余的选言支；4、假言推理充分条件的假言推理规则：（有效推理：必定前件式，否定后件式）必定前件就要必定后件，否定后件就要否定前件；否定前件不克不及否定后件，必定后件不克不及必定前件；需要条件的假言推理规则：（有效推理：否定前件式；必定后件式）否定前件就要否定后件，必定后件就要必定前件；必定前件不克不及必定后件，否定后件不克不及否定前件；充要条件的假言推理规则：必定前件就要必定后件，否定后件就要否定前件；否定前件就要否定后件，必定后件就要必定前件；假言连锁推理：要求：前提中的第一个假言命题的后件必须与第二个假言命题的前件相同.充分条件的假言连锁推理：如果p那末q如果q，那末r所以，如果p，那末r需要条件的假言连锁推理：只有p，才q只有q，才r所以，只有p才r5、模态推理“必定P”与“并不是能够非P”可以互相推出“必定非P”与“并不是能够P”可以相互推出“能够P”与“并不是必定非P”可以相互推出“能够非P”与“并不是必定P”可以相互推出一个模态命题的负命题等值于与该模态命题具有抵触关系的命题.并不是必定P＝＝＝能够非P并不是必定非P＝＝＝能够P并不是能够P＝＝＝必定非P并不是能够非P＝＝＝必定P“必定P”可以推出“能够P”“必定非P”可以推出“能够非P”“并不是能够P”可以推出“并不是必定P”“并不是能够非P”可以推出“并不是必定非P”能够性推理类型：削弱型：最能削弱型、最不克不及削弱型加强型前提与预设型诠释型：最能诠释、最不克不及诠释评价型结论性词项的周延性主项的周延性是由量项来决议的，量项是全称的则主项周延，量项是特称的则主项不周延；谓项的周延性是由联项来决议的，联项是必定的则谓项不周延，联项是否定的，则谓项周延.六种直言命题之间存在的对当关系可以用一个六角图形来暗示，“逻辑方阵图”SAP SEPSaP SePSIP SOP直言命题的真假包含关系（全同关系、真包含于关系、真包含关系、交叉关系、全异关系）合同关系真包含于关系真包含关系交叉关系全异关系SAP 真真假假假SEP 假假假真真SIP 真真真真假SOP 假假真真真四者之间的关系如下：模态方阵必定P 必定非P能够P 能够非P相容的选言推理规则：（只有一种有效的推理形式，即否定必定式）不相容的选言推理规则：（否定必定式、必定否定式）充分条件的假言推理规则：（有效推理：必定前件式，否定后件式）需要条件的假言推理规则：（有效推理：否定前件式；必定后件式）。

判断推理常用公式一、逻辑判断⏹翻译推理关键词形式表达逻辑含义推理规则如果P，那么Q 所有的P都是Q 为了P，一定Q P需要QP离不开Q P→Q P是Q的充分条件肯前必肯后：P→Q否后比否前：非Q→非PP→Q，Q→R 可得P→R非P和Q作为前提的时候，不能得到肯定的结论，能够得到的是可能的结论。

只有Q，才P不Q，不P除非Q，否则不P Q是P必不可少的Q是P的基础P→Q Q是P的必要条件且、和、既…又…A且B AB两者并存或，至少有一个A或B AB中至少有一个存在否定肯定式：非A→B非B→A德摩根定律：并非（A且B）=非A或非B并非（A或B）=非A且非B⏹真假判断题型解题技巧六种关系矛盾关系（主体相同的两句话，必一真一假）①某个S是P，某个S不是P；②所有S都是P，有的S不是P；③所有的S都不是P，有的S是P；④P且Q，非P或非Q。

⑤P或Q，非P且非Q⑥如果P→Q，P→非Q（如果天下雨，路就滑）反对关系⑤有的S是P，有的S不是P（至少有一真）；⑥所有S都是P，所有S都不是P （至少有一假）。

包容关系例：所有A→B 所有老师都会英语A 校长会英语B①一直前假如果题目问只有一个是真的分析，如果A真，B截然为真。

与问题说的只有一真矛盾，哪么A一定为假②一假后真如果题目问只有一个是假的分析，如果B假，A截然为假。

与问题说的只有一假矛盾，哪么B一定为真二、翻译推理1、单句判断①所有（凡是）S都是P 翻译S →P②所有（凡是）S都不是P 翻译S →—P③没有S是P （所有S不是P）翻译P →—S 见没有改所有④没有S不是P （所有S是P）翻译S →P⑤不是S都是P 翻译—S →P⑥不是S都不是P 翻译—S →—P2、否定关系1、并非所有A都是B 等价于有的A不是B（并非所有换成有的，是换不是）2、并非有的A是B 等价于所有A都不是B（并非有的换成所有，是换成不是）3、等价关系1、所有的A都不是B 等价于所有的B都不是A2、有的A是B 等价于有的B是啊五个解题步骤①符号化；②找关系（六种关系）；③推知其余项真假；④根据其余项真假，得出真实情况；⑤带回“矛盾或反对”项，判断其真假。

逻辑命题与推理必然性推理（演绎推理）：对当关系推理、三段论、复合命题推理、关系推理和模态推理可能性推理：归纳推理（枚举归纳、科学归纳）、类比推理命题直言命题的种类：（AEIOae）⑴全称肯定命题：所有S是P（SAP）⑵全称否定命题：所有S不是P（SEP）⑶特称肯定命题：有的S是P（SIP）⑷特称否定命题：有的S不是P（SOP）⑸单称肯定命题：某个S是P（SaP）⑹单称否定命题：某个S不是P（SeP）直言命题间的真假对当关系：矛盾关系、（上）反对关系、（下）反对关系、从属关系矛盾关系：具有矛盾关系的两个命题之间不能同真同假。

主要有三组：SAP与SOP之间。

“所有同学考试都及格了”与“有些同学考试不及格”SEP与SIP之间。

“所有同学考试不及格”与“有些同学考试及格”SaP与SeP之间。

“张三考试及格”与“张三考试不及格”上反对关系：具有上反对关系的两个命题不能同真（必有一假），但是可以同假。

即要么一个是假的，要么都是假的。

存在于SAP与SEP、SAP与SeP、SEP与SaP之间。

下反对关系：具有下反对关系的两个命题不能同假（必有一真），但是可以同真。

即要么一个是真的，要么两个都是真的。

存在于SIP与SOP、SeP与SIP、SaP与SOP之间。

从属关系（可推出关系）：存在于SAP与SIP、SEP与SOP、SAP与SaP、SEP与SeP、SaP与SIP、SeP与SOP六种直言命题之间存在的对当关系可以用一个六角图形来表示，“逻辑方阵图”SAP SEPSaP SePSIP SOP直言命题的真假包含关系全同关系、真包含于关系、真包含关系、交叉关系、全异关系复合命题：负命题、联言命题、选言命题、假言命题负命题的一般公式：并非P联言命题公式：p并且q “并且、…和…、既…又…、不但…而且、虽然…但是…”选言命题：相容的选言命题、不相容的选言命题相容的选言命题公式：p或者q“或、或者…或者…、也许…也许…、可能…可能…”【一个相容的选言命题是真的，只有一个选言支是真的即可。

逻辑命题与推理必然性推理（演绎推理）：对当关系推理、三段论、复合命题推理、关系推理和模态推理可能性推理：归纳推理（枚举归纳、科学归纳）、类比推理命题直言命题的种类：（AEIOae）⑴全称肯定命题：所有S是P（SAP）⑵全称否定命题：所有S不是P（SEP）⑶特称肯定命题：有的S是P（SIP）⑷特称否定命题：有的S不是P（SOP）⑸单称肯定命题：某个S是P（SaP）⑹单称否定命题：某个S不是P（SeP）直言命题间的真假对当关系：矛盾关系、（上）反对关系、（下）反对关系、从属关系矛盾关系：具有矛盾关系的两个命题之间不能同真同假。

主要有三组：SAP与SOP之间。

“所有同学考试都几个了”与“有些同学考试不及格”SEP与SIP之间。

“所有同学考试不及格”与“有些同学考试及格”SaP与SeP之间。

“张三考试及格”与“张三考试不及格”上反对关系：具有上反对关系的两个命题不能同真（必有一假），但是可以同假。

即要么一个是假的，要么都是假的。

存在于SAP与SEP、SAP与SeP、SEP与SaP之间。

下反对关系：具有下反对关系的两个命题不能同假（必有一真），但是可以同真。

即要么一个是真的，要么两个都是真的。

存在于SIP与SOP、SeP与SIP、SaP与SOP之间。

从属关系（可推出关系）：存在于SAP与SIP、SEP与SOP、SAP与SaP、SEP与SeP、SaP与SIP、SeP与SOP六种直言命题之间存在的对当关系可以用一个六角图形来表示，“逻辑方阵图”SAP SEPSaP SePSIP SOP直言命题的真假包含关系全同关系、真包含于关系、真包含关系、交叉关系、全异关系复合命题：负命题、联言命题、选言命题、假言命题负命题的一般公式：并非P联言命题公式：p并且q “并且、…和…、既…又…、不但…而且、虽然…但是…”选言命题：相容的选言命题、不相容的选言命题相容的选言命题公式：p或者q“或、或者…或者…、也许…也许…、可能…可能…”【一个相容的选言命题是真的，只有一个选言支是真的即可。

逻辑命题与推理必然性推理（演绎推理）：对当关系推理、三段论、复合命题推理、关系推理和模态推理可能性推理：归纳推理（枚举归纳、科学归纳）、类比推理命题直言命题的种类：（AEIOae）⑴全称肯定命题：所有S是P（SAP）⑵全称否定命题：所有S不是P（SEP）⑶特称肯定命题：有的S是P（SIP）⑷特称否定命题：有的S不是P（SOP）⑸单称肯定命题：某个S是P（SaP）⑹单称否定命题：某个S不是P（SeP）直言命题间的真假对当关系：矛盾关系、（上）反对关系、（下）反对关系、从属关系矛盾关系：具有矛盾关系的两个命题之间不能同真同假。

主要有三组：SAP与SOP之间。

“所有同学考试都及格了”与“有些同学考试不及格”SEP与SIP之间。

“所有同学考试不及格”与“有些同学考试及格”SaP与SeP之间。

“张三考试及格”与“张三考试不及格”上反对关系：具有上反对关系的两个命题不能同真（必有一假），但是可以同假。

即要么一个是假的，要么都是假的。

存在于SAP与SEP、SAP与SeP、SEP与SaP之间。

下反对关系：具有下反对关系的两个命题不能同假（必有一真），但是可以同真。

即要么一个是真的，要么两个都是真的。

存在于SIP与SOP、SeP与SIP、SaP与SOP之间。

从属关系（可推出关系）：存在于SAP与SIP、SEP与SOP、SAP与SaP、SEP与SeP、SaP与SIP、SeP与SOP六种直言命题之间存在的对当关系可以用一个六角图形来表示，“逻辑方阵图”SAP SEPSaP SePSIP SOP直言命题的真假包含关系全同关系、真包含于关系、真包含关系、交叉关系、全异关系复合命题：负命题、联言命题、选言命题、假言命题负命题的一般公式：并非P联言命题公式：p并且q “并且、…和…、既…又…、不但…而且、虽然…但是…”选言命题：相容的选言命题、不相容的选言命题相容的选言命题公式：p或者q“或、或者…或者…、也许…也许…、可能…可能…”【一个相容的选言命题是真的，只有一个选言支是真的即可。

判断推理公式六句口诀判断推理口诀以不模糊为前提
根据长度分成两句
前提中排中评结论
无充足举反例
对否否定转正义
举例推理论无效
判断推理口诀是指推理公式的六句口诀，用于指导推理过程。

这六句口诀如下：
1.前提中真有假，结论无法成。

即如果前提中存在不真实的情况，那么结论就无法成立。

2.前提中假皆真，结论就成真。

即如果前提中所有的假设都是真实的，那么结论就是真实的。

3.结论非假必真，否定反常见
即如果结论不是假的，那么它就是真的；否定结论可能会引起反常的结果。

4.所有非A即B，宜减非B增A。

即如果所有的情况都是"A不成立即B成立"的关系，那么可以考虑减少"A不成立"的情况，增加"A成立"的情况。

5.若取证实否，先验自圆圈。

即如果想要证明一个命题是否成立，应该先验证它是否与已知事实自圆其说。

6.说假有法讲，须有事实当。

即在论证过程中，不仅要有逻辑正确的推理，还要有确凿的事实作为支持。

逻辑命题与推理之迟辟智美创作肯定性推理（演绎推理）：对当关系推理、三段论、复合命题推理、关系推理和模态推理可能性推理：归纳推理（枚举归纳、科学归纳）、类比推理命题直言命题的种类：（AEIOae）⑴全称肯定数题：所有S是P（SAP）⑵全称否定数题：所有S不是P（SEP）⑶特称肯定数题：有的S是P（SIP）⑷特称否定数题：有的S不是P（SOP）⑸单称肯定数题：某个S是P（SaP）⑹单称否定数题：某个S不是P（SeP）直言命题间的真假对当关系：矛盾关系、（上）反对关系、（下）反对关系、附属关系矛盾关系：具有矛盾关系的两个命题之间不能同真同假.主要有三组：SAP与SOP之间.“所有同学考试都几个了”与“有些同学考试不及格”SEP与SIP之间.“所有同学考试不及格”与“有些同学考试及格”SaP与SeP之间.“张三考试及格”与“张三考试不及格”上反对关系：具有上反对关系的两个命题不能同真（必有一假），可是可以同假.即要么一个是假的，要么都是假的.存在于SAP与SEP、SAP与SeP、SEP与SaP之间.下反对关系：具有下反对关系的两个命题不能同假（必有一真），可是可以同真.即要么一个是真的，要么两个都是真的.存在于SIP与SOP、SeP与SIP、SaP与SOP之间.附属关系（可推出关系）：存在于SAP与SIP、SEP与SOP、SAP与SaP、SEP与SeP、SaP与SIP、SeP与SOP六种直言命题之间存在的对当关系可以用一个六角图形来暗示，“逻辑方阵图”SAP SEPSaP SePSIP SOP直言命题的真假包括关系全同关系、真包括于关系、真包括关系、交叉关系、全异关系合同关系真包括于关系真包括关系交叉关系全异关系SAP 真真假假假SEP 假假假真真SIP 真真真真假SOP 假假真真真复合命题：负命题、联言命题、选言命题、假言命题负命题的一般公式：其实不是P联言命题公式：p而且q “而且、…和…、既…又…、不单…而且、虽然…可是…”选言命题：相容的选言命题、不相容的选言命题相容的选言命题公式：p或者q“或、或者…或者…、也许…也许…、可能…可能…”【一个相容的选言命题是真的，只有一个选言支是真的即可.只有当全部选言支都假时，相容的选言命题才是假的】不相容选言命题公式：要么p要么q“要么…要么…、不是…就是…、或者…或者…二者必居其一、或者…或者…二者不成兼得”【一个不相容的选言命题是真的，有且只有一个选言支是真的.被选言支全真或全假时，此命题为假】假言命题：充沛条件假言命题、需要条件假言命题、充要条件假言命题充沛条件假言命题公式：如果p，那么q“如果…就…、有…就有…、倘若…就…、哪里有…哪里有…、一旦…就…、假若…、只要…就…”【有前件肯定有后件.如果有前件却没有后件，这个充沛条件假言命题就是假的.因此，对一个充沛条件的假言命题来说，只有当其前件真而后件假时，命题才假.】需要条件假言命题公式：只有p，才q“没有…就没有…、不…不…、除非…不…、除非…才…”【没有前件肯定没有后件.如果没有前件也有后件，这个需要假言命题为假.对一个需要条件的假言命题来说，只有当其前件假而后件真时，命题才假.】充要条件假言命题公式：当且仅当p，才q【有前件肯定有后件，没有前件肯定没有后件.充要条件假言命题在前件与后件等值即前件真而且后件真，或者前件假而且后件假时，命题为真，在前件与后件不等值即前真后假，或前假后真时，命题为假】充沛条件与需要条件之间可以相互转化：如果p，那么q＝＝＝只有q，才p只有p，才q，＝＝＝如果q，那么p模态命题：反映事物存在或发展的肯定性或可能性的命题.模态命题包括“肯定”、“可能”等模态词.肯定肯定数题：肯定P肯定否定数题：肯定非P可能肯定数题：可能p可能否定数题：可能非P四者之间的关系如下：模态方阵肯定P 肯定非P可能P 可能非P推理1、直言命题的变形推理：换质推理、换位推理⑴换质推理也就是改变谓项.“是”或者“不是”除改变联项外，同时还需要把结论中的谓项酿成前提谓项的矛盾概念.“所有S是P”可以换质为“所有S不是非P”“所有S不是P”可以换质为“所有S是非P”“有些S是P”可以换质为“有些S不是非P”“有些S不是P”可以换质为“有些S是非P”⑵换位推理就是改变前提中主项与谓项的位置.除交换主项与谓项的位置外，还需要注意的是在前提中不周延的词项在结论中也不能周延.“所有S是P”换位为“有些P是S”“所有S不是P”换位为“所有P不是S”“有些S是P”换位为“有些P是S”注意：“有些S不是P”不能换位为“有些P不是S”2、联言推理：分解式与组合式分解式就是由前提中一个联言命题为真，推出其任一支命题为真的联言命题.组合式就是由前提中一些支命题为真推出这些支命题所组成的联言命题为真的联言推理.3、选言推理：相容的选言推理与不相容的选言推理相容的选言推理规则：（只有一种有效的推理形式，即否定肯定式）否定一部份选言支，就要肯定另一部份选言支；肯定一部份选言支，不能因此而否定另一部份选言支；不相容的选言推理规则：（否定肯定式、肯定否定式）否定除一个选言支以外的其余选言支，就要肯定那个没有被否定的选言支；肯定一个选言支，就要否定其余的选言支；4、假言推理充沛条件的假言推理规则：（有效推理：肯定前件式，否定后件式）肯定前件就要肯定后件，否定后件就要否定前件；否定前件不能否定后件，肯定后件不能肯定前件；需要条件的假言推理规则：（有效推理：否定前件式；肯定后件式）否定前件就要否定后件，肯定后件就要肯定前件；肯定前件不能肯定后件，否定后件不能否定前件；充要条件的假言推理规则：肯定前件就要肯定后件，否定后件就要否定前件；否定前件就要否定后件，肯定后件就要肯定前件；假言连锁推理：要求：前提中的第一个假言命题的后件必需与第二个假言命题的前件相同.充沛条件的假言连锁推理：如果p那么q如果q，那么r所以，如果p，那么r需要条件的假言连锁推理：只有p，才q只有q，才r所以，只有p才r5、模态推理“肯定P”与“其实不是可能非P”可以互相推出“肯定非P”与“其实不是可能P”可以相互推出“可能P”与“其实不是肯定非P”可以相互推出“可能非P”与“其实不是肯定P”可以相互推出一个模态命题的负命题等值于与该模态命题具有矛盾关系的命题.其实不是肯定P＝＝＝可能非P其实不是肯定非P＝＝＝可能P其实不是可能P＝＝＝肯定非P其实不是可能非P＝＝＝肯定P“肯定P”可以推出“可能P”“肯定非P”可以推出“可能非P”“其实不是可能P”可以推出“其实不是肯定P”“其实不是可能非P”可以推出“其实不是肯定非P”可能性推理类型：削弱型：最能削弱型、最不能削弱型加强型前提与预设型解释型：最能解释、最不能解释评价型结论性词项的周延性主项的周延性是由量项来决定的，量项是全称的则主项周延，量项是特称的则主项不周延；谓项的周延性是由联项来决定的，联项是肯定的则谓项不周延，联项是否定的，则谓项周延.六种直言命题之间存在的对当关系可以用一个六角图形来暗示，“逻辑方阵图”SAP SEPSaP SePSIP SOP直言命题的真假包括关系（全同关系、真包括于关系、真包括关系、交叉关系、全异关系）合同关系真包括于关系真包括关系交叉关系全异关系SAP 真真假假假SEP 假假假真真SIP 真真真真假SOP 假假真真真四者之间的关系如下：模态方阵肯定P 肯定非P可能P 可能非P相容的选言推理规则：（只有一种有效的推理形式，即否定肯定式）不相容的选言推理规则：（否定肯定式、肯定否定式）充沛条件的假言推理规则：（有效推理：肯定前件式，否定后件式）需要条件的假言推理规则：（有效推理：否定前件式；肯定后件式）。

逻辑命题与推理必然性推理（演绎推理）：对当关系推理、三段论、复合命题推理、关系推理和模态推理可能性推理：归纳推理（枚举归纳、科学归纳）、类比推理命题直言命题的种类：（AEIOae）⑴全称肯定命题：所有S是P（SAP）⑵全称否定命题：所有S不是P（SEP）⑶特称肯定命题：有的S是P（SIP）⑷特称否定命题：有的S不是P（SOP）⑸单称肯定命题：某个S是P（SaP）⑹单称否定命题：某个S不是P（SeP）直言命题间的真假对当关系：矛盾关系、（上）反对关系、（下）反对关系、从属关系矛盾关系：具有矛盾关系的两个命题之间不能同真同假。

主要有三组：SAP与SOP之间。

“所有同学考试都及格了”与“有些同学考试不及格”SEP与SIP之间。

“所有同学考试不及格”与“有些同学考试及格”SaP与SeP之间。

“张三考试及格”与“张三考试不及格”上反对关系：具有上反对关系的两个命题不能同真（必有一假），但是可以同假。

即要么一个是假的，要么都是假的。

存在于SAP与SEP、SAP与SeP、SEP与SaP之间。

下反对关系：具有下反对关系的两个命题不能同假（必有一真），但是可以同真。

即要么一个是真的，要么两个都是真的。

存在于SIP与SOP、SeP与SIP、SaP与SOP之间。

从属关系（可推出关系）：存在于SAP与SIP、SEP与SOP、SAP与SaP、SEP与SeP、SaP与SIP、SeP与SOP六种直言命题之间存在的对当关系可以用一个六角图形来表示，“逻辑方阵图”SAP SEPSaP SePSIP SOP直言命题的真假包含关系全同关系、真包含于关系、真包含关系、交叉关系、全异关系复合命题：负命题、联言命题、选言命题、假言命题负命题的一般公式：并非P联言命题公式：p并且q “并且、…和…、既…又…、不但…而且、虽然…但是…”选言命题：相容的选言命题、不相容的选言命题相容的选言命题公式：p或者q“或、或者…或者…、也许…也许…、可能…可能…”【一个相容的选言命题是真的，只有一个选言支是真的即可。

逻辑命题与推理必然性推理（演绎推理）：对当关系推理、三段论、复合命题推理、关系推理和模态推理可能性推理：归纳推理（枚举归纳、科学归纳）、类比推理命题直言命题的种类：（AEIOae）⑴全称肯定命题：所有S是P（SAP）⑵全称否定命题：所有S不是P（SEP）⑶特称肯定命题：有的S是P（SIP）⑷特称否定命题：有的S不是P（SOP）⑸单称肯定命题：某个S是P（SaP）⑹单称否定命题：某个S不是P（SeP）直言命题间的真假对当关系：矛盾关系、（上）反对关系、（下）反对关系、从属关系矛盾关系：具有矛盾关系的两个命题之间不能同真同假。

主要有三组：SAP与SOP之间。

“所有同学考试都及格了”与“有些同学考试不及格”SEP与SIP之间。

“所有同学考试不及格”与“有些同学考试及格”SaP与SeP之间。

“张三考试及格”与“张三考试不及格”上反对关系：具有上反对关系的两个命题不能同真（必有一假），但是可以同假。

即要么一个是假的，要么都是假的。

存在于SAP与SEP、SAP与SeP、SEP与SaP之间。

下反对关系：具有下反对关系的两个命题不能同假（必有一真），但是可以同真。

即要么一个是真的，要么两个都是真的。

存在于SIP与SOP、SeP与SIP、SaP与SOP之间。

从属关系（可推出关系）：存在于SAP与SIP、SEP与SOP、SAP与SaP、SEP与SeP、SaP与SIP、SeP与SOP六种直言命题之间存在的对当关系可以用一个六角图形来表示，“逻辑方阵图”SAPSEPSaPSePSIPSOP直言命题的真假包含关系全同关系、真包含于关系、真包含关系、交叉关系、全异关系负命题的一般公式：并非P联言命题公式：p并且q“并且、…和…、既…又…、不但…而且、虽然…但是…”选言命题：相容的选言命题、不相容的选言命题相容的选言命题公式：p或者q“或、或者…或者…、也许…也许…、可能…可能…”【一个相容的选言命题是真的，只有一个选言支是真的即可。

判断推理常用公式一、逻辑判断并非（A或B）=非A且非B⏹真假判断题型解题技巧六种关系矛盾关系（主体相同的两句话，必一真一假）①某个S是P，某个S不是P；②所有S都是P，有的S不是P；③所有的S都不是P，有的S是P；④P且Q，非P或非Q。

⑤P或Q，非P且非Q⑥如果P→Q，P→非Q（如果天下雨，路就滑）反对关系⑤有的S是P，有的S不是P（至少有一真）；⑥所有S都是P，所有S都不是P （至少有一假）。

包容关系例：所有A→B 所有老师都会英语A 校长会英语B①一直前假如果题目问只有一个是真的分析，如果A真，B截然为真。

与问题说的只有一真矛盾，哪么A一定为假②一假后真如果题目问只有一个是假的分析，如果B假，A截然为假。

与问题说的只有一假矛盾，哪么B一定为真二、翻译推理1、单句判断①所有（凡是）S都是P 翻译S →P②所有（凡是）S都不是P 翻译S →—P③没有S是P （所有S不是P）翻译P →—S 见没有改所有④没有S不是P （所有S是P）翻译S →P⑤不是S都是P 翻译—S →P⑥不是S都不是P 翻译—S →—P2、否定关系1、并非所有A都是B 等价于有的A不是B（并非所有换成有的，是换不是）2、并非有的A是B 等价于所有A都不是B（并非有的换成所有，是换成不是）3、等价关系1、所有的A都不是B 等价于所有的B都不是A2、有的A是B 等价于有的B是啊五个解题步骤①符号化；②找关系（六种关系）；③推知其余项真假；④根据其余项真假，得出真实情况；⑤带回“矛盾或反对”项，判断其真假。

排列组合题型1.选项信息充分，运用排除法，2.选项不处分，找推理起点：信息最大优先，特殊信息优先■削弱题型方法：１.否因削弱已知因果推理主线：因→果否因削弱：强调原因不成立或起不到作用。

2.他因已知推理主线：因→果他因削弱：强调存在别的原因会导致该结果，或者导致不了该结果。

3.反例已知推理主线：因→果反例削弱：举出一个反例，即满足了“因”却没有得到所说的“果”。

判断推理常用公式在逻辑学和推理学中，有一些常用的公式和原则可用于进行正确的推理和论证。

这些公式和原则可能包括数学逻辑和形式逻辑中的规则，以及哲学推理和日常生活中的一般原则。

下面将介绍一些常用的推理公式和原则。

1. 矛盾法（Reductio ad absurdum）：矛盾法是一种常用的推理方法，用于证明一些论断的否定。

它通过假设论断的否定，然后通过推理推出一个矛盾的结论，从而证明了原论断的正确性。

这个方法的基本形式是：假设 ~A，然后从这个假设中推出一个矛盾的结论，如B ∧ ~B。

因此可以推断出原论断 A 的正确性。

2. 归谬法（Modus tollens）：归谬法是一种推理方法，通过否定一个推理的结论而否定其前提。

这个方法的基本形式是：如果 A 导致 B，而 ~B 是真的，则可以推断出 ~ A 是真的。

例如，如果一个论断是“如果下雨，那么地面湿”，而地面并不湿，则可以推断出“下雨”这个前提是错误的。

3. 假设法（Modus ponens）：假设法是一种推理方法，通过证明一个条件语句的前提为真来推断出结论的真实性。

这个方法的基本形式是：如果 A 导致 B，而 A 是真的，则可以推断出 B 是真的。

例如，如果一个论断是“如果下雨，那么地面湿”，而已知“下雨”是真的，则可以推断出“地面湿”是真的。

4. 经验归纳（Inductive reasoning）：经验归纳是一种通过观察和实践中的具体事实和例子来得出一般性结论的推理方法。

它基于经验和概率，通过发现一系列的具体案例来推断出普遍性规律或趋势。

但是，经验归纳并不具有绝对的确定性，因为它的结论基于有限的观察。

5. 演绎推理（Deductive reasoning）：演绎推理是从已知前提出发，通过逻辑规则和推理方式得出结论的方法。

它的结论是绝对确定的，因为它基于已知的真实前提和逻辑规则。

例如，如果已知“所有人都会死亡”，以及“张三是一个人”，则可以演绎出“张三将会死亡”的结论。

可能性推理：归纳推理（枚举归纳、科学归纳）、类比推理⑴全称肯定命题：所有SAP)⑵全称否定命题：所有S不是P( SEP)⑶特称肯定命题：有的SIP)⑷特称否定命题：有的S不是P（SOP）⑸单称肯定命题：某个SaP)⑹单称否定命题：某个S不是P（SeP）SaP与SeP之间。

“张三考试及格”与“张三考试不及格” 上反对关系：具有上反对关系的两个命题不能同真（必有一假）存在于SAP与SEP SAP与SeP、SEP与SaP之间。

下反对关系：具有下反对关系的两个命题不能同假（必有一真）的。

存在于SIP与SOP SeP与SIP、SaP与SOP之间。

从属关系（可推出关系）：存在于SAP与SIP、SEP 与SOP 六种直言命题之间存在的对当关系可以用一个六角图形来表示，，但是可以同假。

即要么一个是假的，要么都是假的。

，但是可以同真。

即要么一个是真的，要么两个都是真SAP与SaP SEP与SeP、SaP与SIP、SeP与SOP “逻辑方阵图”逻辑命题与推理必然性推理（演绎推理）：对当关系推理、三段论、复合命题推理、关系推理和模态推理命题直言命题的种类：（AEIOae）直言命题间的真假对当关系：矛盾关系、（上）反对关系、（下）反对关系、从属关系矛盾关系：具有矛盾关系的两个命题之间不能同真同假。

主要有三组：SAP与SOP之间。

“所有同学考试都及格了”与“有些同学考试不及格”SEP与SIP之间。

“所有同学考试不及格”与“有些同学考试及格”SaP SAP SEPSePSIP SOP直言命题的真假包含关系全同关系、真包含于关系、真包含关系、交叉关系、全异关系复合命题：负命题、联言命题、选言命题、假言命题负命题的一般公式：并非P联言命题公式：p并且q “并且、…和…、既…又…、不但…而且、虽然…但是…”选言命题：相容的选言命题、不相容的选言命题相容的选言命题公式：p或者q “或、或者…或者…、也许…也许…、可能…可能…”【一个相容的选言命题是真的，只有一个选言支是真的即可。

判断推理公式速记册子判断推理速记公式技巧集合：一、翻译推理四个翻译（1）“如果...就...”翻译规则前句推出后句替代关联词 1.只要...就/则2.为了...一定3....必须...4.凡是...都5....离不开...（2）”只有...才...”翻译规则后句推出前句替代关联词 1....是...的基础2....是...必不可少的条件/必要条件3.不...不...4.除非...否则不...除非A否则不B B→A除非A否则B－B→A（3）“且”口诀:全真为真，一假全假替代关联词 1....又...2....和...3....但是...4.虽然...但是...5.....并且...6.、（顿号）（4）“或”口诀一真既真，全假为假先否定一个再肯定另外一个替代关联词 1.或者...或者2.至少一个两个推理（1）逆否命题1口诀肯前必肯后，否后必否前否前肯后无必然结果，只能推出可能性结果2公式A→B=－B→－A（2）摩根定公式1.－（A且B）=－A或－B2.－（A或B）=－A且－B二、真假推理矛盾关系：非此即彼必有一真一假对象一直才会存在矛盾六组表现形式 1.A是B——A不是B2.所有的S是P——有的S不是P3.所有的S不是P——有的S是P4.A→B——A且－B①－A→B——－A且－B②A→－B——A且B③－A→－B——－A且B5.A且B——－A或－B6.A或B——－A且－B反对关系：除此以外还有其他两组表现形式1.所有的S是P——所有的S不是P2.有的S是P——有的S不是P两个“所有”必有一假、两个“有的”必有一真三、论证1.因果加强别无他因（排除他因）有因有果无因无果2.因果削弱因果倒置另有他因有因无果无因有果3.非因果加强论据：肯定原论据、补充新论据（最弱）论证方式：搭桥、样本典型、肯定前提（最强）论点：肯定论点（次强）4.非因果削弱论据：否定原论据、补充反论据（最弱）论证方式：拆桥、样本不典型、否定前提（次强）论点：否定论点（最强）▲论证慎选词汇1.感情词（激励、妨碍、倾向于、未发现...）2.没有实际数据显示3.据以往的经验来看4.据古代典籍记载。

逻辑命题与推理必然性推理(演绎推理):对当关系推理、三段论、复合命题推理、关系推理与模态推理可能性推理:归纳推理(枚举归纳、科学归纳)、类比推理命题直言命题得种类:(AEIOae)⑴全称肯定命题:所有S就是P(SAP)⑵全称否定命题:所有Ｓ不就是Ｐ(SEP)⑶特称肯定命题:有得S就是P(ＳＩP)⑷特称否定命题:有得S不就是P(ＳOＰ)⑸单称肯定命题:某个S就是P(SａP)⑹单称否定命题:某个Ｓ不就是P(ＳeP)直言命题间得真假对当关系:矛盾关系、(上)反对关系、(下)反对关系、从属关系矛盾关系:具有矛盾关系得两个命题之间不能同真同假。

主要有三组:SAＰ与ＳOＰ之间。

“所有同学考试都及格了"与“有些同学考试不及格”SＥP与SＩP之间、“所有同学考试不及格”与“有些同学考试及格"SａＰ与SeP之间。

“张三考试及格”与“张三考试不及格”上反对关系:具有上反对关系得两个命题不能同真(必有一假),但就是可以同假、即要么一个就是假得,要么都就是假得、存在于SAP与SEP、SAP与SeP、SＥP与SaP之间。

下反对关系:具有下反对关系得两个命题不能同假(必有一真),但就是可以同真。

即要么一个就是真得,要么两个都就是真得。

存在于ＳIP与SOP、SeＰ与SIP、SaP与ＳＯP之间。

从属关系(可推出关系):存在于SAP与ＳＩＰ、SＥＰ与SＯP、SAP与ＳaP、SEP与SeP、SaP与SIP、SeP与ＳOP 六种直言命题之间存在得对当关系可以用一个六角图形来表示,“逻辑方阵图”SAＰSEPSaP SｅPSIP SOP直言命题得真假包含关系全同关系、真包含于关系、真包含关系、交叉关系、全异关系复合命题:负命题、联言命题、选言命题、假言命题负命题得一般公式:并非P联言命题公式:ｐ并且q“并且、…与…、既…又…、不但…而且、虽然…但就是…”选言命题:相容得选言命题、不相容得选言命题相容得选言命题公式:ｐ或者q“或、或者…或者…、也许…也许…、可能…可能…”【一个相容得选言命题就是真得,只有一个选言支就是真得即可。

判断推理常用公式一、逻辑判断⏹翻译推理德摩根定律：并非（A 且B）=非A 或非B并非（A 或B）=非A 且非B⏹真假判断题型解题技巧六种关系矛盾关系（主体相同的两句话，必一真一假）①某个S 是P，某个S 不是P；②所有S 都是P，有的S 不是P；③所有的S 都不是P，有的S 是P；④P→Q P, 且非Q。

反对关系⑤有的S 是P，有的S 不是P（至少有一真）；⑥所有S 都是P，所有S 都不是P（至少有一假）。

五个解题步骤①符号化；②找关系（六种关系）；③推知其余项真假；④根据其余项真假，得出真实情况；⑤带回“矛盾或反对”项，判断其真假。

⏹排列组合题型1.选项信息充分，运用排除法，2.选项不处分，找推理起点：信息最大优先，特殊信息优先■削弱题型方法：１.否因削弱已知因果推理主线：因→果否因削弱：强调原因不成立或起不到作用。

2.他因已知推理主线：因→果他因削弱：强调存在别的原因会导致该结果，或者导致不了该结果。

3.反例已知推理主线：因→果反例削弱：举出一个反例，即满足了“因”却没有得到所说的“果”。

4.因果倒置已知推理主线：A、B 两个现象同时出现→A 导致了 B因果倒置：很有可能是 B 导致了A。

■假设、支持题型方法：1.排他因已知推理主线：因→果排他因：排除其他因素的干扰，或排除其他可能性，使推理更可信。

2.否因否果已知推理主线：因→果否因否果：非因→非果，会支持“因→果”3.建立联系已知推理主线：因→果建立联系：因果之间有跳跃，唯有建立联系才可行。

4.推论可行已知推理主线：因→果推论可行：因果之间有漏洞，需加前提才可行。

■解释题型关键：解题技巧：抓住需要解释的关键信息。

■归纳题型技巧：1.四项原则：从弱原则，整体原则，就近原则、协调原则2.不能夸大事实3.不能无根据地猜测4.结论越宏观不一定好5.“绝对答案”一般不选：必然、必须、一定、肯定。

二、图形推理■规律推理类解题思路图■立体折叠解题技巧总结1.特殊面法：针对不规则的立体图形（有凸凹），选择一个特殊面。