Part 4-1:组合问题 智巧趣题一
- 格式:ppt
- 大小:2.60 MB
- 文档页数:13
第四讲智巧趣题教学课题:智巧趣题教学课时:两课时教学目标:1.经历“智巧趣题”的探究过程,掌握“智巧趣题”,会用“智巧趣题”解决简单的实际问题。
2. 通过操作发展学生的类推能力,形成比较抽象的数学思维。
3. 通过“智巧趣题”的灵活应用感受数学的魅力。
教学重难点:1.经历“智巧趣题”的探究过程,掌握“智巧趣题”的一般解法。
2.理解“智巧趣题”,并对一些简单实际问题加以“模型化”。
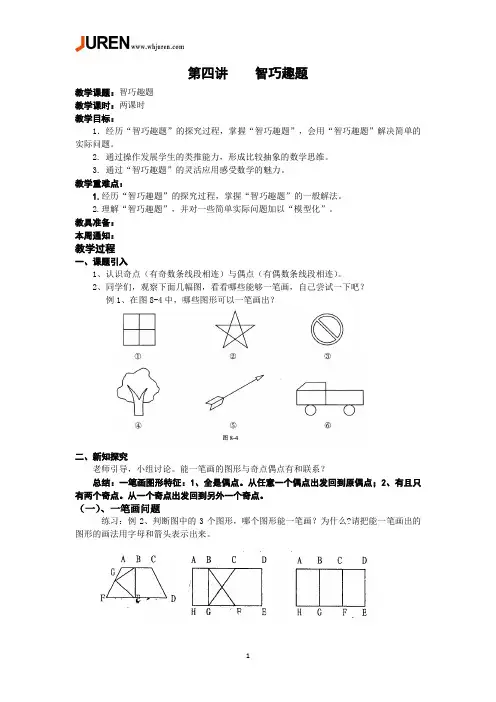
教具准备:本周通知:教学过程一、课题引入1、认识奇点(有奇数条线段相连)与偶点(有偶数条线段相连)。
2、同学们,观察下面几幅图,看看哪些能够一笔画,自己尝试一下吧?例1、在图8-4中,哪些图形可以一笔画出?二、新知探究老师引导,小组讨论。
能一笔画的图形与奇点偶点有和联系?总结:一笔画图形特征:1、全是偶点。
从任意一个偶点出发回到原偶点;2、有且只有两个奇点。
从一个奇点出发回到另外一个奇点。
(一)、一笔画问题练习:例2、判断图中的3个图形,哪个图形能一笔画?为什么?请把能一笔画出的图形的画法用字母和箭头表示出来。
(二)、青蛙跳、蜗牛爬例3、一口井深 10 米,一只蜗牛从井底白天往上爬 2 米,晚上又往下滑 1 米,请问要多长时间,这只蜗牛能爬出这口井?分析:一般情况下,蜗牛每天行进2-1=1米,但这里有个很容易出错的地方,就是最后一次直接爬出来没有下滑,所以每次我们要先减去最后一次往上的然后再做。
因为最后一次爬出井外不会往下滑,所以蜗牛只要往上爬 9 米,晚上下滑 1 米,这时距离井口只有 2米了,这样只要一个白天再往上爬 2 米就到井口了.所以只需要 8 天再加一个白天。
总结:这种爬井问题一定要中点分析最后一次的情况。
(三)、过河问题例4、一个农民携带一只狼,一只羊和一棵白菜,要借助一条小船过河。
小船上除了农民只能再带狼、羊、白菜中的一样.而农民不在时,狼会吃羊,羊会吃白菜.农民如何过河呢?分析:本题直接描述较麻烦,可以用图示法:例5、有四个人在晚上准备通过一座摇摇欲坠的小桥。

第二十一讲 智巧趣题一阿呆阿呆阿呆阿呆阿呆把相应的人物换成红字标明的人物.趣题巧解,把一些看起来不可能实现或者没法解决的问题,通过变换思维解决.今天我们要通过变换思维来解决一些生活中遇到的趣题.例题1河里有一排小鸭:两只后面有两只,两只中间有两只,两只前面有两只.请问河里至少有几只小鸭?【提示】画图试试看.练习1水中有一行小鱼:两条在前,三条在后;三条在前,两条在后;三条在两条中间,排成一条线.请你猜猜水中至少有几条小鱼?例题2把7个梨全部放到大、中、小三个盘子里,大盘要比中盘多3个,中盘要比小盘多3个.应该怎样放?【提示】盘子叠在一起试一试.上面的题目中都用到了共用的数学思想,共用不仅包括位置共用,还有身份共用及图形共用.我们一起来看看下面的题目.【提示】人物身份也会共用哦!练习3王医生有一个儿子,李医生也有一个儿子.两位医生带着自己的儿子一起去超市买东西,每人买了一块蛋糕,放在一起数一数,一共3块蛋糕,这是怎么回事?两个爸爸和两个儿子一同去钓鱼,每人钓到一条大鱼,放在一起数一数,一共只有3条大鱼,这是怎么回事?例题3练习2把5枚棋子全部放到大、中、小三个盒子里,使得每个盒子里都有5枚棋子,应该怎样放?例题4给出如下4个相同的笼子,要装5只小鸭,每个笼子只能装1只小鸭.应该怎么装?【提示】4个笼子能否再拼出来一个笼子?练习4小美在每根小棒上装了3个风车.但是只有2根小棒和5个风车,她是怎么装上的呢?例题5图图帮小美摘了5个一样的椰子.其中有1个椰子被虫子吃成空心的,比较轻.现在给你一架天平,最少称几次保证找到空心椰子?【提示】天平上出现不平衡的状态是不是就可以找到空心椰子了?例题5中运用的称量方法非常巧妙,我们在以后的学习中还会接触到这类的题目.看过了这么多不同类型的共用题目,我们来发散思维,思考一下下面的题目吧!例题65个小朋友排队,横一队3个人,竖一队3个人,他们的队形是什么样的?画一画.【提示】用○代替小朋友!课堂内外中国古代阵法中国古代作战是非常讲究阵法即作战队形的,称之为“布阵”.布阵得法就能充分发挥军队的战斗力,克敌制胜.八卦阵这是战国时大军事家孙膑创造的,据说是受了《易经》八卦图的启发,所以又称八卦阵.具体阵势是大将居中,四面各布一队正兵,正兵之间再派出四队机动作战的奇兵,构成八阵.八阵散布成八,复而为一,分合变化,又可组成六十四阵.当年诸葛亮还用石头在四川奉节布设过八阵的方位,作为教练将士演习阵法之用,名为“八阵图”.撒星阵是南宋名将岳飞破金兵“拐子马”的阵法.撒星阵的队形布列如星,连成一排的“拐子马”冲来时士兵散而不聚,使敌人扑空.等敌人后撤时散开的士兵再聚拢过来,猛力扑击敌人,并用刀专砍马腿,以破“拐子马”.鸳鸯阵是明代将领戚继光为抗击倭寇而创设的一种阵法.他把士兵分为三队,当敌人进到百步时第一队士兵发射火器;敌人进到六十步时第二队士兵发射弩箭;敌人进到十步时第三队士兵用刀矛向敌人冲杀.这些变化反映了中国作战阵法从传统的方阵向多兵种的集团阵法演变的过程.作业1. 草地上有一队奔跑的小鹿:两只在前,一只在后,一只在两只中间,排成一条线,那么草地上至少有几只小鹿呢?2. 把6只小鸭装到大、中、小三个笼子里,大笼子要比中笼子多2只,中笼子要比小笼子多2只.应该怎样放?画一画你的方案.3. 两个妈妈和两个女儿一起去吃饭,每人点了一盘饺子,饺子端来后数一数,一共有3盘饺子,这是怎么回事?4. 你能用3个同样大小的“△”拼出4个形状大小相同的“△”吗?画图表示.5.小美蛙有4个一样的金币,其中一个是假的,比真的重.现在给你一架天平,最少称几次保证找到假金币?换成小美蛙。

第二十一讲 智巧趣题1. 例题1答案:4详解:位置的共用,画图试一试,至少要有4只鸭子才能符合题意.2. 例题2答案:详解:三个盘子重合在一起之后,里面的盘子里面的梨,是外面盘子和里面盘子共用的梨,也就是说,这些梨属于里面的盘子,同时也属于外面的盘子.3. 例题3答案:这三个人的关系是:小朋友、小朋友的爸爸、小朋友的爷爷详解:两个爸爸分别是小朋友的爷爷和小朋友的爸爸,两个儿子分别是小朋友和他的爸爸.4. 例题4答案:详解:装5只鸭子需要5个笼子.要使4个笼子变成5个,则需要用这4个笼子拼出1个笼子,从而产生第5个笼子.5. 例题5答案:2次详解:将5个椰子分别表A 、B 、C 、D 、E ,分成3份,分别为AB 、CD 和E .AB 和CD 先称,如果天平是平的,那么证明被虫子咬了的椰子是E ;如果AB 和CD 不平,则证明被咬了的在轻的一侧,那么再把轻的一侧称一下,较轻的椰子就是被虫子咬了的.那么可知5个椰子的时候,我们最少称2次,不管什么情况,一定能找到被虫子咬的椰子.6. 例题6答案:答案不唯一详解:排队中有的小朋友被共用了,被共用的小朋友既在横一队,又在竖一队.7. 练习1笼子梨答案:5简答:位置的共用,画图试一试,符合题意最少要有5条鱼.8.练习2答案:简答:三个盒子重合在一起之后,里面的盒子的棋子,是外面盒子和里面盒子共用的棋子,也就是说,这些棋子属于里面的盒子,同时也属于外面的盒子.9.练习3答案:王医生和李医生是夫妻,他们带着自己的儿子去买蛋糕(答案不唯一,也可以是奶奶、爸爸和儿子)简答:人物身份关系的共用.10.练习4答案:简答:每根小棒上装了3个风车,2根小棒上应该装6个风车,题目中只装了5个风车,说明有一个风车是被共用了.被共用的风车同时在2根小棒上.11.作业1答案:3简答:通过“两只在前,一只在后”,得到至少有3只小鹿,又通过“一只在两只中间”,同样得到至少有3只小鹿.综合所述,草地上至少有3只小鹿.12.作业2答案:简答:题目只要求大笼子要比中笼子多2只,中笼子要比小笼子多2只而已,而对于笼子怎么放,没有要求,所以可以将大中小笼子叠一起或分开放均可.(答案不唯一)222 132或或024箱子棋子13.作业3答案:这三个人的关系是:小朋友、小朋友的妈妈、小朋友的外婆简答:两个妈妈分别是小朋友的外婆和小朋友的妈妈,两个女儿分别是小朋友和她的妈妈.14.作业4答案:简答:动手摆一摆即可得到答案,注意摆出共用部分.15.作业5答案:2简答:把4个金币分为2堆,各2个,拿其中2堆放到天平上称.如果有1堆重,则假金币就在这一堆里,将其放到天平上再秤一次即可找出重的假金币.。

1.挖掘孩子学习数学的兴趣.2.让孩子掌握各种趣题的不同思考方式.知识点说明智巧趣题顾名思义,就是有趣的一类问题,但回答时要十分小心,稍有不慎,就可能落入“圈套”。
要想正确地解答这类题目,一是细心,善于观察,全面考虑各种情况;二是要充分运用生活中学到的知识;三是需要那么一点思考问题的灵气和非常规的思考方法。
本讲主要是通过数学趣题的研究学习引发学生学习奥数的兴趣,激发学生学习奥数的灵感,充分调动学生学习奥数的积极性。
智巧趣题主要依靠巧妙的构思而解决问题,其中包括火柴棍游戏、数的恰当排列、称量问题及直线或圆周形状的报数问题。
青蛙跳、蜗牛爬【例 1】 青蛙沿着10米高的井往上跳,每次它向上跳半米,然后又落下去,问青蛙爬需要跳几次就能跳出井外?【考点】智巧趣题 【难度】2星 【题型】填空 【解析】 每次青蛙向上跳半米,然后又落下去,等于还在原地,所以永远也跳不出去. 【答案】永远也跳不出去【巩固】 一只树蛙爬树,每次往上爬5厘米,又往下滑2厘米,这只青蛙这样上下了5次,实际往上爬了多少厘米?【考点】智巧趣题 【难度】2星 【题型】填空 【解析】 分析:实际上青蛙每爬行一次只前进了5-2=3(厘米),5次共前进了3×5=15(厘米). 【答案】15厘米【例 2】 一口井深10米,一只蜗牛从井底白天往上爬2米,晚上又往下滑1米,请问要多长时间,这只蜗牛能爬出这口井?【考点】智巧趣题 【难度】2星 【题型】填空 【解析】 “白天往上爬2米,晚上又往下滑1米”其实一天只往上爬1米,如果这样理解,说这只蜗牛爬出这口井需要10天就错了.因为最后一次爬出井外不会往下滑,所以蜗牛只要往上爬9米,晚上下滑1米,这时距离井口只有2米了,这样只要一个白天再往上爬2米就到井口了.所以只需要8天再加一个白天.【答案】8天再加一个白天【巩固】 蜗牛沿着9米高的柱子往上爬,白天它向上爬5米,而晚上又下降4米,问蜗牛爬到柱顶需要几天几夜?【考点】智巧趣题 【难度】2星 【题型】填空 【解析】 一昼夜可以爬1米,爬了4昼夜后再经过一个白天即可爬到柱顶,因此需要5天4夜.例题精讲知识点拨教学目标智巧趣题【答案】5天4夜【巩固】蜗牛沿着10米高的柱子往上爬,白天它向上爬5米,而晚上又下降3米,问蜗牛爬到柱顶需要几天?【考点】智巧趣题【难度】2星【题型】填空【解析】一昼夜可以爬2米,爬了3昼夜后再经过一个白天即可爬到柱顶,因此需要4天3夜.【答案】4天3夜【巩固】有一道关于蜗牛爬墙的题:“日升六尺六,夜降三尺三,墙高一丈九,几日到顶端”。

第一讲 智巧趣题智巧趣味题无固定的解题规律,需要我们根据题意,灵活运用知识,进行分析、推理,巧妙地求出需要的结果,一般方法:1、找“隐藏条件”法解数学问题很关键的一步是审题,这类题看上去很简单,但如果一不小心就会落入圈套。
要找出“隐藏条件”,全面考虑问题。
2、打破“常规”法要从不同的角度去分析,找出解题中关键的一步,很多时候要打破常规,很巧妙地解决问题。
【例1】有一杯牛奶,小萍喝了半杯后,将它加满水,然后她又喝了半杯后,再加满水,最后全部喝完,问:小萍喝的牛奶多,还是喝的水多?【练习1】一杯牛奶,小聪喝了半杯后,将它加满水,然后她又喝了一杯的14后,再加满水,最后全部喝完,问:小聪喝的牛奶多,还是喝的水多?【例2】蜗牛沿着13米高的柱子向上爬,每天白天向上爬6米,晚间又滑下5米,像这样几天爬到柱子顶点?【练习2】有一口枯井,一只蜗牛沿着9米深井壁往上爬,白天它向上爬3米,而晚上它降下2米,蜗牛爬到井口上需要几天几夜?【例3】一个大和尚带着两个小和尚去河对岸的寺院,河上没有桥,他们又都不会游泳,为了过河,他们找来一只空船,船最多载重50千克,大和尚正好重50千克,两个小和尚各重25千克,问:他们怎样才能全部过河?【练习3】37个同学要坐船过河,渡口处只有一只能载5人的小船(无船工),他们要全部渡过河去,至少要使用这只小船渡河多少次?【例4】小华衣服上有5个口袋,每个口袋里都放了几角钱(都不够1元),而且每个口袋里的数目都不同,小华最多有多少钱?最少有多少钱?【练习4】电视台要播放一部30集的电视连续剧,如果要求每天播放的集数互不相等,该电视连续剧最多可以播放几天?【例5】一筐鸡蛋,一个人买走一半又3个后,还剩下9个,这筐鸡蛋原来有多少个?【练习5】爸爸买回一些苹果,全家人吃了其中的一半又6个后,还剩下12个,爸爸开始买回了多少个苹果?【例6】你能用四根筷子摆出一个“田”字吗?【练习6】你能用12根筷子摆出六个同样大小的正方形吗?【例7】三个小朋友三分钟削三支铅笔,照此效率,六个小朋友几分钟削六支铅笔?【练习7】三只猫三天吃三只老鼠,照此效率,六只猫六天吃几只老鼠?1.兔妈妈提来一筐萝卜共21个,要分给6只小兔,使每只小兔分得的个数都不相同。

第一讲 智巧趣题从三年级开始,我们就要系统地学习奥数知识,本讲主要是通过数学趣题的研究学习引发学生学习奥数的兴趣,激发学生学习奥数的灵感,充分调动学生学习奥数的积极性.Ⅰ、过河问题(★★★ 奥数网经典题)【例1】 38个同学要坐船过河,渡口处只有一只能载4人的小船(无船工).他们要全部渡过河去,至少要使用这只小船渡河多少次?分析:根据前面的解答,实际上前面每次过河的人数只有3人,最后一次最多过4人,因为38=3×12+2,所以前面3人一次过了12次,来回一共划了12×2=24(次),最后一次是2人过河,还要用1次.所以最终需要渡河的次数是24+1=25(次).[拓展] 37个同学要坐船过河,渡口处只有一只能载5人的小船(无船工).他们要全部渡过河去,至少要使用这只小船渡河多少次?分析:如果由37÷5=7……2,得出7+1=8次,那么就错了.因为忽视了至少要有1个人将小船划回来这个特定的要求.实际情况是:小船前面的每一个来回至多只能渡4个人过河去,只有最后一次小船不用返回才能渡5个人过河.因为除最后一次可以渡5个人外,前面若干个来回每个来回只能渡过4个人,每个来回是2次渡河,37=4×8+5,所以渡河次数是8×2+1=17(次). (注:由于数据的特殊性,刚好最后一次5个人过河).教学目标专题精讲和想 挑战吗 ?一个人带着一只狐狸、一只鹅和一些玉米渡河,每次只能带一样,可是人不在时,狐狸要吃鹅,鹅要吃玉米.那么应该怎样渡河呢? 分析:先带鹅过河,自己划船回来,第二次带狐狸过去,再把鹅带回来,第三次带玉米过河,自己划船回来,第四次再把鹅带过去即可.【例2】(★★★★奥数网改编题)赵大爷和一个小八路带着一个负伤的红军战士因为叛徒出卖被日本鬼子追到一条小河边,河岸边只有一条能同时乘坐两人的小船,赵大爷划船需要2分钟,小八路划船需要3分钟,负伤的红军战士划船需要5分钟,现在在危机关头,需要尽快过河,采用怎样的过河方式,三个人全部过河用时最少?分析:赵大爷首先跟小八路或者红军战士一起过河,用时2分钟,再由赵大爷把船划过来,用时2分钟,最后把剩下的人一起载过去,再用时2分钟.一共用时6分钟.[拓展] 有四个人在晚上准备通过一座摇摇欲坠的小桥.此桥每次只能让2个人同时通过,否则桥会倒塌.过桥的人必须要用到手电筒,不然会一脚踏空.只有一个手电筒.4个人的行走速度不同:小强用1分种就可以过桥,中强要2分中,大强要5分中,最慢的太强需要10分中.17分钟后桥就要倒塌了.请问:4个人要用什么方法才能全部安全过桥?分析:小强和中强先过桥,用2分钟;再用小强把电筒送过去,用1分钟,现在由大强跟太强一起过桥,用10分钟,过去以后叫中强把电筒送给小强用2分钟,最后小强与中强一起过河再用2分钟,他们一起用时间:2+1+10+2+2=17(分钟),正好在桥倒塌的时候全部过河.(时间最短过河的原则是:时间长的一起过,时间短的来回过.这样保证总的时间是最短的).【例3】有一家五口人要在夜晚过一座独木桥.他们家里的老爷爷行动非常不便,过桥需要12分钟;孩子们的父亲贪吃且不爱运动,体重严重超标,过河需要时间也较长,8分钟;母亲则一直坚持劳作,动作还算敏捷,过桥要6分钟;两个孩子中姐姐需要3分钟,弟弟只要1分钟.当时正是初一夜晚又是阴天,不要说月亮,连一点星光都没有,真所谓伸手不见五指.所幸的是他们有一盏油灯,同时可以有两个人借助灯光过桥.但要命的灯油将尽,这盏灯只能再维持30分钟了!他们焦急万分,该怎样过桥呢?分析:首先姐姐跟弟弟一起过,用时3分钟,姐姐再回去送油灯,用时3分钟,老爷爷跟爸爸一起过河,用时12分钟,弟弟将灯送回去,用时1分钟,弟弟和母亲一起过,用时6分钟,弟弟送灯过河,用时1分钟,最后与姐姐一起过河,用时3分钟.一共用时:3+3+12+1+6+1+3=29分钟.最后能够安全全部过河.【例4】男女二个主人带着二个仆人和一条狗过河,但船每次只能载二个(包活狗),女主人和仆人在一边,女主人会打死仆人;让仆人和狗在一边,狗会咬死仆人:让仆人在一边,他们会逃走.怎么过河?分析:见下表(二)蜗牛与青蛙趣题【例5】(★★★奥数网原创题)蜗牛沿着9米高的柱子往上爬,白天它向上爬5米,而晚上又下降4米,问蜗牛爬到柱顶需要几天?分析:一昼夜可以爬1米,爬了4昼夜后再经过一个白天即可爬到柱顶,因此需要5个白天4昼夜.[巩固]一口井深10米,一只蜗牛从井底白天往上爬2米,晚上又往下滑1米,请问要多长时间,这只蜗牛能爬出这口井?分析:“白天往上爬2米,晚上又往下滑1米”其实一天只往上爬1米,如果这样理解,说这只蜗牛爬出这口井需要10天就错了.因为最后一次爬出井外不会往下滑,所以蜗牛只要往上爬9米,晚上下滑1米,这时距离井口只有2米了,这样只要一个白天再往上爬2米就到井口了.所以只需要8天再加一个白天.【例6】一只青蛙爬树,每次往上爬5厘米,又往下滑2厘米,这只青蛙这样上下了5次,实际往上爬了多少厘米?分析:实际上青蛙没爬行一次只前进了5-2=3(厘米),5次共前进了3×5=15(厘米).[拓展] 青蛙沿着10米高的井往上跳,每次它向上跳半米,然后又落下去,问青蛙爬需要跳几次就能跳出井外?分析:每次青蛙向上跳半米,然后又落下去,等于还在原地,所以永远也跳不出去.Ⅲ、火柴棍趣题【例7】桌子上放着55根火柴,甲、乙二人轮流每次取走1~3根.规定谁取走最后一根火柴谁获胜.如果双方采用最佳方法,甲先取,那么谁将获胜?分析:获胜方在最后一次取走最后一根;往前逆推,在倒数第二次取时,必须留给对方4根,此时无论对方取1,2或3根,获胜方都可以取走最后一根;再往前逆推,获胜方要想留给对方4根,在倒数第三次取时,必须留给对方8根……由此可知,获胜方只要每次留给对方的都是4的倍数根,则必胜.现在桌上有55根火柴,55÷4=13……3,所以只要甲第一次取走3根,剩下52根火柴是4的倍数,以后甲总留给乙4的倍数根火柴,甲必胜.[拓展]将“每次取走1~3根”改为“每次取走1~4根”,其余不变,情形会怎样?分析:由上面的分析,只要始终留给对方(1+4=)5的倍数根火柴,就一定获胜.因为55是5的倍数,甲先取,不可能留给乙5的倍数根,而甲每次取完后,乙再取都可能留给甲5的倍数根,所以在双方都采用最佳策略的情况下,乙必胜.[拓展]将“谁取走最后一根火柴谁获胜”改为“谁取走最后一根火柴谁输”,其余不变,情形又将如何?分析:因为最后留给对方1根火柴者必胜,按照逆推的方法分析,只要每次留给对方4的倍数加1根火柴必胜.甲先取,只要第一次取2根,剩下53根(53除以4余1),以后每次都将除以4余1的根数留给以,甲必胜.【例8】两个人从1开始按自然数顺序轮流依次报数,每人每次只能报1~5个数,谁先报到50谁获胜.你选择先报数还是后报数?怎样才能获胜?分析:因为50(1+5)=8……2,所以要想获胜,应选择先报,第一次报2个数,剩下48个数是(1+5=)6的倍数,以后总把6的倍数个数留给对方,必胜.[拓展] 1111个空格排成一行,最左端空格中放有一枚棋子,甲先乙后轮流向右移动棋子,每次移动1~7个格.规定将棋子移到最后一格者输.甲为了获胜,第一步必须向右移多少格?分析:一开始棋子已占一格,棋子的右面有空格1111-1=1110(个).只要甲始终留给乙(1+7=)8的倍数加1格,就可获胜.(1111-1)(1+7)=138……6,所以甲第一步必须移5格,还剩下1105格,1105是8的倍数加1.以后无论以移几格,甲下次移的格数与乙移的格数之和是8,甲就必胜.【例9】有两堆火柴,一堆35根,另一堆24根.两人轮流在其中一堆中拿取,取得根数不限,但不能不取.规定谁得最后一根火柴谁胜.先取者有何获胜的策略?分析:先取者在35根一堆的火柴中取11根火柴,使得取后剩下两堆的火柴数相同.以后无论对手在某一堆取几根火柴,你只需在另一堆取同样多根火柴.只要对手有火柴可取,你就有火柴可取,也就是说,最后一根火柴总会被你拿到.这样先取者总可获胜.[前铺] 有一堆火柴,甲先乙后轮流每次取走1~3根.取完全部火柴后,如果甲取得火柴总数是偶数,那么甲获胜,否则乙获胜.试分析这堆火柴的根数在1~11根时,谁将获.分析:显然,1根时乙胜,2根或3根时甲胜,4根时乙胜.5根时,甲先取1根,若乙取1根,则甲取3根,若乙取2根或3根,则甲取1根,甲胜.6根时,甲先取1根,若乙取1根或2根,则甲取3根;若乙取3根,则甲取1根,甲胜.7根或8根时,甲先取3根,以后同5根或6根的情况,甲胜.9根时,甲取1~3根,相当于8~6根时乙先取的情况,由上面的分析,最终乙可取得偶数根,则甲为奇数根,乙胜.10根时,甲先取1根,11根时,甲先取2根,转化为9根时乙先取的情况,甲胜.【例10】有3堆火柴,分别有1根,2根与3根火柴.甲先乙后轮流从任意一堆里取火柴,取得根数不限,规定谁能取到最后一根火柴谁获胜.如果采用最佳方法,那么谁将获胜?分析:谁在某次取过火柴之后,恰好留下两堆数目相等的火柴,谁就能获胜.甲先取,共有6种取法:从第1堆里取1根;从第2堆里取1根或2根;从第3堆里取1根、2根或3根.无论那种取法,乙采取正确的取法,都可以留下两堆数目相等的火柴,所以乙采用最佳方法一定获胜.Ⅳ、单循环类趣题【例11】(★★★奥数网题库)学校组织一次乒乓球比赛,一共有10名选手,采用单循环制赛(每两位选手之间都进行一场比赛),那么一共要进行多少场比赛?分析:将十位选手编号,1号将与其他九位选手进行比赛,一共要赛9场,2号要与除了1号以外的所有选手比赛,一共进行8场,……,9号选手只要跟10号选手进行比赛,10号选手跟以前的选手都已经进行过比赛,所以不用再进行比赛.所以一共有比赛场次9+8+7+…+2+1=45(场).【例12】纸上有5个点,任意3点都不在一条直线上,如果把每两个点都连接起来,最多能连成多少条线段?分析:取其中一个点跟其余的4个点相连,就可以得到4条线段;再取一个点跟其他的三个点相连,这样又有3条线段,剩下的点可以组成2条线段和1条线段.这样一共可以组成4+3+2+1=10条线段.[拓展1]在学校的一次小型会议中,每两个人见面都要握手,王校长一共跟别人握了10次手,请问这次会议一共有多少人参加?所有参加会议的人握手的总次数有多少?分析:我校长一共跟别人握手10次,说明除了王校长以外,还有10个人,所以参加这次会议的人一共有11人;11个人一共握手的次数是10+9+8+7+6+5+4+3+2+1=55(次).[拓展2] 10个老朋友通过写信联络感情,一年之中每个人都给其余的人写一封信,请问一年之中这10个老朋友一共要寄出多少封信?一共收到多少封信?分析:这道题个内前面的有点区别,就是每个收到别人的信以后还有写一封信出去,所以每个人都要写9封信,10个人一共写了10×9=90封信.寄出的每一封信都会有人收到,寄出的信和收到的信的数量应该是相等的,也应该是90封.专题展望这一讲内容也许带给同学们无限的乐趣,也容同学们对数学产生了浓厚的兴趣,其实学习数学本身就是一中快乐.我们将在三升四的暑假班继续给大家介绍智巧趣题,更多、更有趣的题目等着大家,当然也会有更多的、更加新颖的解题思路和方法等着大家.练习一1.(例1)42个同学要坐船过河,渡口处只有一只能载4人的小船(无船工).他们要全部渡过河去,至少要使用这只小船渡河多少次?分析:如果由42÷4=10……2,得出10+1=11次,那么就错了.因为忽视了至少要有1个人将小船划回来这个特定的要求.实际情况是:小船前面的每一个来回至多只能渡3个人过河去,只有最后一次小船不用返回才能渡4个人过河.42=3×13+3,所以渡河次数是13×2+1=27(次).2.(例6)蜗牛沿着10米高的柱子往上爬,白天它向上爬5米,而晚上又下降3米,问蜗牛爬到柱顶需要几天?分析:一昼夜可以爬2米,爬了3昼夜后再经过一个白天即可爬到柱顶,因此需要3天1夜.3.(例3)一家人 6 口人,夜间要过一架独木桥,他们仅有一盏油灯照明,借助这盏灯,每次最多两人可以走过独木桥.而这 6 人过桥所需要的时间分别是 1 , 3 , 6 , 8 , 12 , 20 分钟,要命的是这盏灯只能点燃 47 分钟了,而没有灯照明,任何人企图过河那是必然跌落到深谷中.分析:有不同的解法,看其中一个.就用1,3,6,8,12,20表示这6人.共计用时45分钟.4.(例7)桌子上放着50根火柴,甲、乙二人轮流每次取走1~3根.规定谁取走最后一根火柴谁获胜.如果双方采用最佳方法,甲先取,那么谁将获胜?分析:获胜方在最后一次取走最后一根;往前逆推,在倒数第二次取时,必须留给对方4根,此时无论对方取1,2或3根,获胜方都可以取走最后一根;再往前逆推,获胜方要想留给对方4根,在倒数第三次取时,必须留给对方8根……由此可知,获胜方只要每次留给对方的都是4的倍数根,则必胜.现在桌上有55根火柴,50÷4=12……2,所以只要甲第一次取走2根,剩下48根火柴是4的倍数,以后甲总留给乙4的倍数根火柴,甲必胜.5.学校组织一次乒乓球比赛,一共有9名选手,采用单循环制赛(每两位选手之间都进行一场比赛),那么一共要进行多少场比赛?分析:将十位选手编号,1号将与其他九位选手进行比赛,一共要赛8场,2号要与除了1号以外的所有选手比赛,一共进行7场,……,8号选手只要跟9号选手进行比赛,9号选手跟以前的选手都已经进行过比赛,所以不用再进行比赛.所以一共有比赛场次8+7+…+2+1=36(场).成长故事各有所长一只蝙蝠由于懂得一些天文常识,就骄傲起来.它批评大象个头虽大,却大而不当,反而因此行动笨拙缓慢;看见活蹦乱跳的兔子,就说它虽然跳得快,却不懂声纳和气流的原理,光在那儿胡乱跳着;它更不能忍受鸡有翅膀,却不懂得怎么利用它飞行……蝙蝠一天到晚自以为是地说:“我实在无法忍受这些无知又一无是处的家伙!”有一天,蝙蝠不小心落到河里,因为不懂得游泳的技巧,结果被活活淹死了.虽然它懂得天文地理,这时却一点儿也派不上用场.自信并不是自我夸大,唯我独尊.你懂的也许别人不懂,但是别人会的,你也不见得都会.千万不要用自己所具备的条件来衡量别人,这样只会注意到自己的优点,而抹杀了他人的长处.。

小蓝本组合趣题讲解说到“小蓝本组合趣题”,很多人可能会想:“这是什么?听起来有点复杂吧?”其实啊,这个问题呢,乍一听,确实让人有点摸不着头脑。
可你别着急,咱们慢慢捋一捋,保证你看了之后,马上能明白。
咱们先来个引子:想象一下,你去逛超市,看到货架上有好多颜色各异的小盒子,每个盒子里都有不同的小东西,可能是糖果,可能是小玩具,总之种类多得让人眼花缭乱。
你现在要做的事就是,从这些盒子里挑出特定数量的物品,而且每个盒子里你选的东西的组合又有一些限制,怎么样,听起来是不是有点意思?这个小蓝本组合题,其实就是在考察你怎么从众多的选择中挑选出符合条件的组合。
你可能会说,“这不就和选商品一样吗?那有啥难的?”哦,得了吧,真不是你想得那么简单。
举个简单的例子,假设你在一个“蛋糕”的选择题里,市场上有10种蛋糕,你的任务是从这10种里选3个,而每种蛋糕只能选一次。
这个问题不光是考你的选择能力,更考你如何在限定条件下,合理安排你的选项。
有点像是在做一道数独题,既要看整体,又得注意细节。
可能一开始你会觉得有点晕头转向,但掌握了诀窍后,这种题根本难不倒你。
来,再接着往下说,你会发现,虽然每个“小蓝本”上的题目形式不同,最终考的还是同一类思维——组合、排列、分配。
换句话说,无论你是要从20个苹果里挑5个,还是从50个学生中选出4个代表,背后的逻辑都是一样的。
这就好比是在拍电影,演员虽然不同,但导演的手法和拍摄角度差不多。
你要做的,就是从一堆选项中找到合适的搭配,不多也不少,正好符合条件,这个过程还挺有意思的,甚至有时候可以说是巧妙,像解谜一样,每一步都要小心翼翼,不能掉以轻心。
咱们聊聊组合问题常见的一些小陷阱。
想象一下,你正在解题,想着要选4个苹果,但不小心算错了,结果多选了一个,那不就出问题了吗?又或者你选择的苹果有重复的,明明是挑4个不同的,可你却把两颗红苹果算成了两次,这可就尴尬了。
为什么?因为组合题最忌讳的就是重复选择!这种失误,就是所谓的“重复选择”错误。
第一讲 智巧趣题从三年级开始,我们就要系统地学习奥数知识,本讲主要是通过数学趣题的研究学习引发学生学习奥数的兴趣,激发学生学习奥数的灵感,充分调动学生学习奥数的积极性.Ⅰ、蜗牛与青蛙趣题【例1】 (★★★ 奥数网原创题) 一口井深10米,一只蜗牛从井底白天往上爬2米,晚上又往下滑1米,请问要多长时间,这只蜗牛能爬出这口井?分析:“白天往上爬2米,晚上又往下滑1米”其实一天只往上爬1米,如果这样理解,说这只蜗牛爬出这口井需要10天就错了.因为最后一次爬出井外不会往下滑,所以蜗牛只要往上爬9米,晚上下滑1米,这时距离井口只有2米了,这样只要一个白天再往上爬2米就到井口了.所以只需要8天再加一个白天.[拓展] 蜗牛沿着9米高的柱子往上爬,白天它向上爬5米,而晚上又下降4米,问蜗牛爬到柱顶需要几天几夜?分析:一昼夜可以爬1米,爬了4昼夜后再经过一个白天即可爬到柱顶,因此需要5天4夜.教学目标专题精讲和想 挑战吗 ?一个人带着一只狐狸、一只鹅和一些玉米渡河,每次只能带一样,可是人不在时,狐狸要吃鹅,鹅要吃玉米.那么应该怎样渡河呢? 分析:先带鹅过河,自己划船回来,第二次带狐狸过去,再把鹅带回来,第三次带玉米过河,自己划船回来,第四次再把鹅带过去即可.【例2】青蛙沿着10米高的井往上跳,每次它向上跳半米,然后又落下去,问青蛙爬需要跳几次就能跳出井外?分析:每次青蛙向上跳半米,然后又落下去,等于还在原地,所以永远也跳不出去.[拓展]一只树蛙爬树,每次往上爬5厘米,又往下滑2厘米,这只青蛙这样上下了5次,实际往上爬了多少厘米?分析:实际上青蛙没爬行一次只前进了5-2=3(厘米),5次共前进了3×5=15(厘米).Ⅱ、过河问题【例3】一个农民携带一只狼,一只羊和一棵白菜,要借助一条小船过河.小船上除了农民只能再带狼、羊、白菜中的一样.而农民不在时,狼会吃羊,羊会吃白菜.农民如何过河呢?【例4】有一家五口人要在夜晚过一座独木桥.他们家里的老爷爷行动非常不便,过桥需要12分钟;孩子们的父亲贪吃且不爱运动,体重严重超标,过河需要时间也较长,8分钟;母亲则一直坚持劳作,动作还算敏捷,过桥要6分钟;两个孩子中姐姐需要3分钟,弟弟只要1分钟.当时正是初一夜晚又是阴天,不要说月亮,连一点星光都没有,真所谓伸手不见五指.所幸的是他们有一盏油灯,同时可以有两个人借助灯光过桥.但要命的灯油将尽,这盏灯只能再维持30分钟了!他们焦急万分,该怎样过桥呢?分析:首先姐姐跟弟弟一起过,用时3分钟,姐姐再回去送油灯,用时3分钟,老爷爷跟爸爸一起过河,用时12分钟,弟弟将灯送回去,用时1分钟,弟弟和母亲一起过,用时6分钟,弟弟送灯过河,用时1分钟,最后与姐姐一起过河,用时3分钟.一共用时:3+3+12+1+6+1+3=29分钟.最后能够安全全部过河.【例5】(★★★★奥数网改编题)有四个人在晚上准备通过一座摇摇欲坠的小桥.此桥每次只能让2个人同时通过,否则桥会倒塌.过桥的人必须要用到手电筒,不然会一脚踏空.只有一个手电筒.4个人的行走速度不同:小强用1分种就可以过桥,中强要2分中,大强要5分中,最慢的太强需要10分中.17分钟后桥就要倒塌了.请问:4个人要用什么方法才能全部安全过桥?分析:小强和中强先过桥,用2分钟;再用小强把电筒送过去,用1分钟,现在由大强跟太强一起过桥,用10分钟,过去以后叫中强把电筒送给小强用2分钟,最后小强与中强一起过河再用2分钟,他们一起用时间:2+1+10+2+2=17(分钟),正好在桥倒塌的时候全部过河.(时间最短过河的原则是:时间长的一起过,时间短的来回过.这样保证总的时间是最短的).[前铺] 赵大爷和一个小八路带着一个负伤的红军战士因为叛徒出卖被日本鬼子追到一条小河边,河岸边只有一条能同时乘坐两人的小船,赵大爷划船需要2分钟,小八路划船需要3分钟,负伤的红军战士划船需要5分钟,现在在危机关头,需要尽快过河,采用怎样的过河方式,三个人全部过河用时最少?分析:赵大爷首先跟小八路或者红军战士一起过河,用时2分钟,再由赵大爷把船划过来,用时2分钟,最后把剩下的人一起载过去,再用时2分钟.一共用时6分钟.【例6】(★★★奥数网经典题) 37个同学要坐船过河,渡口处只有一只能载5人的小船(无船工).他们要全部渡过河去,至少要使用这只小船渡河多少次?分析:如果由37÷5=7……2,得出7+1=8次,那么就错了.因为忽视了至少要有1个人将小船划回来这个特定的要求.实际情况是:小船前面的每一个来回至多只能渡4个人过河去,只有最后一次小船不用返回才能渡5个人过河.因为除最后一次可以渡5个人外,前面若干个来回每个来回只能渡过4个人,每个来回是2次渡河,37=4×8+5,所以渡河次数是8×2+1=17(次). (注:由于数据的特殊性,刚好最后一次5个人过河).[拓展] 38个同学要坐船过河,渡口处只有一只能载4人的小船(无船工).他们要全部渡过河去,至少要使用这只小船渡河多少次?分析:根据前面的解答,实际上前面每次过河的人数只有3人,最后一次最多过4人,因为38=3×12+2,所以前面3人一次过了12次,来回一共划了12×2=24(次),最后一次是2人过河,还要用1次.所以最终需要渡河的次数是24+1=25(次).Ⅲ、火柴棍趣题【例7】有两堆火柴,一堆3根,另一堆7根.甲、乙两人轮流取火柴,每次可以从每一堆中取任意根火柴,也可以同时从两堆中取相同数目的火柴.每次至少要取走一根火柴.谁取得最后一根火柴谁胜.如果都采用最佳方法,那么谁将获胜?分析:采用逆推法分析,假设甲获胜,甲最终将两堆火柴都变为0,简记(0,0);因为甲至少取1根火柴,所以甲取之前,即乙留给甲的两堆火柴最少的几种情况是(1,0),(2,0)(1,1);要想乙留给甲上述情况,甲应该留给乙(1,2);再往前逆推,当甲留给乙(3,5)时,无论乙怎样取,甲都可以一次取完所有的火柴或留给乙(1,2).所以甲先从7根火柴的一堆取出2根,留给乙(3,5),甲必胜.[前铺]桌子上放着55根火柴,甲、乙二人轮流每次取走1~3根.规定谁取走最后一根火柴谁获胜.如果双方采用最佳方法,甲先取,那么谁将获胜?分析:获胜方在最后一次取走最后一根;往前逆推,在倒数第二次取时,必须留给对方4根,此时无论对方取1,2或3根,获胜方都可以取走最后一根;再往前逆推,获胜方要想留给对方4根,在倒数第三次取时,必须留给对方8根……由此可知,获胜方只要每次留给对方的都是4的倍数根,则必胜.现在桌上有55根火柴,55÷4=13……3,所以只要甲第一次取走3根,剩下52根火柴是4的倍数,以后甲总留给乙4的倍数根火柴,甲必胜.[拓展]将“每次取走1~3根”改为“每次取走1~4根”,其余不变,情形会怎样?分析:由上面的分析,只要始终留给对方(1+4=)5的倍数根火柴,就一定获胜.因为55是5的倍数,甲先取,不可能留给乙5的倍数根,而甲每次取完后,乙再取都可能留给甲5的倍数根,所以在双方都采用最佳策略的情况下,乙必胜.[拓展]将“谁取走最后一根火柴谁获胜”改为“谁取走最后一根火柴谁输”,其余不变,情形又将如何?分析:因为最后留给对方1根火柴者必胜,按照逆推的方法分析,只要每次留给对方4的倍数加1根火柴必胜.甲先取,只要第一次取2根,剩下53根(53除以4余1),以后每次都将除以4余1的根数留给以,甲必胜.【例8】黑板上写着一排相连的自然数1,2,3,…,51.甲、乙两人轮流划掉连续的3个数.规定在谁划过之后另一人再也划不成了,谁就算取胜.问:甲有必胜的策略吗?分析:甲先划,把中间25,26,27这三个数划去,就将1到51这51个数分成了两组,每组有24个数.这样,只要乙在某一组里有数字可划,那么甲在另一组里相对称的位置上就总有数字可划.因此,若甲先划,且按上述策略进行,则甲必能获胜.[前铺] 两个人从1开始按自然数顺序轮流依次报数,每人每次只能报1~5个数,谁先报到50谁获胜.你选择先报数还是后报数?怎样才能获胜?分析:因为50(1+5)=8……2,所以要想获胜,应选择先报,第一次报2个数,剩下48个数是(1+5=)6的倍数,以后总把6的倍数个数留给对方,必胜.【例9】有11根火柴,两人轮流从中拿取,每次至少取1根.先取者第一次取得数目不限(但不能全部取走),以后每人取得数目不得超过另一人上次取得数目的2倍规定取得最后一根者为胜.先取者的获胜策略是什么?分析:甲第一次取3根,可获胜.甲取了3根以后剩下8根,乙如果取3,4,5,6根,那么甲将余下的取完,甲胜;乙如果取1根或者2根,那么甲接着取2根或者1根,此时剩下5根,以后若乙取2,3,4根,加将余下的取完,甲胜;若乙取1根,加再取1根,剩3根,无论乙再如何取,甲必胜.[拓展] 1111个空格排成一行,最左端空格中放有一枚棋子,甲先乙后轮流向右移动棋子,每次移动1~7个格.规定将棋子移到最后一格者输.甲为了获胜,第一步必须向右移多少格?分析:一开始棋子已占一格,棋子的右面有空格1111-1=1110(个).只要甲始终留给乙(1+7=)8的倍数加1格,就可获胜.(1111-1)(1+7)=138……6,所以甲第一步必须移5格,还剩下1105格,1105是8的倍数加1.以后无论以移几格,甲下次移的格数与乙移的格数之和是8,甲就必胜.[拓展] 有一堆火柴,甲先乙后轮流每次取走1~3根.取完全部火柴后,如果甲取得火柴总数是偶数,那么甲获胜,否则乙获胜.试分析这堆火柴的根数在1~11根时,谁将获.分析:显然,1根时乙胜,2根或3根时甲胜,4根时乙胜.5根时,甲先取1根,若乙取1根,则甲取3根,若乙取2根或3根,则甲取1根,甲胜.6根时,甲先取1根,若乙取1根或2根,则甲取3根;若乙取3根,则甲取1根,甲胜.7根或8根时,甲先取3根,以后同5根或6根的情况,甲胜.9根时,甲取1~3根,相当于8~6根时乙先取的情况,由上面的分析,最终乙可取得偶数根,则甲为奇数根,乙胜.10根时,甲先取1根,11根时,甲先取2根,转化为9根时乙先取的情况,甲胜.Ⅳ、卖酒趣题【例10】(★★★★奥数网题库)吝啬的卖酒老板老钱招聘卖酒伙计,他只给伙计两个分别为5升和3升的盛酒杯,要求满足所有顾客的买酒需求(当然顾客只需要整数升的酒),这下难倒了很多前来应聘的人,可是有一个聪明的放牛娃娃却做到了,你知道放牛娃娃是怎么样卖出一升酒的吗?分析:先将5升的酒杯盛满,倒入3升的容器中,再将3升的酒倒入酒缸中,将5升的酒杯中剩余的2升酒倒入3升的酒杯中;再次将5升的酒杯盛满,再将其中的酒倒入3升的容器中,使3升的酒杯装满,这样5升酒杯还剩4升酒;最后把3升酒杯里的酒全部倒入酒缸中,再次将5升酒杯中的酒倒入3升的第一次第二次第三次第四次第五次第六次第七次第八次5升 5 2 2 0 5 4 4 13升0 3 0 2 2 3 0 3还有更简单一方法:用3升的酒杯量2次倒入5升酒杯中,即可量出1升酒.[拓展1] 卖牛奶人有两桶10升装的牛奶.两个顾客各带容器去买2升牛奶.一个带的是5升的容器,另一个带的是4升的容器.这位卖牛奶人如何解决问题?分析:如下表:【例11】某人有12升啤酒一瓶,想从中倒出6升.但是他没有6升的容器,只有一个8升的容器和一个5升的容器.怎样的倒法才能使8升的容器中恰好装好了6升啤酒?分析:这个数学游戏有两种不同的解法,如下面的两个表所示.第一种解法:12 12 4 4 9 9 1 1 68 0 8 3 3 0 8 6 65 0 0 5 0 3 3 5 0第二种解法:12 12 4 0 8 8 3 3 11 11 6 68 0 8 8 0 4 4 8 0 1 1 6 5 0 0 4 4 0 5 1 1 0 5 0这一讲内容也许带给同学们无限的乐趣,也容同学们对数学产生了浓厚的兴趣,其实学习数学本身就是一中快乐.我们将在三升四的暑假班继续给大家介绍智巧趣题,更多、更有趣的题目等着大家,当然也会有更多的、更加新颖的解题思路和方法等着大家.1. (例1)蜗牛沿着10米高的柱子往上爬,白天它向上爬5米,而晚上又下降3米,问蜗牛爬到柱顶需要几天?分析:一昼夜可以爬2米,爬了3昼夜后再经过一个白天即可爬到柱顶,因此需要3天1夜.2. (例10)有大、中、小3个瓶子,最多分别可发装入水1000克、700克和300克.现在大瓶中装满水,希望通过水在3个瓶子间的流动动使得中瓶和小瓶上标出装100克水的刻度线,问最少要倒几次水?分析:63. (例7)桌子上放着50根火柴,甲、乙二人轮流每次取走1~3根.规定谁取走最后一根火柴谁获胜.如果双方采用最佳方法,甲先取,那么谁将获胜?分析:获胜方在最后一次取走最后一根;往前逆推,在倒数第二次取时,必须留给对方4根,此时无论对方取1,2或3根,获胜方都可以取走最后一根;再往前逆推,获胜方要想留给对方4根,在倒数第三次取时,必须留给对方8根……由此可知,获胜方只要每次留给对方的都是4的倍数根,则必胜.现在桌上有55根火柴,50÷4=12……2,所以只要甲第一次取走2根,剩下48根火柴是4的倍数,以后甲总留给乙4的倍数根火柴,甲必胜.4. 学校组织一次乒乓球比赛,一共有9名选手,采用单循环制赛(每两位选手之间都进行一场比赛),那么一共要进行多少场比赛?专题展望练习一分析:将十位选手编号,1号将与其他九位选手进行比赛,一共要赛8场,2号要与除了1号以外的所有选手比赛,一共进行7场,……,8号选手只要跟9号选手进行比赛,9号选手跟以前的选手都已经进行过比赛,所以不用再进行比赛.所以一共有比赛场次8+7+…+2+1=36(场).5.(例5)一家人 6 口人,夜间要过一架独木桥,他们仅有一盏油灯照明,借助这盏灯,每次最多两人可以走过独木桥.而这 6 人过桥所需要的时间分别是 1 , 3 , 6 , 8 , 12 , 20 分钟,要命的是这盏灯只能点燃 47 分钟了,而没有灯照明,任何人企图过河那是必然跌落到深谷中.分析:有不同的解法,看其中一个.就用1,3,6,8,12,20表示这6人.步数此岸过桥彼岸用时1,3,6,8,12,201 1,3> 36,8,12,20 1,32 <1 11,6,8,12,20 33 12,20> 201,6,8 3,12,204 <3 31,3,6,8 12,205 1,3> 36,8 1,3,12,206 <1 11,6,8 3,12,207 6,8> 81 3,6,8,12,208 <3 31,3 6,8,12,209 1,3> 31,3,6,8,12,20共计用时45分钟.成长故事各有所长一只蝙蝠由于懂得一些天文常识,就骄傲起来.它批评大象个头虽大,却大而不当,反而因此行动笨拙缓慢;看见活蹦乱跳的兔子,就说它虽然跳得快,却不懂声纳和气流的原理,光在那儿胡乱跳着;它更不能忍受鸡有翅膀,却不懂得怎么利用它飞行……蝙蝠一天到晚自以为是地说:“我实在无法忍受这些无知又一无是处的家伙!”有一天,蝙蝠不小心落到河里,因为不懂得游泳的技巧,结果被活活淹死了.虽然它懂得天文地理,这时却一点儿也派不上用场.自信并不是自我夸大,唯我独尊.你懂的也许别人不懂,但是别人会的,你也不见得都会.千万不要用自己所具备的条件来衡量别人,这样只会注意到自己的优点,而抹杀了他人的长处.。

组合问题练习题组合问题是离散数学中的一个重要概念,它在组合数学、图论、概率论等领域都有广泛的应用。
组合问题的解决往往需要一定的技巧和数学思维,下面是一些组合问题的练习题,帮助读者提升解决这类问题的能力。
1. 餐厅菜单上有10道菜,你要从中选择3道菜作为晚餐的主菜,请问你有多少种选择的可能性?2. 一副扑克牌有52张牌,你要从中选择5张牌作为手牌,请问你有多少种选择的可能性?3. 一家公司有8名员工,其中3名员工将被选为董事会成员,另外2名员工将被选为监事会成员,请问公司有多少种不同的人员组合方案?4. 一个有序序列中,有8个不同的元素。
从中选择4个元素组成一个子序列,请问有多少种不同的子序列组合方案?5. 在一个班级中,有8名男生和6名女生。
从中选择4名学生组成一个考试小组,请问有多少种不同的小组组合方案?以上是一些组合问题的练习题。
解决这些问题需要运用组合数学中的相关知识,例如排列组合、二项式系数等。
通过练习这些问题,读者可以熟悉组合问题的解决方法,并提升自己解决组合问题的能力。
组合问题的解决思路可以通过数学公式或者直接计数的方法来实现。
在计算组合问题的解的时候,常常需要注意是否需要考虑元素的顺序以及重复的情况。
组合问题在实际生活中有广泛的应用。
例如在排列座位、选择队伍、分配任务等场景中,经常需要考虑组合问题。
解决组合问题可以帮助我们更加合理地组织资源、安排任务,并且能够提高效率。
通过解决上述练习题,可以加深对组合问题的理解,并且提高解决组合问题的能力。
希望读者能够善于运用组合数学的知识,解决生活和工作中的实际问题,提升自己的数学思维能力。
组合问题是离散数学中的一个重要概念,它在组合数学、图论、概率论等领域都有广泛的应用。
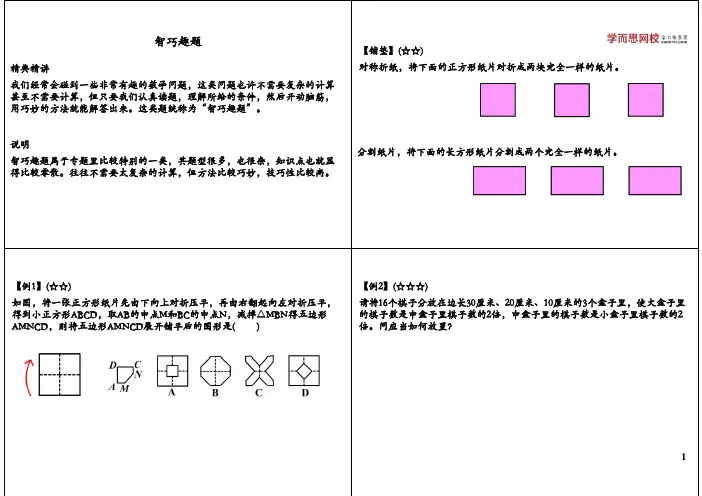
小学数学《智巧趣题》练习题(含答案)【知识要点】智巧趣题靠的就是“智”和“巧”,这类问题一般不需要复杂的计算,问题带有一定的迷惑性,目的就是考考你的智力和思维的灵活性,所以我们不能被一些表面现象或数量所迷惑,关键是开动脑筋,多角度思考问题,灵活地运用自己的智慧,巧妙回答。
解答智巧趣题时,有时看起来很容易,但解题时要小心,关键是要抓住“智”和“巧”。
第一要动脑筋,学会全面考虑各种情况;第二要巧妙运用学过的数学知识;第三需要一些思考问题的灵活性和非常规的思考方法。
解题指导1几个人同时做一件事,需要一定的时间,当人数和事件按相同的倍数增加,仍然是同时做,时间没有增加。
【例1】3个人同时吃3个苹果,用3分钟吃完,9个人同时吃9个苹果,需要几分钟才能吃完?【思路点拨】3个人同时吃3个苹果,用3分钟吃完,说明1人吃一个苹果需要3分钟,9个人同时吃9个苹果,每人一个苹果,需要 3 分钟。
答:需要3分钟才能吃完。
【变式题1】如果有4只猫,同时吃掉4条鱼,需要4分钟的时间,问如果按照同样的速度,100只猫同时吃掉100条鱼,需要多少时间?解题指导2【例2】可可和笑笑到书店买书,两人看中同一本书,但付钱时发现钱不够,可可缺6元4角,笑笑缺1分。
即使两人把钱合起来,钱仍然不够。
问这本书多少元?【思路点拨】笑笑只缺1分钱,两人把钱合起来,只要可可能给笑笑1分钱,就能够买到一本书,现在是合起来后钱还是不够,说明可可一分钱也没能给笑笑,也就是可可一分钱都没有。
那么可可所缺6元4角,就是这本书的定价,这本书6元4角,也就是6.4元。
答:这本书6.4元。
总结:1分钱也沿有,当然合起来和没合起来是一样的。
【变式题2】丽丽和琪琪到书店去买书,两人都看中了一本《格林童话》。
付钱时发现丽丽缺1分钱,琪琪缺10元5角,并且即使两人钱合起来仍然不够。
问《格林童话》售价多少元?解题指导3运送物品过河,还要保护物品不互相损伤,这时就需要考虑带过来,再带回去的思路,使互相会损伤的物品不放在一起。
目录组合题部分 (2)智巧趣题一 (4)智巧趣题二 (7)抽屉原理一 (11)最值问题一 (18)逻辑推理一 (21)构造认证一 (25)抽屉原理二 (28)逻辑推理二 (31)最值问题二 (35)构造论证二 (38)枚举法一 (45)枚举法二 (48)加法原理与乘法原理 (51)排列组合 (54)计数综合一 (56)包含与排除 (59)几何计数 (62)计数综合二 (65)计数综合三 (68)计数综合四 (71)概率初步 (74)组合题部分组合知识网络:()()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⇒⎪⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧+图论方法:染色原理:奇偶分析:最值问题构造论证:找规律:比较法:枚举法:的图片在方格中填数字和最大走棋子圆桌上放硬币抢报数或火柴棒游戏略策多人过沙漠单人过沙漠过沙漠问题排有分支的直线上如何安短直线上如何安排路程最运送货物烙饼问题一个或多个时间最短理发打水合理安排时间筹统策对与筹统保证与至少最不利原则要点原理:个原理:类型抽屉原理一题问合组12m⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⇒⎪⎪⎩⎪⎪⎨⎧-⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⇒⎩⎨⎧推理组题图形推理其它分数相减分数相加分数比较法考试推理得失球对应胜负局对应,平局对应可能分数每队最高分与最低分,所有队总场次,总分比分与得分推理圆形连线场次推理理推育体循环推理:互补性原理:排除性原理:列表法:分析法三者关系二者关系分类理推表列假设法对应推理矛盾分析法假设法目标推理真假推理理推辑逻二题问合组智巧趣题一内容概述:使用火柴棒构造图形的问题;一笔画问题;不涉及专门的数学知识,只需要一些巧妙思路和简单计算即可解决的问题。
8-1智巧趣题知识点说明智巧趣题顾名思义,就是有趣的一类问题,但回答时要十分小心,稍有不慎,就可能落入“圈套”。
要想正确地解答这类题目,一是细心,善于观察,全面考虑各种情况;二是要充分运用生活中学到的知识;三是需要那么一点思考问题的灵气和非常规的思考方法。
本讲主要是通过数学趣题的研究学习引发学生学习奥数的兴趣,激发学生学习奥数的灵感,充分调动学生学习奥数的积极性。
智巧趣题主要依靠巧妙的构思而解决问题,其中包括火柴棍游戏、数的恰当排列、称量问题及直线或圆周形状的报数问题。
【例1】用数字1,1,2,2,3,3拼凑出一个六位数,使两个1之间有1个数字,两个2之间有2个数字,两个3之间有3个数字。
【巩固】把一根线绳对折,对折,再对折,然后从对折后的中间处剪开,这根线绳被剪成了多少段?【例2】12345679999999999【例3】有10张,卡片分别标有从2开始的10个连续偶数。
如果将它们分成5组,每组两张,计算同组中两个偶数和分别得到①34,②22,③16,④30,⑤8。
那么每组中的两张卡片上标的数各是多少?【例4】售货员把29个乒乓球分装在5个盒子里,使得只要顾客所买的乒乓个数小于30,他总可以恰好把其中的一盒或几盒卖出,而不必拆盒。
问这5个盒子里分别装着多少个乒乓球?【例5】一口井深10米,一只蜗牛从井底白天往上爬2米,晚上又往下滑1米,请问要多长时间,这只蜗牛能爬出这口井?【巩固】蜗牛沿着9米高的柱子往上爬,白天它向上爬5米,而晚上又下降4米,问蜗牛爬到柱顶需要几天几夜?【巩固】青蛙沿着10米高的井往上跳,每次它向上跳半米,然后又落下去,问青蛙爬需要跳几次就能跳出井外?【巩固】一只树蛙爬树,每次往上爬5厘米,又往下滑2厘米,这只青蛙这样上下了5次,实际往上爬了多少厘米?【例6】小明的左衣袋和右衣袋中分别装有6枚和8枚硬币,并且两衣袋中硬币的总钱数相等。
当任意从左边衣袋取出两个硬币与右边衣袋的任意两个硬币交换时,左边衣袋的钱总数要么比原来的钱数多2分,要么比原来的钱数少2分,那么两个衣袋中共有多少分钱?【例7】甲和乙分别从东西两地同时出发,相对而行,两地相距100里,甲每小时走6里,乙每小时走4里。
第四讲智巧趣题【知识要点】智巧趣题既有趣味性,又有迷惑性,所以解答趣题时,审题是关键。
看清楚题目中的每一个已知条件和所求问题,就能排除迷惑性。
然后你要充分运用所学过的数学知识就可以轻松地解答了。
【典型例题】例1:在每个小朋友走得快慢相同的情况下,如果2个小朋友一起从学校从儿童乐园需要30分钟,那么6个小朋友一起从学校走到儿童乐园需要多少时间?分析:题目中告诉我们2个小朋友一起从学校到儿童乐园需要30分钟,说明每一个人从学校到儿童乐园都要走30分钟,因为他们是同时出发的,所以无论人数的多少,走这段路所用的时间和一个人走这段路所用的时间是相等的。
答:6个小朋友一起从学校到儿童乐园需要30分钟。
例2:两个父亲和两个儿子,一起去钓鱼。
每人都钓到一条鱼,回去一数一共只有3条鱼。
为什么?分析:“两个父亲”和“两个儿子”初一看好象是四人去钓了鱼,如果你再仔细分析一下,就知道“父亲”、“儿子”的身份相对的,“两个父亲和两个儿子”可能只有3个人:爷爷、爸爸和男孩。
例3:3只小兔同时吃3根萝卜,需要3分钟,按这样的速度,10只小兔同时吃10根萝卜,需要多少时间?分析:有的同学会这样想:3只小兔吃3根萝卜需要3分钟,那么每只小兔吃1根萝卜只需要1分钟,现在有10只小兔同时吃10根萝卜就需要10分钟,其实这样想是不对的。
错在哪里呢?主要是没有注意条件中的“同时”两个字,因为3只小兔同时吃掉3根萝卜,那么每只小兔都吃了1根萝卜,用了3分钟;按同样的速度10只小兔吃10根萝卜,对于每只兔子来说还是都吃了1根萝卜,所用的时间还是3分钟。
例4:在一次计算比赛中,共有30名同学分别获一、二、三奖,第1名到第10名获一等奖,第20名到第30名获三等奖,那么获二等奖的有几人?分析:有的同学看完题目后,可能会脱口而出:“10人获一等奖,10人获三等奖,剩下的10人获二等奖。
”其实这个答案是错误的。
只要仔细读题,你就会发现,获二等奖的应是第11名到第19名的同学,共9人。