电工原理第二章部分习题及答案

精选全文完整版第2章 习题解答(部分)2.3.3 计算图2.13中的电流 I 3。

解: 用电源等值互换法将电流源变换成电压源，将电阻R 2和R 3合并成电阻R 23，其中 V R I U R S S 2125.043,2=⨯=⨯=Ω=参考方向如图2.34所示。

求电路中电流IA R R R U U I S 2.115.012143,211=+++=+++= I 即为原电路中R 1上流过的电流，用分流公式，可求原电路中I 3A I R R R I 6.02.11113223=⨯+=⨯+= 2.4.1 图2.16是两台发电机并联运行的电路。

已知E 1=230V , R 01=0.5Ω，E 2=226V , R 02=0.3 Ω,负载电阻R L =5.5Ω，试分别用支路电流法和结点电压法求各支路电流 。

解:（1）用支路电流法：各支路电流参考方向已画在图2.16中。

列结点电压方程 L I I I =+21列回路电压方程S Ω 图 2.13 习题2.3.3的图U S U 图解 2.34101202图2.16 习题2.4.1的图L L 0222LL 0111R I R I E R I R I E +=+=联立求解上述三各方程式组成的方程组，可得A 40A2021===L I I I验算：按非独立回路方程进行02201121R I R I E E -=-代入数据443.0205.020226230==⨯-⨯=- （正确！）（2）用结点电压法求解：先求端电压U ，有V 2205.513.015.013.02265.02301110201022011=+++=+++=L R R R R E R E U A 405.0220A 205.0220226A 205.022023002220111====-=-==-=-=L L R U I R U E I R U E I 结果与上相同。

2.5.1 试用结点电压法求图2.18所示电路中的各支路电流解:在原图2.18中用O 和O ’标明两个结点，则有A 5.0505025V 505015015015025501005025a O ,O'-=-==++++=I U A 5.0505025A 15050100c b -=-==-=I I 2.6.1 用叠加原理计算图2.19中各支路的电流。

电工学第二章习题一、填空题1． 两个均为40F μ的电容串联后总电容为 80 F μ，它们并联后的总电容为 20 F μ。

2. 表征正弦交流电振荡幅度的量是它的 最大值 ；表征正弦交流电随时间变化快慢程度的量是 角频率ω ；表征正弦交流电起始位置时的量称为它的 初相 。

三者称为正弦量的 三要素 。

3. 电阻元件上任一瞬间的电压电流关系可表示为 u = iR ；电感元件上任一瞬间的电压电流关系可以表示为dtdiLu =L ；电容元件上任一瞬间的电压电流关系可以表示为dtduCi =C 。

由上述三个关系式可得， 电阻 元件为即时元件； 电感 和 电容 元件为动态元件。

4. 在RLC 串联电路中，已知电流为5A ，电阻为30Ω，感抗为40Ω，容抗为80Ω，那么电路的阻抗为 50Ω ，该电路为 容 性电路。

电路中吸收的有功功率为 750W ，吸收的无功功率又为 1000var 。

二、选择题1. 某正弦电压有效值为380V ，频率为50Hz ，计时始数值等于380V ，其瞬时值表达式为（ B ）A 、t u 314sin 380=V ；B 、)45314sin(537︒+=t u V ；C 、)90314sin(380︒+=t u V 。

2. 一个电热器，接在10V 的直流电源上，产生的功率为P 。

把它改接在正弦交流电源上，使其产生的功率为P/2，则正弦交流电源电压的最大值为（ D ） A 、7.07V ； B 、5V ； C 、14V ； D 、10V 。

3. 提高供电电路的功率因数，下列说法正确的是（ D ）A 、减少了用电设备中无用的无功功率；B 、减少了用电设备的有功功率，提高了电源设备的容量；C 、可以节省电能；D 、可提高电源设备的利用率并减小输电线路中的功率损耗。

4. 已知)90314sin(101︒+=t i A ，︒+=30628sin(102t i ）A ，则（ C ）A 、i1超前i260°；B 、i1滞后i260°；C 、相位差无法判断。

电工电子第二章试题及答案一、选择题1.电流的单位是（）A.伏特B.欧姆C.安培D.瓦特答案：C2.简单电路中，电流的方向是（）A.电子流动的方向B.阳极到阴极的方向C.阴极到阳极的方向D.无法确定的方向答案：C3.伏特表的作用是（）A.测量电流B.测量电阻C.测量电压D.测量功率答案：C4.电流的大小受到（）的影响。

A.单位时间内通过导体的电荷数B.导体的长度C.导体的截面积D.导体的材料答案：A5.电阻的单位是（）A.安培B.瓦特C.欧姆D.伏特答案：C二、填空题1.在串联电路中，总电阻等于各个电阻的（）之和。

答案：电阻2.在并联电路中，总电阻等于各个电阻的（）之倒数再取倒数。

答案：电阻3.如果电源电压为12伏特，电路中的总电阻为3欧姆，根据欧姆定律可求出电路中的电流为（）安培。

答案：44.如果电路中的电阻为10欧姆，电路中通过的电流为5安培，根据欧姆定律可求出电路中的电压为（）伏特。

答案：505.根据欧姆定律，电阻与电流成（）关系。

答案：反比三、解答题1.请解释什么是欧姆定律，并列举几个符合欧姆定律的电路现象。

答：欧姆定律是指在一定温度下，电流通过的导体两端的电压与导体两端的电阻成正比关系。

符合欧姆定律的电路现象包括：串联电路中，电流通过的各个电阻之和等于总电压；并联电路中，不同电阻上的电压相等；恒流源电路中，电流经过电阻时，电压与电阻成正比。

2.请简述串联电路和并联电路的区别。

答：串联电路是指电子元件按照一条路径连接起来，电流在元件之间只有一条通路。

并联电路是指电子元件按照多条路径连接起来，电流可以通过不同的路径流过不同的元件。

3.一根电阻为5欧姆的导线接在电源上，通过导线的电流为2安培。

求导线两端的电压。

答：根据欧姆定律，电压等于电阻乘以电流。

所以，导线两端的电压等于5欧姆乘以2安培，即10伏特。

4.某电路中，两个电阻分别为8欧姆和12欧姆，电源电压为20伏特。

请计算电路中的总电阻和电流。

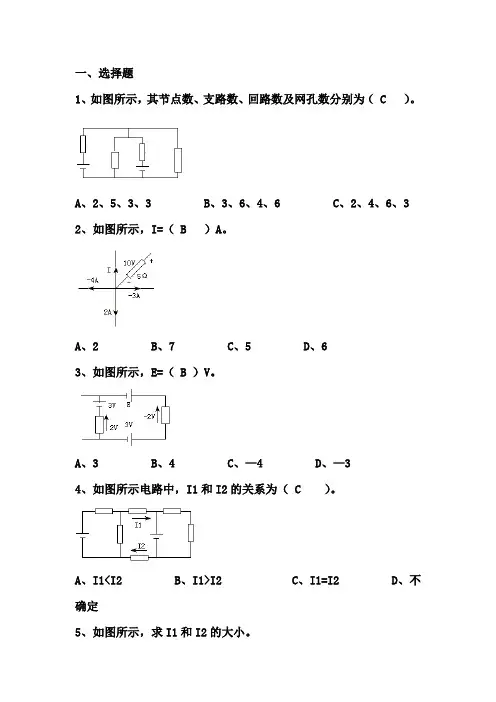
一、选择题1、如图所示，其节点数、支路数、回路数及网孔数分别为（ C ）。

A、2、5、3、3B、3、6、4、6C、2、4、6、32、如图所示，I=（ B ）A。

A、2B、7C、5D、63、如图所示，E=（ B ）V。

A、3B、4C、—4D、—34、如图所示电路中，I1和I2的关系为（ C ）。

A、I1<I2B、I1>I2C、I1=I2D、不确定5、如图所示，求I1和I2的大小。

解：对于左边节点： I1=10+3+5=18A对于右边节点： I2=10+2-5=7A6、基尔霍夫第一定律的依据是（D ）A.欧姆定律B.全电流定律C.法拉第定律D.电荷守恒定7、理想电压源和理想电流源间（C ）A.有等效变换关系B.没有等效变换关系C.有条件下的等效关系D.无法判定8、下列说法错误的是（D ）A.在电路节点处，各支路电流参考方向可以任意设定。

B.基尔霍夫电流定律可以扩展应用于任意假定的封闭面。

C.基尔霍夫电压定律应用于任意闭合路径。

D.∑I=0式中各电流的正负号与事先任意假定的各支路电流方向无关9、实际电压源和电流源模型中，其内阻与理想电压源和电流源之间的正确连接关系是（C）A.理想电压源与内阻串联，理想电流源与内阻串联B.理想电压源与内阻并联，理想电流源与内阻串联C.理想电压源与内阻串联，理想电流源与内阻并联D.理想电压源与内阻并联，理想电流源与内阻并联10、79.下面的叙述正确的是（B ）。

A.理想电压源和理想电流源是不能等效变换的B.理想电压源和理想电流源等效变换后内部是不等效的C.理想电压源和理想电流源等效变换后外部是不等效的D.以上说法都不正确二、填空题1、不能用电阻串、并联化简的电路称为__复杂电路_______。

2、电路中的_____每一分支_______称为支路，____3条或3条以上支路___所汇成的交点称为节点，电路中__________闭合的电路______________都称为回路。

习题二一、判断题1电压的方向是由高电位指向低电位，是电位升高的方向。

2.几个电阻并联后的总电阻等于各并联电阻的倒数之和。

3.在串联电路中，电流处处相等。

4.基尔夫第一定律是节点电流定律，是用来证明电路上各电流之间关系的定律。

5.并联电路中各支路上的电流不一定相等。

6.欧姆定律指出，在一个闭合电路中，当导体温度不变时，通过导体的电流与加在导体两端的电压成反比，与其电阻成正比。

7.当导体温度不变时，通过导体的电流与导体两端的电压成正比，与其电阻成反比。

8.在串联电路中，电路总电压等于各电阻的分电压之和。

9.电流和磁场密不可分，磁场总是伴随着电流而存在，而电流水远被磁场所包围。

10.载流导体在磁场中一定受到磁场力的作用。

11.磁力线是一种闭合曲线。

12.在磁路中，当磁阻大小不变时，磁通与磁动势成反比。

13.若磁场中各点的磁感应强度大小相同，则该磁场为均匀磁场。

二、填空题14.我国正弦交流电的频率为Hz。

15.串联电路中各电阻两端电压的关系是阻值越大两端电压越。

16.水、铜、空气中，属于顺磁性材料的是。

17.感应电流的方向总是使感应电流的磁场阻碍引起感应电流的磁通的变化，这一定律称为。

三、单选题20.下列说法中，不正确的是( )。

A.规定小磁针的北极所指的方向是磁力线的方向B.交流发电机是应用电磁感应的原理发电的C.交流电每交变一周所需的时间叫作周期TD.正弦交流电的周期与角频率的关系互为倒数21.下列说法中，正确的是( )。

A对称的三相电源是由振幅相同、初相依次相差120°的正弦电源连接组成的供电系统B.视在功率就是无功功率加上有功功率C.在三相交流电路中，负载为星形接法时，其相电压等于三相电源的线电压D.导电性能介于导体和绝缘体之间的物体称为半导体22.下列说法中，正确的是( )。

A.右手定则是判定直导体做切割磁力线运动时所产生的感生电流方向C.无论在任何情况下，三极管都具有电流放大功能D二极管只要工作在反向击穿区，一定会被击穿23.下列说法中，正确的是( )。

第二章 电阻电路的分析本章的主要任务是学习电阻电路的分析计算方法，并运用这些方法分析计算各种电阻电路中的电流、电压和功率。

本章基本要求1． 正确理解等效电路的概念，并利用等效变换化简电路。

2． 掌握电阻串、并联等效变换、电源的等效变换。

3． 电阻电路的分压公式和分流公式的应用。

4． 运用支路电流法和结点电压法分析计算电路。

5．运用叠加定理分析计算电路。

6．熟练应用戴维宁定理分析计算电路。

7．应用戴维宁定理求解电路中负载电阻获得的最大功率。

8．学会含有受控源电路的分析计算。

9．了解非线性电阻电路的分析方法。

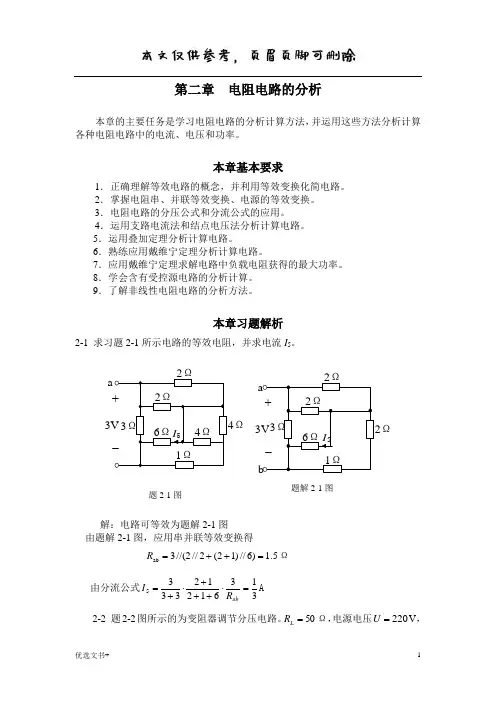
本章习题解析2-1 求习题2-1所示电路的等效电阻，并求电流I 5。

3Ω2Ω2ΩΩ4Ω6Ω1ΩI 5 +-3V b 3Ω2Ω2ΩΩ6Ω1ΩI 5a+-3V解：电路可等效为题解2-1图由题解2-1图，应用串并联等效变换得5.1)6//)12(2//2//(3ab =++=R Ω由分流公式3136********=⋅+++⋅+=ab R I A 2-2 题2-2图所示的为变阻器调节分压电路。

50=L R Ω，电源电压220=U V ，题解2-1图题2-1图中间环节是变阻器。

变阻器的规格是100Ω 3A 。

今把它平分为4段，在图上用a 、b 、c 、d 、e 等点标出。

试求滑动触点分别在a 、b 、c 、d 四点是，负载和变阻器所通过的电流及负载电压，并就流过变阻器的电流与其额定电流比较来说明使用时的安全问题。

+-Ud ab c e L+-U L I L解：1）a 点： 0L =U 0L =I 2.2100220ea ea ===R U I A 2) c 点：75eq =R Ω 93.275220eq ec ===R U I A 47.121ec L ==I I A 5.73L =U V3) d 点：55eq =R Ω 455220eq ed ===R U I A 4.2L =I A 6.1da =I A 120L =U V4) e 点： 2.2100220ea ea ===R U I A 4.450220L ==I A 220L =U V 2-3 试求习题2-3ab 之间的输入电阻。

2-31. 用向量法求取1100sin(31430)u t =+︒与2173sin(314120)u t =+︒之和12u u u =+，并写出它们的相量表示式。

解：11003130()222U i ==+=217313120()222U ==-+=-1290U U U =+==因此，12200sin(31490)u u u t =+=+2-32. 已知某负载的电流的有效值及初相为2A 、45︒，电压的有效值及初相为100V 、45-︒，频率为50Hz ，写出它们的向量表达式，并判断该负载是什么元件，元件参数为多少？解：2452I =∠=10045U =∠-=50Z i ==- 因此，该负载是电容，元件阻抗大小为50。

2-33. 在50Hz 的单相交流电路中，若(a) 090220∠=UV 09010∠=I A ，(b) 090220∠=UV 04510∠=I A ，(c) 090220∠=U V 012010∠=I A 求三种情况下电路中的R 及X ，并写出电路阻抗Z 的复数式。

解：(a) 2202210i Z i== 因此，电路中的22R =Ω，0X =(b)Z ==因此，电路中的R =，X =(c) 11Z i ==因此，电路中的R =，11X =Ω2-34. 一个电感线圈接到20V 的直流电源时，通过电流为0.5A 。

接到50Hz 、100V 的交流电源时通过电流为1.25A ，求线圈的R 和L 。

解：20400.5R ==Ω1.25= L X ∴=又2L X f L π= 0.22L H ∴=2-35. 在R 与L 串联的交流电路中=U 220V ，=R 50Ω，=L 0.282H ，=f 50Hz ，求电路中的电流以及电压与电流间的相位差，作出相量图。

解：288.6L X L f L ωπ===Ω5088.6Z i =+设2200U =∠，则220012.2() 2.2605088.622I i i ∠==-=∠-+ 电压与电流间的相位差为60°。

第二章 电路的分析方法2.1.1 在图2.01的电路中，V 6=E ，Ω=61R ，Ω=32R ，Ω=43R ，Ω=34R ，Ω=15R 。

试求3I 和4I 。

4I ↓图2.01解：图2.01电路可依次等效为图（a ）和图（b ）。

R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。

Ω=1R A2S =图2.12解：根据电压源与电流源的等效变换，图2.12所示电路可依次等效为图（a ）和图（b ），由图（b ）可求得A 2.15.023=+=I由图（a ）可求得：A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中，（1）当将开关S 合在a 点时，求电流1I ，2I 和3I ；（2）当将开关S 合在b 点时，利用（1）的结果，用叠加定理计算电流321,I I I 和 。

I图2.19I (a)I (b)解：（1）当将开关S 合在a 点时，图2.19所示电路即为图（a ），用支路电流法可得：=+=+=+12042130423231321I I I I I I I 解得：===A 25A 10A 15321I I I(2)开关S 合在b 点时，利用叠加原理图2.19所示电路可等效为图（a ）和图（b ），其中图（a ）电路中130V 和120V 两个电压源共同作用时所产生的电流已在（1）中求得，即：A 151=,I A 102=,I A 253=,I由图3（b ）可求得：A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则：A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20（a ）所示，V 10ab ,,V 124321=====U R R R R E 。

习题22.1选择题（1）C （2）D （3）A （4）C （5）B （6）C2.2简答题（1）因为P 1=100W I s2=-4A所以U s2=50VI 1=10A I r2=5AI A =2-（10-4+5）=-9A（2）11101020111136152020R =+=+=++ 所以i=6020=3 i 1＋i 2＝330 i 1＝15i 2i 2=2i 1i 1=1 i 2 =2i 1’=i 2’i 1’=(60-30)/20=1.5i 1+I=i 1’所以I=0.5A(3) ①有三个电容组成一个网络时有SCU(s)+SCU 1(s)=SC ’U(s)得 C ’=3/2C依次 可得如图所示输入端电容Ci=(n+1)/2(n 为电容所组成的网孔数) ②同理可得 Ri ＝2/(n+1) (n 为电阻所组成的网孔数)(4) L=L 11+L 22+2 M =16H(5) 设放大器副端电压为U 3 电流为i 2 正端为i 1 从R 1,R 2端流出得电流为i 则有图可得U 3＝0， i 1＝i 2＝001212+=fU U U i R R R =- 所以01212ff R R U U U R R =--R f /R 1=4 R f /R 2=7由此得R 1＝2.5K Ω,R 2＝10/7（K Ω）（6）设理想变压器输入端线圈电压为U1，输出端线圈电压为U2 有n 1/u 1= n 2/u 2得 u 1＝(n 1/n 2)×u 2＝3u 2n 1i 1+n 2i 2＝0得 i 1＝－（1/3）i 2Ri ＝U/i 1＝4i 1+U 1=4+(3U 2)/(－1/3 i 2)=4－9×（-23/3）=73 K Ω2.3（1）LTI ，双向、单调、有源电阻（2）非线性、时变、单调、有源电阻（3）非线性时不变、单调、单向、有源电容（4）非线性、时不变、单向、流控、有源电感（5）非线性、时不变、有向、有源电感、单调（6）非线性、时不变、单调、单向、有源电阻（7）非线性、时不变、压控、单向、无源电（电流）（8）非线性、时不变、单调、单向、有源电容（9）非线性、时不变、单调、有源电阻（10）非线性、时不变、单调、流控、有源电阻（11）非线性、时不变、荷控、有源电容（12）非线性、时不变、单调、有源电阻2.4①2121U ()U ()1 ()()2t t L di t di t dt dt=== ∴元件1 为电感 ②又2L C 1(0)(0)(0)25(0)252C W W W CU =+=+= 故Uc(0)=0,i 1(0)=i 1(t)t =0= -10A.设元件2 为电阻，则(0)(0) 1.5(0)C L U U R i --==Ω ③元件3 为电容，2111()(0)()(1010)0t t C C t U t U i d e e C Cττ--==-+⎰ 由KVL 又可得：Uc(t)=-U L (t)－U R (t)= －10e-t+10e-2t比较两式系数得C=1F .2.52.6（a ）P R =34 (w),P v =32 (w),P 1= －2（w ）,消耗功率来源于电流源。

第二章 正弦交流电路2.1 基本要求(1) 深入理解正弦量的特征，特别是有效值、初相位和相位差。

(2) 掌握正弦量的各种表示方法及相互关系。

(3) 掌握正弦交流电路的电压电流关系及复数形式。

(4) 掌握三种单一参数（R ，L ，C ）的电压、电流及功率关系。

(5) 能够分析计算一般的单相交流电路，熟练运用相量图和复数法。

(6) 深刻认识提高功率因数的重要性。

(7) 了解交流电路的频率特性和谐振电路。

2.2 基本内容 2.2.1 基本概念 1. 正弦量的三要素(1) 幅值（U m ，E m ，I m ）、瞬时值（u, e, i ）、有效值（U ，E ，I ）。

注：有效值与幅值的关系为：有效值2幅值=。

(2) 频率（f ）、角频率（ω）、周期（T ）。

注：三者的关系是 Tf ππω22==。

(3) 相位（ϕω+t ）、初相角（ϕ）、相位差（21ϕϕ-）。

注：相位差是同频率正弦量的相位之差。

2. 正弦量的表示方法 (1) 函数式表示法：。

)sin();sin();sin(i m e m u m t I i t E e t U u ϕωϕωϕω-=+=+= (2) 波形表示法：例如u 的波形如图2-1-1(a)所示。

(3) 相量（图）表示法：使相量的长度等于正弦量的幅值（或有效值）； 使相量和横轴正方向的夹角等于正弦量的初相角； 使相量旋转的角速度等于正弦量的角速度。

注：例。

)60sin(24,)30sin(2621V t u V t u o o +=+=ωω求?21=+u u解：因为同频率同性质的正弦量相加后仍为正弦量，故)sin(221ϕω+==+t U u u u , 只要求出U 及ϕ问题就解决了。

解1：相量图法求解如下：具体步骤为三步法（如图2-1-2所示）：第一步：画出正弦量u 1、u 2的相量12U U 、（U 1=6，U 2=4）。

第二步：在相量图上进行相量的加法，得到一个新相量U。

习题一元件上的电压和电流分别是A )1(10)(V 2cos 5)(5.0--==e t i t t v ，。

计算：(a)在t=1s 时该元件上的总电荷量； (b)在t=1s 时该元件所消耗的功率。

解:(a)Ce et dt eidt q t tt131.2)221(1001)2(10)1(105.05.015.0=-+=+=-==---⎰⎰(b)We p t i t v t p 188.8)935.3)(081.2()1(102cos 5)1()()()(5.0-=-=-⋅==-2.2.2 图示为一电路元件中的电流与电压波形。

试计算在4s t 0＜＜间元件所吸收的总能量。

|图 习题的图解：mJtt t dt t t t t t mJdt t t dtt dt t dt t t dt t i t v w t t t t t v t t t t t i 7.9163432416250282912250)3(22503250)4(2502324250122250013250)25-)(10010-40()25-(10010)25(10)25(10)()(43 V 10-4031 V 1010V 10t )(42mA 2510020 mA 25)(222432234332211=⎪⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+--++=-+⎪⎪⎭⎫ ⎝⎛-++=+++==⎪⎩⎪⎨⎧=⎩⎨⎧-=⎰⎰⎰⎰⎰⎰＜＜＜＜＜＜，＜＜＜＜2.2.3 求图示电路中各元件的功率。

图 习题的图解:48W)(-4812-432W)(-328-4280W)(028*******W)(1001010300W)(300-30-10-555444333222111该电流源提供的功率为该元件提供的功率为该元件吸收的功率为该元件吸收的功率为该电压源提供的功率为，所以流采用非关联参考方向由于电压源的电压与电W V A U I P W V A U I P W V A U I P W V A U I P W V A U I P =⨯===⨯===⨯===⨯===⨯==^试求图示电路的支路数、基本支路数、节点数与基本节点数。

电工学及电气设备第二章作业（3）19、在交流220V 的供电线上，接有220V 、100W 的电烙铁10把和220V 、400W 的单相电机2台，电机运行时的功率因数为cos ϕ1=0.7(感性)。

试求供电线路上的总电流、总有功功率、无功功率、视在功率及总功率因数λ。

解：以电压U 为参考相量，设U=220/_0°，因为电烙铁为纯电阻，故电烙铁电流I 1与U 同相，电机电流I 2滞后于U 一个ϕ 角。

所以I 1=220100/_0°=0.4545/_0° I 2=220400/_-arccos ϕ1=1.818/_-arccos0.7=1.818/_-45.57° 因此总电流I=10I 1+2I 2=0.4545/_0°+1.818/_-45.57°=7.55/_-20.11°总有功功率P=UIcos ϕ=220×7.55×cos(-20.11°)=1559.74W 总无功功率Q=UIsin ϕ=220×7.55×sin(20.11°)=571.09 var 总视在功率S=UI=220×7.55=1661 VA功率因数λ= cos ϕ=cos(20.11°)=0.93922、在图2-22所示的电路中，R=22Ω，X C =11Ω,X L =22Ω,电源电压U=220V ，试求电路的总电流及功率因数。

解：设U=220/_0°则I R =R U =220/_220︒=10/_0° I L =L X U =j 220/_220︒=10/_-90° I C =CX U =j 110/_220︒=20/_90° 故总电流I=I R +I L +I C =10/_0°+10/_-90°+20/_90°=102/_45° 功率因数λ= cos ϕ=cos(45°)=0.70725、无源二端网络的电压u=2202sin(314t+20°)V ，电流i=102sin(314t -40°)A ，如图2-25所示。

2-1. 列出以下节点的电流方程式，并求出x I 。

解：(a) 由KCL 得：1234()()()0xI I I I I +-+-+-+= ∴2341x I I I I I =++-; (b) 由KCL 得： 39(5)()x I ++-+-= ∴7x I A =(c) 由KCL 之推广得:69()0x I ++-= ∴15x I A = (d) 由KCL 得： 1(2)(3)4xI +-++-+=∴0x I =2-2. 列出以下回路的电压方程式，并标出回路循环方向，求出U 。

解：(a) 回路循环方向与I 方向相同，由KVL 得： U+(2S U -)+I R ⋅=0 ∴U = 2S U -I R ⋅(b) 回路循环方向与3I 、4I 方向相同，由KVL 得： 44I R ⋅+33I R ⋅+(U -)=0 ∴U = 44I R ⋅+33I R ⋅ (c) 回路循环方向为逆时针方向，由KVL 得：U+(9-)+7=0 ∴U = 2V(d) 设回路电流大小为I ，方向为逆时针方向，由KVL 得： 2S U +I ⋅4+I ⋅6+(1S U -)+I ⋅3+I ⋅7=0 ∴I = 0.3A 因此，U=2S U +I ⋅4 = 13.2V2-3. 求出下列电路中的电流I 。

解：(a) 由KCL ，流过2Ω电阻的电流大小为(9+I)，对2Ω电阻与10V 电压源构成的回路，由KVL ，得：(9)I +⋅2+(10-) =0, 因此，I ＝－4A ； (b) (2)I -⋅3+6＝0； ∴I = 4A; (c) 流过3Ω电阻的电流 1I ＝93÷＝3A 流过6Ω电阻的电流 2I ＝(6+9) ÷6＝2.5 A (d) 由KCL ，I + 3-3＝0 ∴I =0;2-4. 求出下列电路中的电压U 。

解：(a) (U/10 + U/10) ⨯5 + U = (4-U/10-U/10) ⨯10 ∴U=10V ；(b) 10⨯2 + 10 + U ＝0 ∴U=－30V(c) 1I =10⨯(64)(46)(64)++++=5A; 2I =10⨯(46)(46)(64)++++=5A;4⨯1I + U + 6⨯(－2I )=0; ∴U = 10V (d) U + 18⨯393+－4.5=0; ∴U = 02-5. 有50个彩色白炽灯接在24V 的交流电源上，每个白炽灯为60W ，求每个白炽灯的电流及总电流，另外消耗的总功率为多少？ 答：每个白炽灯上消耗的功率为2UP U I R==，而U ＝24V ，P ＝60W ，因此每个白炽灯的电流为P I U=＝2.5A ，总电流为I 总＝I ⨯ 50＝125A消耗的总功率为P 总＝P ⨯ 50＝3000W2-6. 在220V 单相交流电源上，接有两台电阻热水器，一台为1.5kW ，一台为3kW ，分别求这两台电热器的电阻。

电工第二章试题及答案一、选择题（每题2分，共10分）1. 电流的单位是（）。

A. 安培（A）B. 伏特（V）C. 瓦特（W）D. 欧姆（Ω）2. 电阻的计算公式是（）。

A. R = V/IB. R = V * IC. R = I^2/VD. R = V^2/I3. 并联电路中，总电阻的倒数等于各分电阻倒数之和，这是（）。

A. 欧姆定律B. 基尔霍夫电压定律C. 基尔霍夫电流定律D. 电阻并联原则4. 交流电的有效值是其最大值的（）。

A. 1/√2B. √2C. 2D. 15. 电路中，功率的计算公式是（）。

A. P = V * IB. P = V^2 / RC. P = I^2 * RD. A 和 C 都是二、填空题（每题2分，共10分）1. 电路中，电压是_______和_______之间的电势差。

2. 纯电阻电路中，电流与电压之间的相位关系是_______。

3. 电感的单位是_______，用符号_______表示。

4. 电容器的充放电过程遵循_______定律。

5. 在串联电路中，总电压等于各分电压之_______。

三、简答题（每题10分，共20分）1. 请简述欧姆定律的内容及其应用场景。

2. 什么是三相交流电？它有哪些优势？四、计算题（每题15分，共30分）1. 一个电阻为10Ω的电阻器与一个电容为5μF的电容器串联，已知电源电压为220V（交流），50Hz。

请计算电路的总阻抗，并求出电路中的电流。

2. 一个星形连接的三相交流电路，每相电阻为10Ω，电感为0.5H，电容为100μF。

若电源线电压为380V，50Hz，求电路的总功率。

五、判断题（每题5分，共10分）1. 在纯电容电路中，电流总是超前于电压。

（）2. 功率因数是衡量电路效率的物理量，它等于电路的视在功率与有功功率之比。

（）六、解答题（每题20分，共20分）请解释什么是谐振频率，并说明在RLC串联电路中，谐振频率是如何影响电路的阻抗和电流的。

第二章电路分析基础2-1 电路如图所示，已知US1=24V，US2=16V，IS=1A，R1=R2=8Ω，R3=4Ω。

试用支路电流法求各支路电流。

解：该题有四条支路其中一条支路是恒流源（设恒流源两端电压为U IS），应列四个方程。

有两个节点，按KCL定理可列一个节点方程： I1+I2 =I S+I3有三个网孔按KVL定理可列三个回路方程：I1R1 =U S1+U ISI2R2 =U S2+U IS I2R2+I3R3 =U S2 U IS=I3R3 解之 I1=2A I2=1A I3=2A U S=8V2-2 电路如图所示。

已知I S=2A，U S=6V，R1=R2=3Ω，R3=R4=6Ω，用叠加原理求a、b两点之间电压U ab。

解：当电压源U S单独作用时，题图变如右图：Uab1=当电流源I S单独作用时，题图变如右图Uab2=3V Uab=Uab1+Uab2=2-3 电路如图所示。

已知R1=6Ω，R2=12Ω，R3=8Ω，R4=4Ω，R5=1电路中流经R3的电流I当电流源I S单独作用时，题图变如右图)(13844434AIRRRI=⨯+=+=''I=)(211AII=+=''+'2-4 在图示电路中，当U S=24V时，Uab=8v. 试用叠加原理求U S=0时的UabIs。

解：当电压源U S单独作用时，题图变如右图)(1841243ARRUI S=+=+='解：以知U S=24V时，Uab=8v.当U S、、I S1、I S2、单独作用时题图分别变作变作下图1、图2、图3由图1可得：Uab1=)(64244VRRUS-=-=⨯；由图2可得：Uab2=)(212411VRIRRISS=⨯；由图3可得：Uab3=)(41422VRIRISS=⨯；UabIs=Uab2+Uab3=8+6=14（V）2-5 用电源等效变换法求图示电路中6Ω电阻中的电流I。