南昌大学历年期末考试试卷

南昌大学 2021～2021学年第二学期期末考试试卷试卷编号：6032(A)卷课程编号：Z5502B011课程名称：数学物理方法考试形式：闭卷适用班级：物理系 08各专业姓名：学号：班级：学院：专业：考试日期：题号一 二 三 四五六七八九十总分 累分人题分484012100签名得分考生考前须知： 1、本试卷共 5页，请查看试卷中是否有缺页或破损。

如有举手报告以便更换。

2、考试结束后，考生不得将试卷、答题纸和草稿纸带出考场。

一、填空题 (每题4分，共48分)得分评阅人1.设i 为虚数单位，复数1 2i/(2 i)__ ; ln(1 i3) 。

2.设i 为虚数单位，且x 和y 为实数，复变函数 f(z) xiy __ (填“是〞或“不是〞)可导的，理由是3. x 2 y 2是否有可能为某解析函数 f(z)的实部？答：__ (填“有可能〞或“不可能〞)，理由是4. 1 [(x 2 1)tan(sinx)(x)]dx 。

20213e z20215. 根据柯西公式，积分z dz|z2021|3 20216. 函数f(z)z 2z 阶极点；在极点处的留数z 2有________个极点，为__________3z4为________________________。

第1页共28页7.当1|z| 2,试以原点为中心将1 做级数展开为z 2 3z21(0 t 1)8. f(t)1( 1 t0)的傅里叶变换为 。

(|t|1)9. 1t 2te t 的拉普拉斯变换为 。

数学物理方程如果没给定解条件，一般会有__________个解；数学物理方程定解问题的适定性是指解的____________，____________，__________。

一根两端(左端为坐标原点而右端xl 〕固定的弦，用手在离弦左端长为l/6处把弦朝横向拨开距离h ，然后放手任其振动。

横向位移u(x,t)的初始条件为。

12.偏微分方程u xx2u xy 4u yy 5u x 7u y 3xy 9 0的类型为 (备选答案：A.双曲型B.抛物型C. 椭圆型D. 混合型)；为了得到标准形，可以采用的自变量函数变换为 。

南昌大学2008～2009学年第二学期期末考试试卷2008～2009学年第二学期有机化学期末考试试卷B 参考答案一、填空题（每空2分，共30分）1．（5702）[解]2．（5704）[解]3．（5719）[解]4．（5728）[解]5．（5746）[解]：NCCH 2CH 2CH(COOEt)2 6．（5752）[解]7．（5759）[解]8．（5786）[解]9．（5775）[解]PhC(CH 2)3CH 3O O NHO O CCH 3O+CH 3OCH 3O COOEt O OOOO C NH 2H 3CPhCH (CH 3)3CCH 2C CH 3CH 2N(CH 3)310．（5785）[解] 11．（5809）[解] 12．（5839）[解] 13．（5845）[解] 14．（5857）[解] 15．（5866）[解]二、选择题（每小题2分，共30分）16．（7601）[解] (C)；17．（7603）[解] (C)；18．（7724）[解] (A)；19．（7629）[解] (B)； 20．（7626）[解] (B)；21．（7651）[解] (D)；22．（7654）[解] (B)；23．（7660）[解] (B) 24．（7718）[解] (A)；25．（7732）[解] (B)；26．（7754）[解] (A)；27．（7810）[解] (D) 28．（7816）[解] (D)；29．（9509）A ；30．（9513）B三、合成题（每小题5分，共20分）31．4分（8625）[解]（1）OH - 缩合；（2）NaBH 4还原；（3）H + Δ, -2H 2O32．4分（9029）[解] ⑴ Cl 2, P ；⑵ OH - / H 2O ；⑶ △ , -H 2ON N Ph CH NO 2NO 2O 2NCHO 2NN N OH COOHBrClOPhNO 22ClCH 2CH 2C CH 33SO 3H33．6分（9034）[解] ⑴ EtONa ，(CH 3)2CHBr ；⑵ EtONa ，CH 3COCl ；⑶ OH - 成酮水解34．6分（9049）[解] ⑴ 苯 → 对硝基苯胺，重氮化得 (A)；⑵ 萘 → 2-萘酚 (B)；⑶ (A) + (B) 偶联四、机理题（每小题5分，共10分）35．6分（2539）[解] 羧酸α-卤化的各步机理为：（1）P 与Br 2 生成催化量的PBr 3 ；（2）36．8分（2680）[解] Hofmann 重排历程为：立体化学实验事实证明氮宾重排时C 1─C 2键的断裂与C 2─N 键的形成是同步的。

南昌大学大学物理期末考试《大学物理》（下）期末统考试题（A卷）说明 1考试答案必须写在答题纸上，否那么无效。

请把答题纸撕下。

一、选择题（30分，每题3分）1．一质点作简谐振动，振动方程x=Acos(ωt+φ)，当时间t=T/4(T为周期)时，质点的速度为：(A) -Aωsinφ；(B) Aωsinφ； (C) -Aωcosφ； (D)Aωcosφ参考解：v =dx/dt = -Aωsin(ωt+φ)vtT/4Asin(2TT)Acos, ∴选(C) 42．一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的(A) 7/6 (B) 9/16(C) 11/16 （D）13/16(E) 15/16 参考解：3.一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运1121A2mv2115 kAk(),2116kA2kA∴选（E）动到最大位移处的过程中：(A)它的动能转换成势能．(B) 它的势能转换成动能．(C) 它从相邻的一段质元获得能量其能量逐渐增大．(D) 它把自己的能量传给相邻的一段质元，其能量逐渐减小．参考解：这里的条件是“平面简谐波在弹性媒质中传播”。

由于弹性媒质的质元在平衡位置时的形变最大，所以势能动能最大，这时动能也最大；由于弹性媒质的质元在最大位移处时形变最小，所以势能也最小，这时动能也最小。

质元的机械能由最大变到最小的过程中，同时也把该机械能传给相邻的一段质元。

∴选（D）4．如下图，折射率为n2、厚度为e的透明介质薄膜的上方和下方的透明介质的折射率分别为n1和n3，n1＜n2＜n3．假设用波长为的单色平行光垂直入射到该薄膜上，那么从薄膜上、下两外表反射的光束①与②的光程差是(A) 2n2 e．(B) 2n2 e－ / 2 .(C) 2n2 e－．(D) 2n2 e－ / (2n2)． n3 参考解：半波损失现象发生在波由波疏媒质到波密媒质的界面的反射现象中。

南昌大学2005～２006学年第二学期期末考试试卷试卷编号：( A )卷课程编号： Ｔ５502000１--03 课程名称: 大学物理 考试形式：闭卷 适用班级: 理工0５级(Ⅰ)、（Ⅱ）、（Ⅲ）姓名:学号： 学院:专业: 班级:考试日期：06年６月题号 一 二 三 四五六总分 累分人 签名题分 30 ２２ 48 １00 得分考生注意事项:1、本试卷共6页，请查看试卷中是否有缺页或破损。

如有立即举手报告以便更换。

2、考试结束后,考生不得将试卷、答题纸和草稿纸带出考场。

一、 填空题(每空 2 分,共 30 分）得分 评阅人1、质点在力j x i y F322+=（SI 制)作用下沿图示路径运动。

则力F在路径oa 上的功A oa =,力在路径ab 上的功A ab ＝。

2、一质点沿直线运动,其运动学方程为x = 8t -２t 2 (SI)，则在ｔ由0至4ｓ的时间间隔内,质点的位移大小为 ＿＿___＿_＿_＿_,在t 由0到4s 的时间间隔内质点走过的路程为_______________＿_． 3、真空中一半径为Ｒ的均匀带电球面带有电荷Ｑ(Q ＞0).今在球面上挖去非常小块的面积△Ｓ(连同电荷）,如图所示,假设不影响其他处原来的电荷分布,则挖去△S 后球 心处电场强度的大小E ＝_____＿＿_＿____，其方向为_＿__＿__＿_＿_＿OR △SQABE 0E 0/3E 0/3第3题图 第4题图b(3,2)o ca xy二、 选择题（每题 ２ 分,共 22分）得分 评阅人1、一光滑的内表面半径为10 cm 的半球形碗，以匀角速度ω绕其对称ＯC 旋转．已知放在碗内表面上的一个小球P 相对于碗静止，其位置高于碗底４ cm,则由此可推知碗旋转的角速度约为 （A) 10 ra ｄ/s. （B) 13 ｒad ／s.（C) 17 rad ／s (D ） 18rad/s ． [］ ωP COAMBF第1题图 第2题图２、如图所示，A 、B 为两个相同的绕着轻绳的定滑轮．A 滑轮挂一质量为Ｍ的物体，B 滑轮受拉力F ，而且F =Mg .设Ａ、B 两滑轮的角加速度分别为βA 和βB ，不计滑轮轴的摩擦，则有 (A) βA ＝βB ． (B ） βＡ>βB .（C) βＡ<βB .(D ） 开始时βA =βＢ,以后βA <βB .[］３、假设卫星环绕地球中心作圆周运动,则在运动过程中,卫星对地球中心的 （A) 角动量守恒,动能也守恒． (B ） 角动量守恒，动能不守恒． (C)角动量不守恒,动能守恒．(D) 角动量不守恒，动量也不守恒. (E ） 角动量守恒,动量也守恒.［］4、如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴Ｏ旋转,初始状态为静止悬挂．现有一个小球自左方水平打击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆与小球这一系统（A) 只有机械能守恒. (B ） 只有动量守恒．(Ｃ）只有对转轴O 的角动量守恒． (Ｄ) 机械能、动量和角动量均守恒.［］OEO r(B) E ∝1/r 2RE O r(A) E ∝1/r 2REOr(C) E ∝1/r 2RE Or(D) E ∝1/r 2第4题图 第5题图５、半径为R 的均匀带电球面的静电场中各点的电场强度的大小E 与距球心的距离ｒ之间的关系曲线为:［B ]后她将两臂收回,使转动惯量减少为31J 0．这时运动员转动的角速度变为 (A ） 31ω０.（B ） ()3/1 ω0． Jw(Ｃ)3 ω0．(Ｄ) 3 ω０． []R OUr U ∝1/r(A)R OUrU ∝1/r(B)R OUrU ∝1/r(C)R OU rU ∝1/r 2(D)ROUrU ∝1/r 2(E)第7题图7、半径为R 的均匀带电球面,总电荷为Q .设无穷远处电势为零，则该带电体所产生的电场的电势U ，随离球心的距离r 变化的分布曲线为［］ 8、有两个大小不相同的金属球,大球直径是小球的两倍,大球带电，小球不带电,两者相距很远．今用细长导线将两者相连,在忽略导线的影响下,大球与小球的带电之比为： (A) 2.（B) １.(C) 1/2． (D) 0.［］9、在点电荷+q 的电场中，若取图中Ｐ点处为电势零点，则M 点的电势为（Ａ）a q 04επ. (Ｂ) a q08επ.(C) a q 04επ-． (D) aq08επ-.［］aa+qPMⅠⅡⅢⅣ第9题图 第10题图1０、图中，六根无限长导线互相绝缘,通过电流均为I ,区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形，哪一个区域指向纸内的磁通量最大?（A) Ⅰ区域.(B) Ⅱ区域. (Ｃ)Ⅲ区域．(D) Ⅳ区域. (E) 最大不止一个．[］ 11、有下列几种说法：(1) 所有惯性系对物理基本规律都是等价的．(２) 在真空中，光的速度与光的频率、光源的运动状态无关． (3) 在任何惯性系中,光在真空中沿任何方向的传播速率都相同. 若问其中哪些说法是正确的, 答案是（A) 只有（１)、(2)是正确的．(B)只有(１)、(３)是正确的. (C ）只有(2)、(3）是正确的.（D) 三种说法都是正确的．[]得分 评阅人1、一物体悬挂在弹簧上作竖直振动,其加速度为-=a k ｙ,式中k 为常量,y 是以平衡位置为原点所测得的坐标. 假定振动的物体在坐标y ０处的速度为v 0,试求速度v 与坐标y 的函数关系式.(本题7分)解:yt y y t a d d d d d d d d v v v v === 又-=a ky ∴ -ｋ=y ｖ d v ／ ｄy 3分⎰⎰+=-=-C ky y ky 222121 , d d v v v 3分已知=y y 0，=v v 0则20202121ky C --=v)(220202y y k -+=v v 1分 2、质量m =１.1kg 的匀质圆盘,可以绕通过其中心且垂直盘面的水平光滑固定轴转动，对轴的转动惯量Ｊ=221mr (ｒ为盘的半径）．圆盘边缘绕有绳子,绳子下端挂一质量ｍ1＝1．0 kg 的物体,如图所示．起初在圆盘上加一恒力矩使物体以速率v 0=0.6m/s 匀速上升，如撤去所加力矩，问经历多少时间圆盘开始作反方向转动.（本题７分)m 1m ,r３、如图所示,一长为１０ cm 的均匀带正电细杆,其电荷为1.５×10－8 C,试求在杆的延长线上距杆的端点5 cm 处的P 点的电场强度.(041επ=9×109 Ｎ·m 2/C ２ )（本题８分)10 cm5 cmP4、一链条总长为 l ，质量为m ，放在桌面上，并使其下垂,下垂一端的长度为ａ,设链条与桌面之间的滑动摩擦系数为μ，令链条由静止开始运动,则 到链条离开桌面的过程中，摩擦力对链条作了多少功?（本题8分)5、半径为Ｒ的半圆线圈AC Ｄ通有电流I 2,置于电流为I １的无限长直线电流的磁场中,直线电流I 1恰过半圆的直径,两导线相互绝缘.求半圆线圈受到长直线电流Ｉ1的磁力． (本题1０分)I 2I 1A DC6、如图所示,有一根长直导线,载有直流电流Ｉ,近旁有一个两条对边与它平行并与它共面的矩形线圈,以匀速度v沿垂直于导线的方向离开导线.设t =0时，线圈位于图示位置,求 (1) 在任意时刻ｔ通过矩形线圈的磁通量 .（2) 在图示位置时矩形线圈中的电动势 .（本题8分）Ia bvl２0０5～2０06-2期末考试Ａ试卷评分参考标准一、１、0 ; 18J 2、 0 m ；1６ ｍ 3、()40216/R S Q ε∆π由圆心O 点指向△S ４、 -2ε０E ０ / ３ ; 4ε0E ０ / 3 5、q / (6πε０R ) 6、 １∶1 ７、 1.2×103 T8、 ２.6０×108 9、狭义相对论的两条原理说的是相对性原理和光速不变原理1０、ADC ＢＡ绕向二、B 、Ｃ、A 、Ｃ、Ｂ、D 、Ａ、Ａ、D 、B 、Ｄ、三、1、解:yt y y t a d d d d d d d d v v v v === 又-=a ｋy ∴ -k =y v ｄv / d y 3分⎰⎰+=-=-C ky y ky 222121 , d d v v v 3分已知=y y 0，=v ｖ0则20202121ky C --=v)(220202y y k -+=v v 1分 2、撤去外加力矩后受力分析如图所示.m 1g -Ｔ＝ｍ1a 1分Tr ＝Ｊβ 2分ａ=r β 1分ａ=m １gr / （ ｍ1ｒ + J / r ) 代入J ＝221mr ,a ＝mm gm 2111+＝ 6.３２ ms -21分 ∵v 0－at =０ １分∴ｔ＝ｖ0 / ａ=0.095 s 1分3、解：设P 点在杆的右边,选取杆的左端为坐标原点O ,x 轴沿杆的方向，如图，并设杆的长度为L .P 点离杆的端点距离为d ．在x 处取一电荷元d q =(q /L )d x ，它在P 点产生场强()()20204d 4d d x d L L xq x d L q E -+π=-+π=εε 3分 Ｐ点处的总场强为()()d L d qx d L x L q E L +π=-+π=⎰00204d 4εε3分 代入题目所给数据,得E ＝1.８×104 N/m 1分E 的方向沿ｘ轴正向．1分 ４、某一时刻的摩擦力为l x l mg f )(-=μ，4分摩擦力作功为:2)(2)(d )(a l lmg dx x l l mg x f A l a l a f --=--=-=⎰⎰μμ4分5、解：长直导线在周围空间产生的磁场分布为)2/(10r I B π=μ取ｘOy 坐标系如图,则在半圆线圈所在处各点产生的磁感强度大小为：θμsin 210R I B π=,方向垂直纸面向里,２分T ax O式中θ为场点至圆心的联线与y 轴的夹角.半圆线圈上d l 段线电流所受的力为：l B I B l I F d d d 22=⨯=θθμd sin 2210R R I I π=2分θcos d d F F y =.根据对称性知： F ｙ=0d =⎰y F 2分θsin d d F F x =，⎰π=0x x dF F ππ=2210I I μ2210I I μ=2分∴半圆线圈受Ｉ1的磁力的大小为:2210I I F μ=，方向:垂直Ｉ1向右．2分6、解：(1) ⎰⎰⋅π==S r l r I S B t d 2d )(0μ Φ⎰++π=tb ta r r l I v v d 20μt a tb l I v v ++π=ln 20μ4分 （2)aba b lI tt π-=-==2)(d d 00v μΦE ４分。

—南昌大学考试试卷一1 •已知|- 二-'■ 'I ■'：2. 孤立奇点可分为 、 、 三类3. 若函数冷）可导，其实部和虚部和出乂 丁 i 必满足条件，这个条件的数学表达式为J^2 S(x — 1) cos [(x 2 + l )7r]dx = 在以-"为中心，" I 的区域上， 的泰勒级数展开为1 + 2，，幕级数二一丄的收敛圆为设八「为'；T 的傅立叶变换像函数，贝u 的傅立叶变换像函数、填空选择题：（每题3分，共27 分）说明：有两个空的题目，其中第一空 1分，第二空2分4. 5. 6.二、复变函数：(每题12分，共36分)(1) / ■1 *，将解用复数的指数形式加以表示；⑵ 对满足U.十的任意上给出此二次方程的解和解的指数形式。

2.计算回路积分"「'『「，其中「代表回路'唱'r g 2JC计算实函数积分和/ -Jo 貳 + 1说明：第1、2题12分，第3题13分1. 「「满足方程：V 丨一3 鮎+：'和初始条件「⑴！ 一 J ，（」一.【，求3. 、数学物理方程及定解问题：（共 37分）得分评阅人丁: r :。

2. 考查下面的无限长弦的振动冋题：u tt -“砂=0—0? t—Q —xc x其中；§ —•—'「，一”・-；.“、。

这是一个达朗贝尔公式定解问题。

(1) 首先给出达朗贝尔公式及相应定解问题的一般形式；(2) 利用达朗贝尔公式求解迫…、「、。

I 3.已知矩形区域0三工W码0壬y壬兀上的函数U(JV T y)满足方程理耳耳+ “叮=0和| 齐次边界条件u\x=o =0. u\x=JI= 0,按以下步骤求解u(.xj)：1 (1)分离变数并找到本问题中包含的本征值问题；!i (2)求解此本征值问题，确定本征值和本征函数；IIi (3)给出满足上述方程和条件的u(xj)的一般解。

南昌大学学期食品化学期末试题附答案文件管理序列号：[K8UY-K9IO69-O6M243-OL889-F88688]—南昌大学考试试卷—【适用时间：20 17 ～20 18 学年第一学期试卷类型：[ A ]卷】参考答案一、填空题：（每空 1 分，共 20 分）1.氢键；水桥。

2.加热；调节pH值；加抑制剂；驱除或隔绝空气。

3.吡喃酮；呋喃；呋喃酮；内酯；羰基化合物。

4. O/W；W/O。

5.氢键；盐键；疏水键；二硫键。

6.凝血维生素；K2；K1。

二、选择题：（每小题 2 分，共 20 分）1-5 BACAD 6-10 BADBC三、名词解释：（每小题 3 分，共 18 分）1.淀粉溶液经缓冲慢冷却成淀粉凝胶经长期放置，会变成不透明甚至产生沉淀的现象，称为淀粉的老化。

2.食品中水分逸出的程度，可以近似地用食品中水的蒸汽分压与同温度下纯水饱和蒸汽压之比表示，也可以用平衡相对湿度表示。

3.同质多晶是指具有相同化学组成但晶体结构不同的一类化合物，这类化合物熔化时可生成相同的液相。

不同形态的固体晶体称为同质多晶体。

4.指蛋白质能自发的迁移到空气－水界面或油－水界面，在界面上形成高黏弹性薄膜，其界面体系比由低分子量德表面活性剂形成的界面更稳定的性质。

5.维生素B11即叶酸，分布较广，绿叶、肝、肾、菜花、酵母中含量都较多，其次为牛肉、麦粒等。

6.绝对阈值又称为感觉阈值，是采用由品尝小组品尝一系列以极小差别递增浓度的水溶液来确定的。

四、简答题：（每小题 4 分，共 24 分）1.答：使氨基酸因形成色素而损失，色素及与糖结合的蛋白质不易被酶分解，降低蛋白质营养价值，水果加工中，维生素C减少，奶粉和脱脂大豆粉中加糖贮存时随着褐变蛋白质的溶解度也随之降低，防止食品中油脂氧化。

2.答：酯交换是改变脂肪酸在三酰基甘油中的分布，使脂肪酸与甘油分子自由连接或定向重排，改善其性能。

它包括在一种三酰基甘油分子内的酯交换和不同分子间的酯交换反应。

南昌大学期末考试试卷(所有答案)XXXX第二学期结束时，南昌大学，试卷一，卷一，选择题。

“A”的ASCII码是65，n是整数，n=“A”，“6”-“3”；之后，n的值是b。

a)“d”b)68c)不确定值d)编译错误2。

在下列变量名中，a是合法的。

在A)中国B)字节之后，n的值是Ba)“d”b)68c)不确定值d)编译错误2。

在下列变量名中，a是合法的。

中国字节:字符通道.a)包含1个字符和2个字符c)包含3个字符是非法的9。

在下面对c和c之间关系的描述中，d是错误的。

a)语言c是c的子集；c语言与c语言兼容；C)c对c语言做了一些改进；c和c语言都是面向对象的。

10.下面对类概念的描述是错误的。

类是C语言中的结构类型；b)类是具有共同行为的几个对象的统一描述；类是创建对象的模板；d)类是抽象数据类型的实现。

11.在下列选项中，符合C语法的赋值表达式是C。

A)d=' 2e A)d=' 2e，' b) c) d 5='1' 1212.；表达式3)可以被理解为b. a)用于(；0 )b)对于(；1 )c)对于(；表达式1) d)表示(；表达式-省略部分-)1.一个错误a1='10a2=20a3=31a4=41 '扣1分2.三角形，得3分* * * * * * * * * * * *3.如果格式不正确，扣1分1220分4.如果顺序不正确，每点:4圆半径:5圆析构函数扣1分！点析构函数！五、程序设计问题(每项10分，共20分)1、# include # define size 10 void main(){ int数据[大小]；m .请输入“[m”数据；int j=0，k=0；对于(int I=1；[[j])j=I；否则，如果(数据[I]0){ int d=数据[0]；数据[0]=数据[k]；数据[k]=d；} if(k2，# include lass date { public : CD ate()函数重载year=' y；月=m；day=d；'(int y，int m='1，int '成员函数设置默认参数void print date()；打印日期无效设置日期(int sy，int sm，int sd)非静态函数设置日期{ year=' sy月=sm。

南昌大学 2005～2006学年第二学期期末物理试卷一、选择题(每题 3 分，共 36 分)1、一平面简谐波表达式为y=－0.05sinπ（t－2x）（SI）则该波的频率υ（HZ）波速u（m/s）及波线上各点振动的振幅A（m）依次为（A）1/2 1/2 －0.05 （B）1/2 1 －0.05（C）1/2 1/2 0.05 （D）2 2 0.05[ ] 2、一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的（A）7/16 （B）9/16（C）11/16 （D）13/16 （E）15/16 [ ] 3、理想气体卡诺循环过程的两条绝热线下的面积大小（图中阴影部分）分别为S 1和S2，则二者的大小关系是：（A）S1＞S2（B）S1＝S2（C）S1＜S2（D）无法确定 [ ]4、在恒定不变的压强下，气体分子的平均碰撞频率Z与气体的热力学温度T的关系为（A）Z与T无关。

（B）Z与成正比。

（C）Z与成反比。

（D）Z与T成正比。

[ ]5、一简谐振动曲线如图所示，则振动周期是（A）2.62s （B）2.40s（C）2.20s （D）2.00s [ ] 6、两偏振片堆叠在一起，一束自然光垂直入射其上时没有光线通过，当其中一偏振片慢慢转动180°时透射光强度发生的变化为：（A）光强单调增加。

（B）光强先增加，后又减小至零。

（C）光强先增加，后减小，再增加。

（D）光强先增加，然后减小，再增加，再减小至零. [ ]7、一束光是自然光和线偏振光的混合光，让它垂直通过一偏振片。

若以此入射光束为轴旋转偏振片，测得透射光强度最大值是最小值的4倍，那么入射光束中自然光占总光强的（A）2/3 （B）2/5 （C）1/3 （D）3/5 [ ] 8、一质点作简谐振动，其振动周期T，则其振动动能变化的周期是（A）T/4。

（B）（1/2）T。

（C）T．（D）2T。

（E）4T。

[ ]9、有两瓶气体：一瓶是氦气，另一瓶是氮气，它们的压强相同，温度也相同，但体积不同，则：（A）它们单位体积内的气体的质量相等。

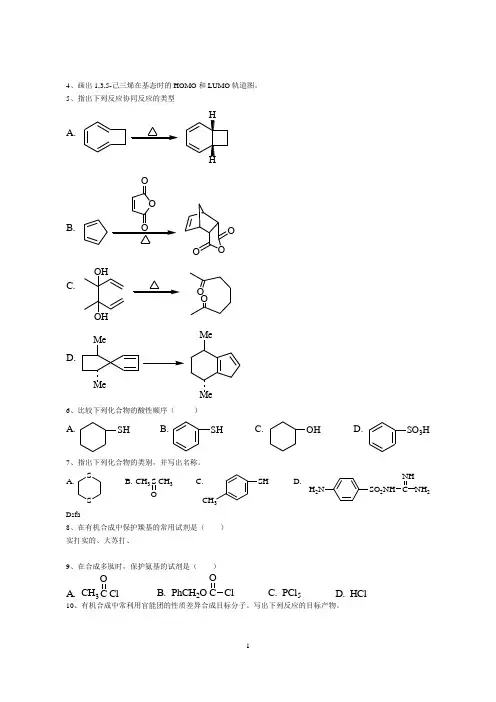
4、画出1,3,5-己三烯在基态时的HOMO 和LUMO 轨道图。

5、指出下列反应协同反应的类型A.HHB.OO OOO OC.OH O OOHD.Me MeMeMe6、比较下列化合物的酸性顺序（ ）A. B.C. D.SHSHOH SO 3H7、指出下列化合物的类别，并写出名称。

A.B. C. D.SS SH S CH 3OCH 3CH 3H 2NSO 2NH C NH 2NHDsfa8、在有机合成中保护羰基的常用试剂是（ ） 实打实的、大苏打、9、在合成多肽时，保护氨基的试剂是（ ）A. B. C. PCl 5D. HCl OC Cl CH 3OPhCH 2O C Cl10、有机合成中常利用官能团的性质差异合成目标分子。

写出下列反应的目标产物。

A.B.ClClNaCN OEtO O Ph 3P +-CH 3CHCH 3C.OEtO O RoNaICH 2CH 2CH 2Cl11、在有机合成中常利用分子的对称性，使合成问题简化。

下列化合物应怎样拆分并合成。

A.CH 3OC C 2H 5H C C 2H 5H O CH 3B.PhC CPhOH CH 3OHCH 3二、完成反应1.N1) KMmO 42) H +―H 2O2.NH NO 3H 2SO 4NaNH 2NH 2甘油, 浓H 2SO 4硝基苯LiAlH 43.4.CH 3CH BrCH 3Ph 3Pn ―BuLi5.NaOHSHC 2H 5Br6.C C H 2SH H 2SH OC CH 2CH 3CH 3H 2兰尼镍7.S S H C 2H 51) n ―BuLi 2) Br(CH 2)4BrH 3O +Hg ++8.1) KMnO 42) H +CH 3SO 2ClNH 39.hvCH 3CH310.LiAlH 4CH 2CH COOEt11.HO CH 2C CHO 干燥 HCl1) Na2) CH 3CH 2CH 2Cl12.1) O 32) Zn/H 2OPh OHH 3PO 413.1) NaOH, H 2O 2) H + ,HCNCH 3C CH 2COOHCH3OC CH 314.2OO15. HCOOC 2H 51) CH 3CH 2CH 2CH 2MgBr 2) H 3O +CrO 3吡啶三、合成1、从n —BuOH 及必要试剂合成CH 3C CH 3OH( CH 2)5CH 3― 2、从C 2H 5Br 及必要试剂合成C 2H 5C OH C 2H 5C 2H 53、从丙醛合成CH 3CH 2CHCH CHO CH 34、从O及必要试剂合成HOOC(CH 2)4C CH 3O5、用切断法合成COOHCHO6、从乙炔及必要试剂合成(meso)—3,4—己二琼7、用切断法合成O 8、用必要试剂合成N N NCH3N NCH3NCH3CH3CH3 CH39、OHOOC OH10、HOCHOO O11、CH3OC CH3OC CH2CH2CH C CH3OCH3南昌大学2004-2005学年第二学期期末考试试卷（B）课程名称：有机化学题号一二三四五总分标准分20 30 6 20 24 100实得分阅卷人一、命名或写出结构式1．β－D－甲基吡喃葡萄糖苷稳定构象式2．2，3，4，6－四－O－甲基－D－吡喃葡萄糖3．谷氨酸4．甘氨酰丙氨酸5．三软脂酸甘油脂6．（+）－纤维二糖7．（+）－蔗糖 8．－果糖9．（Z 、Z ）－9，12－十八碳二烯酸（亚油酸） 10．（Z 、E 、E ）－9。

南昌大学《无机化学》期末试卷2018年南昌大学无机化学期末试卷(专题型版)(一)一.是非题:1.化学变化有新物质产生,而物理变化无新物质产生.2.化学变化是由于构成分子的原子外层电子运动状态的改变而引起的、原子核不变的一类变化3.元素的变化为物理变化而非化学变化.4.化学变化的特点是原子核不变分子组成或原子间结合方式发生变化.5.化学反应常伴有发光现象,但并非所有的发光现象都属于化学反应.二.选择题:1.化学研究的对象是具有宏观实体的物质,它不包括A.希有气体B:混合物C.电子流或γ──射线D.地球外的物质2.纯的无机物不包括A.碳元素B.碳化合物C.二者都对D.二者都错3.下列哪一过程不存在化学变化A.氨溶于水B.蔗糖溶在水中C.电解质溶液导电D.照相底片感光(二)一.是非题1.电子在原子核外运动的能量越高,它与原子核的距离就越远.任何时候,1s电子总比2s电子更靠近原子核,因为E2s>E1s.2.原子中某电子的各种波函数,代表了该电子可能存在的各种运动状态,每一种状态可视为一个轨道.3.氢原子中,2s与2p轨道是简并轨道,其简并度为4;在钪原子中,2s 与2p轨道不是简并轨道,2p x,2p y,2p z为简并轨道,简并度为3.4.从原子轨道能级图上可知,任何原子在相同主量子数的轨道上,能量高低的顺序总是f>d>p>s;在不同主量子数的轨道上,总是(n-1)p>(n-2)f>(n-1)d>ns.5.在元素周期表中,每一周期的元素个数正好等于该周期元素最外电子层轨道可以容纳的电子个数.6.所有非金属元素(H,He除外)都在p区,但p区所有元素并非都是非金属元素.7.就热效应而言,电离能一定是吸热的,电子亲和能一定是放热的.8.铬原子的电子排布为Cr[Ar]4s13d5,由此得出:洪特规则在与能量最低原理出现矛盾时,首先应服从洪特规则.9.s区元素原子丢失最外层的s电子得到相应的离子,d区元素的原子丢失处于最高能级的d电子而得到相应的离子.10.在原子核里因质子数和中子数不同,就组成了不同的核素;同样在原子核里因质子数和中子数不等,就构成了同位素.可见,核素也就是同位素.二.选择题1.玻尔在他的原子理论中A.证明了电子在核外圆形轨道上运动;B.推导出原子半径与量子数平方成反比;C.应用了量子力学的概念和方法;D.解决了氢原子光谱和电子能量之间的关系问题.2.波函数和原子轨道二者之间的关系是A.波函数是函数式,原子轨道是电子轨迹;B.波函数和原子轨道是同义词;C.只有轨道波函数与原子轨道才是同义的;D.以上三种说法都不对.3.多电子原子的原子轨道能级顺序随着原子序数的增加A.轨道能量逐渐降低,但能级顺序不变;B.轨道能量基本不变,但能级顺序改变;C.轨道能量逐渐增加,能级顺序不变;D.轨道能量逐渐降低,能级顺序也会改变.4.周期表中各周期元素数目是由什么决定的A.2n2(n为主量子数);B.相应能级组中所含轨道总数;C.相应能级组中所含电子总数D.n+0.7规则5.下列电子构型中,电离能最低的是A.ns2np3B.ns2np4C.ns2np5D.ns2np66.下列元素中,第一电离能最大的是A.BB.CC.AlD.Si7.原子光谱中存在着不连续的线谱,证明了A.在原子中仅有某些电子能够被激发B.一个原子中的电子只可能有某些特定的能量状态C.原子发射的光,在性质上不同于普通的白光D.白光是由许许多多单色光组成.8.原子轨道中"填充"电子时必须遵循能量最低原理,这里的能量主要是指A.亲合能B.电能C.势能D.动能9.下列哪一原子的原子轨道能量与角量子数无关?A.NaB.NeC.FD.H10.下列哪一种元素性质的周期规律最不明显A.电子亲合能B.电负性C.电离能D.原子体积11.用来表示核外某电子运动状态的下列各组量子数(n l m ms)中哪一组是合理的?A.(2,1,-1,-1/2)B.(0,0,0,+1/2)C.(3,1,2,+1/2)D.(2,1,0,0)12.元素和单质相比较时,正确的说法是A.元素由单质构成;B.元素可分解为单质;C.元素的质量比单质的质量重;D.单质是元素存在的一种形式.13.核素和同位素的相同点是A.它们中的质子数均大于中子数;B.它们中的质子数均小于中子数;C.它们中的质子数和中子数相等;D.它们各自含有相同的质子数.14.关于核素的正确说法是A.具有一定数目的核电荷的一种原子;B.具有一定数目的质子的一种原子;C.具有一定数目的中子的一种原子;D.具有一定数目的中子和一定数目的质子的一种原子.15.测定原子量最直接的方法是A.质谱法B.化合量法C.气体密度法D.α─粒子散射法三.填空题:1.宏观物体的运动可用方程F=ma描述,但微观物体的运动要用量子力学中的()描述.它是一个偏微分方程式.2主量子数为4的一个电子,它的角量子数的可能取值有()种,它的磁量子数的可能取值有()种.3.在氢原子中,4s和3d轨道的能量高低为(),而在19号元素K和26号元素Fe 中,4s和34轨道的能量高低顺序分别为()和().4.填上合理的量子数:n=2,l=(),m=(),ms=+1/2.5.+3价离子的电子层结构与S2-离子相同的元素是().6.微观粒子运动与宏观物质相比具有两大特征,它们是()和(),说明微观粒子运动特点的两个重要实验是().7.ψn,l,m是(),当n,l,m,一定时,处于ψn,l,m状态的一个电子的(),(),()可以确定.n,l,m可以确定一个().8.氢原子的电子能级由()决定,而钠原子的电子能级由()决定.9.Mn原子的价电子构型为(),用四个量子数分别表示每个价电子的一定状态,是().10.在电子构型a.1s22s2,b.1s22s22p54s1,c.1s22s12p13d13s1,d.1s22s22p63s13d 1,e.1s22p2,f.1s22s32p1,g.1s12s22p13d1中,属于原子基态的是(),属于原子激发态的是(),纯属错误的是().11.用元素符号填空:(均以天然存在为准)原子半径最大的元素是(),第一电离能最大的元素是(),原子中3d半充满的元素是(),原子中4p半充满的元素是(),电负性差最大的两个元素是(),化学性质最不活泼的元素是().四.简答题1.第114号元素属于第几周期?第几族?2.为什么碳(6C)的外围电子构型是2s22p2,而不是2s12p3,而铜(29Cu)的外围电子构型是3d104s1,而不是3d94s2?3、气体常数R是否只在气体中使用?五.综合题1.某元素位于周期表中36号元素之前,该元素失去2个电子以后,在角量子数l=2的轨道上正好半充满,试回答:(1).该元素的原子序数,符号,所处周期和族;(2).写出表示全部价电子运动状态的四个量子数;(3).该元素最高价氧化物水合物的分子式及酸碱性.2.某元素原子序数为33,试问:(1).此元素原子的电子总数是多少?有多少个未成对电子?(2).它有多少个电子层?多少个能级?最高能级组中的电子数是多少?(3).它的价电子数是多少?它属于第几周期?第几族?是金属还是非金属?最高化合价是几?3.写出原子序数为24的元素的名称,符号及其基态原子的电子排布式,并用四个量子数分别表示每个价电子的运动状态.（三）一.是非题:1、两原子间可以形成多重键，但两个以上的原子间不可能形成多重键。