北京市延庆区2017-2018年一模考试数学(文)试卷(含答案)

延庆区2017—2018学年度高三模拟试卷数学（文科） 2018.3本试卷共6页，满分150分，考试时间120分钟第Ⅰ卷（选择题）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若集合{|02},{|10}A x x B x x =≤≤=->，则A B = （A ）{|02}x x ≤≤ （B ）{|12}x x <≤（C ）{|0}x x ≥（D ）{|1}x x >2. 在复平面内，复数21i +的对应点位于的象限是（A ） 第一象限 （B ） 第二象限 （C ） 第三象限 （D ）第四象限3. 下列函数在其定义域内是增函数的是（A ）cos y x = （B ）lg(1)y x =+ （C ）xy e -= （D ）1y x =+4. 已知函数()2sin()3f x x πϕ=++,则“23πϕ=”是“()f x 为奇函数”的 （A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件 （D ）既不充分也不必要条件5. 若x ，y 满足030x y x y x ≤≥≥-⎧⎪+⎨⎪⎩则22x y +的最小值为（A ）0 （B ）3 （C ）4.5 （D ）56. 该程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入的,a b 分别为14，4，则输出的a 为（A ）0 （B ）2 （C ）4 （D ）147. 某三棱锥的三视图如图所示，则该三棱锥的最长棱的长为 （A（B（C（D ）8. 某上市股票在30天内每股的交易价格P （元）与时间t （天）所组成的有序数对(),t P ，点(),t P 落在图中的两条线段上；该股票在30天内的日交易量Q （万股）与时间t （天）的部分数据如下表所示,且Q 与t 满足一次函数关系， 那么在这30天中第几天日交易额最大 （A ）10 （B ）15 （C ）20 （D ）25正（主）视图侧（左）视图俯 视 图（7题图） 45tPO 3020106523第Ⅱ卷（非选择题）二、填空题：本大题共6小题，每小题5分，共30分.9. 双曲线2214x y -=的渐近线方程为 ． 10. 已知00x ,y >>,且244x y ⋅=，则xy 的最大值为 ． 11. 已知(1,2)(3,，==a b )x ，()+⊥a b a 则x = ．12. 无偿献血是践行社会主义核心价值观的具体行动,需要在报名的2名男教师和3名女教师中，选取2人参加无偿献血，则恰好选中一名男教师和一名女教师的概率为 ．13. 已知()f x ，()g x 在定义域内均为增函数，但()()f x g x ⋅不一定是增函数，例如当()f x = 且()g x = 时，()()f x g x ⋅不是增函数. 14. 有4个不同国籍的人，他们的名字分别是A 、B 、C 、D ，他们分别来自英国、美国、德国、法国（名字顺序与国籍顺序不一定一致）. 现已知每人只从事一个职业，且：(1)A 和来自美国的人他们俩是医生； (2)B 和来自德国的人他们俩是教师； (3)C 会游泳而来自德国的人不会游泳； (4)A 和来自法国的人他们俩一起去打球.根据以上条件可推测出A 是来自 国的人，D 是来自 国的人.三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤. 15.（本小题满分13分）已知等差数列{}n a 和等比数列{}n b ，其中数列{}n b 的前n 项和为n S ，11a =-，11b =，222a b +=，335a b +=.（Ⅰ）求{}n b 的通项公式和前n 项和n S ；（Ⅱ）设2log n n n c a b =+，求数列{}n c 的前n 项和n T .16.（本小题满分13分）△ABC的内角A，B，C的对边分别为a，b，c，已知sin A A=0，ab=2.（Ⅰ）求角A；（Ⅱ）求边c及△ABC的面积.17.（本小题满分13分）为了鼓励市民节约用电，某市实行“阶梯式”电价，将每户居民的月用电量分为二档，月用电量不超过200度的部分按0.5元/度收费，超过200度的部分按0.8元/度收费.某小区共有居民1000户，为了解居民的用电情况，通过抽样，获得了今年7月份100户居民每户的用电量，统计分析后得到如图所示的频率分布直方图.（Ⅰ）求a的值；（Ⅱ）试估计该小区今年7月份用电费用不超过260元的户数；（Ⅲ）估计7月份该市居民用户的平均用电费用（同一组中的数据用该组区间的中点值作代表）．18.（本小题满分14分）如图，在几何体ABCDE 中，四边形ABCD 是正方形，AB ⊥平面BEC ，BE EC ⊥，2BE EC ==，点,G H 分别是线段,BE EC 的中点，点,F N 分别是线段,CD BC 的中点.（Ⅰ）求证：//GH 平面ADE ； （Ⅱ）求证：AC ⊥平面ENF ；（Ⅲ）在线段CD 上是否存在一点P ，使得D AEP V -DP 的长，若不存在，请说明理由.19.（本小题满分13分）已知椭圆E ：()222210x y a b a b+=>>过点(0,，且离心率2e =.（Ⅰ）求椭圆E 的方程；（Ⅱ）设直线:1,()l x my m R =-∈交椭圆E 于,A B 两点，判断点G 9,04⎛⎫- ⎪⎝⎭与以线段AB 为直径的圆的位置关系，并说明理由.20.（本小题满分14分）已知函数x e x f x -=)(（e 为自然对数的底数）. （Ⅰ）求曲线()=y f x 在点(0,(0))f 处的切线方程；（Ⅱ）当[]0,2x ∈时,不等式ax x f >)(恒成立,求实数a 的取值范围；（Ⅲ）设()()g x f x ax =-，当函数()g x 有且只有一个零点时,求a 的取值范围.（考生务必将答案答在答题卡上，在试卷上作答无效）延庆区2017-2018学年度一模考试数学文评分标准一、选择题：C DBA CBDB 二、填空题：9. 12y x =±10. 1211. -4 12. 35 13. 答案不唯一 14.英, 德（第一空3分，第二空2分）13题参考答案：3,;,;,ln ;,lg ;,xx x x x x x x x x e三、解答题：15．（Ⅰ）设{}n a 公差为d ，{}n b 公比为(0)q q ≠， ………1分则1(1)n a n d =-+-，1n n b q-=⎩⎨⎧=++-=++-,5)21(,2)1(2q d q d 解得⎩⎨⎧==21q d 或⎩⎨⎧==03q d （舍去）. ………4分 所以12n n b -= ，.122112nn n S -==-- ………7分 （Ⅱ） 1(1)2n a n n =-+-=-， ………8分122log 2log 223n n n n c a b n n -=+=-+=- ………10分显然，数列{}n c 是首项为-1，公差为2的等差数列 ………11分 所以，2(123)22n n T n n n -+-==-. ………13分16．（Ⅰ）由sin 0A A =得π2sin 03A ⎛⎫+= ⎪⎝⎭， ………2分 即()ππ3A k k +=∈Z ， ………3分 又()0,πA ∈，∴ππ3A +=，得2π3A =. ………5分 （Ⅱ）由余弦定理2222cos a b c bc A =+-⋅， ………6分(0.0010.0030.004)1001a=0.002a +++⨯=解得又∵12,cos 2a b A ===- ………8分代入并整理得()2125c +=，故4c =； ………11分11sin 2422S bc A ==⨯⨯= ………13分17.（Ⅰ）………3分（Ⅱ）当用电量为400度时，用电费用为2000.5+2000.8100160260⨯⨯=+=元 所以此100户居民中用电费用超过260元的户数为0.0001100100=10⨯⨯户 所以此100户居民中用电费用不超过260元的户数为90户 ………7分 所以该小区1000户居民中用电费用不超过260元的户数为900户………8分 （Ⅲ）该市居民平均用电费用为(1500.32000.7)0.5(500.41500.22500.1)0.8152.5⨯+⨯⨯+⨯+⨯+⨯⨯=元………13分18.（Ⅰ）如图，点,G H 分别是线段,BE EC 的中点所以点GH 是BEC ∆的中位线，所以//GH BC ， ………1分 由ABCD 是正方形得，AB CD =， //AD BC ，所以 //GH AD ，……2分 又AD ⊂平面ADE ，GH ⊄平面ADE 所以//GH 平面ADE ………4分 （Ⅱ）如图，点,F N 分别是线段,CD BC 的中点 所以FN 是BCD ∆的中位线，所以//FN BD ， 由ABCD 是正方形得，A C B D ⊥，所以AC FN ⊥， ………6分又因为 BE EC =，点N 是BC 的中点 所以EN BC ⊥. ………7分 又因为 AB ⊥平面BEC ，EN ⊂平面BEC .EN AB ⊥ABBC B =，EN ⊥平面ABCD ………8分AC ⊂平面ABCD ,EN AC⊥ ………9分FNEN N =,AC ⊥平面ENF ； ………10分（Ⅲ）假设在线段CD 上存在一点P，使得D AEP V -=设DP a =,D AEP E ADP V V --= ………11分13E ADP ADP V S -=4ADP S ∴= ………12分142，ADP S AD DP =⨯=所以DP的长为 ………14分19．（Ⅰ）由已知 解得所以椭圆E的方程为22142x y += . ………4分（Ⅱ）设点1122(y ),B(,y ),A x x AB 中点为00H(,y )x .由221142得x my x y =-⎧⎪⎨+=⎪⎩()222230m y my +--=, ………6分 所以1212222322m y y ,y y m m -+==++ ………7分方法一：从而022my m =+. ………8分所以222222200000095525GH|()y (my )y (m +1)y +my +44216x =++=++=. …10分222b ca ab c⎧=⎪⎪=⎨⎪=+⎪⎩2a b c =⎧⎪=⎨⎪=⎩22222121212()(y )(m +1)(y )|AB|444x x y y -+--==22221212012(m +1)[(y )4y ](m +1)(y y )4y y y +-==-,故 ………12分222222012222|AB|52553(m +1)25172|GH|my (m +1)y 042162(m 2)m 21616(m 2)m m y +-=++=-+=>+++ 所以|AB||GH|>2，故点G 9(4-,0)在以AB 为直径的圆外. ………13分方法二：1212121299554444GA GB x x y y my my y y ⎛⎫⎛⎫⎛⎫⎛⎫⋅=+⋅++=+⋅++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭…9分()()()22121222525352251141641622=m m m y y m y y m m m -++++=+⋅+⋅+++ ()()22222248484025501720162162=m m m m m m --++++=>++ ………12分说明AGB ∠为锐角，故点G 9(4-,0)在以AB 为直径的圆外. ………13分20.（Ⅰ）,1)('-=xe xf 所以切线的斜率()00k f '==又因为()01f =， ………2分所以切线方程为 错误！未找到引用源。

2017-2018延庆区一模考试数学（理）评分标准一、选择题 DCDB DBDB二、填空题 9. 7 10. 1±,2或3- 11. 50 12. 213. 答案不唯一 14.英, 德（第一空3分第二空2分）13题参考答案：3,;,;,ln ;,lg ;,x x x x xx x x x x e L L三、解答题 15. （Ⅰ）由sin 0得A A +=………2分即()ππ3A k k +=∈Z ， ………3分 又()0,πA ∈，∴ππ3A +=，得2π3A =. ………5分 （Ⅱ）由余弦定理2222cos a b c bc A =+-⋅， ………6分又∵12,cos 2a b A ===-………8分 代入并整理得()2125c +=，故4c =； ………11分11sin 2422S bc A ==⨯⨯= ………13分 16.（Ⅰ）事件A 的人数为：400+270=670，该险种有1000人续保，所以P （A ）的估计值为：6700.671000= ………3分 （Ⅱ）X 的可能取值为0，1，2，3， ………4分由出险情况的统计表可知：一辆车一年内不出险的概率为400210005=， 出险的概率为23155-=，则 ………5分 328(0)()5125P x ===，1233236(1)()()55125P x C === 2233254(2)()()55125P x C ===，3327(3)()5125P x === ………9分 π2sin 03A ⎛⎫+= ⎪⎝⎭所以的X 分布列为： X0 1 2 3 P 8125 36125 54125 27125 ………10分（Ⅲ）续保人本年度的平均保费估值为：0.85400270 1.25200 1.580 1.7540210 1.071000a a a a a a a ⨯+⨯+⨯+⨯+⨯+⨯= ………13分17（Ⅰ）如图，取AE 的中点H ，连接,HG HD ，又G 是BE 的中点，所以 //GH AB ，且12GH AB = ………1分 又F 是CD 中点，所以12DF CD =， 由四边形ABCD 是矩形得，AB CD =， //AB CD ， ………2分所以GH DF =， //GH DF ，从而四边形HGFD 是平行四边形，//GF DH ， ………3分又DH ⊂平面ADE ，GF ⊄平面ADE 所以//GF 平面ADE ………4分 法一：（Ⅱ）如图，在平面BEC 内，过点B 作//BQ EC ,因为,BE EC BQ BE ⊥∴⊥又因为AB ⊥平面BEC ，所以AB BE ⊥，AB BQ ⊥ 以B 为原点，分别以,,BE BQ BA u u u r u u u r u u u r 的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系，…5分则(0,0,2)A (0,0,0)B (2,0,0)E (2,2,1).F ………6分因为AB ⊥平面BEC ，所以A=(B u u u r 0,0,2)为平面BEC 的法向量，………7分设(x,y,z)n =r 为平面AEF 的法向量，又AE (2,0,-2)AF=(2,2,-1)=u u u r u u u r ，由2200220,0，得x z n AE x y z n AF ⎧-=⋅=⎧⎨⎨+-=⋅=⎩⎩v u u u v v u u u v 取2z =得=(2,-1,2)n r . ………9分 从而42cos ,323n BA n BA n BA ⋅===⨯⋅v u u u v v u u u v v u u u v………10分 所以平面AEF 与平面BEC 所成锐二面角的余弦值为23. （Ⅲ）假设在线段CD 存在点M ，设点M 的坐标为(2,2,)a . ………11分 因为(0,0,2)A (2,0,0)E (2,2,2).D所以(0,2,2)DE =--u u u r ，(2,2,2)AM a =-u u u u r ………12分因为DE AM ⊥，0DE AM ⋅=u u u r u u u u r 所以0a = .………13分所以2DM = ………14分 法二：（Ⅱ）以E 点为原点，EC 所在直线为x 轴，EB 所在直线为y 轴，过E 做垂直平面BEC 的直线为z 轴，建立空间直角坐标系，则(0,0,0)E ，(0,2,2)A ，(2,0,1)F(2,0,2)D ，1(0,0,1)n v 为平面BEC 的法向量， ………7分设2(,,)n x y z v 为平面AEF 的法向量，又()()0,2,2,2,0,1EA EF u u u v u u u v由2200n EA n EF ⎧⋅=⎪⎨⋅=⎪⎩u u v u u u v u u v u u u v 得22020y z x z +=⎧⎨+=⎩取2z =得2(-1,-2,2)n v ………9分 从而12121222cos ,133n n n n n n ⋅===⨯⋅u u v u u v u u v u u v u u v u u v ………10分 所以平面AEF 与平面BEC 所成锐二面角的余弦值为23. （Ⅲ）假设在线段CD 存在点M ，设点M 的坐标为(2,0,)a . ………11分因为(0,2,2)A (0,0,0)E (2,0,2)D所以(-2,0,2)DE =-u u u r ，(2,-2,2)AM a =-u u u u r ………12分因为DE AM ⊥，0DE AM ⋅=u u u r u u u u r 所以0a = .………13分所以2DM = ………14分18（Ⅰ）,1)('-=xe xf 所以切线的斜率()00k f '== 又因为()01f =， ……2分 所以切线方程为 错误!未找到引用源。

2017-2018延庆区一模考试数学（理）评分标准一、选择题 DCDB DBDB二、填空题 9. 7 10. 1±,2或3- 11. 50 12. 213. 答案不唯一 14.英, 德（第一空3分第二空2分）13题参考答案：3,;,;,ln ;,lg ;,x x x x xx x x x x e L L三、解答题 15. （Ⅰ）由sin 0得A A +=………2分即()ππ3A k k +=∈Z ， ………3分 又()0,πA ∈，∴ππ3A +=，得2π3A =. ………5分 （Ⅱ）由余弦定理2222cos a b c bc A =+-⋅， ………6分又∵12,cos 2a b A ===-………8分 代入并整理得()2125c +=，故4c =； ………11分11sin 2422S bc A ==⨯⨯= ………13分 16.（Ⅰ）事件A 的人数为：400+270=670，该险种有1000人续保，所以P （A ）的估计值为：6700.671000= ………3分 （Ⅱ）X 的可能取值为0，1，2，3， ………4分由出险情况的统计表可知：一辆车一年内不出险的概率为400210005=， 出险的概率为23155-=，则 ………5分 328(0)()5125P x ===，1233236(1)()()55125P x C === 2233254(2)()()55125P x C ===，3327(3)()5125P x === ………9分 π2sin 03A ⎛⎫+= ⎪⎝⎭所以的X 分布列为： X0 1 2 3 P 8125 36125 54125 27125 ………10分（Ⅲ）续保人本年度的平均保费估值为：0.85400270 1.25200 1.580 1.7540210 1.071000a a a a a a a ⨯+⨯+⨯+⨯+⨯+⨯= ………13分17（Ⅰ）如图，取AE 的中点H ，连接,HG HD ，又G 是BE 的中点，所以 //GH AB ，且12GH AB = ………1分 又F 是CD 中点，所以12DF CD =， 由四边形ABCD 是矩形得，AB CD =， //AB CD ， ………2分所以GH DF =， //GH DF ，从而四边形HGFD 是平行四边形，//GF DH ， ………3分又DH ⊂平面ADE ，GF ⊄平面ADE 所以//GF 平面ADE ………4分 法一：（Ⅱ）如图，在平面BEC 内，过点B 作//BQ EC ,因为,BE EC BQ BE ⊥∴⊥又因为AB ⊥平面BEC ，所以AB BE ⊥，AB BQ ⊥ 以B 为原点，分别以,,BE BQ BA u u u r u u u r u u u r 的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系，…5分则(0,0,2)A (0,0,0)B (2,0,0)E (2,2,1).F ………6分因为AB ⊥平面BEC ，所以A=(B u u u r 0,0,2)为平面BEC 的法向量，………7分设(x,y,z)n =r 为平面AEF 的法向量，又AE (2,0,-2)AF=(2,2,-1)=u u u r u u u r ，由2200220,0，得x z n AE x y z n AF ⎧-=⋅=⎧⎨⎨+-=⋅=⎩⎩v u u u v v u u u v 取2z =得=(2,-1,2)n r . ………9分 从而42cos ,323n BA n BA n BA ⋅===⨯⋅v u u u v v u u u v v u u u v………10分 所以平面AEF 与平面BEC 所成锐二面角的余弦值为23. （Ⅲ）假设在线段CD 存在点M ，设点M 的坐标为(2,2,)a . ………11分 因为(0,0,2)A (2,0,0)E (2,2,2).D所以(0,2,2)DE =--u u u r ，(2,2,2)AM a =-u u u u r ………12分因为DE AM ⊥，0DE AM ⋅=u u u r u u u u r 所以0a = .………13分所以2DM = ………14分 法二：（Ⅱ）以E 点为原点，EC 所在直线为x 轴，EB 所在直线为y 轴，过E 做垂直平面BEC 的直线为z 轴，建立空间直角坐标系，则(0,0,0)E ，(0,2,2)A ，(2,0,1)F(2,0,2)D ，1(0,0,1)n v 为平面BEC 的法向量， ………7分设2(,,)n x y z v 为平面AEF 的法向量，又()()0,2,2,2,0,1EA EF u u u v u u u v由2200n EA n EF ⎧⋅=⎪⎨⋅=⎪⎩u u v u u u v u u v u u u v 得22020y z x z +=⎧⎨+=⎩取2z =得2(-1,-2,2)n v ………9分 从而12121222cos ,133n n n n n n ⋅===⨯⋅u u v u u v u u v u u v u u v u u v ………10分 所以平面AEF 与平面BEC 所成锐二面角的余弦值为23. （Ⅲ）假设在线段CD 存在点M ，设点M 的坐标为(2,0,)a . ………11分因为(0,2,2)A (0,0,0)E (2,0,2)D所以(-2,0,2)DE =-u u u r ，(2,-2,2)AM a =-u u u u r ………12分因为DE AM ⊥，0DE AM ⋅=u u u r u u u u r 所以0a = .………13分所以2DM = ………14分18（Ⅰ）,1)('-=xe xf 所以切线的斜率()00k f '== 又因为()01f =， ……2分 所以切线方程为 错误!未找到引用源。

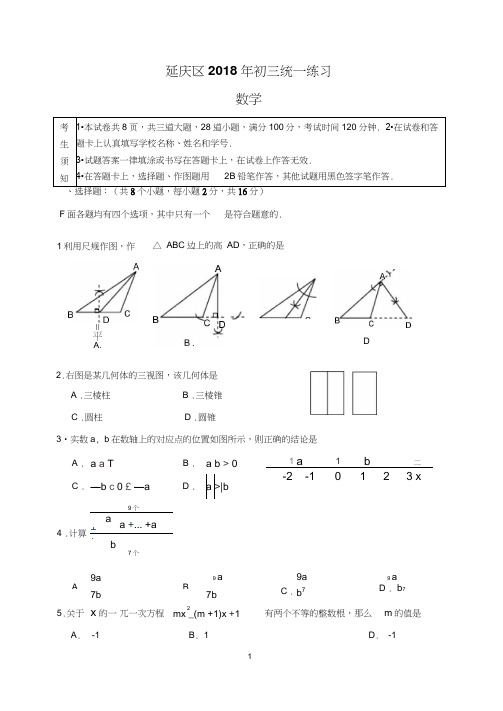
延庆区2018年初三统一练习数学考生须知1•本试卷共8页，共三道大题，28道小题，满分100分，考试时间120分钟. 2•在试卷和答题卡上认真填写学校名称、姓名和学号.3•试题答案一律填涂或书写在答题卡上，在试卷上作答无效.4•在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色签字笔作答.F面各题均有四个选项，其中只有一个是符合题意的.1利用尺规作图，作△ ABC边上的高AD，正确的是2.右图是某几何体的三视图，该几何体是A .三棱柱B .三棱锥C .圆柱D .圆锥3•实数a, b在数轴上的对应点的位置如图所示，则正确的结论是A . a a TB . a b > 0C . —b c 0 £—aD . a>|b9个4 .计算a+a +... +a: —b7个9a9 aA .B .7b7b5.关于x的一兀一次方程2mx _(m +1)x +11a1 b 二-2-10 1 2 3 xC .9a9 ab7 D . b7D. -1II平A.D.A. -1B. 1有两个不等的整数根，那么m的值是6.已知正六边形 ABCDEF ，下列图形中不是.轴对称图形的是7.下面的统计图反映了我国 2013年到2017年国内生产总值情况•（以上数据摘自国家统计局《中华人民共和国2017年国民经济和社会发展统计公报》）根据统计图提供的信息，下列推断不合理• •的是 A .与2016年相比，2017年我国国内生产总值有所增长； B . 2013-2016年，我国国内生产总值的增长率逐年降低； C . 2013-2017年，我国国内生产总值的平均增长率约为6.7% ;D . 2016-2017年比2014-2015年我国国内生产总值增长的多.亿元 1000000800000 600000 400000 200000&某游泳池长25米，小林和小明两个人分别在游泳池的 A , B 两边，同时朝着另一边游泳，他们游泳的时间为 t （秒）,其中0乞t 乞180，到A 边距离为y （米），图中的实 线和虚线分别表示小林和小明在游泳过程中y 与t 的对应关系.下面有四个推断：① 小明游泳的平均速度小于小林游泳的平均速度；2013-2017年国内生产总值及其增长速度%20 15 10 5 0BDB .C .D82712220162014201520172013一 国内生产总值比上年增长（%）14.如图，AB 是O O 的弦，OC 丄AB ，Z AOC=42 °那么/ CDB 的度数为 _____________.② 小明游泳的距离大于小林游泳的距离； ③ 小明游75米时小林游了 90米游泳; ④ 小明与小林共相遇 5次；13. 2017年延庆区农业用水和居民家庭用水的总和为 8亿立方米，其中居民家庭用水比农业用水的2倍还多0.5亿立方米.设农业用水为x 亿立方米，居民家庭用水为y 亿 立方米.依题意，可列方程组为_______________ A .①② B .①③二、填空题（共8个小题，每小题2分，共16分）x 十29.若分式 ------ 有意义，则实数 X 的取值范围是.x _310 .右图是一个正五边形，则/1的度数是 ______________2a _1a 211.如果a 2-a -^0，那么代数式（a） 的值是a a —112.如图，在△ ABC 中，D , E 分别是若AD = 1，BD = 3，贝U 匹的值为BC其中正确的是315.如图，在平面直角坐标系 xOy 中，△ DEF 可以看作是△ ABC 经过若干次图形的变化（平移、轴对称、 旋转）得到的，写出一种由△ ABC 得到△ DEF 的过 程： .16.某农科所在相同条件下做玉米种子发芽实验，结果如下:某位顾客购进这种玉米种子 10千克，那么大约有 _____ 千克种子能发芽.三、解答题（本题共 68分，第17题-22题，每小题5分；第23-26题，每小题6分;第27题，第28题每小题各7分）解答应写出文字说明、证明过程或演算步骤 .17•计算：3tan30°+1 — V3 +（2 —兀）° —（丄）‘.玉米种子发芽的频率发芽率％4p5x -2 ::: 3(x 2),18 •解不等式组：x 5并写出它的所有整数解.3x..219.如图，在△ ABC中，AD平分/ BAC交BC于点D ,过点D作DE // AB交AC于点E.求证：AE=DE .20 .已知：/ AOB及边OB上一点C .求作：/ OCD，使得/ OCD= / AOB .要求：1.尺规作图，保留作图痕迹，不写做法;(说明：作出一个即可)2 .请你写出作图的依据.21.如图，Rt △ ABC 中，/ ABC=90°,点 D , F 分别是 AC , AB 的中点，CE // DB , BE //DC .(1) 求证：四边形 DBEC 是菱形；(2) 若AD =3， DF=1，求四边形 DBEC 面积.在平面直角坐标系 xOy 中，直y = kx • b(k = 0) 与x 轴交于点A ,与y 轴交于点B ,与反比例函 数y = m (m = 0)的图象在第一象限交于点xP (1, 3),连接 OP .(1)求反比例函数y = m (m = 0)的表达式;x22. -3 一2 -1(2)若厶AOB 的面积是厶POB 的面积的2倍,-1 求直线y =kx • b 的表达式.-2 23. 如图，AB 是O O 的直径，D 是O O 上一点，点 中点，过点A 作O O 的切线交BD 的延长线于点 并延长交BF 于点C . (1)求证：AB =BC ; E 是AD 的F .连接AE(2)如果 AB=5, tan/FAC1，求FC 的长.2从北京市环保局证实，为满足 周边的环境污染进行综合治理， 程中，环保部门随机选取了永宁镇和千家店镇进行空气质量监测. 过程如下，请补充完整• 收集数据：24. 2022年冬奥会对环境质量的要求， 率先在部分村镇进行“煤改电”改造•在治理的过 北京延庆正在对其C-3从2016年12月初开始，连续一年对两镇的空气质量进行监测（将30天的空气污染指数（简称：API ）的平均值作为每个月的空气污染指数，12个月的空气污染指数如下：千家店镇：120 115 100 100 95 85 80 70 50 50 50 45永宁镇：110 90 105 80 90 85 90 60 90 45 70 60整理、描述数据：按如下表整理、描述这两镇空气污染指数的数据:（说明：空气污染指数< 50寸，空气质量为优；50V空气污染指数< 100时，空气质量为良；100V空气污染指数<150时，空气质量为轻微污染.）分析数据：两镇的空气污染指数的平均数、中位数、众数如下表所示;请将以上两个表格补充完整;得出结论：可以推断岀镇这一年中环境状况比较好，理由为（至少从两个不同的角度说明推断的合理性）25. 如图，点P是以O为圆心，AB为直径的半圆上的动点，AB=6cm，设弦AP的长为x cm,△ APO的面积为y cm2,（当点P与点A或点B重合时，y的值为0）.小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程，请补充完整；（1）通过取点、画图、测量、计算，得到了x与y的几组值，如下表: x/cm0.5123 3.545 5.5 5.8 y/cm20.8 1.5 2.8 3.9 4.2m 4.2 3.3 2.3那么m=8292 (2)建立平面直角坐标系，描出以表中各组对应值为坐标的点, 画出该函数图象.226. 在平面直角坐标系 xOy 中，抛物线 y=ax-4ax+3a(a >0)与x 轴交于 A , B 两点(A 在 B 的左侧).(1) 求抛物线的对称轴及点 A , B 的坐标；(2) 点C (t , 3)是抛物线y =ax 2-4ax ■ 3a(a 0)上一点，(点C 在对称轴的右侧)，过点C 作x 轴的垂线，垂足为点 D .① 当CD = AD 时，求此时抛物线的表达式； ② 当CD ■ AD 时，求t 的取值范围.L y6 5 4 3(3)结合函数图象说明，当△(保留一位小数)APO 的面积是4时，贝U AP 的值约为27. 如图1正方形ABCD中，点E是BC延长线上一点，连接DE ,过点B作BF丄DE 于点F，连接FC.(1 )求证：/ FBC = Z CDF .(2)作点C关于直线DE的对称点G,连接CG, FG .①依据题意补全图形；②用等式表示线段DF , BF , CG之间的数量关系并加以证明.图1 备用图28.平面直角坐标系xOy 中，点A(X i , yj 与B(% , y 2),如果满足X i= 0 , % - y ? = 0 ,其中X i =X 2，则称点A 与点B 互为反等点. 已知：点C(3, 4)D(-3, - 4), E (3, 4), F ( -3, 4)已知点G ( -5, 4),连接线段CG ,若在线段CG 上存在两点P , Q 互为反等点,求点P 的横坐标X p 的取值范围;1 2 3 4 5 6 X-1 -2 -3 -4(1) F 列各点中,与点C 互为反等点;(2) (3) 已知O O 的半径为r ，若O O 与(2)中线段CG 的两个交点互为反等点，求r的取值范围.i.y6-6 -5 -4 -3 -2 -1 O延庆区2018年初三统一练习评分标准数学一、选择题：（共8个小题，每小题2分，共16分）BACC ADCD二、填空题（共8个小题，每空2分，共16分）x y =89. X M 3 10. 72 °11. 1 12. 1: 4 13.y = 2x + 0.5 14. 21 °15.A ABC沿y轴翻折后，再向上平移4个单位得到△ DEF16. 8.8三、解答题彳3 ―17. 原式=3 +i3-1+1-3 ……4分3=2、3-3 ……汾18 .解：由①得，x<4 . ....... 1分由②得，x> 1 . ••…3分原不等式组的解集为 1 ^x<4. (4)•••原不等式组的所有整数解为 1 , 2, 3. ••…5分19 .证明：T AD平分/ BAC•••/ BAD = Z DAE,•/ DE// AB•••/ BAD = Z ADE••…3 分•••/ DAE=Z ADE …分• - AE=DE …• 5 分20. (1)作图(略) ••…2分(2)到线段两端点距离相等的点在线段的垂直平分线上；垂直平分线上的点到线段两端点距离相等；等边对等角 • ••…5分 21 . ( 1)在Rt A ABC 中，T CE//DC , BE// DC•••四边形DBEC 是平行四边形 •/ D 是 AC 的中点，/ ABC=90° • BD=DC•四边形DBEC 是菱形(2)T F 是AB 的中点• BC=2DF=2,Z AFD=Z ABC=90 °在Rt A AFD 中,错误！未找到引用源。

延庆区2018年初三统一练习数 学一、选择题：（共8个小题，每小题2分，共16分） 下面各题均有四个选项，其中只有一个．．是符合题意的． 1．利用尺规作图，作△ABC 边上的高AD ，正确的是2．右图是某几何体的三视图，该几何体是 A ．三棱柱B ．三棱锥C ．圆柱D ．圆锥 3．实数a ，b 在数轴上的对应点的位置如图所示，则正确的结论是A ．1a >-B ．0a b ⋅>C ．0b a -<<-D ．a b >4．计算：97...a a ab b b b+++=⋅⋅⋅⋅⋅个个A ．97a bB ．97a bC ．79abD ．97a b5．关于x 的一元二次方程2(1)10mx m x -++=有两个不等的整数根，那么m 的值是A ．1-B ．1C ．0D ．1± 6．已知正六边形ABCDEF ，下列图形中不是．．轴对称图形的是7．下面的统计图反映了我国2013年到2017年国内生产总值情况.（以上数据摘自国家统计局《中华人民共和国2017年国民经济和社会发展统计公报》） 根据统计图提供的信息，下列推断不合理．．．的是 A ．与2016年相比，2017年我国国内生产总值有所增长； B ．2013-2016年，我国国内生产总值的增长率逐年降低； C ．2013-2017年，我国国内生产总值的平均增长率约为6.7% ；F A B C E F E D C A F A C D E F AB CDE AB C D AB C DABC DABCDA B ． C ． D ． A ． B ． C ． D ．D ．2016-2017年比2014-2015年我国国内生产总值增长的多．8．某游泳池长25米，小林和小明两个人分别在游泳池的A ，B 两边，同时朝着另一边游泳，他们游泳的时间为t （秒），其中0180t ≤≤，到A 边距离为y （米），图中的实 线和虚线分别表示小林和小明在游泳过程中y 与t 的对应关系．下面有四个推断： ①小明游泳的平均速度小于小林游泳的平均速度； ②小明游泳的距离大于小林游泳的距离； ③小明游75米时小林游了90米游泳； ④小明与小林共相遇5次； 其中正确的是A ．①②B ．①③二、填空题（共8个小题，每小题29．若分式23x x +-有意义，则实数x 10．右图是一个正五边形，则∠111．如果210a a --=，那么代数式()1a a a -⋅-的值是 ． 12．如图，在△ABC 中，D ，E 分别是AB ，AC 上的点，DE ∥BC ，若AD ＝1，BD ＝3，则DEBC的值为 ． 13．2017年延庆区农业用水和居民家庭用水的总和为8亿立方米，其中居民家庭用水比农业用水的2倍还多0.5亿立方米．设农业用水为x 亿立方米，居民家庭用水为y 亿 立方米．依题意，可列方程组为____________． 14．如图，AB 是⊙O 的弦，OC ⊥AB ，∠AOC =42°，那么∠CDB 的度数为____________．15．如图，在平面直角坐标系xOy 中，△DEF 可以看作是△ABC 经过若干次图形的变化（平移、轴对称、 旋转）得到的，写出一种由△ABC 得到△DEF 的过 程： ． 16．某农科所在相同条件下做玉米种子发芽实验，结果如下：某位顾客购进这种玉米种子10千克，那么大约有____千克种子能发芽．三、解答题（本题共68分，第17题-22题，每小题5分；第23-26题，每小题6分；第27题，第28题每小题各7分）解答应写出文字说明、证明过程或演算步骤.17．计算：0113tan 301(2)()3π-︒++--．BCDE18．解不等式组：523(2)53.2x x x x -<+⎧⎪⎨+≤⎪⎩， 并写出它的所有整数解．19．如图，在△ABC 中，AD 平分∠BAC 交BC 于点D ，过点D 作DE ∥AB 交AC 于点E ． 求证：AE=DE ．20．已知：∠AOB 及边OB 上一点C ．求作：∠OCD ，使得∠OCD=∠AOB ．要求：1．尺规作图，保留作图痕迹，不写做法；（说明：作出一个．．即可） 2．请你写出作图的依据．21．如图，Rt △ABC 中，∠ABC =90°，点D ，F分别是AC ，AB 的中点，CE ∥DB ，BE ∥DC ． （1）求证：四边形DBEC 是菱形；（2）若AD =3， DF =1，求四边形DBEC 面积. 22．在平面直角坐标系xOy 中，直(0)y kx b k =+≠与x 轴交于点A ，与y 轴交于点B ，与反比例函 数(0)my m x=≠的图象在第一象限交于点 P （1，3），连接OP ． （1）求反比例函数(0)my m x=≠的表达式； （2）若△AOB 的面积是△POB 的面积的2倍，求直线y kx b =+的表达式．23．如图，AB 是⊙O 的直径，D 是⊙O 上一点，点E 是AD 的中点，过点A 作⊙O 的切线交BD 的延长线于点F ．连接AE 并延长交BF 于点C ． （1）求证：AB BC =；（2）如果AB =5，1tan 2FAC ∠=，求FC 的长． 24．从北京市环保局证实，为满足2022年冬奥会对环境质量的要求，北京延庆正在对其周边的环境污染进行综合治理，率先在部分村镇进行“煤改电”改造．在治理的过 程中，环保部门随机选取了永宁镇和千家店镇进行空气质量监测．过程如下，请补充完整. 收集数据:从2016年12月初开始，连续一年对两镇的空气质量进行监测（将30天的空气污染 指数（简称：API ）的平均值作为每个月的空气污染指数，12个月的空气污染指数FED CB A如下：千家店镇：120 115 100 100 95 85 80 70 50 50 50 45 永宁 镇：110 90 105 80 90 85 90 60 90 45 70 60 整理、描述数据：按如下表整理、描述这两镇空气污染指数的数据：质量为良；100＜空气污染指数≤150时，空气质量为轻微污染．） 分析数据：两镇的空气污染指数的平均数、中位数、众数如下表所示； 请将以上两个表格补充完整；得出结论：可以推断出______镇这一年中环境状况比较好，理由为_____________.（至少从两个不同的角度说明推断的合理性）25．如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB =6cm ，设弦AP 的长为x cm ， △APO 的面积为y cm 2，（当点P 与点A 或 点B 重合时，y 的值为0）．小明根据学习函数的经验，对函数y 随自变量x 的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整；（1）通过取点、画图、测量、计算，得到了x 与y 的几组值，如下表：那么m = ；（保留一位小数） （2）建立平面直角坐标系，描出以表中各组对应值为坐标的点， 画出该函数图象．（3）结合函数图象说明，当△APO（保留一位小数）26．在平面直角坐标系xOy 中，抛物线y 与x 轴交于A ，B 两点（A 在B （1）求抛物线的对称轴及点A ，B （2）点C （t ，3）是抛物线243(0)y ax ax a a =-+>上一点，（点C 在对称轴的右侧），过点C作x轴的垂线，垂足为点D．①当CD AD=时，求此时抛物线的表达式；②当CD AD>时，求t的取值范围．27．如图1，正方形ABCD 中，点E 是BC 延长线上一点，连接DE ，过点B 作BF ⊥DE于点F ，连接FC ．（1）求证：∠FBC =∠CDF ．（2）作点C 关于直线DE 的对称点G ，连接CG ，FG ．①依据题意补全图形；②用等式表示线段DF ，BF ，CG 之间的数量关系并加以证明．图1备用图FDEC BAFDEC BA28．平面直角坐标系xOy 中，点1(A x ，1)y 与2(B x ，2)y ，如果满足120x x +=，120y y -=，其中12x x ≠，则称点A 与点B 互为反等点． 已知：点C (3，4)（1）下列各点中， 与点C 互为反等点；D (-3，-4)，E （3，4），F （-3，4）（2）已知点G （-5，4），连接线段CG ，若在线段CG 上存在两点P ，Q 互为反等点，求点P 的横坐标p x 的取值范围；（3）已知⊙O 的半径为r ，若⊙O 与（2）中线段CG 的两个交点互为反等点， 求r 的取值范围．延庆区2018年初三统一练习评分标准数 学一、选择题：（共8个小题，每小题2分，共16分）BACC ADCD二、填空题 （共8个小题，每空2分，共16分）9．x ≠3 10．72° 11．1 12．1：4 13．820.5x y y x +=⎧⎨=+⎩14．21° 15．△ABC 沿y 轴翻折后，再向上平移4个单位得到△DEF 16．8.8三、解答题 17．原式=3⨯33+3-1+1-3 ……4分 =23-3 ……5分18．解：由①得，x <4． ……1分由②得，x ≥1 ． ……3分∴ 原不等式组的解集为1≤x <4． ……4分 ∴ 原不等式组的所有整数解为1，2，3． ……5分19．证明：∵AD 平分∠BAC∴∠BAD =∠DAE ， ∵DE ∥AB∴∠BAD =∠ADE ……3分 ∴∠DAE =∠ADE ……4分 ∴AE =DE ……5分20． （1）作图（略） ……2分（2）到线段两端点距离相等的点在线段的垂直平分线上；垂直平分线上的点到线段两端点距离相等；等边对等角. ……5分 21．（1）在Rt △ABC 中，∵CE //DC ，BE //DC∴四边形DBEC 是平行四边形∵D 是AC 的中点，∠ABC =90°∴BD =DC ……1分 ∴四边形DBEC 是菱形 ……2分 （2）∵F 是AB 的中点∴BC =2DF =2,∠AFD =∠ABC =90°在Rt △AFD中,……3分∴……4分……5分22．（1）3yx=……1分（2）如图22（1）：∵∴OA=2PE=2∴A（2,0）……2分将A（2,0），P（1,3）代入y=kx+b可得∴……3分图22（1）∴直线AB的表达式为：y=-3x+6同理：如图22（2）直线AB的表达式为：y=x+2 ……4分综上：直线AB的表达式为y=-3x+6或y=x+2 ……5分图22（2）23．证明：（1）连接BE．∵AB是直径，∴∠AEB=90°．∴∠CBE+∠ECB=90°∠EBA+∠EAB=90°．∵点E是AD的中点，∴∠CBE =∠EBA．∴∠ECB =∠EAB．……1分∴AB=BC．……2分（2）∵FA作⊙O的切线，∴FA⊥AB．∴∠FAC+∠EAB=90°．∵∠EBA+∠EAB=90°，∴∠FAC=∠EBA．∵1tan2FAC∠=AB=5，∴AEBE=．……4分过C点作CH⊥AF于点H，∵AB=BC∠AEB=90°，∴AC=2AE=25．∵1 tan2FAC∠=，∴CH=2．……5分AH-16123454321O∵CH ∥AB AB =BC=5， ∴255FCFC =+． ∴FC=310．…6分 24．（1）1，9，2． ……1分 （2） 82.5，90． ……3分 （3）千家店镇 ……4分理由：千家店镇污染指数平均数为80，永宁镇污染指数平均数为81.3，所以千家店镇污染指数平均数较低，空气质量较好；千家店镇空气质量为优的天数是4天，永宁镇空气质量为优的天数是1天，所以千家店镇空气质量为优的天数多，空气质量较好．…6分 25．(1)m = 约4.3 ； ……1分 (2)4.5） (3) 3.15.1 ……6分 26．（1）对称轴：x =2 ……1分 A ）或B （3，0） ……1分（2），∵AD =CD∴AD =3……3分将C （4，3）代入243y ax ax a =-+∴316163a a a =-+∴a =1∴抛物线的表达式为：243y x x =-+ ……4分②34t << ……6分 过程略27.（1）证明：∵四边形ABCD 是正方形，∴∠DCB =90°． ∴∠CDF +∠E =90°． ∵BF ⊥DE ， ∴∠FBC +∠E =90°． ∴∠FBC =∠CDF ．……2分（2）①……3分②猜想：数量关系为：BF =DF +CG ． 证明：在BF 上取点M 使得BM =DF 连接CM ． ∵四边形ABCD 是正方形， ∴BC =DC ．∵∠FBC =∠CDF ，BM =DF ，图1FDEC BA GF DEC BA∴△BMC ≌△DFC ．∴CM =CF ，∠1=∠2．∴△MCF 是等腰直角三角形．∴∠MCF =90°，∠4=45°． ……5分 ∵点C 与点G 关于直线DE 对称，∴CF =GF ，∠5=∠6．∵BF ⊥DE ，∠4=45°，∴∠5=45°，∴∠CFG =90°，∴∠CFG =∠MCF ，∴CM ∥GF ．∵CM =CF ，CF =GF ，∴CM =GF ，∴四边形CGFM 是平行四边形，∴CG =MF ．∴BF =DF +CG ．……7分 28．(1)F……1分 (2) -3≤p x ≤3 且p x ≠0……4分 (3)4 < r≤5 ……7分。

2018年北京市延庆区初三数学一模试卷(含答案)延庆区2018年初三统一练习数学考生须知 1.本试卷共8页，共三道大题，28道小题，满分100分，考试时间120分钟． 2.在试卷和答题卡上认真填写学校名称、姓名和学号． 3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效． 4.在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色签字笔作答．一、选择题：（共8个小题，每小题2分，共16分）下面各题均有四个选项，其中只有一个是符合题意的． 1．利用尺规作图，作△ABC边上的高AD，正确的是2．右图是某几何体的三视图，该几何体是 A．三棱柱 B．三棱锥 C．圆柱 D．圆锥3．实数a，b在数轴上的对应点的位置如图所示，则正确的结论是A． B． C． D． 4．计算： A． B． C． D．5．关于的一元二次方程有两个不等的整数根，那么的值是 A． B．1 C．0 D． 6．已知正六边形ABCDEF，下列图形中不是轴对称图形的是7．下面的统计图反映了我国2013年到2017年国内生产总值情况.（以上数据摘自国家统计局《中华人民共和国2017年国民经济和社会发展统计公报》）根据统计图提供的信息，下列推断不合理的是A．与2016年相比，2017年我国国内生产总值有所增长； B．2013-2016年，我国国内生产总值的增长率逐年降低； C．2013-2017年，我国国内生产总值的平均增长率约为6.7% ； D．2016-2017年比2014-2015年我国国内生产总值增长的多．8．某游泳池长25米，小林和小明两个人分别在游泳池的A，B两边，同时朝着另一边游泳，他们游泳的时间为（秒），其中，到A边距离为y（米），图中的实线和虚线分别表示小林和小明在游泳过程中y与t的对应关系．下面有四个推断：①小明游泳的平均速度小于小林游泳的平均速度；②小明游泳的距离大于小林游泳的距离；③小明游75米时小林游了90米游泳；④小明与小林共相遇5次；其中正确的是 A．①② B．①③ C.③④ D．②④二、填空题（共8个小题，每小题2分，共16分） 9．若分式有意义，则实数的取值范围是． 10．右图是一个正五边形，则∠1的度数是． 11．如果，那么代数式的值是． 12．如图，在△ABC 中，D，E分别是AB，AC上的点，DE∥BC，若AD＝1，BD＝3，则的值为．13．2017年延庆区农业用水和居民家庭用水的总和为8亿立方米，其中居民家庭用水比农业用水的2倍还多0.5亿立方米．设农业用水为x亿立方米，居民家庭用水为y亿立方米．依题意，可列方程组为____________． 14．如图，AB是⊙O的弦，OC⊥AB，∠AOC=42°，那么∠CDB的度数为____________．15．如图，在平面直角坐标系中，△DEF可以看作是△ABC经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△ABC 得到△DEF的过程：．16．某农科所在相同条件下做玉米种子发芽实验，结果如下：某位顾客购进这种玉米种子10千克，那么大约有____千克种子能发芽．三、解答题（本题共68分，第17题-22题，每小题5分；第23-26题，每小题6分；第27题，第28题每小题各7分）解答应写出文字说明、证明过程或演算步骤. 17．计算：． 18．解不等式组：并写出它的所有整数解．19．如图，在△ABC中，AD平分∠BAC交BC于点D，过点D 作DE∥AB 交AC于点E．求证：AE=DE．20．已知：∠AOB及边OB上一点C．求作：∠OCD，使得∠OCD=∠AOB．要求：1．尺规作图，保留作图痕迹，不写做法；（说明：作出一个即可） 2．请你写出作图的依据．21．如图，Rt△ABC中，∠ABC=90°，点D，F 分别是AC，AB的中点，CE∥DB，BE∥DC．（1）求证：四边形DBEC是菱形；（2）若AD=3，DF=1，求四边形DBEC面积.22．在平面直角坐标系xOy中，直与x轴交于点A，与y轴交于点B，与反比例函数的图象在第一象限交于点 P（1，3），连接OP．（1）求反比例函数的表达式；（2）若△AOB的面积是△POB的面积的2倍，求直线的表达式． 23．如图，是⊙O的直径，D是⊙O上一点，点是的中点，过点作⊙O的切线交的延长线于点F．连接并延长交于点．（1）求证：；（2）如果AB=5，，求的长．24．从北京市环保局证实，为满足2022年冬奥会对环境质量的要求，北京延庆正在对其周边的环境污染进行综合治理，率先在部分村镇进行“煤改电”改造．在治理的过程中，环保部门随机选取了永宁镇和千家店镇进行空气质量监测．过程如下，请补充完整. 收集数据: 从2016年12月初开始，连续一年对两镇的空气质量进行监测（将30天的空气污染指数（简称：API）的平均值作为每个月的空气污染指数，12个月的空气污染指数如下：千家店镇：120 115 100 100 95 85 80 70 50 50 50 45 永宁镇：110 90 105 80 90 85 90 60 90 45 70 60 整理、描述数据：按如下表整理、描述这两镇空气污染指数的数据：空气质量为优空气质量为良空气质量为轻微污染千家店镇 4 6 2 永宁镇（说明：空气污染指数≤50时，空气质量为优；50＜空气污染指数≤100时，空气质量为良；100＜空气污染指数≤150时，空气质量为轻微污染．）分析数据：两镇的空气污染指数的平均数、中位数、众数如下表所示；城镇平均数中位数众数千家店 80 50 永宁 81.3 87.5请将以上两个表格补充完整；得出结论：可以推断出______镇这一年中环境状况比较好，理由为_____________. （至少从两个不同的角度说明推断的合理性） 25．如图，点P是以O为圆心，AB为直径的半圆上的动点，AB=6cm，设弦AP的长为 cm，△APO的面积为 cm2，（当点P与点A或点B重合时，y的值为0）．小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整；（1）通过取点、画图、测量、计算，得到了x与y的几组值，如下表： x/cm 0.5 1 2 3 3.5 4 5 5.5 5.8 y/cm2 0.8 1.5 2.8 3.9 4.2 m 4.2 3.3 2.3 那么m= ；（保留一位小数）（2）建立平面直角坐标系，描出以表中各组对应值为坐标的点，画出该函数图象．（3）结合函数图象说明，当△APO的面积是4时，则AP的值约为．（保留一位小数）26．在平面直角坐标系xOy中，抛物线y=ax2-4ax+3a(a＞0) 与x轴交于A，B两点（A在B的左侧）．（1）求抛物线的对称轴及点A，B 的坐标；（2）点C（t，3）是抛物线上一点，（点C在对称轴的右侧），过点C 作x轴的垂线，垂足为点D．①当时，求此时抛物线的表达式；②当时，求t的取值范围．27．如图1，正方形ABCD中，点E是BC延长线上一点，连接DE，过点B作BF⊥DE 于点F，连接FC．（1）求证：∠FBC=∠CDF．（2）作点C关于直线DE的对称点G，连接CG，FG．①依据题意补全图形；②用等式表示线段DF，BF，CG之间的数量关系并加以证明．28．平面直角坐标系xOy中，点，与，，如果满足，，其中，则称点A与点B互为反等点．已知：点C(3，4) （1）下列各点中，与点C互为反等点； D( 3， 4)，E（3，4），F（ 3，4）（2）已知点G（ 5，4），连接线段CG，若在线段CG上存在两点P，Q互为反等点，求点P的横坐标的取值范围；（3）已知⊙O的半径为r，若⊙O与（2）中线段CG的两个交点互为反等点，求r的取值范围．延庆区2018年初三统一练习评分标准数学一、选择题：（共8个小题，每小题2分，共16分） BACC ADCD 二、填空题（共8个小题，每空2分，共16分） 9．x≠3 10．72° 11．1 12．1：4 13． 14．21° 15．△ABC沿y轴翻折后，再向上平移4个单位得到△DEF 16．8.8 三、解答题 17．原式=3 + -1+1-3 ……4分 =2 -3 ……5分18．解：由①得，x<4．……1分由②得，x≥1 ．……3分∴ 原不等式组的解集为1≤x<4．……4分∴ 原不等式组的所有整数解为1，2，3．……5分19．证明：∵AD平分∠BAC ∴∠BAD =∠DAE，∵DE∥AB ∴∠BAD=∠ADE ……3分∴∠DAE =∠ADE ……4分∴AE=DE ……5分 20．（1）作图（略）……2分（2）到线段两端点距离相等的点在线段的垂直平分线上；垂直平分线上的点到线段两端点距离相等；等边对等角. ......5分 21．（1）在Rt△ABC中，∵CE//DC，BE//DC ∴四边形DBEC是平行四边形∵D是AC的中点，∠ABC=90° ∴BD=DC (1)分∴四边形DBEC是菱形……2分（2）∵F是AB的中点∴BC=2DF=2,∠AFD=∠ABC=90° 在Rt△AFD中, ......3分∴ (4)分......5分 22．（1）......1分（2）如图22（1）：∵ ∴OA=2PE=2 ∴A（2,0）......2分将A（2,0），P（1,3）代入y=kx+b 可得∴ (3)分图22（1）∴直线AB的表达式为：y=-3x+6 同理：如图22（2）直线AB的表达式为：y=x+2 ……4分综上：直线AB的表达式为y=-3x+6或y=x+2 ……5分 23．证明：（1）连接BE．∵AB是直径，∴∠AEB=90°．∴∠CBE+∠ECB=90°∠EBA+∠EAB=90°．∵点是的中点，∴∠CBE =∠EBA．∴∠ECB =∠EAB．……1分∴AB=BC．……2分（2）∵FA作⊙O的切线，∴FA⊥AB．∴∠FAC+∠EAB=90°．∵∠EBA+∠EAB=90°，∴∠FAC=∠EBA．∵ AB=5，∴ ．......4分过C点作CH⊥AF于点H，∵AB=BC ∠AEB=90°，∴AC=2AE=2 ．∵ ，∴CH=2． (5)分∵CH∥AB AB=BC=5，∴ ．∴FC= ．…6分24．（1）1，9，2．……1分（2） 82.5，90．……3分（3）千家店镇……4分理由：千家店镇污染指数平均数为80，永宁镇污染指数平均数为81.3，所以千家店镇污染指数平均数较低，空气质量较好；千家店镇空气质量为优的天数是4天，永宁镇空气质量为优的天数是1天，所以千家店镇空气质量为优的天数多，空气质量较好．…6分 25．(1)m= 约4.3 ；……1分（画此函数图象时要体现出x约为4.2时，y有最大值，为4.5） (4)分 (3) 3.1或是5.1 ……6分26．（1）对称轴：x=2 ……1分 A（1，0）或B（3，0）……1分（2）①如图1，∵AD=CD ∴AD=3 ∴C点坐标为（4，3）……3分将C（4，3）代入∴ ∴a=1 ∴抛物线的表达式为：……4分② ……6分过程略27.（1）证明：∵四边形ABCD是正方形，∴∠DCB =90°．∴∠CDF+∠E =90°．∵BF⊥DE，∴∠FBC+∠E =90°．∴∠FBC =∠CDF ． (2)分……3分②猜想：数量关系为：BF=DF+CG．证明：在BF上取点M使得BM=DF连接CM．∵四边形ABCD是正方形，∴BC=DC．∵∠FBC =∠CDF，BM=DF，∴△BMC≌△DFC．∴CM=CF，∠1=∠2．∴△MCF 是等腰直角三角形．∴∠MCF =90°，∠4=45°．……5分∵点C 与点G关于直线DE对称，∴CF=GF，∠5=∠6．∵BF⊥DE，∠4=45°，∴∠5=45°，∴∠CFG =90°，∴∠CFG=∠MCF，∴CM∥GF．∵CM=CF，CF=GF，∴CM=GF，∴四边形CGFM是平行四边形，∴CG=MF．∴BF=DF+CG．……7分 28．(1)F ……1分 (2) -3≤ ≤3 且≠0 ……4分(3)4 < r≤5 ……7分。

2018北京中考数学——延庆一模一、选择题：（共8个小题，每小题2分，共16分）BACC ADCD二、填空题 （共8个小题，每空2分，共16分）9．x ≠3 10．72° 11．1 12．1：4 13．820.5x y y x +=⎧⎨=+⎩14．21° 15．△ABC 沿y 轴翻折后，再向上平移4个单位得到△DEF 16．8.8 三、解答题17．原式=3⨯33+3-1+1-3 ……4分 =23-3 ……5分18．解：由①得，x <4． ……1分 由②得，x ≥1 ． ……3分∴ 原不等式组的解集为1≤x <4． ……4分 ∴ 原不等式组的所有整数解为1，2，3． ……5分19．证明：∵AD 平分∠BAC∴∠BAD =∠DAE ， ∵DE ∥AB∴∠BAD =∠ADE ……3分 ∴∠DAE =∠ADE ……4分 ∴AE =DE ……5分20． （1）作图（略） ……2分（2）到线段两端点距离相等的点在线段的垂直平分线上；垂直平分线上的点到线段两端点距离相等；等边对等角. ……5分21．（1）在Rt△ABC 中，∵CE //DC ，BE //DC∴四边形DBEC 是平行四边形∵D 是AC 的中点，∠ABC =90°∴BD =DC ……1分 ∴四边形DBEC 是菱形 ……2分 （2）∵F 是AB 的中点∴BC =2DF =2,∠AFD =∠ABC =90° 在Rt△AFD 中,……3分 ∴……4分……5分22．（1）3yx=……1分（2）如图22（1）：∵∴OA=2PE=2∴A（2,0）……2分将A（2,0），P（1,3）代入y=kx+b可得∴……3分图22（1）∴直线AB的表达式为：y=-3x+6同理：如图22（2）直线AB的表达式为：y=x+2 ……4分综上：直线AB的表达式为y=-3x+6或y=x+2 ……5分图22（2 23．证明：（1）连接BE．∵AB是直径，∴∠AEB=90°．∴∠CBE+∠ECB=90°∠EBA+∠EAB=90°．∵点E是AD的中点，∴∠CBE=∠EBA．∴∠ECB=∠EAB．……1分∴AB=BC．……2分（2）∵FA作⊙O的切线，∴FA⊥AB．∴∠FAC+∠EAB=90°．∵∠EBA+∠EAB=90°，∴∠FAC=∠EBA．∵1tan2FAC∠=AB=5，∴AE=BE=．……4分过C点作CH⊥AF于点H，∵AB=BC∠AEB=90°，∴AC=2AE=25．∵1 tan2FAC∠=，∴CH=2．……5分∵CH∥AB AB=BC=5，∴255FCFC=+．∴FC=310．…6分AH2018北京中考数学——延庆一模-16123454321O 24．（1）1，9，2． ……1分 （2） 82.5，90． ……3分 （3）千家店镇 ……4分理由：千家店镇污染指数平均数为80，永宁镇污染指数平均数为81.3，所以千家店镇污染指数平均数较低，空气质量较好；千家店镇空气质量为优的天数是4天，永宁镇空气质量为优的天数是1天，所以千家店镇空气质量为优的天数多，空气质量较好．…6分25．(1)m = 约4.3 ； ……1分 (2)（画此函数图象时要体现出x 约为4.2时，有最大值，为4.5） (3) 3.1或是5.1 ……6分 26．（1）对称轴：x =2 ……1分 A （1，0）或B （3，0） ……1分 （2）①如图1，∵AD =CD ∴AD =3∴C 点坐标为（4，3） ……3分 将C （4，3）代入243y ax ax a =-+ ∴316163a a a =-+∴a =1∴抛物线的表达式为：243y x x =-+ ……4分 ②34t << ……6分 过程略27.（1）证明：∵四边形ABCD 是正方形，∴∠DCB=90°． ∴∠CDF +∠E =90°． ∵BF ⊥DE ，∴∠FBC +∠E =90°．∴∠FBC =∠CDF ．……2分图1 FDEBA（2）①……3分②猜想：数量关系为：BF =DF +CG ． 证明：在BF 上取点M 使得BM =DF 连接CM ．∵四边形ABCD 是正方形， ∴BC =DC ．∵∠FBC =∠CDF ，BM =DF ， ∴△BMC ≌△DFC ． ∴CM =CF ，∠1=∠2．∴△MCF 是等腰直角三角形．∴∠MCF =90°，∠4=45°． ……5分 ∵点C 与点G 关于直线DE 对称， ∴CF =GF ，∠5=∠6．∵BF ⊥DE ，∠4=45°， ∴∠5=45°， ∴∠CFG =90°， ∴∠CFG =∠MCF ， ∴CM ∥GF ．∵CM =CF ，CF =GF ， ∴CM =GF ，∴四边形CGFM 是平行四边形， ∴CG =MF ．∴BF =DF +CG ． ……7分 28．(1)F ……1分(2) -3≤p x ≤3 且p x ≠0 ……4分(3)4 < r≤5 ……7分GF DE C BA。

2018北京市延庆区初三（一模）数学考生须知1.本试卷共8页，共三道大题，28道小题，满分100分，考试时间120分钟。

2.在试卷和答题卡上认真填写学校名称、姓名和学号。

3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4.在答题卡上，选择题、做图题用2B铅笔作答，其他试题用黑色签字笔作答。

一、选择题（共8个小题，每小题2分，共16分）下面各题均有四个选项，其中只有一个是符合题意的.1.利用尺规做图，作△ABC边上的高AD，正确的是2.右图是某几何体的三视图，该几何体是A.三棱柱B.三棱锥C.圆柱D.圆锥3.实数a,b在数轴上的对应点的位置如图所示，则正确的结论是A.a>-1B.a.b>0C.-b<0<-aD.∣a∣>∣b∣4.计算：5.关于x的一元二次方程mx2-(m+1)x+1=0有两个不等的整数根，那么m的值是A.-1B.1C.0D.±16.已知正六边形ABCDEF，下列图形中不是轴对称图形的是7.下面的统计图反应了我国2013年到2017年国内生产总值情况（以上数据摘自国家统计局《中华人民共和国2017年国民经济和社会发展统计公报》）根据统计图提供的信息，下列推断不合理的是A.与2016年相比，2017你那我国国内生产总值有所增长；B.2013-2016年，我国国内生产总值的增长率逐年降低；C.2013-2017年，我国国内生产总值的平均增长率约为6.7%；D.2016-2017年比2014-2015年我国国内生产总值增长的多。

8.某游泳池长25米，小林和小明两个人分别在游泳池的A，B两边，同时朝着另一边游泳，他们游泳的时间为t（秒），其中0≤t≤180,到A边距离为y（米），图中的实线和虚线分别表示小林和小明在游泳过程中y与t的对应关系，下面有四个推断；①小明游泳的平均速度小于小林游泳的平均速度②小明游泳的距离大于小林游泳的距离③小明游75米时小林游了90米④小明与小林共相遇5次其中正确的是A. ①②B. ①③C. ③④D. ②④二、填空题（共8个小题，每小题2分，共16分）9.若分式有意义，则实数x的取值范围是 .10.右图是一个正五边形，则∠1的度数是 .11.如果a2-a-1=0,那么代数式（a-）·的值是 .12.如图，在△ABC中，D,E分别是AB,AC上的点，DE∥BC,若AD=1，BD=3,则的值为 .13.2017年延庆区农业用水和居民家庭用水的总和为8亿立方米，期中居民家庭用水比农业用水的2倍还多0.5亿立方米。

延庆区XXXX一模考试答案(数学文)？2q？0(？1？2d)？问？5？？？那么bn？2n？11岁？2n？2n？1.................7分。

sn？1？2(ⅱ)an？？1？(n？1)？n？2，......8分cn？安？log2bn？n？2？log22n？1？2n？3.................10分明显，顺序？cn？第一项是-1，2算术级数的容差.................11分怎么样，Tn？16。

(一)由司南？3科萨？0的2英寸？a。

(？1？2n？3)n？n2？2n。

… … 13点2？？π？？？0，......2分3秒。

a。

π？kπ？k？z？三点，32π？π，得到一个？5分33和a？？0，π？,∴A？(二)通过余弦定理a2？b2？c2？公元前2bc？CosA，......6分高三数学(文科)第1页(共6页)1和÷a？27，b？2、cosA？？… 8分2被替换并整理出来？c？1？？25，那么c？4；… 11分2113秒？新浪？？2？4？？23 .................13分22217。

(一)(0.001？a。

0.003？0.004)？100？A = 0.002 .................3分(ii)当用电量为400度时，用电成本为200？0.5+200？0.8？100？160？那么用电成本超过260元的260元家庭的数量是0.0001？100？100=10户，用电成本不超过260元的户数为90户.......7分，因此用电成本不超过260元的户数为900户.......8分(三)本市居民平均用电成本为(150？0.3？200？0.7)？0.5？(50？0.4？150？0.2？250？0.1)？0.8？152.5元.................13分18。

如图所示，点g和h分别是线段be和EC的中点，那么点GH是什么？BEC的中线，所以GH//公元前，......1点是通过ABCD是正方形得到的。

延庆区2017—2018学年度高三模拟试卷数学（理科） 2018.3本试卷共6页，满分150分，考试时间120分钟第Ⅰ卷（选择题）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若集合2{|02},{|1}A x x B x x =≤≤=>，则AB =（A ）{|01}x x ≤≤ （B ）{|0x x >或1}x <- （C ）{|12}x x <≤ （D ）{|0x x ≥或1}x <-2. 在复平面内，复数-2i1i +的对应点位于的象限是（A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限3. 已知函数()f x 是定义域为R 的奇函数，且(1)2f =-，那么(1)(0)f f -+= （A ）-2 （B ）0 （C ）1 （D ）24. 已知非零向量c b a,,则“()0a b c ⋅=-”是“c b =”的（A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件 （D ）既不充分也不必要条件5. 若x ，y 满足2030x y x y x ≤≥≥-⎧⎪+⎨⎪⎩则22x y +的最小值为（A ）0 （B ）3 （C ）4.5 （D ）56. 该程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b 分别为14,4,则输出的a 为（A ）0 （B ）2 （C ）4 （D ）147. 某三棱锥的三视图如图所示，则该三棱锥的最长棱的长为（A（B（C ） 2 （D8. 若,a b 是函数()()20,0f x x px q p q =-+>>的两个不同的零点，且,,2a b -这三个数适当排序后可成等差数列，且适当排序后也可成等比数列，则a b +的值等于 （A ）4 （B ）5 （C ）6 （D ）7正（主）视图侧（左）视图俯 视 图（7题图）第Ⅱ卷（非选择题）二、填空题：本大题共6小题，每小题5分，共30分.9. 设双曲线2214x y -=的焦点为12，，F F P 为该双曲线上的一点，若13PF =，则2PF = ．10. 已知()2sin 2f x x =ω，其周期为π，则ω= ，当,63x ππ⎡⎤∈⎢⎥⎣⎦时，函数()f x 的最大值为 ．11. 无偿献血是践行社会主义核心价值观的具体行动,需要在报名的2名男教师和6名女教师中，选取5人参加无偿献血，要求男、女教师都有，则不同的选取方法的种数为 ．（结果用数值表示）12. 以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设():cos sin 2l +=ρθθ，M 为l 与224x y +=的交点，则M 的极径为 ．13. 已知()()和f x g x 在定义域内均为增函数，但()()f x g x ⋅不一定是增函数，例如当()f x = 且()g x = 时，()()f x g x ⋅不是增函数.14. 有4个不同国籍的人，他们的名字分别是A 、B 、C 、D ，他们分别来自英国、美国、德国、法国（名字顺序与国籍顺序不一定一致）. 现已知每人只从事一个职业，且：（1）A 和来自美国的人他们俩是医生； （2）B 和来自德国的人他们俩是教师； （3）C 会游泳而来自德国的人不会游泳； （4）A 和来自法国的人他们俩一起去打球.根据以上条件可推测出A 是来自 国的人，D 是来自 国的人.三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.15.（本小题满分13分）△ABC的内角A，B，C的对边分别为a，b，c，已知sin AA=0，a，b=2.（Ⅰ）求角A；（Ⅱ）求边c及△ABC的面积.16.（本小题满分13分）某车险的基本保费为a（单位：元），继续购买车险的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：随机调查了该险种的1000名续保人在一年内的出险情况，得到如下统计表：（Ⅰ）记A为事件：“一续保人本年度的保费不高于基本保费”,求()P A的估计值；（Ⅱ）某公司有三辆汽车,基本保费均为a,根据随机调查表的出险情况,记X为三辆车中一年内出险的车辆个数,写出X的分布列；（Ⅲ）求续保人本年度的平均保费估计值．如图，在几何体ABCDE 中，四边形ABCD 是矩形，AB ⊥平面BEC ，BE EC ⊥，2AB BE EC ===，点,G F 分别是线段,BE DC 的中点.（Ⅰ）求证：//GF 平面ADE ；（Ⅱ）求平面AEF 与平面BEC 所成锐二面角的余弦值；（Ⅲ）在线段CD 上是否存在一点M ，使得DE AM ⊥，若存在，求DM 的长，若不存在，请说明理由.18.（本小题满分13分）已知函数x e x f x-=)(（e 为自然对数的底数）.（Ⅰ）求曲线()=y f x 在点(0,(0))f 处的切线方程；（Ⅱ）设不等式ax x f >)(的解集为P ，且P x x ⊆≤≤}20|{,求实数a 的取值范围； （Ⅲ）设()()g x f x ax =-，写出函数()g x 的零点的个数.（只需写出结论）已知椭圆E ：()222210x y a b a b+=>>过点01（）,且离心率e =.（Ⅰ）求椭圆E 的方程； （Ⅱ）设动直线l 与两定直线1:0l x y -=和2:0l x y +=分别交于,P Q 两点．若直线l 总与椭圆E 有且只有一个公共点，试探究：OPQ ∆的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由．20.（本小题满分13分）设满足以下两个条件的有穷数列12,,,n a a a 为(2,3,4,)n n = 阶“Q 数列”：①120n a a a +++=； ②121n a a a +++=.（Ⅰ）分别写出一个单调递增的3阶和4阶“Q 数列”；（Ⅱ）若2018阶“Q 数列”是递增的等差数列，求该数列的通项公式； （Ⅲ）记n 阶“Q 数列”的前k 项和为(1,2,3,,)k S k n =，试证12k S ≤.（考生务必将答案答在答题卡上，在试卷上作答无效）2017-2018延庆区一模考试数学（理）评分标准一、选择题 DCDB DBDB二、填空题 9. 7 10. 1±,2或3- 11. 50 12. 2 13. 答案不唯一 14.英, 德（第一空3分第二空2分） 13题参考答案：3,;,;,ln ;,lg ;,xx x x x x x x x xe三、解答题15. （Ⅰ）由sin 0得A A +=………2分即()ππ3A k k +=∈Z ， ………3分 又()0,πA ∈，∴ππ3A +=，得2π3A =. ………5分 （Ⅱ）由余弦定理2222cos a b c bc A =+-⋅， ………6分又∵12,cos 2a b A ===-………8分 代入并整理得()2125c +=，故4c =； ………11分11sin 24222S bc A ==⨯⨯⨯= ………13分16.（Ⅰ）事件A 的人数为：400+270=670，该险种有1000人续保，所以P （A ）的估计值为：6700.671000= ………3分 （Ⅱ）X 的可能取值为0，1，2，3， ………4分 由出险情况的统计表可知：一辆车一年内不出险的概率为400210005=， 出险的概率为23155-=，则 ………5分 328(0)()5125P x ===，1233236(1)()()55125P x C ===2233254(2)()()55125P x C ===，3327(3)()5125P x === ………9分 π2sin 03A ⎛⎫+=⎪⎝⎭所以的X 分布列为：………10分 （Ⅲ）续保人本年度的平均保费估值为：0.85400270 1.25200 1.580 1.75402101.071000a a a a a a a ⨯+⨯+⨯+⨯+⨯+⨯=………13分17（Ⅰ）如图，取AE 的中点H ，连接,HG HD ，又G 是BE 的中点， 所以 //GH AB ，且12GH AB =………1分 又F 是CD 中点，所以12DF CD =， 由四边形ABCD 是矩形得，AB CD =， //AB CD ， ………2分 所以GH DF =， //GH DF ，从而四边形HGFD 是平行四边形，//GF DH ， ………3分 又DH ⊂平面ADE ，GF ⊄平面ADE 所以//GF 平面ADE ………4分 法一：（Ⅱ）如图，在平面BEC 内，过点B 作//BQ EC ,因为,B E E C B Q B E ⊥∴⊥又因为AB ⊥平面BEC ，所以AB BE ⊥，AB BQ ⊥ 以B 为原点，分别以,,BE BQ BA 的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系，…5分则(0,0,2)A (0,0,0)B (2,0,0)E (2,2,1).F ………6分 因为AB ⊥平面BEC ，所以A=(B 0,0,2)为平面BEC 的法向量，………7分设(x,y,z)n =为平面AEF 的法向量，又AE (2,0,-2)AF=(2,2,-1)=，由220220,0，得x z n AE x y z n AF ⎧-=⋅=⎧⎨⎨+-=⋅=⎩⎩取2z =得=(2,-1,2)n . ………9分从而42cos ,323n BA n BA n BA⋅===⨯⋅………10分 所以平面AEF 与平面BEC 所成锐二面角的余弦值为23. （Ⅲ）假设在线段CD 存在点M ，设点M 的坐标为(2,2,)a . ………11分 因为(0,0,2)A (2,0,0)E (2,2,2).D所以(0,2,2)DE =--，(2,2,2)AM a =- ………12分 因为DE AM ⊥，0DE AM ⋅=所以0a = .………13分 所以2DM = ………14分 法二：（Ⅱ）以E 点为原点，EC 所在直线为x 轴，EB 所在直线为y 轴，过E 做垂直平面BEC 的直线为z 轴，建立空间直角坐标系，则(0,0,0)E ，(0,2,2)A ，(2,0,1)F (2,0,2)D ，1(0,0,1)n 为平面BEC 的法向量， ………7分设2(,,)n x y z 为平面AEF 的法向量，又()()0,2,2,2,0,1EA EF由2200n EA n EF ⎧⋅=⎪⎨⋅=⎪⎩得22020y z x z +=⎧⎨+=⎩取2z =得2(-1,-2,2)n ………9分从而12121222cos ,133n n n n n n ⋅===⨯⋅ ………10分 所以平面AEF 与平面BEC 所成锐二面角的余弦值为23. （Ⅲ）假设在线段CD 存在点M ，设点M 的坐标为(2,0,)a . ………11分因为(0,2,2)A (0,0,0)E (2,0,2)D所以(-2,0,2)DE =-，(2,-2,2)AM a =- ………12分 因为DE AM ⊥，0DE AM ⋅=所以0a = .………13分 所以2DM = ………14分 18（Ⅰ）,1)('-=xe xf 所以切线的斜率()00k f '==又因为()01f =， ……2分 所以切线方程为 1y =. ……3分 （Ⅱ）因为不等式ax x f >)(的解集为P ，且P x x ⊆≤≤}20|{，所以，对任意的]2,0[∈x ，不等式ax x f >)(恒成立， ………4分由ax x f >)(得xe x a <+)1(.当0=x 时， 上述不等式显然成立，故只需考虑]2,0(∈x 的情况. ………5分将xe x a <+)1(变形得1-<xe a x………6分 令1)(-=x e x g x ，2)1()('x e x x g x-= ………7分 令0)('>x g ，解得1>x ；令0)('<x g ，解得.1<x从而()g x 在（0,1）内单调递减，在（1，2）内单调递增. ………8分 当1=x 时，)(x g 取得最小值1-e ，所以实数的取值范围是)1,(--∞e .……9分 （Ⅲ）当1a <-时有一个零点；当 -11a e ≤<- 无零点当1a e =-时有一个零点；当 1a e >- 时有两个零点. ………13分19 （Ⅰ）由已知得解得222b1acb1ac1a b c=⎧⎧=⎪⎪⎪==⎨⎨⎪⎪=⎩=+⎪⎩所以椭圆的E方程为2212xy+=…………4分（Ⅱ）当直线l的斜率不存在时，直线l为x=或x=都有122OPQS∆=⨯=.………6分当直线l的斜率存在时，设直线:(1)l y kx m k=+≠±，由2212y kx mxy=+⎧⎪⎨+=⎪⎩消去y，可得222(12)4220k x kmx m+++-=228816m k∆=-++，由题可知，0∆=，有2221m k=+………8分又y kx mx y=+⎧⎨-=⎩可得(,)11m mPk k--；同理可得(,)11m mQk k-++.由原点O到直线PQ的距离为d=和2PQ m=可得22121OPQmS d PQk∆==-………10分∵2221m k=+，∴22222111OPQm kSk k∆+==--………11分当210k-<，即11k k><-或时，2222132211OPQkSk k∆+==+>--………12分当210k->，即11k-<<时，222213211OPQkSk k∆+==-+--因为2011k<-≤，所以2331k≥-，所以23211OPQSk∆=-+≥-，当且仅当0k=时等号成立. 综上，当0k =时，OPQ ∆的面积存在最小值为1 ………14分20.解：（Ⅰ）数列11,0,22-为单调递增的3阶“Q 数列”； 数列3113,,,8888--为单调递增的4阶“Q 数列”. （答案不唯一） ┄4分 （Ⅱ）设等差数列122018,,,a a a 的公差为d ，0d > 因为1220180a a a +++=，所以12018()201802a a +=.即120180a a +=. 所以10091010+0a a =. 于是100910100,0a a <>. ┄5分 由于0d >，根据“Q 数列”的条件①②得1210091-2a a a +++=，10101011201812a a a +++= ┄6分 两式相减得210091d =.即211009d = . ┄8分 由1201820172018+02a d ⋅=得12017=-2a d ，即12201721009a =-⋅. ┄10分 所以222201712-2019(1)21009100921009n n a n =-+-=⨯⨯(,2018)n n *∈≤N . ┄11分 （Ⅲ）当k n =时，显然102n S =≤成立；当k n <时，根据条件①得 1212()k k k k n S a a a a a a ++=+++=-+++，所以1212k k k k n S a a a a a a ++=+++=+++ . 所以12122k k k k n S a a a a a a ++=+++++++12121k k k n a a a a a a ++≤+++++++=. 所以12k S ≤(1,2,3,,)k n =. ┄13分。