(2020年编辑)世界数学难题

2020-2021初中数学有理数难题汇编含答案(1)一、选择题1．如果||a a =-，下列成立的是（ ）A ．0a >B ．0a <C ．0a ≥D ．0a ≤【答案】D【解析】【分析】绝对值的性质：正数的绝对值等于它本身，负数的绝对值等于它的相反数，0的绝对值是0．【详解】如果||a a =-，即一个数的绝对值等于它的相反数，则0a ≤．故选D ．【点睛】本题考查绝对值，熟练掌握绝对值的性质是解题关键.2．若x ＜2＋|3－x|的正确结果是( ) A ．－1B ．1C ．2x －5D ．5－2x 【答案】C【解析】a = 的化简得出即可.解析：∵x ＜2+|3﹣x|=2352x x x -+-=- .故选D.3．下列等式一定成立的是( )A =B ．11=C 3=±D ．6=-【答案】B【解析】【分析】根据算术平方根、立方根、绝对值的性质逐项判断即可. 【详解】321-=，故错误；B. 11=，故正确；3=， 故错误；D. ()66=--=，故错误；故答案为：B.【点睛】本题考查了算术平方根的概念、立方根的概念、绝对值的性质，解题的关键是熟练掌握其定义和性质.4．在数轴上，实数a ，b 对应的点的位置如图所示，且这两个点到原点的距离相等，下列结论中，正确的是（ ）A ．0a b +=B ．0a b -=C ．a b <D ．0ab > 【答案】A【解析】由题意可知a<0<1<b ，a=-b ，∴a+b=0，a-b=2a<0，|a|=|b|，ab<0，∴选项A 正确，选项B 、C 、D 错误，故选A.5．－6的绝对值是（ ）A ．-6B ．6C ．- 16D ．16 【答案】B【解析】【分析】在数轴上，表示一个数的点到原点的距离叫做这个数的绝对值.【详解】负数的绝对值等于它的相反数，所以-6的绝对值是6故选B【点睛】考点：绝对值.6．下列各数中，最大的数是（ ）A ．12- B ．14 C ．0D ．-2 【答案】B【解析】【分析】将四个数进行排序，进而确定出最大的数即可．【详解】11 2024 -<-<<，则最大的数是14，故选B．【点睛】此题考查了有理数大小比较，熟练掌握有理数大小比较的方法是解本题的关键．7．在数轴上，与原点的距离是2个单位长度的点所表示的数是（）A．2 B．2-C．2±D．1 2±【答案】C【解析】【分析】与原点距离是2的点有两个，是±2．【详解】解：与原点距离是2的点有两个，是±2．故选：C.【点睛】本题考查数轴的知识点，有两个答案．8．数轴上的A、B、C三点所表示的数分别为a、b、1，且|a﹣1|+|b﹣1|＝|a﹣b|，则下列选项中，满足A、B、C三点位置关系的数轴为（）A．B．C．D．【答案】A【解析】【分析】根据绝对值的意义，在四个答案中分别去掉绝对值进行化简，等式成立的即为答案；【详解】A中a＜1＜b，∴|a﹣1|+|b﹣1|＝1﹣a+b﹣1＝b﹣a，|a﹣b|＝b﹣a，∴A正确；B中a＜b＜1，∴|a﹣1|+|b﹣1|＝1﹣a+1﹣b＝2﹣b﹣a，|a﹣b|＝b﹣a，∴B不正确；C中b＜a＜1，∴|a﹣1|+|b﹣1|＝1﹣a+1﹣b＝2﹣b﹣a，|a﹣b|＝a﹣b，∴C不正确；D中1＜a＜b，∴|a﹣1|+|b﹣1|＝a﹣1+b﹣1＝﹣2+b+a，|a﹣b|＝b﹣a，∴D不正确；故选：A．【点睛】本题考查数轴和绝对值的意义；熟练掌握绝对值的意义是解题的关键．9．如图，下列判断正确的是（）A．a的绝对值大于b的绝对值B．a的绝对值小于b的绝对值C．a的相反数大于b的相反数D．a的相反数小于b的相反数【答案】C【解析】【分析】根据绝对值的性质，相反数的性质，可得答案．【详解】解：没有原点，无法判断|a|，|b|，有可能|a|＞|b|，|a|＝|b|，|a|＜|b|．由数轴上的点表示的数右边的总比左边的大，得a＜b，由不等式的性质，得﹣a＞﹣b，故C符合题意；故选：C．【点睛】本题考查了数轴、绝对值、相反数，利用不等式的性质是解题关键，又利用了有理数大小的比较．10．若（x+y﹣1）2+|x﹣y+5|＝0，则x＝（）A．﹣2 B．2 C．1 D．﹣1【答案】A【解析】【分析】由已知等式，利用非负数的性质列出方程组，求出方程组的解得到x即可.【详解】解：∵（x+y﹣1）2+|x﹣y+5|＝0，∴1050 x yx y+-=⎧⎨-+=⎩，解得：23x y =-⎧⎨=⎩， 故选：A.【点睛】本题主要考查了非负数的性质和二元一次方程组的解法，根据两个非负数的和为零则这两个数均为零得出方程组是解决此题的的关键.11．已知a 、b 、c 都是不等于0的数，求abcabca b c abc +++的所有可能的值有()个．A ．1B ．2C ．3D ．4【答案】C【解析】【分析】根据a b c 、、的符号分情况讨论，再根据绝对值运算进行化简即可得．【详解】由题意，分以下四种情况：①当a b c 、、全为正数时，原式11114=+++=②当a b c 、、中两个正数、一个负数时，原式11110=+--=③当a b c 、、中一个正数、两个负数时，原式11110=--+=④当a b c 、、全为负数时，原式11114=----=-综上所述，所求式子的所有可能的值有3个故选：C ．【点睛】本题考查了绝对值运算，依据题意，正确分情况讨论是解题关键．12．下面说法正确的是( )A ．1是最小的自然数；B ．正分数、0、负分数统称分数C ．绝对值最小的数是0；D ．任何有理数都有倒数【答案】C【解析】【分析】0是最小的自然数，属于整数，没有倒数，在解题过程中，需要关注【详解】最小的自然是为0，A 错误；0是整数，B 错误；任何一个数的绝对值都是非负的，故绝对值最小为0，C 正确；0无倒数，D 错误【点睛】本题是有理数概念的考查，主要需要注意0的特殊存在13．如图，数轴上A ，B 两点分别对应实数a ，b ，则下列结论正确的是( )A ．b ＞aB ．ab ＞0C ．a ＞bD ．|a |＞|b |【答案】C【解析】【分析】本题要先观察a ，b 在数轴上的位置，得b ＜-1＜0＜a ＜1，然后对四个选项逐一分析．【详解】A 、∵b ＜﹣1＜0＜a ＜1，∴b ＜a ，故选项A 错误；B 、∵b ＜﹣1＜0＜a ＜1，∴ab ＜0，故选项B 错误；C 、∵b ＜﹣1＜0＜a ＜1，∴a ＞b ，故选项C 正确；D 、∵b ＜﹣1＜0＜a ＜1，∴|b |＞|a |，即|a |＜|b |，故选项D 错误．故选C ．【点睛】本题考查了实数与数轴的对应关系，数轴上右边的数总是大于左边的数．14．如图，数轴上每相邻两点距离表示1个单位，点A ，B 互为相反数，则点C 表示的数可能是（ ）A ．0B ．1C ．3D ．5 【答案】C【解析】【分析】根据相反数的几何意义：在数轴上，一组相反数所表示的点到原点的距离相等，即可确定原点的位置，进而得出点C 表示的数.【详解】∵点A ，B 互为相反数，∴AB 的中点就是这条数轴的原点，∵数轴上每相邻两点距离表示1个单位，且点C 在正半轴距原点3个单位长度， ∴点C 表示的数为3.故选C.【点睛】本题考查了相反数和数轴的知识.利用相反数的几何意义找出这条数轴的原点是解题的关键.15．实数,,a b c 在数轴上的对应点的位置如图所示，若||||a b ，则下列结论中一定成立的是（ ）A ．0b c +>B ．2a c +>C ．1b a <D ．0abc ≥【答案】A【解析】【分析】利用特殊值法即可判断.【详解】∵a<c<b ，||||a b <，∴0b c +>，故A 正确；若a<c<0，则2a c +>错误，故B 不成立； 若0<a<b ，且||||a b <，则1b a>，故C 不成立； 若a<c<0<b ，则abc<0，故D 不成立，故选：A.【点睛】 此题考查数轴上点的正负，实数的加减乘除法法则，熟记计算法则是解题的关键.16．7-的绝对值是 （ ）A ．17-B ．17C ．7D ．7-【答案】C【解析】【分析】负数的绝对值为这个数的相反数.【详解】|-7|=7,即答案选C.【点睛】掌握负数的绝对值为这个数的相反数这个知识点是解题的关键.17．如图，动点P 在平面直角坐标系中按图中箭头所示的方向运动，第1次从原点运动到点()1,1；第二次接着运动到点()2,0；第三次接着运动到点()3,2，按这样的运动规律，经过2019次运动后，动点P 的坐标为（ ）A ．()2019,0B ．()2019,1C ．()2019,2D ．()2020,0【答案】C【解析】【分析】 分析点P 的运动规律，找到循环次数即可．【详解】解：从图象可以发现，点P 的运动每4次位置循环一次．每循环一次向右移动四个单位． ∴2019=4×504+3， 当第504循环结束时，点P 位置在（2016，0），在此基础之上运动三次到（2019，2），故选：C ．【点睛】本题是规律探究题，解题关键是找到动点运动过程中，每运动多少次形成一个循环．18．实数,a b 在数轴上对应点的位置如图所示，则下列结论正确的是（ ）A ．a b <B ．a b <C ．0a b +>D ．0a b -> 【答案】A【解析】【分析】根据数轴得a<0<b ，且a b >，再根据实数的加法法则，减法法则依次判断即可. 【详解】由数轴得a<0<b ，且a b >，∴a+b<0，a-b<0， 故A 正确，B 、C 、D 错误，故选：A.【点睛】此题考查数轴，实数的大小比较，实数的绝对值的性质，加法法则，减法法则.19．若实数a ，b ，c ，d 在数轴上的对应点的位置如图所示，则正确的结论是( )A ．a <-5B ．b +d <0C ．||||a c <D ．c d <【答案】D【解析】【分析】根据数轴得到-5<a<b<0<c<d ，且a d b c >>>，再依次判断各选项即可得到答案.【详解】由数轴得-5<a<b<0<c<d ，且a d b c >>>，∴A 错误；∵b+d>0，故B 错误； ∵a c >，∴C 错误； ∵d c >，c>0，∴c <D 正确，故选：D.【点睛】此题考查数轴上数的大小关系，绝对值的性质，有理数的加法法则.20．若a 与b 互为相反数，则下列式子不一定正确的是（ ）A ．0a b +=B ．=-a bC ．a b =D ．a b = 【答案】C【解析】【分析】依据相反数的概念及性质可确定正确的式子，再通过举反例可证得不一定正确的式子．【详解】解：∵a 与b 互为相反数，∴0a b +=，∴=-a b ， ∴a b =，故A 、B 、D 正确，当1a =时，1b =-，则1=b ，∴a b =；当1a =-时，1b =，则1=b ，∴a b ≠，故C 不一定正确，故选：C ．【点睛】本题考查了相反数的定义．解此题的关键是灵活运用相反数的定义判定式子是否正确．。

2020-2021初中数学代数式难题汇编附答案解析(1)一、选择题1．填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m 的值应是（ ）A ．110B ．158C ．168D ．178【答案】B【解析】根据排列规律，10下面的数是12，10右面的数是14，∵8=2×4−0，22=4×6−2，44=6×8−4，∴m =12×14−10=158.故选C.2．下列计算正确的是（ ）A ．a 2+a 3=a 5B ．a 2•a 3=a 6C ．（a 2）3=a 6D ．（ab ）2=ab 2【答案】C【解析】试题解析：A.a 2与a 3不是同类项，故A 错误；B.原式=a 5，故B 错误；D.原式=a 2b 2，故D 错误；故选C.考点：幂的乘方与积的乘方；合并同类项；同底数幂的乘法．3．下列运算正确的是（ ）．A ．()2222x y x xy y -=--B ．224a a a +=C ．226a a a ⋅=D ．()2224xy x y =【答案】D【解析】【分析】直接利用合并同类项法则以及积的乘方法则、同底数幂的乘法法则、完全平方公式分别化简求出答案．【详解】解：A.、()2222x y x xy y -=-+，故本选项错误；B.、2222a a a +=，故本选项错误；C.、224a a a ⋅=，故本选项错误；D 、 ()2224xy x y =，故本选项正确；故选：D ．【点睛】本题主要考查合并同类项、积的乘方、同底数幂的乘法、完全平方公式，熟练掌握相关的计算法则是解题的关键．4．下列计算正确的是（ ）A ．235x x x +=B ．236x x x =gC ．633x x x ÷=D ．()239x x = 【答案】C【解析】【分析】根据合并同类项的法则，同底数的乘除法以及幂的乘方的运算法则分别求出结果再起先判断即可得解.【详解】A. 2x 与3x 不能合并，故该选项错误；B. 235x x x =g ，故该选项错误；C. 633x x x ÷=，计算正确，故该选项符合题意；D. ()236x x =，故该选项错误.故选C.【点睛】此题主要考查了合并同类项，同底数的乘除法以及幂的乘方的运算，熟练掌握运算法则是解决此题的关键.5．下列各式中，计算正确的是（ ）A ．835a b ab -=B ．352()a a =C ．842a a a ÷=D ．23a a a ⋅= 【答案】D【解析】【分析】分别根据合并同类项的法则、同底数幂的乘法法则、幂的乘方法则以及同底数幂除法法则解答即可．【详解】解：A 、8a 与3b 不是同类项，故不能合并，故选项A 不合题意；B 、()326a a =，故选项B 不合题意；C 、844a a a ÷=，故选项C 不符合题意；D 、23a a a ⋅=，故选项D 符合题意．故选：D ．【点睛】本题主要考查了幂的运算性质以及合并同类项的法则，熟练掌握运算法则是解答本题的关键．6．下列运算正确的是（）A ．336a a a +=B ．632a a a ÷=C ．()235a a a -⋅=-D ．()336a a = 【答案】C【解析】【分析】分别求出每个式子的值，3332a a a +=，633a a a ÷=，()235aa a -⋅=-，()339a a =再进行判断即可.【详解】解：A: 3332a a a +=，故选项A 错；B ：633a a a ÷=，故选项B 错；C ：()235aa a -⋅=-，故本选项正确； D.：()339a a =，故选项D 错误.故答案为C.【点睛】本题考查了同底数幂的乘除，合并同类项，幂的乘方和积的乘方的应用；掌握乘方的概念，即求n 个相同因数的乘积的运算叫乘方，乘方的结果叫做幂；分清()22n n a a -=，()2121n n a a ++-=-.7．计算 2017201817(5)()736-⨯ 的结果是（ ） A ．736- B ．736 C ．- 1 D ．367【答案】A【解析】【分析】根据积的乘方的逆用进行化简运算即可．【详解】2017201817(5)()736-⨯ 20172018367()()736=-⨯20173677()73636=-⨯⨯ 20177(1)36=-⨯ 736=- 故答案为：A ．【点睛】本题考查了积的乘方的逆用问题，掌握积的乘方的逆用是解题的关键．8．观察等式：232222+=-；23422222++=-；2345222222+++=-⋅⋅⋅已知按一定规律排列的一组数：502、512、522、⋅⋅⋅、992、1002．若502a =，用含a 的式子表示这组数的和是（ ）A ．222a a -B ．2222a a --C ．22a a -D ．22a a +【答案】C【解析】【分析】根据题意，一组数：502、512、522、⋅⋅⋅、992、1002的和为250＋251＋252＋…＋299＋2100＝＝a ＋(2＋22＋…＋250)a ，进而根据所给等式的规律，可以发现2＋22＋…＋250＝251－2，由此即可求得答案.【详解】250＋251＋252＋…＋299＋2100＝a ＋2a ＋22a ＋ (250)＝a ＋(2＋22＋…＋250)a ，∵232222+=-， 23422222++=-，2345222222+++=-，…，∴2＋22＋…＋250＝251－2，∴250＋251＋252＋…＋299＋2100＝a ＋(2＋22＋…＋250)a＝a ＋(251－2)a＝a ＋(2 a －2)a＝2a 2－a ，故选C.【点睛】本题考查了规律题——数字的变化类，仔细观察，发现其中哪些发生了变化，哪些没有发生变化，是按什么规律变化的是解题的关键.9．在长方形内，若两张边长分别为和（）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），长方形总未被这两张正方形纸片覆盖的部分用阴影表示，若图1中阴影部分的面积为，图2中阴影部分的面积和为，则关于，的大小关系表述正确的是（ ）A ．B ．C ．D ．无法确定 【答案】A【解析】【分析】 利用面积的和差分别表示出，，利用整式的混合运算计算他们的差即可比较.【详解】 =（AB-a ）·a+（CD-b ）（AD-a ）=（AB-a ）·a+（AD-a ）（AB-b ）=（AB-a ）（AD-b ）+（CD-b ）（AD-a ）=（AB-a ）（AD-b ）+（AB-b ）（AD-a ） ∴-=（AB-a ）（AD-b ）+（AB-b ）（AD-a ）-（AB-a ）·a-（AD-a ）（AB-b ）=（AB-a ）(AD-a-b)∵AD ＜a+b ， ∴-＜0， 故选A.【点睛】此题主要考查此题主要考查整式的运算，解题的关键是熟知整式的乘法法则.10．若35m =，34n =，则23m n -等于（ ） A ．254 B ．6C ．21D ．20 【答案】A【解析】【分析】根据幂的运算法则转化式子，代入数值计算即可．【详解】解：∵35m =，34n =， ∴222233(3)3253544-==÷÷÷==m n m n m n ， 故选：A ．【点睛】本题考查了同底数幂的除法和幂的乘方的逆用，熟练掌握同底数幂的除法和幂的乘方的运算法则是解题的关键．11．计算1.252 017×2?01945⎛⎫ ⎪⎝⎭的值是( ) A ．45 B ．1625 C ．1 D ．-1【答案】B【解析】【分析】根据同底数幂的乘法底数不变指数相加，可得积的乘方，根据积的乘方等于乘方的积，可得答案．【详解】原式=1.252017×（45）2017×（45）2 =（1.25×45）2012×（45）2 =1625． 故选B ．【点睛】本题考查了积的乘方，利用同底数幂的乘法底数不变指数相加得出积的乘方是解题关键．12．5. 某企业今年3月份产值为万元，4月份比3月份减少了10％，5月份比4月份增加了15％，则5月份的产值是（ ）A ．（－10％）（+15％）万元B ．（1－10％）（1+15％）万元C ．（－10％+15％）万元D ．（1－10％+15％）万元【答案】B【解析】列代数式．据3月份的产值是a 万元，用a 把4月份的产值表示出来a （1－10％），从而得出5月份产值列出式子a 1－10％）（1+15％）．故选B ．13．已知：()()22x 1x 32x px q +-=++，则p ，q 的值分别为（ ） A ．5，3B ．5，−3C ．−5，3D ．−5， −3【答案】D【解析】【分析】 此题可以将等式左边展开和等式右边对照，根据对应项系数相等即可得到p 、q 的值．【详解】由于()()2x 1x 3+-=2x 2-6x+x-3=2 x 2-5x-3=22x px q ++， 则p=-5,q=-3,故答案选D.【点睛】本题考查了多项式乘多项式的法则，根据对应项系数相等求解是关键．14．如图，是一块直径为2a ＋2b 的圆形钢板，从中挖去直径分别为2a 、2b 的两个圆，则剩下的钢板的面积为（ ）A ．ab πB ．2ab πC ．3ab πD ．4ab π【答案】B【解析】【分析】剩下钢板的面积等于大圆的面积减去两个小圆的面积,利用圆的面积公式列出关系式,化简即可.【详解】解:S 剩下=S 大圆- 1S 小圆-2S 小圆 =2222a+2b 2a 2b --222πππ（）（）（） =()222a+b -a -b π⎡⎤⎣⎦=2ab π, 故选：B【点睛】此题考查了整式的混合运算,涉及的知识有:圆的面积公式,完全平方公式,去括号、 合并同类项法则,熟练掌握公式及法则是解本题的关键.15．下列计算，正确的是（ ）A ．2a a a -=B ．236a a a =C ．933a a a ÷=D ．()236a a =【解析】A.2a 和a,和不能合并,故本选项错误;B.2356a a a a ⋅=≠ ,故本选项错误;C.9363a a a a ÷=≠,和不能合并,故本选项错误;D.()236 a a =,故本选项正确;故选D.16．下列图形都是由同样大小的五角星按照一定规律所组成的，按此规律排列下去，第n 个图形中五角星的个数为（ ）A ．31n -B ．3nC ．31n +D ．32n +【答案】C【解析】【分析】 根据前4个图形中五角星的个数得到规律，即可列式得到答案.【详解】观察图形可知：第1个图形中一共是4个五角星，即4311=⨯+，第2个图形中一共是7个五角星，即7321=⨯+，第3个图形中一共是10个五角星，即10331=⨯+，第4个图形中一共是13个五角星，即13341=⨯+，L ，按此规律排列下去，第n 个图形中一共有五角星的个数为31n +，故选：C.【点睛】此题考查图形类规律的探究，观察图形得到五角星的个数的变化规律并运用解题是关键.17．若多项式x 2+mx +4能用完全平方公式分解因式，则m 的值可以是（ ） A ．4B ．﹣4C ．±2D ．±4【答案】D【解析】【分析】利用完全平方公式因式分解2222=()a ab b a b ±+±计算即可．解：∵x2+mx+4＝（x±2）2，即x2+mx+4＝x2±4x+4，∴m＝±4．故选：D．【点睛】本题要熟记完全平方公式，尤其是两种情况的分类讨论．18．有两个正方形A，B，现将B放在A的内部得图甲，将A，B并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和12，则正方形A，B的面积之和为（）A．7 B．12 C．13 D．25【答案】C【解析】【分析】设正方形A的边长为a，正方形B的边长为b，根据图形列式整理得a2＋b2−2ab＝1，2ab ＝12，求出a2＋b2即可．【详解】解：设正方形A的边长为a，正方形B的边长为b，由图甲得：a2−b2−2（a−b）b＝1，即a2＋b2−2ab＝1，由图乙得：（a＋b）2−a2−b2＝12，即2ab＝12，所以a2＋b2＝13，即正方形A，B的面积之和为13，故选：C.【点睛】本题主要考查了完全平方公式在几何图形中的应用，解题的关键是根据图形列出算式．19．已知多项式x-a与x2+2x-1的乘积中不含x2项，则常数a的值是（）A．-1 B．1 C．2 D．-2【答案】C【解析】分析：先计算（x﹣a）（x2+2x﹣1），然后将含x2的项进行合并，最后令其系数为0即可求出a的值．详解：（x﹣a）（x2+2x﹣1）=x3+2x2﹣x﹣ax2﹣2ax+a=x 3+2x 2﹣ax 2﹣x ﹣2ax +a=x 3+（2﹣a ）x 2﹣x ﹣2ax +a令2﹣a =0，∴a =2．故选C ．点睛：本题考查了多项式乘以多项式，解题的关键是熟练运用运算法则，本题属于基础题型．20．小明在利用完全平方公式计算一个二项整式的平方时，不小心用墨水把最后一项染黑了，得到正确的结果变为2412a ab -+（ ），你觉得这一项应是（ ）A ．23bB ．26bC ．29bD ．236b 【答案】C【解析】【分析】根据完全平方公式的形式（a±b ）2=a 2±2ab+b 2可得出缺失平方项．【详解】根据完全平方的形式可得，缺失的平方项为9b 2故选C ．【点睛】本题考查了整式的加减及完全平方式的知识，掌握完全平方公式是解决本题的关键．。

2020年高考数学结束，“金字塔”难倒一大片，考生：比“一朵云”都难高考的第一天就在不知不觉中过去了，很多考生在上午考完语文时还比较开心，但当他们走出数学考场时就开始欲哭无泪了。

纷纷表示：去年的“一朵云”、“维纳斯”还没有今年的“金字塔”难啊！2020年高考数学结束，“金字塔”难倒一大片，考生：比“一朵云”都难！那我们先来回顾一下去年的“一朵云”数学试题：当初2019届的高考生看了这道题，反正无从下手，但2020届的高考生在去年还是准高三学生时做起来并不难。

只不过需要仔细的阅读题目，并且详细的作答。

再来回顾一下去年的“断臂维纳斯”数学试题：这道题虽然是一道选择题，但从题目的长度就能侧面反应出来它有多难。

对于美术生而言就没有什么难度了，毕竟当年画了无数次维纳斯。

但其实仔细阅读题目之后就会发现它跟维纳斯的关系并不大，学生们只要采用排除法，果断选择B就对了。

重点：为今年的全国数学卷“金字塔”点赞！看了一下考生们对2020年数学全国1卷的一些评论发现，大家都在猜测：“去年考维纳斯、一朵云，今年考金字塔，明年是不是该考米开朗基罗的大卫像或者埃菲尔铁塔了？”不过有不少的学生表示这道数学题其实难度不大，并不用太过惊奇。

除了第一页的选择题难度较低，第二页开始题目就开始有难度了。

很多考生走出考场都是笑着的，看来今年的全国1卷深得人心呀！不得不说，今年的全国1卷虽然题目新颖，但好在没有翻车。

填空题的题型到是规规矩矩，几乎考生们平时做真题都能做到相同类型的题目，对于成绩一般的考生而言，这也是能够获得分数的。

但一些答不出答案，企图得步骤分的学渣做填空题就没这么容易了。

接下来就是重头戏解答题，数学解答题对于很多考生而言都是“送分题”，只要按着平时做题那样一步一步写出步骤来，哪怕是最终结果不正确，也可以获得相应的步骤分。

要是多注意一下全国1卷的选答题才会觉得真正有难度的都是压轴题，不过选答题是为了和普通学生拉开差距，是为了选拔更高层次人才而出的题目，所以啊，绝大多数考生不会做也是情有可原的。

2020年六年级数学-六年级数学易错题难题综合训练题一、培优题易错题1．纽约、悉尼与上海的时差如下表（正数表示同一时刻比上海时间早的时数，负数表示同一时刻比上海晚的时数）：城市悉尼纽约时差/时+2-121日上午10时，悉尼时间是________.（2）上海、纽约与悉尼的时差分别为________（正数表示同一时刻比悉尼时间早的时数，负数表示同一时刻比悉尼晚的时数）.（3）王老师2018年9月1日，从纽约Newwark机场，搭乘当地时间上午10:45的班机，前往上海浦东国际机场，飞机飞行的时间为14小时55分钟，问飞机降落上海浦东国际机场的时间.【答案】（1）12（2）-2，-14（3）解：10时45分+14时55分+12时=37时40分.故飞机降落上海浦东国际机场的时间为2018年9月2日下午1:40【解析】【解答】（1）10+（+2）=12时，即当上海是10月1日上午10时，悉尼时间是12时.（ 2 ）12-10=2；-12-2=-14；故上海、纽约与悉尼的时差分别为-2，-14.【分析】（1）根据表格得到悉尼时间是10+（+2）；（2 ）由表格得到上海与悉尼的时差是2，纽约与悉尼的时差-12-2；（3）根据题意得到10时45分+14时55分+12时，得到飞机降落上海浦东国际机场的时间.2．某手机经销商购进甲，乙两种品牌手机共 100 部.（1）已知甲种手机每部进价1500 元，售价2000 元；乙种手机每部进价3500 元，售价4500 元；采购这两种手机恰好用了 27 万元 .把这两种手机全部售完后，经销商共获利多少元？（2）已经购进甲，乙两种手机各一部共用了5000 元，经销商把甲种手机加价50%作为标价，乙种手机加价 40%作为标价.从 A，B 两种中任选一题作答：A：在实际出售时，若同时购买甲，乙手机各一部打九折销售，此时经销商可获利1570 元.求甲，乙两种手机每部的进价.B：经销商采购甲种手机的数量是乙种手机数量的 1.5 倍.由于性能良好，因此在按标价进行销售的情况下，乙种手机很快售完，接着甲种手机的最后10 部按标价的八折全部售完.在这次销售中，经销商获得的利润率为 42.5%.求甲，乙两种手机每部的进价.【答案】（1）解：设购进甲种手机部，乙种手机部，根据题意，得解得：元.答：销商共获利元.（2）解：A: 设每部甲种手机的进价为元，每部乙种手机的进价元，根据题意，得解得：答：求甲，乙两种手机每部的进价分别为：3000元，2000元.B:乙种手机：部，甲种手机部，设每部甲种手机的进价为元，每部乙种手机的进价元，根据题意，得解得：答：求甲，乙两种手机每部的进价分别为：2000元，3000元.【解析】【分析】（1）甲的单价乘以部数加上乙的单价乘以部数等于总数，根据题意列出，然后解方程得到结果。

全世界最难的数学题历史上最难的数学问题之一是“希尔伯特的第十问题”，它是大卫·希尔伯特在1900年提出的23个问题之一。

该问题问的是：是否存在一个通用的算法，能够判断任何给定的多项式方程式是否有整数解。

然而，在1970年，这个问题被证明是无解的。

这意味着没有一个通用的算法可以决定每一个多项式的可解性。

这个结果是由苏联数学家尤里·马蒂亚谢维奇和美国数学家朱莉娅·罗宾逊以及德国数学家希尔伯特·普特拿姆和马丁·戴维斯共同提出的。

除此之外，有一组世界上最难并且最有名的数学问题通常被称为“米勒尼夫挑战”，即“千禧年大奖难题”。

这是七个数学问题，分别是：1. 庞加莱猜想（已解决）- 关于在没有穿孔的情况下将三维空间闭合成一个连续的表面的问题。

格里戈里·佩雷尔曼在2003年解决了这个问题。

2. 黎曼猜想- 断言所有具有某种性质的复数的黎曼ζ函数非平凡零点都具有实部为1/2。

这个猜想至今未证明。

3. P vs NP问题- 关于计算机科学中的问题分类和计算难度的问题。

4. 纳维-斯托克斯方程的存在和光滑性- 涉及流体力学中描述流体内部运动的方程组。

5. 杨-米尔斯理论- 物理学理论，其中的数学问题涉及理解空间中的量子场。

6. 霍奇猜想- 关于代数几何中复代数簇上的某些主要类的理论。

7. 伯奇和斯维尼顿-迪耶尔猜想- 泛称一系列关于算术代数几何中的问题。

这些问题大多未解决，提出的目的是为了激励数学领域的进步和解决重要的理论问题。

对于任何一个能成功解决这些千禧年大奖难题的人，克莱数学研究所（Clay Mathematics Institute，CMI）将颁发一百万美元的奖金。

2020年全国一卷数学金字塔解析一、前言2020年全国一卷数学试卷一直备受瞩目，其中数学金字塔题更是考生们关注的焦点。

本文将对这一题型进行深入分析，并提供解题技巧，帮助考生更好地应对这一挑战。

二、金字塔题目分析金字塔题是数学试卷中常见的题型，题目呈金字塔状排列，要求从顶部到底部依次推理，填入合适的数字。

这一题型考查考生对数学逻辑推理能力的掌握程度，也要求考生具备灵活运用数学知识和解题方法的能力。

2020年全国一卷数学金字塔题一共有3道题，分别是概率统计、空间几何和复数题型。

这三道题目在难度和考点上各有特色，需要考生结合自己的数学基础和解题经验进行分析和解答。

三、解题技巧共享1. 提炼关键信息在做金字塔题时，首先要仔细阅读题目，提炼出关键信息。

理清题目的逻辑关系，明确从顶部到底部的思路，有助于准确推导出正确的结果。

2. 灵活运用数学知识金字塔题考查的不仅是推理能力，更需要考生熟练掌握各种数学知识，并能够将其灵活运用到解题过程中。

因此在平时的学习中，要多做各种类型的数学题目，加强对数学知识的掌握和理解。

3. 深入理解解题思路金字塔题的解题思路往往是层层递进的，要求考生具备一定的逻辑思维能力。

在平时的学习中，要培养自己的逻辑思维能力，多进行逻辑推理训练，提高解题的准确度和速度。

四、具体题目解析1. 概率统计题这些题目主要考查考生对概率与统计知识的掌握，要求考生根据题目信息，进行推理和计算。

在解答此类题型时，考生要深入理解题目背后的统计规律，有针对性地选择解题方法，确保解题的准确性。

2. 空间几何题空间几何题通常涉及立体图形或者空间关系的推理，考查考生在空间几何方面的综合运用能力。

在解答此类题型时，考生要根据题目所给信息，细致地进行测量和计算，注意立体图形的旋转、平移等变化，确保推理的准确性。

3. 复数题复数题主要考查考生对复数运算与性质的掌握，要求考生能够根据题目信息进行复数的推理与运算。

在解答此类题型时，考生要灵活运用复数的运算性质，熟练掌握复数的乘法、除法等运算方法，确保解题的准确性。

2020塞尔维亚数学奥林匹克1. 求所有首一的多项式P x (), 使得-P x ()12可以被+P x (1)整除.2. 给定一个至少有5个顶点的多面体, 且每个顶点恰与3条边相连. 证明, 可以在每个顶点上标记一个有理数, 且满足如下两个条件:(i)至少有一个顶点上标记的数为2020.(ii)对每个面, 这个面上所有顶点上所标记数字的乘积为1.3. 给定△ABC, 在射线BA 上取点D, 射线AB 上取点E, 使得AD ＝AC, BE ＝BC. △DBC 和△EAC 的外接圆再次相交于点X, △DEC 和△ABC 外接圆再次相交于点Y. 若DY ＋EY ＝2XY, 求∠ACB 大小.第一天第二天4. 如图, 梯形ABCD中, 每个角都不为直角. 对角线AC和BD交于E. 作AP⊥BC于P, BQ⊥AD于Q. 过C,E,Q的圆与过D,E,P的圆交于点F.求证: AP, BQ, EF要么互相平行,要么交于一点.5. 对自然数n, 设2()v n 表示满足0,2|k k n ≥的最大自然数k. 若函数**:f →满足如下两个条件: (1)对任意*,()3x f x x ∈≤. (2)对*22,,(()())()x y v f x f y v x y ∀∈+=+. 证明: 对*a ∀∈, 有且仅有一个正整数x, 使得()3f x a =.6. 给定一个正整数k, 将n 个硬币分成若干堆, 并将这些硬币堆从左往右排成一列.(每堆可以有多个硬币)接下来, 在如下两种操作方式中任选一种进行操作:(i) 找到两个非空的硬币堆, 将其中一堆的所有硬币移至另一堆.(ii)找到一个至少有2个硬币的硬币堆, 从中选出两枚硬币,将其中一枚移至其左侧第k 堆, 再将另一枚移至其右侧第k 堆.(空堆也算)这样我们就完成了一步. 随后我们继续从以上两种操作中任选一种进行下去,直到无法进行操作为止.(1)若n ≤k ＋1, 证明我们只能进行有限步操作.(2) 当k 为何值时, 我们可以找到正整数n, 并以某种方式将这n 枚硬币分堆, 使得我们可以进行无限次操作?。

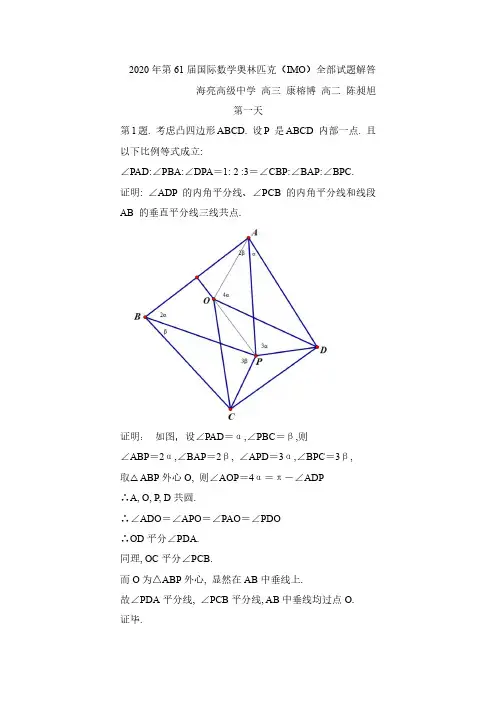
2020年第61届国际数学奥林匹克（IMO）全部试题解答海亮高级中学高三康榕博高二陈昶旭第一天第1题. 考虑凸四边形ABCD. 设P 是ABCD 内部一点. 且以下比例等式成立:∠PAD:∠PBA:∠DPA＝1: 2 :3＝∠CBP:∠BAP:∠BPC.证明: ∠ADP 的内角平分线、∠PCB 的内角平分线和线段AB 的垂直平分线三线共点.证明：如图，设∠PAD＝α,∠PBC＝β,则∠ABP＝2α,∠BAP＝2β, ∠APD＝3α,∠BPC＝3β,取△ABP外心O, 则∠AOP＝4α＝π－∠ADP∴A, O, P, D共圆.∴∠ADO＝∠APO＝∠PAO＝∠PDO∴OD平分∠PDA.同理, OC平分∠PCB.而O为△ABP外心, 显然在AB中垂线上.故∠PDA平分线, ∠PCB平分线, AB中垂线均过点O.证毕.第2题. 设实数a, b, c, d 满足a ≥b ≥c ≥d > 0, 且 a + b + c + d = 1. 证明:(234)1a b c d a b c d a b c d +++<. 证明: 由加权AM －GM 不等式, 我们有2222a b c d a b c d a a b b c c d d a b c d <⋅+⋅+⋅+⋅=+++ 故只需证明22223(234)()()cyca b c d a b c d a ++++++<∑ (*)注意到332()36cyc cyc sym cyca a ab abc =++∑∑∑∑, 及32222cyca ab ad a a ++≥∑2232222222cyca b ab b bc bd b a ++++≥∑2222233333cyca cbc ac cd c a +++≥∑22234444cyc a d a b abd acd bcd d a ++++≥∑∴ (*)成立. 故原不等式成立.第3题. 有4n 枚小石子, 重量分别为1, 2, 3, . . . , 4n. 每一枚小石子都染了n 种颜色之一, 使得每种颜色的小石子恰有四枚. 证明: 我们可以把这些小石子分成两堆, 同时满足以下两个条件:• 两堆小石子有相同的总重量;• 每一堆恰有每种颜色的小石子各两枚.证明: 引理:将n 种颜色的点个4个两两分组, 则可取n 组使得每种颜色的点各2个.即证: n 阶4-正则图G(不一定简单)必有2-正则生成子图. n ＝1, G 为v 的2个自环, 成立.设0n n ≤成立, 则01n n =+时:若G 有点含两自环或有两点含4重边, 对其余部分用归纳假设,该部分取1自环或2重边即可.下设无这样的结构.若G 含三重边,设x,y 间有三条边, 且,(,)xu yv G u y v x ∈≠≠. 考虑将x,y 去掉, 并添入边uv 得到图G ’. 由归纳假设, 图G ’有2-正则生成子图, 若该图含添入的边 uv, 删去该边并加入ux, xy, yv 即可. 若不含, 加入xy, xy 即可.下设无三重边.显然G 有圈. 设最小圈为121,,...,t x x x x . 由G 无2自环,3重边知01t n <+, i x 有两边不指向12,,...t x x x . 设这两边指向,i i u v ，以下下标模t.在G 中删去点12,,...t x x x 并加入边1(1)i i i e u v i t +=≤≤得到G’. 由归纳假设, G ’有2-正则子图G 1.对1≤i ≤t, 若1i e G ∈, 则选择G 中的边11,i i i i x u x v ++, 若1i e G ∉, 则选自1i i x x +, 其余边按G 1中边选择, 则选出的边即为G 的2-正则生成子图的边集.结论成立.回到原题. 将重量为{,41}k n k +-的小石子分为一组.(12)k n ≤≤, 由引理可取n 组使每种颜色的小石子恰2个. 这2n 个分为一组, 其余分为一组, 此即满足条件的分法, 命题成立.第二天第4题. 给定整数n > 1. 在一座山上有n2个高度互不相同的缆车车站. 有两家缆车公司A和B, 各运营k辆缆车; 每辆从一个车站运行到某个更高的车站(中间不停留其他车站). A 公司的k辆缆车的k个起点互不相同，k个终点也互不相同, 并且起点较高的缆车，它的终点也较高. B公司的缆车也满足相同的条件. 我们称两个车站被某个公司连接，如果可以从其中较低的车站通过该公司的一辆或多辆缆车到达较高的车站(中间不允许在车站之间有其他移动). 确定最小的正整数k, 使得一定有两个车站被两个公司同时连接.解: 由题意得, 每个缆车与1或2个缆车相连. (否则有两辆缆车起点不同, 终点相同)∴A, B各自的缆车线路图可划分为若干个链.注意到每条链长度大于等于2, 且首尾两点不能作为终点和起点, 故恰有2n k-条链.若21k n n≥-+, 则A最多由n－1条链.由抽屉原理, 其中至少有一条链上有221nnn⎡⎤=+⎢⎥-⎢⎥个点, 设为P. 而B仅有n－1条链, 故P上一定有两个点同时在B 的一条链上, 则这两点可被两个公司同时连接.另一方面, 2k n n=-时, 记2n个车站高度排序为21,2,...n (从低到高)令A的2n n-辆缆车为2(1)i n i i n n→+≤≤-令B的2n n-辆缆车为21(11,|)i i i n n i→+≤≤-/易见此时任两个车站不能被两个公司同时相连.2 min 1k n n∴=-+.第5题. 有一叠n > 1张卡片. 在每张卡片上写有一个正整数. 这叠卡片具有如下性质：其中任意两张卡片上的数的算术平均值也等于这叠卡片中某一张或几张卡片上的数的几何平均值.确定所有的n, 使得可以推出这叠卡片上的数均相等? 解: 设这n 张卡片上的数为1212,,....(...)n n x x x x x x ≤≤. 若12gcd(,,...)1n x x x d =>, 用i x d 代替i x , 不影响结果. 故不妨设12gcd(,,...)1n x x x =.由题意得, 1,2i jx x i j n +∀≤≤≤为代数整数.则2|i j i x x x +⇒模2同余. 又12gcd(,,...)1n x x x =, 故i x 全为奇数.任取一个素数p, p ≥3.记{|1,|},{|1,|}i i i i A x i n p x B x i n p x =≤≤=≤≤/ 则对,,2x y x A y B +∀∈∈不为p 的倍数. 设121(...)2k k i i i x y x x x +=, 则121|(...)2k k i i i x y p x x x +=/ ∴对1,j i j k x B ∀≤≤∈.max 2i i x B x y x ∈+∴≤. 取max ,max i i i i x A x B x x y x ∈∈==, 则max max i i i i x A x B x x ∈∈≤若1n x ≠, 取n x 的奇素因子p, 由12gcd(,,...)1n x x x =知, i ∃, 使|i p x /.取0max{|1,|}i i i i n p x =≤≤/, 由上述结论知0n i x x ≤, 则o n i x x =. 又0|,|i n p x p x /, 矛盾!1n x ∴=. 则1,1i i n x ∀≤≤=.∴对任意n ≥2, 卡片上的所有数均相等.第6题. 证明: 存在正常数c 具有如下性质:对任意整数n > 1, 以及平面上n 个点的集合S, 若S 中任意两点之间的距离不小于1，则存在一条分离S 的直线ℓ, 使得S 中的每个点到直线ℓ 的距离不小于13cn -.(我们称直线ℓ分离点集S, 如果某条以S 中两点为端点的线段与ℓ 相交.)证明: 以每个点为圆心,12为半径作圆, 则这些圆两两公共部分面积为0.引理1: 对凸多边形P, 其内部最多由421s l π++个点在S 中,其中s,l 代表P 的面积和周长. 证明: 如图, 将P 的每条边往外侧平移12, 并以P 上每个点为圆心, 12为半径作圆, 拓展区域面积为124l π+. ∴P 内部最多1422414S l s l πππ+++=+个点. 现在对于一条直线l, 作S 中每个点在l 上的投影. 任取相邻两个投影点, 则这两点连线的中垂线分离点集S, 且所有的到该直线的距离≥12投影点距离.设S 的直径为D, 则可作一个以D 为边长的正方形覆盖S. 由引理1, 122481()D Dn D n π++≥⇒=Ω 设P,Q ∈S, PQ ＝D. 将PQ 作为上述l, 记我们所能做到的使每个点到一条直线的距离均不小于该数的最大值为d.由于仅与夹角有关, 故d 存在.而l 上除P,Q 外有n －2个投影点.2(1)2D D d n n∴≥>-. 又12()D n =Ω, 故12()d n -=Ω. 需证明13()d n -=Ω .取点集S 的凸包P. 若一直线过P 上一点且使得S 中所有点都在该线一侧, 我们认为其亦分离S. 称其为支撑边. 对于任一常数C, 作两条平行的距离为C 的直线, 满足这两条直线分离S. 作他们的垂线l, 设这个带状区域内有m 个S 中的点, 则11c c d m m d≥⇒≥-+. 不妨设(1)d o =, 则可以认为m 远远大于1. 为使m 尽量小, 应取两直线其中之一为支撑边.∴现在对于一条分离S 的直线l, 设l 与P 围成的区域内部有B 个点. P 中与l 距离最近的点到l 距离为0s , 则01s d B ≥+ (以下用≥代表数量级估计) 我们证明d≥从而311D d n D n ≥⋅= 则13()d n -=Ω. 如图, P 夹在这样一个区域里, 取XY 上一点Z, 使得0YZ s =. 过Z 作MN ⊥XY , 点M,N 在以X 为圆心, D 为半径的圆上. 则B ≤YMN 内S 中点的个数.不妨设XY 为x 轴, 对YMN 内任意两点1122(,),(,)x y x y , 221201212||,()()1x x s x x y y -≤-+-≥, 则12||1y y B -≥⇒≤+.而MN =02s d MN∴≥=+由于0(1)s =Θd ∴≥, 则13d n -≥, 即13()d n -=Ω证毕.。

题目：探讨2020中美洲及加勒比数学奥林匹克试解答---1. 引言2020年的中美洲及加勒比数学奥林匹克试解答，是一个备受关注的事件。

在数学领域，这些试题代表着挑战和机遇。

本文将深入探讨这些试题，给您带来一场关于数学奥赛的知识盛宴。

2. 试题概述2020年中美洲及加勒比地区的数学奥林匹克试题，涵盖了代数、几何、概率等多个领域。

每道题目都设计严谨，考察了考生对数学知识的深度和灵活运用能力。

试题内容不仅注重基础知识的考察，更将数学与现实生活相结合，增加了题目的趣味性和挑战性。

3. 题目解析（1）代数题在代数题部分，考生需要熟练运用代数运算、方程式求解等技巧，解决问题。

一道题目要求计算多项式的值，另一道题目则考察了对齐次方程组的解法。

这些题目旨在考察考生对代数知识的掌握情况，并培养其逻辑推理能力。

（2）几何题几何题部分则考察了考生的空间想象能力和几何推理能力。

题目设计涉及了线段、角度、多边形等几何形状，要求考生在解题过程中画出清晰准确的图形，并通过严密的证明、推理解决问题。

（3）概率题概率题部分考察了考生对概率的理解和应用能力。

题目设计涉及了随机事件、概率计算、独立事件等内容，要求考生通过分析情况、计算概率，解决实际问题。

4. 试题意义2020年中美洲及加勒比数学奥林匹克试题的设计，旨在提高学生的数学综合能力，培养他们的逻辑思维和解决问题的能力。

通过解答这些试题，考生不仅能够巩固已学的数学知识，还能够开拓思维，拓展数学视野，提高解决实际问题的能力。

5. 个人观点作为一名数学爱好者，我认为2020年中美洲及加勒比数学奥林匹克试题的设计非常有价值。

这些试题既考察了考生的数学基础知识，又注重了数学在现实生活中的应用。

通过解答这些试题，我深切感受到数学的魅力和实用性，也在实践中不断提高自己的数学素养。

6. 总结2020年中美洲及加勒比数学奥林匹克试题的内容丰富多样，题目设计严谨合理，体现了数学的广度和深度。

解答这些试题不仅有助于考生巩固数学知识，还能够培养他们的逻辑思维和问题解决能力。

2020-2021初中数学命题与证明的难题汇编附答案一、选择题1．下列命题中是假命题的是（ ）．A ．同旁内角互补，两直线平行B ．直线a b ⊥r r，则a 与b 相交所成的角为直角C ．如果两个角互补，那么这两个角是一个锐角，一个钝角D ．若a b ∥，a c ⊥，那么b c ⊥【答案】C【解析】根据平行线的判定，可知“同旁内角互补，两直线平行”，是真命题；根据垂直的定义，可知“直线a b ⊥，则a 与b 相交所成的角为直角”，是真命题； 根据互补的性质，可知“两个角互补，这两个角可以是两个直角”，是假命题；根据垂直的性质和平行线的性质，可知“若a b P ，a c ⊥，那么b c ⊥”，是真命题． 故选C.2．下列命题中①等腰三角形底边的中点到两腰的距离相等②如果两个三角形全等，则它们必是关于直线成轴对称的图形③如果两个三角形关于某直线成轴对称，那么它们是全等三角形④等腰三角形是关于底边中线成轴对称的图形⑤一条线段是关于经过该线段中点的直线成轴对称的图形正确命题的个数是（ ）A ．2个B ．3个C ．4个D ．5个【答案】A【解析】【分析】根据等腰三角形的性质、轴对称图形的定义、全等三角形的判定逐个判断即可．【详解】根据等腰三角形的三线合一可知，底边中点在顶角角平分线上，再根据角平分线的性质可知，其到两腰的距离相等，则命题①正确全等的三角形不一定是成轴对称，则命题②错误成轴对称的两个三角形一定全等，则命题③正确等腰三角形是以底边中线所在直线为对称轴的轴对称图形，则命题④错误成轴对称的图形必须是两个，一个图形只能是轴对称图形，则命题⑤错误综上，正确命题的个数是2个故选：A ．【点睛】本题考查了等腰三角形的性质、轴对称图形的定义、全等三角形的判定等知识点，掌握理解各定义与性质是解题关键．3．“两条直线相交只有一个交点”的题设是（）A．两条直线 B．相交C．只有一个交点 D．两条直线相交【答案】D【解析】【分析】任何一个命题，都由题设和结论两部分组成．题设，是命题中的已知事项，结论，是由已知事项推出的事项．【详解】“两条直线相交只有一个交点”的题设是两条直线相交．故选D．【点睛】本题考查的知识点是命题和定理，解题关键是理解题设和结论的关系.4．下列命题是真命题的是（）A．如果一个数的相反数等于这个数本身，那么这个数一定是0B．如果一个数的倒数等于这个数本身，那么这个数一定是1C．如果一个数的平方等于这个数本身，那么这个数一定是0D．如果一个数的算术平方根等于这个数本身，那么这个数一定是0【答案】A【解析】【分析】根据相反数是它本身的数为0；倒数等于这个数本身是±1；平方等于它本身的数为1和0；算术平方根等于本身的数为1和0进行分析即可．【详解】A、如果一个数的相反数等于这个数本身，那么这个数一定是0，是真命题；B、如果一个数的倒数等于这个数本身，那么这个数一定是1，是假命题；C、如果一个数的平方等于这个数本身，那么这个数一定是0，是假命题；D、如果一个数的算术平方根等于这个数本身，那么这个数一定是0，是假命题；故选A．【点睛】此题主要考查了命题与定理，关键是掌握正确的命题为真命题，错误的命题为假命题．5．下列命题中真命题是（）A2一定成立B．位似图形不可能全等C．正多边形都是轴对称图形D．圆锥的主视图一定是等边三角形【答案】C【解析】【分析】根据二次根式的性质、位似图形的定义、正多边形的性质及三视图的概念逐一判断即可得．【详解】A）2，当a＜0时不成立，假命题；B、位似图形在位似比为1时全等，假命题；C、正多边形都是轴对称图形，真命题；D、圆锥的主视图不一定是等边三角形，假命题，故选C．【点睛】本题考查了真命题与假命题，涉及到二次根式的性质、位似图形、正多边形、视图等知识，熟练掌握相关知识是解题的关键.6．下列命题中正确的是（）．A．所有等腰三角形都相似B．两边成比例的两个等腰三角形相似C．有一个角相等的两个等腰三角形相似D．有一个角是100°的两个等腰三角形相似【答案】D【解析】【分析】根据相似三角形进行判断即可．【详解】解：A、所有等腰三角形不一定都相似，原命题是假命题；B、两边成比例的两个等腰三角形不一定相似，原命题是假命题；C、有一个角相等的两个等腰三角形不一定相似，原命题是假命题；D、有一个角是100°的两个等腰三角形相似，是真命题；故选：D．【点睛】本题考查了命题与定理：判断事物的语句叫命题；正确的命题称为真命题，错误的命题称为假命题；经过推理论证的真命题称为定理．7．下列命题中，是假命题的是（）A．对顶角相等B．同位角相等C．同角的余角相等D．全等三角形的面积相等【答案】B【解析】【分析】根据对顶角得性质、平行线得性质、余角得等于及全等三角形得性质逐一判断即可得答案．【详解】A.对顶角相等是真命题，故该选项不合题意，B.两直线平行，同位角相等，故该选项是假命题，符合题意，C.同角的余角相等是真命题，故该选项不合题意，D.全等三角形的面积相等是真命题，故该选项不合题意．故选：B ．【点睛】本题主要考查了命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．8．已知：ABC ∆中，AB AC =，求证：90O B ∠<，下面写出可运用反证法证明这个命题的四个步骤：①∴180O A B C ∠+∠+∠>，这与三角形内角和为180O 矛盾,②因此假设不成立．∴90O B ∠<,③假设在ABC ∆中，90O B ∠≥,④由AB AC =，得90O B C ∠=∠≥，即180O B C ∠+∠≥．这四个步骤正确的顺序应是（ ）A ．③④②①B ．③④①②C ．①②③④D ．④③①②【答案】B【解析】【分析】根据反证法的证明步骤“假设、合情推理、导出矛盾、结论”进行分析判断即可.【详解】题目中“已知：△ABC 中，AB=AC ，求证：∠B ＜90°”，用反证法证明这个命题过程中的四个推理步骤：应该为：(1)假设∠B ≥90°，(2)那么，由AB=AC ，得∠B=∠C ≥90°，即∠B+∠C ≥180°，(3)所以∠A+∠B+∠C ＞180°，这与三角形内角和定理相矛盾，(4)因此假设不成立．∴∠B ＜90°，原题正确顺序为：③④①②，故选B ．【点睛】本题考查反证法的证明步骤，弄清反证法的证明环节是解题的关键.9．下列命题中:①等腰三角形底边的中点到两腰的距离相等；②等腰三角形的高、中线、角平分线互相重合； ③若ABC V 与'''A B C V 成轴对称，则ABC V 一定与'''A B C V 全等；④有一个角是60度的三角形是等边三角形；⑤等腰三角形的对称轴是顶角的平分线．正确命题的个数是（ ）A ．2B ．3C ．4D ．5【答案】A【解析】【分析】利用轴对称的性质、等腰三角形的性质、等边三角形的判定等知识分别判断后即可确定正确的选项．【详解】解:①等腰三角形底边的中点到两腰的距离相等；正确；②等腰三角形的底边上的高、底边上的中线、顶角的平分线互相重合；不正确: ③若ABC V 与'''A B C V 成轴对称，则ABC V 一定与'''A B C V 全等；正确； ④有一个角是60度的等腰三角形是等边三角形；不正确；⑤等腰三角形的对称轴是顶角的平分线所在的直线，不正确．正确命题为:2①③，个；故选：A【点睛】本题考查了命题与定理的知识，解题的关键是了解轴对称的性质、等腰三角形的性质、等边三角形的判定等知识，属于基础知识，难度不大．10．下列命题中，是真命题的是（ ）A ．若a b =，则a b =B ．若0a b +>，则a ，b 都是正数C ．两条直线被第三条直线所截，同位角相等D ．垂直于同一条直线的两条直线平行【答案】D【解析】【分析】正确的命题是真命题，根据定义依次判断即可得到答案.【详解】A. 若a b =，则a b =±，故A 错误；B. 若0a b +>，则a ，b 中至少有一个数是正数，且正数绝对值大于负数的绝对值，故B 错误；C. 两条平行线被第三条直线所截，同位角相等，故C 错误；D. 垂直于同一条直线的两条直线平行正确，故选：D.【点睛】此题考查判断真假命题，正确掌握命题的分类并理解事件的正确与否是解题的关键.11．下面命题的逆命题正确的是（ ）A ．对顶角相等B ．邻补角互补C ．矩形的对角线互相平分D ．等腰三角形两腰相等【答案】D【解析】【分析】先分别写出四个命题的逆命题，然后利用对顶角的定义、邻补角的定义、矩形的判断和等腰三角形的判定方法对各命题的真假进行判断．【详解】解：A.对顶角相等的逆命题为相等的角为对顶角，此逆命题为假命题；B.邻补角互补的逆命题为互补的角为邻补角，此逆命题为假命题；C.矩形的对角线互相平分的逆命题为对角线互相平分的四边形为矩形，此逆命题为假命题；D.等腰三角形两腰相等的逆命题为两边相等的三角形为等腰三角形，此逆命题为真命题．故答案为D．【点睛】本题考查了命题与定理,掌握举出反例法是判断命题的真假的重要方法．12．下列命题正确的是( )A．在同一平面内，可以把半径相等的两个圆中的一个看成是由另一个平移得到的. B．两个全等的图形之间必有平移关系.C．三角形经过旋转，对应线段平行且相等.D．将一个封闭图形旋转，旋转中心只能在图形内部.【答案】A【解析】【分析】根据平移的性质：平移后图形的大小、方向、形状均不发生改变结合选项即可得出答案．【详解】解：A、经过旋转后的图形两个图形的大小和形状也不变，半径相等的两个圆是等圆，圆还具有旋转不变性，故本选项正确；B、两个全等的图形位置关系不明确，不能准确判定是否具有平移关系，错误；C、三角形经过旋转，对应线段相等但不一定平行，所以本选项错误；D、旋转中心可能在图形内部，也可能在图形边上或者图形外面，所以本选项错误.故选：A.【点睛】本题考查平移、旋转的基本性质，注意掌握①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．13．已知命题：等边三角形是等腰三角形．则下列说法正确的是（）A．该命题为假命题 B．该命题为真命题C．该命题的逆命题为真命题 D．该命题没有逆命题【答案】B【解析】分析：首先判断该命题的正误，然后判断其逆命题的正误后即可确定正确的选项．详解：等边三角形是等腰三角形，正确，为真命题；其逆命题为等腰三角形是等边三角形，错误，为假命题，故选：B．点睛：本题考查了命题与定理的知识，解题的关键是能够写出该命题的逆命题，难度不大．14．下列命题是真命题的是（）A．若x＞y，则x2＞y2B．若|a|=|b|，则a=b C．若a＞|b|，则a2＞b2D．若a＜1，则a＞1a【答案】C【解析】【分析】根据实数的乘方，绝对值的性质和倒数的意义等，对各选项举反例分析判断后利用排除法求解．【详解】A. x＞y，如x=0，y=-1，02<(-1)2，此时x2<y2，故A选项错误；B. |a|=|b|，如a=2，b=-2，此时a≠b，故B选项错误；C. 若a＞|b|，则a2＞b2，正确；D. a＜1，如a=-1，此时a=1a，故D选项错误，故选C.【点睛】本题考查了命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题，本题主要利用了实数的性质．15．下列说法正确的是（）A．两锐角分别相等的两个直角三角形全等B．两条直角边分别相等的两直角三角形全等C．一个命题是真命题，它的逆命题一定也是真命题D．经过旋转，对应线段平行且相等【答案】B【解析】【分析】A,B利用斜边和一条直角边对应相等的两个直角三角形全等，判定直角三角形全等时，也可以运用其它的方法．C利用命题与定理进行分析即可，D.利用旋转的性质即可解答；【详解】A、两个锐角分别相等的两个直角三角形不一定全等，故A选项错误；B、根据SAS可得，两条直角边分别相等的两个直角三角形全等，故B选项正确；C、一个命题是真命题，它的逆命题不一定是真命题．故C选项错误；D、经过旋转，对应线段相等，故D选项错误；故选：B．【点睛】此题考查命题与定理，解题关键在于掌握判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．16．下列四个命题：①两直线平行，内错角相等；②对顶角相等；③等腰三角形的两个底角相等；④菱形的对角线互相垂直，其中逆命题是真命题的是（）A．①②③④B．①③④C．①③D．①【答案】C【解析】【分析】首先写出各个命题的逆命题，然后进行判断即可．【详解】①两直线平行，内错角相等；其逆命题：内错角相等，两直线平行，是真命题；②对顶角相等，其逆命题：相等的角是对顶角，是假命题；③等腰三角形的两个底角相等，其逆命题：有两个角相等的三角形是等腰三角形，是真命题；④菱形的对角线互相垂直，其逆命题：对角线互相垂直的四边形是菱形，是假命题；故选C．【点睛】本题考查了写一个命题的逆命题的方法，真假命题的判断，弄清命题的题设与结论，掌握相关的定理是解题的关键.17．已知下列命题：①若a＞b，则ac＞bc；②若a=1；③内错角相等；④90°的圆周角所对的弦是直径．其中原命题与逆命题均为真命题的个数是（）A．1个B．2个C．3个D．4个【答案】A【解析】【分析】先对原命题进行判断，再判断出逆命题的真假即可．【详解】解:①若a＞b，则ac＞bc是假命题，逆命题是假命题；②若a=1是真命题，逆命题是假命题；③内错角相等是假命题，逆命题是假命题；④90°的圆周角所对的弦是直径是真命题，逆命题是真命题；其中原命题与逆命题均为真命题的个数是1个；故选A ．点评：主要考查命题与定理，用到的知识点是互逆命题的知识，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题，判断命题的真假关键是要熟悉课本中的性质定理．18．下列命题的逆命题不正确．．．的是（ ） A ．相等的角是对顶角B ．两直线平行，同旁内角互补C ．矩形的对角线相等D ．平行四边形的对角线互相平分 【答案】C【解析】【分析】首先写出各个命题的逆命题，然后进行判断即可．【详解】A 、逆命题是：对顶角相等．正确；B 、逆命题是：同旁内角互补，两直线平行，正确；C 、逆命题是：对角线相等的四边形是矩形，错误；D 、逆命题是：对角线互相平分的四边形是平行四边形，正确．故选：C ．【点睛】本题主要考查了写一个命题的逆命题的方法，首先要分清命题的条件与结论．19．下列命题的逆命题成立的有( )①勾股数是三个正整数 ②全等三角形的三条对应边分别相等③如果两个实数相等，那么它们的平方相等 ④平行四边形的两组对角分别相等 A ．1个B ．2个C ．3个D ．4个【答案】B【解析】【分析】先写出每个命题的逆命题，再分别根据勾股数的定义、三角形全等的判定、平方根的定义、平行四边形的判定逐个判断即可．【详解】①逆命题：如果三个数是正整数，那么它们是勾股数反例：正整数1,2,3，但222123+?，即它们不是勾股数，则此逆命题不成立 ②逆命题：三条对应边分别相等的两个三角形全等由SSS 定理可知，此逆命题成立③逆命题：如果两个实数的平方相等，那么这两个实数相等反例：222(2)4=-=，但22≠-，则此逆命题不成立④逆命题：两组对角分别相等的四边形是平行四边形由平行四边形的判定可知，此逆命题成立综上，逆命题成立的有2个故选：B．【点睛】本题考查了命题的相关概念、勾股数的定义、三角形全等的判定、平方根的定义、平行四边形的判定，正确写出各命题的逆命题是解题关键．20．下列命题是假命题的是( )A．对顶角相等B．两直线平行，同旁内角相等C．平行于同一条直线的两直线平行D．同位角相等，两直线平行【答案】B【解析】解：A．对顶角相等是真命题，故本选项正确，不符合题意；B．两直线平行，同旁内角互补，故本选项错误，符合题意；C．平行于同一条直线的两条直线平行是真命题，故本选项正确，不符合题意；D．同位角相等，两直线平行是真命题，故本选项正确，不符合题意．故选B．。