第三章模拟线性调制

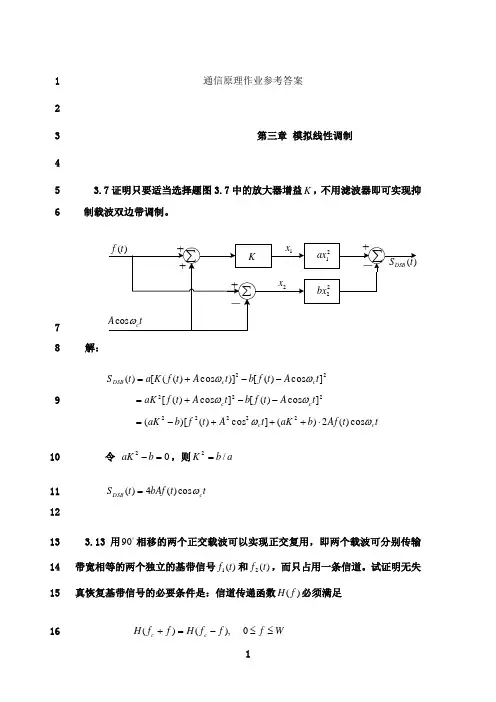
通信原理作业参考答案 12 第三章 模拟线性调制34 3.7证明只要适当选择题图3.7中的放大器增益K ，不用滤波器即可实现抑5 制载波双边带调制。

67 解：8tt Af b aK t A t f b aK t A t f b t A t f aK t A t f b t A t f K a t S c c c c c c DSB ωωωωωωcos )(2)(]cos )()[(]cos )([]cos )([]cos )([)]cos )(([)(2222222222⋅+++-=--+=--+=9令 02=-b aK ，则a b K /2=10 t t bAf t S c DSB ωcos )(4)(=1112 3.13 用 90相移的两个正交载波可以实现正交复用，即两个载波可分别传输13 带宽相等的两个独立的基带信号)(1t f 和)(2t f ，而只占用一条信道。

试证明无失14 真恢复基带信号的必要条件是：信道传递函数)(f H 必须满足15W f f f H f f H c c ≤≤-=+0),()(16证明：)(]sin )([)(]cos )([)(21t h t t f t h t t f t S c c *+*=ωω17)]}()([)()(){(21)(2211c c c c F F j F F H S ωωωωωωωωωω--++++-=18 以t t C c d ωcos )(=相干解调，输出为 19 )(*)()(t C t S t S d p =20)]}()2([)2()(){(41)]}2()([)()2(){(41)]()([21)(22112211ωωωωωωωωωωωωωωωωωωωωωF F j F F H F F j F F H S S S c c c c c c c c p -++++++--++--=++-= 21选择适当滤波器，滤掉上式中c ωω2±项，则22)]()()[(4)]()()[(41)(21c c c c d H H F jH H F S ωωωωωωωωωωω+--+++-=23 要无失真恢复基带信号，必须24⎩⎨⎧=++-+=-常数)()()()(c c c c H H H H ωωωωωωωω 25此时可恢复)(1t f 。

由于双边带信号中的任一个边带都包含调制信号的全部信息，因此就信息传输的目的而言，只要传送其中的一个边带就足够了。

这种只传送一个边带的通信方式称为单边带通信。

相应地，只产生一个边带的调制方式称为单边带调制。

单边带调制的方法主要有滤波法、相移法和修正相移法。

3.3单边带调制不论单边带调制 只产生调幅波的一个边带的调制方式。

它既有抑制载波双边带调制的节约发射功率的优点，又减小了占用信道带宽。

DSB 它上下两个边带携带的是相同的信息，我们只需要其中一个就可以识取我们的基带信号，起带宽比起。

单边带调制有两种实现方法滤波法和相移法。

1. 用滤波法形成单边带信号产生一个抑制载波的双边带信号以后，通过滤波器滤除它的上边带或者下边带就可以得到单边带信号。

滤波法是最简单的也是最常用的方法之一。

因此，用滤波法产生单边带信号就是用基带信号乘以一个载波c （t ），得到一个抑制载波的双边带信号，然后用一个滤波器或者说传递函数滤除一个上边带或者下边带，就可以得到我们需要的单边带调制信号。

图中HSSB 为单边带滤波器的传递函数。

因为边带可取上边带，也可取下边带，所以传递函数有2种形式。

上边带滤波器和下边带滤波器的传递函数分别为我们看一下它的频谱变化的特征，如果我们选择了这样一个滤波器，使其下边带阻断，。

这就是我们通过滤波法形成的一个单边带信号。

再来看看用滤波法产生单边带信号的特点，当然，首先的一个就是简单，只需要构造一个所需要的滤波器，但同时，它的缺点也很明显，就是对滤波器特性要求非常严格，在图上我们看的是理想的滤波器，但像这样没有过渡带的滤波器是不可能存在的，滤波器的频谱没有这样垂直的，普通滤波器的导通和阻断都有一个斜的过渡带，也就是它的导通和阻断不是这样垂直的分隔，而是有一个斜的过渡带，有了过渡带后，这样必然会将上边带内容损耗一点，而下边带内容则包含了一点，显然滤除的信号就不能充分反映基带信号的特征。

因此，用滤波法产生单边带信号的时候就必然要考虑到一个过渡带△f 。

第3章模拟线性调制系统 3.1 概述3.1.1 调制的目的.频谱搬移 － 适应信道传输、合并多路信号； 提高抗干扰性。

3.1.2 基本概念基带信号：由消息直接变换成的电信号。

频带从零频开始，低频端谱能量大，不宜在信道中远距离传输。

调 制：按调制信号（基带信号）的变化规律去改变载波某些参数的过程叫调制。

（频谱搬迁）调制信号：f(t)载 波：c(t)=Acos[ωc t+θ0] 已调信号：s(t)=m (t)·c(t) =A(t)cos[ωc t+φ(t)+θ0] 模拟调制：当调制信号为模拟基带信号m(t)，载波为连续的正弦或余弦高频信号c(t)=Acos[ωc t+θ0]时，称模拟调制。

3.1.3 调制的分类数字调制3.2 双边带调幅一. 常规调幅１． 时域表达式：调制信号f(t)（平均值)(t f ＝0）加直流后对载波幅度调制（称标准或完全调幅）s AM (t)= [A 0+f(t)]·cos[ωc t+θc ]ωc 载波角频率， θc 载波初相位()()()()()()()()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧成比例变化随常数，调相：成比例变化随常数，调频：非线性调制角度调制为常数成比例变化随线性调制幅度调制模拟调制t f t t A t f dt t d t A VSB SSB DSBAM t t f t A φφφ)(,波形图3-1当调制信号f(t)为单频信号时：f(t)= A m cos(ωm t+θm ) 则： s AM (t)= [A 0+ A m cos(ωm t+θm)]cos[ωc t+θc ]= A 0 [1+βAM cos(ωm t+θm)]cos[ωc t+θc ]A A mAM =β称调幅指数，х100%叫调制度 ⎪⎩⎪⎨⎧><=过调幅通常取正常调幅满调幅...1-60%)-30%(...1......1AMβ ２．频域表达式θc =0的时域表达式：s AM (t)= [A 0+ f (t)]cosωc t = A 0 cosωc t+ m (t) cosωc t因m(t) F (ω)A 0 cosωc t [])()(000ωωδωωδπ++-↔A注： ))((21cos )(t j t j c c c e e t f t t f ωωω-+=t j t j c c e t f e t f ωω-+=)(21)(21其付氏变换为因为根据平移故S AM (ω) 的频域表达式为：[])]()([21)()()(00000ωωωωωωδωωδπω++-+++-=F F A S AM 频谱图：()()00ωωω-↔F e t f t j ()()0021ωωωω++-F F [])()(21cos )(00ωωωωω++-↔F F t t f c频谱搬迁到适合通信系统传输的频率范围。

现代通信原理-曹志刚-答案(很重要)通信原理作业参考答案第三章 模拟线性调制3.7证明只要适当选择题图3.7中的放大器增益K，不用滤波器即可实现抑制载波双边带调制。

解：tt Af b aK t A t f b aK t A t f b t A t f aK t A t f b t A t f K a t S c c c c c c DSB ωωωωωωcos )(2)(]cos )()[(]cos )([]cos )([]cos )([)]cos )(([)(2222222222⋅+++-=--+=--+=令2=-b aK ，则ab K/2=t t bAf t S cDSB ωcos )(4)(=3.13 用90相移的两个正交载波可以实现正交复用，即两个载波可分别传输带宽相等的两个独立的基带信号)(1t f 和)(2t f，而只占用一条信道。

试证明无失真恢复基带信号的必要条件是：信道传递函数)(f H 必须满足Wf f f H f f H c c ≤≤-=+0),()(证明：)(]sin )([)(]cos )([)(21t h t t f t h t t f t S c c *+*=ωω)]}()([)()(){(21)(2211c c c c F F j F F H S ωωωωωωωωωω--++++-=以t t C c dωcos )(=相干解调，输出为 )(*)()(t C t S t S dp=)]}()2([)2()(){(41)]}2()([)()2(){(41)]()([21)(22112211ωωωωωωωωωωωωωωωωωωωωωF F j F F H F F j F F H S S S c c c c c c c c p -++++++--++--=++-=选择适当滤波器，滤掉上式中cωω2±项，则)]()()[(4)]()()[(41)(21c c c c d H H F jH H F S ωωωωωωωωωωω+--+++-=要无失真恢复基带信号，必须⎩⎨⎧=++-+=-常数)()()()(c c c c H H H H ωωωωωωωω此时可恢复)(1t f 。

第3章模拟线性调制系统 3.1 概述3.1.1 调制的目的.频谱搬移 － 适应信道传输、合并多路信号； 提高抗干扰性。

3.1.2 基本概念基带信号：由消息直接变换成的电信号。

频带从零频开始，低频端谱能量大，不宜在信道中远距离传输。

调 制：按调制信号（基带信号）的变化规律去改变载波某些参数的过程叫调制。

（频谱搬迁）调制信号：f(t)载 波：c(t)=Acos[ωc t+θ0]已调信号：s(t)=m (t)·c(t) =A(t)cos[ωc t+φ(t)+θ0] 模拟调制：当调制信号为模拟基带信号m(t)，载波为连续的正弦或余弦高频信号c(t)=Acos[ωc t+θ0]时，称模拟调制。

3.1.3 调制的分类数字调制3.2 双边带调幅一. 常规调幅１． 时域表达式：调制信号f(t)（平均值)(t f ＝0）加直流后对载波幅度调制（称标准或完全调幅）s AM (t)= [A 0+f(t)]·cos[ωc t+θc ]ωc 载波角频率， θc 载波初相位()()()()()()()()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧成比例变化随常数，调相：成比例变化随常数，调频：非线性调制角度调制为常数成比例变化随线性调制幅度调制模拟调制t f t t A t f dt t d t A VSBSSB DSBAM t t f t A φφφ)(,波形图3-1当调制信号f(t)为单频信号时：f(t)= A m cos(ωm t+θm )则： s AM (t)= [A 0+ A m cos(ωm t+θm)]cos[ωc t+θc ]= A 0 [1+βAM cos(ωm t+θm)]cos[ωc t+θc ]A A m AM =β称调幅指数，х100%叫调制度⎪⎩⎪⎨⎧><=过调幅通常取正常调幅满调幅...1-60%)-30%(...1......1AMβ ２．频域表达式θc =0的时域表达式：s AM (t)= [A 0+ f (t)]cosωc t = A 0 cosωc t+ m (t) cosωc t因m(t) F (ω)A 0 cosωc t [])()(000ωωδωωδπ++-↔A注： ))((21cos )(tj tj c c c eet f t t f ωωω-+=tj tj c c et f et f ωω-+=)(21)(21其付氏变换为因为根据平移故S AM (ω) 的频域表达式为：[])]()([21)()()(00000ωωωωωωδωωδπω++-+++-=F F A S AM频谱图：()()00ωωω-↔F et f tj ()()0021ωωωω++-F F [])()(21cos )(00ωωωωω++-↔F F t t f c频谱搬迁到适合通信系统传输的频率范围。

第三章（模拟调制原理）习题及其答案【题3－1】已知线性调制信号表示式如下：（1）cos cos c t w t Ω （2）(10.5sin )cos c t w t +Ω 式中，6c w =Ω。

试分别画出它们的波形图和频谱图。

【答案3－1】（1）如图所示，分别是cos cos c t w t Ω的波形图和频谱图设()M S w 是cos cos c t w t Ω的傅立叶变换，有()[()()2()()] [(7)(5)(5)(7)]2M c c c c S w w w w w w w w w w w w w πδδδδπδδδδ=+Ω+++Ω-+-Ω++-Ω-=+Ω+-Ω++Ω+-Ω（2）如图所示分别是(10.5sin )cos c t w t +Ω的波形图和频谱图：设()M S w 是(10.5sin )cos c t w t +Ω的傅立叶变换，有()[()()] [()()2()()] [(6)(6)] [(7)(5)2(7)(5)]M c c c c c c S w w w w w j w w w w w w w w w w j w w w w πδδπδδδδπδδπδδδδ=++-++Ω+++Ω---Ω+--Ω-=+Ω+-Ω++Ω+-Ω--Ω-+Ω【题3－2】根据下图所示的调制信号波形，试画出DSB 及AM 信号的波形图，并比较它们分别通过包络检波器后的波形差别。

【答案3－2】AM 波形如下：通过低通滤波器后，AM 解调波形如下：DSB 波形如下：通过低通滤波器后，DSB 解调波形如下：由图形可知,DSB 采用包络检波法时产生了失真。

【题3－3】已知调制信号()cos(2000)cos(4000)m t t t ππ=+载波为4cos10t π，进行单边带调制，试确定单边带信号的表达式，并画出频谱图。

【答案3－3】可写出上边带的时域表示式4411ˆ()()cos ()sin 221 [cos(2000)cos(4000)]cos1021 [sin(2000)sin(4000)]sin 1021 [cos12000cos 8000cos14000cos 6000]41 [cos 8000co 4m c c s t m t w t mt w t t t t t t tt t t t t πππππππππππ=-=+-+=+++--s12000cos 6000cos14000]11 cos12000cos1400022t t t t tπππππ+-=+其傅立叶变换对()[(14000)(12000)2+(14000)(12000)]M S w w w w w πδπδπδπδπ=+++-+-可写出下边带的时域表示式'4411ˆ()()cos ()cos 221 [cos(2000)cos(4000)]cos1021 [sin(2000)sin(4000)]sin 1021 [cos12000cos 8000cos14000cos 6000]41 +[cos 8000c 4m c c s t m t w t mt w t t t t t t tt t t t t πππππππππππ=+=+++=+++-os12000cos 6000cos14000]11 cos 8000cos1600022t t t t tπππππ+-=+其傅立叶变换对'()[(8000)(6000)2(8000)(6000)]M S w w w w w πδπδπδπδπ=++++-+-两种单边带信号的频谱图分别如下图。