商人安全过河问题a

商人过河数学建模论文摘要4个商人带着4个仆人过河，过河的工具只有一艘小船，只能同时载两个人过河，包括划船的人。

在河的任何一边，只要仆人的数量超过商人的数量，仆人就会联合起来将商人杀死并抢夺其财物，问应如何设计过河顺序才能让所有人都安全地过到河的另一边。

经典的商人过河问题可以看做一个多步决策过程。

每一步由此岸到彼岸或彼岸到此岸船上的人员在安全的前提下(两岸的随从数不比商人多),经有限步使全体人员过河。

用状态变量表示某一岸的人员状况，决策变量表示船上的人员情况，可以找出状态随决策变化的规律。

问题就转换为在状态的允许变化范围内（即安全渡河条件），确定每一步的决策，达到安全渡河的目标。

分别建立两个模型：模型一采用穷举法，对各种过河的方案一一列举，然后根据商人们要安全过河为前提对各种进行了列举，经过层层筛选，最终求出商人安全的方案。

模型二采用图解法，利用图示表示说明该题的解法。

关键词：穷举法多步决策图解法安全渡河一、问题提出4个商人带着4个仆人过河，过河的工具只有一艘小船，只能同时载两个人过河，包括划船的人。

在河的任何一边，只要仆人的数量超过商人的数量，仆人就会联合起来将商人杀死并抢夺其财物，问应如何设计过河顺序才能让所有安全过河。

二、模型的假设和符号说明⑴模型假设：①过河途中不会出现不可抗力的自然因素②当仆人数大于商人数时，随从们不会改变杀人的计划③船很结实，不会发生任何的意外（2）符号的说明（A,B）表示商人和仆人的个数，A表示商人，B表示仆人三、模型的建立模型一(穷举法）：这样如果商人回去，彼岸的商人就比仆人多了，如果仆人过去，此岸的仆人就会比商人多了。

所以无法达到（0,0）这样的最终结果。

1 / 2⑵模型二（图解法）：四人过河模型图允许步骤数L是沿方格线移动1格或2格，L为奇数时向左.下方移动，L 为偶数时向右.上方移动，要确定一系列的L，使初始状态（4，4）最终变为（0，0），无论怎样走都必须经过中间点（2，2），然后奇数次到达Y轴,，而无论怎么变化人数都也只能到达此点后不能继续走下去，只能循环走，达不到最终的目标（0，0）。

做业1、2：之阳早格格创做商人过河一、问题沉述问题一：4个商人戴着4个随从过河，过河的工具惟有一艘小船，只可共时载二部分过河，包罗划船的人.随从们稀约, 正在河的任一岸, 一朝随从的人数比商人多, 便杀人越货.乘船渡河的规划由商人决断.商人们何如才搞仄安过河?问题二：假若小船不妨容3人，请问最多不妨有几名商人各戴一名随从仄安过河.二、问题分解问题不妨瞅搞一个多步计划历程.每一步由此岸到此岸或者此岸到此岸船上的人员正在仄安的前提下(二岸的随从数没有比商人多),经有限步使部分人员过河.用状态变量表示某一岸的人员情景，计划变量表示船上的人员情况，不妨找出状态随计划变更的顺序.问题便变换为正在状态的允许变更范畴内（即仄安渡河条件），决定每一步的计划，达到仄安渡河的目标.三．问题假设1. 过河途中没有会出现没有成抗力的自然果素.2. 当随从人数大于商人数时，随从们没有会改变杀人的计划.3．船的品量很佳，正在多次谦载的情况下也能仄常运做.4. 随从会听从商人的调动.四、模型形成x(k)~第k 次渡河前此岸的商人数 x(k),y(k)=0,1,2,3,4; y(k)~第k 次渡河前此岸的随从数 k=1,2,…..s(k)=[ x(k), y(k)]~历程的状态 S~允许状态集中 S={(x,y)|x=0,y=0,1,2,3,4; x=4,y=0,1,2,3,4;x=y=1,2,3} u(k)~第k 次渡船上的商人数 u(k), v(k)=0,1,2;v(k)~ 第k 次渡船上的随从数 k=1,2…..d(k)=( u(k), v(k))~历程的计划 D~允许计划集中 D={u,v|u+v=1,2,u,v=0,1,2}状态果计划而改变s(k+1)=s(k)+(-1)^k*d(k)~状态变化律供d(k)ÎD(k=1,2,….n),使s(k)ÎS 并按变化律s(k+1)=s(k)+(-1)^k*d(k)由（4,4）到达（0,0）数教模型： k+1kS =S +k k D （-1）（1）'4k k x x += （2）'4k k y y +=（3）k.k x y ≥ （4）''k k x y ≥（5）模型分解：由（2）（3）（5）可得化简得概括（4）可得k k x y =战 {}(,)|0,0,1,2,3,4k k k k k S x y x y ===（6） 还要思量{}'(',')|'0,'0,1,2,3,4k k k k k S x y x y === （7）把（2）（3）戴进（7）可得化简得{}(,)|4,0,1,2,3,4k k k k k S x y x y === （8）概括（6）（7）（8）式可得谦脚条件的情况谦脚下式 {}(,)|0,4,0,1,2,3,4;k k k k k k k S x y x y x y ====（9） 所以咱们知讲谦脚条件的面如上图所示：面移动由{}(,)|4,0,1,2,3,4k k k k k S x y x y === （8）到达{}(,)|0,0,1,2,3,4k k k k k S x y x y ===（6）时，不妨认为完毕渡河.果为移动的格数小于等于2，惟有核心面（2，2）到（6）面战（8）面的距离为2，所以核心面（2,2）成为渡河的闭键面.当咱们移动到（2,2）面时，便无法举止下去.故4个商人，4个随从，船容量为2人时，无法仄安渡河. 对付于问题二，咱们不妨修坐模型为：k+1k S =S +k k D （-1）（10）'k k x x M += （11）'k k y y M += （12）k.k x y ≥（13）''k k x y ≥ （14）u(k), v(k)=0,1,2,3; （15）通过类似于问题一的步调不妨知讲：坐标上的闭键面是（3,3），最多不妨五名商人戴五名随从往日.需要决定五名商人戴五名随从的规划可止再决定六名商人戴六名随从的规划没有成止1、五名商人戴五名随从的情况：（1）最先没有成能有三名商人先过河，二名商人一名随从过河，一名商人二名随从过河（2）三个随从先过河（5,2），回去一个随从（5,3），往日二个随从（5,1）回去一个随从（5,2），再往日三个商人（2,2），回去一个商人一个随从（3,3），再往日三个商人（0,3），回去一个随从（0,4），往日三个随从（0,1），回去一个随从（0,2）再往日二个随从（0,0）综上可知：五名商人戴五名随从，小船不妨载三部分不妨过河2、六名商人戴六名随从的情况：（1）最先没有成能有三名商人先过河，二名商人一名随从过河，一名商人二名随从过河（2）三个随从先过河（6,3），回去一个随从（6,4），往日二个随从（6,2）回去一个随从（6,3），往日三个商人（3,3），此时二岸皆是（3,3），由坐标法分解知，那是最交近末面的临界面，然而是如果回去的时间一定是回去一个商人战一个随从，如果那一步可止，后里便举止没有去综上所述，六个商人戴六个随从，小船载三部分的情况下没有克没有及渡河分离1、2知，当小船最多载三部分的时间，最多五名商人各戴一个随从不妨过河.五、模型的考验取评介由少量人的过河问题推广到了更普遍人的过河问题，使得问题变得明白有顺序.六、参照文件[1]章胤，2014年燕山大教世界大教死数教修模竞赛训练ppt，2014年4月17日。

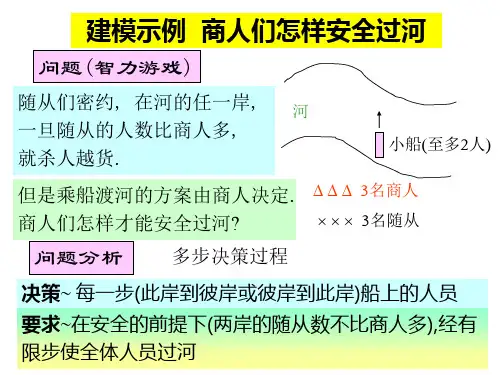
8.7 动态规划：商人过河问题问题提出三名商人各带一个随从乘船渡河（A岸到B岸）。

现此岸有一小船只能容纳两人，由他们自己划行。

若在河的任一岸随从人数比商人多，他们就可能杀人越货。

不过如何乘船渡河的大权由商人们掌握。

商人们怎样才能安全过河呢?模型建立此问题可视为一个多步决策模型建立决策变量:(a,b)a------船上的商人数b ------船上的随从数a,b的取值范围：{0，1，2}且满足a+b<=2，且均为整数。

允许决策集合：D={(a,b)|a+b=1,2}={(0,1), (0,2), (1,1), (1,0), (2,0)}模型求解这样问题要求由(3，3，1)变到(0，0，0)的一条道路。

根据题意，状态转移时要满足一定的规则：1. Z从1变为0与从0变为1交替进行(船在哪个岸)；2. 当Z从1变为0时，即船从A岸到B岸，A岸人数减少1或2个；即(x,y,1)→(u,v,0)时, u≤x, v≤y, u+v=x+y-1 oru+v=x+y-23. 当Z从0变为1时，即船从B岸到A岸，A岸人数增加1或2个；即(x,y,0)→(u,v,1)时, u≥x, v≥y,u+v=x+y+1 oru+v=x+y+24. 不重复已出现过的状态，如(3,3,1)→(3,1,0)→(3,3,1)；按照以上规则，求解过程如下从(3，2，0)只能到达(3，3，1)/*不必考虑*/从(3,3,1)出发(3,2,0)(3,1,0)如右图(2,2,0)(3,3,1)(3,2,0)(3,1,0)(2,2,0)从(3,1,0)出发(3,3,1) /*不必考虑*/(3,2,1)/*可取*/从(2,2,0)出发(3,3,1) /*不必考虑*/(3,2,1)/*可取*/模型求解如下图所示：逐步求解，可得:模型求解由此可得到渡河策略:(3,3,1) (3,2,1)→(3,0,0)→(3,1,1)→(1,1,0)→(2,2,1)→(0,2,0)→(0,3,1)→(0,1,0) (0,0,0)(2,2,0)(3,1,0)(1,1,1)(0,2,1)模型求解思考(1) 夫妻过河问题有三对夫妻要过河，船最多可载两人。

《数学建模实验》课程考试试题----商人安全过河数学建模与求解一．问题提出：4名商人带4名随从乘一条小船过河，小船每次自能承载至多两人。

随从们密约, 在河的任一岸, 一旦随从的人数比商人多, 就杀人越货.乘船渡河的方案由商人决定，商人们如何才能安全渡河呢二．模型假设：商人和随从都会划船，天气很好，无大风大浪，且船的质量很好，可以保证很多次安全的运载商人和随从。

三．问题分析：商随过河问题可以视为一个多步决策过程，通过多次优化，最后获取一个全局最优的决策方案。

对于每一步，即船由此岸驶向彼岸或由彼岸驶向此岸，都要对船上的人员作出决策，在保证两岸的商人数不少于随从数的前提下，在有限步内使全部人员过河。

用状态变量表示某一岸的人员状况，决策变量表示船上的人员状况，可以找出状态随决策变化的规律，问题转化为在状态的允许变化范围内(即安全渡河条件)，确定每一步的决策，达到安全渡河的目标。

四．模型构成：k x ~第k 次渡河前此岸的商人数，k y ~第k 次渡河前此岸的随从数 k x , k y =0,1,2,3,4; k =1,2,… …k S =(k x , k y )~过程的状态,S ~ 允许状态集合，S={(x , y )| x =0, y =0,1,2,3,4; x =4 ,y =0,1,2,3,4; x =y =1,2,3} k u ~第k 次渡船上的商人数k v ~第k 次渡船上的随从数k d =(k u , k v )~决策，D={(u , v )| 21≤+≤v u ,k u , k v =0,1,2} ~允许决策集合 k =1,2,… …因为k 为奇数时船从此岸驶向彼岸，k 为偶数时船从彼岸驶向此岸，所以状态k S 随决策k d 的变化规律是1+k S =k S +k )1(-k d ~状态转移律求k d ∈D(k =1,2, …n), 使k S ∈S, 并按转移律由1S =(4,4)到达状态1+n S =(0,0)。

商人过河问题一、三名商人各带一名随从的情况1．问题（略）2．模型假设①当一边岸满足随从数大于商人数，但商人数为0时仍为一种安全状态；②小船至多可容纳2人，且渡河时由随从（或者商人）来划船。

3．分析与建模商人过河需要一步一步实现，比如第一步：两个仆人过河，第二步：一个仆人驾船回来，第三步：又是两个仆人过河，第四步：……其中每一步都使当前状态发生变化，而且是从一种安全状态变为另一种安全状态。

如果我们把每一种安全状态看成一个点，又如果存在某种过河方式使状态a变到状态b，则在点a和点b之间连一条边，这样我们把商人过河问题和图联系起来，有可能用图论方法来解决商人过河问题。

建模步骤：⑴首先要确定过河过程中的所有安全状态，我们用二元数组(,)x y 表示一个安全状态（不管此岸还是彼岸），其中x表示留在此岸的主人数，y表示留在此岸的随从数。

两岸各有十种安全状态：(0,0),(0,1),(0,2),(0,3),(2,2),(1,1),(3,0),(3,1),(3,2),(3,3)⑵在两岸的安全状态之间，如存在一种渡河方法能使一种状态变为另一种安全状态，则在这两种状态之间连一条边。

这样，得到如下一个二部图（图1），其中下方顶点表示此岸状态，上方顶点表示彼岸状态。

我们的目的是要找出一条从此岸(3,3)到彼岸(0,0)的最短路。

⑶观察发现此岸的状态(0,0)，(3,0)和彼岸的状态(0,3)，(3,3)都是孤立点，在求最短路的过程中不涉及这些点，把它们删去。

两岸的点用1,2, (16)新标号。

（3,3）（3,2）（3,1）（3,0）（1,1）（2,2）（0,3）（0,2）（0,3）（0,0）○②④⑥⑧⑩○○12○14○16①③⑤○⑦⑨○11○13○15○（3,3）（3,2）（3,1）（3,0）（1,1）（2,2）（0,3）（0,2）（0,3）（0,0）(图1)4．模型求解求最短路程的matlab程序如下：function route=sroute(G,opt)%求图的最短路的Dijkstra算法程序，规定起点为1，顶点连续编号%G是给定图的邻接矩阵或弧表矩阵，程序能够自动识别%当opt=0（或缺省）时求无向图的最短路，当opt=1时求有向图的最短路%d——标记最短距离%route是一个矩阵，第一行标记顶点，第二行标记1到该点的最短路，第三行标记最短路上该点的先驱顶点while 1 %此循环自动识别或由弧表矩阵生成邻接矩阵if G(1,1)==0A=G;breakelsee=Gn=max([e(:,1);e(:,2)]); %顶点数m=size(e,1); %边数M=sum(e(:,3)); %代表无穷大A=M*ones(n,n);for k=1:mA(e(k,1),e(k,2))=e(k,3);if opt==0A(e(k,2),e(k,1))=e(k,3); %形成无向图的邻接矩阵endendA=A-M*eye(n) %形成图的邻接矩阵endbreakendpb(1:length(A))=0;pb(1)=1;index1=1;index2=ones(1,length(A));d(1:length(A))=M;d(1)=0; %标记距离temp=1;while sum(pb)<length(A)tb=find(pb==0);d(tb)=min(d(tb),d(temp)+A(temp,tb)); %更新距离temp=find(d(tb)==min(d(tb))); %确定新最小距离点temp=tb(temp(1));pb(temp)=1;index1=[index1,temp];index=index1(find(d(index1)==d(temp)-A(temp,index1)));if length(index)>=2index=index(1);endindex2(temp)=index; %记录前驱顶点endroute=[1:n;d;index2];在matlab的命令窗口输入图（1）的弧表矩阵e:e=[1 2;1 4;1 10;3 4;3 6;3 10;5 6;5 8;7 14;7 16;9 8;9 12;11 12;11 14;13 14;13 16;15 16];e=[e,ones(17,1)]; %边权都设为1调用程序：route=sroute(e,0)运行结果：e =1 2 11 4 11 10 13 4 13 6 13 10 15 6 15 8 17 14 17 16 19 8 19 12 111 12 111 14 113 14 113 16 115 16 1route =1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 160 1 2 1 4 3 10 5 6 1 8 7 10 9 12 111 1 4 1 6 3 14 5 8 1 12 9 14 11 16 7这表示存在一条从1到16的长度为11的路：1 4 3 6 5 8 912 11 14 7 16，此路对应商人成功渡河的一个方案：（3,3）变为（3,1）变为（3,2）变为（3,0）变为（3,1）变为（1,1）变为（2,2）变为（0,2）变为（0,3）变为（0,1）变为（1,1）变为（0,0）即：两个仆人过河，一个仆人回来；有两个仆人过河，一个仆人回来；两个主人过河，一主一仆回来；有两个主人过河，一个仆人回来；两个仆人过河，一个仆人回来；最后两个仆人过河。

1、我们建立的“商人怎样安全过河”模型是（ A ）。

A.允许决策模型B.状态转移模型C.马氏链模型D.多步决策模型4、“公平合理的席位分配”模型中，以下说法错误的（ D ）。

A.参照惯例的席位分配结果是较合理的B.提出的相对不公平程度对席位分配有改进效果C. 席位分配一类问题的Q 值法是较公平的D.存在满足四个公平分配公理的分配方法 10、“层次分析模型”中成比对矩阵)(ij a A =如果满足如下（ D ）式，则称为一致阵。

A 、0>ij aB 、jiij a a 1=C 、11=∑=ni ijaD 、ik jk ij a a a =⋅二、填空题（2分/空×10空=20分）1、“商人怎样安全过河”模型中状态随决策变化的规律是k k k k d s s )1(1-+=+。

2、“公平的席位分配”模型中的Q 值法计算公式是)1(2+=i i i i n n p Q 。

7、“传染病模型”中SIS 模型是指被传染者康复以后，还有可能再次感染该传染病。

三、问答题（40分）1、请用简练的语言全面的描述数学建模的过程和数学模型的特点。

(10’)答：（1）建模过程：模型准备→模型假设→模型构成→模型求解→模型检验→模型应用。

（2）数学模型的特点：逼真性和可行性；渐进性；强健性；可转移性；非预制性；条理性；技艺性；局限性；2、某家具厂生产桌子和椅子两种家具，桌子售价50元/个，椅子销售价格30元/个，生产桌子和椅子要求需要木工和油漆工两种工种。

生产一个桌子需要木工4小时，油漆工2小时。

生产一个椅子需要木工3小时，油漆工1小时。

该厂每个月可用木工工时为120小时，油漆工工时为50小时。

问该厂如何组织生产才能使每月的销售收入最大？（建立模型不计算）(10’) 解：（1）确定决策变量：x1=生产桌子的数量x2=生产椅子的数量 4分 （2）确定目标函数：家具厂的目标是销售收入最大max z=50x1+30x2（3）确定约束条件：4x1+3x2<120（木工工时限制） 2x1+x2>50（油漆工工时限制）（4）建立的数学模型为：max S=50x1+30x2 s.t. 4x1+3x2<120 2x1+ x2>50 x1, x2 >03、有四个工人，要分别指派他们完成四项不同的工作，每人做各项工作所消耗的时间如下表所示，问应如何指派工作，才能使总的消耗时间为最少？（建立模型不计算）(10’) 解：令0,1,ij i j x i ⎧=⎨⎩指派第人完成第项工作不指折派第项工作目标函数：111231421222431323334414244min 1518212419231826171619192117Z x x x x x x x x x x x x x x =++++++++++++约束条件：1121314112223242132333431424344411..11x x x x x x x x st x x x x x x x x +++=⎧⎪+++=⎪⎨+++=⎪⎪+++=⎩4、结合自身的实际情况，谈谈数学建模的方法和自身能力的培训。

实验1 怎样安全过河问题一、问题3名商人各带1名随从乘船渡河，一只小船只能容纳2人，由他们自己划行。

随从们密约，在河的任一岸，一旦随从人数比商人多，就杀商人。

此密约被商人知道，如何乘船渡河的大权掌握在商人们手中，商人们怎样安排每次乘船方案，才能安全渡河呢？二、实验目的使学生进一步巩固和理解向量的定义、运算规则及多步决策理论及其应用。

三、预备知识向量定义及运算，多步决策理论。

四、实验内容与要求建立起商人安全渡河的数学模型，并给出商人们如何安全渡河的一个方案，使得渡河的次数尽量少。

五、思考问题在上述的约束条件下，若商人有4名时，问商人们是否能实现安全渡河？更一般地，若商人数是m，小船最多只能坐n（1〈n〈m〉人，m和n有何关系时，商人们才能实现安全渡河？问题解答一、问题分析与建立模型由于这个问题已经理想化了，所以不必再作假设。

这个问题可以看作一个多步决策的过程。

设第k次渡河前此岸的商人数为X K，随从数为Y K，k=1,2,…。

X K，Y K=0,1,2,3。

将二维向量S K=( X K,Y K)定义为状态。

安全渡河条件下的状态集合称为允许状态集合，记为S，则S={(x,y)|x=0或3,y=0,1,2,3;x=y=1,2} (1) 又设第k次渡船上的商人数为U K，随从数为V K，将二维向量D K=(U K,V K)定义为决策,则允许决策集合为:D={(u,v)|u+v=1,2} （2）因为k为奇数时船从此岸驶向彼岸，k为偶数时船由彼岸驶回此岸，所以状态S K随着决策D K变化的规律即状态转移规律是：S K+1=S K+（—1）K D K （3）这样，制定安全渡河方案归结为如下的多步决策问题：求决策D K∈D（k=1，2，…，n），使S K∈S按照转移律（3），由初始状态S1=（3，3）经有限步（设为n）到达状态S n+1=（0，0）。

二、计算过程下面通过Mathematica的程序给出这个多步决策问题的一个解，同时满足了渡河次数尽量少的条件。

商人安全过河摘要商人安全过河问题通过逻辑思索求解起来比较繁琐，而用建立数学模型并采用计算机编制算法进行求解就比较方便了，并且还容易推广。

本题为多步决策模型，每一次过河都是状态量的转移过程，转移即为决策，通过一步步决策使所有人员安全到达彼岸。

关键字：多步决策模型状态量的转移栈递归一、问题重述随从们密约, 在河的任一岸, 一旦随从的人数比商人多, 就杀人越货。

现有3名商人各带一个随从一起渡河一只船只能容纳两个人，但如何乘船渡河的大权掌握在商人的手里，商人怎样安排才能在有限步内安全渡河？数据及其关系？如何存储？过程中数据上的操作？操作过程中需借助什么结构实现？二、问题分析把商人过河问题视为一个多步决策的过程。

每一步即船由此岸驶向彼岸，都是对船上的人员（商人、随从）做出决策，在保证安全的前提下即两岸的商人数都不比随从少，用有限步使人员全部过河。

用状态变量表示某一岸的人员状况，决策变量表示船上的人员状况，可以找出状态随决策变化的规律。

这样商人过河问题就转化为在状态的允许变化范围内即满足安全渡河的条件下，确定每一步的决策，达到安全过河的目标。

三、模型假设1、在商人人数多于随从时乘船渡河的大权掌握在商人的手里；2、商人和随从都会划船。

四．符号说明记第k次过河前此岸的商人数为x k，随从数为y k，其中k=1,2，…，x k，y k=0,1,2,3,。

将二维向量S k=（x k，y k）定义为状态，满足安全条件下的状态集合称为允许状态集合S，则S={（x，y）}。

记第k次过河船上的商人数为u k，随从数为v k，将向量d k=（u k，v k）定义为决策，因为小船最多只能容两个人，即u+v=1,2，故允许决策的集合D为：D{（u，v）}。

因为k为奇数时，船是从此岸到彼岸，k为偶数时，船从彼岸驶回此岸。

解决商人过河问题就是求决策D，使得S按照状态转移率由初始状态（3,3）经过有限步到达状态（0，0）。

五、模型的建立与求解本题为多步决策模型，每一次过河都是状态量的转移过程。

商人过河问题摘要本文就商人们如何能够安全过河问题, 采用多步决策建立了数学模型，求解得到商人们安全过河的方案。

将经典的商人过河问题进行了更广的讨论，在此基础上着重分析了安全渡河的状态空间，建立了满足问题需求的规则，从而得出了要求解问题的方案。

模型主要通过穷举的方法对各种过河的方案进行一一列举，然后根据小船的容量和商人们要安全渡河为前提对各种方案进行层层筛选。

最终，得到商人安全渡河的方案。

最后本文就此问题进行推广，当有m名商人m名随从且小船的容量为k时，将会得到几种解决方案给出了说明。

关键词：穷举法多步决策图解法商人过河状态空间一、问题重述三名商人各带一名随从过河，随从们密约, 在河的任一岸, 一旦随从的人数比商人多, 就杀人越货.但乘船渡河的方案由商人决定.现在需要解决的问题如下：1.1 3名商人在不被随从谋杀和小船最多能容2人的情况下，商人们将如何安全过河?1.2如果有m名商人n名随从，小船的容量为k时，商人们又将如何安全过河？二、模型的假设2.1 假设过河的过程中不会发生意外事故。

2.2 假设当随从人数多过商人时，不会改变杀人越货计划。

2.3假设所有人最终都必须到达河对岸。

三、符号说明M表示商人的数量::N表示随从的数量Z表示河的此岸和彼岸:K表示小船的容量:m表示此岸的商人数量::n表示此岸随从的数量:u表示彼岸的商人数量:v表示彼岸的随从数量四、模型分析本题针对商人们能否安全过河问题，需要选择一种合理的过河方案。

对该问题可视为一个多步决策模型，通过对每一次过河的方案的筛选优化，最终得到商人们全部安全过到河对岸的最优决策方案。

对于每一次的过河过程都看成一个随机决策状态量，商人们能够安全到达彼岸或此岸我们可以看成目标决策允许的状态量，通过对允许的状态量的层层筛选，从而得到过河的目标。

五、模型建立与求解5.1模型的建立本题为多步决策模型，每一次过河都是状态量的转移过程。

可以用三维向量表示（,,m n Z ）m 的取值范围:{0,1,2,3}n 的取值范围:{0,1,2,3}1,0,Z ⎧=⎨⎩表示划船到河的彼岸表示划船到河的此岸那么允许状态量（即两岸同时必须满足（m n ≥））可以表示为（1） 当m =0或3, n ={0,1,2,3}，（2） 当m =1或2，m =n或用三维向量表示允许状态量如下表格1：表（1）过河安全状态量5.2模型的求解模型的要求从（3,3,1）开始经过对每次过河的安全状态量的选择最终安全到达（0,0,0）。

商人们怎样安全过河的数学模型示例文章篇一：话说啊，商人们遇到了一个棘手的问题：他们得带着随从们一起过河，但随从们可不是省油的灯，一有机会就想着害商人抢货。

这河又不宽不窄，一只小船每次只能载两个人，怎么过河才能确保安全呢？咱们来聊聊这个问题吧。

首先，商人们得明白，随从们人多势众，要是他们比商人多了，那可就危险了。

所以，商人们得想个法子，让随从们没法儿耍花招。

其实啊，这个问题可以变成一个数学模型。

想象一下，我们把每次过河的人都看成是一个状态，就像打游戏一样，每过一次河就是进入了一个新的关卡。

在这个关卡里，商人们得保证自己的人数不能少于随从们。

那具体怎么做呢？咱们得先设定一些规则。

比如说，每次过河的人数只能是两个，这是小船的容量决定的。

然后，商人们得选择让哪些人过河，这就得靠他们的智慧和策略了。

想象一下这个场景：商人们先让两个随从过河，然后一个商人再带一个随从回来。

这样，河对岸的随从人数虽然多了，但商人这边还有足够的人手可以应对。

接下来，两个商人再过河，这样河对岸的商人数就比随从数多了，安全就得到了保障。

然后，再让一个商人带一个随从回来，这样河这边也有足够的商人保护随从不敢造次。

最后，两个随从再过河，问题就解决了。

这个数学模型虽然简单，但却非常实用。

它告诉我们，在面对困难和挑战时，只要我们善于运用智慧和策略，就一定能够找到解决问题的方法。

所以，商人们要想安全过河，就得靠他们的智慧和勇气了。

示例文章篇二：话说啊，有这么一个古老的谜题，叫做“商人过河”。

话说有三名聪明的商人，他们各自带着一个狡猾的随从，准备乘船过河。

这船啊，一次只能载两个人，问题就在于，这些随从们心里都有个小九九，他们密谋着，只要到了河的对岸，随从人数多于商人人数，就立马动手抢货。

这商人们也不是吃素的，他们知道随从们的阴谋，但他们毕竟都是聪明人，于是就想出了一个绝妙的策略。

咱们来想想啊，这过河其实就是一个多步决策的过程。

每次渡河，船上的人员选择都至关重要。

商人过河问题摘要：为了求解3个商人和3个随从的过河问题，用数学分析方法，建立数学模型，并且加以求解，展示动态规划思想的应用步骤。

最后利用计算机编程进行求解，获得过河问题的完整求解过程；有效地求解类似多步决策问题的作用。

关键词：多步决策计算机求解状态转移律图解法 MATLAB程序一．问题提出S个商人各带一个随从乘船过河，一只小船只能容纳K人，由他们自己划船。

商人们窃听到随从们密谋，在河的任意一岸上，只要随从的人数比商人多，就杀掉商人。

但是如何乘船渡河的决策权在商人手中，商人们如何安排渡河计划确保自身安全？二．问题的关键解决的关键集中在商人和随从的数量上，以及小船的容量上，该问题就是考虑过河步骤的安排和数量上。

各个步骤对应的状态及决策的表示法也是关键。

三．问题的分析在安全的前提下(两岸的随从数不比商人多),经有限步使全体人员过河。

由于船上人数限制，这需要多步决策过程，必须考虑每一步船上的人员。

动态规划法正是求解多步决策的有效方法。

它要求把解的问题一层一层地分解成一级一级、规模逐步缩小的子问题。

直到可以直接求出其解的子问题为止。

分解成所有子问题按层次关系构成一棵子问题树．树根是原问题。

原问题的解依赖于子问题树中所有子问题的解。

四．模型假设记第k次过河前A岸的商人数为XK，随从数为YK k=1，2，⋯ XK ,YK=0，1，2，3，将二维向量SK=(XK，YK)定义为状态．把满足安全渡河条件下的状态集合称作为允许状态集合。

记作S。

则 S={(XK ,YK)|(XK =0,YK =0,1,2,3),(XK =3,YK =0,1,2,3),(XK =YK =1)(XK =YK =2)}记第k次过河船上的商人数为UK，随从数为VK将二维向量DK=(UK ,VK)定义为决策。

由小船的容量可知允许决策集合（记作D)为D={(UK ,VK)|UK +VK=l,2}={(O,1);(O,2);(1,O);(1,1);(2,O)}五．模型建立：动态规划法正是求解多步决策的有效方法。

作业1、2：商人过河一、问题重述问题一：4个商人带着4个随从过河，过河的工具只有一艘小船，只能同时载两个人过河，包括划船的人。

随从们密约, 在河的任一岸, 一旦随从的人数比商人多, 就杀人越货。

乘船渡河的方案由商人决定。

商人们怎样才能安全过河?问题二：假如小船可以容3人，请问最多可以有几名商人各带一名随从安全过河。

二、问题分析问题可以看做一个多步决策过程。

每一步由此岸到彼岸或彼岸到此岸船上的人员在安全的前提下(两岸的随从数不比商人多),经有限步使全体人员过河。

用状态变量表示某一岸的人员状况，决策变量表示船上的人员情况，可以找出状态随决策变化的规律。

问题就转换为在状态的允许变化范围内（即安全渡河条件），确定每一步的决策，达到安全渡河的目标。

三．问题假设1. 过河途中不会出现不可抗力的自然因素。

2. 当随从人数大于商人数时，随从们不会改变杀人的计划。

3．船的质量很好，在多次满载的情况下也能正常运作。

4. 随从会听从商人的调度。

四、模型构成x(k)~第k次渡河前此岸的商人数x(k),y(k)=0,1,2,3,4;y(k)~第k次渡河前此岸的随从数k=1,2,…..s(k)=[ x(k), y(k)]~过程的状态S~允许状态集合S={(x,y) x=0,y=0,1,2,3,4; x=4,y=0,1,2,3,4;x=y=1,2,3}u(k)~第k次渡船上的商人数u(k), v(k)=0,1,2;v(k)~ 第k次渡船上的随从数k=1,2…..d(k)=( u(k), v(k))~过程的决策 D~允许决策集合D={u,v |u+v=1,2,u,v=0,1,2}状态因决策而改变s(k+1)=s(k)+(-1)^k*d(k)~状态转移律求d(k) ∈D(k=1,2,….n),使s(k)∈S 并按转移律s(k+1)=s(k)+(-1)^k*d(k)由（4,4）到达（0,0）数学模型：k+1k S =S +k k D （-1） （1）'4k k x x += （2）'4k k y y += （3）k.k x y ≥ （4）''k k x y ≥ （5）模型分析：由（2）（3）（5）可得44kk x y -≥- 化简得k k x y ≤综合（4）可得k k x y = 和 {}(,)|0,0,1,2,3,4k k k k k S x y x y === （6）还要考虑 {}'(',')|'0,'0,1,2,3,4kk k k k S x y x y === （7） 把（2）（3）带入（7）可得{}(4,4)|40,40,1,2,3,4k k k k k S x y x y =---=-=化简得{}(,)|4,0,1,2,3,4k k k k k S x y x y === （8） 综合（6）（7）（8）式可得满足条件的情况满足下式{}(,)|0,4,0,1,2,3,4;k k k k k k k S x y x y x y ==== （9）所以我们知道满足条件的点如上图所示：点移动由{}(,)|4,0,1,2,3,4k k k k k S x y x y === （8） 到达{}(,)|0,0,1,2,3,4k k k k k S x y x y === （6）时，可以认为完成渡河。

数学建模作业（四）——商人过河问题一．问题描述有四名商人各带一名仆人过河，但船最多能载二人，商人已获得仆人的阴谋：在河的任一岸，只要仆人数超过商人数，仆人会将商人杀死并窃取财物且安排如何乘船的权力掌握在商人手中。

试为商人制定一个安全过河的方案。

二．解决方案用递归的源程序如下：开始时商人，强盗所在的河的这边设为0状态，另一边设为1状态（也就是船开始时的一边设为0，当船驶到对岸是设为1状态，在这两个状态时，都必须符合条件）#include <stdlib.h>struct node /*建立一个类似栈的数据结构并且可以浏览每一个数据点*/ {int x;int y;int state;struct node *next;};typedef struct node state;typedef state *link;link PPointer1=NULL;link PPointer2=NULL;int a1,b1;int a2,b2;/*栈中每个数据都分为0，1状态*/void Push(int a,int b,int n){link newnode;newnode=(link)malloc(sizeof(state));newnode-> x=a;newnode-> y=b;newnode-> state=n;newnode-> next=NULL;if(PPointer1==NULL){PPointer1=newnode;PPointer2=newnode;}else{PPointer2-> next=newnode;PPointer2=newnode;}}void Pop()/*弹栈*/{link pointer;if(PPointer1==PPointer2){free(PPointer1);PPointer1=NULL;PPointer2=NULL;}pointer=PPointer1;while(pointer-> next!=PPointer2)pointer=pointer-> next;free(PPointer2);PPointer2=pointer;PPointer2-> next=NULL;}int history(int a,int b,int n) /*比较输入的数据和栈中是否有重复的*/ {link pointer;if(PPointer1==NULL)return 1;else{pointer=PPointer1;while(pointer!=NULL){if(pointer-> x==a&&pointer-> y==b&&pointer-> state==n)return 0;pointer=pointer-> next;}return 1;}}int judge(int a,int b,int c,int d,int n)/*判断这个状态是否可行，其中使用了history函数*/{if(history(a,b,n)==0) return 0;if(a> =0&&b> =0&&a <=3&&b <=3&&c> =0&&d> =0&&c <=3&&d <=3&&a+c==3&&b+d==3){switch(n){case 1:{if(a==3){Push(a,b,n);return 1;}else if(a==0){Push(a,b,n);return 1;}else if(a==b){Push(a,b,n);return 1;}else return 0;}case 0:{if(a==3){Push(a,b,n);return 1;}else if(a==0){Push(a,b,n);return 1;}else if(a> =b){Push(a,b,n);return 1;}else return 0;}}}else return 0;}int Duhe(int a,int b,int n)/*递归法解决商人渡河问题，如果这一个状态符合*/ {/*则判断下一个状态，直至问题解决*/ if(a==0&&b==0) return 1;if(n==0)/*判断0状态时，商匪状态是否符合要求*/{if(judge(a-1,b-1,4-a,4-b,1)){if(Duhe(a-1,b-1,1)==1)return 1;}if(judge(a,b-2,3-a,5-b,1)){if(Duhe(a,b-2,1)==1)return 1;}if(judge(a-2,b,5-a,3-b,1)){if(Duhe(a-2,b,1)==1)return 1;if(judge(a-1,b,4-a,3-b,1)){if(Duhe(a-1,b,1)==1)return 1;}if(judge(a,b-1,3-a,4-b,1)){if(Duhe(a,b-1,1)==1)return 1;}else{Pop(0);return 0;}}if(n==1)/*判断0状态时，商匪状态是否符合要求*/{if(judge(a+1,b+1,2-a,2-b,0)){if(Duhe(a+1,b+1,0)==1)return 1;}if(judge(a,b+2,3-a,1-b,0)){if(Duhe(a,b+2,0)==1)return 1;}if(judge(a+2,b,1-a,3-b,0)){if(Duhe(a+2,b,0)==1)return 1;}if(judge(a+1,b,2-a,3-b,0)){if(Duhe(a+1,b,0)==1)return 1;}if(judge(a,b+1,3-a,2-b,0))if(Duhe(a,b+1,0)==1)return 1;}else{Pop(1);return 0;}}return 0;}main(){link pointer;Push(3,3,0);Duhe(3,3,0);pointer=PPointer1;while(pointer!=NULL){printf( "%d,%d---%d\n ",pointer-> x,pointer-> y,pointer-> state);pointer=pointer-> next;}getch();}。