立体构成—几何多面体(阿基米德变形多面体).

学习立体几何中的多面体特性在数学的世界中，立体几何是一个既有趣又具有挑战性的领域。

而多面体则是立体几何中一类重要的几何体，它由多个平面多边形组成。

本文将探讨学习立体几何中多面体的特性。

一、多面体的定义及分类多面体是由多个平面多边形组成的立体图形。

它的边界由多个平面多边形构成，其中每个平面多边形都共用同一个边界。

多面体的每个面都是平面多边形，而且每个顶点都是三条或更多条边的交点。

根据多面体的特性，我们可以将其分为以下几类：1. 三角柱、四棱锥、四棱柱、四面体等。

2. 正多面体，它的各个面都是相等且全等的正多边形，如正四面体、正六面体等。

3. 正/非正多面锥，它的底面是一个正/非正多边形，而侧面都是由自底面的每个顶点与一个共同顶点相连接形成的三角形。

4. 锥体和棱台，它们都是由一个多边形绕着一条轴旋转而成的。

二、多面体的性质与特点1. 基本元素：多面体由面、边和顶点组成。

每个面都由若干个边连接而成，而每条边都是两个顶点的连接线，且每个顶点都是三条或更多条边的交点。

2. 面的数量：多面体的面的数量与其种类有关。

例如，四面体有四个面，六面体有六个面。

3. 线的数量：多面体的线的数量等于边的数量。

边的数量与多面体的类型有关。

4. 顶点的数量：多面体的顶点数量与其种类和拓扑结构有关。

5. 特殊性质：正多面体的各个面都是相等且全等的正多边形，每个顶点都是相等的。

6. 对称性：许多多面体都拥有对称性，比如正多面体具有高度的对称性。

三、多面体的应用多面体在生活中和科学领域中有着广泛应用。

以下几个例子展示了多面体应用的实际意义：1. 晶体学：多面体是描述晶体形态的常用工具。

通过研究多面体的形状和结构，可以推导出晶体中的原子间距离和晶体面的朝向。

2. 建筑设计：建筑师常常运用多面体的形状设计建筑物，如球体、棱柱等。

多面体丰富了建筑物的外观，使其更加美观与富有创意。

3. 游戏设计：许多益智游戏和拼图游戏都使用多面体作为关卡设计的基础。

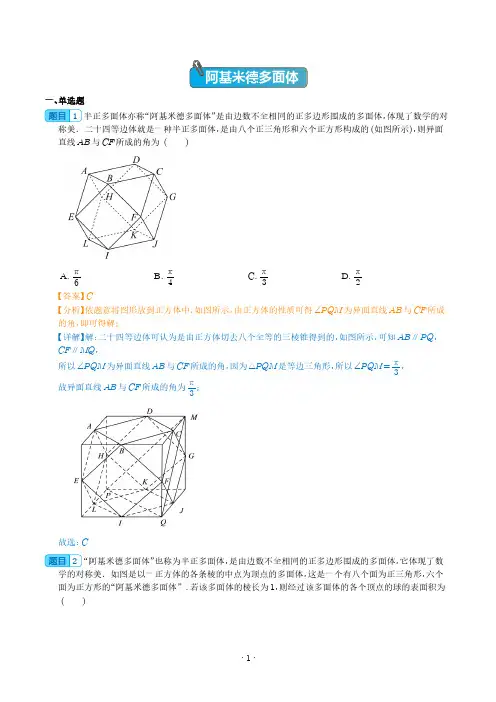
阿基米德多面体一、单选题1半正多面体亦称“阿基米德多面体”是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由八个正三角形和六个正方形构成的(如图所示)，则异面直线AB 与CF 所成的角为()A.π6B.π4C.π3D.π2【答案】C【分析】依题意将图形放到正方体中，如图所示，由正方体的性质可得∠PQM 为异面直线AB 与CF 所成的角，即可得解；【详解】解：二十四等边体可认为是由正方体切去八个全等的三棱锥得到的，如图所示，可知AB ⎳PQ ，CF ⎳MQ ，所以∠PQM 为异面直线AB 与CF 所成的角，因为△PQM 是等边三角形，所以∠PQM =π3，故异面直线AB 与CF 所成的角为π3；故选：C2“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形围成的多面体，它体现了数学的对称美．如图是以一正方体的各条棱的中点为顶点的多面体，这是一个有八个面为正三角形，六个面为正方形的“阿基米德多面体”.若该多面体的棱长为1，则经过该多面体的各个顶点的球的表面积为()A.8πB.4πC.3πD.2π【答案】B【分析】将该多面体补形为正方体，得到经过该多面体的各个顶点的球为正方体ABCD-EFGH的棱切球，求出该正方体的边长，求出棱切球的半径，得到表面积.【详解】将该多面体补形为正方体，则由OR=1，AO=AR,AO⊥AR，所以由勾股定理得：AO=AR=22，所以正方体的边长为22×2=2，所以经过该多面体的各个顶点的球为正方体ABCD-EFGH的棱切球，所以棱切球的直径为该正方体的面对角线，长度为2×2=2，故过该多面体的各个顶点的球的半径为1，球的表面积为4π×12=4π.故选：B3半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，它是由正方体的各条棱的中点连接形成的几何体、它由八个正三角形和六个正方形围成(如图所示)，若它所有棱的长都为2，则下列说法错误的是()A.该二十四等边体的表面积为24+83B.QH⊥平面ABEC.直线AH与PN的夹角为60°D.该半正多面体的顶点数V、面数F、棱数E，满足关系式V+F-E=2【答案】B【分析】由三角形和正方形面积公式即可求出二十四等边体的表面积，线面垂直判定定理，利用平移求异面直线夹角，推理分析即可判断结果.【详解】对于A，S□ABCD=22=4，S△ABE=12×32×2×2=3，S表=6S□ABCD+8S△ABE=6×4+8×3=24+83，故A正确；对于B，由图可知QH⎳BF,BF⊥EB,但BF与AB和AE都不垂直，所以QH不可能与平面ABE垂直，故B错误；对于C，由图可知AH⎳AD，而直线AH与AD的夹角为60°，所以直线AH与PN的夹角为60°，故C正确；对于D，该半正多面体的顶点数为12、面数为14、棱数为24，满足12+14-24=2，故D正确；故选：B.4“阿基米德多面体”也称为半正多面体，半正多面体是由两种或多种正多边形面组成，而又不属于正多面体的凸多面体．如图，某广场的一张石凳就是一个阿基米德多面体，它是由正方体截去八个一样的四面体得到的．若被截正方体的棱长为40cm，则该阿基米德多面体的表面积为()A.4800+16003cm2 B.4800+48003cm2C.3600+36003cm2 D.3600+12003cm2【答案】A【分析】通过图形可知阿基米德多面体是由六个全等的正方形和八个全等的等边三角形构成，分别求解正方形和等边三角形面积，加和即可.【详解】由题意知：阿基米德多面体是由六个全等的正方形和八个全等的等边三角形构成，其中正方形边长和等边三角形的边长均为202+202=202；∴阿基米德多面体的表面积S=6×2022+8×12×202×202×32=4800+16003cm2.故选：A.5“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.如图，将一个正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形，六个面为正方形的“阿基米德多面体”，则该多面体中具有公共顶点的两个正三角形所在平面的夹角正切值为()A.22B.1C.2D.22【答案】D【分析】将该多面体放在正方体中，利用空间向量的坐标运算，求出平面EFG 和平面GHK 的法向量，即可求平面EFG 和平面GHK 夹角的余弦值，进而可求解.【详解】将该“阿基米德多面体”放入正方体中，如图，平面EFG 和平面GHK 为有公共顶点的两个正三角形所在平面，建立如图所示空间直角坐标系，设正方体的棱长为2，则E (1,0,2),F (2,1,2),G (2,0,1),H (2,1,0),K (1,0,0),设平面EFG 的法向量为m=(x ,y ,z ),EF =(1,1,0),EG =(1,0,-1),所以EF ⋅m=x +y =0EG ⋅m=x -z =0，令x =1,y =-1,z =1，所以m =(1,-1,1),设平面GHK 的法向量为n=(a ,b ,c ),GH =(0,1,-1),GK =(-1,0,-1),所以GH ⋅n=b -c =0GK ⋅n=-a -c =0，令a =1,b =-1,c =-1，所以n =(1,-1,-1),设平面平面EFG 和平面GHK 的夹角为θ，则cos <m ,n >=m ⋅n m ⋅n=13×3=13，因为平面EFG 和平面GHK 的夹角为锐角，所以cos θ=cos <m ,n > =13，所以sin θ=1-cos 2θ=223,tan θ=sin θcos θ=22，故选：D6如图，将正方体沿交于同一顶点的三条棱的中点截去一个三棱锥，如此共可截去八个三棱锥，截取后的剩余部分称为“阿基米德多面体”，它是一个24等边半正多面体．从它的棱中任取两条，则这两条棱所在的直线为异面直线的概率为()A.1023B.1223C.2969D.5069【答案】B【分析】分一条直线位置于上(或下)底面，另一条不在底面；两条直线都位于上下底面时；两条直线都不在上下底面时计数，再根据古典概型公式求解即可.【详解】解：当一条直线位置于上(或下)底面，另一条不在底面时，共有10×8=80对异面直线，当两条直线都位于上下底面时，有4×2=8对异面直线，当两条直线都不在上下底面时，有7×8=56对异面直线，所以，两条棱所在的直线为异面直线的概率为P=80+56+8C224=1223故选：B7半正多面体(semiregular solid)亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．下图是棱长为2的正方体截去八个一样的四面体，得到的一个半正多面体，则下列说法错误的是()A.该半正多面体是十四面体B.该几何体外接球的体积为4π3C.该几何体的体积与原正方体的体积比为5∶6D.原正方体的表面积比该几何体的表面积小【答案】D【分析】由题意求该几何体的体积与表面积，由外接球的半径求体积，对选项逐一判断即得.【详解】由图可知该半正多面体的表面是由6个正方形和8个等边三角形构成，所以为十四面体，该半正多面体是十四面体，故A正确；该几何体外接球的球心为原正方体的中心，故外接球半径为1，外接球的体积为4π3，故B正确；对于C，该几何体的体积V=V正方体-8V四面体=(2)3-8×13×12×12×22=523，正方体体积为22，故该几何体的体积与原正方体的体积比为5∶6，故C正确；对于D，该几何体有6个面为正方形，8个面为等边三角形，S表=6×12+8×34×1=6+23<12，即原正方体的表面积比该几何体的表面积大，故D 错误．故选：D ．8“阿基米德多面体”这称为半正多面体(semi -regularsolid )，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.如图所示，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形、六个面为正方形的一种半正多面体.已知AB =322，则该半正多面体外接球的表面积为()A.18πB.16πC.14πD.12π【答案】A【分析】根据正方体的对称性可知：该半正多面体外接球的球心为正方体的中心O ，进而可求球的半径和表面积.【详解】如图，在正方体EFGH -E 1F 1G 1H 1中，取正方体、正方形E 1F 1G 1H 1的中心O 、O 1，连接E 1G 1,OO 1,OA ,O 1A ，∵A ,B 分别为E 1H 1,H 1G 1的中点，则E 1G 1=2AB =32，∴正方体的边长为EF =3，故OO 1=O 1A =32，可得OA =OO 21+O 1A 2=322，根据对称性可知：点O 到该半正多面体的顶点的距离相等，则该半正多面体外接球的球心为O ，半径R =OA =322，故该半正多面体外接球的表面积为S =4πR 2=4π×3222=18π.故选：A .9中国有悠久的金石文化，印信是金石文化代表之一，印信的形状多为长方体､正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”.半正多面体是由两种或两种以上的正多边形围成的多面体，古希腊著名数学家阿基米德研究过此类多面体的性质，故半正多面体又被称为“阿基米德多面体”.半正多面体体现了数学的对称美，如图，是一个棱数为24的半正多面体，它的所有顶点都在同一个正方体的棱上，且此正方体的棱长为1.则下列关于该多面体的说法中错误的是()A.多面体有12个顶点，14个面B.多面体的表面积为3C.多面体的体积为56 D.多面体有外接球(即经过多面体所有顶点的球)【答案】B【分析】求得一个棱数为24的半正多面体的顶点数和面数，可判断A ；将半正多面体补成棱长为1的正方体，故其顶点是正方体各棱的中点，求得半正多面体的棱长，计算表面积和体积，可判断B ，C ；再由正方体的中心到多面体各顶点的距离相等，可判断D ．【详解】解：一个棱数为24的半正多面体有12个顶点，14个面；可将半正多面体补成棱长为1的正方体，故其顶点是正方体各棱的中点．半正多面体的棱长为22，表面积为S =8×34×22 2+6×22 2=3+3，体积可看作正方体的体积减去八个三棱锥的体积，则V =1-8×16×12 3=56，又因为正方体的中心到多面体各顶点的距离相等，所以有外接球．故选：B ．10半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形围成(如图所示)，若它所有棱的长都为2，则()A.BC ⊥平面ABEB.该二十四等边体的体积为3223C.ME 与PN 所成的角为45°D.该二十四等边体的外接球的表面积为16π【答案】D【分析】依题意补齐正方体，对于A ，假设BC ⊥平面ABE ，得到∠EBC =90°，根据六边形EBCGQM 为正六边形，∠EBC =120°，得出矛盾判断A ；对于B ，结合集合图形，该二十四等边体的体积为正方体体积去掉八个三棱锥体积，从而求出B ；对于C ，由平移法找出异面直线所成角为∠NPF =60°，判断C ；对于D ，取正方形ACPM 对角线交点为O ，即为该二十四等边体的外接球球心，从而求出半径大小，进而求出外接球体积，判断D .【详解】依题意，补齐正方体，如下图，对于A ，假设BC ⊥平面ABE ，∵BE ⊂平面ABE ，∴BE ⊥BC ，∴∠EBC =90°，∵二十四等边体就是一种半正多面体，由对称性可知，六边形EBCGQM 为正六边形，∴∠EBC =120°，这与“∠EBC =90°”矛盾，所以假设不成立，A 错误；对于B ，∵BF =FN =2，∴正方体的棱长为22，∴该二十四等边体的体积为正方体体积去掉8个三棱锥体积，即22 3-8×13×12×2×2×2=4023，B 错误；对于C ，∵EM ⎳PF ，∴∠NPF 为异面直线ME 与PN 所成角(或补角)，在等边△NFP 中，∠NPF =60°，C 错误；对于D ，如图，取正方形ACPM 对角线交点为O ，即为该二十四等边体的外接球球心，在等腰Rt △PFC 中，PC =22，在正方形ACPM 中，AO =2，即外接球半径R =2，∴该二十四等边体的外接球的表面积S =4πR 2=16π，D 正确.故选：D .11有很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体.如图，这是一个棱数为24，棱长为2的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得.若点E 为线段BC 上的动点，则直线DE 与直线AF 所成角的余弦值的取值范围为()A.13,22B.13,32C.12,22D.12,32【答案】C【分析】将半正多面体补成正方体并建立空间直角坐标系，确定相关点坐标，设BE =λBC=-λ,λ,0 ,λ∈0,1 ，利用向量夹角的坐标表示及二次函数性质求所成角的余弦值的取值范围.【详解】将半正多面体补成正方体，建立如图所示的空间直角坐标系.因为半正多面体的棱长为2，故正方体的棱长为2.所以A 2,1,0 ,F 2,2,1 ，B 1,0,2 ,C 0,1,2 ,D 1,2,2 ,AF =0,1,1 ,BC =-1,1,0 .设BE =λBC =-λ,λ,0 ,λ∈0,1 ，则E 1-λ,λ,2 ,DE =-λ,λ-2,0 .所以cos AF ,DE =AF ⋅DEAF DE =λ-22λ2+(λ-2)2=-12(λ-2)2(λ-2)2+2λ-2 +2=-1211+2λ-2+2(λ-2)2.令t =1λ-2∈-1,-12 ，则cos AF ,DE =-122t 2+2t +1，因为2t 2+2t +1∈12,1 ，所以cos AF ,DE ∈-22,-12.故直线DE 与直线AF 所成角的余弦值的取值范围为12,22.故选：C 12半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美.二十四等边体就是一种半正多面体，它是由正方体的各条棱的中点连接形成的几何体.它由八个正三角形和六个正方形围成(如图所示)，若它的棱长为2，则下列说法错误的是()A.该二十四等边体的外接球的表面积为16πB.该半正多面体的顶点数V、面数F、棱数E，满足关系式V+F-E=2C.直线AH与PN的夹角为60°D.QH⊥平面ABE【答案】D【分析】将二十四等边体补齐成正方体，根据空间几何相关知识进行判断.【详解】由已知，补齐二十四等边体所在的正方体如图所示记正方体体心为O，取下底面ABCD中心为O1，二十四等边体的棱长为2易知OO1=BO1=2，则外接球半径R=OB=2+2=2所以外接球的表面积S=4πR2=16π，故A正确.由欧拉公式可知：顶点数+面数-棱数=2，故B正确.又因为PN∥AD，易知直线AH与PN的夹角即为∠HAD=60°直线AH与PN的夹角为60°，故C正确.又因为QH∥EN，AB∥MN，易知直线QH与直线AB的夹角为∠ENM=60°可知直线QH与直线AB不垂直，故直线QH与平面ABE不垂直，故D错误.故选：D13“阿基米德多面体”是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.如图，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形，六个面为正方形的“阿基米德多面体”.若该多面体的棱长为2，则其外接球的表面积为()A.16πB.8πC.16π3D.32π3【答案】A 【分析】根据其外接球为正四棱柱的外接球，再结合球的表面积公式，即可得到结果.【详解】由题意可得AB =2，根据该几何体的对称性可知，该几何体的外接球即为底面棱长为2，侧棱长为22的正四棱柱的外接球，即2R 2=22+22+22 2，所以R =2，则该正多面体外接球的表面积S =4πR 2=4π×22=16π故选:A14“阿基米德多面体”也称半正多面体，是由边数不全相同的正多边形围成的多面体，它体现了数学的对称美.如图是以一正方体的各条棱的中点为顶点的多面体，这是一个有八个面为正三角形，六个面为正方形的“阿基米德多面体”，若该多面体的棱长为1，则经过该多面体的各个顶点的球的体积为()A.43πB.82π3C.4πD.8π【答案】A 【分析】根据给定条件，把多面体放在棱长为2的正方体中，结合正方体的结构特征确定球心，求出球半径作答.【详解】把该多面体放入正方体中，如图，由于多面体的棱长为1，则正方体的棱长为2，因此该多面体是由棱长为2的正方体连接各棱中点所得，于是得该多面体的外接球球心是正方体体对角线中点，该多面体外接球半径R 等于球心到一个顶点的距离，即正方体面对角线的一半，则2R =2×2，解得R =1，所以经过该多面体的各个顶点的球的体积为V =4π3R 3=4π3.故选：A【点睛】关键点睛：解决与球有关的内切或外接问题时，关键是确定球心的位置，再利用球的截面小圆性质求解.15有很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体.如图，这是一个棱数为24，棱长为2的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得.若点E 为线段BC 上的动点，则下列结论不正确的是()A.存在点E 、使得A 、F 、D 、E 四点共面；B.存在点E ，使DE ⊥DF ；C.存在点E ，使得直线DE 与平面CDF 所成角为π3；D.存在点E ，使得直线DE 与直线AF 所成角的余弦值3510.【答案】C【分析】将半正多面体补成一个棱长为2的正方体，当点E 在点C 时，根据DF ⎳AC ，得A 、F 、D 、E 四点共面，故A 正确；当点E 在点B 时，根据正方体的性质易得DE ⊥DF ，故B 正确；对C ，建立空间直角坐标系，利用线面角的向量公式计算，可知C 不对；对于D ，根据直面值直线夹角的向量公式计算，可知D 正确.【详解】将半正多面体补成一个棱长为2的正方体，如图：则半正多面体的所有顶点都是正方体的棱的中点，对A ，当点E 在点C 时，DF ⎳AC ，则A 、F 、D 、E 四点共面，A 正确；对B ，当点E 在点B 时，易得DE ⊥DF ，B 正确；以O 为原点，过O 的三条棱所在直线分别为x ,y ,z 轴建立如图所示的空间直角坐标系.则A 2,1,0 ，F 2,2,1 ，B 1,0,2 ，C 0,1,2 ，D 1,2,2 ，对C ，设BE =λBC (0≤λ≤1)，则DE =DB +BE =DB +λBC =(0,-2,0)+λ(-1,1,0)=(-λ,λ-2,0)，设平面CDF 的一个法向量为n =x ,y ,z ，CD =1,1,0 ，CF =2,1,-1 ，则n ⋅CD =x +y =0n ⋅CF =2x +y -z =0 ，令x =1，得y =-1，z =1，∴n =1,-1,1 ，设直线DE 与平面CDF 所成角为θ，则sin θ=n ⋅DE DE ⋅n=-λ+2-λλ2+(λ-2)2×3 ，若θ=π3，则sin θ=32，则2-2λ 3⋅2λ2-4λ+4=32,化简得λ2-2λ+10=0，此方程无解，故不存在点E ，使得直线DE 与平面CDF 所成角为π3，C 不对；对D ，AF =0,1,1 ，由C 可知，DE =(-λ,λ-2,0)，所以cos <AF ,DE >=AF ⋅DE AF DE =λ-22⋅λ2+λ-2 2=3510，∴λ=12，即E 为BC 的中点时，直线DE 与直线AF 所成角的余弦值3510，故D 正确.故选：C二、多选题16半正多面体(semiregular solid )亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，半正多面体有且只有13种．最早用于1970年世界杯比赛的足球就可以近似看作是由12个正五边形和20个正六边形组成的半正面体，半正多面体体现了数学的对称美．如图所示的二十四等边体就是一种半正多面体，它由8个正三角形和6个正方形围成，它是通过对正方体进行八次切截而得到的．若这个二十四等边体的棱长都为2，则下列结论正确的是()A.MQ 与平面AEMH 不可能垂直B.异面直线BC 和EA 所成角为60°C.该二十四等边体的体积为4023D.该二十四等边体外接球的表面积为18π【答案】ABC 【分析】根据线面垂直得线线垂直，即可找到矛盾进而判断A ,根据异面直线的夹角即可求解B ,根据割补法即可求解C ,根据外接球的半径即可求解表面积.【详解】对于A ，若MQ ⊥平面AEMH ，因为MH ⊂平面AEMH ，所以MQ ⊥MH ，又因为△MQH 为等边三角形，所以∠QMH =60°，这与MQ ⊥MH 矛盾，故MQ 与平面AEMH 不可能垂直，所以A 正确；对于B ，因为BC ∥AD ，所以异面直线BC 和EA 所成的角即为直线AD 和EA 所成的角，设角∠EAD =θ，在正六边形ADGPNE 中，可得θ=120°，所以异面直线BC 和EA 所成角为60°，所以B 正确；对于C ，补全八个角构成一个棱长为22的一个正方体，则该正方体的体积为V =(22)3=162，其中每个小三棱锥的体积为V 1=13×12×2×2×2=23，所以该二十四面体的体积为162-8×23=4023，所以C 正确；对于D ，取正方形ACPM 对角线的交点为O ，即为该二十四面体的外接球的球心，其半径为R =12AC 2+AM 2=12(22)2+(22)2=2，所以该二十四面体的外接球的表面积为S =4πR 2=4π×22=16π，所以D 不正确．故选：ABC .17“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美．如图，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共截去八个三棱锥，得到的半正多面体的表面积为12+43，则关于该半正多面体的下列说法中正确的是( )．A.AB =2B.该半正多面体的外接球的表面积为6πC.AB 与平面BCD 所成的角为π4 D.与AB 所成的角是π3的棱共有16条【答案】ACD 【分析】补全该半正多面体得到一正方体，根据条件计算正方体的棱长，再求AB 的长，判断A ;利用几何体的对称性确定该半正多面体的外接球的球心及半径,判断B ；根据线面角的定义找到线面角，解三角形求其大小,判断C ；利用平行关系，确定与AB 所成的角是π3的棱的条数，判断D .【详解】补全该半正多面体得到一正方体，设正方体的棱长为a ，则AB =22a ，对选项A ：由题意知，该半正多面体由6个全等的正方形和8个全等的正三角形构成.则由半正多面体的表面积为12+43，得8×34×22a 2+6×22a2=12+43，解得a =2，∵a =2，∴AB =2，故A 正确；对选项B ：由半正多面体的对称性可知，其对称中心与相应的正方体的对称中心是同一点，其对称中心为正方体的体对角线的中点O ，点O 在平面ABE 的投影点为O 1，则有OO 1=1，AO 1=1，所以AO =OO 12+AO 12=2，故该半正多面体的外接球的半径为2，面积为4π×2 2=8π，故B 错误；对选项C ：因为AE ⊥平面BCD ，所以∠ABE 为AB 与平面BCD 的夹角，因为△AEB 为直角三角形，且AE =BE ，所以∠ABE =π4所以AB 与平面BCD 所成的角为∠ABE =π4，故C 正确；对选项D ：在与AB 相交的6条棱中，与AB 所成的角是π3的棱有4条，又这4条棱中，每一条棱都有3条平行的棱，故与AB 所成的角是π3的棱共有16条，故D 正确；故选：ACD .18半正多面体(semiregularsolid)亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美，二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形构成(如图所示)，若它的所有棱长都为2，则()A.BF⊥平面EABB.AB与PF所成角为45°C.该二十四等边体的体积为20D.该二十四等边体多面体有12个顶点，14个面3【答案】CD【分析】将该二十四等边体补形为正方体, 利用RS与BF是异面直线判定选项A错误，利用PF∥AH和△ABH的形状判定选项B错误，利用正方体和等二十四等边体的关系和分割法判定选项C正确，利用该二十四等边体顶点数和面数判定选项D正确.【详解】将该二十四等边体补形为正方体(如图所示)，因为该二十四等边体的所有棱长都为2，所以正方体的棱长为2，对于A：正方体的体对角线RS⊥平面EAB，而RS与BF是异面直线，所以BF⊥平面EAB不成立，即选项A错误；对于B：因为PF∥AH，所以∠HAB是AB与PF所成角或其补角，在△ABH中，AH=AB=2，BH2=12+22+12=6，因为AH 2+AB 2≠BH 2，所以∠HAB ≠45°，即选项B 错误；对于C ：因为该二十四等边体的所有棱长都为2，所以正方体的棱长为2，所以该二十四等边体的体积为V =23-13×13×8=203，即选项C 正确；对于D ：该二十四等边体多面体有A ,B ,C ,D ,E ,F ,G ,H ,M ,N ,P ,Q 共12个顶点，有面ABCD ，面ABE ，面BCF ，面GCD ，面ADH ，面BENF ，面CFPG ，面DGQH ，面AHME ，面EMN ，面NFP ，面PQG ，面MHQ ，面MNPQ 共14个面，即选项D 正确.故选：CD .19“阿基米德多面体”也称为半正多面体，它是由边数不全相同的正多边形为面围成的多面体，体现了数学的对称美．如图，将正方体沿交于同一顶点的三条棱的中点截去一个三棱锥，共截去八个三棱锥，得到的半正多面体的表面积为12+43，则关于该半正多面体的下列说法中正确的是()A.AB 与平面BCD 所成的角为π4 B.AB =22C.与AB 所成的角是π3的棱共有16条 D.该半正多面体的外接球的表面积为6π【答案】AC 【分析】补全该半正多面体得到一正方体，根据线面角的定义找到线面角，解三角形求其大小,判断A ；根据条件计算正方体的棱长，再求AB 的长，判断B ;利用平行关系，确定与AB 所成的角是π3的棱的条数，判定C ，利用几何体的对称性确定半正方体的外接球的球心及半径,判定D ；【详解】补全该半正多面体得到一正方体，设正方体的棱长为a ，由题意知，该半正多面体由6个全等的正方形和8个全等的正三角形构成.则由半正多面体的表面积为12+43，得8×34×22a 2+6×22a2=12+43，解得a =2，∵a =2，因为AE ⊥平面BCD ，∠ABE 为AB 与平面BCD 的夹角，因为△AEB 为直角三角形，且AE =BE ，所以∠ABE =π4所以AB 与平面BCD 所成的角为∠ABE =π4，故A 正确；∴AB =AE 2+BE 2=2，故B 错误；在与AB 相交的6条棱中，与AB 所成的角是π3的棱有4条，又这4条棱中，每一条棱都有3条平行的棱，故与AB 所成的角是π3的棱共有16条，故C 正确；由半正多面体的对称性可知，其对称中心与相应的正方体的对称中心是同一点，其对称中心为正方体的体对角线的中点O ，点O 在平面ABE 的投影点为O 1，则有OO 1=1，AO 1=1，所以AO =OO 12+AO 12=2，故该半正多面体的外接球的半径为2，面积为4π×2 2=8π，故D 错误；故选：AC .20半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形围成(如图所示)，若它所有棱的长都为2，则()A.BC ⊥平面ABEB.该二十四等边体的体积为4023C.ME 与NP 的夹角为60°D.该二十四等边体的外接球的表面积为16π【答案】BD 【分析】依题意补齐正方体，对于A ，假设BC ⊥平面ABE ，得到∠EBC =90°，根据六边形EBCGQM 为正六边形，∠EBC =120°，得出矛盾判断A ；对于B ，结合集合图形，该二十四等边体的体积为正方体体积去掉八个三棱锥体积，从而求出B ；对于C ，由平移法找出异面直线所成角为∠NPF =60°，判断C ；对于D ，取正方形ACPM 对角线交点为O ，即为该二十四等边体的外接球球心，从而求出半径大小，进而求出外接球体积，判断D .【详解】依题意，补齐正方体，如下图，对于A ，假设BC ⊥平面ABE ，∵BE ⊂平面ABE ，∴BE ⊥BC ，∴∠EBC =90°，∵二十四等边体就是一种半正多面体，由对称性可知，六边形EBCGQM 为正六边形，∴∠EBC =120°，这与“∠EBC =90°”矛盾，所以假设不成立，A 错误；对于B ，∵BF =FN =2，∴正方体的棱长为22，∴该二十四等边体的体积为正方体体积去掉8个三棱锥体积，。