数电第五版(阎石)第三章课后习题及答案

第3章逻辑门电路3.1 概述逻辑门电路:用以实现基本和常用逻辑运算的电子电路。

简称门电路.用逻辑1和0 分别来表示电子电路中的高、低电平的逻辑赋值方式，称为正逻辑,目前在数字技术中，大都采用正逻辑工作；若用低、高电平来表示，则称为负逻辑。

本课程采用正逻辑。

获得高、低电平的基本方法：利用半导体开关元件的导通、截止（即开、关）两种工作状态.在数字集成电路的发展过程中，同时存在着两种类型器件的发展。

一种是由三极管组成的双极型集成电路,例如晶体管-晶体管逻辑电路（简称TTL电路）及射极耦合逻辑电路（简称ECL电路）.另一种是由MOS管组成的单极型集成电路，例如N-MOS逻辑电路和互补MOS(简称COMS）逻辑电路。

3。

2 分立元件门电路3。

3.1二极管的开关特性3.2.2三极管的开关特性NPN型三极管截止、放大、饱和3种工作状态的特点工作状态截止放大饱和条件i B＝0 0＜i B＜I BS i B＞I BS工作特点偏置情况发射结反偏集电结反偏u BE〈0，u BC〈0发射结正偏集电结反偏u BE>0，u BC〈0发射结正偏集电结正偏u BE〉0，u BC〉集电极电流i C＝0 i C＝βi B i C＝I CSce间电压u CE＝V CC u CE＝V CC－i C R cu CE＝U CES＝0.3Vce间等效电阻很大，相当开关断开可变很小，相当开关闭合3.2。

3二极管门电路1、二极管与门2、二极管或门u A u B u Y D1D20V 0V 0V 5V 5V 0V 5V 5V0V4。

3V4。

3V4.3V截止截止截止导通导通截止导通导通3。

2.4三极管非门3。

2。

5组合逻辑门电路1、与非门电路2、或非门电路3.3 集成逻辑门电路一、TTL与非门1、电路结构(1）抗饱和三极管作用：使三极管工作在浅饱和状态。

因为三极管饱和越深，其工作速度越慢，为了提高工作速度，需要采用抗饱和三极管。

构成:在普通三极管的基极B和集电极C之间并接了一个肖特基二极管(简称SBD）。

习 题1题1.1 数字信号的波形如图题1.1.1图所示，若波形的高，低电平用正逻辑赋值。

试用二进制数序列表示该脉冲波形（每一时间段用一位二进制数表示）。

解：从时间段1~8的数字序列为:10011011。

题1.2 若用正逻辑赋值。

高电平等于3伏，低电平等于0.3伏，将下述二进制数序列用脉冲波形表示（一位二进制数用每一相等的时间段表示）。

（a ） 110110101 （b ） 1011001 （c ） 10101011 （d ） 10001110解：对于各个数字序列，用脉冲波形表示如图1.1(a)、(b)、(c)、(d)所示。

题1.3 有一脉冲信号，脉冲信号的高电平维持时间为0.1μS,低电平维持时间为0.4μS 求信号的脉冲周期T ，占空比q 。

解：脉冲周期T=高电平维持时间+低电平维持时间＝0.1μS+0.4μS ＝0.5μS ；占空比q ＝高电平维持时间/脉冲周期T=0.1/0.5=0.2。

题1.4 有一正弦模拟信号，u(t)=9sinωt 伏，若以0.5伏作为基本转换单位，试问在t=T/4，T/2，3T/4，T/6时，将该模拟量的瞬时值转换数字量，则数字量为多大？解：在t=T/4，T/2，3T/4，T/6时，u(t)=9sinωt 伏的瞬时值分别为：9V ，0V ，－9V ，7.94V ，采用四舍五入进行量化：则数字量分别为：18，0，－18，16。

题1.5 将下述十进制数转换成为八进制数(保留小数点后二位)，再转换成为二进制数。

（a ） 658.95D （b ） 135.16D （c ） 63.24D （d ） 1027.67D解：658D ＝1×83+2×82+2×81+2×80，而 0.95×8＝7.6，0.6×8＝4.8,所以： 658.95D ＝1222.74O ＝1010010010.1111B ;同理：135.16D =207.12O =10000111.00101B ;63.24D =77.17O =111111.001111B ;1027.67D =2003.52O =10000000011.10101B ;题1.6 将下述十进制数转换成为十六进制数(保留小数点后二位)，再转换成为二进制数。

第一章数字逻辑习题1．1 数字电路与数字信号图形代表的二进制数1．1．4 一周期性数字波形如图题所示，试计算：（1）周期；（2）频率；（3）占空比例MSB LSB0 1 2 11 12 （ms）解：因为图题所示为周期性数字波，所以两个相邻的上升沿之间持续的时间为周期，T=10ms 频率为周期的倒数，f=1/T=1/=100HZ占空比为高电平脉冲宽度与周期的百分比，q=1ms/10ms*100%=10%数制将下列十进制数转换为二进制数，八进制数和十六进制数（要求转换误差不大于2−4（2）127 （4）解：（2）（127）D= 27 -1=（）B-1=（1111111）B=（177）O=（7F）H（4）（）D=B=O=H二进制代码将下列十进制数转换为 8421BCD 码：（1）43 （3）解：（43）D=（01000011）BCD试用十六进制写书下列字符繁荣ASCⅡ码的表示：P28（1）+ （2）@ （3）you (4)43解：首先查出每个字符所对应的二进制表示的ASCⅡ码，然后将二进制码转换为十六进制数表示。

（1）“+”的ASCⅡ码为 0101011，则（00101011）B=（2B）H（2）@的ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,33逻辑函数及其表示方法在图题 1. 中，已知输入信号 A，B`的波形，画出各门电路输出 L 的波形。

解: (a)为与非， (b)为同或非，即异或第二章逻辑代数习题解答用真值表证明下列恒等式(3)A⊕ =B AB AB+ （A⊕B）=AB+AB解：真值表如下由最右边2栏可知，A⊕B与AB+AB的真值表完全相同。

用逻辑代数定律证明下列等式(3)A+ABC ACD C D E A CD E++ +( ) = + +解：A+ABC ACD C D E++ +( )=A(1+BC ACD CDE)+ += +A ACD CDE+= +A CD CDE+ = +A CD+ E用代数法化简下列各式 (3)ABC B( +C)解：ABCB( +C)= + +(A B C B C)( + )=AB AC BB BC CB C+ + + + +=AB C A B B+ ( + + +1)=AB C+(6)(A + + + +B A B AB AB ) ( ) ( )() 解：(A + + + +B A B AB AB ) () ( )( )= A B ⋅+ A B ⋅+(A + B A )(+ B )=AB(9)ABCD ABD BCD ABCBD BC + + + +解：ABCD ABD BCD ABCBD BC +++ +=ABC D D ABD BC D C ( + +) + ( + ) =B AC AD C D ( + + + ) =B A C AD ( + + + ) =B A C D ( + + ) =AB BC BD + +画出实现下列逻辑表达式的逻辑电路图，限使用非门和二输入与非门B AB AB = + + AB B = + A B = +(1)L AB AC =(2) ( ) L DAC = +已知函数L （A ，B ，C ，D ）的卡诺图如图所示，试写出函数L 的最简与或表达式用卡诺图化简下列个式(3) ( )() L ABCD=+ +解： ( , , , ) L ABCDBCDBCDBCDABD = + + +（1）ABCD ABCD AB AD ABC+ + + +解：ABCD ABCD AB AD ABC+ + + +=ABCD ABCD ABC C D D AD B B C C ABC D D++ ( + )( + +)( + )( + +)( + )=ABCD ABCD ABCD ABCD ABCD ABCD ABCD+ + + + + +（6）L A B C D( , , , )=∑m(0,2,4,6,9,13)+∑d(1,3,5,7,11,15)解：L= +A D（7）L A B C D( , , , )=∑m(0,13,14,15)+∑d(1,2,3,9,10,11)解:L AD AC AB= + +已知逻辑函数L AB BC CA=+ + ，试用真值表,卡诺图和逻辑图（限用非门和与非门）表示解:1>由逻辑函数写出真值表用摩根定理将与或化为与非表达式L = AB + BC + AC = AB BC AC ⋅ ⋅4>由已知函数的与非-与非表达式画出逻辑图2> 由真值表画出卡诺图3> 由卡诺图,得逻辑表达式 LABBCAC = + +第三章习题MOS 逻辑门电路根据表题所列的三种逻辑门电路的技术参数，试选择一种最合适工作在高噪声环境下的门电路。

【最新整理，下载后即可编辑】第一章1.1 二进制到十六进制、十进制(1)(10010111)2=(97)16=(151)10 (2)(1101101)2=(6D)16=(109)10(3)(0.01011111)2=(0.5F)16=(0.37109375)10 (4)(11.001)2=(3.2)16=(3.125)10 1.2 十进制到二进制、十六进制(1)(17)10=(10001)2=(11)16(2)(127)10=(1111111)2=(7F)16(3) (0.39) 10 (0.0110 0011 1101 0111 0000 101 0)2 (0.63 D70 A )161.8 用公式化简逻辑函数(1)Y=A+B(2)Y ABC A B C 解：Y BC A B C C A B C （1 A＋A＝1）(4)Y ABCD ABD ACD 解：Y AD(BC B C ) AD(B C C) AD(5)Y=0(4) (25.7) 10 (11001.101 1 0011)2 (19.B3)16(3)Y=1(7)Y=A+CD(6)Y AC(CD AB) BC(B AD CE) 解：Y BC(B AD CE) BC(B AD) CE ABCD(C E ) ABCDE（8）Y A (B C)(A B C)(A B C) 解：Y A (B C)(A B C)(A B C) A (ABC BC)(A B C) A BC( A B C) A ABC BC A BC(9)Y BC AD AD(10)Y AC AD AEF BDE BDE1.9 (a) Y ABC BC(b)(c) Y1 AB AC D,Y2 AB AC D ACD ACD (d) Y1 AB AC BC,Y2 ABC ABC ABC ABC 1.10 求下列函数的反函数并化简为最简与或式Y ABC ABC(1) (2)Y A C DY AC BC(3)Y (A B)(A C)AC BC 解：Y ( A B)(A C)AC BC [(A B)(A C) AC] BC(4)Y A B C ( AB AC BC AC)(B C) B C【最新整理，下载后即可编辑】(5)Y AD AC BCD C 解：Y (A D)(A C)(B C D)C AC(A D)(B C D) ACD(B C D) ABCD1.11 将函数化简为最小项之和的形式(6)Y 0(1)Y ABC AC BC 解：Y ABC AC BC ABC A(B B )C ( A A)BC ABC ABC ABC ABC ABC ABC ABC ABC ABC（2）Y ABCD ABCD ABCD ABCD ABCD ABCD （3）Y A B CD解：Y A(BC D BCD BCD BCD BC D BCD BCD BCD) B( ACD ACD ACD ACD AC D ACD ACD ACD) (AB AB AB AB)CD ABC D ABCD ABCD ABCD ABC D ABCD ABCD ABCD ABC D ABCD ABCD ABCD ABCD (13)(4)Y ABCD ABCD ABCD ABC D ABCD ABCD ABCD ABCD (5)Y LM N LMN LMN LMN L M N LMN1.12 将下列各函数式化为最大项之积的形式(1)Y (A B C )( A B C)( A B C )(2)Y (A B C)( A B C)( A B C)(3)Y M 0 M 3 M 4 M 6 M 7(4) Y M 0 M 4 M 6 M 9 M12 M13(5)Y M 0 M 3 M 51.13 用卡诺图化简法将下列函数化为最简与或形式：(1)Y A D(3)Y 1(2)Y AB AC BC CD(4)Y AB AC BC(5)Y B C DY C D AB(7)(9)Y B D AD BC ACD (8)Y ( A, B, C, D) m (0,1,2,3,4,6,8,9,10,11,14)Y AB AC(6)Y AB AC BCY C(10)Y ( A, B, C) (m1,m4 , m7 )Y B CD AD 【最新整理，下载后即可编辑】Y ABC ABC ABC1.14 化简下列逻辑函数 (1)Y A B C D (3)Y AB D AC (5)Y AB DE CE BDE AD ACDE1.20 将下列函数化为最简与或式 (1)Y ACD BCD AD (3)Y A B C (5)Y 1 第三章3.1 解：由图可写出 Y1、Y2 的逻辑表达式：Y1 ABC ( A B C) AB AC BC ABC ABC ABC ABCY2 AB AC BC真值表：(2)Y CD ACD (4)Y BC BD(2)Y B AD AC (4)Y A B D (6)Y CD B D AC3.2 解： ， comp 1、Z 0 时，Y1 A，Y2 A2，Y3 A2 A3 A2 A3，Y4 A2 A3 A4comp 0、Z 0 时，Y1 A1，Y2 A2，Y3 A3，Y4 A真值表：3.3 解：【最新整理，下载后即可编辑】3.4 解：采用正逻辑，低电平＝0，高电平＝1。

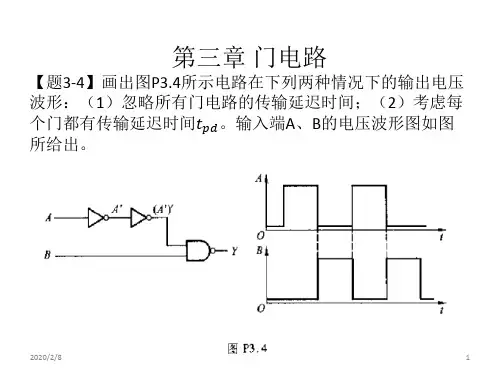
第1章数制和码制1.1复习笔记一、数字信号与数字电路1.模拟信号和数字信号模拟信号：幅度和时间连续变化的信号。

例如，正弦波信号。

数字信号：在幅度和时间上取值离散的信号。

例如，统计一座桥上通过的汽车数量。

模拟信号经过抽样、量化、编码后可转化为数字信号。

数字信号的表示方式：（1）采用二值数字来表示，即0、1数字；0为逻辑0，1为逻辑1。

（2）采用逻辑电平来表示，即H（高电平）和L（低电平）。

（3）采用数字波形来表示。

2.模拟电路和数字电路模拟电路：工作在模拟信号下的电路统称为数字电路。

数字电路：工作在数字信号下的电路统称为数字电路。

数字电路的主要研究对象是电路的输入和输出之间的逻辑关系；主要分析工具是逻辑代数关系；表达电路的功能的方法有真值表，逻辑表达式及波形图等。

二、几种常用的进制不同的数码既可以用来表示不同数量的大小，又可以用来表示不同的事物。

在用数码表示数量的大小时，采用的各种计数进位制规则称为数制，主要包括进位制、基数和位权三个方面。

进位制：多位数码每一位的构成以及从低位到高位的进位规则。

基数：在进位制中可能用到的数码个数。

位权：在某一进位制的数中，每一位的大小都对应着该位上的数码乘上一个固定的数，这个固定的数就是这一位的权数，权数是一个幂。

常用的数制有十进制、二进制、八进制和十六进制几种。

1.十进制在十进制数中，每一位有0～9十个数码，所以计数基数为10。

超过9的数必须用多位数表示，其中低位和相邻高位之间的关系是“逢十进一”，故称为十进制。

十进制的展开形式为式中，是第i位的系数，可以是0～9十个数码中的任何一个。

任意N进制的展开形式为式中，是第i位的系数，N为计数的基数，为第i位的权。

2.二进制在二进制数中，每一位仅有0和1两个可能的数码，计数基数为2。

低位和相邻高位间的进位关系是“逢二进一”。

二进制的展开形式为例如，（101.11）2=1×22＋0×21＋1×20＋1×2-1＋0×2-2=（5.75）10。