2014年秋季新版苏科版七年级数学上学期3.3、代数式的值同步练习4

随堂测试3.3代数式的值一、单选题1．若a 是最大的负整数，b 是绝对值最小的有理数，c 是倒数等于它本身的自然数，则代数式201920192020a b c ++的值为（）A ．0B ．2C ．2019D ．20202．当2m =，3n =时，多项式()()12m n m n ---的值是（）.A ．12B ．12-C ．32D ．32-3．若2x =，则318x 的值是（）.A ．12B ．1C ．4D ．84．若a 、b 互为相反数，c 、d 互为倒数，则223a b cd +-的值是（）.A ．0B ．-3C ．3D ．25．当1x =-时，代数式323ax bx -值为10，则代数式962b a -+的值为()A ．28B ．28-C ．32D ．32-6．已知x ﹣2y ＝2，则代数式3x ﹣6y+2014的值是（）A ．2016B ．2018C ．2020D ．20217．当x ＝1时，代数式ax 2+bx+3的值为1，当x ＝﹣1时，代数式ax 2﹣bx ﹣3的值为（）A ．1B ．﹣1C ．5D ．﹣58．若a ，b 互为相反数，c ，d 互为倒数，则（a ＋b ＋d ）÷1c 等于（）A ．0B ．1C ．2D ．39．当a ，b 互为相反数时，代数式22a ab +-的值为（）A ．2B ．0C ．-2D ．110．当1x =时，代数式31px qx ++的值为2021，则当1x =-时，代数式31px qx ++的值为（）A ．2020B ．-2020C ．2019D ．-2019二、填空题11．已知a ﹣2b ＝1，则3﹣2a+4b ＝____．12．已知a 、b 互为相反数，m 、n 互为倒数，则()3a b mn ++=____________．13．若a 和b 互为相反数，c 和d 互为倒数，则20192020()()a b cd ++=_________．14．若关于x 的五次四项式ax 5＋bx 3＋（x ﹣6），当x ＝﹣2时的值是7，则当x ＝2时的值是__．15．当a ＝5，b ＝23时，代数式5（a 2+ab ）﹣（5a 2﹣ab ）的值为_____．16．在数轴上，点(A 表示整数)a 在原点的左侧，点(B 表示整数)b 在原点的右侧.若2016a b -=，且2AO BO =，则a b +的值为______．17．（1）当1x =-，2y =时，代数式3x y -的值是_______；（2）当2x =，3y =-时，代数式3x y -的值是_______；18．若多项式()()4322311x a x x b x --+-+-中不含3x 和x 项，则a+b=_______.19．当3x =时，代数式33ax bx -+的值为12，则当3x =-时，代数式37ax bx -+的值为___.三、解答题20．图中正方形的边长为2㎝，求下图中阴影部分的面积．21．底面为正方形的长方体，体积为332cm ，底面边长为cm x ，请用含x 的式子表示这个长方体的高h ，并求当底面边长2cm x =时，h 的值．22．若a 5=，b 7=．（1）求a ，b 的值（2）若ab 0>，求a b +的值．22．已知a b 、互为倒数，,c d 互为相反数，2m =，求4m c d ab m+++23．已知当2x =-时，代数式31ax bx ++的值为6.求当2x =时，代数式31ax bx ++的值.25．()1若3a =，4b =，且a b <，求a b -的值．()2已知3520a b c -+++-=，计算2a b c ++的值．26．已知代数式535ax bx cx ++-，当2x =-时的值为7，那么当2x =时，该代数式的值是多少？27．已知当2x =-时，代数式21ax bx ++的值为6，利用等式的性质求代数式84a b -+的值.28．公安人员在破案时，常常根据案发现场作案人员留下的脚印推断犯人的身高，如果用(cm)a 表示脚印长度，(cm)b 表示身高，关系类似于 3.7 07b a =-．（1）某人脚印长度为24.5cm ，则他的身高约为多少厘米？（2）在某次案件中，抓获了两个可疑人员，一个身高为1.87m ，另一个身高为1.79m ，现场测量的脚印长度为26.3cm ，请你帮助侦察一下，哪个可疑人员的可能性更大？参考答案1．A2．A3．B4．B5．C6．C7．D8．B9．C10．D11．112．113．114．﹣1915．2016．672-17．-5；9.18．119．-220．阴影的面积=正方形面积-四个四分之一圆面积即：阴影的面积=正方形面积2144r p -´=2×2-3.14×1×1=4-3.14=0．86∴阴影部分的面积为0.86平方厘米．21．2V x h =，223232h x x=¸=，当2cm x =，23282h ==cm 22．解：()1a |5= ，b 7=，a 5\=±，b 7=±；()2ab 0> ，①5a =时，b 7=，∴a b 5712+=+=；②a 5=-时，b 7=-，∴()a b 5712+=-+-=-；a b \+的值为：12±．23．解：,a b 互为倒数，1ab \=,c d 互为相反数，0c d \+=2,22m m m =\==- 或()1当2m =时，原式231042=++=()2当2m =-时，原式211042=-++=所以原式3122=或24．解：将2x =-代入31ax bx ++得：318216ax bx a b ++=--+=，所以825a b +=-，当2x =时，31821514ax bx a b ++=++=-+=-25．解：()1根据题意得：3a =，4b =或3a =-，4b =，则1a b -=-或7-；()23520a b c -+++-= ，3a \=，5b =-，2c =，则26523a b c ++=-+=．26．解：当2x =-时，()()535352225328257ax bx cx a b c a b c ++-=-+---=----=，∴328212a b c ---=，即328212a b c ++=-当2x =时，535ax bx cx ++-532225a b c =++-32825a b c =++-125=--17=-.27．因为当x=-2时，21ax bx ++=4a-2b+1=6,所以4a-2b=5,所以84a b -+=-2(4a-2b)=-10.28．（1）当24.5a =时，7 3.07168.43b a =-=，所以他的身高约为168.43cm ；（2）当脚印的长度为26.3cm 时，7 3.07181.03b a =-=，因为179cm 更接近181.03cm ，所以身高为1.79m 的可疑人员可能性更大．。

3.3 代数式的值知识平台1．理解代数式的值的概念．2．掌握求代数式的值的方法．思维点击求代数式的值时应注意以下问题:1．严格按求值的步骤和格式去做．2．一个代数式中的同一个字母，只能用同一个数值代替，若有多个字母，•代入时要注意对应关系，千万不能混淆．3．在代入值时，原来省略的乘号要恢复，而数字和其他运算符号不变．4．求有乘方运算的代数式的值，在代入时要注意加括号．5．运算时要注意运算顺序．考点浏览☆考点用具体的数值代替代数式中的字母，求出代数式的值．例1 当x=13，y=3时，求下列代数式的值:（1）3x2-2y2+1；（2）2 ()1x yxy--。

【解析】分别将x，y的值替换代数式中对应的字母，并注意添括号．（1）当x=-13，y=3时，原式=3×（-13）2-2×32+1=13-18+1=-1623．（2）当x=13，y=3时，原式=21100(3)5039129 ()313--==---⨯-。

例2 下面是由一些火柴棒拼出的一系列图形，第n个图形由n个正方形组成，•通过观察图形：2+2x( )+1( )2输出（ ）输入y 输入x（1）用n 表示火柴棒根数s 的公式． （2）当n=20时，计算s 的值．【解析】 n 表示正方形的个数，每个正方形由四根火柴棒组成，而当n ≥2时，•每两个正方形有一条公共边，即每个图形除第一个正方形外，其余正方形只需三根火柴棒，这样每个图形所需火柴棒是：正方形个数×3+1． （1）s=3n+1．（2）当n=20时，s=3×20+1=61（根）．（本题还有一种解法，想一想!）在线检测 1.填表．23 （1）根据上述图形填写下表．（2）第n 个图形需要火柴棒根数为s ，写出用n 表示s 的公式．（3）当n=10时，求出s 值．n=4n=3n=2n=1③②①4．当x=3，y=12时，求下列代数式的值:（1）2x2-4xy2+4y；（2）2242x xyxy y+-.5．当x-y=2时，求代数式（x-y）2+2（y-x）+5的值．6．小明读一本共m页的书，第一天读了该书的13，第二天读了剩下的15．（1）用代数式表示小明两天共读了多少页．（2）求当m=120时，小明两天读的页数．7．当m=2，n=1时，（1）求代数式（m+2）2和m2+2mn+n2的值．（2）写出这两个代数式值的关系．（3）当m=5，n=-2时，上述的结论是否仍成立？（4）根据（1）、（2），你能用简便方法算出，当m=0.125，n=0．875时，m2+2mn+n2的值吗？3．3 代数式的值（答案）1．略 2．略 3．（1）7 12 17 （2）s=5n+2 （3）524．（1）17 （2）60115．5 6．（1）715m （2）567．（1）9 9 （2）相等（3）成立（4）1。

巧求计算机里的代数式的值随着社会的发展，电脑已进入了寻常百姓家，为既能培养学生学习电脑的兴趣，又能培养学生的应用意识，各地中考试题出现了以计算机为背景的许多题目，解决这类题目的关键在于搞清计算机程序与数学之间的联系，本文以“求代数式的值”为例加以说明，供同学们参考．例1． 下面是一个简单的数值运算程序，当输入x 的值为2时，输出的数值是 ．析解：根据运算程序，若输入x 最后输出的代数式是：-x+3，然后当x=2时，计算的结果为1 例2． 小王利用计算机设计了一个计算程序，输入和输出的数据如下表：那么，当输入数据为8时，输出的数据为 ．析解：由112 2 25，3 310，不难发现规律：n 21n n ，所以当输入的数是8时，输出的数是865． 例3． 按下列程序计算，把答案写在表格内：(1)填写表格：(2)请将题中计算程序用代数式表达出来，并给予化简．析解：本题是一道以计算机程序为背景的探究题，背景新颖独特，只要按照程序的流程就能写出符合要求的代数式，然后再进行计算、填表，最后再利用整式的除法法则进行验证，答案为：代数式为：2()n n n n +÷-输入x(1)⨯- 3+ 输出化简结果为：1例4． 根据如图的程序，计算当输入3x =时，输出的结果y = ．析解：将这个流程图转化为数学表达式，可能同学们就会感觉比较亲切了，即：)1(5)1(5{>+-≤+=x x x x y ，由于x=3，所以，y=-x+5= -3+5=2例5． 定义一种对正整数n 的“F”运算：①当n 为奇数时，结果为3n ＋5；②当n 为偶数时，结果为k n 2（其中k 是使k n2为奇数的正整数），并且运算重复进行．例如，取n ＝26，则：若n ＝449，则第449次“F 运算”的结果是_________．析解：根据运算程序提供的信息，可以发现循环的规律，最后计算出结果为：826134411 第一次F ② 第二次F ① 第三次F ② …七年级下学期期末数学试卷一、选择题（每题只有一个答案正确）1．将某图形的各顶点的横坐标保持不变，纵坐标减去3，可将该图形（）A．横向向右平移3个单位B．横向向左平移3个单位C．纵向向上平移3个单位D．纵向向下平移3个单位【答案】D【解析】根据向下平移，纵坐标减，横坐标不变解答．【详解】解：∵某图形的各顶点的横坐标保持不变，纵坐标减去3，∴将该图形向下平移了3个单位．故选：D．【点睛】本题考查了坐标与图形的变化-平移，平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．2．二元一次方程2x+3y=10的正整数解有（）A．0个B．1个C．3个D．无数多个【答案】B【解析】将x看做已知数求出y，即可确定出方程的正整数解．【详解】2x+3y=10，解得：y=，当x=2时，y=2，则方程的正整数解有1个．故选B【点睛】此题考查了解二元一次方程，解题的关键是将x看做已知数求出y．3．如图，AB⊥BC，∠ABD的度数比∠DBC的度数的两倍少15°，设∠ABD和∠DBC的度数分别为x°、y°，那么下面可以求出这两个角的度数的方程组是（）A ．9015x y x y +=⎧⎨=-⎩B ．90215x y x y +=⎧⎨=-⎩C ．90152x y x y +=⎧⎨=-⎩D ．290215x x y =⎧⎨=-⎩【答案】B【解析】∵AB ⊥BC ， ∴∠ABD+∠DBC=90°，又∵∠ABD 的度数比∠DBC 的度数的两倍少15度， ∴当设∠ABD 和∠DBC 度数分别为x y 、时，由题意可得：180215x y x y +=⎧⎨=-⎩ . 故选B.4．下列调查中，最适合采用全面调查方式的是（ ）A ．了解某市居民日平均用水量B ．了解某学校七年级一班学生数学成绩C ．了解全国中小学生课外阅读时间D ．了解某工厂一批节能灯使用寿命 【答案】B【解析】根据普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似进行判断．【详解】A ．了解某市居民日平均用水量适合抽样调查； B ．了解某学校七年级一班学生数学成绩适合全面调查； C ．了解全国中小学生课外阅读时间适合抽样调查； D ．了解某工厂一批节能灯使用寿命适合抽样调查． 故选B ． 【点睛】本题考查了抽样调查和全面调查的区别，选择普查（全面调查）还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．5．对于实数x ，我们规定[x]表示不大于x 的最大整数，例如[1.2]=1，[3]=3，[-2.5]=-3，若[1-12x -]=5，则x 的取值范围是( )A ．-7＜x ≤-5B ．-7≤x ＜-5C ．-9≤x ＜-7D ．-9＜x ≤-7【答案】D【解析】根据新定义得出不等式组，求出不等式组的解集即可． 【详解】∵[1-12x -]=5， ∴5≤1-12x -＜6， 解得：-9＜x≤-7， 故选D ． 【点睛】本题考查了解一元一次不等式组，根据新定义得出关于x 的不等式组是解此题的关键．6．把边长相等的正五边形ABCDE 和正方形ABFG 按照如图所示的方式叠合在一起，则∠EAG 的度数是（ ）A ．18°B ．20°C ．28°D ．30°【答案】A【解析】∠EAG=180°-360°÷5-90°=18°. 故选A.7．如图，为估计池塘岸边A 、B 的距离，小方在池塘的一侧选取一点O ，测得OA ＝15米，OB ＝10米，A 、B 间的距离不可能是( )A ．20米B ．15米C ．10米D ．5米【答案】D【解析】∵5<AB<25，∴A 、B 间的距离不可能是5，故选D. 8．化简2211444a aa a a --÷-+-，其结果是（ ）A ．22a a -+B ．22a a +-C ．22a a +-D ．22a a 【答案】C【解析】原式=()()()2221·12a a a a a +----=22a a +-， 故选C.9．已知2()11m n +=，2mn =；则22m n +的值为（ ） A ．15 B ．11 C ．7 D ．3【答案】C【解析】原式利用完全平方公式化简即可求出值． 【详解】解：222(147m )21m n n mn =+-=-=+， 故选：C. 【点睛】此题考查了完全平方公式，熟练掌握公式是解本题的关键． 10．如图，能够判定AD ∥BC 的是( )A ．∠1＝∠3B ．∠B ＝∠DC ．∠2＝∠4D ．∠B+∠BCD ＝180【答案】C【解析】根据内错角相等，两直线平行，即可得到正确结论． 【详解】解：根据∠2＝∠4，可得AD ∥BC ； 根据∠B ＝∠D ，不能得到AD ∥BC ；根据∠1＝∠3，可得AB ∥CD ，不能得到AD ∥BC ；根据∠B+∠BCD ＝180°，能得到AB ∥CD ，不能得到AD ∥BC ； 故选：C ． 【点睛】本题主要考查了平行线的判定，解题时注意：内错角相等，两直线平行． 二、填空题题11．如图所示，转盘被等分成4个扇形，并在上面依次写上数字1，2，3，5，若自由转动转盘，当它停止转动时，指针指向奇数区的概率是___________。

3.3代数式的值（一）一、基础训练1.用__________代替代数式中的________，按照代数式中的运算关系计算，所得的结果是代数式的值.2．当x＝_______时，代数式53x的值为0.3.当a＝4，b＝12时，代数式a2－ba的值是___________.4.小张在计算31＋a的值时，误将“＋”号看成“－”号，结果得12，那么31＋a的值应为_____________.5.三角形的底边为a ，底边上的高为h ，则它的面积s＝_______，若s＝6cm2，h＝5cm，则a＝_______cm.二、典型例题例1 已知a2＋5ab＝76，3b2＋2ab＝51，求代数式a2＋11ab＋9b2的值.分析首先将原代数式变形成（a2＋5ab）+3（3b2＋2ab），然后将整体代入.例2当m=2，n=1时，（1）求代数式（m+2）2和m2+2mn+n2的值；（2）写出这两个代数式值的关系．（3）当m=5，n=-2时，上述的结论是否仍成立？（4）根据（1）（2），你能用简便方法算出：当m=0.125，n=0．875时，m2+2mn+n2的值吗？分析通过代入具体数值，得知（m+2）2=m2+2mn+n2，再运用此等式求值.三、拓展提升例小明读一本共m页的书，第一天读了该书的13，第二天读了剩下的15．（1）用代数式表示小明两天共读了多少页；（2）求当m=120时，小明两天读的页数．四、课后作业1．当a ＝2，b ＝1，c ＝－3时，代数式2c b a b-+的值为___________. 2.若x ＝4时，代数式x 2－2x ＋a 的值为0，则a 的值为________.3.若5a b +=，6ab =，则ab a b --=________.4.当7x =时，代数式357ax bx +-=.则当7x =时，35ax bx ++=_____.5.如果某船行驶第1千米的运费是25元，以后每增加1千米，运费增加5元.现在某人租船要行驶s 千米（s 为整数，s ≥1），所需运费表示为___________________.当s ＝6千米时，运费为________元.6.若代数式2a 2+3a +1的值为5，求代数式4a 2+6a +8的值.7.已知2a b a b+=-，求224()a b a b a b a b +---+的值.8.从2开始，连续的偶数相加，和的情况如下表：n .并由此计算下列各题：(1) 2＋4＋6＋8＋…＋202(2) 126＋128＋130＋…＋3003.3代数式的值（一）一、基础训练1．具体数值字母2. 53. 134. 505. 12ah125二、典型例题例1a2＋11a＋9b2＝（a2＋5ab）＋3（3b2＋2ab）＝76＋3×51＝229 例2 （1）99（2）相等（3）成立（4）1三、拓展提升例3（1）715m（2）56四、课后作业1．4 32.－83. 14. 175. 20＋5s50元6. 167.7 3 88.S＝n（n＋1）(1)101×（101＋1）＝10302；(2)150×（150＋1）－62（62＋1）＝18744.3.3代数式的值（二）一、基础训练1.已知a，b互为相反数，c、d互为倒数，则代数式2（a＋b）－3cd的值为______.2.填表：÷2+2x( )+1( )2输出（ ）输入y 输入x.3.右图是一个数值转换机，写出图中的输出结果：输入2- 0 0.5 输出4.当x .5.当x y x y -+＝2时，代数式x y x y -+－22x y x y+-的值是___________. 二、典型例题 例1根据右边的数值转换器，按要求填写下表． x 1- 0 1 2- y 1 12- 0 12 输出 例2 填写下表，并观察下列两个代数式的值的变化情况： n 1 2 3 4 5 6 7 8 …5n +6 …n 2 …(1)(2)估计一下，哪个代数式的值先超过100？三、拓展提升例 已知311=-y x ，求代数式yxy x y xy x ---+2232的值. 分析 变形后运用整体的思想带入，可使分子分母同除以“xy ”.四、课后作业1.当x =1，y =32，z =53时，代数式y (x －y +z )的值为_______. 2.若23250x y -+=，那么23(321)x y -+=______.2x 2 14 2x +1 9 3 12x 1163.定义a*b ＝ab b a+，则2*（2*2）＝ . 4.如图所示，某计算装置有一数据入口和计算结果出口，根据图中的程序， 计算函数值，若输入的x 值为75，则输出的结果是________.5.在下列计算程序中填写适当的数或转换步骤：6.若7:4:3::=z y x ，且182=+-z y x ，求代数式z y x -+2的值.3.3代数式的值（二）一、基础训练1．－3 y =x 2 －1≤x y =5x －2≤x ≤－1 y =－x +2 1≤x ≤2输出y 值 输入x 值2．3 1281816 17 2125443．－15 －3 0 4．45．17 5二、典型例题：例1 2 0 1 3例2 （1）6或－1 （2）n2三、拓展提升：例3 3 5四、课后作业：1．4 32．－123．3 24．3 55．略6．8。

3.3代数式的值1同步练习姓名_____________班级____________学号____________分数_____________一、选择题1 ．化简()221a a -+-的结果是( )A. 41a --B.41a -C.1D.1-2 ．若23(2)0m n -++=,则2m n +的值为( )A.1-B.4-C.0D.43 ．若3-=b a ,则a b -的值是( )A.3B.3-C.0D.6 4 ．当1x =时,代数式1x +的值是( )A.1B.2C.3 D ,4 5 ．下列各式中,去括号对的是( )A.y x n m y x n m -++=-+-+)(B.y x n m y x n m +++=-+--)(C.c b a c b a +-=+-2)(2D. c b a c b a 22)(2+-=--6 ．已知3257x y -+=,那么代数式15102x y -+的值为( ) A 、8 B 、10 C 、12 D 、357 ．下列运算中,正确的是A. 325a b ab +=B. 323323÷⨯= C. 22321x x -= D. (3)(4)1---= 8 ．如果1a b +=,且,a b 都是整数,则a b +的值为 ( ) A 、0 B 、1 C 、1- D 、1±9 ．下列运算正确的是( )A.5a 2－3a 2=2B.2a 2+3a 2=5a 4C.3a +2b =5abD.7ab －6ab =ab 10．当,1-=m 时()[]22242mm m -+---等于( )(A )－7 (B )3 (C )1 (D )211．当x =3时,代数式px 3+qx +1的值为2002,则当x =－3时,代数式px 3+qx +1的值为 ( ) A 、2000 B 、－2002 C 、－2000 D 、200112．当1=a 时,a a a a a a 10099432-++-+- 的值为( )A. 5050B. 100C. 50D. －50 二、填空题13．若m n ，互为相反数,则555m n +-=____________. 14．已知,|x |=5,y =3,则=-y x ____. 15．当x =2,代数式21x -的值为_______.16．若代数式23x x -+的值是5,则代数式2223x x --的值是________.17．请写出两个整式,使它们的和为2321x x -+,它们可以是______________________和____________________.18．如图所示是计算机程序计算,若开始输入x =－1,则最后输出的结果是________.19．给出下列程序:若输入的x 值为1时,输出值为1;若输入的x 值为－1时,输出值为－3;则当输入的x 值为12时,输出值为_________.20．当5,4x y ==-时,代数式2yx -的值是__________ ｡ 21．若()2120x y -++=,则x y +的值为________.22．()2230a a b -++-=,则代数式()3a a b +的值为_________｡ 23．已知2a 2－3b +2=5,则8a 2－12b +16=______. 三、解答题24．3x 2－x +2x 2+3x ,其中x =225．已知:x 是|－3|的相反数,y 是－2的绝对值,求 2x 2－y 2 的值｡26．)145(2)286(1022-+-+--x x x x ,其中2-=x .27．x =－21时,求 x 2+(5x 2－4x )－ 2(x 2－3x )的值.28．当x =－14, y =0.5时,求代数式2x －2y －2x 的值｡29．若正数 a 的倒数等于其本身,负数 b 的绝对值等于 3,且 c <a ,c 2=36,求代数式 2 (a －2b 2)－5c 的值｡30．已知A =x 2－2x －1, B =2x 2－6x +3,求3A －[(2A －B )－2(A －B )]的值,其中x =－7参考答案一、选择题1 ．D2 ．A3 ．A4 ．B5 ．D6 ．C7 ．D8 ．B9 ．D 10．C 11．C 12．D 二、填空题13．5-; 14．2或－8 15．3 ; 16．1 17．23,21x x -+等;18．－11 19．34-20．7 21．1- 22．18 23．28 三、解答题24．原式= 5x 2+2x把x =2代入上式,原式=2425．∵x =－3,y =2,∴2x 2－y 2=2 (－3)2－22=2×9－4=18－4=14｡ 26．101422+--x x ,30. 27．原式=4x 2+2 x ,把x =－21代入,得原式 = 0 28．解:当x =―41, y =0.5时,x 2―y 2―2x=(―41)2－(21)2－2×(―41)=161－41+21 =16841+-=－16529．∵a =1,b =－3,c =－6 ,∴2 (a －2b 2)－5c =2[1－2×(－3)2]－5×(－6)=2[1－18]+30=－34+30=－4｡ 30．43。

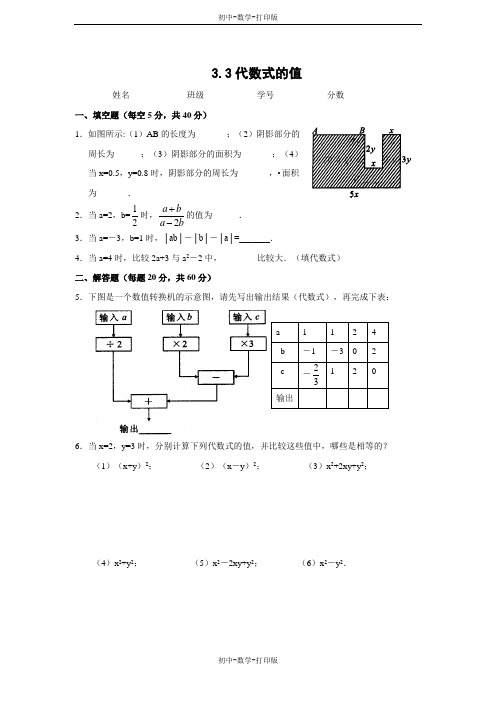
3.3代数式的值姓名_____________班级____________学号____________分数_____________一、填空题（每空5分，共40分）1．如图所示:（1）AB 的长度为_______；（2）阴影部分的周长为______；（3）阴影部分的面积为_______；（4）当x=0.5，y=0.8时，阴影部分的周长为_______，•面积为_______． 2．当a=2，b=12时，2a b a b+-的值为______． 3．当a=－3，b=1时，│ab│－│b│－│a│=_______．4．当a=4时，比较2a+3与a 2－2中，________比较大．（填代数式） 二、解答题（每题20分，共60分）5．下图是一个数值转换机的示意图，请先写出输出结果（代数式），再完成下表：6．当x=2，y=3时，分别计算下列代数式的值，并比较这些值中，哪些是相等的？（1）（x+y ）2； （2）（x －y ）2； （3）x 2+2xy+y 2；（4）x 2+y 2； （5）x 2－2xy+y 2； （6）x 2－y 2．a 1 1 2 4b －1 －3 02 c－2312 0 输出7．当a=－4，－3，－2，－1，0，1，2，3，4时，分别求出1－a2的值，通过这些值，•你发现了什么？你能求出代数式1－a2的最大值吗？8．已知：m－n=3，求代数式：－（m－n）2+4（m－n）的值．9．已知：│a+5│+│b+3│=0，求代数式－a2+3ab2－2b3的值．答案:一、1．（1）3x （2）10y+10x （3）13xy （4）13 5．2分析：（1）AB=5x－x－x=3x，（2）3y×2+2y×2+5x×2=6y+4y+10x=10y+10x，（3）•面积可看成大长方形中挖去一个小长方形，∴5x·3y－2y·x=15xy－2xy=13xy．（4）当x=0.5，y=0.8时，10x+10y=0.5×10+0.8×10=5+8=13，13xy=13×0.5×0.8=5.2．点拨：此题在求周长、面积的代数式时，要适当的化简，既为合并同类项做准备，又简化运算量．2．212分析：112222121222a ba b+++==--⨯=212．点拨：将a，b值代入求值．3．－1 分析：将a，b的值代入得│ab│－│b│－│a│=│－3×1│－│1│－│－3│=3－1－3=－1．点拨：此题考查了代数式求值和绝对值的化简．4．a2－2 分析：把a=4分别代入这两个代数式中，2a+3=2×4+3=11，a2－2=16－2=14，•∵11<14，∴a2－2比较大．点拨：代数式本身是无法比较大小的，但若已知了代数式中字母的值，就可以求出代数式的值，也就可以比较代数式的值的大小了．二、5．分析：先分析数值转换机的运算步骤来写出输出结果，再根据此结果进入代入求值．解：输出结果：+（2b－3c）．填表得：点拨：此题关键在于如何写出输出结果，对此一定要分析清楚数值的运算关系．6．分析：先代入求值，再比较结果．解：把x=2，y=3分别代入题中代数式中，（1）（x+y）2=（2+3）2=25；（2）（x－y）2=（2－3）2=1；（3）x2+2xy+y2=22+2×2×3+32=25；（4）x2+y2=22+32=4+9=13；（5）x2－2xy+y2=22－2×2×3+32=1；（6）x2－y2=22－32=－5，∴当x=2，y=3时，代数式（x+y）2=x2+2xy+y2，（x－y）2=x2－2xy+y2．点拨：此题在代入求值过程中，要细心运算．7．分析：先求值，再根据值探究规律．解：当a=－4时，1－a2=1－（－4）2=1－16=－15；•当a=－3时，1－a2=1－（－3）2=1－9=－8；当a=－2时，1－a2=1－（－2）2=1－4=－3；当a=－1时，1－a2=1－（－1）2=1－1=0；当a=0时，1－a2=1－02=1；当a=1时，1－a2=1－1=0；当a=2时，1－a2=1－22=－3；当a=3时，1－a2=1－32=－8；当a=4时，1－a2=1－42=－15．通过上述求值运算，发现a取互为相反数的值时，代数式1－a2的值是相等的；当a<0时，随着a增大，代数式1－a2的值增大，当a>0时，•随着a增大，代数式1－a2的值减小．比较上述结果：代数式1－a2的最大值是1．点拨：在考虑值的变化趋势时，要整体分析，此题不能单纯地说增大或减小．另外，在求最值时，先根据值的变化猜想，然后进行数值推导．8．39．106。

初中数学试卷3.3 代数式的值2 同步练习姓名班级学号分数_____________一、选择题1 ．用代数式表示“ 2a 与 3 的差”为 ()C.2(a-3)D.2(3-a)2 ．已知代数式 x 2y 的值是3,则代数式 2x 4 y 1的值是C. 7D.不可以确立3． x 是一个两位数,y是一个一位数,假如把y放在 x 的左侧,那么所成的三位数表示为A. yxB. y xC.10 y xD.100 y x4 ．已知a是一个一位数,b是一个两位数,若将a置于b的左侧构成一个三位数,则此三位数为 ()A、abB、10a bC、10 a bD、100a b 5．已知代数式 x+2 y 的值是5,则代数式2 x+4 y+1的值是A.6B.7C.11D.126 ．格兰仕微波炉降价25% 后 ,每台售价 a 元 ,则这类微波炉的原价为每台()元元 Ca 元D.a元7 ．假如某长方形草坪的周长是m 米 ,宽是 n 米 ,则它的长是 ()Ａ．2n) 米 Ｂ．mn 米Ｃ．m2n 米Ｄ．mn 米(m22228 ．根据右图所示的程序计算代数式的值 ,若输入的 n 值为 5, 则输出的结果为 ( )9 ．有一种石棉瓦 (如图 4),每块宽 60 厘米 ,用于铺盖屋顶时 ,每相邻两块重叠部分的宽都为10 厘米 ,那么 n (n 为正整数 )块石棉瓦覆盖的宽度为 A. 60 n 厘米B. 50 n 厘米C. (50 n+ 10) 厘米D. (60 n -10) 厘米图 410 ．当前 ,财政部将证券交易印花税税率由本来的 1 ‰ (千分之一 )提升到 3 ‰ .假如税率提升后的某一天的交易额为 a 亿元,则该天的证券交易印花税(交易印花税 = 印花税率×交易额 )比按原税率计算增添了多少亿元( )A.a ‰B. 2a ‰C. 3a ‰D.4a ‰二、填空题11 ．“ x 的 2 倍与 5 的差小于 0 ”用不等式表示为 _________________.12 ．一件商品本来价钱为x 元,降价10%后,则这件商品的实质价钱是_______元.13 ．某种商品的零售价为m 元 ,顾客以八折的优惠价购置此商品,共需付款 _______元.14 ．某件商品进价为 a 元,现涨价20% 后销售 ,则每件可获收益_______元.15 ．一台电视机的原价为 a 元,降价4%后的价钱为元 .16 ．加拿大数学家约翰? 菲尔兹正在看一本数学书,他从第a页看起,向来看到第n页(a<n),他看了 _________页书?三、解答题17 ．某地电话拨号入网有两种收费方式,用户可任选其一 :(A)计时制 :3 元/时 ;(B) 包月制 :50元/月(限一部个人住所电话入网); 别的 ,每一种上网方式都得加收通讯费1.2 元/时.⑴某用户某月上网时间为x 小时,请写出两种收费方式下该用户应当支付的花费;⑵若某用户预计一个月上网的时间为25 小时 ,你以为哪一种方式比较合算.参照答案一、选择题1．A2．C3．D4．D;5．C6．D7．C8．A9．C10． B二、填空题11． 2x-5<012． 0． 9x(或9x );10813 ．m1014 ．15 ． (1 –4%) a元或 0.96 a元16 ．n-a+1三、解答题17 ． (1) 计时制包月制(2) 当 x=25时,计时制 :4.2 ×25=105(元)包月制 :50+1.2 ×25=80( 元 ) ∴包月制较合算。

3.3代数式的值（2）1．如图，是一个数值转换机，输入x ，输出3（x －１）. 下列四种转换步骤中，不正确的是（ ）A ．先减去1，再乘以3B ．先乘以3，再减去1C ．先乘以3，再减去3D ．先加上－1，再乘以3 2．在如图所示的计算程序中填写适当的数或计算步骤3．如图是两个计算程序：（1）写出图①的输出结果为_________，找出图②中的转换步骤；_________________. （2）当输入x ＝－3是，图①输出_________，图②输出__________.4． 如图是一个数值转换机的示意图，写出计算过程并填写下表.5．请你设计求代数式2a 2＋6的值的计算程序，并计算当a 分别取－3，0，12时，代数式的值.6．当a ＝－0.5，b ＝0.25时，求下列代数式的值：（1）(a ＋b )2（2）a 2＋2ab ＋b 2.运算过程：______________________________)2第2题图 第3题图图① 图②7．根据第6题的计算结果，回答下问题： （1）这两个代数式的值有什么关系？（2）当a ＝2，b ＝－3时，上述结论是否仍然成立？ （3）再自选一组a 、b 的值试一试．（4）你能用简便的方法算出当a ＝－0.875，b ＝－0.125时，代数式a 2＋2ab ＋b 2的值吗？备助学习单：2．当x ＋y ＝－2，xy ＝－4时，求代数式xy x ＋y －12xy 的值．二、备助方略：1．阅读课本p80页的内容，并尝试完成“试一试”.2．将如图两个框中的同类项用线段连起来：3．下列单项式中，与－3a 3b 为同类项的是 （ ）A ．－3a 2bB ．12ba 3 C ．2ab 3 D ．3a 2b 24．判断下列各题中的两个单项式是不是同类项，是的打“√”，不是的打“×”.①－ab 与12ab ；（ ） ②4x 2y 与4x y 2；（ ）③2xy 与2xyz ；（ ） ④3ts 与2st ；（ ） ⑤－0.3与4；（ ） ⑥0.2x 2y 与－0.2yx 2；（ ）第2题图。

3.3代数式的值—2023-2024学年苏科版数学七年级上册堂堂练1.按照如图所示的计算程序，若，则输出的结果是( )A.16B.26C.-16D.-262.按如图所示的运算程序，若，，则输出结果y为( )A.9B.11C.17D.193.规定，则( )A.-12B.12C.D.4.如果，那么代数式的值是( )A.-2021B.2021C.-1D.15.当与时，代数式的两个值( )A.相等B.互为倒数C.互为相反数D.既不相等也不互为相反数6.已知，那么的值为________.7.若，则________.8.余姚金泰商厦销售一种西装和领带，西装每套定价1000元，领带每条定价200元，当双十一来临之际，商场决定开展促销活动，可以同时向客户提供两种优惠方案：方案一：买一套西装送一条领带；方案二：西装和领带都按定价的90%付款.现某客户要到该商场购买西装20套，领带x条(x超过20)(1)若该客户按方案一购买，需付款_________元(用含x的式子表示)；若该客户按方案二购买，需付款__________元(用含x的式子表示)；(2)若，通过计算说明此时按哪种方案购买较为合算？答案以及解析1.答案：D解析：当时，，不输出；当时，，符合题意，输出结果，故选D.2.答案：A解析：输入，，，即走“否”的路径，，输出结果为9，故选A.3.答案：D解析：规定，.故选D.4.答案：C解析：，，，解得，，.故选C.5.答案：A解析：当时，，，.当时，，，.相等.故答案为：A.6.答案：5解析：，，，解得：，，，故答案为：5.7.答案：1解析：，.8.答案：(1)，(2)方案一解析：(1)方案一：元，方案二：元，故答案为，.(2)当时，元，元，，故选择方案一.。